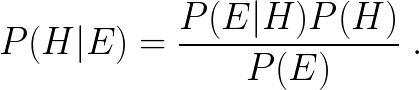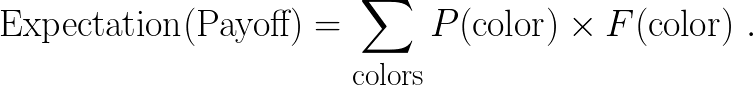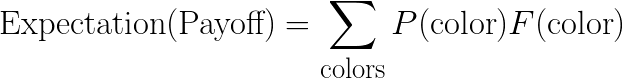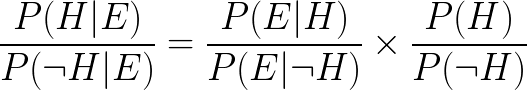Biases: An Introduction
by Rob Bensinger

It’s not a secret. For some reason, though, it rarely comes up in conversation, and few people are asking what we should do about it. It’s a pattern, hidden unseen behind all our triumphs and failures, unseen behind our eyes. What is it?

Imagine reaching into an urn that contains seventy white balls and thirty red ones, and plucking out ten mystery balls. Perhaps three of the ten balls will be red, and you’ll correctly guess how many red balls total were in the urn. Or perhaps you’ll happen to grab four red balls, or some other number. Then you’ll probably get the total number wrong.

This random error is the cost of incomplete knowledge, and as errors go, it’s not so bad. Your estimates won’t be incorrect on average, and the more you learn, the smaller your error will tend to be.

On the other hand, suppose that the white balls are heavier, and sink to the bottom of the urn. Then your sample may be unrepresentative in a consistent direction.

That sort of error is called “statistical bias.” When your method of learning about the world is biased, learning more may not help. Acquiring more data can even consistently worsen a biased prediction.

If you’re used to holding knowledge and inquiry in high esteem, this is a scary prospect. If we want to be sure that learning more will help us, rather than making us worse off than we were before, we need to discover and correct for biases in our data.

The idea of cognitive bias in psychology works in an analogous way. A cognitive bias is a systematic error in how we think, as opposed to a random error or one that’s merely caused by our ignorance. Whereas statistical bias skews a sample so that it less closely resembles a larger population, cognitive biases skew our beliefs so that they less accurately represent the facts, and they skew our decision-making so that it less reliably achieves our goals.

Maybe you have an optimism bias, and you find out that the red balls can be used to treat a rare tropical disease besetting your brother. You may then overestimate how many red balls the urn contains because you wish the balls were mostly red. Here, your sample isn’t what’s biased. You’re what’s biased.

Now that we’re talking about biased people, however, we have to be careful. Usually, when we call individuals or groups “biased,” we do it to chastise them for being unfair or partial. Cognitive bias is a different beast altogether. Cognitive biases are a basic part of how humans in general think, not the sort of defect we could blame on a terrible upbringing or a rotten personality.¹

A cognitive bias is a systematic way that your innate patterns of thought fall short of truth (or some other attainable goal, such as happiness). Like statistical biases, cognitive biases can distort our view of reality, they can’t always be fixed by just gathering more data, and their effects can add up over time. But when the miscalibrated measuring instrument you’re trying to fix is you, debiasing is a unique challenge.

Still, this is an obvious place to start. For if you can’t trust your brain, how can you trust anything else?

It would be useful to have a name for this project of overcoming cognitive bias, and of overcoming all species of error where our minds can come to undermine themselves.

We could call this project whatever we’d like. For the moment, though, I suppose “rationality” is as good a name as any.

Rational Feelings

In a Hollywood movie, being “rational” usually means that you’re a stern, hyperintellectual stoic. Think Spock from Star Trek, who “rationally” suppresses his emotions, “rationally” refuses to rely on intuitions or impulses, and is easily dumbfounded and outmaneuvered upon encountering an erratic or “irrational” opponent.²

There’s a completely different notion of “rationality” studied by mathematicians, psychologists, and social scientists. Roughly, it’s the idea of doing the best you can with what you’ve got. A rational person, no matter how out of their depth they are, forms the best beliefs they can with the evidence they’ve got. A rational person, no matter how terrible a situation they’re stuck in, makes the best choices they can to improve their odds of success.

Real-world rationality isn’t about ignoring your emotions and intuitions. For a human, rationality often means becoming more self-aware about your feelings, so you can factor them into your decisions.

Rationality can even be about knowing when not to overthink things. When selecting a poster to put on their wall, or predicting the outcome of a basketball game, experimental subjects have been found to perform worse if they carefully analyzed their reasons.³^,⁴ There are some problems where conscious deliberation serves us better, and others where snap judgments serve us better.

Psychologists who work on dual process theories distinguish the brain’s “System 1” processes (fast, implicit, associative, automatic cognition) from its “System 2” processes (slow, explicit, intellectual, controlled cognition).⁵ The stereotype is for rationalists to rely entirely on System 2, disregarding their feelings and impulses. Looking past the stereotype, someone who is actually being rational—actually achieving their goals, actually mitigating the harm from their cognitive biases—would rely heavily on System-1 habits and intuitions where they’re reliable.

Unfortunately, System 1 on its own seems to be a terrible guide to “when should I trust System 1?” Our untrained intuitions don’t tell us when we ought to stop relying on them. Being biased and being unbiased feel the same.⁶

On the other hand, as behavioral economist Dan Ariely notes: we’re predictably irrational. We screw up in the same ways, again and again, systematically.

If we can’t use our gut to figure out when we’re succumbing to a cognitive bias, we may still be able to use the sciences of mind.

The Many Faces of Bias

To solve problems, our brains have evolved to employ cognitive heuristics—rough shortcuts that get the right answer often, but not all the time. Cognitive biases arise when the corners cut by these heuristics result in a relatively consistent and discrete mistake.

The representativeness heuristic, for example, is our tendency to assess phenomena by how representative they seem of various categories. This can lead to biases like the conjunction fallacy. Tversky and Kahneman found that experimental subjects considered it less likely that a strong tennis player would “lose the first set” than that he would “lose the first set but win the match.”⁷ Making a comeback seems more typical of a strong player, so we overestimate the probability of this complicated-but-sensible-sounding narrative compared to the probability of a strictly simpler scenario.

The representativeness heuristic can also contribute to base rate neglect, where we ground our judgments in how intuitively “normal” a combination of attributes is, neglecting how common each attribute is in the population at large.⁸ Is it more likely that Steve is a shy librarian, or that he’s a shy salesperson? Most people answer this kind of question by thinking about whether “shy” matches their stereotypes of those professions. They fail to take into consideration how much more common salespeople are than librarians—seventy-five times as common, in the United States.⁹

Other examples of biases include duration neglect (evaluating experiences without regard to how long they lasted), the sunk cost fallacy (feeling committed to things you’ve spent resources on in the past, when you should be cutting your losses and moving on), and confirmation bias (giving more weight to evidence that confirms what we already believe).¹⁰^,¹¹

Knowing about a bias, however, is rarely enough to protect you from it. In a study of bias blindness, experimental subjects predicted that if they learned a painting was the work of a famous artist, they’d have a harder time neutrally assessing the quality of the painting. And, indeed, subjects who were told a painting’s author and were asked to evaluate its quality exhibited the very bias they had predicted, relative to a control group. When asked afterward, however, the very same subjects claimed that their assessments of the paintings had been objective and unaffected by the bias—in all groups!¹²^,¹³

We’re especially loathe to think of our views as inaccurate compared to the views of others. Even when we correctly identify others’ biases, we have a special bias blind spot when it comes to our own flaws.¹⁴ We fail to detect any “biased-feeling thoughts” when we introspect, and so draw the conclusion that we must just be more objective than everyone else.¹⁵

Studying biases can in fact make you more vulnerable to overconfidence and confirmation bias, as you come to see the influence of cognitive biases all around you—in everyone but yourself. And the bias blind spot, unlike many biases, is especially severe among people who are especially intelligent, thoughtful, and open-minded.¹⁶^,¹⁷

This is cause for concern.

Still . . . it does seem like we should be able to do better. It’s known that we can reduce base rate neglect by thinking of probabilities as frequencies of objects or events. We can minimize duration neglect by directing more attention to duration and depicting it graphically.¹⁸ People vary in how strongly they exhibit different biases, so there should be a host of yet-unknown ways to influence how biased we are.

If we want to improve, however, it’s not enough for us to pore over lists of cognitive biases. The approach to debiasing in Rationality: From AI to Zombies is to communicate a systematic understanding of why good reasoning works, and of how the brain falls short of it. To the extent this volume does its job, its approach can be compared to the one described in Serfas, who notes that “years of financially related work experience” didn’t affect people’s susceptibility to the sunk cost bias, whereas “the number of accounting courses attended” did help.

As a consequence, it might be necessary to distinguish between experience and expertise, with expertise meaning “the development of a schematic principle that involves conceptual understanding of the problem,” which in turn enables the decision maker to recognize particular biases. However, using expertise as countermeasure requires more than just being familiar with the situational content or being an expert in a particular domain. It requires that one fully understand the underlying rationale of the respective bias, is able to spot it in the particular setting, and also has the appropriate tools at hand to counteract the bias.¹⁹

The goal of this book is to lay the groundwork for creating rationality “expertise.” That means acquiring a deep understanding of the structure of a very general problem: human bias, self-deception, and the thousand paths by which sophisticated thought can defeat itself.

A Word About This Text

Rationality: From AI to Zombies began its life as a series of essays by Eliezer Yudkowsky, published between 2006 and 2009 on the economics blog Overcoming Bias and its spin-off community blog Less Wrong. I’ve worked with Yudkowsky for the last year at the Machine Intelligence Research Institute (MIRI), a nonprofit he founded in 2000 to study the theoretical requirements for smarter-than-human artificial intelligence (AI).

Reading his blog posts got me interested in his work. He impressed me with his ability to concisely communicate insights it had taken me years of studying analytic philosophy to internalize. In seeking to reconcile science’s anarchic and skeptical spirit with a rigorous and systematic approach to inquiry, Yudkowsky tries not just to refute but to understand the many false steps and blind alleys bad philosophy (and bad lack-of-philosophy) can produce. My hope in helping organize these essays into a book is to make it easier to dive in to them, and easier to appreciate them as a coherent whole.

The resultant rationality primer is frequently personal and irreverent—drawing, for example, from Yudkowsky’s experiences with his Orthodox Jewish mother (a psychiatrist) and father (a physicist), and from conversations on chat rooms and mailing lists. Readers who are familiar with Yudkowsky from Harry Potter and the Methods of Rationality, his science-oriented take-off of J.K. Rowling’s Harry Potter books, will recognize the same irreverent iconoclasm, and many of the same core concepts.

Stylistically, the essays in this book run the gamut from “lively textbook” to “compendium of thoughtful vignettes” to “riotous manifesto,” and the content is correspondingly varied. Rationality: From AI to Zombies collects hundreds of Yudkowsky’s blog posts into twenty-six “sequences,” chapter-like series of thematically linked posts. The sequences in turn are grouped into six books, covering the following topics:

Book 1—Map and Territory. What is a belief, and what makes some beliefs work better than others? These four sequences explain the Bayesian notions of rationality, belief, and evidence. A running theme: the things we call “explanations” or “theories” may not always function like maps for navigating the world. As a result, we risk mixing up our mental maps with the other objects in our toolbox.

Book 2—How to Actually Change Your Mind. This truth thing seems pretty handy. Why, then, do we keep jumping to conclusions, digging our heels in, and recapitulating the same mistakes? Why are we so bad at acquiring accurate beliefs, and how can we do better? These seven sequences discuss motivated reasoning and confirmation bias, with a special focus on hard-to-spot species of self-deception and the trap of “using arguments as soldiers.”

Book 3—The Machine in the Ghost. Why haven’t we evolved to be more rational? Even taking into account resource constraints, it seems like we could be getting a lot more epistemic bang for our evidential buck. To get a realistic picture of how and why our minds execute their biological functions, we need to crack open the hood and see how evolution works, and how our brains work, with more precision. These three sequences illustrate how even philosophers and scientists can be led astray when they rely on intuitive, non-technical evolutionary or psychological accounts. By locating our minds within a larger space of goal-directed systems, we can identify some of the peculiarities of human reasoning and appreciate how such systems can “lose their purpose.”

Book 4—Mere Reality. What kind of world do we live in? What is our place in that world? Building on the previous sequences’ examples of how evolutionary and cognitive models work, these six sequences explore the nature of mind and the character of physical law. In addition to applying and generalizing past lessons on scientific mysteries and parsimony, these essays raise new questions about the role science should play in individual rationality.

Book 5—Mere Goodness. What makes something valuable—morally, or aesthetically, or prudentially? These three sequences ask how we can justify, revise, and naturalize our values and desires. The aim will be to find a way to understand our goals without compromising our efforts to actually achieve them. Here the biggest challenge is knowing when to trust your messy, complicated case-by-case impulses about what’s right and wrong, and when to replace them with simple exceptionless principles.

Book 6—Becoming Stronger. How can individuals and communities put all this into practice? These three sequences begin with an autobiographical account of Yudkowsky’s own biggest philosophical blunders, with advice on how he thinks others might do better. The book closes with recommendations for developing evidence-based applied rationality curricula, and for forming groups and institutions to support interested students, educators, researchers, and friends.

The sequences are also supplemented with “interludes,” essays taken from Yudkowsky’s personal website, http://www.yudkowsky.net. These tie in to the sequences in various ways; e.g., The Twelve Virtues of Rationality poetically summarizes many of the lessons of Rationality: From AI to Zombies, and is often quoted in other essays.

Clicking the asterisk at the bottom of an essay will take you to the original version of it on Less Wrong (where you can leave comments) or on Yudkowsky’s website. You can also find a glossary for Rationality: From AI to Zombies terminology online, at http://wiki.lesswrong.com/wiki/RAZ_Glossary.

Map and Territory

This, the first book, begins with a sequence on cognitive bias: “Predictably Wrong.” The rest of the book won’t stick to just this topic; bad habits and bad ideas matter, even when they arise from our minds’ contents as opposed to our minds’ structure. Thus evolved and invented errors will both be on display in subsequent sequences, beginning with a discussion in “Fake Beliefs” of ways that one’s expectations can come apart from one’s professed beliefs.

An account of irrationality would also be incomplete if it provided no theory about how rationality works—or if its “theory” only consisted of vague truisms, with no precise explanatory mechanism. The “Noticing Confusion” sequence asks why it’s useful to base one’s behavior on “rational” expectations, and what it feels like to do so.

“Mysterious Answers” next asks whether science resolves these problems for us. Scientists base their models on repeatable experiments, not speculation or hearsay. And science has an excellent track record compared to anecdote, religion, and . . . pretty much everything else. Do we still need to worry about “fake” beliefs, confirmation bias, hindsight bias, and the like when we’re working with a community of people who want to explain phenomena, not just tell appealing stories?

This is then followed by The Simple Truth, a stand-alone allegory on the nature of knowledge and belief.

It is cognitive bias, however, that provides the clearest and most direct glimpse into the stuff of our psychology, into the shape of our heuristics and the logic of our limitations. It is with bias that we will begin.

There is a passage in the Zhuangzi, a proto-Daoist philosophical text, that says: “The fish trap exists because of the fish; once you’ve gotten the fish, you can forget the trap.”²⁰

I invite you to explore this book in that spirit. Use it like you’d use a fish trap, ever mindful of the purpose you have for it. Carry with you what you can use, so long as it continues to have use; discard the rest. And may your purpose serve you well.

Acknowledgments

I am stupendously grateful to Nate Soares, Elizabeth Tarleton, Paul Crowley, Brienne Strohl, Adam Freese, Helen Toner, and dozens of volunteers for proofreading portions of this book.

Special and sincere thanks to Alex Vermeer, who steered this book to completion, and Tsvi Benson-Tilsen, who combed through the entire book to ensure its readability and consistency.

1. The idea of personal bias, media bias, etc. resembles statistical bias in that it’s an error. Other ways of generalizing the idea of “bias” focus instead on its association with nonrandomness. In machine learning, for example, an inductive bias is just the set of assumptions a learner uses to derive predictions from a data set. Here, the learner is “biased” in the sense that it’s pointed in a specific direction; but since that direction might be truth, it isn’t a bad thing for an agent to have an inductive bias. It’s valuable and necessary. This distinguishes inductive “bias” quite clearly from the other kinds of bias.

2. A sad coincidence: Leonard Nimoy, the actor who played Spock, passed away just a few days before the release of this book. Though we cite his character as a classic example of fake “Hollywood rationality,” we mean no disrespect to Nimoy’s memory.

3. Timothy D. Wilson et al., “Introspecting About Reasons Can Reduce Post-choice Satisfaction,” Personality and Social Psychology Bulletin 19 (1993): 331–331.

4. Jamin Brett Halberstadt and Gary M. Levine, “Effects of Reasons Analysis on the Accuracy of Predicting Basketball Games,” Journal of Applied Social Psychology 29, no. 3 (1999): 517–530.

5. Keith E. Stanovich and Richard F. West, “Individual Differences in Reasoning: Implications for the Rationality Debate?,” Behavioral and Brain Sciences 23, no. 5 (2000): 645–665, http://journals.cambridge.org/abstract_S0140525X00003435.

6. Timothy D. Wilson, David B. Centerbar, and Nancy Brekke, “Mental Contamination and the Debiasing Problem,” in Heuristics and Biases: The Psychology of Intuitive Judgment, ed. Thomas Gilovich, Dale Griffin, and Daniel Kahneman (Cambridge University Press, 2002).

7. Amos Tversky and Daniel Kahneman, “Extensional Versus Intuitive Reasoning: The Conjunction Fallacy in Probability Judgment,” Psychological Review 90, no. 4 (1983): 293–315, doi:10.1037/0033-295X.90.4.293.

8. Richards J. Heuer, Psychology of Intelligence Analysis (Center for the Study of Intelligence, Central Intelligence Agency, 1999).

9. Wayne Weiten, Psychology: Themes and Variations, Briefer Version, Eighth Edition (Cengage Learning, 2010).

10. Raymond S. Nickerson, “Confirmation Bias: A Ubiquitous Phenomenon in Many Guises,” Review of General Psychology 2, no. 2 (1998): 175.

11. Probability neglect is another cognitive bias. In the months and years following the September 11 attacks, many people chose to drive long distances rather than fly. Hijacking wasn’t likely, but it now felt like it was on the table; the mere possibility of hijacking hugely impacted decisions. By relying on black-and-white reasoning (cars and planes are either “safe” or “unsafe,” full stop), people actually put themselves in much more danger. Where they should have weighed the probability of dying on a cross-country car trip against the probability of dying on a cross-country flight—the former is hundreds of times more likely—they instead relied on their general feeling of worry and anxiety (the affect heuristic). We can see the same pattern of behavior in children who, hearing arguments for and against the safety of seat belts, hop back and forth between thinking seat belts are a completely good idea or a completely bad one, instead of trying to compare the strengths of the pro and con considerations.²¹

Some more examples of biases are: the peak/end rule (evaluating remembered events based on their most intense moment, and how they ended); anchoring (basing decisions on recently encountered information, even when it’s irrelevant)²² and self-anchoring (using yourself as a model for others’ likely characteristics, without giving enough thought to ways you’re atypical);²³ and status quo bias (excessively favoring what’s normal and expected over what’s new and different).²⁴

12. Katherine Hansen et al., “People Claim Objectivity After Knowingly Using Biased Strategies,” Personality and Social Psychology Bulletin 40, no. 6 (2014): 691–699.

13. Similarly, Pronin writes of gender bias blindness:

In one study, participants considered a male and a female candidate for a police-chief job and then assessed whether being “streetwise” or “formally educated” was more important for the job. The result was that participants favored whichever background they were told the male candidate possessed (e.g., if told he was “streetwise,” they viewed that as more important). Participants were completely blind to this gender bias; indeed, the more objective they believed they had been, the more bias they actually showed.²⁵

Even when we know about biases, Pronin notes, we remain “naive realists” about our own beliefs. We reliably fall back into treating our beliefs as distortion-free representations of how things actually are.²⁶

14. In a survey of 76 people waiting in airports, individuals rated themselves much less susceptible to cognitive biases on average than a typical person in the airport. In particular, people think of themselves as unusually unbiased when the bias is socially undesirable or has difficult-to-notice consequences.²⁷ Other studies find that people with personal ties to an issue see those ties as enhancing their insight and objectivity; but when they see other people exhibiting the same ties, they infer that those people are overly attached and biased.

15. Joyce Ehrlinger, Thomas Gilovich, and Lee Ross, “Peering Into the Bias Blind Spot: People’s Assessments of Bias in Themselves and Others,” Personality and Social Psychology Bulletin 31, no. 5 (2005): 680–692.

16. Richard F. West, Russell J. Meserve, and Keith E. Stanovich, “Cognitive Sophistication Does Not Attenuate the Bias Blind Spot,” Journal of Personality and Social Psychology 103, no. 3 (2012): 506.

17. . . . Not to be confused with people who think they’re unusually intelligent, thoughtful, etc. because of the illusory superiority bias.

18. Michael J. Liersch and Craig R. M. McKenzie, “Duration Neglect by Numbers and Its Elimination by Graphs,” Organizational Behavior and Human Decision Processes 108, no. 2 (2009): 303–314.

19. Sebastian Serfas, Cognitive Biases in the Capital Investment Context: Theoretical Considerations and Empirical Experiments on Violations of Normative Rationality (Springer, 2010).

20. Zhuangzi and Burton Watson, The Complete Works of Zhuangzi (Columbia University Press, 1968).

21. Cass R. Sunstein, “Probability Neglect: Emotions, Worst Cases, and Law,” Yale Law Journal (2002): 61–107.

22. Dan Ariely, Predictably Irrational: The Hidden Forces That Shape Our Decisions (HarperCollins, 2008).

23. Boaz Keysar and Dale J. Barr, “Self-Anchoring in Conversation: Why Language Users Do Not Do What They ‘Should,’” in Heuristics and Biases: The Psychology of Intuitive Judgment, ed. Thomas Gilovich, Dale Griffin, and Daniel Kahneman (New York: Cambridge University Press, 2002), 150–166, doi:10.2277/0521796792.

24. Scott Eidelman and Christian S. Crandall, “Bias in Favor of the Status Quo,” Social and Personality Psychology Compass 6, no. 3 (2012): 270–281.

25. Eric Luis Uhlmann and Geoffrey L. Cohen, “‘I think it, therefore it’s true’: Effects of Self-perceived Objectivity on Hiring Discrimination,” Organizational Behavior and Human Decision Processes 104, no. 2 (2007): 207–223.

26. Emily Pronin, “How We See Ourselves and How We See Others,” Science 320 (2008): 1177–1180, http://psych.princeton.edu/psychology/research/pronin/pubs/2008%20Self%20and%20Other.pdf.

27. Emily Pronin, Daniel Y. Lin, and Lee Ross, “The Bias Blind Spot: Perceptions of Bias in Self versus Others,” Personality and Social Psychology Bulletin 28, no. 3 (2002): 369–381.

Book I
Map and Territory

A. Predictably Wrong
1. What Do I Mean By “Rationality”?
2. Feeling Rational
3. Why Truth? And . . .
4. . . . What’s a Bias, Again?
5. Availability
6. Burdensome Details
7. Planning Fallacy
8. Illusion of Transparency: Why No One Understands You
9. Expecting Short Inferential Distances
10. The Lens That Sees Its Own Flaws

B. Fake Beliefs
11. Making Beliefs Pay Rent (in Anticipated Experiences)
12. A Fable of Science and Politics
13. Belief in Belief
14. Bayesian Judo
15. Pretending to be Wise
16. Religion’s Claim to be Non-Disprovable
17. Professing and Cheering
18. Belief as Attire
19. Applause Lights

C. Noticing Confusion
20. Focus Your Uncertainty
21. What Is Evidence?
22. Scientific Evidence, Legal Evidence, Rational Evidence
23. How Much Evidence Does It Take?
24. Einstein’s Arrogance
25. Occam’s Razor
26. Your Strength as a Rationalist
27. Absence of Evidence Is Evidence of Absence
28. Conservation of Expected Evidence
29. Hindsight Devalues Science

D. Mysterious Answers
30. Fake Explanations
31. Guessing the Teacher’s Password
32. Science as Attire
33. Fake Causality
34. Semantic Stopsigns
35. Mysterious Answers to Mysterious Questions
36. The Futility of Emergence
37. Say Not “Complexity”
38. Positive Bias: Look into the Dark
39. Lawful Uncertainty
40. My Wild and Reckless Youth
41. Failing to Learn from History
42. Making History Available
43. Explain/Worship/Ignore?
44. “Science” as Curiosity-Stopper
45. Truly Part of You

Interlude: The Simple Truth

Part A
Predictably Wrong

1
What Do I Mean By “Rationality”?

I mean:

Epistemic rationality: systematically improving the accuracy of your beliefs.
Instrumental rationality: systematically achieving your values.

When you open your eyes and look at the room around you, you’ll locate your laptop in relation to the table, and you’ll locate a bookcase in relation to the wall. If something goes wrong with your eyes, or your brain, then your mental model might say there’s a bookcase where no bookcase exists, and when you go over to get a book, you’ll be disappointed.

This is what it’s like to have a false belief, a map of the world that doesn’t correspond to the territory. Epistemic rationality is about building accurate maps instead. This correspondence between belief and reality is commonly called “truth,” and I’m happy to call it that.

Instrumental rationality, on the other hand, is about steering reality—sending the future where you want it to go. It’s the art of choosing actions that lead to outcomes ranked higher in your preferences. I sometimes call this “winning.”

So rationality is about forming true beliefs and making winning decisions.

Pursuing “truth” here doesn’t mean dismissing uncertain or indirect evidence. Looking at the room around you and building a mental map of it isn’t different, in principle, from believing that the Earth has a molten core, or that Julius Caesar was bald. Those questions, being distant from you in space and time, might seem more airy and abstract than questions about your bookcase. Yet there are facts of the matter about the state of the Earth’s core in 2015 CE and about the state of Caesar’s head in 50 BCE. These facts may have real effects upon you even if you never find a way to meet Caesar or the core face-to-face.

And “winning” here need not come at the expense of others. The project of life can be about collaboration or self-sacrifice, rather than about competition. “Your values” here means anything you care about, including other people. It isn’t restricted to selfish values or unshared values.

When people say “X is rational!” it’s usually just a more strident way of saying “I think X is true” or “I think X is good.” So why have an additional word for “rational” as well as “true” and “good”?

An analogous argument can be given against using “true.” There is no need to say “it is true that snow is white” when you could just say “snow is white.” What makes the idea of truth useful is that it allows us to talk about the general features of map-territory correspondence. “True models usually produce better experimental predictions than false models” is a useful generalization, and it’s not one you can make without using a concept like “true” or “accurate.”

Similarly, “Rational agents make decisions that maximize the probabilistic expectation of a coherent utility function” is the kind of thought that depends on a concept of (instrumental) rationality, whereas “It’s rational to eat vegetables” can probably be replaced with “It’s useful to eat vegetables” or “It’s in your interest to eat vegetables.” We need a concept like “rational” in order to note general facts about those ways of thinking that systematically produce truth or value—and the systematic ways in which we fall short of those standards.

Sometimes experimental psychologists uncover human reasoning that seems very strange. For example, someone rates the probability “Bill plays jazz” as less than the probability “Bill is an accountant who plays jazz.” This seems like an odd judgment, since any particular jazz-playing accountant is obviously a jazz player. But to what higher vantage point do we appeal in saying that the judgment is wrong?

Experimental psychologists use two gold standards: probability theory, and decision theory.

Probability theory is the set of laws underlying rational belief. The mathematics of probability describes equally and without distinction (a) figuring out where your bookcase is, (b) figuring out the temperature of the Earth’s core, and (c) estimating how many hairs were on Julius Caesar’s head. It’s all the same problem of how to process the evidence and observations to revise (“update”) one’s beliefs. Similarly, decision theory is the set of laws underlying rational action, and is equally applicable regardless of what one’s goals and available options are.

Let “P(such-and-such)” stand for “the probability that such-and-such happens,” and P(A,B) for “the probability that both A and B happen.” Since it is a universal law of probability theory that P(A) ≥ P(A,B), the judgment that P(Bill plays jazz) is less than P(Bill plays jazz, Bill is an accountant) is labeled incorrect.

To keep it technical, you would say that this probability judgment is non-Bayesian. Beliefs and actions that are rational in this mathematically well-defined sense are called “Bayesian.”

Note that the modern concept of rationality is not about reasoning in words. I gave the example of opening your eyes, looking around you, and building a mental model of a room containing a bookcase against the wall. The modern concept of rationality is general enough to include your eyes and your brain’s visual areas as things-that-map. It includes your wordless intuitions as well. The math doesn’t care whether we use the same English-language word, “rational,” to refer to Spock and to refer to Bayesianism. The math models good ways of achieving goals or mapping the world, regardless of whether those ways fit our preconceptions and stereotypes about what “rationality” is supposed to be.

This does not quite exhaust the problem of what is meant in practice by “rationality,” for two major reasons:

First, the Bayesian formalisms in their full form are computationally intractable on most real-world problems. No one can actually calculate and obey the math, any more than you can predict the stock market by calculating the movements of quarks.

This is why there is a whole site called “Less Wrong,” rather than a single page that simply states the formal axioms and calls it a day. There’s a whole further art to finding the truth and accomplishing value from inside a human mind: we have to learn our own flaws, overcome our biases, prevent ourselves from self-deceiving, get ourselves into good emotional shape to confront the truth and do what needs doing, et cetera, et cetera.

Second, sometimes the meaning of the math itself is called into question. The exact rules of probability theory are called into question by, e.g., anthropic problems in which the number of observers is uncertain. The exact rules of decision theory are called into question by, e.g., Newcomblike problems in which other agents may predict your decision before it happens.¹

In cases like these, it is futile to try to settle the problem by coming up with some new definition of the word “rational” and saying, “Therefore my preferred answer, by definition, is what is meant by the word ‘rational.’” This simply raises the question of why anyone should pay attention to your definition. I’m not interested in probability theory because it is the holy word handed down from Laplace. I’m interested in Bayesian-style belief-updating (with Occam priors) because I expect that this style of thinking gets us systematically closer to, you know, accuracy, the map that reflects the territory.

And then there are questions of how to think that seem not quite answered by either probability theory or decision theory—like the question of how to feel about the truth once you have it. Here, again, trying to define “rationality” a particular way doesn’t support an answer, but merely presumes one.

I am not here to argue the meaning of a word, not even if that word is “rationality.” The point of attaching sequences of letters to particular concepts is to let two people communicate—to help transport thoughts from one mind to another. You cannot change reality, or prove the thought, by manipulating which meanings go with which words.

So if you understand what concept I am generally getting at with this word “rationality,” and with the sub-terms “epistemic rationality” and “instrumental rationality,” we have communicated: we have accomplished everything there is to accomplish by talking about how to define “rationality.” What’s left to discuss is not what meaning to attach to the syllables “ra-tio-na-li-ty”; what’s left to discuss is what is a good way to think.

If you say, “It’s (epistemically) rational for me to believe X, but the truth is Y,” then you are probably using the word “rational” to mean something other than what I have in mind. (E.g., “rationality” should be consistent under reflection—“rationally” looking at the evidence, and “rationally” considering how your mind processes the evidence, shouldn’t lead to two different conclusions.)

Similarly, if you find yourself saying, “The (instrumentally) rational thing for me to do is X, but the right thing for me to do is Y,” then you are almost certainly using some other meaning for the word “rational” or the word “right.” I use the term “rationality” normatively, to pick out desirable patterns of thought.

In this case—or in any other case where people disagree about word meanings—you should substitute more specific language in place of “rational”: “The self-benefiting thing to do is to run away, but I hope I would at least try to drag the child off the railroad tracks,” or “Causal decision theory as usually formulated says you should two-box on Newcomb’s Problem, but I’d rather have a million dollars.”

In fact, I recommend reading back through this essay, replacing every instance of “rational” with “foozal,” and seeing if that changes the connotations of what I’m saying any. If so, I say: strive not for rationality, but for foozality.

The word “rational” has potential pitfalls, but there are plenty of non-borderline cases where “rational” works fine to communicate what I’m getting at. Likewise “irrational.” In these cases I’m not afraid to use it.

Yet one should be careful not to overuse that word. One receives no points merely for pronouncing it loudly. If you speak overmuch of the Way, you will not attain it.

1. Editor’s Note: For a good introduction to Newcomb’s Problem, see Holt.² More generally, you can find definitions and explanations for many of the terms in this book at the website wiki.lesswrong.com/wiki/RAZ_Glossary.

2. Jim Holt, “Thinking Inside the Boxes,” Slate (2002), http://www.slate.com/articles/arts/egghead/2002/02/thinkinginside%5C_the%5C_boxes.single.html.

2
Feeling Rational

A popular belief about “rationality” is that rationality opposes all emotion—that all our sadness and all our joy are automatically anti-logical by virtue of being feelings. Yet strangely enough, I can’t find any theorem of probability theory which proves that I should appear ice-cold and expressionless.

So is rationality orthogonal to feeling? No; our emotions arise from our models of reality. If I believe that my dead brother has been discovered alive, I will be happy; if I wake up and realize it was a dream, I will be sad. P. C. Hodgell said: “That which can be destroyed by the truth should be.” My dreaming self’s happiness was opposed by truth. My sadness on waking is rational; there is no truth which destroys it.

Rationality begins by asking how-the-world-is, but spreads virally to any other thought which depends on how we think the world is. Your beliefs about “how-the-world-is” can concern anything you think is out there in reality, anything that either does or does not exist, any member of the class “things that can make other things happen.” If you believe that there is a goblin in your closet that ties your shoes’ laces together, then this is a belief about how-the-world-is. Your shoes are real—you can pick them up. If there’s something out there that can reach out and tie your shoelaces together, it must be real too, part of the vast web of causes and effects we call the “universe.”

Feeling angry at the goblin who tied your shoelaces involves a state of mind that is not just about how-the-world-is. Suppose that, as a Buddhist or a lobotomy patient or just a very phlegmatic person, finding your shoelaces tied together didn’t make you angry. This wouldn’t affect what you expected to see in the world—you’d still expect to open up your closet and find your shoelaces tied together. Your anger or calm shouldn’t affect your best guess here, because what happens in your closet does not depend on your emotional state of mind; though it may take some effort to think that clearly.

But the angry feeling is tangled up with a state of mind that is about how-the-world-is; you become angry because you think the goblin tied your shoelaces. The criterion of rationality spreads virally, from the initial question of whether or not a goblin tied your shoelaces, to the resulting anger.

Becoming more rational—arriving at better estimates of how-the-world-is—can diminish feelings or intensify them. Sometimes we run away from strong feelings by denying the facts, by flinching away from the view of the world that gave rise to the powerful emotion. If so, then as you study the skills of rationality and train yourself not to deny facts, your feelings will become stronger.

In my early days I was never quite certain whether it was all right to feel things strongly—whether it was allowed, whether it was proper. I do not think this confusion arose only from my youthful misunderstanding of rationality. I have observed similar troubles in people who do not even aspire to be rationalists; when they are happy, they wonder if they are really allowed to be happy, and when they are sad, they are never quite sure whether to run away from the emotion or not. Since the days of Socrates at least, and probably long before, the way to appear cultured and sophisticated has been to never let anyone see you care strongly about anything. It’s embarrassing to feel—it’s just not done in polite society. You should see the strange looks I get when people realize how much I care about rationality. It’s not the unusual subject, I think, but that they’re not used to seeing sane adults who visibly care about anything.

But I know, now, that there’s nothing wrong with feeling strongly. Ever since I adopted the rule of “That which can be destroyed by the truth should be,” I’ve also come to realize “That which the truth nourishes should thrive.” When something good happens, I am happy, and there is no confusion in my mind about whether it is rational for me to be happy. When something terrible happens, I do not flee my sadness by searching for fake consolations and false silver linings. I visualize the past and future of humankind, the tens of billions of deaths over our history, the misery and fear, the search for answers, the trembling hands reaching upward out of so much blood, what we could become someday when we make the stars our cities, all that darkness and all that light—I know that I can never truly understand it, and I haven’t the words to say. Despite all my philosophy I am still embarrassed to confess strong emotions, and you’re probably uncomfortable hearing them. But I know, now, that it is rational to feel.

3
Why Truth? And . . .

Some of the comments on Overcoming Bias have touched on the question of why we ought to seek truth. (Thankfully not many have questioned what truth is.) Our shaping motivation for configuring our thoughts to rationality, which determines whether a given configuration is “good” or “bad,” comes from whyever we wanted to find truth in the first place.

It is written: “The first virtue is curiosity.” Curiosity is one reason to seek truth, and it may not be the only one, but it has a special and admirable purity. If your motive is curiosity, you will assign priority to questions according to how the questions, themselves, tickle your personal aesthetic sense. A trickier challenge, with a greater probability of failure, may be worth more effort than a simpler one, just because it is more fun.

As I noted, people often think of rationality and emotion as adversaries. Since curiosity is an emotion, I suspect that some people will object to treating curiosity as a part of rationality. For my part, I label an emotion as “not rational” if it rests on mistaken beliefs, or rather, on mistake-producing epistemic conduct: “If the iron approaches your face, and you believe it is hot, and it is cool, the Way opposes your fear. If the iron approaches your face, and you believe it is cool, and it is hot, the Way opposes your calm.” Conversely, then, an emotion that is evoked by correct beliefs or epistemically rational thinking is a “rational emotion”; and this has the advantage of letting us regard calm as an emotional state, rather than a privileged default.

When people think of “emotion” and “rationality” as opposed, I suspect that they are really thinking of System 1 and System 2—fast perceptual judgments versus slow deliberative judgments. Deliberative judgments aren’t always true, and perceptual judgments aren’t always false; so it is very important to distinguish that dichotomy from “rationality.” Both systems can serve the goal of truth, or defeat it, depending on how they are used.

Besides sheer emotional curiosity, what other motives are there for desiring truth? Well, you might want to accomplish some specific real-world goal, like building an airplane, and therefore you need to know some specific truth about aerodynamics. Or more mundanely, you want chocolate milk, and therefore you want to know whether the local grocery has chocolate milk, so you can choose whether to walk there or somewhere else. If this is the reason you want truth, then the priority you assign to your questions will reflect the expected utility of their information—how much the possible answers influence your choices, how much your choices matter, and how much you expect to find an answer that changes your choice from its default.

To seek truth merely for its instrumental value may seem impure—should we not desire the truth for its own sake?—but such investigations are extremely important because they create an outside criterion of verification: if your airplane drops out of the sky, or if you get to the store and find no chocolate milk, it’s a hint that you did something wrong. You get back feedback on which modes of thinking work, and which don’t. Pure curiosity is a wonderful thing, but it may not linger too long on verifying its answers, once the attractive mystery is gone. Curiosity, as a human emotion, has been around since long before the ancient Greeks. But what set humanity firmly on the path of Science was noticing that certain modes of thinking uncovered beliefs that let us manipulate the world. As far as sheer curiosity goes, spinning campfire tales of gods and heroes satisfied that desire just as well, and no one realized that anything was wrong with that.

Are there motives for seeking truth besides curiosity and pragmatism? The third reason that I can think of is morality: You believe that to seek the truth is noble and important and worthwhile. Though such an ideal also attaches an intrinsic value to truth, it’s a very different state of mind from curiosity. Being curious about what’s behind the curtain doesn’t feel the same as believing that you have a moral duty to look there. In the latter state of mind, you are a lot more likely to believe that someone else should look behind the curtain, too, or castigate them if they deliberately close their eyes. For this reason, I would also label as “morality” the belief that truthseeking is pragmatically important to society, and therefore is incumbent as a duty upon all. Your priorities, under this motivation, will be determined by your ideals about which truths are most important (not most useful or most intriguing), or about when, under what circumstances, the duty to seek truth is at its strongest.

I tend to be suspicious of morality as a motivation for rationality, not because I reject the moral ideal, but because it invites certain kinds of trouble. It is too easy to acquire, as learned moral duties, modes of thinking that are dreadful missteps in the dance. Consider Mr. Spock of Star Trek, a naive archetype of rationality. Spock’s emotional state is always set to “calm,” even when wildly inappropriate. He often gives many significant digits for probabilities that are grossly uncalibrated. (E.g., “Captain, if you steer the Enterprise directly into that black hole, our probability of surviving is only 2.234%.” Yet nine times out of ten the Enterprise is not destroyed. What kind of tragic fool gives four significant digits for a figure that is off by two orders of magnitude?) Yet this popular image is how many people conceive of the duty to be “rational”—small wonder that they do not embrace it wholeheartedly. To make rationality into a moral duty is to give it all the dreadful degrees of freedom of an arbitrary tribal custom. People arrive at the wrong answer, and then indignantly protest that they acted with propriety, rather than learning from their mistake.

And yet if we’re going to improve our skills of rationality, go beyond the standards of performance set by hunter-gatherers, we’ll need deliberate beliefs about how to think with propriety. When we write new mental programs for ourselves, they start out in System 2, the deliberate system, and are only slowly—if ever—trained into the neural circuitry that underlies System 1. So if there are certain kinds of thinking that we find we want to avoid—like, say, biases—it will end up represented, within System 2, as an injunction not to think that way; a professed duty of avoidance.

If we want the truth, we can most effectively obtain it by thinking in certain ways, rather than others; these are the techniques of rationality. And some of the techniques of rationality involve overcoming a certain class of obstacles, the biases . . .

4
. . . What’s a Bias, Again?

A bias is a certain kind of obstacle to our goal of obtaining truth. (Its character as an “obstacle” stems from this goal of truth.) However, there are many obstacles that are not “biases.”

If we start right out by asking “What is bias?,” it comes at the question in the wrong order. As the proverb goes, “There are forty kinds of lunacy but only one kind of common sense.” The truth is a narrow target, a small region of configuration space to hit. “She loves me, she loves me not” may be a binary question, but E = mc² is a tiny dot in the space of all equations, like a winning lottery ticket in the space of all lottery tickets. Error is not an exceptional condition; it is success that is a priori so improbable that it requires an explanation.

We don’t start out with a moral duty to “reduce bias,” because biases are bad and evil and Just Not Done. This is the sort of thinking someone might end up with if they acquired a deontological duty of “rationality” by social osmosis, which leads to people trying to execute techniques without appreciating the reason for them. (Which is bad and evil and Just Not Done, according to Surely You’re Joking, Mr. Feynman, which I read as a kid.)

Rather, we want to get to the truth, for whatever reason, and we find various obstacles getting in the way of our goal. These obstacles are not wholly dissimilar to each other—for example, there are obstacles that have to do with not having enough computing power available, or information being expensive. It so happens that a large group of obstacles seem to have a certain character in common—to cluster in a region of obstacle-to-truth space—and this cluster has been labeled “biases.”

What is a bias? Can we look at the empirical cluster and find a compact test for membership? Perhaps we will find that we can’t really give any explanation better than pointing to a few extensional examples, and hoping the listener understands. If you are a scientist just beginning to investigate fire, it might be a lot wiser to point to a campfire and say “Fire is that orangey-bright hot stuff over there,” rather than saying “I define fire as an alchemical transmutation of substances which releases phlogiston.” You should not ignore something just because you can’t define it. I can’t quote the equations of General Relativity from memory, but nonetheless if I walk off a cliff, I’ll fall. And we can say the same of biases—they won’t hit any less hard if it turns out we can’t define compactly what a “bias” is. So we might point to conjunction fallacies, to overconfidence, to the availability and representativeness heuristics, to base rate neglect, and say: “Stuff like that.”

With all that said, we seem to label as “biases” those obstacles to truth which are produced, not by the cost of information, nor by limited computing power, but by the shape of our own mental machinery. Perhaps the machinery is evolutionarily optimized to purposes that actively oppose epistemic accuracy; for example, the machinery to win arguments in adaptive political contexts. Or the selection pressure ran skew to epistemic accuracy; for example, believing what others believe, to get along socially. Or, in the classic heuristic-and-bias, the machinery operates by an identifiable algorithm that does some useful work but also produces systematic errors: the availability heuristic is not itself a bias, but it gives rise to identifiable, compactly describable biases. Our brains are doing something wrong, and after a lot of experimentation and/or heavy thinking, someone identifies the problem in a fashion that System 2 can comprehend; then we call it a “bias.” Even if we can do no better for knowing, it is still a failure that arises, in an identifiable fashion, from a particular kind of cognitive machinery—not from having too little machinery, but from the machinery’s shape.

“Biases” are distinguished from errors that arise from cognitive content, such as adopted beliefs, or adopted moral duties. These we call “mistakes,” rather than “biases,” and they are much easier to correct, once we’ve noticed them for ourselves. (Though the source of the mistake, or the source of the source of the mistake, may ultimately be some bias.)

“Biases” are distinguished from errors that arise from damage to an individual human brain, or from absorbed cultural mores; biases arise from machinery that is humanly universal.

Plato wasn’t “biased” because he was ignorant of General Relativity—he had no way to gather that information, his ignorance did not arise from the shape of his mental machinery. But if Plato believed that philosophers would make better kings because he himself was a philosopher—and this belief, in turn, arose because of a universal adaptive political instinct for self-promotion, and not because Plato’s daddy told him that everyone has a moral duty to promote their own profession to governorship, or because Plato sniffed too much glue as a kid—then that was a bias, whether Plato was ever warned of it or not.

Biases may not be cheap to correct. They may not even be correctable. But where we look upon our own mental machinery and see a causal account of an identifiable class of errors; and when the problem seems to come from the evolved shape of the machinery, rather from there being too little machinery, or bad specific content; then we call that a bias.

Personally, I see our quest in terms of acquiring personal skills of rationality, in improving truthfinding technique. The challenge is to attain the positive goal of truth, not to avoid the negative goal of failure. Failurespace is wide, infinite errors in infinite variety. It is difficult to describe so huge a space: “What is true of one apple may not be true of another apple; thus more can be said about a single apple than about all the apples in the world.” Success-space is narrower, and therefore more can be said about it.

While I am not averse (as you can see) to discussing definitions, we should remember that is not our primary goal. We are here to pursue the great human quest for truth: for we have desperate need of the knowledge, and besides, we’re curious. To this end let us strive to overcome whatever obstacles lie in our way, whether we call them “biases” or not.

5
Availability

The availability heuristic is judging the frequency or probability of an event by the ease with which examples of the event come to mind.

A famous 1978 study by Lichtenstein, Slovic, Fischhoff, Layman, and Combs, “Judged Frequency of Lethal Events,” studied errors in quantifying the severity of risks, or judging which of two dangers occurred more frequently.¹ Subjects thought that accidents caused about as many deaths as disease; thought that homicide was a more frequent cause of death than suicide. Actually, diseases cause about sixteen times as many deaths as accidents, and suicide is twice as frequent as homicide.

An obvious hypothesis to account for these skewed beliefs is that murders are more likely to be talked about than suicides—thus, someone is more likely to recall hearing about a murder than hearing about a suicide. Accidents are more dramatic than diseases—perhaps this makes people more likely to remember, or more likely to recall, an accident. In 1979, a followup study by Combs and Slovic showed that the skewed probability judgments correlated strongly (0.85 and 0.89) with skewed reporting frequencies in two newspapers.² This doesn’t disentangle whether murders are more available to memory because they are more reported-on, or whether newspapers report more on murders because murders are more vivid (hence also more remembered). But either way, an availability bias is at work. Selective reporting is one major source of availability biases. In the ancestral environment, much of what you knew, you experienced yourself; or you heard it directly from a fellow tribe-member who had seen it. There was usually at most one layer of selective reporting between you, and the event itself. With today’s Internet, you may see reports that have passed through the hands of six bloggers on the way to you—six successive filters. Compared to our ancestors, we live in a larger world, in which far more happens, and far less of it reaches us—a much stronger selection effect, which can create much larger availability biases.

In real life, you’re unlikely to ever meet Bill Gates. But thanks to selective reporting by the media, you may be tempted to compare your life success to his—and suffer hedonic penalties accordingly. The objective frequency of Bill Gates is 0.00000000015, but you hear about him much more often. Conversely, 19% of the planet lives on less than $1/day, and I doubt that one fifth of the blog posts you read are written by them.

Using availability seems to give rise to an absurdity bias; events that have never happened are not recalled, and hence deemed to have probability zero. When no flooding has recently occurred (and yet the probabilities are still fairly calculable), people refuse to buy flood insurance even when it is heavily subsidized and priced far below an actuarially fair value. Kunreuther et al. suggest underreaction to threats of flooding may arise from “the inability of individuals to conceptualize floods that have never occurred . . . Men on flood plains appear to be very much prisoners of their experience . . . Recently experienced floods appear to set an upward bound to the size of loss with which managers believe they ought to be concerned.”³

Burton et al. report that when dams and levees are built, they reduce the frequency of floods, and thus apparently create a false sense of security, leading to reduced precautions.⁴ While building dams decreases the frequency of floods, damage per flood is afterward so much greater that average yearly damage increases. The wise would extrapolate from a memory of small hazards to the possibility of large hazards. Instead, past experience of small hazards seems to set a perceived upper bound on risk. A society well-protected against minor hazards takes no action against major risks, building on flood plains once the regular minor floods are eliminated. A society subject to regular minor hazards treats those minor hazards as an upper bound on the size of the risks, guarding against regular minor floods but not occasional major floods.

Memory is not always a good guide to probabilities in the past, let alone in the future.

1. Sarah Lichtenstein et al., “Judged Frequency of Lethal Events,” Journal of Experimental Psychology: Human Learning and Memory 4, no. 6 (1978): 551–578, doi:10.1037/0278-7393.4.6.551.

2. Barbara Combs and Paul Slovic, “Newspaper Coverage of Causes of Death,” Journalism & Mass Communication Quarterly 56, no. 4 (1979): 837–849, doi:10.1177/107769907905600420.

3. Howard Kunreuther, Robin Hogarth, and Jacqueline Meszaros, “Insurer Ambiguity and Market Failure,” Journal of Risk and Uncertainty 7 (1 1993): 71–87, doi:10.1007/BF01065315.

4. Ian Burton, Robert W. Kates, and Gilbert F. White, The Environment as Hazard, 1st ed. (New York: Oxford University Press, 1978).

6
Burdensome Details

Merely corroborative detail, intended to give artistic verisimilitude to an otherwise bald and unconvincing narrative . . .

—Pooh-Bah, in Gilbert and Sullivan’s The Mikado¹

The conjunction fallacy is when humans rate the probability P(A,B) higher than the probability P(B), even though it is a theorem that P(A,B) ≤ P(B). For example, in one experiment in 1981, 68% of the subjects ranked it more likely that “Reagan will provide federal support for unwed mothers and cut federal support to local governments” than that “Reagan will provide federal support for unwed mothers.”

A long series of cleverly designed experiments, which weeded out alternative hypotheses and nailed down the standard interpretation, confirmed that conjunction fallacy occurs because we “substitute judgment of representativeness for judgment of probability.” By adding extra details, you can make an outcome seem more characteristic of the process that generates it. You can make it sound more plausible that Reagan will support unwed mothers, by adding the claim that Reagan will also cut support to local governments. The implausibility of one claim is compensated by the plausibility of the other; they “average out.”

Which is to say: Adding detail can make a scenario SOUND MORE PLAUSIBLE, even though the event necessarily BECOMES LESS PROBABLE.

If so, then, hypothetically speaking, we might find futurists spinning unconscionably plausible and detailed future histories, or find people swallowing huge packages of unsupported claims bundled with a few strong-sounding assertions at the center. If you are presented with the conjunction fallacy in a naked, direct comparison, then you may succeed on that particular problem by consciously correcting yourself. But this is only slapping a band-aid on the problem, not fixing it in general.

In the 1982 experiment where professional forecasters assigned systematically higher probabilities to “Russia invades Poland, followed by suspension of diplomatic relations between the USA and the USSR” than to “Suspension of diplomatic relations between the USA and the USSR,” each experimental group was only presented with one proposition.² What strategy could these forecasters have followed, as a group, that would have eliminated the conjunction fallacy, when no individual knew directly about the comparison? When no individual even knew that the experiment was about the conjunction fallacy? How could they have done better on their probability judgments?

Patching one gotcha as a special case doesn’t fix the general problem. The gotcha is the symptom, not the disease.

What could the forecasters have done to avoid the conjunction fallacy, without seeing the direct comparison, or even knowing that anyone was going to test them on the conjunction fallacy? It seems to me, that they would need to notice the word “and.” They would need to be wary of it—not just wary, but leap back from it. Even without knowing that researchers were afterward going to test them on the conjunction fallacy particularly. They would need to notice the conjunction of two entire details, and be shocked by the audacity of anyone asking them to endorse such an insanely complicated prediction. And they would need to penalize the probability substantially—a factor of four, at least, according to the experimental details.

It might also have helped the forecasters to think about possible reasons why the US and Soviet Union would suspend diplomatic relations. The scenario is not “The US and Soviet Union suddenly suspend diplomatic relations for no reason,” but “The US and Soviet Union suspend diplomatic relations for any reason.”

And the subjects who rated “Reagan will provide federal support for unwed mothers and cut federal support to local governments”? Again, they would need to be shocked by the word “and.” Moreover, they would need to add absurdities—where the absurdity is the log probability, so you can add it—rather than averaging them. They would need to think, “Reagan might or might not cut support to local governments (1 bit), but it seems very unlikely that he will support unwed mothers (4 bits). Total absurdity: 5 bits.” Or maybe, “Reagan won’t support unwed mothers. One strike and it’s out. The other proposition just makes it even worse.”

Similarly, consider the six-sided die with four green faces and two red faces. The subjects had to bet on the sequence (1) RGRRR, (2) GRGRRR, or (3) GRRRRR appearing anywhere in twenty rolls of the dice.³ Sixty-five percent of the subjects chose GRGRRR, which is strictly dominated by RGRRR, since any sequence containing GRGRRR also pays off for RGRRR. How could the subjects have done better? By noticing the inclusion? Perhaps; but that is only a band-aid, it does not fix the fundamental problem. By explicitly calculating the probabilities? That would certainly fix the fundamental problem, but you can’t always calculate an exact probability.

The subjects lost heuristically by thinking: “Aha! Sequence 2 has the highest proportion of green to red! I should bet on Sequence 2!” To win heuristically, the subjects would need to think: “Aha! Sequence 1 is short! I should go with Sequence 1!”

They would need to feel a stronger emotional impact from Occam’s Razor—feel every added detail as a burden, even a single extra roll of the dice.

Once upon a time, I was speaking to someone who had been mesmerized by an incautious futurist (one who adds on lots of details that sound neat). I was trying to explain why I was not likewise mesmerized by these amazing, incredible theories. So I explained about the conjunction fallacy, specifically the “suspending relations ± invading Poland” experiment. And he said, “Okay, but what does this have to do with—” And I said, “It is more probable that universes replicate for any reason, than that they replicate via black holes because advanced civilizations manufacture black holes because universes evolve to make them do it.” And he said, “Oh.”

Until then, he had not felt these extra details as extra burdens. Instead they were corroborative detail, lending verisimilitude to the narrative. Someone presents you with a package of strange ideas, one of which is that universes replicate. Then they present support for the assertion that universes replicate. But this is not support for the package, though it is all told as one story.

You have to disentangle the details. You have to hold up every one independently, and ask, “How do we know this detail?” Someone sketches out a picture of humanity’s descent into nanotechnological warfare, where China refuses to abide by an international control agreement, followed by an arms race . . . Wait a minute—how do you know it will be China? Is that a crystal ball in your pocket or are you just happy to be a futurist? Where are all these details coming from? Where did that specific detail come from?

For it is written:

If you can lighten your burden you must do so.

There is no straw that lacks the power to break your back.

1. William S. Gilbert and Arthur Sullivan, The Mikado, Opera, 1885.

2. Tversky and Kahneman, “Extensional Versus Intuitive Reasoning.”

3. Amos Tversky and Daniel Kahneman, “Judgments of and by Representativeness,” in Judgment Under Uncertainty: Heuristics and Biases, ed. Daniel Kahneman, Paul Slovic, and Amos Tversky (New York: Cambridge University Press, 1982), 84–98.

7
Planning Fallacy

The Denver International Airport opened 16 months late, at a cost overrun of $2 billion. (I’ve also seen $3.1 billion asserted.) The Eurofighter Typhoon, a joint defense project of several European countries, was delivered 54 months late at a cost of $19 billion instead of $7 billion. The Sydney Opera House may be the most legendary construction overrun of all time, originally estimated to be completed in 1963 for $7 million, and finally completed in 1973 for $102 million.¹

Are these isolated disasters brought to our attention by selective availability? Are they symptoms of bureaucracy or government incentive failures? Yes, very probably. But there’s also a corresponding cognitive bias, replicated in experiments with individual planners.

Buehler et al. asked their students for estimates of when they (the students) thought they would complete their personal academic projects.² Specifically, the researchers asked for estimated times by which the students thought it was 50%, 75%, and 99% probable their personal projects would be done. Would you care to guess how many students finished on or before their estimated 50%, 75%, and 99% probability levels?

13% of subjects finished their project by the time they had assigned a 50% probability level;
19% finished by the time assigned a 75% probability level;
and only 45% (less than half!) finished by the time of their 99% probability level.

As Buehler et al. wrote, “The results for the 99% probability level are especially striking: Even when asked to make a highly conservative forecast, a prediction that they felt virtually certain that they would fulfill, students’ confidence in their time estimates far exceeded their accomplishments.”³

More generally, this phenomenon is known as the “planning fallacy.” The planning fallacy is that people think they can plan, ha ha.

A clue to the underlying problem with the planning algorithm was uncovered by Newby-Clark et al., who found that

Asking subjects for their predictions based on realistic “best guess” scenarios; and
Asking subjects for their hoped-for “best case” scenarios . . .

. . . produced indistinguishable results.⁴

When people are asked for a “realistic” scenario, they envision everything going exactly as planned, with no unexpected delays or unforeseen catastrophes—the same vision as their “best case.”

Reality, it turns out, usually delivers results somewhat worse than the “worst case.”

Unlike most cognitive biases, we know a good debiasing heuristic for the planning fallacy. It won’t work for messes on the scale of the Denver International Airport, but it’ll work for a lot of personal planning, and even some small-scale organizational stuff. Just use an “outside view” instead of an “inside view.”

People tend to generate their predictions by thinking about the particular, unique features of the task at hand, and constructing a scenario for how they intend to complete the task—which is just what we usually think of as planning. When you want to get something done, you have to plan out where, when, how; figure out how much time and how much resource is required; visualize the steps from beginning to successful conclusion. All this is the “inside view,” and it doesn’t take into account unexpected delays and unforeseen catastrophes. As we saw before, asking people to visualize the “worst case” still isn’t enough to counteract their optimism—they don’t visualize enough Murphyness.

The outside view is when you deliberately avoid thinking about the special, unique features of this project, and just ask how long it took to finish broadly similar projects in the past. This is counterintuitive, since the inside view has so much more detail—there’s a temptation to think that a carefully tailored prediction, taking into account all available data, will give better results.

But experiment has shown that the more detailed subjects’ visualization, the more optimistic (and less accurate) they become. Buehler et al. asked an experimental group of subjects to describe highly specific plans for their Christmas shopping—where, when, and how.⁵ On average, this group expected to finish shopping more than a week before Christmas. Another group was simply asked when they expected to finish their Christmas shopping, with an average response of four days. Both groups finished an average of three days before Christmas.

Likewise, Buehler et al., reporting on a cross-cultural study, found that Japanese students expected to finish their essays ten days before deadline. They actually finished one day before deadline. Asked when they had previously completed similar tasks, they responded, “one day before deadline.”⁶ This is the power of the outside view over the inside view.

A similar finding is that experienced outsiders, who know less of the details, but who have relevant memory to draw upon, are often much less optimistic and much more accurate than the actual planners and implementers.

So there is a fairly reliable way to fix the planning fallacy, if you’re doing something broadly similar to a reference class of previous projects. Just ask how long similar projects have taken in the past, without considering any of the special properties of this project. Better yet, ask an experienced outsider how long similar projects have taken.

You’ll get back an answer that sounds hideously long, and clearly reflects no understanding of the special reasons why this particular task will take less time. This answer is true. Deal with it.

1. Roger Buehler, Dale Griffin, and Michael Ross, “Inside the Planning Fallacy: The Causes and Consequences of Optimistic Time Predictions,” in Gilovich, Griffin, and Kahneman, Heuristics and Biases, 250–270.

2. Roger Buehler, Dale Griffin, and Michael Ross, “Exploring the ‘Planning Fallacy’: Why People Underestimate Their Task Completion Times,” Journal of Personality and Social Psychology 67, no. 3 (1994): 366–381, doi:10.1037/0022-3514.67.3.366; Roger Buehler, Dale Griffin, and Michael Ross, “It’s About Time: Optimistic Predictions in Work and Love,” European Review of Social Psychology 6, no. 1 (1995): 1–32, doi:10.1080/14792779343000112.

3. Buehler, Griffin, and Ross, “Inside the Planning Fallacy.”

4. Ian R. Newby-Clark et al., “People Focus on Optimistic Scenarios and Disregard Pessimistic Scenarios While Predicting Task Completion Times,” Journal of Experimental Psychology: Applied 6, no. 3 (2000): 171–182, doi:10.1037/1076-898X.6.3.171.

5. Buehler, Griffin, and Ross, “Inside the Planning Fallacy.”

6. Ibid.

8
Illusion of Transparency: Why No One Understands You

In hindsight bias, people who know the outcome of a situation believe the outcome should have been easy to predict in advance. Knowing the outcome, we reinterpret the situation in light of that outcome. Even when warned, we can’t de-interpret to empathize with someone who doesn’t know what we know.

Closely related is the illusion of transparency: We always know what we mean by our words, and so we expect others to know it too. Reading our own writing, the intended interpretation falls easily into place, guided by our knowledge of what we really meant. It’s hard to empathize with someone who must interpret blindly, guided only by the words.

June recommends a restaurant to Mark; Mark dines there and discovers (a) unimpressive food and mediocre service or (b) delicious food and impeccable service. Then Mark leaves the following message on June’s answering machine: “June, I just finished dinner at the restaurant you recommended, and I must say, it was marvelous, just marvelous.” Keysar presented a group of subjects with scenario (a), and 59% thought that Mark’s message was sarcastic and that Jane would perceive the sarcasm.¹ Among other subjects, told scenario (b), only 3% thought that Jane would perceive Mark’s message as sarcastic. Keysar and Barr seem to indicate that an actual voice message was played back to the subjects.² Keysar showed that if subjects were told that the restaurant was horrible but that Mark wanted to conceal his response, they believed June would not perceive sarcasm in the (same) message:³

They were just as likely to predict that she would perceive sarcasm when he attempted to conceal his negative experience as when he had a positive experience and was truly sincere. So participants took Mark’s communicative intention as transparent. It was as if they assumed that June would perceive whatever intention Mark wanted her to perceive.⁴

“The goose hangs high” is an archaic English idiom that has passed out of use in modern language. Keysar and Bly told one group of subjects that “the goose hangs high” meant that the future looks good; another group of subjects learned that “the goose hangs high” meant the future looks gloomy.⁵ Subjects were then asked which of these two meanings an uninformed listener would be more likely to attribute to the idiom. Each group thought that listeners would perceive the meaning presented as “standard.”

(Other idioms tested included “come the uncle over someone,” “to go by the board,” and “to lay out in lavender.” Ah, English, such a lovely language.)

Keysar and Henly tested the calibration of speakers: Would speakers underestimate, overestimate, or correctly estimate how often listeners understood them?⁶ Speakers were given ambiguous sentences (“The man is chasing a woman on a bicycle.”) and disambiguating pictures (a man running after a cycling woman), then asked the speakers to utter the words in front of addressees, then asked speakers to estimate how many addressees understood the intended meaning. Speakers thought that they were understood in 72% of cases and were actually understood in 61% of cases. When addressees did not understand, speakers thought they did in 46% of cases; when addressees did understand, speakers thought they did not in only 12% of cases.

Additional subjects who overheard the explanation showed no such bias, expecting listeners to understand in only 56% of cases.

As Keysar and Barr note, two days before Germany’s attack on Poland, Chamberlain sent a letter intended to make it clear that Britain would fight if any invasion occurred.⁷ The letter, phrased in polite diplomatese, was heard by Hitler as conciliatory—and the tanks rolled.

Be not too quick to blame those who misunderstand your perfectly clear sentences, spoken or written. Chances are, your words are more ambiguous than you think.

1. Boaz Keysar, “The Illusory Transparency of Intention: Linguistic Perspective Taking in Text,” Cognitive Psychology 26 (2 1994): 165–208, doi:10.1006/cogp.1994.1006.

2. Keysar and Barr, “Self-Anchoring in Conversation.”

3. Boaz Keysar, “Language Users as Problem Solvers: Just What Ambiguity Problem Do They Solve?,” in Social and Cognitive Approaches to Interpersonal Communication, ed. Susan R. Fussell and Roger J. Kreuz (Mahwah, NJ: Lawrence Erlbaum Associates, 1998), 175–200.

4. Keysar and Barr, “Self-Anchoring in Conversation.”

5. Boaz Keysar and Bridget Bly, “Intuitions of the Transparency of Idioms: Can One Keep a Secret by Spilling the Beans?,” Journal of Memory and Language 34 (1 1995): 89–109, doi:10.1006/jmla.1995.1005.

6. Boaz Keysar and Anne S. Henly, “Speakers’ Overestimation of Their Effectiveness,” Psychological Science 13 (3 2002): 207–212, doi:10.1111/1467-9280.00439.

7. Keysar and Barr, “Self-Anchoring in Conversation.”

9
Expecting Short Inferential Distances

Homo sapiens’s environment of evolutionary adaptedness (a.k.a. EEA or “ancestral environment”) consisted of hunter-gatherer bands of at most 200 people, with no writing. All inherited knowledge was passed down by speech and memory.

In a world like that, all background knowledge is universal knowledge. All information not strictly private is public, period.

In the ancestral environment, you were unlikely to end up more than one inferential step away from anyone else. When you discover a new oasis, you don’t have to explain to your fellow tribe members what an oasis is, or why it’s a good idea to drink water, or how to walk. Only you know where the oasis lies; this is private knowledge. But everyone has the background to understand your description of the oasis, the concepts needed to think about water; this is universal knowledge. When you explain things in an ancestral environment, you almost never have to explain your concepts. At most you have to explain one new concept, not two or more simultaneously.

In the ancestral environment there were no abstract disciplines with vast bodies of carefully gathered evidence generalized into elegant theories transmitted by written books whose conclusions are a hundred inferential steps removed from universally shared background premises.

In the ancestral environment, anyone who says something with no obvious support is a liar or an idiot. You’re not likely to think, “Hey, maybe this person has well-supported background knowledge that no one in my band has even heard of,” because it was a reliable invariant of the ancestral environment that this didn’t happen.

Conversely, if you say something blatantly obvious and the other person doesn’t see it, they’re the idiot, or they’re being deliberately obstinate to annoy you.

And to top it off, if someone says something with no obvious support and expects you to believe it—acting all indignant when you don’t—then they must be crazy.

Combined with the illusion of transparency and selfanchoring, I think this explains a lot about the legendary difficulty most scientists have in communicating with a lay audience—or even communicating with scientists from other disciplines. When I observe failures of explanation, I usually see the explainer taking one step back, when they need to take two or more steps back. Or listeners assume that things should be visible in one step, when they take two or more steps to explain. Both sides act as if they expect very short inferential distances from universal knowledge to any new knowledge.

A biologist, speaking to a physicist, can justify evolution by saying it is the simplest explanation. But not everyone on Earth has been inculcated with that legendary history of science, from Newton to Einstein, which invests the phrase “simplest explanation” with its awesome import: a Word of Power, spoken at the birth of theories and carved on their tombstones. To someone else, “But it’s the simplest explanation!” may sound like an interesting but hardly knockdown argument; it doesn’t feel like all that powerful a tool for comprehending office politics or fixing a broken car. Obviously the biologist is infatuated with their own ideas, too arrogant to be open to alternative explanations which sound just as plausible. (If it sounds plausible to me, it should sound plausible to any sane member of my band.)

And from the biologist’s perspective, they can understand how evolution might sound a little odd at first—but when someone rejects evolution even after the biologist explains that it’s the simplest explanation, well, it’s clear that nonscientists are just idiots and there’s no point in talking to them.

A clear argument has to lay out an inferential pathway, starting from what the audience already knows or accepts. If you don’t recurse far enough, you’re just talking to yourself.

If at any point you make a statement without obvious justification in arguments you’ve previously supported, the audience just thinks you’re crazy.

This also happens when you allow yourself to be seen visibly attaching greater weight to an argument than is justified in the eyes of the audience at that time. For example, talking as if you think “simpler explanation” is a knockdown argument for evolution (which it is), rather than a sorta-interesting idea (which it sounds like to someone who hasn’t been raised to revere Occam’s Razor).

Oh, and you’d better not drop any hints that you think you’re working a dozen inferential steps away from what the audience knows, or that you think you have special background knowledge not available to them. The audience doesn’t know anything about an evolutionary-psychological argument for a cognitive bias to underestimate inferential distances leading to traffic jams in communication. They’ll just think you’re condescending.

And if you think you can explain the concept of “systematically underestimated inferential distances” briefly, in just a few words, I’ve got some sad news for you . . .

10
The Lens That Sees Its Own Flaws

Light leaves the Sun and strikes your shoelaces and bounces off; some photons enter the pupils of your eyes and strike your retina; the energy of the photons triggers neural impulses; the neural impulses are transmitted to the visual-processing areas of the brain; and there the optical information is processed and reconstructed into a 3D model that is recognized as an untied shoelace; and so you believe that your shoelaces are untied.

Here is the secret of deliberate rationality—this whole process is not magic, and you can understand it. You can understand how you see your shoelaces. You can think about which sort of thinking processes will create beliefs which mirror reality, and which thinking processes will not.

Mice can see, but they can’t understand seeing. You can understand seeing, and because of that, you can do things that mice cannot do. Take a moment to marvel at this, for it is indeed marvelous.

Mice see, but they don’t know they have visual cortexes, so they can’t correct for optical illusions. A mouse lives in a mental world that includes cats, holes, cheese and mousetraps—but not mouse brains. Their camera does not take pictures of its own lens. But we, as humans, can look at a seemingly bizarre image, and realize that part of what we’re seeing is the lens itself. You don’t always have to believe your own eyes, but you have to realize that you have eyes—you must have distinct mental buckets for the map and the territory, for the senses and reality. Lest you think this a trivial ability, remember how rare it is in the animal kingdom.

The whole idea of Science is, simply, reflective reasoning about a more reliable process for making the contents of your mind mirror the contents of the world. It is the sort of thing mice would never invent. Pondering this business of “performing replicable experiments to falsify theories,” we can see why it works. Science is not a separate magisterium, far away from real life and the understanding of ordinary mortals. Science is not something that only applies to the inside of laboratories. Science, itself, is an understandable processin-the-world that correlates brains with reality.

Science makes sense, when you think about it. But mice can’t think about thinking, which is why they don’t have Science. One should not overlook the wonder of this—or the potential power it bestows on us as individuals, not just scientific societies.

Admittedly, understanding the engine of thought may be a little more complicated than understanding a steam engine—but it is not a fundamentally different task.

Once upon a time, I went to EFNet’s #philosophy chatroom to ask, “Do you believe a nuclear war will occur in the next 20 years? If no, why not?” One person who answered the question said he didn’t expect a nuclear war for 100 years, because “All of the players involved in decisions regarding nuclear war are not interested right now.” “But why extend that out for 100 years?” I asked. “Pure hope,” was his reply.

Reflecting on this whole thought process, we can see why the thought of nuclear war makes the person unhappy, and we can see how his brain therefore rejects the belief. But if you imagine a billion worlds—Everett branches, or Tegmark duplicates¹—this thought process will not systematically correlate optimists to branches in which no nuclear war occurs. (Some clever fellow is bound to say, “Ah, but since I have hope, I’ll work a little harder at my job, pump up the global economy, and thus help to prevent countries from sliding into the angry and hopeless state where nuclear war is a possibility. So the two events are related after all.” At this point, we have to drag in Bayes’s Theorem and measure the relationship quantitatively. Your optimistic nature cannot have that large an effect on the world; it cannot, of itself, decrease the probability of nuclear war by 20%, or however much your optimistic nature shifted your beliefs. Shifting your beliefs by a large amount, due to an event that only slightly increases your chance of being right, will still mess up your mapping.)

To ask which beliefs make you happy is to turn inward, not outward—it tells you something about yourself, but it is not evidence entangled with the environment. I have nothing against happiness, but it should follow from your picture of the world, rather than tampering with the mental paintbrushes.

If you can see this—if you can see that hope is shifting your first-order thoughts by too large a degree—if you can understand your mind as a mapping engine that has flaws—then you can apply a reflective correction. The brain is a flawed lens through which to see reality. This is true of both mouse brains and human brains. But a human brain is a flawed lens that can understand its own flaws—its systematic errors, its biases—and apply second-order corrections to them. This, in practice, makes the lens far more powerful. Not perfect, but far more powerful.

1. Max Tegmark, “Parallel Universes,” in Science and Ultimate Reality: Quantum Theory, Cosmology, and Complexity, ed. John D. Barrow, Paul C. W. Davies, and Charles L. Harper Jr. (New York: Cambridge University Press, 2004), 459–491.

11
Making Beliefs Pay Rent (in Anticipated Experiences)

Thus begins the ancient parable:

If a tree falls in a forest and no one hears it, does it make a sound? One says, “Yes it does, for it makes vibrations in the air.” Another says, “No it does not, for there is no auditory processing in any brain.”

Suppose that, after the tree falls, the two walk into the forest together. Will one expect to see the tree fallen to the right, and the other expect to see the tree fallen to the left? Suppose that before the tree falls, the two leave a sound recorder next to the tree. Would one, playing back the recorder, expect to hear something different from the other? Suppose they attach an electroencephalograph to any brain in the world; would one expect to see a different trace than the other? Though the two argue, one saying “No,” and the other saying “Yes,” they do not anticipate any different experiences. The two think they have different models of the world, but they have no difference with respect to what they expect will happen to them.

It’s tempting to try to eliminate this mistake class by insisting that the only legitimate kind of belief is an anticipation of sensory experience. But the world does, in fact, contain much that is not sensed directly. We don’t see the atoms underlying the brick, but the atoms are in fact there. There is a floor beneath your feet, but you don’t experience the floor directly; you see the light reflected from the floor, or rather, you see what your retina and visual cortex have processed of that light. To infer the floor from seeing the floor is to step back into the unseen causes of experience. It may seem like a very short and direct step, but it is still a step.

You stand on top of a tall building, next to a grandfather clock with an hour, minute, and ticking second hand. In your hand is a bowling ball, and you drop it off the roof. On which tick of the clock will you hear the crash of the bowling ball hitting the ground?

To answer precisely, you must use beliefs like Earth’s gravity is 9.8 meters per second per second, and This building is around 120 meters tall. These beliefs are not wordless anticipations of a sensory experience; they are verbal-ish, propositional. It probably does not exaggerate much to describe these two beliefs as sentences made out of words. But these two beliefs have an inferential consequence that is a direct sensory anticipation—if the clock’s second hand is on the 12 numeral when you drop the ball, you anticipate seeing it on the 1 numeral when you hear the crash five seconds later. To anticipate sensory experiences as precisely as possible, we must process beliefs that are not anticipations of sensory experience.

It is a great strength of Homo sapiens that we can, better than any other species in the world, learn to model the unseen. It is also one of our great weak points. Humans often believe in things that are not only unseen but unreal.

The same brain that builds a network of inferred causes behind sensory experience can also build a network of causes that is not connected to sensory experience, or poorly connected. Alchemists believed that phlogiston caused fire—we could oversimply their minds by drawing a little node labeled “Phlogiston,” and an arrow from this node to their sensory experience of a crackling campfire—but this belief yielded no advance predictions; the link from phlogiston to experience was always configured after the experience, rather than constraining the experience in advance. Or suppose your postmodern English professor teaches you that the famous writer Wulky Wilkinsen is actually a “post-utopian.” What does this mean you should expect from his books? Nothing. The belief, if you can call it that, doesn’t connect to sensory experience at all. But you had better remember the propositional assertion that “Wulky Wilkinsen” has the “post-utopian” attribute, so you can regurgitate it on the upcoming quiz. Likewise if “post-utopians” show “colonial alienation”; if the quiz asks whether Wulky Wilkinsen shows colonial alienation, you’d better answer yes. The beliefs are connected to each other, though still not connected to any anticipated experience.

We can build up whole networks of beliefs that are connected only to each other—call these “floating” beliefs. It is a uniquely human flaw among animal species, a perversion of Homo sapiens’s ability to build more general and flexible belief networks.

The rationalist virtue of empiricism consists of constantly asking which experiences our beliefs predict—or better yet, prohibit. Do you believe that phlogiston is the cause of fire? Then what do you expect to see happen, because of that? Do you believe that Wulky Wilkinsen is a post-utopian? Then what do you expect to see because of that? No, not “colonial alienation”; what experience will happen to you? Do you believe that if a tree falls in the forest, and no one hears it, it still makes a sound? Then what experience must therefore befall you?

It is even better to ask: what experience must not happen to you? Do you believe that élan vital explains the mysterious aliveness of living beings? Then what does this belief not allow to happen—what would definitely falsify this belief? A null answer means that your belief does not constrain experience; it permits anything to happen to you. It floats.

When you argue a seemingly factual question, always keep in mind which difference of anticipation you are arguing about. If you can’t find the difference of anticipation, you’re probably arguing about labels in your belief network—or even worse, floating beliefs, barnacles on your network. If you don’t know what experiences are implied by Wulky Wilkinsen being a post-utopian, you can go on arguing forever.

Above all, don’t ask what to believe—ask what to anticipate. Every question of belief should flow from a question of anticipation, and that question of anticipation should be the center of the inquiry. Every guess of belief should begin by flowing to a specific guess of anticipation, and should continue to pay rent in future anticipations. If a belief turns deadbeat, evict it.

12
A Fable of Science and Politics

In the time of the Roman Empire, civic life was divided between the Blue and Green factions. The Blues and the Greens murdered each other in single combats, in ambushes, in group battles, in riots. Procopius said of the warring factions: “So there grows up in them against their fellow men a hostility which has no cause, and at no time does it cease or disappear, for it gives place neither to the ties of marriage nor of relationship nor of friendship, and the case is the same even though those who differ with respect to these colors be brothers or any other kin.”¹ Edward Gibbon wrote: “The support of a faction became necessary to every candidate for civil or ecclesiastical honors.”²

Who were the Blues and the Greens? They were sports fans—the partisans of the blue and green chariot-racing teams.

Imagine a future society that flees into a vast underground network of caverns and seals the entrances. We shall not specify whether they flee disease, war, or radiation; we shall suppose the first Undergrounders manage to grow food, find water, recycle air, make light, and survive, and that their descendants thrive and eventually form cities. Of the world above, there are only legends written on scraps of paper; and one of these scraps of paper describes the sky, a vast open space of air above a great unbounded floor. The sky is cerulean in color, and contains strange floating objects like enormous tufts of white cotton. But the meaning of the word “cerulean” is controversial; some say that it refers to the color known as “blue,” and others that it refers to the color known as “green.”

In the early days of the underground society, the Blues and Greens contested with open violence; but today, truce prevails—a peace born of a growing sense of pointlessness. Cultural mores have changed; there is a large and prosperous middle class that has grown up with effective law enforcement and become unaccustomed to violence. The schools provide some sense of historical perspective; how long the battle between Blues and Greens continued, how many died, how little changed as a result. Minds have been laid open to the strange new philosophy that people are people, whether they be Blue or Green.

The conflict has not vanished. Society is still divided along Blue and Green lines, and there is a “Blue” and a “Green” position on almost every contemporary issue of political or cultural importance. The Blues advocate taxes on individual incomes, the Greens advocate taxes on merchant sales; the Blues advocate stricter marriage laws, while the Greens wish to make it easier to obtain divorces; the Blues take their support from the heart of city areas, while the more distant farmers and watersellers tend to be Green; the Blues believe that the Earth is a huge spherical rock at the center of the universe, the Greens that it is a huge flat rock circling some other object called a Sun. Not every Blue or every Green citizen takes the “Blue” or “Green” position on every issue, but it would be rare to find a city merchant who believed the sky was blue, and yet advocated an individual tax and freer marriage laws.

The Underground is still polarized; an uneasy peace. A few folk genuinely think that Blues and Greens should be friends, and it is now common for a Green to patronize a Blue shop, or for a Blue to visit a Green tavern. Yet from a truce originally born of exhaustion, there is a quietly growing spirit of tolerance, even friendship.

One day, the Underground is shaken by a minor earthquake. A sightseeing party of six is caught in the tremblor while looking at the ruins of ancient dwellings in the upper caverns. They feel the brief movement of the rock under their feet, and one of the tourists trips and scrapes her knee. The party decides to turn back, fearing further earthquakes. On their way back, one person catches a whiff of something strange in the air, a scent coming from a long-unused passageway. Ignoring the well-meant cautions of fellow travellers, the person borrows a powered lantern and walks into the passageway. The stone corridor wends upward . . . and upward . . . and finally terminates in a hole carved out of the world, a place where all stone ends. Distance, endless distance, stretches away into forever; a gathering space to hold a thousand cities. Unimaginably far above, too bright to look at directly, a searing spark casts light over all visible space, the naked filament of some huge light bulb. In the air, hanging unsupported, are great incomprehensible tufts of white cotton. And the vast glowing ceiling above . . . the color . . . is . . .

Now history branches, depending on which member of the sightseeing party decided to follow the corridor to the surface.

Aditya the Blue stood under the blue forever, and slowly smiled. It was not a pleasant smile. There was hatred, and wounded pride; it recalled every argument she’d ever had with a Green, every rivalry, every contested promotion. “You were right all along,” the sky whispered down at her, “and now you can prove it.” For a moment Aditya stood there, absorbing the message, glorying in it, and then she turned back to the stone corridor to tell the world. As Aditya walked, she curled her hand into a clenched fist. “The truce,” she said, “is over.”

Barron the Green stared incomprehendingly at the chaos of colors for long seconds. Understanding, when it came, drove a pile-driver punch into the pit of his stomach. Tears started from his eyes. Barron thought of the Massacre of Cathay, where a Blue army had massacred every citizen of a Green town, including children; he thought of the ancient Blue general, Annas Rell, who had declared Greens “a pit of disease; a pestilence to be cleansed”; he thought of the glints of hatred he’d seen in Blue eyes and something inside him cracked. “How can you be on their side?” Barron screamed at the sky, and then he began to weep; because he knew, standing under the malevolent blue glare, that the universe had always been a place of evil.

Charles the Blue considered the blue ceiling, taken aback. As a professor in a mixed college, Charles had carefully emphasized that Blue and Green viewpoints were equally valid and deserving of tolerance: The sky was a metaphysical construct, and cerulean a color that could be seen in more than one way. Briefly, Charles wondered whether a Green, standing in this place, might not see a green ceiling above; or if perhaps the ceiling would be green at this time tomorrow; but he couldn’t stake the continued survival of civilization on that. This was merely a natural phenomenon of some kind, having nothing to do with moral philosophy or society . . . but one that might be readily misinterpreted, Charles feared. Charles sighed, and turned to go back into the corridor. Tomorrow he would come back alone and block off the passageway.

Daria, once Green, tried to breathe amid the ashes of her world. I will not flinch, Daria told herself, I will not look away. She had been Green all her life, and now she must be Blue. Her friends, her family, would turn from her. Speak the truth, even if your voice trembles, her father had told her; but her father was dead now, and her mother would never understand. Daria stared down the calm blue gaze of the sky, trying to accept it, and finally her breathing quietened. I was wrong, she said to herself mournfully; it’s not so complicated, after all. She would find new friends, and perhaps her family would forgive her . . . or, she wondered with a tinge of hope, rise to this same test, standing underneath this same sky? “The sky is blue,” Daria said experimentally, and nothing dire happened to her; but she couldn’t bring herself to smile. Daria the Blue exhaled sadly, and went back into the world, wondering what she would say.

Eddin, a Green, looked up at the blue sky and began to laugh cynically. The course of his world’s history came clear at last; even he couldn’t believe they’d been such fools. “Stupid,” Eddin said, “stupid, stupid, and all the time it was right here.” Hatred, murders, wars, and all along it was just a thing somewhere, that someone had written about like they’d write about any other thing. No poetry, no beauty, nothing that any sane person would ever care about, just one pointless thing that had been blown out of all proportion. Eddin leaned against the cave mouth wearily, trying to think of a way to prevent this information from blowing up the world, and wondering if they didn’t all deserve it.

Ferris gasped involuntarily, frozen by sheer wonder and delight. Ferris’s eyes darted hungrily about, fastening on each sight in turn before moving reluctantly to the next; the blue sky, the white clouds, the vast unknown outside, full of places and things (and people?) that no Undergrounder had ever seen. “Oh, so that’s what color it is,” Ferris said, and went exploring.

1. Procopius, History of the Wars, ed. Henry B. Dewing, vol. 1 (Harvard University Press, 1914).

2. Edward Gibbon, The History of the Decline and Fall of the Roman Empire, vol. 4 (J. & J. Harper, 1829).

13
Belief in Belief

Carl Sagan once told a parable of someone who comes to us and claims: “There is a dragon in my garage.” Fascinating! We reply that we wish to see this dragon—let us set out at once for the garage! “But wait,” the claimant says to us, “it is an invisible dragon.”

Now as Sagan points out, this doesn’t make the hypothesis unfalsifiable. Perhaps we go to the claimant’s garage, and although we see no dragon, we hear heavy breathing from no visible source; footprints mysteriously appear on the ground; and instruments show that something in the garage is consuming oxygen and breathing out carbon dioxide.

But now suppose that we say to the claimant, “Okay, we’ll visit the garage and see if we can hear heavy breathing,” and the claimant quickly says no, it’s an inaudible dragon. We propose to measure carbon dioxide in the air, and the claimant says the dragon does not breathe. We propose to toss a bag of flour into the air to see if it outlines an invisible dragon, and the claimant immediately says, “The dragon is permeable to flour.”

Carl Sagan used this parable to illustrate the classic moral that poor hypotheses need to do fast footwork to avoid falsification. But I tell this parable to make a different point: The claimant must have an accurate model of the situation somewhere in their mind, because they can anticipate, in advance, exactly which experimental results they’ll need to excuse.

Some philosophers have been much confused by such scenarios, asking, “Does the claimant really believe there’s a dragon present, or not?” As if the human brain only had enough disk space to represent one belief at a time! Real minds are more tangled than that. There are different types of belief; not all beliefs are direct anticipations. The claimant clearly does not anticipate seeing anything unusual upon opening the garage door. Otherwise they wouldn’t make advance excuses. It may also be that the claimant’s pool of propositional beliefs contains There is a dragon in my garage. It may seem, to a rationalist, that these two beliefs should collide and conflict even though they are of different types. Yet it is a physical fact that you can write “The sky is green!” next to a picture of a blue sky without the paper bursting into flames.

The rationalist virtue of empiricism is supposed to prevent us from making this class of mistake. We’re supposed to constantly ask our beliefs which experiences they predict, make them pay rent in anticipation. But the dragon-claimant’s problem runs deeper, and cannot be cured with such simple advice. It’s not exactly difficult to connect belief in a dragon to anticipated experience of the garage. If you believe there’s a dragon in your garage, then you can expect to open up the door and see a dragon. If you don’t see a dragon, then that means there’s no dragon in your garage. This is pretty straightforward. You can even try it with your own garage.

No, this invisibility business is a symptom of something much worse.

Depending on how your childhood went, you may remember a time period when you first began to doubt Santa Claus’s existence, but you still believed that you were supposed to believe in Santa Claus, so you tried to deny the doubts. As Daniel Dennett observes, where it is difficult to believe a thing, it is often much easier to believe that you ought to believe it. What does it mean to believe that the Ultimate Cosmic Sky is both perfectly blue and perfectly green? The statement is confusing; it’s not even clear what it would mean to believe it—what exactly would be believed, if you believed. You can much more easily believe that it is proper, that it is good and virtuous and beneficial, to believe that the Ultimate Cosmic Sky is both perfectly blue and perfectly green. Dennett calls this “belief in belief.”¹

And here things become complicated, as human minds are wont to do—I think even Dennett oversimplifies how this psychology works in practice. For one thing, if you believe in belief, you cannot admit to yourself that you only believe in belief, because it is virtuous to believe, not to believe in belief, and so if you only believe in belief, instead of believing, you are not virtuous. Nobody will admit to themselves, “I don’t believe the Ultimate Cosmic Sky is blue and green, but I believe I ought to believe it”—not unless they are unusually capable of acknowledging their own lack of virtue. People don’t believe in belief in belief, they just believe in belief.

(Those who find this confusing may find it helpful to study mathematical logic, which trains one to make very sharp distinctions between the proposition P, a proof of P, and a proof that P is provable. There are similarly sharp distinctions between P, wanting P, believing P, wanting to believe P, and believing that you believe P.)

There’s different kinds of belief in belief. You may believe in belief explicitly; you may recite in your deliberate stream of consciousness the verbal sentence “It is virtuous to believe that the Ultimate Cosmic Sky is perfectly blue and perfectly green.” (While also believing that you believe this, unless you are unusually capable of acknowledging your own lack of virtue.) But there are also less explicit forms of belief in belief. Maybe the dragon-claimant fears the public ridicule that they imagine will result if they publicly confess they were wrong (although, in fact, a rationalist would congratulate them, and others are more likely to ridicule the claimant if they go on claiming there’s a dragon in their garage). Maybe the dragon-claimant flinches away from the prospect of admitting to themselves that there is no dragon, because it conflicts with their self-image as the glorious discoverer of the dragon, who saw in their garage what all others had failed to see.

If all our thoughts were deliberate verbal sentences like philosophers manipulate, the human mind would be a great deal easier for humans to understand. Fleeting mental images, unspoken flinches, desires acted upon without acknowledgement—these account for as much of ourselves as words.

While I disagree with Dennett on some details and complications, I still think that Dennett’s notion of belief in belief is the key insight necessary to understand the dragon-claimant. But we need a wider concept of belief, not limited to verbal sentences. “Belief” should include unspoken anticipation-controllers. “Belief in belief” should include unspoken cognitive-behavior-guiders. It is not psychologically realistic to say, “The dragon-claimant does not believe there is a dragon in their garage; they believe it is beneficial to believe there is a dragon in their garage.” But it is realistic to say the dragon-claimant anticipates as if there is no dragon in their garage, and makes excuses as if they believed in the belief.

You can possess an ordinary mental picture of your garage, with no dragons in it, which correctly predicts your experiences on opening the door, and never once think the verbal phrase There is no dragon in my garage. I even bet it’s happened to you—that when you open your garage door or bedroom door or whatever, and expect to see no dragons, no such verbal phrase runs through your mind.

And to flinch away from giving up your belief in the dragon—or flinch away from giving up your self-image as a person who believes in the dragon—it is not necessary to explicitly think I want to believe there’s a dragon in my garage. It is only necessary to flinch away from the prospect of admitting you don’t believe.

To correctly anticipate, in advance, which experimental results shall need to be excused, the dragon-claimant must (a) possess an accurate anticipation-controlling model somewhere in their mind, and (b) act cognitively to protect either (b1) their free-floating propositional belief in the dragon or (b2) their self-image of believing in the dragon.

If someone believes in their belief in the dragon, and also believes in the dragon, the problem is much less severe. They will be willing to stick their neck out on experimental predictions, and perhaps even agree to give up the belief if the experimental prediction is wrong—although belief in belief can still interfere with this, if the belief itself is not absolutely confident. When someone makes up excuses in advance, it would seem to require that belief and belief in belief have become unsynchronized.

1. Daniel C. Dennett, Breaking the Spell: Religion as a Natural Phenomenon (Penguin, 2006).

14
Bayesian Judo

You can have some fun with people whose anticipations get out of sync with what they believe they believe.

I was once at a dinner party, trying to explain to a man what I did for a living, when he said: “I don’t believe Artificial Intelligence is possible because only God can make a soul.”

At this point I must have been divinely inspired, because I instantly responded: “You mean if I can make an Artificial Intelligence, it proves your religion is false?”

He said, “What?”

I said, “Well, if your religion predicts that I can’t possibly make an Artificial Intelligence, then, if I make an Artificial Intelligence, it means your religion is false. Either your religion allows that it might be possible for me to build an AI; or, if I build an AI, that disproves your religion.”

There was a pause, as the one realized he had just made his hypothesis vulnerable to falsification, and then he said, “Well, I didn’t mean that you couldn’t make an intelligence, just that it couldn’t be emotional in the same way we are.”

I said, “So if I make an Artificial Intelligence that, without being deliberately preprogrammed with any sort of script, starts talking about an emotional life that sounds like ours, that means your religion is wrong.”

He said, “Well, um, I guess we may have to agree to disagree on this.”

I said: “No, we can’t, actually. There’s a theorem of rationality called Aumann’s Agreement Theorem which shows that no two rationalists can agree to disagree. If two people disagree with each other, at least one of them must be doing something wrong.”

We went back and forth on this briefly. Finally, he said, “Well, I guess I was really trying to say that I don’t think you can make something eternal.”

I said, “Well, I don’t think so either! I’m glad we were able to reach agreement on this, as Aumann’s Agreement Theorem requires.” I stretched out my hand, and he shook it, and then he wandered away.

A woman who had stood nearby, listening to the conversation, said to me gravely, “That was beautiful.”

“Thank you very much,” I said.

15
Pretending to be Wise

The hottest place in Hell is reserved for those who in time of crisis remain neutral.

—Dante Alighieri, famous hell expert
John F. Kennedy, misquoter

It’s common to put on a show of neutrality or suspended judgment in order to signal that one is mature, wise, impartial, or just has a superior vantage point.

An example would be the case of my parents, who respond to theological questions like “Why does ancient Egypt, which had good records on many other matters, lack any records of Jews having ever been there?” with “Oh, when I was your age, I also used to ask that sort of question, but now I’ve grown out of it.”

Another example would be the principal who, faced with two children who were caught fighting on the playground, sternly says: “It doesn’t matter who started the fight, it only matters who ends it.” Of course it matters who started the fight. The principal may not have access to good information about this critical fact, but if so, the principal should say so, not dismiss the importance of who threw the first punch. Let a parent try punching the principal, and we’ll see how far “It doesn’t matter who started it” gets in front of a judge. But to adults it is just inconvenient that children fight, and it matters not at all to their convenience which child started it. It is only convenient that the fight end as rapidly as possible.

A similar dynamic, I believe, governs the occasions in international diplomacy where Great Powers sternly tell smaller groups to stop that fighting right now. It doesn’t matter to the Great Power who started it—who provoked, or who responded disproportionately to provocation—because the Great Power’s ongoing inconvenience is only a function of the ongoing conflict. Oh, can’t Israel and Hamas just get along?

This I call “pretending to be Wise.” Of course there are many ways to try and signal wisdom. But trying to signal wisdom by refusing to make guesses—refusing to sum up evidence—refusing to pass judgment—refusing to take sides—staying above the fray and looking down with a lofty and condescending gaze—which is to say, signaling wisdom by saying and doing nothing—well, that I find particularly pretentious.

Paolo Freire said, “Washing one’s hands of the conflict between the powerful and the powerless means to side with the powerful, not to be neutral.”¹ A playground is a great place to be a bully, and a terrible place to be a victim, if the teachers don’t care who started it. And likewise in international politics: A world where the Great Powers refuse to take sides and only demand immediate truces is a great world for aggressors and a terrible place for the aggressed. But, of course, it is a very convenient world in which to be a Great Power or a school principal.

So part of this behavior can be chalked up to sheer selfishness on the part of the Wise.

But part of it also has to do with signaling a superior vantage point. After all—what would the other adults think of a principal who actually seemed to be taking sides in a fight between mere children? Why, it would lower the principal’s status to a mere participant in the fray!

Similarly with the revered elder—who might be a CEO, a prestigious academic, or a founder of a mailing list—whose reputation for fairness depends on their refusal to pass judgment themselves, when others are choosing sides. Sides appeal to them for support, but almost always in vain; for the Wise are revered judges on the condition that they almost never actually judge—then they would just be another disputant in the fray, no better than any other mere arguer.

(Oddly, judges in the actual legal system can repeatedly hand down real verdicts without automatically losing their reputation for impartiality. Maybe because of the understood norm that they have to judge, that it’s their job. Or maybe because judges don’t have to repeatedly rule on issues that have split a tribe on which they depend for their reverence.)

There are cases where it is rational to suspend judgment, where people leap to judgment only because of their biases. As Michael Rooney said:

The error here is similar to one I see all the time in beginning philosophy students: when confronted with reasons to be skeptics, they instead become relativists. That is, when the rational conclusion is to suspend judgment about an issue, all too many people instead conclude that any judgment is as plausible as any other.

But then how can we avoid the (related but distinct) pseudo-rationalist behavior of signaling your unbiased impartiality by falsely claiming that the current balance of evidence is neutral? “Oh, well, of course you have a lot of passionate Darwinists out there, but I think the evidence we have doesn’t really enable us to make a definite endorsement of natural selection over intelligent design.”

On this point I’d advise remembering that neutrality is a definite judgment. It is not staying above anything. It is putting forth the definite and particular position that the balance of evidence in a particular case licenses only one summation, which happens to be neutral. This, too, can be wrong; propounding neutrality is just as attackable as propounding any particular side.

Likewise with policy questions. If someone says that both pro-life and pro-choice sides have good points and that they really should try to compromise and respect each other more, they are not taking a position above the two standard sides in the abortion debate. They are putting forth a definite judgment, every bit as particular as saying “pro-life!” or “pro-choice!”

If your goal is to improve your general ability to form more accurate beliefs, it might be useful to avoid focusing on emotionally charged issues like abortion or the Israeli-Palestinian conflict. But it’s not that a rationalist is too mature to talk about politics. It’s not that a rationalist is above this foolish fray in which only mere political partisans and youthful enthusiasts would stoop to participate.

As Robin Hanson describes it, the ability to have potentially divisive conversations is a limited resource. If you can think of ways to pull the rope sideways, you are justified in expending your limited resources on relatively less common issues where marginal discussion offers relatively higher marginal payoffs.

But then the responsibilities that you deprioritize are a matter of your limited resources. Not a matter of floating high above, serene and Wise.

My reply to Paul Graham’s comment on Hacker News seems like a summary worth repeating:

There’s a difference between:

Passing neutral judgment;

Declining to invest marginal resources;

Pretending that either of the above is a mark of deep wisdom, maturity, and a superior vantage point; with the corresponding implication that the original sides occupy lower vantage points that are not importantly different from up there.

1. Paulo Freire, The Politics of Education: Culture, Power, and Liberation (Greenwood Publishing Group, 1985), 122.

16
Religion’s Claim to be NonDisprovable

The earliest account I know of a scientific experiment is, ironically, the story of Elijah and the priests of Baal.

The people of Israel are wavering between Jehovah and Baal, so Elijah announces that he will conduct an experiment to settle it—quite a novel concept in those days! The priests of Baal will place their bull on an altar, and Elijah will place Jehovah’s bull on an altar, but neither will be allowed to start the fire; whichever God is real will call down fire on His sacrifice. The priests of Baal serve as control group for Elijah—the same wooden fuel, the same bull, and the same priests making invocations, but to a false god. Then Elijah pours water on his altar—ruining the experimental symmetry, but this was back in the early days—to signify deliberate acceptance of the burden of proof, like needing a 0.05 significance level. The fire comes down on Elijah’s altar, which is the experimental observation. The watching people of Israel shout “The Lord is God!”—peer review.

And then the people haul the 450 priests of Baal down to the river Kishon and slit their throats. This is stern, but necessary. You must firmly discard the falsified hypothesis, and do so swiftly, before it can generate excuses to protect itself. If the priests of Baal are allowed to survive, they will start babbling about how religion is a separate magisterium which can be neither proven nor disproven.

Back in the old days, people actually believed their religions instead of just believing in them. The biblical archaeologists who went in search of Noah’s Ark did not think they were wasting their time; they anticipated they might become famous. Only after failing to find confirming evidence—and finding disconfirming evidence in its place—did religionists execute what William Bartley called the retreat to commitment, “I believe because I believe.”

Back in the old days, there was no concept of religion’s being a separate magisterium. The Old Testament is a stream-of-consciousness culture dump: history, law, moral parables, and yes, models of how the universe works. In not one single passage of the Old Testament will you find anyone talking about a transcendent wonder at the complexity of the universe. But you will find plenty of scientific claims, like the universe being created in six days (which is a metaphor for the Big Bang), or rabbits chewing their cud. (Which is a metaphor for . . .)

Back in the old days, saying the local religion “could not be proven” would have gotten you burned at the stake. One of the core beliefs of Orthodox Judaism is that God appeared at Mount Sinai and said in a thundering voice, “Yeah, it’s all true.” From a Bayesian perspective that’s some darned unambiguous evidence of a superhumanly powerful entity. (Although it doesn’t prove that the entity is God per se, or that the entity is benevolent—it could be alien teenagers.) The vast majority of religions in human history—excepting only those invented extremely recently—tell stories of events that would constitute completely unmistakable evidence if they’d actually happened. The orthogonality of religion and factual questions is a recent and strictly Western concept. The people who wrote the original scriptures didn’t even know the difference.

The Roman Empire inherited philosophy from the ancient Greeks; imposed law and order within its provinces; kept bureaucratic records; and enforced religious tolerance. The New Testament, created during the time of the Roman Empire, bears some traces of modernity as a result. You couldn’t invent a story about God completely obliterating the city of Rome (a la Sodom and Gomorrah), because the Roman historians would call you on it, and you couldn’t just stone them.

In contrast, the people who invented the Old Testament stories could make up pretty much anything they liked. Early Egyptologists were genuinely shocked to find no trace whatsoever of Hebrew tribes having ever been in Egypt—they weren’t expecting to find a record of the Ten Plagues, but they expected to find something. As it turned out, they did find something. They found out that, during the supposed time of the Exodus, Egypt ruled much of Canaan. That’s one huge historical error, but if there are no libraries, nobody can call you on it.

The Roman Empire did have libraries. Thus, the New Testament doesn’t claim big, showy, large-scale geopolitical miracles as the Old Testament routinely did. Instead the New Testament claims smaller miracles which nonetheless fit into the same framework of evidence. A boy falls down and froths at the mouth; the cause is an unclean spirit; an unclean spirit could reasonably be expected to flee from a true prophet, but not to flee from a charlatan; Jesus casts out the unclean spirit; therefore Jesus is a true prophet and not a charlatan. This is perfectly ordinary Bayesian reasoning, if you grant the basic premise that epilepsy is caused by demons (and that the end of an epileptic fit proves the demon fled).

Not only did religion used to make claims about factual and scientific matters, religion used to make claims about everything. Religion laid down a code of law—before legislative bodies; religion laid down history—before historians and archaeologists; religion laid down the sexual morals—before Women’s Lib; religion described the forms of government—before constitutions; and religion answered scientific questions from biological taxonomy to the formation of stars. The Old Testament doesn’t talk about a sense of wonder at the complexity of the universe—it was busy laying down the death penalty for women who wore men’s clothing, which was solid and satisfying religious content of that era. The modern concept of religion as purely ethical derives from every other area’s having been taken over by better institutions. Ethics is what’s left.

Or rather, people think ethics is what’s left. Take a culture dump from 2,500 years ago. Over time, humanity will progress immensely, and pieces of the ancient culture dump will become ever more glaringly obsolete. Ethics has not been immune to human progress—for example, we now frown upon such Bible-approved practices as keeping slaves. Why do people think that ethics is still fair game?

Intrinsically, there’s nothing small about the ethical problem with slaughtering thousands of innocent first-born male children to convince an unelected Pharaoh to release slaves who logically could have been teleported out of the country. It should be more glaring than the comparatively trivial scientific error of saying that grasshoppers have four legs. And yet, if you say the Earth is flat, people will look at you like you’re crazy. But if you say the Bible is your source of ethics, women will not slap you. Most people’s concept of rationality is determined by what they think they can get away with; they think they can get away with endorsing Bible ethics; and so it only requires a manageable effort of self-deception for them to overlook the Bible’s moral problems. Everyone has agreed not to notice the elephant in the living room, and this state of affairs can sustain itself for a time.

Maybe someday, humanity will advance further, and anyone who endorses the Bible as a source of ethics will be treated the same way as Trent Lott endorsing Strom Thurmond’s presidential campaign. And then it will be said that religion’s “true core” has always been genealogy or something.

The idea that religion is a separate magisterium that cannot be proven or disproven is a Big Lie—a lie which is repeated over and over again, so that people will say it without thinking; yet which is, on critical examination, simply false. It is a wild distortion of how religion happened historically, of how all scriptures present their beliefs, of what children are told to persuade them, and of what the majority of religious people on Earth still believe. You have to admire its sheer brazenness, on a par with Oceania has always been at war with Eastasia. The prosecutor whips out the bloody axe, and the defendant, momentarily shocked, thinks quickly and says: “But you can’t disprove my innocence by mere evidence—it’s a separate magisterium!”

And if that doesn’t work, grab a piece of paper and scribble yourself a Get Out of Jail Free card.

17
Professing and Cheering

I once attended a panel on the topic, “Are science and religion compatible?” One of the women on the panel, a pagan, held forth interminably upon how she believed that the Earth had been created when a giant primordial cow was born into the primordial abyss, who licked a primordial god into existence, whose descendants killed a primordial giant and used its corpse to create the Earth, etc. The tale was long, and detailed, and more absurd than the Earth being supported on the back of a giant turtle. And the speaker clearly knew enough science to know this.

I still find myself struggling for words to describe what I saw as this woman spoke. She spoke with . . . pride? Self-satisfaction? A deliberate flaunting of herself?

The woman went on describing her creation myth for what seemed like forever, but was probably only five minutes. That strange pride/satisfaction/flaunting clearly had something to do with her knowing that her beliefs were scientifically outrageous. And it wasn’t that she hated science; as a panelist she professed that religion and science were compatible. She even talked about how it was quite understandable that the Vikings talked about a primordial abyss, given the land in which they lived—explained away her own religion!—and yet nonetheless insisted this was what she “believed,” said with peculiar satisfaction.

I’m not sure that Daniel Dennett’s concept of “belief in belief” stretches to cover this event. It was weirder than that. She didn’t recite her creation myth with the fanatical faith of someone who needs to reassure herself. She didn’t act like she expected us, the audience, to be convinced—or like she needed our belief to validate her.

Dennett, in addition to suggesting belief in belief, has also suggested that much of what is called “religious belief” should really be studied as “religious profession.” Suppose an alien anthropologist studied a group of postmodernist English students who all seemingly believed that Wulky Wilkensen was a post-utopian author. The appropriate question may not be “Why do the students all believe this strange belief?” but “Why do they all write this strange sentence on quizzes?” Even if a sentence is essentially meaningless, you can still know when you are supposed to chant the response aloud.

I think Dennett may be slightly too cynical in suggesting that religious profession is just saying the belief aloud—most people are honest enough that, if they say a religious statement aloud, they will also feel obligated to say the verbal sentence into their own stream of consciousness.

But even the concept of “religious profession” doesn’t seem to cover the pagan woman’s claim to believe in the primordial cow. If you had to profess a religious belief to satisfy a priest, or satisfy a co-religionist—heck, to satisfy your own self-image as a religious person—you would have to pretend to believe much more convincingly than this woman was doing. As she recited her tale of the primordial cow, with that same strange flaunting pride, she wasn’t even trying to be persuasive—wasn’t even trying to convince us that she took her own religion seriously. I think that’s the part that so took me aback. I know people who believe they believe ridiculous things, but when they profess them, they’ll spend much more effort to convince themselves that they take their beliefs seriously.

It finally occurred to me that this woman wasn’t trying to convince us or even convince herself. Her recitation of the creation story wasn’t about the creation of the world at all. Rather, by launching into a five-minute diatribe about the primordial cow, she was cheering for paganism, like holding up a banner at a football game. A banner saying GO BLUES isn’t a statement of fact, or an attempt to persuade; it doesn’t have to be convincing—it’s a cheer.

That strange flaunting pride . . . it was like she was marching naked in a gay pride parade. (Not that there’s anything wrong with marching naked in a gay pride parade. Lesbianism is not something that truth can destroy.) It wasn’t just a cheer, like marching, but an outrageous cheer, like marching naked—believing that she couldn’t be arrested or criticized, because she was doing it for her pride parade.

That’s why it mattered to her that what she was saying was beyond ridiculous. If she’d tried to make it sound more plausible, it would have been like putting on clothes.

18
Belief as Attire

I have so far distinguished between belief as anticipation-controller, belief in belief, professing, and cheering. Of these, we might call anticipation-controlling beliefs “proper beliefs” and the other forms “improper beliefs.” A proper belief can be wrong or irrational, as when someone genuinely anticipates that prayer will cure their sick baby. But the other forms are arguably “not belief at all.”

Yet another form of improper belief is belief as group identification—as a way of belonging. Robin Hanson uses the excellent metaphor of wearing unusual clothing, a group uniform like a priest’s vestments or a Jewish skullcap, and so I will call this “belief as attire.”

In terms of humanly realistic psychology, the Muslims who flew planes into the World Trade Center undoubtedly saw themselves as heroes defending truth, justice, and the Islamic Way from hideous alien monsters a la the movie Independence Day. Only a very inexperienced nerd, the sort of nerd who has no idea how non-nerds see the world, would say this out loud in an Alabama bar. It is not an American thing to say. The American thing to say is that the terrorists “hate our freedom” and that flying a plane into a building is a “cowardly act.” You cannot say the phrases “heroic self-sacrifice” and “suicide bomber” in the same sentence, even for the sake of accurately describing how the Enemy sees the world. The very concept of the courage and altruism of a suicide bomber is Enemy attire—you can tell, because the Enemy talks about it. The cowardice and sociopathy of a suicide bomber is American attire. There are no quote marks you can use to talk about how the Enemy sees the world; it would be like dressing up as a Nazi for Halloween.

Belief-as-attire may help explain how people can be passionate about improper beliefs. Mere belief in belief, or religious professing, would have some trouble creating genuine, deep, powerful emotional effects. Or so I suspect; I confess I’m not an expert here. But my impression is this: People who’ve stopped anticipating-as-if their religion is true, will go to great lengths to convince themselves they are passionate, and this desperation can be mistaken for passion. But it’s not the same fire they had as a child.

On the other hand, it is very easy for a human being to genuinely, passionately, gut-level belong to a group, to cheer for their favorite sports team. (This is the foundation on which rests the swindle of “Republicans vs. Democrats” and analogous false dilemmas in other countries, but that’s a topic for another time.) Identifying with a tribe is a very strong emotional force. People will die for it. And once you get people to identify with a tribe, the beliefs which are attire of that tribe will be spoken with the full passion of belonging to that tribe.

19
Applause Lights

At the Singularity Summit 2007, one of the speakers called for democratic, multinational development of Artificial Intelligence. So I stepped up to the microphone and asked:

Suppose that a group of democratic republics form a consortium to develop AI, and there’s a lot of politicking during the process—some interest groups have unusually large influence, others get shafted—in other words, the result looks just like the products of modern democracies. Alternatively, suppose a group of rebel nerds develops an AI in their basement, and instructs the AI to poll everyone in the world—dropping cellphones to anyone who doesn’t have them—and do whatever the majority says. Which of these do you think is more “democratic,” and would you feel safe with either?

I wanted to find out whether he believed in the pragmatic adequacy of the democratic political process, or if he believed in the moral rightness of voting. But the speaker replied:

The first scenario sounds like an editorial in Reason magazine, and the second sounds like a Hollywood movie plot.

Confused, I asked:

Then what kind of democratic process did you have in mind?

The speaker replied:

Something like the Human Genome Project—that was an internationally sponsored research project.

I asked:

How would different interest groups resolve their conflicts in a structure like the Human Genome Project?

And the speaker said:

I don’t know.

This exchange puts me in mind of a quote from some dictator or other, who was asked if he had any intentions to move his pet state toward democracy:

We believe we are already within a democratic system. Some factors are still missing, like the expression of the people’s will.

The substance of a democracy is the specific mechanism that resolves policy conflicts. If all groups had the same preferred policies, there would be no need for democracy—we would automatically cooperate. The resolution process can be a direct majority vote, or an elected legislature, or even a voter-sensitive behavior of an Artificial Intelligence, but it has to be something. What does it mean to call for a “democratic” solution if you don’t have a conflict-resolution mechanism in mind?

I think it means that you have said the word “democracy,” so the audience is supposed to cheer. It’s not so much a propositional statement, as the equivalent of the “Applause” light that tells a studio audience when to clap.

This case is remarkable only in that I mistook the applause light for a policy suggestion, with subsequent embarrassment for all. Most applause lights are much more blatant, and can be detected by a simple reversal test. For example, suppose someone says:

We need to balance the risks and opportunities of AI.

If you reverse this statement, you get:

We shouldn’t balance the risks and opportunities of AI.

Since the reversal sounds abnormal, the unreversed statement is probably normal, implying it does not convey new information. There are plenty of legitimate reasons for uttering a sentence that would be uninformative in isolation. “We need to balance the risks and opportunities of AI” can introduce a discussion topic; it can emphasize the importance of a specific proposal for balancing; it can criticize an unbalanced proposal. Linking to a normal assertion can convey new information to a bounded rationalist—the link itself may not be obvious. But if no specifics follow, the sentence is probably an applause light.

I am tempted to give a talk sometime that consists of nothing but applause lights, and see how long it takes for the audience to start laughing:

I am here to propose to you today that we need to balance the risks and opportunities of advanced Artificial Intelligence. We should avoid the risks and, insofar as it is possible, realize the opportunities. We should not needlessly confront entirely unnecessary dangers. To achieve these goals, we must plan wisely and rationally. We should not act in fear and panic, or give in to technophobia; but neither should we act in blind enthusiasm. We should respect the interests of all parties with a stake in the Singularity. We must try to ensure that the benefits of advanced technologies accrue to as many individuals as possible, rather than being restricted to a few. We must try to avoid, as much as possible, violent conflicts using these technologies; and we must prevent massive destructive capability from falling into the hands of individuals. We should think through these issues before, not after, it is too late to do anything about them . . .

Part C
Noticing Confusion

20
Focus Your Uncertainty

Will bond yields go up, or down, or remain the same? If you’re a TV pundit and your job is to explain the outcome after the fact, then there’s no reason to worry. No matter which of the three possibilities comes true, you’ll be able to explain why the outcome perfectly fits your pet market theory. There’s no reason to think of these three possibilities as somehow opposed to one another, as exclusive, because you’ll get full marks for punditry no matter which outcome occurs.

But wait! Suppose you’re a novice TV pundit, and you aren’t experienced enough to make up plausible explanations on the spot. You need to prepare remarks in advance for tomorrow’s broadcast, and you have limited time to prepare. In this case, it would be helpful to know which outcome will actually occur—whether bond yields will go up, down, or remain the same—because then you would only need to prepare one set of excuses.

Alas, no one can possibly foresee the future. What are you to do? You certainly can’t use “probabilities.” We all know from school that “probabilities” are little numbers that appear next to a word problem, and there aren’t any little numbers here. Worse, you feel uncertain. You don’t remember feeling uncertain while you were manipulating the little numbers in word problems. College classes teaching math are nice clean places, therefore math itself can’t apply to life situations that aren’t nice and clean. You wouldn’t want to inappropriately transfer thinking skills from one context to another. Clearly, this is not a matter for “probabilities.”

Nonetheless, you only have 100 minutes to prepare your excuses. You can’t spend the entire 100 minutes on “up,” and also spend all 100 minutes on “down,” and also spend all 100 minutes on “same.” You’ve got to prioritize somehow.

If you needed to justify your time expenditure to a review committee, you would have to spend equal time on each possibility. Since there are no little numbers written down, you’d have no documentation to justify spending different amounts of time. You can hear the reviewers now: And why, Mr. Finkledinger, did you spend exactly 42 minutes on excuse #3? Why not 41 minutes, or 43? Admit it—you’re not being objective! You’re playing subjective favorites!

But, you realize with a small flash of relief, there’s no review committee to scold you. This is good, because there’s a major Federal Reserve announcement tomorrow, and it seems unlikely that bond prices will remain the same. You don’t want to spend 33 precious minutes on an excuse you don’t anticipate needing.

Your mind keeps drifting to the explanations you use on television, of why each event plausibly fits your market theory. But it rapidly becomes clear that plausibility can’t help you here—all three events are plausible. Fittability to your pet market theory doesn’t tell you how to divide your time. There’s an uncrossable gap between your 100 minutes of time, which are conserved; versus your ability to explain how an outcome fits your theory, which is unlimited.

And yet . . . even in your uncertain state of mind, it seems that you anticipate the three events differently; that you expect to need some excuses more than others. And—this is the fascinating part—when you think of something that makes it seem more likely that bond prices will go up, then you feel less likely to need an excuse for bond prices going down or remaining the same.

It even seems like there’s a relation between how much you anticipate each of the three outcomes, and how much time you want to spend preparing each excuse. Of course the relation can’t actually be quantified. You have 100 minutes to prepare your speech, but there isn’t 100 of anything to divide up in this anticipation business. (Although you do work out that, if some particular outcome occurs, then your utility function is logarithmic in time spent preparing the excuse.)

Still . . . your mind keeps coming back to the idea that anticipation is limited, unlike excusability, but like time to prepare excuses. Maybe anticipation should be treated as a conserved resource, like money. Your first impulse is to try to get more anticipation, but you soon realize that, even if you get more anticiptaion, you won’t have any more time to prepare your excuses. No, your only course is to allocate your limited supply of anticipation as best you can.

You’re pretty sure you weren’t taught anything like that in your statistics courses. They didn’t tell you what to do when you felt so terribly uncertain. They didn’t tell you what to do when there were no little numbers handed to you. Why, even if you tried to use numbers, you might end up using any sort of numbers at all—there’s no hint what kind of math to use, if you should be using math! Maybe you’d end up using pairs of numbers, right and left numbers, which you’d call DS for Dexter-Sinister . . . or who knows what else? (Though you do have only 100 minutes to spend preparing excuses.)

If only there were an art of focusing your uncertainty—of squeezing as much anticipation as possible into whichever outcome will actually happen!

But what could we call an art like that? And what would the rules be like?

21
What Is Evidence?

The sentence “snow is white” is true if and only if snow is white.

—Alfred Tarski

To say of what is, that it is, or of what is not, that it is not, is true.

—Aristotle, Metaphysics IV

If these two quotes don’t seem like a sufficient definition of “truth,” skip ahead to The Simple Truth. Here I’m going to talk about “evidence.” (I also intend to discuss beliefs-of-fact, not emotions or morality, as distinguished in Feeling Rational.)

Walking along the street, your shoelaces come untied. Shortly thereafter, for some odd reason, you start believing your shoelaces are untied. Light leaves the Sun and strikes your shoelaces and bounces off; some photons enter the pupils of your eyes and strike your retina; the energy of the photons triggers neural impulses; the neural impulses are transmitted to the visual-processing areas of the brain; and there the optical information is processed and reconstructed into a 3D model that is recognized as an untied shoelace. There is a sequence of events, a chain of cause and effect, within the world and your brain, by which you end up believing what you believe. The final outcome of the process is a state of mind which mirrors the state of your actual shoelaces.

What is evidence? It is an event entangled, by links of cause and effect, with whatever you want to know about. If the target of your inquiry is your shoelaces, for example, then the light entering your pupils is evidence entangled with your shoelaces. This should not be confused with the technical sense of “entanglement” used in physics—here I’m just talking about “entanglement” in the sense of two things that end up in correlated states because of the links of cause and effect between them.

Not every influence creates the kind of “entanglement” required for evidence. It’s no help to have a machine that beeps when you enter winning lottery numbers, if the machine also beeps when you enter losing lottery numbers. The light reflected from your shoes would not be useful evidence about your shoelaces, if the photons ended up in the same physical state whether your shoelaces were tied or untied.

To say it abstractly: For an event to be evidence about a target of inquiry, it has to happen differently in a way that’s entangled with the different possible states of the target. (To say it technically: There has to be Shannon mutual information between the evidential event and the target of inquiry, relative to your current state of uncertainty about both of them.)

Entanglement can be contagious when processed correctly, which is why you need eyes and a brain. If photons reflect off your shoelaces and hit a rock, the rock won’t change much. The rock won’t reflect the shoelaces in any helpful way; it won’t be detectably different depending on whether your shoelaces were tied or untied. This is why rocks are not useful witnesses in court. A photographic film will contract shoelace-entanglement from the incoming photons, so that the photo can itself act as evidence. If your eyes and brain work correctly, you will become tangled up with your own shoelaces.

This is why rationalists put such a heavy premium on the paradoxical-seeming claim that a belief is only really worthwhile if you could, in principle, be persuaded to believe otherwise. If your retina ended up in the same state regardless of what light entered it, you would be blind. Some belief systems, in a rather obvious trick to reinforce themselves, say that certain beliefs are only really worthwhile if you believe them unconditionally—no matter what you see, no matter what you think. Your brain is supposed to end up in the same state regardless. Hence the phrase, “blind faith.” If what you believe doesn’t depend on what you see, you’ve been blinded as effectively as by poking out your eyeballs.

If your eyes and brain work correctly, your beliefs will end up entangled with the facts. Rational thought produces beliefs which are themselves evidence.

If your tongue speaks truly, your rational beliefs, which are themselves evidence, can act as evidence for someone else. Entanglement can be transmitted through chains of cause and effect—and if you speak, and another hears, that too is cause and effect. When you say “My shoelaces are untied” over a cellphone, you’re sharing your entanglement with your shoelaces with a friend.

Therefore rational beliefs are contagious, among honest folk who believe each other to be honest. And it’s why a claim that your beliefs are not contagious—that you believe for private reasons which are not transmissible—is so suspicious. If your beliefs are entangled with reality, they should be contagious among honest folk.

If your model of reality suggests that the outputs of your thought processes should not be contagious to others, then your model says that your beliefs are not themselves evidence, meaning they are not entangled with reality. You should apply a reflective correction, and stop believing.

Indeed, if you feel, on a gut level, what this all means, you will automatically stop believing. Because “my belief is not entangled with reality” means “my belief is not accurate.” As soon as you stop believing “‘snow is white’ is true,” you should (automatically!) stop believing “snow is white,” or something is very wrong.

So go ahead and explain why the kind of thought processes you use systematically produce beliefs that mirror reality. Explain why you think you’re rational. Why you think that, using thought processes like the ones you use, minds will end up believing “snow is white” if and only if snow is white. If you don’t believe that the outputs of your thought processes are entangled with reality, why do you believe the outputs of your thought processes? It’s the same thing, or it should be.

22
Scientific Evidence, Legal Evidence, Rational Evidence

Suppose that your good friend, the police commissioner, tells you in strictest confidence that the crime kingpin of your city is Wulky Wilkinsen. As a rationalist, are you licensed to believe this statement? Put it this way: if you go ahead and insult Wulky, I’d call you foolhardy. Since it is prudent to act as if Wulky has a substantially higher-than-default probability of being a crime boss, the police commissioner’s statement must have been strong Bayesian evidence.

Our legal system will not imprison Wulky on the basis of the police commissioner’s statement. It is not admissible as legal evidence. Maybe if you locked up every person accused of being a crime boss by a police commissioner, you’d initially catch a lot of crime bosses, plus some people that a police commissioner didn’t like. Power tends to corrupt: over time, you’d catch fewer and fewer real crime bosses (who would go to greater lengths to ensure anonymity) and more and more innocent victims (unrestrained power attracts corruption like honey attracts flies).

This does not mean that the police commissioner’s statement is not rational evidence. It still has a lopsided likelihood ratio, and you’d still be a fool to insult Wulky. But on a social level, in pursuit of a social goal, we deliberately define “legal evidence” to include only particular kinds of evidence, such as the police commissioner’s own observations on the night of April 4th. All legal evidence should ideally be rational evidence, but not the other way around. We impose special, strong, additional standards before we anoint rational evidence as “legal evidence.”

As I write this sentence at 8:33 p.m., Pacific time, on August 18th, 2007, I am wearing white socks. As a rationalist, are you licensed to believe the previous statement? Yes. Could I testify to it in court? Yes. Is it a scientific statement? No, because there is no experiment you can perform yourself to verify it. Science is made up of generalizations which apply to many particular instances, so that you can run new real-world experiments which test the generalization, and thereby verify for yourself that the generalization is true, without having to trust anyone’s authority. Science is the publicly reproducible knowledge of humankind.

Like a court system, science as a social process is made up of fallible humans. We want a protected pool of beliefs that are especially reliable. And we want social rules that encourage the generation of such knowledge. So we impose special, strong, additional standards before we canonize rational knowledge as “scientific knowledge,” adding it to the protected belief pool. Is a rationalist licensed to believe in the historical existence of Alexander the Great? Yes. We have a rough picture of ancient Greece, untrustworthy but better than maximum entropy. But we are dependent on authorities such as Plutarch; we cannot discard Plutarch and verify everything for ourselves. Historical knowledge is not scientific knowledge.

Is a rationalist licensed to believe that the Sun will rise on September 18th, 2007? Yes—not with absolute certainty, but that’s the way to bet. (Pedants: interpret this as the Earth’s rotation and orbit remaining roughly constant relative to the Sun.) Is this statement, as I write this essay on August 18th, 2007, a scientific belief?

It may seem perverse to deny the adjective “scientific” to statements like “The Sun will rise on September 18th, 2007.” If Science could not make predictions about future events—events which have not yet happened—then it would be useless; it could make no prediction in advance of experiment. The prediction that the Sun will rise is, definitely, an extrapolation from scientific generalizations. It is based upon models of the Solar System that you could test for yourself by experiment.

But imagine that you’re constructing an experiment to verify prediction #27, in a new context, of an accepted theory Q. You may not have any concrete reason to suspect the belief is wrong; you just want to test it in a new context. It seems dangerous to say, before running the experiment, that there is a “scientific belief” about the result. There is a “conventional prediction” or “theory Q’s prediction.” But if you already know the “scientific belief” about the result, why bother to run the experiment?

You begin to see, I hope, why I identify Science with generalizations, rather than the history of any one experiment. A historical event happens once; generalizations apply over many events. History is not reproducible; scientific generalizations are.

Is my definition of “scientific knowledge” true? That is not a well-formed question. The special standards we impose upon science are pragmatic choices. Nowhere upon the stars or the mountains is it written that p < 0.05 shall be the standard for scientific publication. Many now argue that 0.05 is too weak, and that it would be useful to lower it to 0.01 or 0.001.

Perhaps future generations, acting on the theory that science is the public, reproducible knowledge of humankind, will only label as “scientific” papers published in an open-access journal. If you charge for access to the knowledge, is it part of the knowledge of humankind? Can we trust a result if people must pay to criticize it? Is it really science?

The question “Is it really science?” is ill-formed. Is a $20,000/year closed-access journal really Bayesian evidence? As with the police commissioner’s private assurance that Wulky is the kingpin, I think we must answer “Yes.” But should the closed-access journal be further canonized as “science”? Should we allow it into the special, protected belief pool? For myself, I think science would be better served by the dictum that only open knowledge counts as the public, reproducible knowledge pool of humankind.

23
How Much Evidence Does It Take?

Previously, I defined evidence as “an event entangled, by links of cause and effect, with whatever you want to know about,” and entangled as “happening differently for different possible states of the target.” So how much entanglement—how much evidence—is required to support a belief?

Let’s start with a question simple enough to be mathematical: How hard would you have to entangle yourself with the lottery in order to win? Suppose there are seventy balls, drawn without replacement, and six numbers to match for the win. Then there are 131,115,985 possible winning combinations, hence a randomly selected ticket would have a 1/131,115,985 probability of winning (0.0000007%). To win the lottery, you would need evidence selective enough to visibly favor one combination over 131,115,984 alternatives.

Suppose there are some tests you can perform which discriminate, probabilistically, between winning and losing lottery numbers. For example, you can punch a combination into a little black box that always beeps if the combination is the winner, and has only a 1/4 (25%) chance of beeping if the combination is wrong. In Bayesian terms, we would say the likelihood ratio is 4 to 1. This means that the box is 4 times as likely to beep when we punch in a correct combination, compared to how likely it is to beep for an incorrect combination.

There are still a whole lot of possible combinations. If you punch in 20 incorrect combinations, the box will beep on 5 of them by sheer chance (on average). If you punch in all 131,115,985 possible combinations, then while the box is certain to beep for the one winning combination, it will also beep for 32,778,996 losing combinations (on average).

So this box doesn’t let you win the lottery, but it’s better than nothing. If you used the box, your odds of winning would go from 1 in 131,115,985 to 1 in 32,778,997. You’ve made some progress toward finding your target, the truth, within the huge space of possibilities.

Suppose you can use another black box to test combinations twice, independently. Both boxes are certain to beep for the winning ticket. But the chance of a box beeping for a losing combination is 1/4 independently for each box; hence the chance of both boxes beeping for a losing combination is 1/16. We can say that the cumulative evidence, of two independent tests, has a likelihood ratio of 16:1. The number of losing lottery tickets that pass both tests will be (on average) 8,194,749.

Since there are 131,115,985 possible lottery tickets, you might guess that you need evidence whose strength is around 131,115,985 to 1—an event, or series of events, which is 131,115,985 times more likely to happen for a winning combination than a losing combination. Actually, this amount of evidence would only be enough to give you an even chance of winning the lottery. Why? Because if you apply a filter of that power to 131 million losing tickets, there will be, on average, one losing ticket that passes the filter. The winning ticket will also pass the filter. So you’ll be left with two tickets that passed the filter, only one of them a winner. Fifty percent odds of winning, if you can only buy one ticket.

A better way of viewing the problem: In the beginning, there is 1 winning ticket and 131,115,984 losing tickets, so your odds of winning are 1:131,115,984. If you use a single box, the odds of it beeping are 1 for a winning ticket and 0.25 for a losing ticket. So we multiply 1:131,115,984 by 1:0.25 and get 1:32,778,996. Adding another box of evidence multiplies the odds by 1:0.25 again, so now the odds are 1 winning ticket to 8,194,749 losing tickets.

It is convenient to measure evidence in bits—not like bits on a hard drive, but mathematician’s bits, which are conceptually different. Mathematician’s bits are the logarithms, base 1/2, of probabilities. For example, if there are four possible outcomes A, B, C, and D, whose probabilities are 50%, 25%, 12.5%, and 12.5%, and I tell you the outcome was “D,” then I have transmitted three bits of information to you, because I informed you of an outcome whose probability was 1/8.

It so happens that 131,115,984 is slightly less than 2 to the 27th power. So 14 boxes or 28 bits of evidence—an event 268,435,456:1 times more likely to happen if the ticket-hypothesis is true than if it is false—would shift the odds from 1:131,115,984 to 268,435,456:131,115,984, which reduces to 2:1. Odds of 2 to 1 mean two chances to win for each chance to lose, so the probability of winning with 28 bits of evidence is 2/3. Adding another box, another 2 bits of evidence, would take the odds to 8:1. Adding yet another two boxes would take the chance of winning to 128:1.

So if you want to license a strong belief that you will win the lottery—arbitrarily defined as less than a 1% probability of being wrong—34 bits of evidence about the winning combination should do the trick.

In general, the rules for weighing “how much evidence it takes” follow a similar pattern: The larger the space of possibilities in which the hypothesis lies, or the more unlikely the hypothesis seems a priori compared to its neighbors, or the more confident you wish to be, the more evidence you need.

You cannot defy the rules; you cannot form accurate beliefs based on inadequate evidence. Let’s say you’ve got 10 boxes lined up in a row, and you start punching combinations into the boxes. You cannot stop on the first combination that gets beeps from all 10 boxes, saying, “But the odds of that happening for a losing combination are a million to one! I’ll just ignore those ivory-tower Bayesian rules and stop here.” On average, 131 losing tickets will pass such a test for every winner. Considering the space of possibilities and the prior improbability, you jumped to a too-strong conclusion based on insufficient evidence. That’s not a pointless bureaucratic regulation; it’s math.

Of course, you can still believe based on inadequate evidence, if that is your whim; but you will not be able to believe accurately. It is like trying to drive your car without any fuel, because you don’t believe in the silly-dilly fuddy-duddy concept that it ought to take fuel to go places. It would be so much more fun, and so much less expensive, if we just decided to repeal the law that cars need fuel. Isn’t it just obviously better for everyone? Well, you can try, if that is your whim. You can even shut your eyes and pretend the car is moving. But to really arrive at accurate beliefs requires evidence-fuel, and the further you want to go, the more fuel you need.

24
Einstein’s Arrogance

In 1919, Sir Arthur Eddington led expeditions to Brazil and to the island of Principe, aiming to observe solar eclipses and thereby test an experimental prediction of Einstein’s novel theory of General Relativity. A journalist asked Einstein what he would do if Eddington’s observations failed to match his theory. Einstein famously replied: “Then I would feel sorry for the good Lord. The theory is correct.”

It seems like a rather foolhardy statement, defying the trope of Traditional Rationality that experiment above all is sovereign. Einstein seems possessed of an arrogance so great that he would refuse to bend his neck and submit to Nature’s answer, as scientists must do. Who can know that the theory is correct, in advance of experimental test?

Of course, Einstein did turn out to be right. I try to avoid criticizing people when they are right. If they genuinely deserve criticism, I will not need to wait long for an occasion where they are wrong.

And Einstein may not have been quite so foolhardy as he sounded . . .

To assign more than 50% probability to the correct candidate from a pool of 100,000,000 possible hypotheses, you need at least 27 bits of evidence (or thereabouts). You cannot expect to find the correct candidate without tests that are this strong, because lesser tests will yield more than one candidate that passes all the tests. If you try to apply a test that only has a million-to-one chance of a false positive (~20 bits), you’ll end up with a hundred candidates. Just finding the right answer, within a large space of possibilities, requires a large amount of evidence.

Traditional Rationality emphasizes justification: “If you want to convince me of X, you’ve got to present me with Y amount of evidence.” I myself often slip into this phrasing, whenever I say something like, “To justify believing in this proposition, at more than 99% probability, requires 34 bits of evidence.” Or, “In order to assign more than 50% probability to your hypothesis, you need 27 bits of evidence.” The Traditional phrasing implies that you start out with a hunch, or some private line of reasoning that leads you to a suggested hypothesis, and then you have to gather “evidence” to confirm it—to convince the scientific community, or justify saying that you believe in your hunch.

But from a Bayesian perspective, you need an amount of evidence roughly equivalent to the complexity of the hypothesis just to locate the hypothesis in theory-space. It’s not a question of justifying anything to anyone. If there’s a hundred million alternatives, you need at least 27 bits of evidence just to focus your attention uniquely on the correct answer.

This is true even if you call your guess a “hunch” or “intuition.” Hunchings and intuitings are real processes in a real brain. If your brain doesn’t have at least 10 bits of genuinely entangled valid Bayesian evidence to chew on, your brain cannot single out a correct 10-bit hypothesis for your attention—consciously, subconsciously, whatever. Subconscious processes can’t find one out of a million targets using only 19 bits of entanglement any more than conscious processes can. Hunches can be mysterious to the huncher, but they can’t violate the laws of physics.

You see where this is going: At the time of first formulating the hypothesis—the very first time the equations popped into his head—Einstein must have had, already in his possession, sufficient observational evidence to single out the complex equations of General Relativity for his unique attention. Or he couldn’t have gotten them right.

Now, how likely is it that Einstein would have exactly enough observational evidence to raise General Relativity to the level of his attention, but only justify assigning it a 55% probability? Suppose General Relativity is a 29.3-bit hypothesis. How likely is it that Einstein would stumble across exactly 29.5 bits of evidence in the course of his physics reading?

Not likely! If Einstein had enough observational evidence to single out the correct equations of General Relativity in the first place, then he probably had enough evidence to be damn sure that General Relativity was true.

In fact, since the human brain is not a perfectly efficient processor of information, Einstein probably had overwhelmingly more evidence than would, in principle, be required for a perfect Bayesian to assign massive confidence to General Relativity.

“Then I would feel sorry for the good Lord; the theory is correct.” It doesn’t sound nearly as appalling when you look at it from that perspective. And remember that General Relativity was correct, from all that vast space of possibilities.

25
Occam’s Razor

The more complex an explanation is, the more evidence you need just to find it in belief-space. (In Traditional Rationality this is often phrased misleadingly, as “The more complex a proposition is, the more evidence is required to argue for it.”) How can we measure the complexity of an explanation? How can we determine how much evidence is required?

Occam’s Razor is often phrased as “The simplest explanation that fits the facts.” Robert Heinlein replied that the simplest explanation is “The lady down the street is a witch; she did it.”

One observes that the length of an English sentence is not a good way to measure “complexity.” And “fitting” the facts by merely failing to prohibit them is insufficient.

Why, exactly, is the length of an English sentence a poor measure of complexity? Because when you speak a sentence aloud, you are using labels for concepts that the listener shares—the receiver has already stored the complexity in them. Suppose we abbreviated Heinlein’s whole sentence as “Tldtsiawsdi!” so that the entire explanation can be conveyed in one word; better yet, we’ll give it a short arbitrary label like “Fnord!” Does this reduce the complexity? No, because you have to tell the listener in advance that “Tldtsiawsdi!” stands for “The lady down the street is a witch; she did it.” “Witch,” itself, is a label for some extraordinary assertions—just because we all know what it means doesn’t mean the concept is simple.

An enormous bolt of electricity comes out of the sky and hits something, and the Norse tribesfolk say, “Maybe a really powerful agent was angry and threw a lightning bolt.” The human brain is the most complex artifact in the known universe. If anger seems simple, it’s because we don’t see all the neural circuitry that’s implementing the emotion. (Imagine trying to explain why Saturday Night Live is funny, to an alien species with no sense of humor. But don’t feel superior; you yourself have no sense of fnord.) The complexity of anger, and indeed the complexity of intelligence, was glossed over by the humans who hypothesized Thor the thunder-agent.

To a human, Maxwell’s equations take much longer to explain than Thor. Humans don’t have a built-in vocabulary for calculus the way we have a built-in vocabulary for anger. You’ve got to explain your language, and the language behind the language, and the very concept of mathematics, before you can start on electricity.

And yet it seems that there should be some sense in which Maxwell’s equations are simpler than a human brain, or Thor the thunder-agent.

There is. It’s enormously easier (as it turns out) to write a computer program that simulates Maxwell’s equations, compared to a computer program that simulates an intelligent emotional mind like Thor.

The formalism of Solomonoff induction measures the “complexity of a description” by the length of the shortest computer program which produces that description as an output. To talk about the “shortest computer program” that does something, you need to specify a space of computer programs, which requires a language and interpreter. Solomonoff induction uses Turing machines, or rather, bitstrings that specify Turing machines. What if you don’t like Turing machines? Then there’s only a constant complexity penalty to design your own universal Turing machine that interprets whatever code you give it in whatever programming language you like. Different inductive formalisms are penalized by a worst-case constant factor relative to each other, corresponding to the size of a universal interpreter for that formalism.

In the better (in my humble opinion) versions of Solomonoff induction, the computer program does not produce a deterministic prediction, but assigns probabilities to strings. For example, we could write a program to explain a fair coin by writing a program that assigns equal probabilities to all 2^N strings of length N. This is Solomonoff induction’s approach to fitting the observed data. The higher the probability a program assigns to the observed data, the better that program fits the data. And probabilities must sum to 1, so for a program to better “fit” one possibility, it must steal probability mass from some other possibility which will then “fit” much more poorly. There is no superfair coin that assigns 100% probability to heads and 100% probability to tails.

How do we trade off the fit to the data, against the complexity of the program? If you ignore complexity penalties, and think only about fit, then you will always prefer programs that claim to deterministically predict the data, assign it 100% probability. If the coin shows HTTHHT, then the program that claims that the coin was fixed to show HTTHHT fits the observed data 64 times better than the program which claims the coin is fair. Conversely, if you ignore fit, and consider only complexity, then the “fair coin” hypothesis will always seem simpler than any other hypothesis. Even if the coin turns up HTHHTHHHTHHHHTHHHHHT . . . Indeed, the fair coin is simpler and it fits this data exactly as well as it fits any other string of 20 coinflips—no more, no less—but we see another hypothesis, seeming not too complicated, that fits the data much better.

If you let a program store one more binary bit of information, it will be able to cut down a space of possibilities by half, and hence assign twice as much probability to all the points in the remaining space. This suggests that one bit of program complexity should cost at least a “factor of two gain” in the fit. If you try to design a computer program that explicitly stores an outcome like HTTHHT, the six bits that you lose in complexity must destroy all plausibility gained by a 64-fold improvement in fit. Otherwise, you will sooner or later decide that all fair coins are fixed.

Unless your program is being smart, and compressing the data, it should do no good just to move one bit from the data into the program description.

The way Solomonoff induction works to predict sequences is that you sum up over all allowed computer programs—if any program is allowed, Solomonoff induction becomes uncomputable—with each program having a prior probability of (1/2) to the power of its code length in bits, and each program is further weighted by its fit to all data observed so far. This gives you a weighted mixture of experts that can predict future bits.

The Minimum Message Length formalism is nearly equivalent to Solomonoff induction. You send a string describing a code, and then you send a string describing the data in that code. Whichever explanation leads to the shortest total message is the best. If you think of the set of allowable codes as a space of computer programs, and the code description language as a universal machine, then Minimum Message Length is nearly equivalent to Solomonoff induction. (Nearly, because it chooses the shortest program, rather than summing up over all programs.)

This lets us see clearly the problem with using “The lady down the street is a witch; she did it” to explain the pattern in the sequence 0101010101. If you’re sending a message to a friend, trying to describe the sequence you observed, you would have to say: “The lady down the street is a witch; she made the sequence come out 0101010101.” Your accusation of witchcraft wouldn’t let you shorten the rest of the message; you would still have to describe, in full detail, the data which her witchery caused.

Witchcraft may fit our observations in the sense of qualitatively permitting them; but this is because witchcraft permits everything, like saying “Phlogiston!” So, even after you say “witch,” you still have to describe all the observed data in full detail. You have not compressed the total length of the message describing your observations by transmitting the message about witchcraft; you have simply added a useless prologue, increasing the total length.

The real sneakiness was concealed in the word “it” of “A witch did it.” A witch did what?

Of course, thanks to hindsight bias and anchoring and fake explanations and fake causality and positive bias and motivated cognition, it may seem all too obvious that if a woman is a witch, of course she would make the coin come up 0101010101. But I’ll get to that soon enough. . .

26
Your Strength as a Rationalist

The following happened to me in an IRC chatroom, long enough ago that I was still hanging around in IRC chatrooms. Time has fuzzed the memory and my report may be imprecise.

So there I was, in an IRC chatroom, when someone reports that a friend of his needs medical advice. His friend says that he’s been having sudden chest pains, so he called an ambulance, and the ambulance showed up, but the paramedics told him it was nothing, and left, and now the chest pains are getting worse. What should his friend do?

I was confused by this story. I remembered reading about homeless people in New York who would call ambulances just to be taken someplace warm, and how the paramedics always had to take them to the emergency room, even on the 27th iteration. Because if they didn’t, the ambulance company could be sued for lots and lots of money. Likewise, emergency rooms are legally obligated to treat anyone, regardless of ability to pay. (And the hospital absorbs the costs, which are enormous, so hospitals are closing their emergency rooms . . . It makes you wonder what’s the point of having economists if we’re just going to ignore them.) So I didn’t quite understand how the described events could have happened. Anyone reporting sudden chest pains should have been hauled off by an ambulance instantly.

And this is where I fell down as a rationalist. I remembered several occasions where my doctor would completely fail to panic at the report of symptoms that seemed, to me, very alarming. And the Medical Establishment was always right. Every single time. I had chest pains myself, at one point, and the doctor patiently explained to me that I was describing chest muscle pain, not a heart attack. So I said into the IRC channel, “Well, if the paramedics told your friend it was nothing, it must really be nothing—they’d have hauled him off if there was the tiniest chance of serious trouble.”

Thus I managed to explain the story within my existing model, though the fit still felt a little forced . . .

Later on, the fellow comes back into the IRC chatroom and says his friend made the whole thing up. Evidently this was not one of his more reliable friends.

I should have realized, perhaps, that an unknown acquaintance of an acquaintance in an IRC channel might be less reliable than a published journal article. Alas, belief is easier than disbelief; we believe instinctively, but disbelief requires a conscious effort.¹

So instead, by dint of mighty straining, I forced my model of reality to explain an anomaly that never actually happened. And I knew how embarrassing this was. I knew that the usefulness of a model is not what it can explain, but what it can’t. A hypothesis that forbids nothing, permits everything, and thereby fails to constrain anticipation.

Your strength as a rationalist is your ability to be more confused by fiction than by reality. If you are equally good at explaining any outcome, you have zero knowledge.

We are all weak, from time to time; the sad part is that I could have been stronger. I had all the information I needed to arrive at the correct answer, I even noticed the problem, and then I ignored it. My feeling of confusion was a Clue, and I threw my Clue away.

I should have paid more attention to that sensation of still feels a little forced. It’s one of the most important feelings a truthseeker can have, a part of your strength as a rationalist. It is a design flaw in human cognition that this sensation manifests as a quiet strain in the back of your mind, instead of a wailing alarm siren and a glowing neon sign reading:

EITHER YOUR MODEL IS FALSE OR THIS STORY IS WRONG.

1. Daniel T. Gilbert, Romin W. Tafarodi, and Patrick S. Malone, “You Can’t Not Believe Everything You Read,” Journal of Personality and Social Psychology 65 (2 1993): 221–233, doi:10.1037/0022-3514.65.2.221.

27
Absence of Evidence Is Evidence of Absence

From Robyn Dawes’s Rational Choice in an Uncertain World:¹

In fact, this post-hoc fitting of evidence to hypothesis was involved in a most grievous chapter in United States history: the internment of Japanese-Americans at the beginning of the Second World War. When California governor Earl Warren testified before a congressional hearing in San Francisco on February 21, 1942, a questioner pointed out that there had been no sabotage or any other type of espionage by the Japanese-Americans up to that time. Warren responded, “I take the view that this lack [of subversive activity] is the most ominous sign in our whole situation. It convinces me more than perhaps any other factor that the sabotage we are to get, the Fifth Column activities are to get, are timed just like Pearl Harbor was timed . . . I believe we are just being lulled into a false sense of security.”

Consider Warren’s argument from a Bayesian perspective. When we see evidence, hypotheses that assigned a higher likelihood to that evidence gain probability at the expense of hypotheses that assigned a lower likelihood to the evidence. This is a phenomenon of relative likelihoods and relative probabilities. You can assign a high likelihood to the evidence and still lose probability mass to some other hypothesis, if that other hypothesis assigns a likelihood that is even higher.

Warren seems to be arguing that, given that we see no sabotage, this confirms that a Fifth Column exists. You could argue that a Fifth Column might delay its sabotage. But the likelihood is still higher that the absence of a Fifth Column would perform an absence of sabotage.

Let E stand for the observation of sabotage, and ¬E for the observation of no sabotage. The symbol H₁ stands for the hypothesis of a Japanese-American Fifth Column, and H₂ for the hypothesis that no Fifth Column exists. The conditional probability P(E|H), or “E given H,” is how confidently we’d expect to see the evidence E if we assumed the hypothesis H were true.

Whatever the likelihood that a Fifth Column would do no sabotage, the probability P(¬E|H₁), it won’t be as large as the likelihood that there’s no sabotage given that there’s no Fifth Column, the probability P(¬E|H₂). So observing a lack of sabotage increases the probability that no Fifth Column exists.

A lack of sabotage doesn’t prove that no Fifth Column exists. Absence of proof is not proof of absence. In logic, (A ⇒ B), read “A implies B,” is not equivalent to (¬A ⇒ ¬B), read “not-A implies not-B.”

But in probability theory, absence of evidence is always evidence of absence. If E is a binary event and P(H|E) > P(H), i.e., seeing E increases the probability of H, then P(H|¬E) < P(H), i.e., failure to observe E decreases the probability of H. The probability P(H) is a weighted mix of P(H|E) and P(H|¬E), and necessarily lies between the two. If any of this sounds at all confusing, see An Intuitive Explanation of Bayesian Reasoning.

Under the vast majority of real-life circumstances, a cause may not reliably produce signs of itself, but the absence of the cause is even less likely to produce the signs. The absence of an observation may be strong evidence of absence or very weak evidence of absence, depending on how likely the cause is to produce the observation. The absence of an observation that is only weakly permitted (even if the alternative hypothesis does not allow it at all) is very weak evidence of absence (though it is evidence nonetheless). This is the fallacy of “gaps in the fossil record”—fossils form only rarely; it is futile to trumpet the absence of a weakly permitted observation when many strong positive observations have already been recorded. But if there are no positive observations at all, it is time to worry; hence the Fermi Paradox.

Your strength as a rationalist is your ability to be more confused by fiction than by reality; if you are equally good at explaining any outcome you have zero knowledge. The strength of a model is not what it can explain, but what it can’t, for only prohibitions constrain anticipation. If you don’t notice when your model makes the evidence unlikely, you might as well have no model, and also you might as well have no evidence; no brain and no eyes.

1. Robyn M. Dawes, Rational Choice in An Uncertain World, 1st ed., ed. Jerome Kagan (San Diego, CA: Harcourt Brace Jovanovich, 1988), 250-251.

28
Conservation of Expected Evidence

Friedrich Spee von Langenfeld, a priest who heard the confessions of condemned witches, wrote in 1631 the Cautio Criminalis (“prudence in criminal cases”), in which he bitingly described the decision tree for condemning accused witches: If the witch had led an evil and improper life, she was guilty; if she had led a good and proper life, this too was a proof, for witches dissemble and try to appear especially virtuous. After the woman was put in prison: if she was afraid, this proved her guilt; if she was not afraid, this proved her guilt, for witches characteristically pretend innocence and wear a bold front. Or on hearing of a denunciation of witchcraft against her, she might seek flight or remain; if she ran, that proved her guilt; if she remained, the devil had detained her so she could not get away.

Spee acted as confessor to many witches; he was thus in a position to observe every branch of the accusation tree, that no matter what the accused witch said or did, it was held as proof against her. In any individual case, you would only hear one branch of the dilemma. It is for this reason that scientists write down their experimental predictions in advance.

But you can’t have it both ways—as a matter of probability theory, not mere fairness. The rule that “absence of evidence is evidence of absence” is a special case of a more general law, which I would name Conservation of Expected Evidence: The expectation of the posterior probability, after viewing the evidence, must equal the prior probability.

P(H) = P(H,E) + P(H,¬E)

P(H) = P(H|E) × P(E) + P(H,¬E) × P(¬E)

Therefore, for every expectation of evidence, there is an equal and opposite expectation of counterevidence.

If you expect a strong probability of seeing weak evidence in one direction, it must be balanced by a weak expectation of seeing strong evidence in the other direction. If you’re very confident in your theory, and therefore anticipate seeing an outcome that matches your hypothesis, this can only provide a very small increment to your belief (it is already close to 1); but the unexpected failure of your prediction would (and must) deal your confidence a huge blow. On average, you must expect to be exactly as confident as when you started out. Equivalently, the mere expectation of encountering evidence—before you’ve actually seen it—should not shift your prior beliefs. (Again, if this is not intuitively obvious, see An Intuitive Explanation of Bayesian Reasoning.)

So if you claim that “no sabotage” is evidence for the existence of a Japanese-American Fifth Column, you must conversely hold that seeing sabotage would argue against a Fifth Column. If you claim that “a good and proper life” is evidence that a woman is a witch, then an evil and improper life must be evidence that she is not a witch. If you argue that God, to test humanity’s faith, refuses to reveal His existence, then the miracles described in the Bible must argue against the existence of God.

Doesn’t quite sound right, does it? Pay attention to that feeling of this seems a little forced, that quiet strain in the back of your mind. It’s important.

For a true Bayesian, it is impossible to seek evidence that confirms a theory. There is no possible plan you can devise, no clever strategy, no cunning device, by which you can legitimately expect your confidence in a fixed proposition to be higher (on average) than before. You can only ever seek evidence to test a theory, not to confirm it.

This realization can take quite a load off your mind. You need not worry about how to interpret every possible experimental result to confirm your theory. You needn’t bother planning how to make any given iota of evidence confirm your theory, because you know that for every expectation of evidence, there is an equal and oppositive expectation of counterevidence. If you try to weaken the counterevidence of a possible “abnormal” observation, you can only do it by weakening the support of a “normal” observation, to a precisely equal and opposite degree. It is a zero-sum game. No matter how you connive, no matter how you argue, no matter how you strategize, you can’t possibly expect the resulting game plan to shift your beliefs (on average) in a particular direction.

You might as well sit back and relax while you wait for the evidence to come in.

. . . Human psychology is so screwed up.

29
Hindsight Devalues Science

This essay is closely based on an excerpt from Meyers’s Exploring Social Psychology;¹ the excerpt is worth reading in its entirety.

Cullen Murphy, editor of The Atlantic, said that the social sciences turn up “no ideas or conclusions that can’t be found in [any] encyclopedia of quotations . . . Day after day social scientists go out into the world. Day after day they discover that people’s behavior is pretty much what you’d expect.”

Of course, the “expectation” is all hindsight. (Hindsight bias: Subjects who know the actual answer to a question assign much higher probabilities they “would have” guessed for that answer, compared to subjects who must guess without knowing the answer.)

The historian Arthur Schlesinger, Jr. dismissed scientific studies of World War II soldiers’ experiences as “ponderous demonstrations” of common sense. For example:

Better educated soldiers suffered more adjustment problems than less educated soldiers. (Intellectuals were less prepared for battle stresses than street-smart people.)
Southern soldiers coped better with the hot South Sea Island climate than Northern soldiers. (Southerners are more accustomed to hot weather.)
White privates were more eager to be promoted to noncommissioned officers than Black privates. (Years of oppression take a toll on achievement motivation.)
Southern Blacks preferred Southern to Northern White officers. (Southern officers were more experienced and skilled in interacting with Blacks.)
As long as the fighting continued, soldiers were more eager to return home than after the war ended. (During the fighting, soldiers knew they were in mortal danger.)

How many of these findings do you think you could have predicted in advance? Three out of five? Four out of five? Are there any cases where you would have predicted the opposite—where your model takes a hit? Take a moment to think before continuing . . .

. . .

In this demonstration (from Paul Lazarsfeld by way of Meyers), all of the findings above are the opposite of what was actually found.² How many times did you think your model took a hit? How many times did you admit you would have been wrong? That’s how good your model really was. The measure of your strength as a rationalist is your ability to be more confused by fiction than by reality.

Unless, of course, I reversed the results again. What do you think?

Do your thought processes at this point, where you really don’t know the answer, feel different from the thought processes you used to rationalize either side of the “known” answer?

Daphna Baratz exposed college students to pairs of supposed findings, one true (“In prosperous times people spend a larger portion of their income than during a recession”) and one the truth’s opposite.³ In both sides of the pair, students rated the supposed finding as what they “would have predicted.” Perfectly standard hindsight bias.

Which leads people to think they have no need for science, because they “could have predicted” that.

(Just as you would expect, right?)

Hindsight will lead us to systematically undervalue the surprisingness of scientific findings, especially the discoveries we understand—the ones that seem real to us, the ones we can retrofit into our models of the world. If you understand neurology or physics and read news in that topic, then you probably underestimate the surprisingness of findings in those fields too. This unfairly devalues the contribution of the researchers; and worse, will prevent you from noticing when you are seeing evidence that doesn’t fit what you really would have expected.

We need to make a conscious effort to be shocked enough.

1. David G. Meyers, Exploring Social Psychology (New York: McGraw-Hill, 1994), 15–19.

2. Paul F. Lazarsfeld, “The American Solidier—An Expository Review,” Public Opinion Quarterly 13, no. 3 (1949): 377–404.

3. Daphna Baratz, How Justified Is the “Obvious” Reaction? (Stanford University, 1983).

Part D
Mysterious Answers

30
Fake Explanations

Once upon a time, there was an instructor who taught physics students. One day the instructor called them into the classroom and showed them a wide, square plate of metal, next to a hot radiator. The students each put their hand on the plate and found the side next to the radiator cool, and the distant side warm. And the instructor said, Why do you think this happens? Some students guessed convection of air currents, and others guessed strange metals in the plate. They devised many creative explanations, none stooping so low as to say “I don’t know” or “This seems impossible.”

And the answer was that before the students entered the room, the instructor turned the plate around.¹

Consider the student who frantically stammers, “Eh, maybe because of the heat conduction and so?” I ask: Is this answer a proper belief? The words are easily enough professed—said in a loud, emphatic voice. But do the words actually control anticipation?

Ponder that innocent little phrase, “because of,” which comes before “heat conduction.” Ponder some of the other things we could put after it. We could say, for example, “Because of phlogiston,” or “Because of magic.”

“Magic!” you cry. “That’s not a scientific explanation!” Indeed, the phrases “because of heat conduction” and “because of magic” are readily recognized as belonging to different literary genres. “Heat conduction” is something that Spock might say on Star Trek, whereas “magic” would be said by Giles in Buffy the Vampire Slayer.

However, as Bayesians, we take no notice of literary genres. For us, the substance of a model is the control it exerts on anticipation. If you say “heat conduction,” what experience does that lead you to anticipate? Under normal circumstances, it leads you to anticipate that, if you put your hand on the side of the plate near the radiator, that side will feel warmer than the opposite side. If “because of heat conduction” can also explain the radiator-adjacent side feeling cooler, then it can explain pretty much anything.

And as we all know by this point (I do hope), if you are equally good at explaining any outcome, you have zero knowledge. “Because of heat conduction,” used in such fashion, is a disguised hypothesis of maximum entropy. It is anticipation-isomorphic to saying “magic.” It feels like an explanation, but it’s not.

Suppose that instead of guessing, we measured the heat of the metal plate at various points and various times. Seeing a metal plate next to the radiator, we would ordinarily expect the point temperatures to satisfy an equilibrium of the diffusion equation with respect to the boundary conditions imposed by the environment. You might not know the exact temperature of the first point measured, but after measuring the first points—I’m not physicist enough to know how many would be required—you could take an excellent guess at the rest.

A true master of the art of using numbers to constrain the anticipation of material phenomena—a “physicist”—would take some measurements and say, “This plate was in equilibrium with the environment two and a half minutes ago, turned around, and is now approaching equilibrium again.”

The deeper error of the students is not simply that they failed to constrain anticipation. Their deeper error is that they thought they were doing physics. They said the phrase “because of,” followed by the sort of words Spock might say on Star Trek, and thought they thereby entered the magisterium of science.

Not so. They simply moved their magic from one literary genre to another.

1. Search for “heat conduction.” Taken from Joachim Verhagen, http://web.archive.org/web/20060424082937/http://www.nvon.nl/scheik/best/diversen/scijokes/scijokes.txt, archived version, October 27, 2001.

31
Guessing the Teacher’s Password

When I was young, I read popular physics books such as Richard Feynman’s QED: The Strange Theory of Light and Matter. I knew that light was waves, sound was waves, matter was waves. I took pride in my scientific literacy, when I was nine years old.

When I was older, and I began to read the Feynman Lectures on Physics, I ran across a gem called “the wave equation.” I could follow the equation’s derivation, but, looking back, I couldn’t see its truth at a glance. So I thought about the wave equation for three days, on and off, until I saw that it was embarrassingly obvious. And when I finally understood, I realized that the whole time I had accepted the honest assurance of physicists that light was waves, sound was waves, matter was waves, I had not had the vaguest idea of what the word “wave” meant to a physicist.

There is an instinctive tendency to think that if a physicist says “light is made of waves,” and the teacher says “What is light made of?,” and the student says “Waves!,” then the student has made a true statement. That’s only fair, right? We accept “waves” as a correct answer from the physicist; wouldn’t it be unfair to reject it from the student? Surely, the answer “Waves!” is either true or false, right?

Which is one more bad habit to unlearn from school. Words do not have intrinsic definitions. If I hear the syllables “bea-ver” and think of a large rodent, that is a fact about my own state of mind, not a fact about the syllables “bea-ver.” The sequence of syllables “made of waves” (or “because of heat conduction”) is not a hypothesis, it is a pattern of vibrations traveling through the air, or ink on paper. It can associate to a hypothesis in someone’s mind, but it is not, of itself, right or wrong. But in school, the teacher hands you a gold star for saying “made of waves,” which must be the correct answer because the teacher heard a physicist emit the same sound-vibrations. Since verbal behavior (spoken or written) is what gets the gold star, students begin to think that verbal behavior has a truth-value. After all, either light is made of waves, or it isn’t, right?

And this leads into an even worse habit. Suppose the teacher presents you with a confusing problem involving a metal plate next to a radiator; the far side feels warmer than the side next to the radiator. The teacher asks “Why?” If you say “I don’t know,” you have no chance of getting a gold star—it won’t even count as class participation. But, during the current semester, this teacher has used the phrases “because of heat convection,” “because of heat conduction,” and “because of radiant heat.” One of these is probably what the teacher wants. You say, “Eh, maybe because of heat conduction?”

This is not a hypothesis about the metal plate. This is not even a proper belief. It is an attempt to guess the teacher’s password.

Even visualizing the symbols of the diffusion equation (the math governing heat conduction) doesn’t mean you’ve formed a hypothesis about the metal plate. This is not school; we are not testing your memory to see if you can write down the diffusion equation. This is Bayescraft; we are scoring your anticipations of experience. If you use the diffusion equation, by measuring a few points with a thermometer and then trying to predict what the thermometer will say on the next measurement, then it is definitely connected to experience. Even if the student just visualizes something flowing, and therefore holds a match near the cooler side of the plate to try to measure where the heat goes, then this mental image of flowing-ness connects to experience; it controls anticipation.

If you aren’t using the diffusion equation—putting in numbers and getting out results that control your anticipation of particular experiences—then the connection between map and territory is severed as though by a knife. What remains is not a belief, but a verbal behavior.

In the school system, it’s all about verbal behavior, whether written on paper or spoken aloud. Verbal behavior gets you a gold star or a failing grade. Part of unlearning this bad habit is becoming consciously aware of the difference between an explanation and a password.

Does this seem too harsh? When you’re faced by a confusing metal plate, can’t “heat conduction?” be a first step toward finding the answer? Maybe, but only if you don’t fall into the trap of thinking that you are looking for a password. What if there is no teacher to tell you that you failed? Then you may think that “Light is wakalixes” is a good explanation, that “wakalixes” is the correct password. It happened to me when I was nine years old—not because I was stupid, but because this is what happens by default. This is how human beings think, unless they are trained not to fall into the trap. Humanity stayed stuck in holes like this for thousands of years.

Maybe, if we drill students that words don’t count, only anticipation-controllers, the student will not get stuck on “heat conduction? No? Maybe heat convection? That’s not it either?” Maybe then, thinking the phrase “heat conduction” will lead onto a genuinely helpful path, like:

“Heat conduction?”
But that’s only a phrase—what does it mean?
The diffusion equation?
But those are only symbols—how do I apply them?
What does applying the diffusion equation lead me to anticipate?
It sure doesn’t lead me to anticipate that the side of a metal plate farther away from a radiator would feel warmer.
I notice that I am confused. Maybe the near side just feels cooler, because it’s made of more insulative material and transfers less heat to my hand? I’ll try measuring the temperature . . .
Okay, that wasn’t it. Can I try to verify whether the diffusion equation holds true of this metal plate, at all? Is heat flowing the way it usually does, or is something else going on?
I could hold a match to the plate and try to measure how heat spreads over time . . .

If we are not strict about “Eh, maybe because of heat conduction?” being a fake explanation, the student will very probably get stuck on some wakalixes-password. This happens by default: it happened to the whole human species for thousands of years.

32
Science as Attire

The preview for the X-Men movie has a voice-over saying: “In every human being . . . there is the genetic code . . . for mutation.” Apparently you can acquire all sorts of neat abilities by mutation. The mutant Storm, for example, has the ability to throw lightning bolts.

I beg you, dear reader, to consider the biological machinery necessary to generate electricity; the biological adaptations necessary to avoid being harmed by electricity; and the cognitive circuitry required for finely tuned control of lightning bolts. If we actually observed any organism acquiring these abilities in one generation, as the result of mutation, it would outright falsify the neo-Darwinian model of natural selection. It would be worse than finding rabbit fossils in the pre-Cambrian. If evolutionary theory could actually stretch to cover Storm, it would be able to explain anything, and we all know what that would imply.

The X-Men comics use terms like “evolution,” “mutation,” and “genetic code,” purely to place themselves in what they conceive to be the literary genre of science. The part that scares me is wondering how many people, especially in the media, understand science only as a literary genre.

I encounter people who very definitely believe in evolution, who sneer at the folly of creationists. And yet they have no idea of what the theory of evolutionary biology permits and prohibits. They’ll talk about “the next step in the evolution of humanity,” as if natural selection got here by following a plan. Or even worse, they’ll talk about something completely outside the domain of evolutionary biology, like an improved design for computer chips, or corporations splitting, or humans uploading themselves into computers, and they’ll call that “evolution.” If evolutionary biology could cover that, it could cover anything.

Probably an actual majority of the people who believe in evolution use the phrase “because of evolution” because they want to be part of the scientific in-crowd—belief as scientific attire, like wearing a lab coat. If the scientific in-crowd instead used the phrase “because of intelligent design,” they would just as cheerfully use that instead—it would make no difference to their anticipation-controllers. Saying “because of evolution” instead of “because of intelligent design” does not, for them, prohibit Storm. Its only purpose, for them, is to identify with a tribe.

I encounter people who are quite willing to entertain the notion of dumber-than-human Artificial Intelligence, or even mildly smarter-than-human Artificial Intelligence. Introduce the notion of strongly superhuman Artificial Intelligence, and they’ll suddenly decide it’s “pseudoscience.” It’s not that they think they have a theory of intelligence which lets them calculate a theoretical upper bound on the power of an optimization process. Rather, they associate strongly superhuman AI to the literary genre of apocalyptic literature; whereas an AI running a small corporation associates to the literary genre of Wired magazine. They aren’t speaking from within a model of cognition. They don’t realize they need a model. They don’t realize that science is about models. Their devastating critiques consist purely of comparisons to apocalyptic literature, rather than, say, known laws which prohibit such an outcome. They understand science only as a literary genre, or in-group to belong to. The attire doesn’t look to them like a lab coat; this isn’t the football team they’re cheering for.

Is there any idea in science that you are proud of believing, though you do not use the belief professionally? You had best ask yourself which future experiences your belief prohibits from happening to you. That is the sum of what you have assimilated and made a true part of yourself. Anything else is probably passwords or attire.

33
Fake Causality

Phlogiston was the eighteenth century’s answer to the Elemental Fire of the Greek alchemists. Ignite wood, and let it burn. What is the orangey-bright “fire” stuff? Why does the wood transform into ash? To both questions, the eighteenth-century chemists answered, “phlogiston.”

. . . and that was it, you see, that was their answer: “Phlogiston.”

Phlogiston escaped from burning substances as visible fire. As the phlogiston escaped, the burning substances lost phlogiston and so became ash, the “true material.” Flames in enclosed containers went out because the air became saturated with phlogiston, and so could not hold any more. Charcoal left little residue upon burning because it was nearly pure phlogiston.

Of course, one didn’t use phlogiston theory to predict the outcome of a chemical transformation. You looked at the result first, then you used phlogiston theory to explain it. It’s not that phlogiston theorists predicted a flame would extinguish in a closed container; rather they lit a flame in a container, watched it go out, and then said, “The air must have become saturated with phlogiston.” You couldn’t even use phlogiston theory to say what you ought not to see; it could explain everything.

This was an earlier age of science. For a long time, no one realized there was a problem. Fake explanations don’t feel fake. That’s what makes them dangerous.

Modern research suggests that humans think about cause and effect using something like the directed acyclic graphs (DAGs) of Bayes nets. Because it rained, the sidewalk is wet; because the sidewalk is wet, it is slippery:

From this we can infer—or, in a Bayes net, rigorously calculate in probabilities—that when the sidewalk is slippery, it probably rained; but if we already know that the sidewalk is wet, learning that the sidewalk is slippery tells us nothing more about whether it rained.

Why is fire hot and bright when it burns?

Phlogiston to Fire hot and bright

It feels like an explanation. It’s represented using the same cognitive data format. But the human mind does not automatically detect when a cause has an unconstraining arrow to its effect. Worse, thanks to hindsight bias, it may feel like the cause constrains the effect, when it was merely fitted to the effect.

Interestingly, our modern understanding of probabilistic reasoning about causality can describe precisely what the phlogiston theorists were doing wrong. One of the primary inspirations for Bayesian networks was noticing the problem of double-counting evidence if inference resonates between an effect and a cause. For example, let’s say that I get a bit of unreliable information that the sidewalk is wet. This should make me think it’s more likely to be raining. But, if it’s more likely to be raining, doesn’t that make it more likely that the sidewalk is wet? And wouldn’t that make it more likely that the sidewalk is slippery? But if the sidewalk is slippery, it’s probably wet; and then I should again raise my probability that it’s raining . . .

Judea Pearl uses the metaphor of an algorithm for counting soldiers in a line.¹ Suppose you’re in the line, and you see two soldiers next to you, one in front and one in back. That’s three soldiers, including you. So you ask the soldier behind you, “How many soldiers do you see?” They look around and say, “Three.” So that’s a total of six soldiers. This, obviously, is not how to do it.

A smarter way is to ask the soldier in front of you, “How many soldiers forward of you?” and the soldier in back, “How many soldiers backward of you?” The question “How many soldiers forward?” can be passed on as a message without confusion. If I’m at the front of the line, I pass the message “1 soldier forward,” for myself. The person directly in back of me gets the message “1 soldier forward,” and passes on the message “2 soldiers forward” to the soldier behind them. At the same time, each soldier is also getting the message “N soldiers backward” from the soldier behind them, and passing it on as “N + 1 soldiers backward” to the soldier in front of them. How many soldiers in total? Add the two numbers you receive, plus one for yourself: that is the total number of soldiers in line.

The key idea is that every soldier must separately track the two messages, the forward-message and backward-message, and add them together only at the end. You never add any soldiers from the backward-message you receive to the forward-message you pass back. Indeed, the total number of soldiers is never passed as a message—no one ever says it aloud.

An analogous principle operates in rigorous probabilistic reasoning about causality. If you learn something about whether it’s raining, from some source other than observing the sidewalk to be wet, this will send a forward-message from Rain to Sidewalk wet and raise our expectation of the sidewalk being wet. If you observe the sidewalk to be wet, this sends a backward-message to our belief that it is raining, and this message propagates from Rain to all neighboring nodes except the Sidewalk wet node. We count each piece of evidence exactly once; no update message ever “bounces” back and forth. The exact algorithm may be found in Judea Pearl’s classic Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference.

So what went wrong in phlogiston theory? When we observe that fire is hot, the Fire node can send a backward-evidence to the Phlogiston node, leading us to update our beliefs about phlogiston. But if so, we can’t count this as a successful forward-prediction of phlogiston theory. The message should go in only one direction, and not bounce back.

Alas, human beings do not use a rigorous algorithm for updating belief networks. We learn about parent nodes from observing children, and predict child nodes from beliefs about parents. But we don’t keep rigorously separate books for the backward-message and forward-message. We just remember that phlogiston is hot, which causes fire to be hot. So it seems like phlogiston theory predicts the hotness of fire. Or, worse, it just feels like phlogiston makes the fire hot.

Until you notice that no advance predictions are being made, the non-constraining causal node is not labeled “fake.” It’s represented the same way as any other node in your belief network. It feels like a fact, like all the other facts you know: Phlogiston makes the fire hot.

A properly designed AI would notice the problem instantly. This wouldn’t even require special-purpose code, just correct bookkeeping of the belief network. (Sadly, we humans can’t rewrite our own code, the way a properly designed AI could.)

Speaking of “hindsight bias” is just the nontechnical way of saying that humans do not rigorously separate forward and backward messages, allowing forward messages to be contaminated by backward ones.

Those who long ago went down the path of phlogiston were not trying to be fools. No scientist deliberately wants to get stuck in a blind alley. Are there any fake explanations in your mind? If there are, I guarantee they’re not labeled “fake explanation,” so polling your thoughts for the “fake” keyword will not turn them up.

Thanks to hindsight bias, it’s also not enough to check how well your theory “predicts” facts you already know. You’ve got to predict for tomorrow, not yesterday. It’s the only way a messy human mind can be guaranteed of sending a pure forward message.

1. Judea Pearl, Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference (San Mateo, CA: Morgan Kaufmann, 1988).

34
Semantic Stopsigns

And the child asked:

Q: Where did this rock come from?

A: I chipped it off the big boulder, at the center of the village.

Q: Where did the boulder come from?

A: It probably rolled off the huge mountain that towers over our village.

Q: Where did the mountain come from?

A: The same place as all stone: it is the bones of Ymir, the primordial giant.

Q: Where did the primordial giant, Ymir, come from?

A: From the great abyss, Ginnungagap.

Q: Where did the great abyss, Ginnungagap, come from?

A: Never ask that question.

Consider the seeming paradox of the First Cause. Science has traced events back to the Big Bang, but why did the Big Bang happen? It’s all well and good to say that the zero of time begins at the Big Bang—that there is nothing before the Big Bang in the ordinary flow of minutes and hours. But saying this presumes our physical law, which itself appears highly structured; it calls out for explanation. Where did the physical laws come from? You could say that we’re all a computer simulation, but then the computer simulation is running on some other world’s laws of physics—where did those laws of physics come from?

At this point, some people say, “God!”

What could possibly make anyone, even a highly religious person, think this even helped answer the paradox of the First Cause? Why wouldn’t you automatically ask, “Where did God come from?” Saying “God is uncaused” or “God created Himself” leaves us in exactly the same position as “Time began with the Big Bang.” We just ask why the whole metasystem exists in the first place, or why some events but not others are allowed to be uncaused.

My purpose here is not to discuss the seeming paradox of the First Cause, but to ask why anyone would think “God!” could resolve the paradox. Saying “God!” is a way of belonging to a tribe, which gives people a motive to say it as often as possible—some people even say it for questions like “Why did this hurricane strike New Orleans?” Even so, you’d hope people would notice that on the particular puzzle of the First Cause, saying “God!” doesn’t help. It doesn’t make the paradox seem any less paradoxical even if true. How could anyone not notice this?

Jonathan Wallace suggested that “God!” functions as a semantic stopsign—that it isn’t a propositional assertion, so much as a cognitive traffic signal: do not think past this point. Saying “God!” doesn’t so much resolve the paradox, as put up a cognitive traffic signal to halt the obvious continuation of the question-and-answer chain.

Of course you’d never do that, being a good and proper atheist, right? But “God!” isn’t the only semantic stopsign, just the obvious first example.

The transhuman technologies—molecular nanotechnology, advanced biotech, genetech, Artificial Intelligence, et cetera—pose tough policy questions. What kind of role, if any, should a government take in supervising a parent’s choice of genes for their child? Could parents deliberately choose genes for schizophrenia? If enhancing a child’s intelligence is expensive, should governments help ensure access, to prevent the emergence of a cognitive elite? You can propose various institutions to answer these policy questions—for example, that private charities should provide financial aid for intelligence enhancement—but the obvious next question is, “Will this institution be effective?” If we rely on product liability lawsuits to prevent corporations from building harmful nanotech, will that really work?

I know someone whose answer to every one of these questions is “Liberal democracy!” That’s it. That’s his answer. If you ask the obvious question of “How well have liberal democracies performed, historically, on problems this tricky?” or “What if liberal democracy does something stupid?” then you’re an autocrat, or libertopian, or otherwise a very very bad person. No one is allowed to question democracy.

I once called this kind of thinking “the divine right of democracy.” But it is more precise to say that “Democracy!” functioned for him as a semantic stopsign. If anyone had said to him “Turn it over to the Coca-Cola corporation!,” he would have asked the obvious next questions: “Why? What will the Coca-Cola corporation do about it? Why should we trust them? Have they done well in the past on equally tricky problems?”

Or suppose that someone says “Mexican-Americans are plotting to remove all the oxygen in Earth’s atmosphere.” You’d probably ask, “Why would they do that? Don’t Mexican-Americans have to breathe too? Do Mexican-Americans even function as a unified conspiracy?” If you don’t ask these obvious next questions when someone says, “Corporations are plotting to remove Earth’s oxygen,” then “Corporations!” functions for you as a semantic stopsign.

Be careful here not to create a new generic counterargument against things you don’t like—“Oh, it’s just a stopsign!” No word is a stopsign of itself; the question is whether a word has that effect on a particular person. Having strong emotions about something doesn’t qualify it as a stopsign. I’m not exactly fond of terrorists or fearful of private property; that doesn’t mean “Terrorists!” or “Capitalism!” are cognitive traffic signals unto me. (The word “intelligence” did once have that effect on me, though no longer.) What distinguishes a semantic stopsign is failure to consider the obvious next question.

35
Mysterious Answers to Mysterious Questions

Imagine looking at your hand, and knowing nothing of cells, nothing of biochemistry, nothing of DNA. You’ve learned some anatomy from dissection, so you know your hand contains muscles; but you don’t know why muscles move instead of lying there like clay. Your hand is just . . . stuff . . . and for some reason it moves under your direction. Is this not magic?

The animal body does not act as a thermodynamic engine . . . consciousness teaches every individual that they are, to some extent, subject to the direction of his will. It appears therefore that animated creatures have the power of immediately applying to certain moving particles of matter within their bodies, forces by which the motions of these particles are directed to produce derived mechanical effects . . . The influence of animal or vegetable life on matter is infinitely beyond the range of any scientific inquiry hitherto entered on. Its power of directing the motions of moving particles, in the demonstrated daily miracle of our human free-will, and in the growth of generation after generation of plants from a single seed, are infinitely different from any possible result of the fortuitous concurrence of atoms . . . Modern biologists were coming once more to the acceptance of something and that was a vital principle.

—Lord Kelvin¹

This was the theory of vitalism; that the mysterious difference between living matter and non-living matter was explained by an élan vital or vis vitalis. élan vital infused living matter and caused it to move as consciously directed. élan vital participated in chemical transformations which no mere non-living particles could undergo—Wöhler’s later synthesis of urea, a component of urine, was a major blow to the vitalistic theory because it showed that mere chemistry could duplicate a product of biology.

Calling “élan vital” an explanation, even a fake explanation like phlogiston, is probably giving it too much credit. It functioned primarily as a curiosity-stopper. You said “Why?” and the answer was “Élan vital!”

When you say “Élan vital!,” it feels like you know why your hand moves. You have a little causal diagram in your head that says:

But actually you know nothing you didn’t know before. You don’t know, say, whether your hand will generate heat or absorb heat, unless you have observed the fact already; if not, you won’t be able to predict it in advance. Your curiosity feels sated, but it hasn’t been fed. Since you can say “Why? Élan vital!” to any possible observation, it is equally good at explaining all outcomes, a disguised hypothesis of maximum entropy, et cetera.

But the greater lesson lies in the vitalists’ reverence for the élan vital, their eagerness to pronounce it a mystery beyond all science. Meeting the great dragon Unknown, the vitalists did not draw their swords to do battle, but bowed their necks in submission. They took pride in their ignorance, made biology into a sacred mystery, and thereby became loath to relinquish their ignorance when evidence came knocking.

The Secret of Life was infinitely beyond the reach of science! Not just a little beyond, mind you, but infinitely beyond! Lord Kelvin sure did get a tremendous emotional kick out of not knowing something.

But ignorance exists in the map, not in the territory. If I am ignorant about a phenomenon, that is a fact about my own state of mind, not a fact about the phenomenon itself. A phenomenon can seem mysterious to some particular person. There are no phenomena which are mysterious of themselves. To worship a phenomenon because it seems so wonderfully mysterious is to worship your own ignorance.

Vitalism shared with phlogiston the error of encapsulating the mystery as a substance. Fire was mysterious, and the phlogiston theory encapsulated the mystery in a mysterious substance called “phlogiston.” Life was a sacred mystery, and vitalism encapsulated the sacred mystery in a mysterious substance called “élan vital.” Neither answer helped concentrate the model’s probability density—make some outcomes easier to explain than others. The “explanation” just wrapped up the question as a small, hard, opaque black ball.

In a comedy written by Moliére, a physician explains the power of a soporific by saying that it contains a “dormitive potency.” Same principle. It is a failure of human psychology that, faced with a mysterious phenomenon, we more readily postulate mysterious inherent substances than complex underlying processes.

But the deeper failure is supposing that an answer can be mysterious. If a phenomenon feels mysterious, that is a fact about our state of knowledge, not a fact about the phenomenon itself. The vitalists saw a mysterious gap in their knowledge, and postulated a mysterious stuff that plugged the gap. In doing so, they mixed up the map with the territory. All confusion and bewilderment exist in the mind, not in encapsulated substances.

This is the ultimate and fully general explanation for why, again and again in humanity’s history, people are shocked to discover that an incredibly mysterious question has a non-mysterious answer. Mystery is a property of questions, not answers.

Therefore I call theories such as vitalism mysterious answers to mysterious questions.

These are the signs of mysterious answers to mysterious questions:

First, the explanation acts as a curiosity-stopper rather than an anticipation-controller.
Second, the hypothesis has no moving parts—the model is not a specific complex mechanism, but a blankly solid substance or force. The mysterious substance or mysterious force may be said to be here or there, to cause this or that; but the reason why the mysterious force behaves thus is wrapped in a blank unity.
Third, those who proffer the explanation cherish their ignorance; they speak proudly of how the phenomenon defeats ordinary science or is unlike merely mundane phenomena.
Fourth, even after the answer is given, the phenomenon is still a mystery and possesses the same quality of wonderful inexplicability that it had at the start.

1. Silvanus Phillips Thompson, The Life of Lord Kelvin (American Mathematical Society, 2005).

36
The Futility of Emergence

The failures of phlogiston and vitalism are historical hindsight. Dare I step out on a limb, and name some current theory which I deem analogously flawed?

I name emergence or emergent phenomena—usually defined as the study of systems whose high-level behaviors arise or “emerge” from the interaction of many low-level elements. (Wikipedia: “The way complex systems and patterns arise out of a multiplicity of relatively simple interactions.”) Taken literally, that description fits every phenomenon in our universe above the level of individual quarks, which is part of the problem. Imagine pointing to a market crash and saying “It’s not a quark!” Does that feel like an explanation? No? Then neither should saying “It’s an emergent phenomenon!”

It’s the noun “emergence” that I protest, rather than the verb “emerges from.” There’s nothing wrong with saying “X emerges from Y,” where Y is some specific, detailed model with internal moving parts. “Arises from” is another legitimate phrase that means exactly the same thing: Gravity arises from the curvature of spacetime, according to the specific mathematical model of General Relativity. Chemistry arises from interactions between atoms, according to the specific model of quantum electrodynamics.

Now suppose I should say that gravity is explained by “arisence” or that chemistry is an “arising phenomenon,” and claim that as my explanation.

The phrase “emerges from” is acceptable, just like “arises from” or “is caused by” are acceptable, if the phrase precedes some specific model to be judged on its own merits.

However, this is not the way “emergence” is commonly used. “Emergence” is commonly used as an explanation in its own right.

I have lost track of how many times I have heard people say, “Intelligence is an emergent phenomenon!” as if that explained intelligence. This usage fits all the checklist items for a mysterious answer to a mysterious question. What do you know, after you have said that intelligence is “emergent”? You can make no new predictions. You do not know anything about the behavior of real-world minds that you did not know before. It feels like you believe a new fact, but you don’t anticipate any different outcomes. Your curiosity feels sated, but it has not been fed. The hypothesis has no moving parts—there’s no detailed internal model to manipulate. Those who proffer the hypothesis of “emergence” confess their ignorance of the internals, and take pride in it; they contrast the science of “emergence” to other sciences merely mundane.

And even after the answer of “Why? Emergence!” is given, the phenomenon is still a mystery and possesses the same sacred impenetrability it had at the start.

A fun exercise is to eliminate the adjective “emergent” from any sentence in which it appears, and see if the sentence says anything different:

Before: Human intelligence is an emergent product of neurons firing.
After: Human intelligence is a product of neurons firing.

Before: The behavior of the ant colony is the emergent outcome of the interactions of many individual ants.
After: The behavior of the ant colony is the outcome of the interactions of many individual ants.
Even better: A colony is made of ants. We can successfully predict some aspects of colony behavior using models that include only individual ants, without any global colony variables, showing that we understand how those colony behaviors arise from ant behaviors.

Another fun exercise is to replace the word “emergent” with the old word, the explanation that people had to use before emergence was invented:

Before: Life is an emergent phenomenon.
After: Life is a magical phenomenon.

Before: Human intelligence is an emergent product of neurons firing.
After: Human intelligence is a magical product of neurons firing.

Does not each statement convey exactly the same amount of knowledge about the phenomenon’s behavior? Does not each hypothesis fit exactly the same set of outcomes?

“Emergence” has become very popular, just as saying “magic” used to be very popular. “Emergence” has the same deep appeal to human psychology, for the same reason. “Emergence” is such a wonderfully easy explanation, and it feels good to say it; it gives you a sacred mystery to worship. Emergence is popular because it is the junk food of curiosity. You can explain anything using emergence, and so people do just that; for it feels so wonderful to explain things. Humans are still humans, even if they’ve taken a few science classes in college. Once they find a way to escape the shackles of settled science, they get up to the same shenanigans as their ancestors—dressed up in the literary genre of “science,” but humans are still humans, and human psychology is still human psychology.

37
Say Not “Complexity”

Once upon a time . . .

This is a story from when I first met Marcello, with whom I would later work for a year on AI theory; but at this point I had not yet accepted him as my apprentice. I knew that he competed at the national level in mathematical and computing olympiads, which sufficed to attract my attention for a closer look; but I didn’t know yet if he could learn to think about AI.

I had asked Marcello to say how he thought an AI might discover how to solve a Rubik’s Cube. Not in a preprogrammed way, which is trivial, but rather how the AI itself might figure out the laws of the Rubik universe and reason out how to exploit them. How would an AI invent for itself the concept of an “operator,” or “macro,” which is the key to solving the Rubik’s Cube?

At some point in this discussion, Marcello said: “Well, I think the AI needs complexity to do X, and complexity to do Y—”

And I said, “Don’t say ‘complexity.’”

Marcello said, “Why not?”

I said, “Complexity should never be a goal in itself. You may need to use a particular algorithm that adds some amount of complexity, but complexity for the sake of complexity just makes things harder.” (I was thinking of all the people whom I had heard advocating that the Internet would “wake up” and become an AI when it became “sufficiently complex.”)

And Marcello said, “But there’s got to be some amount of complexity that does it.”

I closed my eyes briefly, and tried to think of how to explain it all in words. To me, saying “complexity” simply felt like the wrong move in the AI dance. No one can think fast enough to deliberate, in words, about each sentence of their stream of consciousness; for that would require an infinite recursion. We think in words, but our stream of consciousness is steered below the level of words, by the trained-in remnants of past insights and harsh experience . . .

I said, “Did you read A Technical Explanation of Technical Explanation?”

“Yes,” said Marcello.

“Okay,” I said. “Saying ‘complexity’ doesn’t concentrate your probability mass.”

“Oh,” Marcello said, “like ‘emergence.’ Huh. So . . . now I’ve got to think about how X might actually happen . . .”

That was when I thought to myself, “Maybe this one is teachable.”

Complexity is not a useless concept. It has mathematical definitions attached to it, such as Kolmogorov complexity and Vapnik-Chervonenkis complexity. Even on an intuitive level, complexity is often worth thinking about—you have to judge the complexity of a hypothesis and decide if it’s “too complicated” given the supporting evidence, or look at a design and try to make it simpler.

But concepts are not useful or useless of themselves. Only usages are correct or incorrect. In the step Marcello was trying to take in the dance, he was trying to explain something for free, get something for nothing. It is an extremely common misstep, at least in my field. You can join a discussion on Artificial General Intelligence and watch people doing the same thing, left and right, over and over again—constantly skipping over things they don’t understand, without realizing that’s what they’re doing.

In an eyeblink it happens: putting a non-controlling causal node behind something mysterious, a causal node that feels like an explanation but isn’t. The mistake takes place below the level of words. It requires no special character flaw; it is how human beings think by default, how they have thought since the ancient times.

What you must avoid is skipping over the mysterious part; you must linger at the mystery to confront it directly. There are many words that can skip over mysteries, and some of them would be legitimate in other contexts—“complexity,” for example. But the essential mistake is that skip-over, regardless of what causal node goes behind it. The skip-over is not a thought, but a microthought. You have to pay close attention to catch yourself at it. And when you train yourself to avoid skipping, it will become a matter of instinct, not verbal reasoning. You have to feel which parts of your map are still blank, and more importantly, pay attention to that feeling.

I suspect that in academia there is a huge pressure to sweep problems under the rug so that you can present a paper with the appearance of completeness. You’ll get more kudos for a seemingly complete model that includes some “emergent phenomena,” versus an explicitly incomplete map where the label says “I got no clue how this part works” or “then a miracle occurs.” A journal may not even accept the latter paper, since who knows but that the unknown steps are really where everything interesting happens? And yes, it sometimes happens that all the non-magical parts of your map turn out to also be non-important. That’s the price you sometimes pay, for entering into terra incognita and trying to solve problems incrementally. But that makes it even more important to know when you aren’t finished yet. Mostly, people don’t dare to enter terra incognita at all, for the deadly fear of wasting their time.

And if you’re working on a revolutionary AI startup, there is an even huger pressure to sweep problems under the rug; or you will have to admit to yourself that you don’t know how to build an AI yet, and your current life plans will come crashing down in ruins around your ears. But perhaps I am over-explaining, since skip-over happens by default in humans; if you’re looking for examples, just watch people discussing religion or philosophy or spirituality or any science in which they were not professionally trained.

Marcello and I developed a convention in our AI work: when we ran into something we didn’t understand, which was often, we would say “magic”—as in, “X magically does Y”—to remind ourselves that here was an unsolved problem, a gap in our understanding. It is far better to say “magic,” than “complexity” or “emergence”; the latter words create an illusion of understanding. Wiser to say “magic,” and leave yourself a placeholder, a reminder of work you will have to do later.

38
Positive Bias: Look into the Dark

I am teaching a class, and I write upon the blackboard three numbers: 2-4-6. “I am thinking of a rule,” I say, “which governs sequences of three numbers. The sequence 2-4-6, as it so happens, obeys this rule. Each of you will find, on your desk, a pile of index cards. Write down a sequence of three numbers on a card, and I’ll mark it ‘Yes’ for fits the rule, or ‘No’ for not fitting the rule. Then you can write down another set of three numbers and ask whether it fits again, and so on. When you’re confident that you know the rule, write down the rule on a card. You can test as many triplets as you like.”

Here’s the record of one student’s guesses:

4-6-2 No
4-6-8 Yes
10-12-14 Yes

At this point the student wrote down their guess at the rule. What do you think the rule is? Would you have wanted to test another triplet, and if so, what would it be? Take a moment to think before continuing.

The challenge above is based on a classic experiment due to Peter Wason, the 2-4-6 task. Although subjects given this task typically expressed high confidence in their guesses, only 21% of the subjects successfully guessed the experimenter’s real rule, and replications since then have continued to show success rates of around 20%.¹

The study was called “On the failure to eliminate hypotheses in a conceptual task.” Subjects who attempt the 2-4-6 task usually try to generate positive examples, rather than negative examples—they apply the hypothetical rule to generate a representative instance, and see if it is labeled “Yes.”

Thus, someone who forms the hypothesis “numbers increasing by two” will test the triplet 8-10-12, hear that it fits, and confidently announce the rule. Someone who forms the hypothesis X-2X-3X will test the triplet 3-6-9, discover that it fits, and then announce that rule.

In every case the actual rule is the same: the three numbers must be in ascending order.

But to discover this, you would have to generate triplets that shouldn’t fit, such as 20-23-26, and see if they are labeled “No.” Which people tend not to do, in this experiment. In some cases, subjects devise, “test,” and announce rules far more complicated than the actual answer.

This cognitive phenomenon is usually lumped in with “confirmation bias.” However, it seems to me that the phenomenon of trying to test positive rather than negative examples, ought to be distinguished from the phenomenon of trying to preserve the belief you started with. “Positive bias” is sometimes used as a synonym for “confirmation bias,” and fits this particular flaw much better.

It once seemed that phlogiston theory could explain a flame going out in an enclosed box (the air became saturated with phlogiston and no more could be released), but phlogiston theory could just as well have explained the flame not going out. To notice this, you have to search for negative examples instead of positive examples, look into zero instead of one; which goes against the grain of what experiment has shown to be human instinct.

For by instinct, we human beings only live in half the world.

One may be lectured on positive bias for days, and yet overlook it in-the-moment. Positive bias is not something we do as a matter of logic, or even as a matter of emotional attachment. The 2-4-6 task is “cold,” logical, not affectively “hot.” And yet the mistake is subverbal, on the level of imagery, of instinctive reactions. Because the problem doesn’t arise from following a deliberate rule that says “Only think about positive examples,” it can’t be solved just by knowing verbally that “We ought to think about both positive and negative examples.” Which example automatically pops into your head? You have to learn, wordlessly, to zag instead of zig. You have to learn to flinch toward the zero, instead of away from it.

I have been writing for quite some time now on the notion that the strength of a hypothesis is what it can’t explain, not what it can—if you are equally good at explaining any outcome, you have zero knowledge. So to spot an explanation that isn’t helpful, it’s not enough to think of what it does explain very well—you also have to search for results it couldn’t explain, and this is the true strength of the theory.

So I said all this, and then I challenged the usefulness of “emergence” as a concept. One commenter cited superconductivity and ferromagnetism as examples of emergence. I replied that non-superconductivity and non-ferromagnetism were also examples of emergence, which was the problem. But be it far from me to criticize the commenter! Despite having read extensively on “confirmation bias,” I didn’t spot the “gotcha” in the 2-4-6 task the first time I read about it. It’s a subverbal blink-reaction that has to be retrained. I’m still working on it myself.

So much of a rationalist’s skill is below the level of words. It makes for challenging work in trying to convey the Art through words. People will agree with you, but then, in the next sentence, do something subdeliberative that goes in the opposite direction. Not that I’m complaining! A major reason I’m writing this is to observe what my words haven’t conveyed.

Are you searching for positive examples of positive bias right now, or sparing a fraction of your search on what positive bias should lead you to not see? Did you look toward light or darkness?

1. Peter Cathcart Wason, “On the Failure to Eliminate Hypotheses in a Conceptual Task,” Quarterly Journal of Experimental Psychology 12, no. 3 (1960): 129–140, doi:10.1080/17470216008416717.

39
Lawful Uncertainty

In Rational Choice in an Uncertain World, Robyn Dawes describes an experiment by Tversky:¹^,²

Many psychological experiments were conducted in the late 1950s and early 1960s in which subjects were asked to predict the outcome of an event that had a random component but yet had base-rate predictability—for example, subjects were asked to predict whether the next card the experimenter turned over would be red or blue in a context in which 70% of the cards were blue, but in which the sequence of red and blue cards was totally random.

In such a situation, the strategy that will yield the highest proportion of success is to predict the more common event. For example, if 70% of the cards are blue, then predicting blue on every trial yields a 70% success rate.

What subjects tended to do instead, however, was match probabilities—that is, predict the more probable event with the relative frequency with which it occurred. For example, subjects tended to predict 70% of the time that the blue card would occur and 30% of the time that the red card would occur. Such a strategy yields a 58% success rate, because the subjects are correct 70% of the time when the blue card occurs (which happens with probability .70) and 30% of the time when the red card occurs (which happens with probability .30); (.70 × .70) + (.30 × .30) = .58.

In fact, subjects predict the more frequent event with a slightly higher probability than that with which it occurs, but do not come close to predicting its occurrence 100% of the time, even when they are paid for the accuracy of their predictions . . . For example, subjects who were paid a nickel for each correct prediction over a thousand trials . . . predicted [the more common event] 76% of the time.

Do not think that this experiment is about a minor flaw in gambling strategies. It compactly illustrates the most important idea in all of rationality.

Subjects just keep guessing red, as if they think they have some way of predicting the random sequence. Of this experiment Dawes goes on to say, “Despite feedback through a thousand trials, subjects cannot bring themselves to believe that the situation is one in which they cannot predict.”

But the error must go deeper than that. Even if subjects think they’ve come up with a hypothesis, they don’t have to actually bet on that prediction in order to test their hypothesis. They can say, “Now if this hypothesis is correct, the next card will be red”—and then just bet on blue. They can pick blue each time, accumulating as many nickels as they can, while mentally noting their private guesses for any patterns they thought they spotted. If their predictions come out right, then they can switch to the newly discovered sequence.

I wouldn’t fault a subject for continuing to invent hypotheses—how could they know the sequence is truly beyond their ability to predict? But I would fault a subject for betting on the guesses, when this wasn’t necessary to gather information, and literally hundreds of earlier guesses had been disconfirmed.

Can even a human be that overconfident?

I would suspect that something simpler is going on—that the all-blue strategy just didn’t occur to the subjects.

People see a mix of mostly blue cards with some red, and suppose that the optimal betting strategy must be a mix of mostly blue cards with some red.

It is a counterintuitive idea that, given incomplete information, the optimal betting strategy does not resemble a typical sequence of cards.

It is a counterintuitive idea that the optimal strategy is to behave lawfully, even in an environment that has random elements.

It seems like your behavior ought to be unpredictable, just like the environment—but no! A random key does not open a random lock just because they are “both random.”

You don’t fight fire with fire; you fight fire with water. But this thought involves an extra step, a new concept not directly activated by the problem statement, and so it’s not the first idea that comes to mind.

In the dilemma of the blue and red cards, our partial knowledge tells us—on each and every round—that the best bet is blue. This advice of our partial knowledge is the same on each and every round. If 30% of the time we go against our partial knowledge and bet on red instead, then we will do worse thereby—because now we’re being outright stupid, betting on what we know is the less probable outcome.

If you bet on red every round, you would do as badly as you could possibly do; you would be 100% stupid. If you bet on red 30% of the time, faced with 30% red cards, then you’re making yourself 30% stupid.

When your knowledge is incomplete—meaning that the world will seem to you to have an element of randomness—randomizing your actions doesn’t solve the problem. Randomizing your actions takes you further from the target, not closer. In a world already foggy, throwing away your intelligence just makes things worse.

It is a counterintuitive idea that the optimal strategy can be to think lawfully, even under conditions of uncertainty.

And so there are not many rationalists, for most who perceive a chaotic world will try to fight chaos with chaos. You have to take an extra step, and think of something that doesn’t pop right into your mind, in order to imagine fighting fire with something that is not itself fire.

You have heard the unenlightened ones say, “Rationality works fine for dealing with rational people, but the world isn’t rational.” But faced with an irrational opponent, throwing away your own reason is not going to help you. There are lawful forms of thought that still generate the best response, even when faced with an opponent who breaks those laws. Decision theory does not burst into flames and die when faced with an opponent who disobeys decision theory.

This is no more obvious than the idea of betting all blue, faced with a sequence of both blue and red cards. But each bet that you make on red is an expected loss, and so too with every departure from the Way in your own thinking.

How many Star Trek episodes are thus refuted? How many theories of AI?

1. Dawes, Rational Choice in An Uncertain World; Yaacov Schul and Ruth Mayo, “Searching for Certainty in an Uncertain World: The Difficulty of Giving Up the Experiential for the Rational Mode of Thinking,” Journal of Behavioral Decision Making 16, no. 2 (2003): 93–106, doi:10.1002/bdm.434.

2. Amos Tversky and Ward Edwards, “Information versus Reward in Binary Choices,” Journal of Experimental Psychology 71, no. 5 (1966): 680–683, doi:10.1037/h0023123.

40
My Wild and Reckless Youth

It is said that parents do all the things they tell their children not to do, which is how they know not to do them.

Long ago, in the unthinkably distant past, I was a devoted Traditional Rationalist, conceiving myself skilled according to that kind, yet I knew not the Way of Bayes. When the young Eliezer was confronted with a mysterious-seeming question, the precepts of Traditional Rationality did not stop him from devising a Mysterious Answer. It is, by far, the most embarrassing mistake I made in my life, and I still wince to think of it.

What was my mysterious answer to a mysterious question? This I will not describe, for it would be a long tale and complicated. I was young, and a mere Traditional Rationalist who knew not the teachings of Tversky and Kahneman. I knew about Occam’s Razor, but not the conjunction fallacy. I thought I could get away with thinking complicated thoughts myself, in the literary style of the complicated thoughts I read in science books, not realizing that correct complexity is only possible when every step is pinned down overwhelmingly. Today, one of the chief pieces of advice I give to aspiring young rationalists is “Do not attempt long chains of reasoning or complicated plans.”

Nothing more than this need be said: Even after I invented my “answer,” the phenomenon was still a mystery unto me, and possessed the same quality of wondrous impenetrability that it had at the start.

Make no mistake, that younger Eliezer was not stupid. All the errors of which the young Eliezer was guilty are still being made today by respected scientists in respected journals. It would have taken a subtler skill to protect him than ever he was taught as a Traditional Rationalist.

Indeed, the young Eliezer diligently and painstakingly followed the injunctions of Traditional Rationality in the course of going astray.

As a Traditional Rationalist, the young Eliezer was careful to ensure that his Mysterious Answer made a bold prediction of future experience. Namely, I expected future neurologists to discover that neurons were exploiting quantum gravity, a la Sir Roger Penrose. This required neurons to maintain a certain degree of quantum coherence, which was something you could look for, and find or not find. Either you observe that or you don’t, right?

But my hypothesis made no retrospective predictions. According to Traditional Science, retrospective predictions don’t count—so why bother making them? To a Bayesian, on the other hand, if a hypothesis does not today have a favorable likelihood ratio over “I don’t know,” it raises the question of why you today believe anything more complicated than “I don’t know.” But I knew not the Way of Bayes, so I was not thinking about likelihood ratios or focusing probability density. I had Made a Falsifiable Prediction; was this not the Law?

As a Traditional Rationalist, the young Eliezer was careful not to believe in magic, mysticism, carbon chauvinism, or anything of that sort. I proudly professed of my Mysterious Answer, “It is just physics like all the rest of physics!” As if you could save magic from being a cognitive isomorph of magic, by calling it quantum gravity. But I knew not the Way of Bayes, and did not see the level on which my idea was isomorphic to magic. I gave my allegiance to physics, but this did not save me; what does probability theory know of allegiances? I avoided everything that Traditional Rationality told me was forbidden, but what was left was still magic.

Beyond a doubt, my allegiance to Traditional Rationality helped me get out of the hole I dug myself into. If I hadn’t been a Traditional Rationalist, I would have been completely screwed. But Traditional Rationality still wasn’t enough to get it right. It just led me into different mistakes than the ones it had explicitly forbidden.

When I think about how my younger self very carefully followed the rules of Traditional Rationality in the course of getting the answer wrong, it sheds light on the question of why people who call themselves “rationalists” do not rule the world. You need one whole hell of a lot of rationality before it does anything but lead you into new and interesting mistakes.

Traditional Rationality is taught as an art, rather than a science; you read the biography of famous physicists describing the lessons life taught them, and you try to do what they tell you to do. But you haven’t lived their lives, and half of what they’re trying to describe is an instinct that has been trained into them.

The way Traditional Rationality is designed, it would have been acceptable for me to spend thirty years on my silly idea, so long as I succeeded in falsifying it eventually, and was honest with myself about what my theory predicted, and accepted the disproof when it arrived, et cetera. This is enough to let the Ratchet of Science click forward, but it’s a little harsh on the people who waste thirty years of their lives. Traditional Rationality is a walk, not a dance. It’s designed to get you to the truth eventually, and gives you all too much time to smell the flowers along the way.

Traditional Rationalists can agree to disagree. Traditional Rationality doesn’t have the ideal that thinking is an exact art in which there is only one correct probability estimate given the evidence. In Traditional Rationality, you’re allowed to guess, and then test your guess. But experience has taught me that if you don’t know, and you guess, you’ll end up being wrong.

The Way of Bayes is also an imprecise art, at least the way I’m holding forth upon it. These essays are still fumbling attempts to put into words lessons that would be better taught by experience. But at least there’s underlying math, plus experimental evidence from cognitive psychology on how humans actually think. Maybe that will be enough to cross the stratospherically high threshold required for a discipline that lets you actually get it right, instead of just constraining you into interesting new mistakes.

41
Failing to Learn from History

Once upon a time, in my wild and reckless youth, when I knew not the Way of Bayes, I gave a Mysterious Answer to a mysterious-seeming question. Many failures occurred in sequence, but one mistake stands out as most critical: My younger self did not realize that solving a mystery should make it feel less confusing. I was trying to explain a Mysterious Phenomenon—which to me meant providing a cause for it, fitting it into an integrated model of reality. Why should this make the phenomenon less Mysterious, when that is its nature? I was trying to explain the Mysterious Phenomenon, not render it (by some impossible alchemy) into a mundane phenomenon, a phenomenon that wouldn’t even call out for an unusual explanation in the first place.

As a Traditional Rationalist, I knew the historical tales of astrologers and astronomy, of alchemists and chemistry, of vitalists and biology. But the Mysterious Phenomenon was not like this. It was something new, something stranger, something more difficult, something that ordinary science had failed to explain for centuries—

—as if stars and matter and life had not been mysteries for hundreds of years and thousands of years, from the dawn of human thought right up until science finally solved them—

We learn about astronomy and chemistry and biology in school, and it seems to us that these matters have always been the proper realm of science, that they have never been mysterious. When science dares to challenge a new Great Puzzle, the children of that generation are skeptical, for they have never seen science explain something that feels mysterious to them. Science is only good for explaining scientific subjects, like stars and matter and life.

I thought the lesson of history was that astrologers and alchemists and vitalists had an innate character flaw, a tendency toward mysterianism, which led them to come up with mysterious explanations for non-mysterious subjects. But surely, if a phenomenon really was very weird, a weird explanation might be in order?

It was only afterward, when I began to see the mundane structure inside the mystery, that I realized whose shoes I was standing in. Only then did I realize how reasonable vitalism had seemed at the time, how surprising and embarrassing had been the universe’s reply of, “Life is mundane, and does not need a weird explanation.”

We read history but we don’t live it, we don’t experience it. If only I had personally postulated astrological mysteries and then discovered Newtonian mechanics, postulated alchemical mysteries and then discovered chemistry, postulated vitalistic mysteries and then discovered biology. I would have thought of my Mysterious Answer and said to myself: No way am I falling for that again.

42
Making History Available

There is a habit of thought which I call the logical fallacy of generalization from fictional evidence. Journalists who, for example, talk about the Terminator movies in a report on AI, do not usually treat Terminator as a prophecy or fixed truth. But the movie is recalled—is available—as if it were an illustrative historical case. As if the journalist had seen it happen on some other planet, so that it might well happen here. More on this in Section 7 of ”Cognitive biases potentially affecting judgment of global risks.”¹

There is an inverse error to generalizing from fictional evidence: failing to be sufficiently moved by historical evidence. The trouble with generalizing from fictional evidence is that it is fiction—it never actually happened. It’s not drawn from the same distribution as this, our real universe; fiction differs from reality in systematic ways. But history has happened, and should be available.

In our ancestral environment, there were no movies; what you saw with your own eyes was true. Is it any wonder that fictions we see in lifelike moving pictures have too great an impact on us? Conversely, things that really happened, we encounter as ink on paper; they happened, but we never saw them happen. We don’t remember them happening to us.

The inverse error is to treat history as mere story, process it with the same part of your mind that handles the novels you read. You may say with your lips that it is “truth,” rather than “fiction,” but that doesn’t mean you are being moved as much as you should be. Many biases involve being insufficiently moved by dry, abstract information.

Once upon a time, I gave a Mysterious Answer to a mysterious question, not realizing that I was making exactly the same mistake as astrologers devising mystical explanations for the stars, or alchemists devising magical properties of matter, or vitalists postulating an opaque “élan vital” to explain all of biology.

When I finally realized whose shoes I was standing in, there was a sudden shock of unexpected connection with the past. I realized that the invention and destruction of vitalism—which I had only read about in books—had actually happened to real people, who experienced it much the same way I experienced the invention and destruction of my own mysterious answer. And I also realized that if I had actually experienced the past—if I had lived through past scientific revolutions myself, rather than reading about them in history books—I probably would not have made the same mistake again. I would not have come up with another mysterious answer; the first thousand lessons would have hammered home the moral.

So (I thought), to feel sufficiently the force of history, I should try to approximate the thoughts of an Eliezer who had lived through history—I should try to think as if everything I read about in history books had actually happened to me. (With appropriate reweighting for the availability bias of history books—I should remember being a thousand peasants for every ruler.) I should immerse myself in history, imagine living through eras I only saw as ink on paper.

Why should I remember the Wright Brothers’ first flight? I was not there. But as a rationalist, could I dare to not remember, when the event actually happened? Is there so much difference between seeing an event through your eyes—which is actually a causal chain involving reflected photons, not a direct connection—and seeing an event through a history book? Photons and history books both descend by causal chains from the event itself.

I had to overcome the false amnesia of being born at a particular time. I had to recall—make available—all the memories, not just the memories which, by mere coincidence, belonged to myself and my own era.

The Earth became older, of a sudden.

To my former memory, the United States had always existed—there was never a time when there was no United States. I had not remembered, until that time, how the Roman Empire rose, and brought peace and order, and lasted through so many centuries, until I forgot that things had ever been otherwise; and yet the Empire fell, and barbarians overran my city, and the learning that I had possessed was lost. The modern world became more fragile to my eyes; it was not the first modern world.

So many mistakes, made over and over and over again, because I did not remember making them, in every era I never lived . . .

And to think, people sometimes wonder if overcoming bias is important.

Don’t you remember how many times your biases have killed you? You don’t? I’ve noticed that sudden amnesia often follows a fatal mistake. But take it from me, it happened. I remember; I wasn’t there.

So the next time you doubt the strangeness of the future, remember how you were born in a hunter-gatherer tribe ten thousand years ago, when no one knew of Science at all. Remember how you were shocked, to the depths of your being, when Science explained the great and terrible sacred mysteries that you once revered so highly. Remember how you once believed that you could fly by eating the right mushrooms, and then you accepted with disappointment that you would never fly, and then you flew. Remember how you had always thought that slavery was right and proper, and then you changed your mind. Don’t imagine how you could have predicted the change, for that is amnesia. Remember that, in fact, you did not guess. Remember how, century after century, the world changed in ways you did not guess.

Maybe then you will be less shocked by what happens next.

1. Eliezer Yudkowsky, “Cognitive Biases Potentially Affecting Judgment of Global Risks,” in Global Catastrophic Risks, ed. Nick Bostrom and Milan M. Ćirković (New York: Oxford University Press, 2008), 91–119.

43
Explain/Worship/Ignore?

As our tribe wanders through the grasslands, searching for fruit trees and prey, it happens every now and then that water pours down from the sky.

“Why does water sometimes fall from the sky?” I ask the bearded wise man of our tribe.

He thinks for a moment, this question having never occurred to him before, and then says, “From time to time, the sky spirits battle, and when they do, their blood drips from the sky.”

“Where do the sky spirits come from?” I ask.

His voice drops to a whisper. “From the before time. From the long long ago.”

When it rains, and you don’t know why, you have several options. First, you could simply not ask why—not follow up on the question, or never think of the question in the first place. This is the Ignore command, which the bearded wise man originally selected. Second, you could try to devise some sort of explanation, the Explain command, as the bearded man did in response to your first question. Third, you could enjoy the sensation of mysteriousness—the Worship command.

Now, as you are bound to notice from this story, each time you select Explain, the best-case scenario is that you get an explanation, such as “sky spirits.” But then this explanation itself is subject to the same dilemma—Explain, Worship, or Ignore? Each time you hit Explain, science grinds for a while, returns an explanation, and then another dialog box pops up. As good rationalists, we feel duty-bound to keep hitting Explain, but it seems like a road that has no end.

You hit Explain for life, and get chemistry; you hit Explain for chemistry, and get atoms; you hit Explain for atoms, and get electrons and nuclei; you hit Explain for nuclei, and get quantum chromodynamics and quarks; you hit Explain for how the quarks got there, and get back the Big Bang . . .

We can hit Explain for the Big Bang, and wait while science grinds through its process, and maybe someday it will return a perfectly good explanation. But then that will just bring up another dialog box. So, if we continue long enough, we must come to a special dialog box, a new option, an Explanation That Needs No Explanation, a place where the chain ends—and this, maybe, is the only explanation worth knowing.

There—I just hit Worship.

Never forget that there are many more ways to worship something than lighting candles around an altar.

If I’d said, “Huh, that does seem paradoxical. I wonder how the apparent paradox is resolved?” then I would have hit Explain, which does sometimes take a while to produce an answer.

And if the whole issue seems to you unimportant, or irrelevant, or if you’d rather put off thinking about it until tomorrow, than you have hit Ignore.

Select your option wisely.

44
“Science” as CuriosityStopper

Imagine that I, in full view of live television cameras, raised my hands and chanted abracadabra and caused a brilliant light to be born, flaring in empty space beyond my outstretched hands. Imagine that I committed this act of blatant, unmistakeable sorcery under the full supervision of James Randi and all skeptical armies. Most people, I think, would be fairly curious as to what was going on.

But now suppose instead that I don’t go on television. I do not wish to share the power, nor the truth behind it. I want to keep my sorcery secret. And yet I also want to cast my spells whenever and wherever I please. I want to cast my brilliant flare of light so that I can read a book on the train—without anyone becoming curious. Is there a spell that stops curiosity?

Yes indeed! Whenever anyone asks “How did you do that?,” I just say “Science!”

It’s not a real explanation, so much as a curiositystopper. It doesn’t tell you whether the light will brighten or fade, change color in hue or saturation, and it certainly doesn’t tell you how to make a similar light yourself. You don’t actually know anything more than you knew before I said the magic word. But you turn away, satisfied that nothing unusual is going on.

Better yet, the same trick works with a standard light switch.

Flip a switch and a light bulb turns on. Why?

In school, one is taught that the password to the light bulb is “Electricity!” By now, I hope, you’re wary of marking the light bulb “understood” on such a basis. Does saying “Electricity!” let you do calculations that will control your anticipation of experience? There is, at the least, a great deal more to learn. (Physicists should ignore this paragraph and substitute a problem in evolutionary theory, where the substance of the theory is again in calculations that few people know how to perform.)

If you thought the light bulb was scientifically inexplicable, it would seize the entirety of your attention. You would drop whatever else you were doing, and focus on that light bulb.

But what does the phrase “scientifically explicable” mean? It means that someone else knows how the light bulb works. When you are told the light bulb is “scientifically explicable,” you don’t know more than you knew earlier; you don’t know whether the light bulb will brighten or fade. But because someone else knows, it devalues the knowledge in your eyes. You become less curious.

Someone is bound to say, “If the light bulb were unknown to science, you could gain fame and fortune by investigating it.” But I’m not talking about greed. I’m not talking about career ambition. I’m talking about the raw emotion of curiosity—the feeling of being intrigued. Why should your curiosity be diminished because someone else, not you, knows how the light bulb works? Is this not spite? It’s not enough for you to know; other people must also be ignorant, or you won’t be happy?

There are goods that knowledge may serve besides curiosity, such as the social utility of technology. For these instrumental goods, it matters whether some other entity in local space already knows. But for my own curiosity, why should it matter?

Besides, consider the consequences if you permit “Someone else knows the answer” to function as a curiositystopper. One day you walk into your living room and see a giant green elephant, seemingly hovering in midair, surrounded by an aura of silver light.

“What the heck?” you say.

And a voice comes from above the elephant, saying,

SOMEBODY ALREADY KNOWS WHY THIS ELEPHANT IS HERE.

“Oh,” you say, “in that case, never mind,” and walk on to the kitchen.

I don’t know the grand unified theory for this universe’s laws of physics. I also don’t know much about human anatomy with the exception of the brain. I couldn’t point out on my body where my kidneys are, and I can’t recall offhand what my liver does. (I am not proud of this. Alas, with all the math I need to study, I’m not likely to learn anatomy anytime soon.)

Should I, so far as curiosity is concerned, be more intrigued by my ignorance of the ultimate laws of physics, than the fact that I don’t know much about what goes on inside my own body?

If I raised my hands and cast a light spell, you would be intrigued. Should you be any less intrigued by the very fact that I raised my hands? When you raise your arm and wave a hand around, this act of will is coordinated by (among other brain areas) your cerebellum. I bet you don’t know how the cerebellum works. I know a little—though only the gross details, not enough to perform calculations . . . but so what? What does that matter, if you don’t know? Why should there be a double standard of curiosity for sorcery and hand motions?

Look at yourself in the mirror. Do you know what you’re looking at? Do you know what looks out from behind your eyes? Do you know what you are? Some of that answer, Science knows, and some of it Science does not. But why should that distinction matter to your curiosity, if you don’t know?

Do you know how your knees work? Do you know how your shoes were made? Do you know why your computer monitor glows? Do you know why water is wet?

The world around you is full of puzzles. Prioritize, if you must. But do not complain that cruel Science has emptied the world of mystery. With reasoning such as that, I could get you to overlook an elephant in your living room.

45
Truly Part of You

A classic paper by Drew McDermott, “Artificial Intelligence Meets Natural Stupidity,” criticized AI programs that would try to represent notions like happiness is a state of mind using a semantic network:¹

HAPPINESS ---IS-A---> STATE-OF-MIND

And of course there’s nothing inside the HAPPINESS node; it’s just a naked LISP token with a suggestive English name.

So, McDermott says, “A good test for the disciplined programmer is to try using gensyms in key places and see if he still admires his system. For example, if STATE-OF-MIND is renamed G1073 . . .” then we would have IS-A(HAPPINESS, G1073) “which looks much more dubious.”

Or as I would slightly rephrase the idea: If you substituted randomized symbols for all the suggestive English names, you would be completely unable to figure out what G1071(G1072, G1073) meant. Was the AI program meant to represent hamburgers? Apples? Happiness? Who knows? If you delete the suggestive English names, they don’t grow back.

Suppose a physicist tells you that “Light is waves,” and you believe the physicist. You now have a little network in your head that says:

IS-A(LIGHT, WAVES).

If someone asks you “What is light made of?” you’ll be able to say “Waves!”

As McDermott says, “The whole problem is getting the hearer to notice what it has been told. Not ‘understand,’ but ‘notice.’” Suppose that instead the physicist told you, “Light is made of little curvy things.” (Not true, by the way.) Would you notice any difference of anticipated experience?

How can you realize that you shouldn’t trust your seeming knowledge that “light is waves”? One test you could apply is asking, “Could I regenerate this knowledge if it were somehow deleted from my mind?”

This is similar in spirit to scrambling the names of suggestively named LISP tokens in your AI program, and seeing if someone else can figure out what they allegedly “refer” to. It’s also similar in spirit to observing that an Artificial Arithmetician programmed to record and play back

Plus-Of(Seven, Six) = Thirteen

can’t regenerate the knowledge if you delete it from memory, until another human re-enters it in the database. Just as if you forgot that “light is waves,” you couldn’t get back the knowledge except the same way you got the knowledge to begin with—by asking a physicist. You couldn’t generate the knowledge for yourself, the way that physicists originally generated it.

The same experiences that lead us to formulate a belief, connect that belief to other knowledge and sensory input and motor output. If you see a beaver chewing a log, then you know what this thing-that-chews-through-logs looks like, and you will be able to recognize it on future occasions whether it is called a “beaver” or not. But if you acquire your beliefs about beavers by someone else telling you facts about “beavers,” you may not be able to recognize a beaver when you see one.

This is the terrible danger of trying to tell an Artificial Intelligence facts that it could not learn for itself. It is also the terrible danger of trying to tell someone about physics that they cannot verify for themselves. For what physicists mean by “wave” is not “little squiggly thing” but a purely mathematical concept.

As Davidson observes, if you believe that “beavers” live in deserts, are pure white in color, and weigh 300 pounds when adult, then you do not have any beliefs about beavers, true or false. Your belief about “beavers” is not right enough to be wrong.² If you don’t have enough experience to regenerate beliefs when they are deleted, then do you have enough experience to connect that belief to anything at all? Wittgenstein: “A wheel that can be turned though nothing else moves with it, is not part of the mechanism.”

Almost as soon as I started reading about AI—even before I read McDermott—I realized it would be a really good idea to always ask myself: “How would I regenerate this knowledge if it were deleted from my mind?”

The deeper the deletion, the stricter the test. If all proofs of the Pythagorean Theorem were deleted from my mind, could I re-prove it? I think so. If all knowledge of the Pythagorean Theorem were deleted from my mind, would I notice the Pythagorean Theorem to re-prove? That’s harder to boast, without putting it to the test; but if you handed me a right triangle with sides of length 3 and 4, and told me that the length of the hypotenuse was calculable, I think I would be able to calculate it, if I still knew all the rest of my math.

What about the notion of mathematical proof? If no one had ever told it to me, would I be able to reinvent that on the basis of other beliefs I possess? There was a time when humanity did not have such a concept. Someone must have invented it. What was it that they noticed? Would I notice if I saw something equally novel and equally important? Would I be able to think that far outside the box?

How much of your knowledge could you regenerate? From how deep a deletion? It’s not just a test to cast out insufficiently connected beliefs. It’s a way of absorbing a fountain of knowledge, not just one fact.

A shepherd builds a counting system that works by throwing a pebble into a bucket whenever a sheep leaves the fold, and taking a pebble out whenever a sheep returns. If you, the apprentice, do not understand this system—if it is magic that works for no apparent reason—then you will not know what to do if you accidentally drop an extra pebble into the bucket. That which you cannot make yourself, you cannot remake when the situation calls for it. You cannot go back to the source, tweak one of the parameter settings, and regenerate the output, without the source. If “two plus four equals six” is a brute fact unto you, and then one of the elements changes to “five,” how are you to know that “two plus five equals seven” when you were simply told that “two plus four equals six”?

If you see a small plant that drops a seed whenever a bird passes it, it will not occur to you that you can use this plant to partially automate the sheep-counter. Though you learned something that the original maker would use to improve on their invention, you can’t go back to the source and re-create it.

When you contain the source of a thought, that thought can change along with you as you acquire new knowledge and new skills. When you contain the source of a thought, it becomes truly a part of you and grows along with you.

Strive to make yourself the source of every thought worth thinking. If the thought originally came from outside, make sure it comes from inside as well. Continually ask yourself: “How would I regenerate the thought if it were deleted?” When you have an answer, imagine that knowledge being deleted as well. And when you find a fountain, see what else it can pour.

1. Drew McDermott, “Artificial Intelligence Meets Natural Stupidity,” SIGART Newsletter, no. 57 (1976): 4–9, doi:10.1145/1045339.1045340.

2. Richard Rorty, “Out of the Matrix: How the Late Philosopher Donald Davidson Showed That Reality Can’t Be an Illusion,” The Boston Globe (October 2003).

Interlude
The Simple Truth

I remember this paper I wrote on existentialism. My teacher gave it back with an F. She’d underlined true and truth wherever it appeared in the essay, probably about twenty times, with a question mark beside each. She wanted to know what I meant by truth.

—Danielle Egan, journalist

This essay is meant to restore a naive view of truth.

Someone says to you: “My miracle snake oil can rid you of lung cancer in just three weeks.” You reply: “Didn’t a clinical study show this claim to be untrue?” The one returns: “This notion of ‘truth’ is quite naive; what do you mean by ‘true’?”

Many people, so questioned, don’t know how to answer in exquisitely rigorous detail. Nonetheless they would not be wise to abandon the concept of “truth.” There was a time when no one knew the equations of gravity in exquisitely rigorous detail, yet if you walked off a cliff, you would fall.

Often I have seen—especially on Internet mailing lists—that amidst other conversation, someone says “X is true,” and then an argument breaks out over the use of the word “true.” This essay is not meant as an encyclopedic reference for that argument. Rather, I hope the arguers will read this essay, and then go back to whatever they were discussing before someone questioned the nature of truth.

In this essay I pose questions. If you see what seems like a really obvious answer, it’s probably the answer I intend. The obvious choice isn’t always the best choice, but sometimes, by golly, it is. I don’t stop looking as soon I find an obvious answer, but if I go on looking, and the obvious-seeming answer still seems obvious, I don’t feel guilty about keeping it. Oh, sure, everyone thinks two plus two is four, everyone says two plus two is four, and in the mere mundane drudgery of everyday life everyone behaves as if two plus two is four, but what does two plus two really, ultimately equal? As near as I can figure, four. It’s still four even if I intone the question in a solemn, portentous tone of voice. Too simple, you say? Maybe, on this occasion, life doesn’t need to be complicated. Wouldn’t that be refreshing?

If you are one of those fortunate folk to whom the question seems trivial at the outset, I hope it still seems trivial at the finish. If you find yourself stumped by deep and meaningful questions, remember that if you know exactly how a system works, and could build one yourself out of buckets and pebbles, it should not be a mystery to you.

If confusion threatens when you interpret a metaphor as a metaphor, try taking everything completely literally.

Imagine that in an era before recorded history or formal mathematics, I am a shepherd and I have trouble tracking my sheep. My sheep sleep in an enclosure, a fold; and the enclosure is high enough to guard my sheep from wolves that roam by night. Each day I must release my sheep from the fold to pasture and graze; each night I must find my sheep and return them to the fold. If a sheep is left outside, I will find its body the next morning, killed and half-eaten by wolves. But it is so discouraging, to scour the fields for hours, looking for one last sheep, when I know that probably all the sheep are in the fold. Sometimes I give up early, and usually I get away with it; but around a tenth of the time there is a dead sheep the next morning.

If only there were some way to divine whether sheep are still grazing, without the inconvenience of looking! I try several methods: I toss the divination sticks of my tribe; I train my psychic powers to locate sheep through clairvoyance; I search carefully for reasons to believe all the sheep are in the fold. It makes no difference. Around a tenth of the times I turn in early, I find a dead sheep the next morning. Perhaps I realize that my methods aren’t working, and perhaps I carefully excuse each failure; but my dilemma is still the same. I can spend an hour searching every possible nook and cranny, when most of the time there are no remaining sheep; or I can go to sleep early and lose, on the average, one-tenth of a sheep.

Late one afternoon I feel especially tired. I toss the divination sticks and the divination sticks say that all the sheep have returned. I visualize each nook and cranny, and I don’t imagine scrying any sheep. I’m still not confident enough, so I look inside the fold and it seems like there are a lot of sheep, and I review my earlier efforts and decide that I was especially diligent. This dissipates my anxiety, and I go to sleep. The next morning I discover two dead sheep. Something inside me snaps, and I begin thinking creatively.

That day, loud hammering noises come from the gate of the sheepfold’s enclosure.

The next morning, I open the gate of the enclosure only a little way, and as each sheep passes out of the enclosure, I drop a pebble into a bucket nailed up next to the door. In the afternoon, as each returning sheep passes by, I take one pebble out of the bucket. When there are no pebbles left in the bucket, I can stop searching and turn in for the night. It is a brilliant notion. It will revolutionize shepherding.

That was the theory. In practice, it took considerable refinement before the method worked reliably. Several times I searched for hours and didn’t find any sheep, and the next morning there were no stragglers. On each of these occasions it required deep thought to figure out where my bucket system had failed. On returning from one fruitless search, I thought back and realized that the bucket already contained pebbles when I started; this, it turned out, was a bad idea. Another time I randomly tossed pebbles into the bucket, to amuse myself, between the morning and the afternoon; this too was a bad idea, as I realized after searching for a few hours. But I practiced my pebblecraft, and became a reasonably proficient pebblecrafter.

One afternoon, a man richly attired in white robes, leafy laurels, sandals, and business suit trudges in along the sandy trail that leads to my pastures.

“Can I help you?” I inquire.

The man takes a badge from his coat and flips it open, proving beyond the shadow of a doubt that he is Markos Sophisticus Maximus, a delegate from the Senate of Rum. (One might wonder whether another could steal the badge; but so great is the power of these badges that if any other were to use them, they would in that instant be transformed into Markos.)

“Call me Mark,” he says. “I’m here to confiscate the magic pebbles, in the name of the Senate; artifacts of such great power must not fall into ignorant hands.”

“That bleedin’ apprentice,” I grouse under my breath, “he’s been yakkin’ to the villagers again.” Then I look at Mark’s stern face, and sigh. “They aren’t magic pebbles,” I say aloud. “Just ordinary stones I picked up from the ground.”

A flicker of confusion crosses Mark’s face, then he brightens again. “I’m here for the magic bucket!” he declares.

“It’s not a magic bucket,” I say wearily. “I used to keep dirty socks in it.”

Mark’s face is puzzled. “Then where is the magic?” he demands.

An interesting question. “It’s hard to explain,” I say.

My current apprentice, Autrey, attracted by the commotion, wanders over and volunteers his explanation: “It’s the level of pebbles in the bucket,” Autrey says. “There’s a magic level of pebbles, and you have to get the level just right, or it doesn’t work. If you throw in more pebbles, or take some out, the bucket won’t be at the magic level anymore. Right now, the magic level is,” Autrey peers into the bucket, “about one-third full.”

“I see!” Mark says excitedly. From his back pocket Mark takes out his own bucket, and a heap of pebbles. Then he grabs a few handfuls of pebbles, and stuffs them into the bucket. Then Mark looks into the bucket, noting how many pebbles are there. “There we go,” Mark says, “the magic level of this bucket is half full. Like that?”

“No!” Autrey says sharply. “Half full is not the magic level. The magic level is about one-third. Half full is definitely unmagic. Furthermore, you’re using the wrong bucket.”

Mark turns to me, puzzled. “I thought you said the bucket wasn’t magic?”

“It’s not,” I say. A sheep passes out through the gate, and I toss another pebble into the bucket. “Besides, I’m watching the sheep. Talk to Autrey.”

Mark dubiously eyes the pebble I tossed in, but decides to temporarily shelve the question. Mark turns to Autrey and draws himself up haughtily. “It’s a free country,” Mark says, “under the benevolent dictatorship of the Senate, of course. I can drop whichever pebbles I like into whatever bucket I like.”

Autrey considers this. “No you can’t,” he says finally, “there won’t be any magic.”

“Look,” says Mark patiently, “I watched you carefully. You looked in your bucket, checked the level of pebbles, and called that the magic level. I did exactly the same thing.”

“That’s not how it works,” says Autrey.

“Oh, I see,” says Mark, “It’s not the level of pebbles in my bucket that’s magic, it’s the level of pebbles in your bucket. Is that what you claim? What makes your bucket so much better than mine, huh?”

“Well,” says Autrey, “if we were to empty your bucket, and then pour all the pebbles from my bucket into your bucket, then your bucket would have the magic level. There’s also a procedure we can use to check if your bucket has the magic level, if we know that my bucket has the magic level; we call that a bucket compare operation.”

Another sheep passes, and I toss in another pebble.

“He just tossed in another pebble!” Mark says. “And I suppose you claim the new level is also magic? I could toss pebbles into your bucket until the level was the same as mine, and then our buckets would agree. You’re just comparing my bucket to your bucket to determine whether you think the level is ‘magic’ or not. Well, I think your bucket isn’t magic, because it doesn’t have the same level of pebbles as mine. So there!”

“Wait,” says Autrey, “you don’t understand—”

“By ‘magic level,’ you mean simply the level of pebbles in your own bucket. And when I say ‘magic level,’ I mean the level of pebbles in my bucket. Thus you look at my bucket and say it ‘isn’t magic,’ but the word ‘magic’ means different things to different people. You need to specify whose magic it is. You should say that my bucket doesn’t have ‘Autrey’s magic level,’ and I say that your bucket doesn’t have ‘Mark’s magic level.’ That way, the apparent contradiction goes away.”

“But—” says Autrey helplessly.

“Different people can have different buckets with different levels of pebbles, which proves this business about ‘magic’ is completely arbitrary and subjective.”

“Mark,” I say, “did anyone tell you what these pebbles do?”

“Do?” says Mark. “I thought they were just magic.”

“If the pebbles didn’t do anything,” says Autrey, “our ISO 9000 process efficiency auditor would eliminate the procedure from our daily work.”

“What’s your auditor’s name?”

“Darwin,” says Autrey.

“Hm,” says Mark. “Charles does have a reputation as a strict auditor. So do the pebbles bless the flocks, and cause the increase of sheep?”

“No,” I say. “The virtue of the pebbles is this; if we look into the bucket and see the bucket is empty of pebbles, we know the pastures are likewise empty of sheep. If we do not use the bucket, we must search and search until dark, lest one last sheep remain. Or if we stop our work early, then sometimes the next morning we find a dead sheep, for the wolves savage any sheep left outside. If we look in the bucket, we know when all the sheep are home, and we can retire without fear.”

Mark considers this. “That sounds rather implausible,” he says eventually. “Did you consider using divination sticks? Divination sticks are infallible, or at least, anyone who says they are fallible is burned at the stake. This is an extremely painful way to die; it follows that divination sticks are infallible.”

“You’re welcome to use divination sticks if you like,” I say.

“Oh, good heavens, of course not,” says Mark. “They work infallibly, with absolute perfection on every occasion, as befits such blessed instruments; but what if there were a dead sheep the next morning? I only use the divination sticks when there is no possibility of their being proven wrong. Otherwise I might be burned alive. So how does your magic bucket work?”

How does the bucket work . . . ? I’d better start with the simplest possible case. “Well,” I say, “suppose the pastures are empty, and the bucket isn’t empty. Then we’ll waste hours looking for a sheep that isn’t there. And if there are sheep in the pastures, but the bucket is empty, then Autrey and I will turn in too early, and we’ll find dead sheep the next morning. So an empty bucket is magical if and only if the pastures are empty—”

“Hold on,” says Autrey. “That sounds like a vacuous tautology to me. Aren’t an empty bucket and empty pastures obviously the same thing?”

“It’s not vacuous,” I say. “Here’s an analogy: The logician Alfred Tarski once said that the assertion ‘Snow is white’ is true if and only if snow is white. If you can understand that, you should be able to see why an empty bucket is magical if and only if the pastures are empty of sheep.”

“Hold on,” says Mark. “These are buckets. They don’t have anything to do with sheep. Buckets and sheep are obviously completely different. There’s no way the sheep can ever interact with the bucket.”

“Then where do you think the magic comes from?” inquires Autrey.

Mark considers. “You said you could compare two buckets to check if they had the same level . . . I can see how buckets can interact with buckets. Maybe when you get a large collection of buckets, and they all have the same level, that’s what generates the magic. I’ll call that the coherentist theory of magic buckets.”

“Interesting,” says Autrey. “I know that my master is working on a system with multiple buckets—he says it might work better because of ‘redundancy’ and ‘error correction.’ That sounds like coherentism to me.”

“They’re not quite the same—” I start to say.

“Let’s test the coherentism theory of magic,” says Autrey. “I can see you’ve got five more buckets in your back pocket. I’ll hand you the bucket we’re using, and then you can fill up your other buckets to the same level—”

Mark recoils in horror. “Stop! These buckets have been passed down in my family for generations, and they’ve always had the same level! If I accept your bucket, my bucket collection will become less coherent, and the magic will go away!”

“But your current buckets don’t have anything to do with the sheep!” protests Autrey.

Mark looks exasperated. “Look, I’ve explained before, there’s obviously no way that sheep can interact with buckets. Buckets can only interact with other buckets.”

“I toss in a pebble whenever a sheep passes,” I point out.

“When a sheep passes, you toss in a pebble?” Mark says. “What does that have to do with anything?”

“It’s an interaction between the sheep and the pebbles,” I reply.

“No, it’s an interaction between the pebbles and you,” Mark says. “The magic doesn’t come from the sheep, it comes from you. Mere sheep are obviously nonmagical. The magic has to come from somewhere, on the way to the bucket.”

I point at a wooden mechanism perched on the gate. “Do you see that flap of cloth hanging down from that wooden contraption? We’re still fiddling with that—it doesn’t work reliably—but when sheep pass through, they disturb the cloth. When the cloth moves aside, a pebble drops out of a reservoir and falls into the bucket. That way, Autrey and I won’t have to toss in the pebbles ourselves.”

Mark furrows his brow. “I don’t quite follow you . . . is the cloth magical?”

I shrug. “I ordered it online from a company called Natural Selections. The fabric is called Sensory Modality.” I pause, seeing the incredulous expressions of Mark and Autrey. “I admit the names are a bit New Agey. The point is that a passing sheep triggers a chain of cause and effect that ends with a pebble in the bucket. Afterward you can compare the bucket to other buckets, and so on.”

“I still don’t get it,” Mark says. “You can’t fit a sheep into a bucket. Only pebbles go in buckets, and it’s obvious that pebbles only interact with other pebbles.”

“The sheep interact with things that interact with pebbles . . .” I search for an analogy. “Suppose you look down at your shoelaces. A photon leaves the Sun; then travels down through Earth’s atmosphere; then bounces off your shoelaces; then passes through the pupil of your eye; then strikes the retina; then is absorbed by a rod or a cone. The photon’s energy makes the attached neuron fire, which causes other neurons to fire. A neural activation pattern in your visual cortex can interact with your beliefs about your shoelaces, since beliefs about shoelaces also exist in neural substrate. If you can understand that, you should be able to see how a passing sheep causes a pebble to enter the bucket.”

“At exactly which point in the process does the pebble become magic?” says Mark.

“It . . . um . . .” Now I’m starting to get confused. I shake my head to clear away cobwebs. This all seemed simple enough when I woke up this morning, and the pebble-and-bucket system hasn’t gotten any more complicated since then. “This is a lot easier to understand if you remember that the point of the system is to keep track of sheep.”

Mark sighs sadly. “Never mind . . . it’s obvious you don’t know. Maybe all pebbles are magical to start with, even before they enter the bucket. We could call that position panpebblism.”

“Ha!” Autrey says, scorn rich in his voice. “Mere wishful thinking! Not all pebbles are created equal. The pebbles in your bucket are not magical. They’re only lumps of stone!”

Mark’s face turns stern. “Now,” he cries, “now you see the danger of the road you walk! Once you say that some people’s pebbles are magical and some are not, your pride will consume you! You will think yourself superior to all others, and so fall! Many throughout history have tortured and murdered because they thought their own pebbles supreme!” A tinge of condescension enters Mark’s voice. “Worshipping a level of pebbles as ‘magical’ implies that there’s an absolute pebble level in a Supreme Bucket. Nobody believes in a Supreme Bucket these days.”

“One,” I say. “Sheep are not absolute pebbles. Two, I don’t think my bucket actually contains the sheep. Three, I don’t worship my bucket level as perfect—I adjust it sometimes—and I do that because I care about the sheep.”

“Besides,” says Autrey, “someone who believes that possessing absolute pebbles would license torture and murder, is making a mistake that has nothing to do with buckets. You’re solving the wrong problem.”

Mark calms himself down. “I suppose I can’t expect any better from mere shepherds. You probably believe that snow is white, don’t you.”

“Um . . . yes?” says Autrey.

“It doesn’t bother you that Joseph Stalin believed that snow is white?”

“Um . . . no?” says Autrey.

Mark gazes incredulously at Autrey, and finally shrugs. “Let’s suppose, purely for the sake of argument, that your pebbles are magical and mine aren’t. Can you tell me what the difference is?”

“My pebbles represent the sheep!” Autrey says triumphantly. “Your pebbles don’t have the representativeness property, so they won’t work. They are empty of meaning. Just look at them. There’s no aura of semantic content; they are merely pebbles. You need a bucket with special causal powers.”

“Ah!” Mark says. “Special causal powers, instead of magic.”

“Exactly,” says Autrey. “I’m not superstitious. Postulating magic, in this day and age, would be unacceptable to the international shepherding community. We have found that postulating magic simply doesn’t work as an explanation for shepherding phenomena. So when I see something I don’t understand, and I want to explain it using a model with no internal detail that makes no predictions even in retrospect, I postulate special causal powers. If that doesn’t work, I’ll move on to calling it an emergent phenomenon.”

“What kind of special powers does the bucket have?” asks Mark.

“Hm,” says Autrey. “Maybe this bucket is imbued with an about-ness relation to the pastures. That would explain why it worked—when the bucket is empty, it means the pastures are empty.”

“Where did you find this bucket?” says Mark. “And how did you realize it had an about-ness relation to the pastures?”

“It’s an ordinary bucket,” I say. “I used to climb trees with it . . . I don’t think this question needs to be difficult.”

“I’m talking to Autrey,” says Mark.

“You have to bind the bucket to the pastures, and the pebbles to the sheep, using a magical ritual—pardon me, an emergent process with special causal powers—that my master discovered,” Autrey explains.

Autrey then attempts to describe the ritual, with Mark nodding along in sage comprehension.

“You have to throw in a pebble every time a sheep leaves through the gate?” says Mark. “Take out a pebble every time a sheep returns?”

Autrey nods. “Yeah.”

“That must be really hard,” Mark says sympathetically.

Autrey brightens, soaking up Mark’s sympathy like rain. “Exactly!” says Autrey. “It’s extremely hard on your emotions. When the bucket has held its level for a while, you . . . tend to get attached to that level.”

A sheep passes then, leaving through the gate. Autrey sees; he stoops, picks up a pebble, holds it aloft in the air. “Behold!” Autrey proclaims. “A sheep has passed! I must now toss a pebble into this bucket, my dear bucket, and destroy that fond level which has held for so long—” Another sheep passes. Autrey, caught up in his drama, misses it; so I plunk a pebble into the bucket. Autrey is still speaking: “—for that is the supreme test of the shepherd, to throw in the pebble, be it ever so agonizing, be the old level ever so precious. Indeed, only the best of shepherds can meet a requirement so stern—”

“Autrey,” I say, “if you want to be a great shepherd someday, learn to shut up and throw in the pebble. No fuss. No drama. Just do it.”

“And this ritual,” says Mark, “it binds the pebbles to the sheep by the magical laws of Sympathy and Contagion, like a voodoo doll.”

Autrey winces and looks around. “Please! Don’t call it Sympathy and Contagion. We shepherds are an anti-superstitious folk. Use the word ‘intentionality,’ or something like that.”

“Can I look at a pebble?” says Mark.

“Sure,” I say. I take one of the pebbles out of the bucket, and toss it to Mark. Then I reach to the ground, pick up another pebble, and drop it into the bucket.

Autrey looks at me, puzzled. “Didn’t you just mess it up?”

I shrug. “I don’t think so. We’ll know I messed it up if there’s a dead sheep next morning, or if we search for a few hours and don’t find any sheep.”

“But—” Autrey says.

“I taught you everything you know, but I haven’t taught you everything I know,” I say.

Mark is examining the pebble, staring at it intently. He holds his hand over the pebble and mutters a few words, then shakes his head. “I don’t sense any magical power,” he says. “Pardon me. I don’t sense any intentionality.”

“A pebble only has intentionality if it’s inside a ma—an emergent bucket,” says Autrey. “Otherwise it’s just a mere pebble.”

“Not a problem,” I say. I take a pebble out of the bucket, and toss it away. Then I walk over to where Mark stands, tap his hand holding a pebble, and say: “I declare this hand to be part of the magic bucket!” Then I resume my post at the gates.

Autrey laughs. “Now you’re just being gratuitously evil.”

I nod, for this is indeed the case.

“Is that really going to work, though?” says Autrey.

I nod again, hoping that I’m right. I’ve done this before with two buckets, and in principle, there should be no difference between Mark’s hand and a bucket. Even if Mark’s hand is imbued with the élan vital that distinguishes live matter from dead matter, the trick should work as well as if Mark were a marble statue.

Mark is looking at his hand, a bit unnerved. “So . . . the pebble has intentionality again, now?”

“Yep,” I say. “Don’t add any more pebbles to your hand, or throw away the one you have, or you’ll break the ritual.”

Mark nods solemnly. Then he resumes inspecting the pebble. “I understand now how your flocks grew so great,” Mark says. “With the power of this bucket, you could keep on tossing pebbles, and the sheep would keep returning from the fields. You could start with just a few sheep, let them leave, then fill the bucket to the brim before they returned. And if tending so many sheep grew tedious, you could let them all leave, then empty almost all the pebbles from the bucket, so that only a few returned . . . increasing the flocks again when it came time for shearing . . . dear heavens, man! Do you realize the sheer power of this ritual you’ve discovered? I can only imagine the implications; humankind might leap ahead a decade—no, a century!”

“It doesn’t work that way,” I say. “If you add a pebble when a sheep hasn’t left, or remove a pebble when a sheep hasn’t come in, that breaks the ritual. The power does not linger in the pebbles, but vanishes all at once, like a soap bubble popping.”

Mark’s face is terribly disappointed. “Are you sure?”

I nod. “I tried that and it didn’t work.”

Mark sighs heavily. “And this . . . math . . . seemed so powerful and useful until then . . . Oh, well. So much for human progress.”

“Mark, it was a brilliant idea,” Autrey says encouragingly. “The notion didn’t occur to me, and yet it’s so obvious . . . it would save an enormous amount of effort . . . there must be a way to salvage your plan! We could try different buckets, looking for one that would keep the magical pow—the intentionality in the pebbles, even without the ritual. Or try other pebbles. Maybe our pebbles just have the wrong properties to have inherent intentionality. What if we tried it using stones carved to resemble tiny sheep? Or just write ‘sheep’ on the pebbles; that might be enough.”

“Not going to work,” I predict dryly.

Autrey continues. “Maybe we need organic pebbles, instead of silicon pebbles . . . or maybe we need to use expensive gemstones. The price of gemstones doubles every eighteen months, so you could buy a handful of cheap gemstones now, and wait, and in twenty years they’d be really expensive.”

“You tried adding pebbles to create more sheep, and it didn’t work?” Mark asks me. “What exactly did you do?”

“I took a handful of dollar bills. Then I hid the dollar bills under a fold of my blanket, one by one; each time I hid another bill, I took another paperclip from a box, making a small heap. I was careful not to keep track in my head, so that all I knew was that there were ‘many’ dollar bills, and ‘many’ paperclips. Then when all the bills were hidden under my blanket, I added a single additional paperclip to the heap, the equivalent of tossing an extra pebble into the bucket. Then I started taking dollar bills from under the fold, and putting the paperclips back into the box. When I finished, a single paperclip was left over.”

“What does that result mean?” asks Autrey.

“It means the trick didn’t work. Once I broke ritual by that single misstep, the power did not linger, but vanished instantly; the heap of paperclips and the pile of dollar bills no longer went empty at the same time.”

“You actually tried this?” asks Mark.

“Yes,” I say, “I actually performed the experiment, to verify that the outcome matched my theoretical prediction. I have a sentimental fondness for the scientific method, even when it seems absurd. Besides, what if I’d been wrong?”

“If it had worked,” says Mark, “you would have been guilty of counterfeiting! Imagine if everyone did that; the economy would collapse! Everyone would have billions of dollars of currency, yet there would be nothing for money to buy!”

“Not at all,” I reply. “By that same logic whereby adding another paperclip to the heap creates another dollar bill, creating another dollar bill would create an additional dollar’s worth of goods and services.”

Mark shakes his head. “Counterfeiting is still a crime . . . You should not have tried.”

“I was reasonably confident I would fail.”

“Aha!” says Mark. “You expected to fail! You didn’t believe you could do it!”

“Indeed,” I admit. “You have guessed my expectations with stunning accuracy.”

“Well, that’s the problem,” Mark says briskly. “Magic is fueled by belief and willpower. If you don’t believe you can do it, you can’t. You need to change your belief about the experimental result; that will change the result itself.”

“Funny,” I say nostalgically, “that’s what Autrey said when I told him about the pebble-and-bucket method. That it was too ridiculous for him to believe, so it wouldn’t work for him.”

“How did you persuade him?” inquires Mark.

“I told him to shut up and follow instructions,” I say, “and when the method worked, Autrey started believing in it.”

Mark frowns, puzzled. “That makes no sense. It doesn’t resolve the essential chicken-and-egg dilemma.”

“Sure it does. The bucket method works whether or not you believe in it.”

“That’s absurd!” sputters Mark. “I don’t believe in magic that works whether or not you believe in it!”

“I said that too,” chimes in Autrey. “Apparently I was wrong.”

Mark screws up his face in concentration. “But . . . if you didn’t believe in magic that works whether or not you believe in it, then why did the bucket method work when you didn’t believe in it? Did you believe in magic that works whether or not you believe in it whether or not you believe in magic that works whether or not you believe in it?”

“I don’t . . . think so . . .” says Autrey doubtfully.

“Then if you didn’t believe in magic that works whether or not you . . . hold on a second, I need to work this out with paper and pencil—” Mark scribbles frantically, looks skeptically at the result, turns the piece of paper upside down, then gives up. “Never mind,” says Mark. “Magic is difficult enough for me to comprehend; metamagic is out of my depth.”

“Mark, I don’t think you understand the art of bucketcraft,” I say. “It’s not about using pebbles to control sheep. It’s about making sheep control pebbles. In this art, it is not necessary to begin by believing the art will work. Rather, first the art works, then one comes to believe that it works.”

“Or so you believe,” says Mark.

“So I believe,” I reply, “because it happens to be a fact. The correspondence between reality and my beliefs comes from reality controlling my beliefs, not the other way around.”

Another sheep passes, causing me to toss in another pebble.

“Ah! Now we come to the root of the problem,” says Mark. “What’s this so-called ‘reality’ business? I understand what it means for a hypothesis to be elegant, or falsifiable, or compatible with the evidence. It sounds to me like calling a belief ‘true’ or ‘real’ or ‘actual’ is merely the difference between saying you believe something, and saying you really really believe something.”

I pause. “Well . . .” I say slowly. “Frankly, I’m not entirely sure myself where this ‘reality’ business comes from. I can’t create my own reality in the lab, so I must not understand it yet. But occasionally I believe strongly that something is going to happen, and then something else happens instead. I need a name for whatever-it-is that determines my experimental results, so I call it ‘reality’. This ‘reality’ is somehow separate from even my very best hypotheses. Even when I have a simple hypothesis, strongly supported by all the evidence I know, sometimes I’m still surprised. So I need different names for the thingies that determine my predictions and the thingy that determines my experimental results. I call the former thingies ‘belief,’ and the latter thingy ‘reality.’”

Mark snorts. “I don’t even know why I bother listening to this obvious nonsense. Whatever you say about this so-called ‘reality,’ it is merely another belief. Even your belief that reality precedes your beliefs is a belief. It follows, as a logical inevitability, that reality does not exist; only beliefs exist.”

“Hold on,” says Autrey, “could you repeat that last part? You lost me with that sharp swerve there in the middle.”

“No matter what you say about reality, it’s just another belief,” explains Mark. “It follows with crushing necessity that there is no reality, only beliefs.”

“I see,” I say. “The same way that no matter what you eat, you need to eat it with your mouth. It follows that there is no food, only mouths.”

“Precisely,” says Mark. “Everything that you eat has to be in your mouth. How can there be food that exists outside your mouth? The thought is nonsense, proving that ‘food’ is an incoherent notion. That’s why we’re all starving to death; there’s no food.”

Autrey looks down at his stomach. “But I’m not starving to death.”

“Aha!” shouts Mark triumphantly. “And how did you utter that very objection? With your mouth, my friend! With your mouth! What better demonstration could you ask that there is no food?”

“What’s this about starvation?” demands a harsh, rasping voice from directly behind us. Autrey and I stay calm, having gone through this before. Mark leaps a foot in the air, startled almost out of his wits.

Inspector Darwin smiles tightly, pleased at achieving surprise, and makes a small tick on his clipboard.

“Just a metaphor!” Mark says quickly. “You don’t need to take away my mouth, or anything like that—”

“Why do you need a mouth if there is no food?” demands Darwin angrily. “Never mind. I have no time for this foolishness. I am here to inspect the sheep.”

“Flock’s thriving, sir,” I say. “No dead sheep since January.”

“Excellent. I award you 0.12 units of fitness. Now what is this person doing here? Is he a necessary part of the operations?”

“As far as I can see, he would be of more use to the human species if hung off a hot-air balloon as ballast,” I say.

“Ouch,” says Autrey mildly.

“I do not care about the human species. Let him speak for himself.”

Mark draws himself up haughtily. “This mere shepherd,” he says, gesturing at me, “has claimed that there is such a thing as reality. This offends me, for I know with deep and abiding certainty that there is no truth. The concept of ‘truth’ is merely a stratagem for people to impose their own beliefs on others. Every culture has a different ‘truth,’ and no culture’s ‘truth’ is superior to any other. This that I have said holds at all times in all places, and I insist that you agree.”

“Hold on a second,” says Autrey. “If nothing is true, why should I believe you when you say that nothing is true?”

“I didn’t say that nothing is true—” says Mark.

“Yes, you did,” interjects Autrey, “I heard you.”

“—I said that ‘truth’ is an excuse used by some cultures to enforce their beliefs on others. So when you say something is ‘true,’ you mean only that it would be advantageous to your own social group to have it believed.”

“And this that you have said,” I say, “is it true?”

“Absolutely, positively true!” says Mark emphatically. “People create their own realities.”

“Hold on,” says Autrey, sounding puzzled again, “saying that people create their own realities is, logically, a completely separate issue from saying that there is no truth, a state of affairs I cannot even imagine coherently, perhaps because you still have not explained how exactly it is supposed to work—”

“There you go again,” says Mark exasperatedly, “trying to apply your Western concepts of logic, rationality, reason, coherence, and self-consistency.”

“Great,” mutters Autrey, “now I need to add a third subject heading, to keep track of this entirely separate and distinct claim—”

“It’s not separate,” says Mark. “Look, you’re taking the wrong attitude by treating my statements as hypotheses, and carefully deriving their consequences. You need to think of them as fully general excuses, which I apply when anyone says something I don’t like. It’s not so much a model of how the universe works, as a Get Out of Jail Free card. The key is to apply the excuse selectively. When I say that there is no such thing as truth, that applies only to your claim that the magic bucket works whether or not I believe in it. It does not apply to my claim that there is no such thing as truth.”

“Um . . . why not?” inquires Autrey.

Mark heaves a patient sigh. “Autrey, do you think you’re the first person to think of that question? To ask us how our own beliefs can be meaningful if all beliefs are meaningless? That’s the same thing many students say when they encounter this philosophy, which, I’ll have you know, has many adherents and an extensive literature.”

“So what’s the answer?” says Autrey.

“We named it the ‘reflexivity problem,’” explains Mark.

“But what’s the answer?” persists Autrey.

Mark smiles condescendingly. “Believe me, Autrey, you’re not the first person to think of such a simple question. There’s no point in presenting it to us as a triumphant refutation.”

“But what’s the actual answer?”

“Now, I’d like to move on to the issue of how logic kills cute baby seals—”

“You are wasting time,” snaps Inspector Darwin.

“Not to mention, losing track of sheep,” I say, tossing in another pebble.

Inspector Darwin looks at the two arguers, both apparently unwilling to give up their positions. “Listen,” Darwin says, more kindly now, “I have a simple notion for resolving your dispute. You say,” says Darwin, pointing to Mark, “that people’s beliefs alter their personal realities. And you fervently believe,” his finger swivels to point at Autrey, “that Mark’s beliefs can’t alter reality. So let Mark believe really hard that he can fly, and then step off a cliff. Mark shall see himself fly away like a bird, and Autrey shall see him plummet down and go splat, and you shall both be happy.”

We all pause, considering this.

“It sounds reasonable . . .” Mark says finally.

“There’s a cliff right there,” observes Inspector Darwin.

Autrey is wearing a look of intense concentration. Finally he shouts: “Wait! If that were true, we would all have long since departed into our own private universes, in which case the other people here are only figments of your imagination—there’s no point in trying to prove anything to us—”

A long dwindling scream comes from the nearby cliff, followed by a dull and lonely splat. Inspector Darwin flips his clipboard to the page that shows the current gene pool and pencils in a slightly lower frequency for Mark’s alleles.

Autrey looks slightly sick. “Was that really necessary?”

“Necessary?” says Inspector Darwin, sounding puzzled. “It just happened . . . I don’t quite understand your question.”

Autrey and I turn back to our bucket. It’s time to bring in the sheep. You wouldn’t want to forget about that part. Otherwise what would be the point?

Book II
How to Actually Change Your Mind

Rationality: An Introduction

E. Overly Convenient Excuses
46. The Proper Use of Humility
47. The Third Alternative
48. Lotteries: A Waste of Hope
49. New Improved Lottery
50. But There’s Still a Chance, Right?
51. The Fallacy of Gray
52. Absolute Authority
53. How to Convince Me That 2 + 2 = 3
54. Infinite Certainty
55. 0 And 1 Are Not Probabilities
56. Your Rationality Is My Business

F. Politics and Rationality
57. Politics is the Mind-Killer
58. Policy Debates Should Not Appear One-Sided
59. The Scales of Justice, the Notebook of Rationality
60. Correspondence Bias
61. Are Your Enemies Innately Evil?
62. Reversed Stupidity Is Not Intelligence
63. Argument Screens Off Authority
64. Hug the Query
65. Rationality and the English Language
66. Human Evil and Muddled Thinking

G. Against Rationalization
67. Knowing About Biases Can Hurt People
68. Update Yourself Incrementally
69. One Argument Against An Army
70. The Bottom Line
71. What Evidence Filtered Evidence?
72. Rationalization
73. A Rational Argument
74. Avoiding Your Belief’s Real Weak Points
75. Motivated Stopping and Motivated Continuation
76. Fake Justification
77. Is That Your True Rejection?
78. Entangled Truths, Contagious Lies
79. Of Lies and Black Swan Blowups
80. Dark Side Epistemology

H. Against Doublethink
81. Singlethink
82. Doublethink (Choosing to be Biased)
83. No, Really, I’ve Deceived Myself
84. Belief in Self-Deception
85. Moore’s Paradox
86. Don’t Believe You’ll Self-Deceive

I. Seeing with Fresh Eyes
87. Anchoring and Adjustment
88. Priming and Contamination
89. Do We Believe Everything We’re Told?
90. Cached Thoughts
91. The “Outside the Box” Box
92. Original Seeing
93. Stranger than History
94. The Logical Fallacy of Generalization from Fictional Evidence
95. The Virtue of Narrowness
96. How to Seem (and Be) Deep
97. We Change Our Minds Less Often Than We Think
98. Hold Off On Proposing Solutions
99. The Genetic Fallacy

J. Death Spirals
100. The Affect Heuristic
101. Evaluability (and Cheap Holiday Shopping)
102. Unbounded Scales, Huge Jury Awards, and Futurism
103. The Halo Effect
104. Superhero Bias
105. Mere Messiahs
106. Affective Death Spirals
107. Resist the Happy Death Spiral
108. Uncritical Supercriticality
109. Evaporative Cooling of Group Beliefs
110. When None Dare Urge Restraint
111. The Robbers Cave Experiment
112. Every Cause Wants to Be a Cult
113. Guardians of the Truth
114. Guardians of the Gene Pool
115. Guardians of Ayn Rand
116. Two Cult Koans
117. Asch’s Conformity Experiment
118. On Expressing Your Concerns
119. Lonely Dissent
120. Cultish Countercultishness

K. Letting Go
121. The Importance of Saying “Oops”
122. The Crackpot Offer
123. Just Lose Hope Already
124. The Proper Use of Doubt
125. You Can Face Reality
126. The Meditation on Curiosity
127. No One Can Exempt You From Rationality’s Laws
128. Leave a Line of Retreat
129. Crisis of Faith
130. The Ritual

Rationality: An Introduction
by Rob Bensinger

What should I believe?

As it turns out, that question has a right answer.

It has a right answer when you’re wracked with uncertainty, not just when you have a conclusive proof. There is always a correct amount of confidence to have in a statement, even when it looks like a “personal belief” and not like an expert-verified “fact.”

Yet we often talk as though the existence of uncertainty and disagreement make beliefs a mere matter of taste. We say “that’s just my opinion” or “you’re entitled to your opinion,” as though the assertions of science and math existed on a different and higher plane than beliefs that are merely “private” or “subjective.” But, writes Robin Hanson:¹

You are never entitled to your opinion. Ever! You are not even entitled to “I don’t know.” You are entitled to your desires, and sometimes to your choices. You might own a choice, and if you can choose your preferences, you may have the right to do so. But your beliefs are not about you; beliefs are about the world. Your beliefs should be your best available estimate of the way things are; anything else is a lie. [ . . . ]

It is true that some topics give experts stronger mechanisms for resolving disputes. On other topics our biases and the complexity of the world make it harder to draw strong conclusions. [ . . . ]

But never forget that on any question about the way things are (or should be), and in any information situation, there is always a best estimate. You are only entitled to your best honest effort to find that best estimate; anything else is a lie.

Suppose you find out that one of six people has a crush on you—perhaps you get a letter from a secret admirer and you’re sure it’s from one of those six—but you have no idea which of those six it is. Your classmate Bob is one of the six candidates, but you have no special evidence for or against him being the one with the crush. In that case, the odds that Bob is the one with the crush are 1:5.

Because there are six possibilities, a wild guess would result in you getting it right once for every five times you got it wrong, on average. This is what we mean by “the odds are 1:5.” You can’t say, “Well, I have no idea who has a crush on me; maybe it’s Bob, or maybe it’s not. So I’ll just say the odds are fifty-fifty.” Even if you’d rather say “I don’t know” or “Maybe” and stop there, the answer is still 1:5.²

Suppose also that you’ve noticed you get winked at by people ten times as often when they have a crush on you. If Bob then winks at you, that’s a new piece of evidence. In that case, it would be a mistake to stay skeptical about whether Bob is your secret admirer; the 10:1 odds in favor of “a random person who winks at me has a crush on me” outweigh the 1:5 odds against “Bob has a crush on me.”

It would also be a mistake to say, “That evidence is so strong, it’s a sure bet that he’s the one who has the crush on me! I’ll just assume from now on that Bob is into me.” Overconfidence is just as bad as underconfidence.

In fact, there’s only one possible answer to this question that’s mathematically consistent. To change our mind from the 1:5 prior odds based on the evidence’s 10:1 likelihood ratio, we multiply the left sides together and the right sides together, getting 10:5 posterior odds, or 2:1 odds in favor of “Bob has a crush on me.” Given our assumptions and the available evidence, guessing that Bob has a crush on you will turn out to be correct 2 times for every 1 time it turns out to be wrong. Equivalently: the probability that he’s attracted to you is 2/3. Any other confidence level would be inconsistent.

Our culture hasn’t internalized the lessons of probability theory—that the correct answer to questions like “How sure can I be that Bob has a crush on me?” is just as logically constrained as the correct answer to a question on an algebra quiz or in a geology textbook. Our clichés are out of step with the discovery that “what beliefs should I hold?” has an objectively right answer, whether your question is “does my classmate have a crush on me?” or “do I have an immortal soul?” There really is a right way to change your mind. And it’s a precise way.

How to Not Actually Change Your Mind

Revising our beliefs in anything remotely like this idealized way is a tricky task, however.

In the first volume of Rationality: From AI to Zombies, we discussed the value of “proper” beliefs. There’s nothing intrinsically wrong with expressing your support for something you care about—like a group you identify with, or a spiritual experience you find exalting. When we conflate cheers with factual beliefs, however, those misunderstood cheers can help shield an entire ideology from contamination by the evidence.

Even beliefs that seem to elegantly explain our observations aren’t immune to this problem. It’s all too easy for us to see a vaguely scientific-sounding (or otherwise authoritative) phrase and conclude that it has “explained” something, even when it doesn’t affect the odds we implicitly assign to our possible future experiences.

Worst of all, prosaic beliefs—beliefs that are in principle falsifiable, beliefs that do constrain what we expect to see—can still get stuck in our heads, reinforced by a network of illusions and biases.

In 1951, a football game between Dartmouth and Princeton turned unusually rough. Psychologists Hastorf and Cantril asked students from each school who had started the rough play. Nearly all agreed that Princeton hadn’t started it; but 86% of Princeton students believed that Dartmouth had started it, whereas only 36% of Dartmouth students blamed Dartmouth. (Most Dartmouth students believed “both started it.”)

There’s no reason to think this was a cheer, as opposed to a real belief. The students were probably led by their different beliefs to make different predictions about the behavior of players in future games. And yet somehow the perfectly ordinary factual beliefs at Dartmouth were wildly different from the perfectly ordinary factual beliefs at Princeton.

Can we blame this on the different sources Dartmouth and Princeton students had access to? On its own, bias in the different news sources that groups rely on is a pretty serious problem.

However, there is more than that at work in this case. When actually shown a film of the game later and asked to count the infractions they saw, Dartmouth students claimed to see a mean of 4.3 infractions by the Dartmouth team (and identified half as “mild”), whereas Princeton students claimed to see a mean of 9.8 Dartmouth infractions (and identified a third as “mild”).

Never mind getting rival factions to agree about complicated propositions in national politics or moral philosophy; students with different group loyalties couldn’t even agree on what they were seeing.³

When something we care about is threatened—our world-view, our in-group, our social standing, or anything else—our thoughts and perceptions rally to their defense.⁴^,⁵ Some psychologists these days go so far as to hypothesize that our ability to come up with explicit justifications for our conclusions evolved specifically to help us win arguments.⁶

One of the defining insights of 20th-century psychology, animating everyone from the disciples of Freud to present-day cognitive psychologists, is that human behavior is often driven by sophisticated unconscious processes, and the stories we tell ourselves about our motives and reasons are much more biased and confabulated than we realize.

We often fail, in fact, to realize that we’re doing any story-telling. When we seem to “directly perceive” things about ourselves in introspection, it often turns out to rest on tenuous implicit causal models.⁷^,⁸ When we try to argue for our beliefs, we can come up with shaky reasoning bearing no relation to how we first arrived at the belief.⁹ Rather than judging our explanations by their predictive power, we tell stories to make sense of what we think we know.

How can we do better? How can we arrive at a realistic view of the world, when our minds are so prone to rationalization? How can we come to a realistic view of our mental lives, when our thoughts about thinking are also suspect? How can we become less biased, when our efforts to debias ourselves can turn out to have biases of their own?

What’s the least shaky place we could put our weight down?

The Mathematics of Rationality

At the turn of the 20th century, coming up with simple (e.g., set-theoretic) axioms for arithmetic gave mathematicians a clearer standard by which to judge the correctness of their conclusions. If a human or calculator outputs “2 + 2 = 4,” we can now do more than just say “that seems intuitively right.” We can explain why it’s right, and we can prove that its rightness is tied in systematic ways to the rightness of the rest of arithmetic.

But mathematics and logic let us model the behaviors of physical systems that are a lot more interesting than a pocket calculator. We can also formalize rational belief in general, using probability theory to pick out features held in common by all successful forms of inference. We can even formalize rational behavior in general by drawing upon decision theory.

Probability theory defines how we would ideally reason in the face of uncertainty, if we had the time, the computing power, and the self-control. Given some background knowledge (priors) and a new piece of evidence, probability theory uniquely defines the best set of new beliefs (posterior) I could adopt. Likewise, decision theory defines what action I should take based on my beliefs. For any consistent set of beliefs and preferences I could have about Bob, there is a decision-theoretic answer to how I should then act in order to satisfy my preferences.

Humans aren’t perfect reasoners or perfect decision-makers, any more than we’re perfect calculators. Our brains are kludges slapped together by natural selection. Even at our best, we don’t compute the exact right answer to “what should I think?” and “what should I do?” We lack the time and computing power, and evolution lacked the engineering expertise and foresight, to iron out all our bugs.

A maximally efficient bug-free reasoner in the real world, in fact, would still need to rely on heuristics and approximations. The optimal computationally tractable algorithms for changing beliefs fall short of probability theory’s consistency.

And yet, knowing we can’t become fully consistent, we can certainly still get better. Knowing that there’s an ideal standard we can compare ourselves to—what researchers call “Bayesian rationality”—can guide us as we improve our thoughts and actions. Though we’ll never be perfect Bayesians, the mathematics of rationality can help us understand why a certain answer is correct, and help us spot exactly where we messed up.

Imagine trying to learn math through rote memorization alone. You might be told that “10 + 3 = 13,” “31 + 108 = 139,” and so on, but it won’t do you a lot of good unless you understand the pattern behind the squiggles. It can be a lot harder to seek out methods for improving your rationality when you don’t have a general framework for judging a method’s success. The purpose of this book is to help people build for themselves such frameworks.

Rationality Applied

In a blog post discussing how rationality-enthusiast “rationalists” differ from anti-empiricist “rationalists,” Scott Alexander observed:¹⁰

[O]bviously it’s useful to have as much evidence as possible, in the same way it’s useful to have as much money as possible. But equally obviously it’s useful to be able to use a limited amount of evidence wisely, in the same way it’s useful to be able to use a limited amount of money wisely.

Rationality techniques help us get more mileage out of the evidence we have, in cases where the evidence is inconclusive or our biases and attachments are distorting how we interpret the evidence. This applies to our personal lives, as in the tale of Bob. It applies to disagreements between political factions (and between sports fans). And it applies to technological and philosophical puzzles, as in debates over transhumanism, the position that we should use technology to radically refurbish the human condition. Recognizing that the same mathematical rules apply to each of these domains—and that the same cognitive biases in many cases hold sway—How to Actually Change Your Mind draws on a wide range of example problems.

The first sequence of essays in How to Actually Change Your Mind, “Overly Convenient Excuses,” focuses on questions that are as probabilistically clear-cut as questions get. The Bayes-optimal answer is often infeasible to compute, but errors like confirmation bias can take root even in cases where the available evidence is overwhelming and we have plenty of time to think things over.

From there, we move into murkier waters with a sequence on “Politics and Rationality.” Mainstream national politics, as debated by TV pundits, is famous for its angry, unproductive discussions. On the face of it, there’s something surprising about that. Why do we take political disagreements so personally, even when the machinery and effects of national politics are so distant from us in space or in time? For that matter, why do we not become more careful and rigorous with the evidence when we’re dealing with issues we deem important?

The Dartmouth-Princeton game hints at an answer. Much of our reasoning process is really rationalization—story-telling that makes our current beliefs feel more coherent and justified, without necessarily improving their accuracy. “Against Rationalization” speaks to this problem, followed by “Against Doublethink” (on self-deception) and “Seeing with Fresh Eyes” (on the challenge of recognizing evidence that doesn’t fit our expectations and assumptions).

Leveling up in rationality means encountering a lot of interesting and powerful new ideas. In many cases, it also means making friends who you can bounce ideas off of and finding communities that encourage you to better yourself. “Death Spirals” discusses some important hazards that can afflict groups united around common interests and amazing shiny ideas, which will need to be overcome if we’re to get the full benefits out of rationalist communities. How to Actually Change Your Mind then concludes with a sequence on “Letting Go.”

Our natural state isn’t to change our minds like a Bayesian would. Getting the Dartmouth and Princeton students to notice what they’re really seeing won’t be as easy as reciting the axioms of probability theory to them. As Luke Muehlhauser writes, in The Power of Agency:¹¹

You are not a Bayesian homunculus whose reasoning is “corrupted” by cognitive biases.

You just are cognitive biases.

Confirmation bias, status quo bias, correspondence bias, and the like are not tacked on to our reasoning; they are its very substance.

That doesn’t mean that debiasing is impossible. We aren’t perfect calculators underneath all our arithmetic errors, either. Many of our mathematical limitations result from very deep facts about how the human brain works. Yet we can train our mathematical abilities; we can learn when to trust and distrust our mathematical intuitions, and share our knowledge, and help one another; we can shape our environments to make things easier on us, and build tools to offload much of the work.

Our biases are part of us. But there is a shadow of Bayesianism present in us as well, a flawed apparatus that really can bring us closer to truth. No homunculus—but still, some truth. Enough, perhaps, to get started.

1. Robin Hanson, “You Are Never Entitled to Your Opinion,” Overcoming Bias (blog) (2006), http://www.overcomingbias.com/2006/12/you_are_never_e.html.

2. This follows from the assumption that there are six possibilities and you have no reason to favor one of them over any of the others. We’re also assuming, unrealistically, that you can really be certain the admirer is one of those six people, and that you aren’t neglecting other possibilities. (What if more than one of the six people has a crush on you?)

3. Albert Hastorf and Hadley Cantril, “They Saw a Game: A Case Study,” Journal of Abnormal and Social Psychology 49 (1954): 129–134, http://www2.psych.ubc.ca/~schaller/Psyc590Readings/Hastorf1954.pdf.

4. Pronin, “How We See Ourselves and How We See Others.”

5. Robert P. Vallone, Lee Ross, and Mark R. Lepper, “The Hostile Media Phenomenon: Biased Perception and Perceptions of Media Bias in Coverage of the Beirut Massacre,” Journal of Personality and Social Psychology 49 (1985): 577–585, http://ssc.wisc.edu/~jpiliavi/965/hwang.pdf.

6. Hugo Mercier and Dan Sperber, “Why Do Humans Reason? Arguments for an Argumentative Theory,” Behavioral and Brain Sciences 34 (2011): 57–74, https://hal.archives-ouvertes.fr/file/index/docid/904097/filename/MercierSperberWhydohumansreason.pdf.

7. Richard E. Nisbett and Timothy D. Wilson, “Telling More than We Can Know: Verbal Reports on Mental Processes,” Psychological Review 84 (1977): 231–259, http://people.virginia.edu/~tdw/nisbett&wilson.pdf.

8. Eric Schwitzgebel, Perplexities of Consciousness (MIT Press, 2011).

9. Jonathan Haidt, “The Emotional Dog and Its Rational Tail: A Social Intuitionist Approach to Moral Judgment,” Psychological Review 108, no. 4 (2001): 814–834, doi:10.1037/0033-295X.108.4.814.

10. Scott Alexander, “Why I Am Not Rene Descartes,” Slate Star Codex (blog) (2014), http://slatestarcodex.com/2014/11/27/why-i-am-not-rene-descartes/.

11. Luke Muehlhauser, “The Power of Agency,” Less Wrong (blog) (2011), http://lesswrong.com/lw/5i8/the_power_of_agency/.

Part E
Overly Convenient Excuses

46
The Proper Use of Humility

It is widely recognized that good science requires some kind of humility. What sort of humility is more controversial.

Consider the creationist who says: “But who can really know whether evolution is correct? It is just a theory. You should be more humble and open-minded.” Is this humility? The creationist practices a very selective underconfidence, refusing to integrate massive weights of evidence in favor of a conclusion they find uncomfortable. I would say that whether you call this “humility” or not, it is the wrong step in the dance.

What about the engineer who humbly designs fail-safe mechanisms into machinery, even though they’re damn sure the machinery won’t fail? This seems like a good kind of humility to me. Historically, it’s not unheard-of for an engineer to be damn sure a new machine won’t fail, and then it fails anyway.

What about the student who humbly double-checks the answers on their math test? Again I’d categorize that as good humility.

What about a student who says, “Well, no matter how many times I check, I can’t ever be certain my test answers are correct,” and therefore doesn’t check even once? Even if this choice stems from an emotion similar to the emotion felt by the previous student, it is less wise.

You suggest studying harder, and the student replies: “No, it wouldn’t work for me; I’m not one of the smart kids like you; nay, one so lowly as myself can hope for no better lot.” This is social modesty, not humility. It has to do with regulating status in the tribe, rather than scientific process. If you ask someone to “be more humble,” by default they’ll associate the words to social modesty—which is an intuitive, everyday, ancestrally relevant concept. Scientific humility is a more recent and rarefied invention, and it is not inherently social. Scientific humility is something you would practice even if you were alone in a spacesuit, light years from Earth with no one watching. Or even if you received an absolute guarantee that no one would ever criticize you again, no matter what you said or thought of yourself. You’d still double-check your calculations if you were wise.

The student says: “But I’ve seen other students double-check their answers and then they still turned out to be wrong. Or what if, by the problem of induction, 2 + 2 = 5 this time around? No matter what I do, I won’t be sure of myself.” It sounds very profound, and very modest. But it is not coincidence that the student wants to hand in the test quickly, and go home and play video games.

The end of an era in physics does not always announce itself with thunder and trumpets; more often it begins with what seems like a small, small flaw . . . But because physicists have this arrogant idea that their models should work all the time, not just most of the time, they follow up on small flaws. Usually, the small flaw goes away under closer inspection. Rarely, the flaw widens to the point where it blows up the whole theory. Therefore it is written: “If you do not seek perfection you will halt before taking your first steps.”

But think of the social audacity of trying to be right all the time! I seriously suspect that if Science claimed that evolutionary theory is true most of the time but not all of the time—or if Science conceded that maybe on some days the Earth is flat, but who really knows—then scientists would have better social reputations. Science would be viewed as less confrontational, because we wouldn’t have to argue with people who say the Earth is flat—there would be room for compromise. When you argue a lot, people look upon you as confrontational. If you repeatedly refuse to compromise, it’s even worse. Consider it as a question of tribal status: scientists have certainly earned some extra status in exchange for such socially useful tools as medicine and cellphones. But this social status does not justify their insistence that only scientific ideas on evolution be taught in public schools. Priests also have high social status, after all. Scientists are getting above themselves—they won a little status, and now they think they’re chiefs of the whole tribe! They ought to be more humble, and compromise a little.

Many people seem to possess rather hazy views of “rationalist humility.” It is dangerous to have a prescriptive principle which you only vaguely comprehend; your mental picture may have so many degrees of freedom that it can adapt to justify almost any deed. Where people have vague mental models that can be used to argue anything, they usually end up believing whatever they started out wanting to believe. This is so convenient that people are often reluctant to give up vagueness. But the purpose of our ethics is to move us, not be moved by us.

“Humility” is a virtue that is often misunderstood. This doesn’t mean we should discard the concept of humility, but we should be careful using it. It may help to look at the actions recommended by a “humble” line of thinking, and ask: “Does acting this way make you stronger, or weaker?” If you think about the problem of induction as applied to a bridge that needs to stay up, it may sound reasonable to conclude that nothing is certain no matter what precautions are employed; but if you consider the real-world difference between adding a few extra cables, and shrugging, it seems clear enough what makes the stronger bridge.

The vast majority of appeals that I witness to “rationalist’s humility” are excuses to shrug. The one who buys a lottery ticket, saying, “But you can’t know that I’ll lose.” The one who disbelieves in evolution, saying, “But you can’t prove to me that it’s true.” The one who refuses to confront a difficult-looking problem, saying, “It’s probably too hard to solve.” The problem is motivated skepticism a.k.a. disconfirmation bias—more heavily scrutinizing assertions that we don’t want to believe. Humility, in its most commonly misunderstood form, is a fully general excuse not to believe something; since, after all, you can’t be sure. Beware of fully general excuses!

A further problem is that humility is all too easy to profess. Dennett, in Breaking the Spell: Religion as a Natural Phenomenon, points out that while many religious assertions are very hard to believe, it is easy for people to believe that they ought to believe them. Dennett terms this “belief in belief.” What would it mean to really assume, to really believe, that three is equal to one? It’s a lot easier to believe that you should, somehow, believe that three equals one, and to make this response at the appropriate points in church. Dennett suggests that much “religious belief” should be studied as “religious profession”—what people think they should believe and what they know they ought to say.

It is all too easy to meet every counterargument by saying, “Well, of course I could be wrong.” Then, having dutifully genuflected in the direction of Modesty, having made the required obeisance, you can go on about your way without changing a thing.

The temptation is always to claim the most points with the least effort. The temptation is to carefully integrate all incoming news in a way that lets us change our beliefs, and above all our actions, as little as possible. John Kenneth Galbraith said: “Faced with the choice of changing one’s mind and proving that there is no need to do so, almost everyone gets busy on the proof.”¹ And the greater the inconvenience of changing one’s mind, the more effort people will expend on the proof.

But y’know, if you’re gonna do the same thing anyway, there’s no point in going to such incredible lengths to rationalize it. Often I have witnessed people encountering new information, apparently accepting it, and then carefully explaining why they are going to do exactly the same thing they planned to do previously, but with a different justification. The point of thinking is to shape our plans; if you’re going to keep the same plans anyway, why bother going to all that work to justify it? When you encounter new information, the hard part is to update, to react, rather than just letting the information disappear down a black hole. And humility, properly misunderstood, makes a wonderful black hole—all you have to do is admit you could be wrong. Therefore it is written: “To be humble is to take specific actions in anticipation of your own errors. To confess your fallibility and then do nothing about it is not humble; it is boasting of your modesty.”

1. John Kenneth Galbraith, Economics, Peace and Laughter (Plume, 1981), 50.

47
The Third Alternative

Believing in Santa Claus gives children a sense of wonder and encourages them to behave well in hope of receiving presents. If Santa-belief is destroyed by truth, the children will lose their sense of wonder and stop behaving nicely. Therefore, even though Santa-belief is false-to-fact, it is a Noble Lie whose net benefit should be preserved for utilitarian reasons.

Classically, this is known as a false dilemma, the fallacy of the excluded middle, or the package-deal fallacy. Even if we accept the underlying factual and moral premises of the above argument, it does not carry through. Even supposing that the Santa policy (encourage children to believe in Santa Claus) is better than the null policy (do nothing), it does not follow that Santa-ism is the best of all possible alternatives. Other policies could also supply children with a sense of wonder, such as taking them to watch a Space Shuttle launch or supplying them with science fiction novels. Likewise (if I recall correctly), offering children bribes for good behavior encourages the children to behave well only when adults are watching, while praise without bribes leads to unconditional good behavior.

Noble Lies are generally package-deal fallacies; and the response to a package-deal fallacy is that if we really need the supposed gain, we can construct a Third Alternative for getting it.

How can we obtain Third Alternatives? The first step in obtaining a Third Alternative is deciding to look for one, and the last step is the decision to accept it. This sounds obvious, and yet most people fail on these two steps, rather than within the search process. Where do false dilemmas come from? Some arise honestly, because superior alternatives are cognitively hard to see. But one factory for false dilemmas is justifying a questionable policy by pointing to a supposed benefit over the null action. In this case, the justifier does not want a Third Alternative; finding a Third Alternative would destroy the justification. The last thing a Santa-ist wants to hear is that praise works better than bribes, or that spaceships can be as inspiring as flying reindeer.

The best is the enemy of the good. If the goal is really to help people, then a superior alternative is cause for celebration—once we find this better strategy, we can help people more effectively. But if the goal is to justify a particular strategy by claiming that it helps people, a Third Alternative is an enemy argument, a competitor.

Modern cognitive psychology views decision-making as a search for alternatives. In real life, it’s not enough to compare options; you have to generate the options in the first place. On many problems, the number of alternatives is huge, so you need a stopping criterion for the search. When you’re looking to buy a house, you can’t compare every house in the city; at some point you have to stop looking and decide.

But what about when our conscious motives for the search—the criteria we can admit to ourselves—don’t square with subconscious influences? When we are carrying out an allegedly altruistic search, a search for an altruistic policy, and we find a strategy that benefits others but disadvantages ourselves—well, we don’t stop looking there; we go on looking. Telling ourselves that we’re looking for a strategy that brings greater altruistic benefit, of course. But suppose we find a policy that has some defensible benefit, and also just happens to be personally convenient? Then we stop the search at once! In fact, we’ll probably resist any suggestion that we start looking again—pleading lack of time, perhaps. (And yet somehow, we always have cognitive resources for coming up with justifications for our current policy.)

Beware when you find yourself arguing that a policy is defensible rather than optimal; or that it has some benefit compared to the null action, rather than the best benefit of any action.

False dilemmas are often presented to justify unethical policies that are, by some vast coincidence, very convenient. Lying, for example, is often much more convenient than telling the truth; and believing whatever you started out with is more convenient than updating. Hence the popularity of arguments for Noble Lies; it serves as a defense of a pre-existing belief—one does not find Noble Liars who calculate an optimal new Noble Lie; they keep whatever lie they started with. Better stop that search fast!

To do better, ask yourself straight out: If I saw that there was a superior alternative to my current policy, would I be glad in the depths of my heart, or would I feel a tiny flash of reluctance before I let go? If the answers are “no” and “yes,” beware that you may not have searched for a Third Alternative.

Which leads into another good question to ask yourself straight out: Did I spend five minutes with my eyes closed, brainstorming wild and creative options, trying to think of a better alternative? It has to be five minutes by the clock, because otherwise you blink—close your eyes and open them again—and say, “Why, yes, I searched for alternatives, but there weren’t any.” Blinking makes a good black hole down which to dump your duties. An actual, physical clock is recommended.

And those wild and creative options—were you careful not to think of a good one? Was there a secret effort from the corner of your mind to ensure that every option considered would be obviously bad?

It’s amazing how many Noble Liars and their ilk are eager to embrace ethical violations—with all due bewailing of their agonies of conscience—when they haven’t spent even five minutes by the clock looking for an alternative. There are some mental searches that we secretly wish would fail; and when the prospect of success is uncomfortable, people take the earliest possible excuse to give up.

48
Lotteries: A Waste of Hope

The classic criticism of the lottery is that the people who play are the ones who can least afford to lose; that the lottery is a sink of money, draining wealth from those who most need it. Some lottery advocates, and even some commentors on Overcoming Bias, have tried to defend lottery-ticket buying as a rational purchase of fantasy—paying a dollar for a day’s worth of pleasant anticipation, imagining yourself as a millionaire.

But consider exactly what this implies. It would mean that you’re occupying your valuable brain with a fantasy whose real probability is nearly zero—a tiny line of likelihood which you, yourself, can do nothing to realize. The lottery balls will decide your future. The fantasy is of wealth that arrives without effort—without conscientiousness, learning, charisma, or even patience.

Which makes the lottery another kind of sink: a sink of emotional energy. It encourages people to invest their dreams, their hopes for a better future, into an infinitesimal probability. If not for the lottery, maybe they would fantasize about going to technical school, or opening their own business, or getting a promotion at work—things they might be able to actually do, hopes that would make them want to become stronger. Their dreaming brains might, in the 20th visualization of the pleasant fantasy, notice a way to really do it. Isn’t that what dreams and brains are for? But how can such reality-limited fare compete with the artificially sweetened prospect of instant wealth—not after herding a dot-com startup through to IPO, but on Tuesday?

Seriously, why can’t we just say that buying lottery tickets is stupid? Human beings are stupid, from time to time—it shouldn’t be so surprising a hypothesis.

Unsurprisingly, the human brain doesn’t do 64-bit floating-point arithmetic, and it can’t devalue the emotional force of a pleasant anticipation by a factor of 0.00000001 without dropping the line of reasoning entirely. Unsurprisingly, many people don’t realize that a numerical calculation of expected utility ought to override or replace their imprecise financial instincts, and instead treat the calculation as merely one argument to be balanced against their pleasant anticipations—an emotionally weak argument, since it’s made up of mere squiggles on paper, instead of visions of fabulous wealth.

This seems sufficient to explain the popularity of lotteries. Why do so many arguers feel impelled to defend this classic form of selfdestruction?

The process of overcoming bias requires (1) first noticing the bias, (2) analyzing the bias in detail, (3) deciding that the bias is bad, (4) figuring out a workaround, and then (5) implementing it. It’s unfortunate how many people get through steps 1 and 2 and then bog down in step 3, which by rights should be the easiest of the five. Biases are lemons, not lemonade, and we shouldn’t try to make lemonade out of them—just burn those lemons down.

49
New Improved Lottery

People are still suggesting that the lottery is not a waste of hope, but a service which enables purchase of fantasy—“daydreaming about becoming a millionaire for much less money than daydreaming about hollywood stars in movies.” One commenter wrote: “There is a big difference between zero chance of becoming wealthy, and epsilon. Buying a ticket allows your dream of riches to bridge that gap.”

Actually, one of the points I was trying to make is that between zero chance of becoming wealthy, and epsilon chance, there is an order-of-epsilon difference. If you doubt this, let epsilon equal one over googolplex.

Anyway, if we pretend that the lottery sells epsilon hope, this suggests a design for a New Improved Lottery. The New Improved Lottery pays out every five years on average, at a random time—determined, say, by the decay of a not-very-radioactive element. You buy in once, for a single dollar, and get not just a few days of epsilon chance of becoming rich, but a few years of epsilon. Not only that, your wealth could strike at any time! At any minute, the phone could ring to inform you that you, yes, you are a millionaire!

Think of how much better this would be than an ordinary lottery drawing, which only takes place at defined times, a few times per week. Let’s say the boss comes in and demands you rework a proposal, or restock inventory, or something similarly annoying. Instead of getting to work, you could turn to the phone and stare, hoping for that call—because there would be epsilon chance that, at that exact moment, you yes you would be awarded the Grand Prize! And even if it doesn’t happen this minute, why, there’s no need to be disappointed—it might happen the next minute!

Think of how many more fantasies this New Improved Lottery would enable. You could shop at the store, adding expensive items to your shopping cart—if your cellphone doesn’t ring with news of a lottery win, you could always put the items back, right?

Maybe the New Improved Lottery could even show a constantly fluctuating probability distribution over the likelihood of a win occurring, and the likelihood of particular numbers being selected, with the overall expectation working out to the aforesaid Poisson distribution. Think of how much fun that would be! Oh, goodness, right this minute the chance of a win occurring is nearly ten times higher than usual! And look, the number 42 that I selected for the Mega Ball has nearly twice the usual chance of winning! You could feed it to a display on people’s cellphones, so they could just flip open the cellphone and see their chances of winning. Think of how exciting that would be! Much more exciting than trying to balance your checkbook! Much more exciting than doing your homework! This new dream would be so much tastier that it would compete with, not only hopes of going to technical school, but even hopes of getting home from work early. People could just stay glued to the screen all day long, why, they wouldn’t need to dream about anything else!

Yep, offering people tempting daydreams that will not actually happen sure is a valuable service, all right. People are willing to pay; it must be valuable. The alternative is that consumers are making mistakes, and we all know that can’t happen.

And yet current governments, with their vile monopoly on lotteries, don’t offer this simple and obvious service. Why? Because they want to overcharge people. They want them to spend money every week. They want them to spend a hundred dollars for the thrill of believing their chance of winning is a hundred times as large, instead of being able to stare at a cellphone screen waiting for the likelihood to spike. So if you believe that the lottery is a service, it is clearly an enormously overpriced service—charged to the poorest members of society—and it is your solemn duty as a citizen to demand the New Improved Lottery instead.

50
But There’s Still a Chance, Right?

Years ago, I was speaking to someone when he casually remarked that he didn’t believe in evolution. And I said, “This is not the nineteenth century. When Darwin first proposed evolution, it might have been reasonable to doubt it. But this is the twenty-first century. We can read the genes. Humans and chimpanzees have 98% shared DNA. We know humans and chimps are related. It’s over.”

He said, “Maybe the DNA is just similar by coincidence.”

I said, “The odds of that are something like two to the power of seven hundred and fifty million to one.”

He said, “But there’s still a chance, right?”

Now, there’s a number of reasons my past self cannot claim a strict moral victory in this conversation. One reason is that I have no memory of whence I pulled that 2^750,000,000 figure, though it’s probably the right meta-order of magnitude. The other reason is that my past self didn’t apply the concept of a calibrated confidence. Of all the times over the history of humanity that a human being has calculated odds of 2^750,000,000:1 against something, they have undoubtedly been wrong more often than once in 2^750,000,000 times. E.g. the shared genes estimate was revised to 95%, not 98%—and that may even apply only to the 30,000 known genes and not the entire genome, in which case it’s the wrong meta-order of magnitude.

But I think the other guy’s reply is still pretty funny.

I don’t recall what I said in further response—probably something like “No”—but I remember this occasion because it brought me several insights into the laws of thought as seen by the unenlightened ones.

It first occurred to me that human intuitions were making a qualitative distinction between “No chance” and “A very tiny chance, but worth keeping track of.” You can see this in the Overcoming Bias lottery debate, where someone said, “There’s a big difference between zero chance of winning and epsilon chance of winning,” and I replied, “No, there’s an order-of-epsilon difference; if you doubt this, let epsilon equal one over googolplex.”

The problem is that probability theory sometimes lets us calculate a chance which is, indeed, too tiny to be worth the mental space to keep track of it—but by that time, you’ve already calculated it. People mix up the map with the territory, so that on a gut level, tracking a symbolically described probability feels like “a chance worth keeping track of,” even if the referent of the symbolic description is a number so tiny that if it was a dust speck, you couldn’t see it. We can use words to describe numbers that small, but not feelings—a feeling that small doesn’t exist, doesn’t fire enough neurons or release enough neurotransmitters to be felt. This is why people buy lottery tickets—no one can feel the smallness of a probability that small.

But what I found even more fascinating was the qualitative distinction between “certain” and “uncertain” arguments, where if an argument is not certain, you’re allowed to ignore it. Like, if the likelihood is zero, then you have to give up the belief, but if the likelihood is one over googol, you’re allowed to keep it.

Now it’s a free country and no one should put you in jail for illegal reasoning, but if you’re going to ignore an argument that says the likelihood is one over googol, why not also ignore an argument that says the likelihood is zero? I mean, as long as you’re ignoring the evidence anyway, why is it so much worse to ignore certain evidence than uncertain evidence?

I have often found, in life, that I have learned from other people’s nicely blatant bad examples, duly generalized to more subtle cases. In this case, the flip lesson is that, if you can’t ignore a likelihood of one over googol because you want to, you can’t ignore a likelihood of 0.9 because you want to. It’s all the same slippery cliff.

Consider his example if you ever you find yourself thinking, “But you can’t prove me wrong.” If you’re going to ignore a probabilistic counterargument, why not ignore a proof, too?

51
The Fallacy of Gray

The Sophisticate: “The world isn’t black and white. No one does pure good or pure bad. It’s all gray. Therefore, no one is better than anyone else.”

The Zetet: “Knowing only gray, you conclude that all grays are the same shade. You mock the simplicity of the two-color view, yet you replace it with a one-color view . . .”

—Marc Stiegler, David’s Sling¹

I don’t know if the Sophisticate’s mistake has an official name, but I call it the Fallacy of Gray. We saw it manifested in the previous essay—the one who believed that odds of two to the power of seven hundred and fifty millon to one, against, meant “there was still a chance.” All probabilities, to him, were simply “uncertain” and that meant he was licensed to ignore them if he pleased.

“The Moon is made of green cheese” and “the Sun is made of mostly hydrogen and helium” are both uncertainties, but they are not the same uncertainty.

Everything is shades of gray, but there are shades of gray so light as to be very nearly white, and shades of gray so dark as to be very nearly black. Or even if not, we can still compare shades, and say “it is darker” or “it is lighter.”

Years ago, one of the strange little formative moments in my career as a rationalist was reading this paragraph from Player of Games by Iain M. Banks, especially the sentence in bold:²

A guilty system recognizes no innocents. As with any power apparatus which thinks everybody’s either for it or against it, we’re against it. You would be too, if you thought about it. The very way you think places you amongst its enemies. This might not be your fault, because every society imposes some of its values on those raised within it, but the point is that some societies try to maximize that effect, and some try to minimize it. You come from one of the latter and you’re being asked to explain yourself to one of the former. Prevarication will be more difficult than you might imagine; neutrality is probably impossible. You cannot choose not to have the politics you do; they are not some separate set of entities somehow detachable from the rest of your being; they are a function of your existence. I know that and they know that; you had better accept it.

Now, don’t write angry comments saying that, if societies impose fewer of their values, then each succeeding generation has more work to start over from scratch. That’s not what I got out of the paragraph.

What I got out of the paragraph was something which seems so obvious in retrospect that I could have conceivably picked it up in a hundred places; but something about that one paragraph made it click for me.

It was the whole notion of the Quantitative Way applied to life-problems like moral judgments and the quest for personal self-improvement. That, even if you couldn’t switch something from on to off, you could still tend to increase it or decrease it.

Is this too obvious to be worth mentioning? I say it is not too obvious, for many bloggers have said of Overcoming Bias: “It is impossible, no one can completely eliminate bias.” I don’t care if the one is a professional economist, it is clear that they have not yet grokked the Quantitative Way as it applies to everyday life and matters like personal self-improvement. That which I cannot eliminate may be well worth reducing.

Or consider this exchange between Robin Hanson and Tyler Cowen. Robin Hanson said that he preferred to put at least 75% weight on the prescriptions of economic theory versus his intuitions: “I try to mostly just straightforwardly apply economic theory, adding little personal or cultural judgment.” Tyler Cowen replied:

In my view there is no such thing as “straightforwardly applying economic theory” . . . theories are always applied through our personal and cultural filters and there is no other way it can be.

Yes, but you can try to minimize that effect, or you can do things that are bound to increase it. And if you try to minimize it, then in many cases I don’t think it’s unreasonable to call the output “straightforward”—even in economics.

“Everyone is imperfect.” Mohandas Gandhi was imperfect and Joseph Stalin was imperfect, but they were not the same shade of imperfection. “Everyone is imperfect” is an excellent example of replacing a two-color view with a one-color view. If you say, “No one is perfect, but some people are less imperfect than others,” you may not gain applause; but for those who strive to do better, you have held out hope. No one is perfectly imperfect, after all.

(Whenever someone says to me, “Perfectionism is bad for you,” I reply: “I think it’s okay to be imperfect, but not so imperfect that other people notice.”)

Likewise the folly of those who say, “Every scientific paradigm imposes some of its assumptions on how it interprets experiments,” and then act like they’d proven science to occupy the same level with witchdoctoring. Every worldview imposes some of its structure on its observations, but the point is that there are worldviews which try to minimize that imposition, and worldviews which glory in it. There is no white, but there are shades of gray that are far lighter than others, and it is folly to treat them as if they were all on the same level.

If the Moon has orbited the Earth these past few billion years, if you have seen it in the sky these last years, and you expect to see it in its appointed place and phase tomorrow, then that is not a certainty. And if you expect an invisible dragon to heal your daughter of cancer, that too is not a certainty. But they are rather different degrees of uncertainty—this business of expecting things to happen yet again in the same way you have previously predicted to twelve decimal places, versus expecting something to happen that violates the order previously observed. Calling them both “faith” seems a little too un-narrow.

It’s a most peculiar psychology—this business of “Science is based on faith too, so there!” Typically this is said by people who claim that faith is a good thing. Then why do they say “Science is based on faith too!” in that angry-triumphal tone, rather than as a compliment? And a rather dangerous compliment to give, one would think, from their perspective. If science is based on “faith,” then science is of the same kind as religion—directly comparable. If science is a religion, it is the religion that heals the sick and reveals the secrets of the stars. It would make sense to say, “The priests of science can blatantly, publicly, verifiably walk on the Moon as a faith-based miracle, and your priests’ faith can’t do the same.” Are you sure you wish to go there, oh faithist? Perhaps, on further reflection, you would prefer to retract this whole business of “Science is a religion too!”

There’s a strange dynamic here: You try to purify your shade of gray, and you get it to a point where it’s pretty light-toned, and someone stands up and says in a deeply offended tone, “But it’s not white! It’s gray!” It’s one thing when someone says, “This isn’t as light as you think, because of specific problems X, Y, and Z.” It’s a different matter when someone says angrily “It’s not white! It’s gray!” without pointing out any specific dark spots.

In this case, I begin to suspect psychology that is more imperfect than usual—that someone may have made a devil’s bargain with their own mistakes, and now refuses to hear of any possibility of improvement. When someone finds an excuse not to try to do better, they often refuse to concede that anyone else can try to do better, and every mode of improvement is thereafter their enemy, and every claim that it is possible to move forward is an offense against them. And so they say in one breath proudly, “I’m glad to be gray,” and in the next breath angrily, “And you’re gray too!”

If there is no black and white, there is yet lighter and darker, and not all grays are the same.

G2 points us to Asimov’s “The Relativity of Wrong”:³

When people thought the earth was flat, they were wrong. When people thought the earth was spherical, they were wrong. But if you think that thinking the earth is spherical is just as wrong as thinking the earth is flat, then your view is wronger than both of them put together.

1. Marc Stiegler, David’s Sling (Baen, 1988).

2. Iain Banks, The Player of Games (Orbit, 1989).

3. Isaac Asimov, The Relativity of Wrong (Oxford University Press, 1989).

52
Absolute Authority

The one comes to you and loftily says: “Science doesn’t really know anything. All you have are theories—you can’t know for certain that you’re right. You scientists changed your minds about how gravity works—who’s to say that tomorrow you won’t change your minds about evolution?”

Behold the abyssal cultural gap. If you think you can cross it in a few sentences, you are bound to be sorely disappointed.

In the world of the unenlightened ones, there is authority and unauthority. What can be trusted, can be trusted; what cannot be trusted, you may as well throw away. There are good sources of information and bad sources of information. If scientists have changed their stories ever in their history, then science cannot be a true Authority, and can never again be trusted—like a witness caught in a contradiction, or like an employee found stealing from the till.

Plus, the one takes for granted that a proponent of an idea is expected to defend it against every possible counterargument and confess nothing. All claims are discounted accordingly. If even the proponent of science admits that science is less than perfect, why, it must be pretty much worthless.

When someone has lived their life accustomed to certainty, you can’t just say to them, “Science is probabilistic, just like all other knowledge.” They will accept the first half of the statement as a confession of guilt; and dismiss the second half as a flailing attempt to accuse everyone else to avoid judgment.

You have admitted you are not trustworthy—so begone, Science, and trouble us no more!

One obvious source for this pattern of thought is religion, where the scriptures are alleged to come from God; therefore to confess any flaw in them would destroy their authority utterly; so any trace of doubt is a sin, and claiming certainty is mandatory whether you’re certain or not.

But I suspect that the traditional school regimen also has something to do with it. The teacher tells you certain things, and you have to believe them, and you have to recite them back on the test. But when a student makes a suggestion in class, you don’t have to go along with it—you’re free to agree or disagree (it seems) and no one will punish you.

This experience, I fear, maps the domain of belief onto the social domains of authority, of command, of law. In the social domain, there is a qualitative difference between absolute laws and nonabsolute laws, between commands and suggestions, between authorities and unauthorities. There seems to be strict knowledge and unstrict knowledge, like a strict regulation and an unstrict regulation. Strict authorities must be yielded to, while unstrict suggestions can be obeyed or discarded as a matter of personal preference. And Science, since it confesses itself to have a possibility of error, must belong in the second class.

(I note in passing that I see a certain similarity to they who think that if you don’t get an Authoritative probability written on a piece of paper from the teacher in class, or handed down from some similar Unarguable Source, then your uncertainty is not a matter for Bayesian probability theory. Someone might—gasp!—argue with your estimate of the prior probability. It thus seems to the not-fully-enlightened ones that Bayesian priors belong to the class of beliefs proposed by students, and not the class of beliefs commanded you by teachers—it is not proper knowledge.)

The abyssal cultural gap between the Authoritative Way and the Quantitative Way is rather annoying to those of us staring across it from the rationalist side. Here is someone who believes they have knowledge more reliable than science’s mere probabilistic guesses—such as the guess that the Moon will rise in its appointed place and phase tomorrow, just like it has every observed night since the invention of astronomical record-keeping, and just as predicted by physical theories whose previous predictions have been successfully confirmed to fourteen decimal places. And what is this knowledge that the unenlightened ones set above ours, and why? It’s probably some musty old scroll that has been contradicted eleventeen ways from Sunday, and from Monday, and from every day of the week. Yet this is more reliable than Science (they say) because it never admits to error, never changes its mind, no matter how often it is contradicted. They toss around the word “certainty” like a tennis ball, using it as lightly as a feather—while scientists are weighed down by dutiful doubt, struggling to achieve even a modicum of probability. “I’m perfect,” they say without a care in the world, “I must be so far above you, who must still struggle to improve yourselves.”

There is nothing simple you can say to them—no fast crushing rebuttal. By thinking carefully, you may be able to win over the audience, if this is a public debate. Unfortunately you cannot just blurt out, “Foolish mortal, the Quantitative Way is beyond your comprehension, and the beliefs you lightly name ‘certain’ are less assured than the least of our mighty hypotheses.” It’s a difference of life-gestalt that isn’t easy to describe in words at all, let alone quickly.

What might you try, rhetorically, in front of an audience? Hard to say . . . maybe:

“The power of science comes from having the ability to change our minds and admit we’re wrong. If you’ve never admitted you’re wrong, it doesn’t mean you’ve made fewer mistakes.”
“Anyone can say they’re absolutely certain. It’s a bit harder to never, ever make any mistakes. Scientists understand the difference, so they don’t say they’re absolutely certain. That’s all. It doesn’t mean that they have any specific reason to doubt a theory—absolutely every scrap of evidence can be going the same way, all the stars and planets lined up like dominos in support of a single hypothesis, and the scientists still won’t say they’re absolutely sure, because they’ve just got higher standards. It doesn’t mean scientists are less entitled to certainty than, say, the politicians who always seem so sure of everything.”
“Scientists don’t use the phrase ‘not absolutely certain’ the way you’re used to from regular conversation. I mean, suppose you went to the doctor, and got a blood test, and the doctor came back and said, ‘We ran some tests, and it’s not absolutely certain that you’re not made out of cheese, and there’s a non-zero chance that twenty fairies made out of sentient chocolate are singing the “I love you” song from Barney inside your lower intestine.’ Run for the hills, your doctor needs a doctor. When a scientist says the same thing, it means that they think the probability is so tiny that you couldn’t see it with an electron microscope, but the scientist is willing to see the evidence in the extremely unlikely event that you have it.”
“Would you be willing to change your mind about the things you call ‘certain’ if you saw enough evidence? I mean, suppose that God himself descended from the clouds and told you that your whole religion was true except for the Virgin Birth. If that would change your mind, you can’t say you’re absolutely certain of the Virgin Birth. For technical reasons of probability theory, if it’s theoretically possible for you to change your mind about something, it can’t have a probability exactly equal to one. The uncertainty might be smaller than a dust speck, but it has to be there. And if you wouldn’t change your mind even if God told you otherwise, then you have a problem with refusing to admit you’re wrong that transcends anything a mortal like me can say to you, I guess.”

But, in a way, the more interesting question is what you say to someone not in front of an audience. How do you begin the long process of teaching someone to live in a universe without certainty?

I think the first, beginning step should be understanding that you can live without certainty—that if, hypothetically speaking, you couldn’t be certain of anything, it would not deprive you of the ability to make moral or factual distinctions. To paraphrase Lois Bujold, “Don’t push harder, lower the resistance.”

One of the common defenses of Absolute Authority is something I call “The Argument From The Argument From Gray,” which runs like this:

Moral relativists say:
- The world isn’t black and white, therefore:
- Everything is gray, therefore:
- No one is better than anyone else, therefore:
- I can do whatever I want and you can’t stop me bwahahaha.
But we’ve got to be able to stop people from committing murder.
Therefore there has to be some way of being absolutely certain, or the moral relativists win.

Reversed stupidity is not intelligence. You can’t arrive at a correct answer by reversing every single line of an argument that ends with a bad conclusion—it gives the fool too much detailed control over you. Every single line must be correct for a mathematical argument to carry. And it doesn’t follow, from the fact that moral relativists say “The world isn’t black and white,” that this is false, any more than it follows, from Stalin’s belief that 2 + 2 = 4, that “2 + 2 = 4” is false. The error (and it only takes one) is in the leap from the two-color view to the single-color view, that all grays are the same shade.

It would concede far too much (indeed, concede the whole argument) to agree with the premise that you need absolute knowledge of absolutely good options and absolutely evil options in order to be moral. You can have uncertain knowledge of relatively better and relatively worse options, and still choose. It should be routine, in fact, not something to get all dramatic about.

I mean, yes, if you have to choose between two alternatives A and B, and you somehow succeed in establishing knowably certain well-calibrated 100% confidence that A is absolutely and entirely desirable and that B is the sum of everything evil and disgusting, then this is a sufficient condition for choosing A over B. It is not a necessary condition.

Oh, and: Logical fallacy: Appeal to consequences of belief.

Let’s see, what else do they need to know? Well, there’s the entire rationalist culture which says that doubt, questioning, and confession of error are not terrible shameful things.

There’s the whole notion of gaining information by looking at things, rather than being proselytized. When you look at things harder, sometimes you find out that they’re different from what you thought they were at first glance; but it doesn’t mean that Nature lied to you, or that you should give up on seeing.

Then there’s the concept of a calibrated confidence—that “probability” isn’t the same concept as the little progress bar in your head that measures your emotional commitment to an idea. It’s more like a measure of how often, pragmatically, in real life, people in a certain state of belief say things that are actually true. If you take one hundred people and ask them each to make a statement of which they are “absolutely certain,” how many of these statements will be correct? Not one hundred.

If anything, the statements that people are really fanatic about are far less likely to be correct than statements like “the Sun is larger than the Moon” that seem too obvious to get excited about. For every statement you can find of which someone is “absolutely certain,” you can probably find someone “absolutely certain” of its opposite, because such fanatic professions of belief do not arise in the absence of opposition. So the little progress bar in people’s heads that measures their emotional commitment to a belief does not translate well into a calibrated confidence—it doesn’t even behave monotonically.

As for “absolute certainty”—well, if you say that something is 99.9999% probable, it means you think you could make one million equally strong independent statements, one after the other, over the course of a solid year or so, and be wrong, on average, around once. This is incredible enough. (It’s amazing to realize we can actually get that level of confidence for “Thou shalt not win the lottery.”) So let us say nothing of probability 1.0. Once you realize you don’t need probabilities of 1.0 to get along in life, you’ll realize how absolutely ridiculous it is to think you could ever get to 1.0 with a human brain. A probability of 1.0 isn’t just certainty, it’s infinite certainty.

In fact, it seems to me that to prevent public misunderstanding, maybe scientists should go around saying “We are not INFINITELY certain” rather than “We are not certain.” For the latter case, in ordinary discourse, suggests you know some specific reason for doubt.

53
How to Convince Me That 2 + 2 = 3

In What is Evidence? I wrote:

This is why rationalists put such a heavy premium on the paradoxical-seeming claim that a belief is only really worthwhile if you could, in principle, be persuaded to believe otherwise. If your retina ended up in the same state regardless of what light entered it, you would be blind . . . Hence the phrase, “blind faith.” If what you believe doesn’t depend on what you see, you’ve been blinded as effectively as by poking out your eyeballs.

Cihan Baran replied:

I can not conceive of a situation that would make 2 + 2 = 4 false. Perhaps for that reason, my belief in 2 + 2 = 4 is unconditional.

I admit, I cannot conceive of a “situation” that would make 2 + 2 = 4 false. (There are redefinitions, but those are not “situations,” and then you’re no longer talking about 2, 4, =, or +.) But that doesn’t make my belief unconditional. I find it quite easy to imagine a situation which would convince me that 2 + 2 = 3.

Suppose I got up one morning, and took out two earplugs, and set them down next to two other earplugs on my nighttable, and noticed that there were now three earplugs, without any earplugs having appeared or disappeared—in contrast to my stored memory that 2 + 2 was supposed to equal 4. Moreover, when I visualized the process in my own mind, it seemed that making XX and XX come out to XXXX required an extra X to appear from nowhere, and was, moreover, inconsistent with other arithmetic I visualized, since subtracting XX from XXX left XX, but subtracting XX from XXXX left XXX. This would conflict with my stored memory that 3 - 2 = 1, but memory would be absurd in the face of physical and mental confirmation that XXX - XX = XX.

I would also check a pocket calculator, Google, and perhaps my copy of 1984 where Winston writes that “Freedom is the freedom to say two plus two equals three.” All of these would naturally show that the rest of the world agreed with my current visualization, and disagreed with my memory, that 2 + 2 = 3.

How could I possibly have ever been so deluded as to believe that 2 + 2 = 4? Two explanations would come to mind: First, a neurological fault (possibly caused by a sneeze) had made all the additive sums in my stored memory go up by one. Second, someone was messing with me, by hypnosis or by my being a computer simulation. In the second case, I would think it more likely that they had messed with my arithmetic recall than that 2 + 2 actually equalled 4. Neither of these plausible-sounding explanations would prevent me from noticing that I was very, very, very confused.

What would convince me that 2 + 2 = 3, in other words, is exactly the same kind of evidence that currently convinces me that 2 + 2 = 4: The evidential crossfire of physical observation, mental visualization, and social agreement.

There was a time when I had no idea that 2 + 2 = 4. I did not arrive at this new belief by random processes—then there would have been no particular reason for my brain to end up storing “2 + 2 = 4” instead of “2 + 2 = 7.” The fact that my brain stores an answer surprisingly similar to what happens when I lay down two earplugs alongside two earplugs, calls forth an explanation of what entanglement produces this strange mirroring of mind and reality.

There’s really only two possibilities, for a belief of fact—either the belief got there via a mind-reality entangling process, or not. If not, the belief can’t be correct except by coincidence. For beliefs with the slightest shred of internal complexity (requiring a computer program of more than 10 bits to simulate), the space of possibilities is large enough that coincidence vanishes.

Unconditional facts are not the same as unconditional beliefs. If entangled evidence convinces me that a fact is unconditional, this doesn’t mean I always believed in the fact without need of entangled evidence.

I believe that 2 + 2 = 4, and I find it quite easy to conceive of a situation which would convince me that 2 + 2 = 3. Namely, the same sort of situation that currently convinces me that 2 + 2 = 4. Thus I do not fear that I am a victim of blind faith.

If there are any Christians in the audience who know Bayes’s Theorem (no numerophobes, please), might I inquire of you what situation would convince you of the truth of Islam? Presumably it would be the same sort of situation causally responsible for producing your current belief in Christianity: We would push you screaming out of the uterus of a Muslim woman, and have you raised by Muslim parents who continually told you that it is good to believe unconditionally in Islam. Or is there more to it than that? If so, what situation would convince you of Islam, or at least, non-Christianity?

54
Infinite Certainty

In Absolute Authority, I argued that you don’t need infinite certainty:

If you have to choose between two alternatives A and B, and you somehow succeed in establishing knowably certain well-calibrated 100% confidence that A is absolutely and entirely desirable and that B is the sum of everything evil and disgusting, then this is a sufficient condition for choosing A over B. It is not a necessary condition . . . You can have uncertain knowledge of relatively better and relatively worse options, and still choose. It should be routine, in fact.

Concerning the proposition that 2 + 2 = 4, we must distinguish between the map and the territory. Given the seeming absolute stability and universality of physical laws, it’s possible that never, in the whole history of the universe, has any particle exceeded the local lightspeed limit. That is, the lightspeed limit may be, not just true 99% of the time, or 99.9999% of the time, or (1 - 1/googolplex) of the time, but simply always and absolutely true.

But whether we can ever have absolute confidence in the lightspeed limit is a whole ’nother question. The map is not the territory.

It may be entirely and wholly true that a student plagiarized their assignment, but whether you have any knowledge of this fact at all—let alone absolute confidence in the belief—is a separate issue. If you flip a coin and then don’t look at it, it may be completely true that the coin is showing heads, and you may be completely unsure of whether the coin is showing heads or tails. A degree of uncertainty is not the same as a degree of truth or a frequency of occurrence.

The same holds for mathematical truths. It’s questionable whether the statement “2 + 2 = 4” or “In Peano arithmetic, SS0 + SS0 = SSSS0” can be said to be true in any purely abstract sense, apart from physical systems that seem to behave in ways similar to the Peano axioms. Having said this, I will charge right ahead and guess that, in whatever sense “2 + 2 = 4” is true at all, it is always and precisely true, not just roughly true (“2 + 2 actually equals 4.0000004”) or true 999,999,999,999 times out of 1,000,000,000,000.

I’m not totally sure what “true” should mean in this case, but I stand by my guess. The credibility of “2 + 2 = 4 is always true” far exceeds the credibility of any particular philosophical position on what “true,” “always,” or “is” means in the statement above.

This doesn’t mean, though, that I have absolute confidence that 2 + 2 = 4. See the previous discussion on how to convince me that 2 + 2 = 3, which could be done using much the same sort of evidence that convinced me that 2 + 2 = 4 in the first place. I could have hallucinated all that previous evidence, or I could be misremembering it. In the annals of neurology there are stranger brain dysfunctions than this.

So if we attach some probability to the statement “2 + 2 = 4,” then what should the probability be? What you seek to attain in a case like this is good calibration—statements to which you assign “99% probability” come true 99 times out of 100. This is actually a hell of a lot more difficult than you might think. Take a hundred people, and ask each of them to make ten statements of which they are “99% confident.” Of the 1,000 statements, do you think that around 10 will be wrong?

I am not going to discuss the actual experiments that have been done on calibration—you can find them in my book chapter “Cognitive biases potentially affecting judgment of global risks”—because I’ve seen that when I blurt this out to people without proper preparation, they thereafter use it as a Fully General Counterargument, which somehow leaps to mind whenever they have to discount the confidence of someone whose opinion they dislike, and fails to be available when they consider their own opinions. So I try not to talk about the experiments on calibration except as part of a structured presentation of rationality that includes warnings against motivated skepticism.

But the observed calibration of human beings who say they are “99% confident” is not 99% accuracy.

Suppose you say that you’re 99.99% confident that 2 + 2 = 4. Then you have just asserted that you could make 10,000 independent statements, in which you repose equal confidence, and be wrong, on average, around once. Maybe for 2 + 2 = 4 this extraordinary degree of confidence would be possible: “2 + 2 = 4” is extremely simple, and mathematical as well as empirical, and widely believed socially (not with passionate affirmation but just quietly taken for granted). So maybe you really could get up to 99.99% confidence on this one.

I don’t think you could get up to 99.99% confidence for assertions like “53 is a prime number.” Yes, it seems likely, but by the time you tried to set up protocols that would let you assert 10,000 independent statements of this sort—that is, not just a set of statements about prime numbers, but a new protocol each time—you would fail more than once. Peter de Blanc has an amusing anecdote on this point. (I told him not to do it again.)

Yet the map is not the territory: if I say that I am 99% confident that 2 + 2 = 4, it doesn’t mean that I think “2 + 2 = 4” is true to within 99% precision, or that “2 + 2 = 4” is true 99 times out of 100. The proposition in which I repose my confidence is the proposition that “2 + 2 = 4 is always and exactly true,” not the proposition “2 + 2 = 4 is mostly and usually true.”

As for the notion that you could get up to 100% confidence in a mathematical proposition—well, really now! If you say 99.9999% confidence, you’re implying that you could make one million equally fraught statements, one after the other, and be wrong, on average, about once. That’s around a solid year’s worth of talking, if you can make one assertion every 20 seconds and you talk for 16 hours a day.

Assert 99.9999999999% confidence, and you’re taking it up to a trillion. Now you’re going to talk for a hundred human lifetimes, and not be wrong even once?

Assert a confidence of (1 - 1/googolplex) and your ego far exceeds that of mental patients who think they’re God.

And a googolplex is a lot smaller than even relatively small inconceivably huge numbers like 3 ↑↑↑ 3. But even a confidence of (1 - 1∕3 ↑↑↑ 3) isn’t all that much closer to PROBABILITY 1 than being 90% sure of something.

If all else fails, the hypothetical Dark Lords of the Matrix, who are right now tampering with your brain’s credibility assessment of this very sentence, will bar the path and defend us from the scourge of infinite certainty.

Am I absolutely sure of that?

Why, of course not.

As Rafal Smigrodski once said:

I would say you should be able to assign a less than 1 certainty level to the mathematical concepts which are necessary to derive Bayes’s rule itself, and still practically use it. I am not totally sure I have to be always unsure. Maybe I could be legitimately sure about something. But once I assign a probability of 1 to a proposition, I can never undo it. No matter what I see or learn, I have to reject everything that disagrees with the axiom. I don’t like the idea of not being able to change my mind, ever.

55
0 And 1 Are Not Probabilities

One, two, and three are all integers, and so is negative four. If you keep counting up, or keep counting down, you’re bound to encounter a whole lot more integers. You will not, however, encounter anything called “positive infinity” or “negative infinity,” so these are not integers.

Positive and negative infinity are not integers, but rather special symbols for talking about the behavior of integers. People sometimes say something like, “5 + infinity = infinity,” because if you start at 5 and keep counting up without ever stopping, you’ll get higher and higher numbers without limit. But it doesn’t follow from this that “infinity - infinity = 5.” You can’t count up from 0 without ever stopping, and then count down without ever stopping, and then find yourself at 5 when you’re done.

From this we can see that infinity is not only not-an-integer, it doesn’t even behave like an integer. If you unwisely try to mix up infinities with integers, you’ll need all sorts of special new inconsistent-seeming behaviors which you don’t need for 1, 2, 3 and other actual integers.

Even though infinity isn’t an integer, you don’t have to worry about being left at a loss for numbers. Although people have seen five sheep, millions of grains of sand, and septillions of atoms, no one has ever counted an infinity of anything. The same with continuous quantities—people have measured dust specks a millimeter across, animals a meter across, cities kilometers across, and galaxies thousands of lightyears across, but no one has ever measured anything an infinity across. In the real world, you don’t need a whole lot of infinity.

(I should note for the more sophisticated readers in the audience that they do not need to write me with elaborate explanations of, say, the difference between ordinal numbers and cardinal numbers. Yes, I possess various advanced set-theoretic definitions of infinity, but I don’t see a good use for them in probability theory. See below.)

In the usual way of writing probabilities, probabilities are between 0 and 1. A coin might have a probability of 0.5 of coming up tails, or the weatherman might assign probability 0.9 to rain tomorrow.

This isn’t the only way of writing probabilities, though. For example, you can transform probabilities into odds via the transformation O = (P∕(1 - P)). So a probability of 50% would go to odds of 0.5/0.5 or 1, usually written 1:1, while a probability of 0.9 would go to odds of 0.9/0.1 or 9, usually written 9:1. To take odds back to probabilities you use P = (O∕(1 + O)), and this is perfectly reversible, so the transformation is an isomorphism—a two-way reversible mapping. Thus, probabilities and odds are isomorphic, and you can use one or the other according to convenience.

For example, it’s more convenient to use odds when you’re doing Bayesian updates. Let’s say that I roll a six-sided die: If any face except 1 comes up, there’s a 10% chance of hearing a bell, but if the face 1 comes up, there’s a 20% chance of hearing the bell. Now I roll the die, and hear a bell. What are the odds that the face showing is 1? Well, the prior odds are 1:5 (corresponding to the real number 1/5 = 0.20) and the likelihood ratio is 0.2:0.1 (corresponding to the real number 2) and I can just multiply these two together to get the posterior odds 2:5 (corresponding to the real number 2/5 or 0.40). Then I convert back into a probability, if I like, and get (0.4∕1.4) = 2∕7 = ~29%.

So odds are more manageable for Bayesian updates—if you use probabilities, you’ve got to deploy Bayes’s Theorem in its complicated version. But probabilities are more convenient for answering questions like “If I roll a six-sided die, what’s the chance of seeing a number from 1 to 4?” You can add up the probabilities of 1/6 for each side and get 4/6, but you can’t add up the odds ratios of 0.2 for each side and get an odds ratio of 0.8.

Why am I saying all this? To show that “odd ratios” are just as legitimate a way of mapping uncertainties onto real numbers as “probabilities.” Odds ratios are more convenient for some operations, probabilities are more convenient for others. A famous proof called Cox’s Theorem (plus various extensions and refinements thereof) shows that all ways of representing uncertainties that obey some reasonable-sounding constraints, end up isomorphic to each other.

Why does it matter that odds ratios are just as legitimate as probabilities? Probabilities as ordinarily written are between 0 and 1, and both 0 and 1 look like they ought to be readily reachable quantities—it’s easy to see 1 zebra or 0 unicorns. But when you transform probabilities onto odds ratios, 0 goes to 0, but 1 goes to positive infinity. Now absolute truth doesn’t look like it should be so easy to reach.

A representation that makes it even simpler to do Bayesian updates is the log odds—this is how E. T. Jaynes recommended thinking about probabilities. For example, let’s say that the prior probability of a proposition is 0.0001—this corresponds to a log odds of around -40 decibels. Then you see evidence that seems 100 times more likely if the proposition is true than if it is false. This is 20 decibels of evidence. So the posterior odds are around -40 dB + 20 dB = -20 dB, that is, the posterior probability is ~0.01.

When you transform probabilities to log odds, 0 goes onto negative infinity and 1 goes onto positive infinity. Now both infinite certainty and infinite improbability seem a bit more out-of-reach.

In probabilities, 0.9999 and 0.99999 seem to be only 0.00009 apart, so that 0.502 is much further away from 0.503 than 0.9999 is from 0.99999. To get to probability 1 from probability 0.99999, it seems like you should need to travel a distance of merely 0.00001.

But when you transform to odds ratios, 0.502 and 0.503 go to 1.008 and 1.012, and 0.9999 and 0.99999 go to 9,999 and 99,999. And when you transform to log odds, 0.502 and 0.503 go to 0.03 decibels and 0.05 decibels, but 0.9999 and 0.99999 go to 40 decibels and 50 decibels.

When you work in log odds, the distance between any two degrees of uncertainty equals the amount of evidence you would need to go from one to the other. That is, the log odds gives us a natural measure of spacing among degrees of confidence.

Using the log odds exposes the fact that reaching infinite certainty requires infinitely strong evidence, just as infinite absurdity requires infinitely strong counterevidence.

Furthermore, all sorts of standard theorems in probability have special cases if you try to plug 1s or 0s into them—like what happens if you try to do a Bayesian update on an observation to which you assigned probability 0.

So I propose that it makes sense to say that 1 and 0 are not in the probabilities; just as negative and positive infinity, which do not obey the field axioms, are not in the real numbers.

The main reason this would upset probability theorists is that we would need to rederive theorems previously obtained by assuming that we can marginalize over a joint probability by adding up all the pieces and having them sum to 1.

However, in the real world, when you roll a die, it doesn’t literally have infinite certainty of coming up some number between 1 and 6. The die might land on its edge; or get struck by a meteor; or the Dark Lords of the Matrix might reach in and write “37” on one side.

If you made a magical symbol to stand for “all possibilities I haven’t considered,” then you could marginalize over the events including this magical symbol, and arrive at a magical symbol “T” that stands for infinite certainty.

But I would rather ask whether there’s some way to derive a theorem without using magic symbols with special behaviors. That would be more elegant. Just as there are mathematicians who refuse to believe in the law of the excluded middle or infinite sets, I would like to be a probability theorist who doesn’t believe in absolute certainty.

56
Your Rationality Is My Business

Some responses to Lotteries: A Waste of Hope chided me for daring to criticize others’ decisions; if someone else chooses to buy lottery tickets, who am I to disagree? This is a special case of a more general question: What business is it of mine, if someone else chooses to believe what is pleasant rather than what is true? Can’t we each choose for ourselves whether to care about the truth?

An obvious snappy comeback is: “Why do you care whether I care whether someone else cares about the truth?” It is somewhat inconsistent for your utility function to contain a negative term for anyone else’s utility function having a term for someone else’s utility function. But that is only a snappy comeback, not an answer.

So here then is my answer: I believe that it is right and proper for me, as a human being, to have an interest in the future, and what human civilization becomes in the future. One of those interests is the human pursuit of truth, which has strengthened slowly over the generations (for there was not always Science). I wish to strengthen that pursuit further, in this generation. That is a wish of mine, for the Future. For we are all of us players upon that vast gameboard, whether we accept the responsibility or not.

And that makes your rationality my business.

Is this a dangerous idea? Yes, and not just pleasantly edgy “dangerous.” People have been burned to death because some priest decided that they didn’t think the way they should. Deciding to burn people to death because they “don’t think properly”—that’s a revolting kind of reasoning, isn’t it? You wouldn’t want people to think that way, why, it’s disgusting. People who think like that, well, we’ll have to do something about them . . .

I agree! Here’s my proposal: Let’s argue against bad ideas but not set their bearers on fire.

The syllogism we desire to avoid runs: “I think Susie said a bad thing, therefore, Susie should be set on fire.” Some try to avoid the syllogism by labeling it improper to think that Susie said a bad thing. No one should judge anyone, ever; anyone who judges is committing a terrible sin, and should be publicly pilloried for it.

As for myself, I deny the therefore. My syllogism runs, “I think Susie said something wrong, therefore, I will argue against what she said, but I will not set her on fire, or try to stop her from talking by violence or regulation . . .”

We are all of us players upon that vast gameboard; and one of my interests for the Future is to make the game fair. The counterintuitive idea underlying science is that factual disagreements should be fought out with experiments and mathematics, not violence and edicts. This incredible notion can be extended beyond science, to a fair fight for the whole Future. You should have to win by convincing people, and should not be allowed to burn them. This is one of the principles of Rationality, to which I have pledged my allegiance.

People who advocate relativism or selfishness do not appear to me to be truly relativistic or selfish. If they were really relativistic, they would not judge. If they were really selfish, they would get on with making money instead of arguing passionately with others. Rather, they have chosen the side of Relativism, whose goal upon that vast gameboard is to prevent the players—all the players—from making certain kinds of judgments. Or they have chosen the side of Selfishness, whose goal is to make all players selfish. And then they play the game, fairly or unfairly according to their wisdom.

If there are any true Relativists or Selfishes, we do not hear them—they remain silent, non-players.

I cannot help but care how you think, because—as I cannot help but see the universe—each time a human being turns away from the truth, the unfolding story of humankind becomes a little darker. In many cases, it is a small darkness only. (Someone doesn’t always end up getting hurt.) Lying to yourself, in the privacy of your own thoughts, does not shadow humanity’s history so much as telling public lies or setting people on fire. Yet there is a part of me which cannot help but mourn. And so long as I don’t try to set you on fire—only argue with your ideas—I believe that it is right and proper to me, as a human, that I care about my fellow humans. That, also, is a position I defend into the Future.

Part F
Politics and Rationality

57
Politics is the MindKiller

People go funny in the head when talking about politics. The evolutionary reasons for this are so obvious as to be worth belaboring: In the ancestral environment, politics was a matter of life and death. And sex, and wealth, and allies, and reputation . . . When, today, you get into an argument about whether “we” ought to raise the minimum wage, you’re executing adaptations for an ancestral environment where being on the wrong side of the argument could get you killed. Being on the right side of the argument could let you kill your hated rival!

If you want to make a point about science, or rationality, then my advice is to not choose a domain from contemporary politics if you can possibly avoid it. If your point is inherently about politics, then talk about Louis XVI during the French Revolution. Politics is an important domain to which we should individually apply our rationality—but it’s a terrible domain in which to learn rationality, or discuss rationality, unless all the discussants are already rational.

Politics is an extension of war by other means. Arguments are soldiers. Once you know which side you’re on, you must support all arguments of that side, and attack all arguments that appear to favor the enemy side; otherwise it’s like stabbing your soldiers in the back—providing aid and comfort to the enemy. People who would be level-headed about evenhandedly weighing all sides of an issue in their professional life as scientists, can suddenly turn into slogan-chanting zombies when there’s a Blue or Green position on an issue.

In Artificial Intelligence, and particularly in the domain of nonmonotonic reasoning, there’s a standard problem: “All Quakers are pacifists. All Republicans are not pacifists. Nixon is a Quaker and a Republican. Is Nixon a pacifist?”

What on Earth was the point of choosing this as an example? To rouse the political emotions of the readers and distract them from the main question? To make Republicans feel unwelcome in courses on Artificial Intelligence and discourage them from entering the field? (And no, I am not a Republican. Or a Democrat.)

Why would anyone pick such a distracting example to illustrate nonmonotonic reasoning? Probably because the author just couldn’t resist getting in a good, solid dig at those hated Greens. It feels so good to get in a hearty punch, y’know, it’s like trying to resist a chocolate cookie.

As with chocolate cookies, not everything that feels pleasurable is good for you.

I’m not saying that I think we should be apolitical, or even that we should adopt Wikipedia’s ideal of the Neutral Point of View. But try to resist getting in those good, solid digs if you can possibly avoid it. If your topic legitimately relates to attempts to ban evolution in school curricula, then go ahead and talk about it—but don’t blame it explicitly on the whole Republican Party; some of your readers may be Republicans, and they may feel that the problem is a few rogues, not the entire party. As with Wikipedia’s NPOV, it doesn’t matter whether (you think) the Republican Party really is at fault. It’s just better for the spiritual growth of the community to discuss the issue without invoking color politics.

58
Policy Debates Should Not Appear OneSided

Robin Hanson proposed stores where banned products could be sold. There are a number of excellent arguments for such a policy—an inherent right of individual liberty, the career incentive of bureaucrats to prohibit everything, legislators being just as biased as individuals. But even so (I replied), some poor, honest, not overwhelmingly educated mother of five children is going to go into these stores and buy a “Dr. Snakeoil’s Sulfuric Acid Drink” for her arthritis and die, leaving her orphans to weep on national television.

I was just making a simple factual observation. Why did some people think it was an argument in favor of regulation?

On questions of simple fact (for example, whether Earthly life arose by natural selection) there’s a legitimate expectation that the argument should be a onesided battle; the facts themselves are either one way or another, and the so-called “balance of evidence” should reflect this. Indeed, under the Bayesian definition of evidence, “strong evidence” is just that sort of evidence which we only expect to find on one side of an argument.

But there is no reason for complex actions with many consequences to exhibit this onesidedness property. Why do people seem to want their policy debates to be onesided?

Politics is the mind-killer. Arguments are soldiers. Once you know which side you’re on, you must support all arguments of that side, and attack all arguments that appear to favor the enemy side; otherwise it’s like stabbing your soldiers in the back. If you abide within that pattern, policy debates will also appear onesided to you—the costs and drawbacks of your favored policy are enemy soldiers, to be attacked by any means necessary.

One should also be aware of a related failure pattern, thinking that the course of Deep Wisdom is to compromise with perfect evenness between whichever two policy positions receive the most airtime. A policy may legitimately have lopsided costs or benefits. If policy questions were not tilted one way or the other, we would be unable to make decisions about them. But there is also a human tendency to deny all costs of a favored policy, or deny all benefits of a disfavored policy; and people will therefore tend to think policy tradeoffs are tilted much further than they actually are.

If you allow shops that sell otherwise banned products, some poor, honest, poorly educated mother of five kids is going to buy something that kills her. This is a prediction about a factual consequence, and as a factual question it appears rather straightforward—a sane person should readily confess this to be true regardless of which stance they take on the policy issue. You may also think that making things illegal just makes them more expensive, that regulators will abuse their power, or that her individual freedom trumps your desire to meddle with her life. But, as a matter of simple fact, she’s still going to die.

We live in an unfair universe. Like all primates, humans have strong negative reactions to perceived unfairness; thus we find this fact stressful. There are two popular methods of dealing with the resulting cognitive dissonance. First, one may change one’s view of the facts—deny that the unfair events took place, or edit the history to make it appear fair. (This is mediated by the affect heuristic and the just-world fallacy.) Second, one may change one’s morality—deny that the events are unfair.

Some libertarians might say that if you go into a “banned products shop,” passing clear warning labels that say THINGS IN THIS STORE MAY KILL YOU, and buy something that kills you, then it’s your own fault and you deserve it. If that were a moral truth, there would be no downside to having shops that sell banned products. It wouldn’t just be a net benefit, it would be a onesided tradeoff with no drawbacks.

Others argue that regulators can be trained to choose rationally and in harmony with consumer interests; if those were the facts of the matter then (in their moral view) there would be no downside to regulation.

Like it or not, there’s a birth lottery for intelligence—though this is one of the cases where the universe’s unfairness is so extreme that many people choose to deny the facts. The experimental evidence for a purely genetic component of 0.6–0.8 is overwhelming, but even if this were to be denied, you don’t choose your parental upbringing or your early schools either.

I was raised to believe that denying reality is a moral wrong. If I were to engage in wishful optimism about how Sulfuric Acid Drink was likely to benefit me, I would be doing something that I was warned against and raised to regard as unacceptable. Some people are born into environments—we won’t discuss their genes, because that part is too unfair—where the local witch doctor tells them that it is right to have faith and wrong to be skeptical. In all goodwill, they follow this advice and die. Unlike you, they weren’t raised to believe that people are responsible for their individual choices to follow society’s lead. Do you really think you’re so smart that you would have been a proper scientific skeptic even if you’d been born in 500 CE? Yes, there is a birth lottery, no matter what you believe about genes.

Saying “People who buy dangerous products deserve to get hurt!” is not tough-minded. It is a way of refusing to live in an unfair universe. Real tough-mindedness is saying, “Yes, sulfuric acid is a horrible painful death, and no, that mother of five children didn’t deserve it, but we’re going to keep the shops open anyway because we did this cost-benefit calculation.” Can you imagine a politician saying that? Neither can I. But insofar as economists have the power to influence policy, it might help if they could think it privately—maybe even say it in journal articles, suitably dressed up in polysyllabismic obfuscationalization so the media can’t quote it.

I don’t think that when someone makes a stupid choice and dies, this is a cause for celebration. I count it as a tragedy. It is not always helping people, to save them from the consequences of their own actions; but I draw a moral line at capital punishment. If you’re dead, you can’t learn from your mistakes.

Unfortunately the universe doesn’t agree with me. We’ll see which one of us is still standing when this is over.

59
The Scales of Justice, the Notebook of Rationality

Lady Justice is widely depicted as carrying scales. A set of scales has the property that whatever pulls one side down pushes the other side up. This makes things very convenient and easy to track. It’s also usually a gross distortion.

In human discourse there is a natural tendency to treat discussion as a form of combat, an extension of war, a sport; and in sports you only need to keep track of how many points have been scored by each team. There are only two sides, and every point scored against one side is a point in favor of the other. Everyone in the audience keeps a mental running count of how many points each speaker scores against the other. At the end of the debate, the speaker who has scored more points is, obviously, the winner; so everything that speaker says must be true, and everything the loser says must be wrong.

“The Affect Heuristic in Judgments of Risks and Benefits” studied whether subjects mixed up their judgments of the possible benefits of a technology (e.g., nuclear power), and the possible risks of that technology, into a single overall good or bad feeling about the technology.¹ Suppose that I first tell you that a particular kind of nuclear reactor generates less nuclear waste than competing reactor designs. But then I tell you that the reactor is more unstable than competing designs, with a greater danger of melting down if a sufficient number of things go wrong simultaneously.

If the reactor is more likely to melt down, this seems like a “point against” the reactor, or a “point against” someone who argues for building the reactor. And if the reactor produces less waste, this is a “point for” the reactor, or a “point for” building it. So are these two facts opposed to each other? No. In the real world, no. These two facts may be cited by different sides of the same debate, but they are logically distinct; the facts don’t know whose side they’re on.

If it’s a physical fact about a reactor design that it’s passively safe (won’t go supercritical even if the surrounding coolant systems and so on break down), this doesn’t imply that the reactor will necessarily generate less waste, or produce electricity at a lower cost. All these things would be good, but they are not the same good thing. The amount of waste produced by the reactor arises from the properties of that reactor. Other physical properties of the reactor make the nuclear reaction more unstable. Even if some of the same design properties are involved, you have to separately consider the probability of meltdown, and the expected annual waste generated. These are two different physical questions with two different factual answers.

But studies such as the above show that people tend to judge technologies—and many other problems—by an overall good or bad feeling. If you tell people a reactor design produces less waste, they rate its probability of meltdown as lower. This means getting the wrong answer to physical questions with definite factual answers, because you have mixed up logically distinct questions—treated facts like human soldiers on different sides of a war, thinking that any soldier on one side can be used to fight any soldier on the other side.

A set of scales is not wholly inappropriate for Lady Justice if she is investigating a strictly factual question of guilt or innocence. Either John Smith killed John Doe, or not. We are taught (by E. T. Jaynes) that all Bayesian evidence consists of probability flows between hypotheses; there is no such thing as evidence that “supports” or “contradicts” a single hypothesis, except insofar as other hypotheses do worse or better. So long as Lady Justice is investigating a single, strictly factual question with a binary answer space, a set of scales would be an appropriate tool. If Justitia must consider any more complex issue, she should relinquish her scales or relinquish her sword.

Not all arguments reduce to mere up or down. Lady Rationality carries a notebook, wherein she writes down all the facts that aren’t on anyone’s side.

1. Melissa L. Finucane et al., “The Affect Heuristic in Judgments of Risks and Benefits,” Journal of Behavioral Decision Making 13, no. 1 (2000): 1–17.

60
Correspondence Bias

The correspondence bias is the tendency to draw inferences about a person’s unique and enduring dispositions from behaviors that can be entirely explained by the situations in which they occur.

—Gilbert and Malone¹

We tend to see far too direct a correspondence between others’ actions and personalities. When we see someone else kick a vending machine for no visible reason, we assume they are “an angry person.” But when you yourself kick the vending machine, it’s because the bus was late, the train was early, your report is overdue, and now the damned vending machine has eaten your lunch money for the second day in a row. Surely, you think to yourself, anyone would kick the vending machine, in that situation.

We attribute our own actions to our situations, seeing our behaviors as perfectly normal responses to experience. But when someone else kicks a vending machine, we don’t see their past history trailing behind them in the air. We just see the kick, for no reason we know about, and we think this must be a naturally angry person—since they lashed out without any provocation.

Yet consider the prior probabilities. There are more late buses in the world, than mutants born with unnaturally high anger levels that cause them to sometimes spontaneously kick vending machines. Now the average human is, in fact, a mutant. If I recall correctly, an average individual has two to ten somatically expressed mutations. But any given DNA location is very unlikely to be affected. Similarly, any given aspect of someone’s disposition is probably not very far from average. To suggest otherwise is to shoulder a burden of improbability.

Even when people are informed explicitly of situational causes, they don’t seem to properly discount the observed behavior. When subjects are told that a pro-abortion or anti-abortion speaker was randomly assigned to give a speech on that position, subjects still think the speakers harbor leanings in the direction randomly assigned.²

It seems quite intuitive to explain rain by water spirits; explain fire by a fire-stuff (phlogiston) escaping from burning matter; explain the soporific effect of a medication by saying that it contains a “dormitive potency.” Reality usually involves more complicated mechanisms: an evaporation and condensation cycle underlying rain, oxidizing combustion underlying fire, chemical interactions with the nervous system for soporifics. But mechanisms sound more complicated than essences; they are harder to think of, less available. So when someone kicks a vending machine, we think they have an innate vending-machine-kicking-tendency.

Unless the “someone” who kicks the machine is us—in which case we’re behaving perfectly normally, given our situations; surely anyone else would do the same. Indeed, we overestimate how likely others are to respond the same way we do—the “false consensus effect.” Drinking students considerably overestimate the fraction of fellow students who drink, but nondrinkers considerably underestimate the fraction. The “fundamental attribution error” refers to our tendency to overattribute others’ behaviors to their dispositions, while reversing this tendency for ourselves.

To understand why people act the way they do, we must first realize that everyone sees themselves as behaving normally. Don’t ask what strange, mutant disposition they were born with, which directly corresponds to their surface behavior. Rather, ask what situations people see themselves as being in. Yes, people do have dispositions—but there are not enough heritable quirks of disposition to directly account for all the surface behaviors you see.

Suppose I gave you a control with two buttons, a red button and a green button. The red button destroys the world, and the green button stops the red button from being pressed. Which button would you press? The green one. Anyone who gives a different answer is probably overcomplicating the question.

And yet people sometimes ask me why I want to save the world. Like I must have had a traumatic childhood or something. Really, it seems like a pretty obvious decision . . . if you see the situation in those terms.

I may have non-average views which call for explanation—why do I believe such things, when most people don’t?—but given those beliefs, my reaction doesn’t seem to call forth an exceptional explanation. Perhaps I am a victim of false consensus; perhaps I overestimate how many people would press the green button if they saw the situation in those terms. But y’know, I’d still bet there’d be at least a substantial minority.

Most people see themselves as perfectly normal, from the inside. Even people you hate, people who do terrible things, are not exceptional mutants. No mutations are required, alas. When you understand this, you are ready to stop being surprised by human events.

1. Daniel T. Gilbert and Patrick S. Malone, “The Correspondence Bias,” Psychological Bulletin 117, no. 1 (1995): 21–38, http://www.wjh.harvard.edu/~dtg/Gilbert%20&%20Malone%20(CORRESPONDENCE%20BIAS).pdf.

2. Edward E. Jones and Victor A. Harris, “The Attribution of Attitudes,” Journal of Experimental Social Psychology 3 (1967): 1–24, http://www.radford.edu/~jaspelme/443/spring-2007/Articles/Jones_n_Harris_1967.pdf.

61
Are Your Enemies Innately Evil?

We see far too direct a correspondence between others’ actions and their inherent dispositions. We see unusual dispositions that exactly match the unusual behavior, rather than asking after real situations or imagined situations that could explain the behavior. We hypothesize mutants.

When someone actually offends us—commits an action of which we (rightly or wrongly) disapprove—then, I observe, the correspondence bias redoubles. There seems to be a very strong tendency to blame evil deeds on the Enemy’s mutant, evil disposition. Not as a moral point, but as a strict question of prior probability, we should ask what the Enemy might believe about their situation that would reduce the seeming bizarrity of their behavior. This would allow us to hypothesize a less exceptional disposition, and thereby shoulder a lesser burden of improbability.

On September 11th, 2001, nineteen Muslim males hijacked four jet airliners in a deliberately suicidal effort to hurt the United States of America. Now why do you suppose they might have done that? Because they saw the USA as a beacon of freedom to the world, but were born with a mutant disposition that made them hate freedom?

Realistically, most people don’t construct their life stories with themselves as the villains. Everyone is the hero of their own story. The Enemy’s story, as seen by the Enemy, is not going to make the Enemy look bad. If you try to construe motivations that would make the Enemy look bad, you’ll end up flat wrong about what actually goes on in the Enemy’s mind.

But politics is the mind-killer. Debate is war; arguments are soldiers. Once you know which side you’re on, you must support all arguments of that side, and attack all arguments that appear to favor the opposing side; otherwise it’s like stabbing your soldiers in the back.

If the Enemy did have an evil disposition, that would be an argument in favor of your side. And any argument that favors your side must be supported, no matter how silly—otherwise you’re letting up the pressure somewhere on the battlefront. Everyone strives to outshine their neighbor in patriotic denunciation, and no one dares to contradict. Soon the Enemy has horns, bat wings, flaming breath, and fangs that drip corrosive venom. If you deny any aspect of this on merely factual grounds, you are arguing the Enemy’s side; you are a traitor. Very few people will understand that you aren’t defending the Enemy, just defending the truth.

If it took a mutant to do monstrous things, the history of the human species would look very different. Mutants would be rare.

Or maybe the fear is that understanding will lead to forgiveness. It’s easier to shoot down evil mutants. It is a more inspiring battle cry to scream, “Die, vicious scum!” instead of “Die, people who could have been just like me but grew up in a different environment!” You might feel guilty killing people who weren’t pure darkness.

This looks to me like the deep-seated yearning for a one-sided policy debate in which the best policy has no drawbacks. If an army is crossing the border or a lunatic is coming at you with a knife, the policy alternatives are (a) defend yourself or (b) lie down and die. If you defend yourself, you may have to kill. If you kill someone who could, in another world, have been your friend, that is a tragedy. And it is a tragedy. The other option, lying down and dying, is also a tragedy. Why must there be a non-tragic option? Who says that the best policy available must have no downside? If someone has to die, it may as well be the initiator of force, to discourage future violence and thereby minimize the total sum of death.

If the Enemy has an average disposition, and is acting from beliefs about their situation that would make violence a typically human response, then that doesn’t mean their beliefs are factually accurate. It doesn’t mean they’re justified. It means you’ll have to shoot down someone who is the hero of their own story, and in their novel the protagonist will die on page 80. That is a tragedy, but it is better than the alternative tragedy. It is the choice that every police officer makes, every day, to keep our neat little worlds from dissolving into chaos.

When you accurately estimate the Enemy’s psychology—when you know what is really in the Enemy’s mind—that knowledge won’t feel like landing a delicious punch on the opposing side. It won’t give you a warm feeling of righteous indignation. It won’t make you feel good about yourself. If your estimate makes you feel unbearably sad, you may be seeing the world as it really is. More rarely, an accurate estimate may send shivers of serious horror down your spine, as when dealing with true psychopaths, or neurologically intact people with beliefs that have utterly destroyed their sanity (Scientologists or Jesus Campers).

So let’s come right out and say it—the 9/11 hijackers weren’t evil mutants. They did not hate freedom. They, too, were the heroes of their own stories, and they died for what they believed was right—truth, justice, and the Islamic way. If the hijackers saw themselves that way, it doesn’t mean their beliefs were true. If the hijackers saw themselves that way, it doesn’t mean that we have to agree that what they did was justified. If the hijackers saw themselves that way, it doesn’t mean that the passengers of United Flight 93 should have stood aside and let it happen. It does mean that in another world, if they had been raised in a different environment, those hijackers might have been police officers. And that is indeed a tragedy. Welcome to Earth.

62
Reversed Stupidity Is Not Intelligence

“. . . then our people on that time-line went to work with corrective action. Here.”

He wiped the screen and then began punching combinations. Page after page appeared, bearing accounts of people who had claimed to have seen the mysterious disks, and each report was more fantastic than the last.

“The standard smother-out technique,” Verkan Vall grinned. “I only heard a little talk about the ‘flying saucers,’ and all of that was in joke. In that order of culture, you can always discredit one true story by setting up ten others, palpably false, parallel to it.”

—H. Beam Piper, Police Operation¹

Piper had a point. Pers’nally, I don’t believe there are any poorly hidden aliens infesting these parts. But my disbelief has nothing to do with the awful embarrassing irrationality of flying saucer cults—at least, I hope not.

You and I believe that flying saucer cults arose in the total absence of any flying saucers. Cults can arise around almost any idea, thanks to human silliness. This silliness operates orthogonally to alien intervention: We would expect to see flying saucer cults whether or not there were flying saucers. Even if there were poorly hidden aliens, it would not be any less likely for flying saucer cults to arise. The conditional probability P(cults|aliens) isn’t less than P(cults|¬aliens), unless you suppose that poorly hidden aliens would deliberately suppress flying saucer cults. By the Bayesian definition of evidence, the observation “flying saucer cults exist” is not evidence against the existence of flying saucers. It’s not much evidence one way or the other.

This is an application of the general principle that, as Robert Pirsig puts it, “The world’s greatest fool may say the Sun is shining, but that doesn’t make it dark out.”²

If you knew someone who was wrong 99.99% of the time on yes-or-no questions, you could obtain 99.99% accuracy just by reversing their answers. They would need to do all the work of obtaining good evidence entangled with reality, and processing that evidence coherently, just to anticorrelate that reliably. They would have to be superintelligent to be that stupid.

A car with a broken engine cannot drive backward at 200 mph, even if the engine is really really broken.

If stupidity does not reliably anticorrelate with truth, how much less should human evil anticorrelate with truth? The converse of the halo effect is the horns effect: All perceived negative qualities correlate. If Stalin is evil, then everything he says should be false. You wouldn’t want to agree with Stalin, would you?

Stalin also believed that 2 + 2 = 4. Yet if you defend any statement made by Stalin, even “2 + 2 = 4,” people will see only that you are “agreeing with Stalin”; you must be on his side.

Corollaries of this principle:

To argue against an idea honestly, you should argue against the best arguments of the strongest advocates. Arguing against weaker advocates proves nothing, because even the strongest idea will attract weak advocates. If you want to argue against transhumanism or the intelligence explosion, you have to directly challenge the arguments of Nick Bostrom or Eliezer Yudkowsky post-2003. The least convenient path is the only valid one.
Exhibiting sad, pathetic lunatics, driven to madness by their apprehension of an Idea, is no evidence against that Idea. Many New Agers have been made crazier by their personal apprehension of quantum mechanics.
Someone once said, “Not all conservatives are stupid, but most stupid people are conservatives.” If you cannot place yourself in a state of mind where this statement, true or false, seems completely irrelevant as a critique of conservatism, you are not ready to think rationally about politics.
Ad hominem argument is not valid.
You need to be able to argue against genocide without saying “Hitler wanted to exterminate the Jews.” If Hitler hadn’t advocated genocide, would it thereby become okay?
In Hansonian terms: Your instinctive willingness to believe something will change along with your willingness to affiliate with people who are known for believing it—quite apart from whether the belief is actually true. Some people may be reluctant to believe that God does not exist, not because there is evidence that God does exist, but rather because they are reluctant to affiliate with Richard Dawkins or those darned “strident” atheists who go around publicly saying “God does not exist.”
If your current computer stops working, you can’t conclude that everything about the current system is wrong and that you need a new system without an AMD processor, an ATI video card, a Maxtor hard drive, or case fans—even though your current system has all these things and it doesn’t work. Maybe you just need a new power cord.
If a hundred inventors fail to build flying machines using metal and wood and canvas, it doesn’t imply that what you really need is a flying machine of bone and flesh. If a thousand projects fail to build Artificial Intelligence using electricity-based computing, this doesn’t mean that electricity is the source of the problem. Until you understand the problem, hopeful reversals are exceedingly unlikely to hit the solution.

1. Henry Beam Piper, “Police Operation,” Astounding Science Fiction (July 1948).

2. Robert M. Pirsig, Zen and the Art of Motorcycle Maintenance: An Inquiry Into Values, 1st ed. (New York: Morrow, 1974).

63
Argument Screens Off Authority

Scenario 1: Barry is a famous geologist. Charles is a fourteen-year-old juvenile delinquent with a long arrest record and occasional psychotic episodes. Barry flatly asserts to Arthur some counterintuitive statement about rocks, and Arthur judges it 90% probable. Then Charles makes an equally counterintuitive flat assertion about rocks, and Arthur judges it 10% probable. Clearly, Arthur is taking the speaker’s authority into account in deciding whether to believe the speaker’s assertions.

Scenario 2: David makes a counterintuitive statement about physics and gives Arthur a detailed explanation of the arguments, including references. Ernie makes an equally counterintuitive statement, but gives an unconvincing argument involving several leaps of faith. Both David and Ernie assert that this is the best explanation they can possibly give (to anyone, not just Arthur). Arthur assigns 90% probability to David’s statement after hearing his explanation, but assigns a 10% probability to Ernie’s statement.

It might seem like these two scenarios are roughly symmetrical: both involve taking into account useful evidence, whether strong versus weak authority, or strong versus weak argument.

But now suppose that Arthur asks Barry and Charles to make full technical cases, with references; and that Barry and Charles present equally good cases, and Arthur looks up the references and they check out. Then Arthur asks David and Ernie for their credentials, and it turns out that David and Ernie have roughly the same credentials—maybe they’re both clowns, maybe they’re both physicists.

Assuming that Arthur is knowledgeable enough to understand all the technical arguments—otherwise they’re just impressive noises—it seems that Arthur should view David as having a great advantage in plausibility over Ernie, while Barry has at best a minor advantage over Charles.

Indeed, if the technical arguments are good enough, Barry’s advantage over Charles may not be worth tracking. A good technical argument is one that eliminates reliance on the personal authority of the speaker.

Similarly, if we really believe Ernie that the argument he gave is the best argument he could give, which includes all of the inferential steps that Ernie executed, and all of the support that Ernie took into account—citing any authorities that Ernie may have listened to himself—then we can pretty much ignore any information about Ernie’s credentials. Ernie can be a physicist or a clown, it shouldn’t matter. (Again, this assumes we have enough technical ability to process the argument. Otherwise, Ernie is simply uttering mystical syllables, and whether we “believe” these syllables depends a great deal on his authority.)

So it seems there’s an asymmetry between argument and authority. If we know authority we are still interested in hearing the arguments; but if we know the arguments fully, we have very little left to learn from authority.

Clearly (says the novice) authority and argument are fundamentally different kinds of evidence, a difference unaccountable in the boringly clean methods of Bayesian probability theory. For while the strength of the evidences—90% versus 10%—is just the same in both cases, they do not behave similarly when combined. How will we account for this?

Here’s half a technical demonstration of how to represent this difference in probability theory. (The rest you can take on my personal authority, or look up in the references.)

If P(H|E₁) = 90% and P(H|E₂) = 9%, what is the probability P(H|E₁,E₂)? If learning E₁ is true leads us to assign 90% probability to H, and learning E₂ is true leads us to assign 9% probability to H, then what probability should we assign to H if we learn both E₁ and E₂? This is simply not something you can calculate in probability theory from the information given. No, the missing information is not the prior probability of H. The events E₁ and E₂ may not be independent of each other.

Suppose that H is “My sidewalk is slippery,” E₁ is “My sprinkler is running,” and E₂ is “It’s night.” The sidewalk is slippery starting from one minute after the sprinkler starts, until just after the sprinkler finishes, and the sprinkler runs for ten minutes. So if we know the sprinkler is on, the probability is 90% that the sidewalk is slippery. The sprinkler is on during 10% of the nighttime, so if we know that it’s night, the probability of the sidewalk being slippery is 9%. If we know that it’s night and the sprinkler is on—that is, if we know both facts—the probability of the sidewalk being slippery is 90%.

We can represent this in a graphical model as follows:

Whether or not it’s Night causes the Sprinkler to be on or off, and whether the Sprinkler is on causes the sidewalk to be Slippery or unSlippery.

The direction of the arrows is meaningful. Say we had:

This would mean that, if I didn’t know anything about the sprinkler, the probability of Nighttime and Slipperiness would be independent of each other. For example, suppose that I roll Die One and Die Two, and add up the showing numbers to get the Sum:

If you don’t tell me the sum of the two numbers, and you tell me the first die showed 6, this doesn’t tell me anything about the result of the second die, yet. But if you now also tell me the sum is 7, I know the second die showed 1.

Figuring out when various pieces of information are dependent or independent of each other, given various background knowledge, actually turns into a quite technical topic. The books to read are Judea Pearl’s Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference¹ and Causality: Models, Reasoning, and Inference.² (If you only have time to read one book, read the first one.)

If you know how to read causal graphs, then you look at the dice-roll graph and immediately see:

P(Die 1, Die 2) = P(Die 1) × P(Die 2)

P(Die 1, Die 2|Sum) ≠ P(Die 1|Sum) × P(Die 2|Sum)

If you look at the correct sidewalk diagram, you see facts like:

P(Slippery|Night) ≠ P(Slippery)

P(Slippery|Sprinkler) ≠ P(Slippery)

P(Slippery|Night, Sprinkler) = P(Slippery|Sprinkler).

That is, the probability of the sidewalk being Slippery, given knowledge about the Sprinkler and the Night, is the same probability we would assign if we knew only about the Sprinkler. Knowledge of the Sprinkler has made knowledge of the Night irrelevant to inferences about Slipperiness.

This is known as screening off, and the criterion that lets us read such conditional independences off causal graphs is known as D-separation.

For the case of argument and authority, the causal diagram looks like this:

If something is true, then it therefore tends to have arguments in favor of it, and the experts therefore observe these evidences and change their opinions. (In theory!)

If we see that an expert believes something, we infer back to the existence of evidence-in-the-abstract (even though we don’t know what that evidence is exactly), and from the existence of this abstract evidence, we infer back to the truth of the proposition.

But if we know the value of the Argument node, this D-separates the node “Truth” from the node “Expert Belief” by blocking all paths between them, according to certain technical criteria for “path blocking” that seem pretty obvious in this case. So even without checking the exact probability distribution, we can read off from the graph that:

P(truth|argument, expert) = P(truth|argument).

This does not represent a contradiction of ordinary probability theory. It’s just a more compact way of expressing certain probabilistic facts. You could read the same equalities and inequalities off an unadorned probability distribution—but it would be harder to see it by eyeballing. Authority and argument don’t need two different kinds of probability, any more than sprinklers are made out of ontologically different stuff than sunlight.

In practice you can never completely eliminate reliance on authority. Good authorities are more likely to know about any counterevidence that exists and should be taken into account; a lesser authority is less likely to know this, which makes their arguments less reliable. This is not a factor you can eliminate merely by hearing the evidence they did take into account.

It’s also very hard to reduce arguments to pure math; and otherwise, judging the strength of an inferential step may rely on intuitions you can’t duplicate without the same thirty years of experience.

There is an ineradicable legitimacy to assigning slightly higher probability to what E. T. Jaynes tells you about Bayesian probability, than you assign to Eliezer Yudkowsky making the exact same statement. Fifty additional years of experience should not count for literally zero influence.

But this slight strength of authority is only ceteris paribus, and can easily be overwhelmed by stronger arguments. I have a minor erratum in one of Jaynes’s books—because algebra trumps authority.

1. Pearl, Probabilistic Reasoning in Intelligent Systems.

2. Judea Pearl, Causality: Models, Reasoning, and Inference, 2nd ed. (New York: Cambridge University Press, 2009).

64
Hug the Query

In the art of rationality there is a discipline of closeness-to-the-issue—trying to observe evidence that is as near to the original question as possible, so that it screens off as many other arguments as possible.

The Wright Brothers say, “My plane will fly.” If you look at their authority (bicycle mechanics who happen to be excellent amateur physicists) then you will compare their authority to, say, Lord Kelvin, and you will find that Lord Kelvin is the greater authority.

If you demand to see the Wright Brothers’ calculations, and you can follow them, and you demand to see Lord Kelvin’s calculations (he probably doesn’t have any apart from his own incredulity), then authority becomes much less relevant.

If you actually watch the plane fly, the calculations themselves become moot for many purposes, and Kelvin’s authority not even worth considering.

The more directly your arguments bear on a question, without intermediate inferences—the closer the observed nodes are to the queried node, in the Great Web of Causality—the more powerful the evidence. It’s a theorem of these causal graphs that you can never get more information from distant nodes, than from strictly closer nodes that screen off the distant ones.

Jerry Cleaver said: “What does you in is not failure to apply some high-level, intricate, complicated technique. It’s overlooking the basics. Not keeping your eye on the ball.”¹

Just as it is superior to argue physics than credentials, it is also superior to argue physics than rationality. Who was more rational, the Wright Brothers or Lord Kelvin? If we can check their calculations, we don’t have to care! The virtue of a rationalist cannot directly cause a plane to fly.

If you forget this principle, learning about more biases will hurt you, because it will distract you from more direct arguments. It’s all too easy to argue that someone is exhibiting Bias #182 in your repertoire of fully generic accusations, but you can’t settle a factual issue without closer evidence. If there are biased reasons to say the Sun is shining, that doesn’t make it dark out.

Just as you can’t always experiment today, you can’t always check the calculations today. Sometimes you don’t know enough background material, sometimes there’s private information, sometimes there just isn’t time. There’s a sadly large number of times when it’s worthwhile to judge the speaker’s rationality. You should always do it with a hollow feeling in your heart, though, a sense that something’s missing.

Whenever you can, dance as near to the original question as possible—press yourself up against it—get close enough to hug the query!

1. Jerry Cleaver, Immediate Fiction: A Complete Writing Course (Macmillan, 2004).

65
Rationality and the English Language

Responding to my discussion of applause lights, someone said that my writing reminded them of George Orwell’s Politics and the English Language.¹ I was honored. Especially since I’d already thought of today’s topic.

If you really want an artist’s perspective on rationality, then read Orwell; he is mandatory reading for rationalists as well as authors. Orwell was not a scientist, but a writer; his tools were not numbers, but words; his adversary was not Nature, but human evil. If you wish to imprison people for years without trial, you must think of some other way to say it than “I’m going to imprison Mr. Jennings for years without trial.” You must muddy the listener’s thinking, prevent clear images from outraging conscience. You say, “Unreliable elements were subjected to an alternative justice process.”

Orwell was the outraged opponent of totalitarianism and the muddy thinking in which evil cloaks itself—which is how Orwell’s writings on language ended up as classic rationalist documents on a level with Feynman, Sagan, or Dawkins.

“Writers are told to avoid usage of the passive voice.” A rationalist whose background comes exclusively from science may fail to see the flaw in the previous sentence; but anyone who’s done a little writing should see it right away. I wrote the sentence in the passive voice, without telling you who tells authors to avoid passive voice. Passive voice removes the actor, leaving only the acted-upon. “Unreliable elements were subjected to an alternative justice process”—subjected by whom? What does an “alternative justice process” do? With enough static noun phrases, you can keep anything unpleasant from actually happening.

Journal articles are often written in passive voice. (Pardon me, some scientists write their journal articles in passive voice. It’s not as if the articles are being written by no one, with no one to blame.) It sounds more authoritative to say “The subjects were administered Progenitorivox” than “I gave each college student a bottle of 20 Progenitorivox, and told them to take one every night until they were gone.” If you remove the scientist from the description, that leaves only the all-important data. But in reality the scientist is there, and the subjects are college students, and the Progenitorivox wasn’t “administered” but handed over with instructions. Passive voice obscures reality.

Judging from the comments I get, someone will protest that using the passive voice in a journal article is hardly a sin—after all, if you think about it, you can realize the scientist is there. It doesn’t seem like a logical flaw. And this is why rationalists need to read Orwell, not just Feynman or even Jaynes.

Nonfiction conveys knowledge, fiction conveys experience. Medical science can extrapolate what would happen to a human unprotected in a vacuum. Fiction can make you live through it.

Some rationalists will try to analyze a misleading phrase, try to see if there might possibly be anything meaningful to it, try to construct a logical interpretation. They will be charitable, give the author the benefit of the doubt. Authors, on the other hand, are trained not to give themselves the benefit of the doubt. Whatever the audience thinks you said is what you said, whether you meant to say it or not; you can’t argue with the audience no matter how clever your justifications.

A writer knows that readers will not stop for a minute to think. A fictional experience is a continuous stream of first impressions. A writer-rationalist pays attention to the experience words create. If you are evaluating the public rationality of a statement, and you analyze the words deliberatively, rephrasing propositions, trying out different meanings, searching for nuggets of truthiness, then you’re losing track of the first impression—what the audience sees, or rather feels.

A novelist would notice the screaming wrongness of “The subjects were administered Progenitorivox.” What life is here for a reader to live? This sentence creates a distant feeling of authoritativeness, and that’s all—the only experience is the feeling of being told something reliable. A novelist would see nouns too abstract to show what actually happened—the postdoc with the bottle in their hand, trying to look stern; the student listening with a nervous grin.

My point is not to say that journal articles should be written like novels, but that a rationalist should become consciously aware of the experiences which words create. A rationalist must understand the mind and how to operate it. That includes the stream of consciousness, the part of yourself that unfolds in language. A rationalist must become consciously aware of the actual, experiential impact of phrases, beyond their mere propositional semantics.

Or to say it more bluntly: Meaning does not excuse impact!

I don’t care what rational interpretation you can construct for an applause light like “AI should be developed through democratic processes.” That cannot excuse its irrational impact of signaling the audience to applaud, not to mention its cloudy question-begging vagueness.

Here is Orwell, railing against the impact of cliches, their effect on the experience of thinking:

When one watches some tired hack on the platform mechanically repeating the familiar phrases—BESTIAL, ATROCITIES, IRON HEEL, BLOODSTAINED TYRANNY, FREE PEOPLES OF THE WORLD, STAND SHOULDER TO SHOULDER—one often has a curious feeling that one is not watching a live human being but some kind of dummy . . . A speaker who uses that kind of phraseology has gone some distance toward turning himself into a machine. The appropriate noises are coming out of his larynx, but his brain is not involved, as it would be if he were choosing his words for himself . . .

What is above all needed is to let the meaning choose the word, and not the other way around. In prose, the worst thing one can do with words is surrender to them. When you think of a concrete object, you think wordlessly, and then, if you want to describe the thing you have been visualising you probably hunt about until you find the exact words that seem to fit it. When you think of something abstract you are more inclined to use words from the start, and unless you make a conscious effort to prevent it, the existing dialect will come rushing in and do the job for you, at the expense of blurring or even changing your meaning. Probably it is better to put off using words as long as possible and get one’s meaning as clear as one can through pictures and sensations.

Charles Sanders Peirce might have written that last paragraph. More than one path can lead to the Way.

1. George Orwell, “Politics and the English Language,” Horizon (April 1946).

66
Human Evil and Muddled Thinking

George Orwell saw the descent of the civilized world into totalitarianism, the conversion or corruption of one country after another; the boot stamping on a human face, forever, and remember that it is forever. You were born too late to remember a time when the rise of totalitarianism seemed unstoppable, when one country after another fell to secret police and the thunderous knock at midnight, while the professors of free universities hailed the Soviet Union’s purges as progress. It feels as alien to you as fiction; it is hard for you to take seriously. Because, in your branch of time, the Berlin Wall fell. And if Orwell’s name is not carved into one of those stones, it should be.

Orwell saw the destiny of the human species, and he put forth a convulsive effort to wrench it off its path. Orwell’s weapon was clear writing. Orwell knew that muddled language is muddled thinking; he knew that human evil and muddled thinking intertwine like conjugate strands of DNA:¹

In our time, political speech and writing are largely the defence of the indefensible. Things like the continuance of British rule in India, the Russian purges and deportations, the dropping of the atom bombs on Japan, can indeed be defended, but only by arguments which are too brutal for most people to face, and which do not square with the professed aims of the political parties. Thus political language has to consist largely of euphemism, question-begging and sheer cloudy vagueness. Defenceless villages are bombarded from the air, the inhabitants driven out into the countryside, the cattle machine-gunned, the huts set on fire with incendiary bullets: this is called PACIFICATION . . .

Orwell was clear on the goal of his clarity:

If you simplify your English, you are freed from the worst follies of orthodoxy. You cannot speak any of the necessary dialects, and when you make a stupid remark its stupidity will be obvious, even to yourself.

To make our stupidity obvious, even to ourselves—this is the heart of Overcoming Bias.

Evil sneaks, hidden, through the unlit shadows of the mind. We look back with the clarity of history, and weep to remember the planned famines of Stalin and Mao, which killed tens of millions. We call this evil, because it was done by deliberate human intent to inflict pain and death upon innocent human beings. We call this evil, because of the revulsion that we feel against it, looking back with the clarity of history. For perpetrators of evil to avoid its natural opposition, the revulsion must remain latent. Clarity must be avoided at any cost. Even as humans of clear sight tend to oppose the evil that they see; so too does human evil, wherever it exists, set out to muddle thinking.

1984 sets this forth starkly: Orwell’s ultimate villains are cutters and airbrushers of photographs (based on historical cutting and airbrushing in the Soviet Union). At the peak of all darkness in the Ministry of Love, O’Brien tortures Winston to admit that two plus two equals five:²

“Do you remember,” he went on, “writing in your diary, ‘Freedom is the freedom to say that two plus two make four’?”

“Yes,” said Winston.

O’Brien held up his left hand, its back towards Winston, with the thumb hidden and the four fingers extended.

“How many fingers am I holding up, Winston?”

“Four.”

“And if the party says that it is not four but five—then how many?”

“Four.”

The word ended in a gasp of pain. The needle of the dial had shot up to fifty-five. The sweat had sprung out all over Winston’s body. The air tore into his lungs and issued again in deep groans which even by clenching his teeth he could not stop. O’Brien watched him, the four fingers still extended. He drew back the lever. This time the pain was only slightly eased.

I am continually aghast at apparently intelligent folks—such as Robin Hanson’s colleague Tyler Cowen—who don’t think that overcoming bias is important. This is your mind we’re talking about. Your human intelligence. It separates you from an ape. It built this world. You don’t think how the mind works is important? You don’t think the mind’s systematic malfunctions are important? Do you think the Inquisition would have tortured witches, if all were ideal Bayesians?

Tyler Cowen apparently feels that overcoming bias is just as biased as bias: “I view Robin’s blog as exemplifying bias, and indeed showing that bias can be very useful.” I hope this is only the result of thinking too abstractly while trying to sound clever. Does Tyler seriously think that scope insensitivity to the value of human life is on the same level with trying to create plans that will really save as many lives as possible?

Orwell was forced to fight a similar attitude—that to admit to any distinction is youthful naiveté:

Stuart Chase and others have come near to claiming that all abstract words are meaningless, and have used this as a pretext for advocating a kind of political quietism. Since you don’t know what Fascism is, how can you struggle against Fascism?

Maybe overcoming bias doesn’t look quite exciting enough, if it’s framed as a struggle against mere accidental mistakes. Maybe it’s harder to get excited if there isn’t some clear evil to oppose. So let us be absolutely clear that where there is human evil in the world, where there is cruelty and torture and deliberate murder, there are biases enshrouding it. Where people of clear sight oppose these biases, the concealed evil fights back. The truth does have enemies. If Overcoming Bias were a newsletter in the old Soviet Union, every poster and commenter of Overcoming Bias would have been shipped off to labor camps.

In all human history, every great leap forward has been driven by a new clarity of thought. Except for a few natural catastrophes, every great woe has been driven by a stupidity. Our last enemy is ourselves; and this is a war, and we are soldiers.

1. Ibid.

2. George Orwell, 1984 (Signet Classic, 1950).

Part G
Against Rationalization

67
Knowing About Biases Can Hurt People

Once upon a time I tried to tell my mother about the problem of expert calibration, saying: “So when an expert says they’re 99% confident, it only happens about 70% of the time.” Then there was a pause as, suddenly, I realized I was talking to my mother, and I hastily added: “Of course, you’ve got to make sure to apply that skepticism evenhandedly, including to yourself, rather than just using it to argue against anything you disagree with—”

And my mother said: “Are you kidding? This is great! I’m going to use it all the time!”

Taber and Lodge’s “Motivated skepticism in the evaluation of political beliefs” describes the confirmation of six predictions:¹

Prior attitude effect. Subjects who feel strongly about an issue—even when encouraged to be objective—will evaluate supportive arguments more favorably than contrary arguments.
Disconfirmation bias. Subjects will spend more time and cognitive resources denigrating contrary arguments than supportive arguments.
Confirmation bias. Subjects free to choose their information sources will seek out supportive rather than contrary sources.
Attitude polarization. Exposing subjects to an apparently balanced set of pro and con arguments will exaggerate their initial polarization.
Attitude strength effect. Subjects voicing stronger attitudes will be more prone to the above biases.
Sophistication effect. Politically knowledgeable subjects, because they possess greater ammunition with which to counter-argue incongruent facts and arguments, will be more prone to the above biases.

If you’re irrational to start with, having more knowledge can hurt you. For a true Bayesian, information would never have negative expected utility. But humans aren’t perfect Bayes-wielders; if we’re not careful, we can cut ourselves.

I’ve seen people severely messed up by their own knowledge of biases. They have more ammunition with which to argue against anything they don’t like. And that problem—too much ready ammunition—is one of the primary ways that people with high mental agility end up stupid, in Stanovich’s “dysrationalia” sense of stupidity.

You can think of people who fit this description, right? People with high g-factor who end up being less effective because they are too sophisticated as arguers? Do you think you’d be helping them—making them more effective rationalists—if you just told them about a list of classic biases?

I recall someone who learned about the calibration/overconfidence problem. Soon after he said: “Well, you can’t trust experts; they’re wrong so often—as experiments have shown. So therefore, when I predict the future, I prefer to assume that things will continue historically as they have—” and went off into this whole complex, error-prone, highly questionable extrapolation. Somehow, when it came to trusting his own preferred conclusions, all those biases and fallacies seemed much less salient—leapt much less readily to mind—than when he needed to counter-argue someone else.

I told the one about the problem of disconfirmation bias and sophisticated argument, and lo and behold, the next time I said something he didn’t like, he accused me of being a sophisticated arguer. He didn’t try to point out any particular sophisticated argument, any particular flaw—just shook his head and sighed sadly over how I was apparently using my own intelligence to defeat itself. He had acquired yet another Fully General Counterargument.

Even the notion of a “sophisticated arguer” can be deadly, if it leaps all too readily to mind when you encounter a seemingly intelligent person who says something you don’t like.

I endeavor to learn from my mistakes. The last time I gave a talk on heuristics and biases, I started out by introducing the general concept by way of the conjunction fallacy and representativeness heuristic. And then I moved on to confirmation bias, disconfirmation bias, sophisticated argument, motivated skepticism, and other attitude effects. I spent the next thirty minutes hammering on that theme, reintroducing it from as many different perspectives as I could.

I wanted to get my audience interested in the subject. Well, a simple description of conjunction fallacy and representativeness would suffice for that. But suppose they did get interested. Then what? The literature on bias is mostly cognitive psychology for cognitive psychology’s sake. I had to give my audience their dire warnings during that one lecture, or they probably wouldn’t hear them at all.

Whether I do it on paper, or in speech, I now try to never mention calibration and overconfidence unless I have first talked about disconfirmation bias, motivated skepticism, sophisticated arguers, and dysrationalia in the mentally agile. First, do no harm!

1. Charles S. Taber and Milton Lodge, “Motivated Skepticism in the Evaluation of Political Beliefs,” American Journal of Political Science 50, no. 3 (2006): 755–769, doi:10.1111/j.1540-5907.2006.00214.x.

68
Update Yourself Incrementally

Politics is the mind-killer. Debate is war, arguments are soldiers. There is the temptation to search for ways to interpret every possible experimental result to confirm your theory, like securing a citadel against every possible line of attack. This you cannot do. It is mathematically impossible. For every expectation of evidence, there is an equal and opposite expectation of counterevidence.

But it’s okay if your cherished belief isn’t perfectly defended. If the hypothesis is that the coin comes up heads 95% of the time, then one time in twenty you will expect to see what looks like contrary evidence. This is okay. It’s normal. It’s even expected, so long as you’ve got nineteen supporting observations for every contrary one. A probabilistic model can take a hit or two, and still survive, so long as the hits don’t keep on coming in.

Yet it is widely believed, especially in the court of public opinion, that a true theory can have no failures and a false theory no successes.

You find people holding up a single piece of what they conceive to be evidence, and claiming that their theory can “explain” it, as though this were all the support that any theory needed. Apparently a false theory can have no supporting evidence; it is impossible for a false theory to fit even a single event. Thus, a single piece of confirming evidence is all that any theory needs.

It is only slightly less foolish to hold up a single piece of probabilistic counterevidence as disproof, as though it were impossible for a correct theory to have even a slight argument against it. But this is how humans have argued for ages and ages, trying to defeat all enemy arguments, while denying the enemy even a single shred of support. People want their debates to be one-sided; they are accustomed to a world in which their preferred theories have not one iota of antisupport. Thus, allowing a single item of probabilistic counterevidence would be the end of the world.

I just know someone in the audience out there is going to say, “But you can’t concede even a single point if you want to win debates in the real world! If you concede that any counterarguments exist, the Enemy will harp on them over and over—you can’t let the Enemy do that! You’ll lose! What could be more viscerally terrifying than that?”

Whatever. Rationality is not for winning debates, it is for deciding which side to join. If you’ve already decided which side to argue for, the work of rationality is done within you, whether well or poorly. But how can you, yourself, decide which side to argue? If choosing the wrong side is viscerally terrifying, even just a little viscerally terrifying, you’d best integrate all the evidence.

Rationality is not a walk, but a dance. On each step in that dance your foot should come down in exactly the correct spot, neither to the left nor to the right. Shifting belief upward with each iota of confirming evidence. Shifting belief downward with each iota of contrary evidence. Yes, down. Even with a correct model, if it is not an exact model, you will sometimes need to revise your belief down.

If an iota or two of evidence happens to countersupport your belief, that’s okay. It happens, sometimes, with probabilistic evidence for non-exact theories. (If an exact theory fails, you are in trouble!) Just shift your belief downward a little—the probability, the odds ratio, or even a nonverbal weight of credence in your mind. Just shift downward a little, and wait for more evidence. If the theory is true, supporting evidence will come in shortly, and the probability will climb again. If the theory is false, you don’t really want it anyway.

The problem with using black-and-white, binary, qualitative reasoning is that any single observation either destroys the theory or it does not. When not even a single contrary observation is allowed, it creates cognitive dissonance and has to be argued away. And this rules out incremental progress; it rules out correct integration of all the evidence. Reasoning probabilistically, we realize that on average, a correct theory will generate a greater weight of support than countersupport. And so you can, without fear, say to yourself: “This is gently contrary evidence, I will shift my belief downward.” Yes, down. It does not destroy your cherished theory. That is qualitative reasoning; think quantitatively.

For every expectation of evidence, there is an equal and opposite expectation of counterevidence. On every occasion, you must, on average, anticipate revising your beliefs downward as much as you anticipate revising them upward. If you think you already know what evidence will come in, then you must already be fairly sure of your theory—probability close to 1—which doesn’t leave much room for the probability to go further upward. And however unlikely it seems that you will encounter disconfirming evidence, the resulting downward shift must be large enough to precisely balance the anticipated gain on the other side. The weighted mean of your expected posterior probability must equal your prior probability.

How silly is it, then, to be terrified of revising your probability downward, if you’re bothering to investigate a matter at all? On average, you must anticipate as much downward shift as upward shift from every individual observation.

It may perhaps happen that an iota of antisupport comes in again, and again and again, while new support is slow to trickle in. You may find your belief drifting downward and further downward. Until, finally, you realize from which quarter the winds of evidence are blowing against you. In that moment of realization, there is no point in constructing excuses. In that moment of realization, you have already relinquished your cherished belief. Yay! Time to celebrate! Pop a champagne bottle or send out for pizza! You can’t become stronger by keeping the beliefs you started with, after all.

69
One Argument Against An Army

I talked about a style of reasoning in which not a single contrary argument is allowed, with the result that every non-supporting observation has to be argued away. Here I suggest that when people encounter a contrary argument, they prevent themselves from downshifting their confidence by rehearsing already-known support.

Suppose the country of Freedonia is debating whether its neighbor, Sylvania, is responsible for a recent rash of meteor strikes on its cities. There are several pieces of evidence suggesting this: the meteors struck cities close to the Sylvanian border; there was unusual activity in the Sylvanian stock markets before the strikes; and the Sylvanian ambassador Trentino was heard muttering about “heavenly vengeance.”

Someone comes to you and says: “I don’t think Sylvania is responsible for the meteor strikes. They have trade with us of billions of dinars annually.” “Well,” you reply, “the meteors struck cities close to Sylvania, there was suspicious activity in their stock market, and their ambassador spoke of heavenly vengeance afterward.” Since these three arguments outweigh the first, you keep your belief that Sylvania is responsible—you believe rather than disbelieve, qualitatively. Clearly, the balance of evidence weighs against Sylvania.

Then another comes to you and says: “I don’t think Sylvania is responsible for the meteor strikes. Directing an asteroid strike is really hard. Sylvania doesn’t even have a space program.” You reply, “But the meteors struck cities close to Sylvania, and their investors knew it, and the ambassador came right out and admitted it!” Again, these three arguments outweigh the first (by three arguments against one argument), so you keep your belief that Sylvania is responsible.

Indeed, your convictions are strengthened. On two separate occasions now, you have evaluated the balance of evidence, and both times the balance was tilted against Sylvania by a ratio of 3 to 1.

You encounter further arguments by the pro-Sylvania traitors—again, and again, and a hundred times again—but each time the new argument is handily defeated by 3 to 1. And on every occasion, you feel yourself becoming more confident that Sylvania was indeed responsible, shifting your prior according to the felt balance of evidence.

The problem, of course, is that by rehearsing arguments you already knew, you are double-counting the evidence. This would be a grave sin even if you double-counted all the evidence. (Imagine a scientist who does an experiment with 50 subjects and fails to obtain statistically significant results, so the scientist counts all the data twice.)

But to selectively double-count only some evidence is sheer farce. I remember seeing a cartoon as a child, where a villain was dividing up loot using the following algorithm: “One for you, one for me. One for you, one-two for me. One for you, one-two-three for me.”

As I emphasized in the last essay, even if a cherished belief is true, a rationalist may sometimes need to downshift the probability while integrating all the evidence. Yes, the balance of support may still favor your cherished belief. But you still have to shift the probability down—yes, down—from whatever it was before you heard the contrary evidence. It does no good to rehearse supporting arguments, because you have already taken those into account.

And yet it does appear to me that when people are confronted by a new counterargument, they search for a justification not to downshift their confidence, and of course they find supporting arguments they already know. I have to keep constant vigilance not to do this myself! It feels as natural as parrying a sword-strike with a handy shield.

With the right kind of wrong reasoning, a handful of support—or even a single argument—can stand off an army of contradictions.

70
The Bottom Line

There are two sealed boxes up for auction, box A and box B. One and only one of these boxes contains a valuable diamond. There are all manner of signs and portents indicating whether a box contains a diamond; but I have no sign which I know to be perfectly reliable. There is a blue stamp on one box, for example, and I know that boxes which contain diamonds are more likely than empty boxes to show a blue stamp. Or one box has a shiny surface, and I have a suspicion—I am not sure—that no diamond-containing box is ever shiny.

Now suppose there is a clever arguer, holding a sheet of paper, and they say to the owners of box A and box B: “Bid for my services, and whoever wins my services, I shall argue that their box contains the diamond, so that the box will receive a higher price.” So the box-owners bid, and box B’s owner bids higher, winning the services of the clever arguer.

The clever arguer begins to organize their thoughts. First, they write, “And therefore, box B contains the diamond!” at the bottom of their sheet of paper. Then, at the top of the paper, the clever arguer writes, “Box B shows a blue stamp,” and beneath it, “Box A is shiny,” and then, “Box B is lighter than box A,” and so on through many signs and portents; yet the clever arguer neglects all those signs which might argue in favor of box A. And then the clever arguer comes to me and recites from their sheet of paper: “Box B shows a blue stamp, and box A is shiny,” and so on, until they reach: “and therefore, box B contains the diamond.”

But consider: At the moment when the clever arguer wrote down their conclusion, at the moment they put ink on their sheet of paper, the evidential entanglement of that physical ink with the physical boxes became fixed.

It may help to visualize a collection of worlds—Everett branches or Tegmark duplicates—within which there is some objective frequency at which box A or box B contains a diamond. There’s likewise some objective frequency within the subset “worlds with a shiny box A” where box B contains the diamond; and some objective frequency in “worlds with shiny box A and blue-stamped box B” where box B contains the diamond.

The ink on paper is formed into odd shapes and curves, which look like this text: “And therefore, box B contains the diamond.” If you happened to be a literate English speaker, you might become confused, and think that this shaped ink somehow meant that box B contained the diamond. Subjects instructed to say the color of printed pictures and shown the picture GREEN often say “green” instead of “red.” It helps to be illiterate, so that you are not confused by the shape of the ink.

To us, the true import of a thing is its entanglement with other things. Consider again the collection of worlds, Everett branches or Tegmark duplicates. At the moment when all clever arguers in all worlds put ink to the bottom line of their paper—let us suppose this is a single moment—it fixed the correlation of the ink with the boxes. The clever arguer writes in non-erasable pen; the ink will not change. The boxes will not change. Within the subset of worlds where the ink says “And therefore, box B contains the diamond,” there is already some fixed percentage of worlds where box A contains the diamond. This will not change regardless of what is written in on the blank lines above.

So the evidential entanglement of the ink is fixed, and I leave to you to decide what it might be. Perhaps box owners who believe a better case can be made for them are more liable to hire advertisers; perhaps box owners who fear their own deficiencies bid higher. If the box owners do not themselves understand the signs and portents, then the ink will be completely unentangled with the boxes’ contents, though it may tell you something about the owners’ finances and bidding habits.

Now suppose another person present is genuinely curious, and they first write down all the distinguishing signs of both boxes on a sheet of paper, and then apply their knowledge and the laws of probability and write down at the bottom: “Therefore, I estimate an 85% probability that box B contains the diamond.” Of what is this handwriting evidence? Examining the chain of cause and effect leading to this physical ink on physical paper, I find that the chain of causality wends its way through all the signs and portents of the boxes, and is dependent on these signs; for in worlds with different portents, a different probability is written at the bottom.

So the handwriting of the curious inquirer is entangled with the signs and portents and the contents of the boxes, whereas the handwriting of the clever arguer is evidence only of which owner paid the higher bid. There is a great difference in the indications of ink, though one who foolishly read aloud the ink-shapes might think the English words sounded similar.

Your effectiveness as a rationalist is determined by whichever algorithm actually writes the bottom line of your thoughts. If your car makes metallic squealing noises when you brake, and you aren’t willing to face up to the financial cost of getting your brakes replaced, you can decide to look for reasons why your car might not need fixing. But the actual percentage of you that survive in Everett branches or Tegmark worlds—which we will take to describe your effectiveness as a rationalist—is determined by the algorithm that decided which conclusion you would seek arguments for. In this case, the real algorithm is “Never repair anything expensive.” If this is a good algorithm, fine; if this is a bad algorithm, oh well. The arguments you write afterward, above the bottom line, will not change anything either way.

This is intended as a caution for your own thinking, not a Fully General Counterargument against conclusions you don’t like. For it is indeed a clever argument to say “My opponent is a clever arguer,” if you are paying yourself to retain whatever beliefs you had at the start. The world’s cleverest arguer may point out that the Sun is shining, and yet it is still probably daytime.

71
What Evidence Filtered Evidence?

I discussed the dilemma of the clever arguer, hired to sell you a box that may or may not contain a diamond. The clever arguer points out to you that the box has a blue stamp, and it is a valid known fact that diamond-containing boxes are more likely than empty boxes to bear a blue stamp. What happens at this point, from a Bayesian perspective? Must you helplessly update your probabilities, as the clever arguer wishes?

If you can look at the box yourself, you can add up all the signs yourself. What if you can’t look? What if the only evidence you have is the word of the clever arguer, who is legally constrained to make only true statements, but does not tell you everything they know? Each statement that the clever arguer makes is valid evidence—how could you not update your probabilities? Has it ceased to be true that, in such-and-such a proportion of Everett branches or Tegmark duplicates in which box B has a blue stamp, box B contains a diamond? According to Jaynes, a Bayesian must always condition on all known evidence, on pain of paradox. But then the clever arguer can make you believe anything they choose, if there is a sufficient variety of signs to selectively report. That doesn’t sound right.

Consider a simpler case, a biased coin, which may be biased to come up 2/3 heads and 1/3 tails, or 1/3 heads and 2/3 tails, both cases being equally likely a priori. Each H observed is 1 bit of evidence for an H-biased coin; each T observed is 1 bit of evidence for a T-biased coin. I flip the coin ten times, and then I tell you, “The 4th flip, 6th flip, and 9th flip came up heads.” What is your posterior probability that the coin is H-biased?

And the answer is that it could be almost anything, depending on what chain of cause and effect lay behind my utterance of those words—my selection of which flips to report.

I might be following the algorithm of reporting the result of the 4th, 6th, and 9th flips, regardless of the result of those and all other flips. If you know that I used this algorithm, the posterior odds are 8:1 in favor of an H-biased coin.
I could be reporting on all flips, and only flips, that came up heads. In this case, you know that all 7 other flips came up tails, and the posterior odds are 1:16 against the coin being H-biased.
I could have decided in advance to say the result of the 4th, 6th, and 9th flips only if the probability of the coin being H-biased exceeds 98%. And so on.

Or consider the Monty Hall problem:

On a game show, you are given the choice of three doors leading to three rooms. You know that in one room is $100,000, and the other two are empty. The host asks you to pick a door, and you pick door #1. Then the host opens door #2, revealing an empty room. Do you want to switch to door #3, or stick with door #1?

The answer depends on the host’s algorithm. If the host always opens a door and always picks a door leading to an empty room, then you should switch to door #3. If the host always opens door #2 regardless of what is behind it, #1 and #3 both have 50% probabilities of containing the money. If the host only opens a door, at all, if you initially pick the door with the money, then you should definitely stick with #1.

You shouldn’t just condition on #2 being empty, but this fact plus the fact of the host choosing to open door #2. Many people are confused by the standard Monty Hall problem because they update only on #2 being empty, in which case #1 and #3 have equal probabilities of containing the money. This is why Bayesians are commanded to condition on all of their knowledge, on pain of paradox.

When someone says, “The 4th coinflip came up heads,” we are not conditioning on the 4th coinflip having come up heads—we are not taking the subset of all possible worlds where the 4th coinflip came up heads—rather we are conditioning on the subset of all possible worlds where a speaker following some particular algorithm said “The 4th coinflip came up heads.” The spoken sentence is not the fact itself; don’t be led astray by the mere meanings of words.

Most legal processes work on the theory that every case has exactly two opposed sides and that it is easier to find two biased humans than one unbiased one. Between the prosecution and the defense, someone has a motive to present any given piece of evidence, so the court will see all the evidence; that is the theory. If there are two clever arguers in the box dilemma, it is not quite as good as one curious inquirer, but it is almost as good. But that is with two boxes. Reality often has many-sided problems, and deep problems, and nonobvious answers, which are not readily found by Blues and Greens screaming at each other.

Beware lest you abuse the notion of evidence-filtering as a Fully General Counterargument to exclude all evidence you don’t like: “That argument was filtered, therefore I can ignore it.” If you’re ticked off by a contrary argument, then you are familiar with the case, and care enough to take sides. You probably already know your own side’s strongest arguments. You have no reason to infer, from a contrary argument, the existence of new favorable signs and portents which you have not yet seen. So you are left with the uncomfortable facts themselves; a blue stamp on box B is still evidence.

But if you are hearing an argument for the first time, and you are only hearing one side of the argument, then indeed you should beware! In a way, no one can really trust the theory of natural selection until after they have listened to creationists for five minutes; and then they know it’s solid.

72
Rationalization

In The Bottom Line, I presented the dilemma of two boxes, only one of which contains a diamond, with various signs and portents as evidence. I dichotomized the curious inquirer and the clever arguer. The curious inquirer writes down all the signs and portents, and processes them, and finally writes down “Therefore, I estimate an 85% probability that box B contains the diamond.” The clever arguer works for the highest bidder, and begins by writing, “Therefore, box B contains the diamond,” and then selects favorable signs and portents to list on the lines above.

The first procedure is rationality. The second procedure is generally known as “rationalization.”

“Rationalization.” What a curious term. I would call it a wrong word. You cannot “rationalize” what is not already rational. It is as if “lying” were called “truthization.”

On a purely computational level, there is a rather large difference between:

Starting from evidence, and then crunching probability flows, in order to output a probable conclusion. (Writing down all the signs and portents, and then flowing forward to a probability on the bottom line which depends on those signs and portents.)
Starting from a conclusion, and then crunching probability flows, in order to output evidence apparently favoring that conclusion. (Writing down the bottom line, and then flowing backward to select signs and portents for presentation on the lines above.)

What fool devised such confusingly similar words, “rationality” and “rationalization,” to describe such extraordinarily different mental processes? I would prefer terms that made the algorithmic difference obvious, like “rationality” versus “giant sucking cognitive black hole.”

Not every change is an improvement, but every improvement is necessarily a change. You cannot obtain more truth for a fixed proposition by arguing it; you can make more people believe it, but you cannot make it more true. To improve our beliefs, we must necessarily change our beliefs. Rationality is the operation that we use to obtain more accuracy for our beliefs by changing them. Rationalization operates to fix beliefs in place; it would be better named “anti-rationality,” both for its pragmatic results and for its reversed algorithm.

“Rationality” is the forward flow that gathers evidence, weighs it, and outputs a conclusion. The curious inquirer used a forward-flow algorithm: first gathering the evidence, writing down a list of all visible signs and portents, which they then processed forward to obtain a previously unknown probability for the box containing the diamond. During the entire time that the rationality-process was running forward, the curious inquirer did not yet know their destination, which was why they were curious. In the Way of Bayes, the prior probability equals the expected posterior probability: If you know your destination, you are already there.

“Rationalization” is a backward flow from conclusion to selected evidence. First you write down the bottom line, which is known and fixed; the purpose of your processing is to find out which arguments you should write down on the lines above. This, not the bottom line, is the variable unknown to the running process.

I fear that Traditional Rationality does not properly sensitize its users to the difference between forward flow and backward flow. In Traditional Rationality, there is nothing wrong with the scientist who arrives at a pet hypothesis and then sets out to find an experiment that proves it. A Traditional Rationalist would look at this approvingly, and say, “This pride is the engine that drives Science forward.” Well, it is the engine that drives Science forward. It is easier to find a prosecutor and defender biased in opposite directions, than to find a single unbiased human.

But just because everyone does something, doesn’t make it okay. It would be better yet if the scientist, arriving at a pet hypothesis, set out to test that hypothesis for the sake of curiosity—creating experiments that would drive their own beliefs in an unknown direction.

If you genuinely don’t know where you are going, you will probably feel quite curious about it. Curiosity is the first virtue, without which your questioning will be purposeless and your skills without direction.

Feel the flow of the Force, and make sure it isn’t flowing backwards.

73
A Rational Argument

You are, by occupation, a campaign manager, and you’ve just been hired by Mortimer Q. Snodgrass, the Green candidate for Mayor of Hadleyburg. As a campaign manager reading a book on rationality, one question lies foremost on your mind: “How can I construct an impeccable rational argument that Mortimer Q. Snodgrass is the best candidate for Mayor of Hadleyburg?”

Sorry. It can’t be done.

“What?” you cry. “But what if I use only valid support to construct my structure of reason? What if every fact I cite is true to the best of my knowledge, and relevant evidence under Bayes’s Rule?”

Sorry. It still can’t be done. You defeated yourself the instant you specified your argument’s conclusion in advance.

This year, the Hadleyburg Trumpet sent out a 16-item questionnaire to all mayoral candidates, with questions like “Can you paint with all the colors of the wind?” and “Did you inhale?” Alas, the Trumpet’s offices are destroyed by a meteorite before publication. It’s a pity, since your own candidate, Mortimer Q. Snodgrass, compares well to his opponents on 15 out of 16 questions. The only sticking point was Question 11, “Are you now, or have you ever been, a supervillain?”

So you are tempted to publish the questionnaire as part of your own campaign literature . . . with the 11th question omitted, of course.

Which crosses the line between rationality and rationalization. It is no longer possible for the voters to condition on the facts alone; they must condition on the additional fact of their presentation, and infer the existence of hidden evidence.

Indeed, you crossed the line at the point where you considered whether the questionnaire was favorable or unfavorable to your candidate, before deciding whether to publish it. “What!” you cry. “A campaign should publish facts unfavorable to their candidate?” But put yourself in the shoes of a voter, still trying to select a candidate—why would you censor useful information? You wouldn’t, if you were genuinely curious. If you were flowing forward from the evidence to an unknown choice of candidate, rather than flowing backward from a fixed candidate to determine the arguments.

A “logical” argument is one that follows from its premises. Thus the following argument is illogical:

All rectangles are quadrilaterals.
All squares are quadrilaterals.
Therefore, all squares are rectangles.

This syllogism is not rescued from illogic by the truth of its premises or even the truth of its conclusion. It is worth distinguishing logical deductions from illogical ones, and to refuse to excuse them even if their conclusions happen to be true. For one thing, the distinction may affect how we revise our beliefs in light of future evidence. For another, sloppiness is habit-forming.

Above all, the syllogism fails to state the real explanation. Maybe all squares are rectangles, but, if so, it’s not because they are both quadrilaterals. You might call it a hypocritical syllogism—one with a disconnect between its stated reasons and real reasons.

If you really want to present an honest, rational argument for your candidate, in a political campaign, there is only one way to do it:

Before anyone hires you, gather up all the evidence you can about the different candidates.
Make a checklist which you, yourself, will use to decide which candidate seems best.
Process the checklist.
Go to the winning candidate.
Offer to become their campaign manager.
When they ask for campaign literature, print out your checklist.

Only in this way can you offer a rational chain of argument, one whose bottom line was written flowing forward from the lines above it. Whatever actually decides your bottom line, is the only thing you can honestly write on the lines above.

74
Avoiding Your Belief’s Real Weak Points

A few years back, my great-grandmother died, in her nineties, after a long, slow, and cruel disintegration. I never knew her as a person, but in my distant childhood, she cooked for her family; I remember her gefilte fish, and her face, and that she was kind to me. At her funeral, my grand-uncle, who had taken care of her for years, spoke. He said, choking back tears, that God had called back his mother piece by piece: her memory, and her speech, and then finally her smile; and that when God finally took her smile, he knew it wouldn’t be long before she died, because it meant that she was almost entirely gone.

I heard this and was puzzled, because it was an unthinkably horrible thing to happen to anyone, and therefore I would not have expected my grand-uncle to attribute it to God. Usually, a Jew would somehow just-not-think-about the logical implication that God had permitted a tragedy. According to Jewish theology, God continually sustains the universe and chooses every event in it; but ordinarily, drawing logical implications from this belief is reserved for happier occasions. By saying “God did it!” only when you’ve been blessed with a baby girl, and just-not-thinking “God did it!” for miscarriages and stillbirths and crib deaths, you can build up quite a lopsided picture of your God’s benevolent personality.

Hence I was surprised to hear my grand-uncle attributing the slow disintegration of his mother to a deliberate, strategically planned act of God. It violated the rules of religious self-deception as I understood them.

If I had noticed my own confusion, I could have made a successful surprising prediction. Not long afterward, my grand-uncle left the Jewish religion. (The only member of my extended family besides myself to do so, as far as I know.)

Modern Orthodox Judaism is like no other religion I have ever heard of, and I don’t know how to describe it to anyone who hasn’t been forced to study Mishna and Gemara. There is a tradition of questioning, but the kind of questioning . . . It would not be at all surprising to hear a rabbi, in his weekly sermon, point out the conflict between the seven days of creation and the 13.7 billion years since the Big Bang—because he thought he had a really clever explanation for it, involving three other Biblical references, a Midrash, and a half-understood article in Scientific American. In Orthodox Judaism you’re allowed to notice inconsistencies and contradictions, but only for purposes of explaining them away, and whoever comes up with the most complicated explanation gets a prize.

There is a tradition of inquiry. But you only attack targets for purposes of defending them. You only attack targets you know you can defend.

In Modern Orthodox Judaism I have not heard much emphasis of the virtues of blind faith. You’re allowed to doubt. You’re just not allowed to successfully doubt.

I expect that the vast majority of educated Orthodox Jews have questioned their faith at some point in their lives. But the questioning probably went something like this: “According to the skeptics, the Torah says that the universe was created in seven days, which is not scientifically accurate. But would the original tribespeople of Israel, gathered at Mount Sinai, have been able to understand the scientific truth, even if it had been presented to them? Did they even have a word for ‘billion’? It’s easier to see the seven-days story as a metaphor—first God created light, which represents the Big Bang . . .”

Is this the weakest point at which to attack one’s own Judaism? Read a bit further on in the Torah, and you can find God killing the firstborn male children of Egypt to convince an unelected Pharaoh to release slaves who logically could have been teleported out of the country. An Orthodox Jew is most certainly familiar with this episode, because they are supposed to read through the entire Torah in synagogue once per year, and this event has an associated major holiday. The name “Passover” (“Pesach”) comes from God passing over the Jewish households while killing every male firstborn in Egypt.

Modern Orthodox Jews are, by and large, kind and civilized people; far more civilized than the several editors of the Old Testament. Even the old rabbis were more civilized. There’s a ritual in the Seder where you take ten drops of wine from your cup, one drop for each of the Ten Plagues, to emphasize the suffering of the Egyptians. (Of course, you’re supposed to be sympathetic to the suffering of the Egyptians, but not so sympathetic that you stand up and say, “This is not right! It is wrong to do such a thing!”) It shows an interesting contrast—the rabbis were sufficiently kinder than the compilers of the Old Testament that they saw the harshness of the Plagues. But Science was weaker in these days, and so rabbis could ponder the more unpleasant aspects of Scripture without fearing that it would break their faith entirely.

You don’t even ask whether the incident reflects poorly on God, so there’s no need to quickly blurt out “The ways of God are mysterious!” or “We’re not wise enough to question God’s decisions!” or “Murdering babies is okay when God does it!” That part of the question is just-not-thought-about.

The reason that educated religious people stay religious, I suspect, is that when they doubt, they are subconsciously very careful to attack their own beliefs only at the strongest points—places where they know they can defend. Moreover, places where rehearsing the standard defense will feel strengthening.

It probably feels really good, for example, to rehearse one’s prescripted defense for “Doesn’t Science say that the universe is just meaningless atoms bopping around?,” because it confirms the meaning of the universe and how it flows from God, etc. Much more comfortable to think about than an illiterate Egyptian mother wailing over the crib of her slaughtered son. Anyone who spontaneously thinks about the latter, when questioning their faith in Judaism, is really questioning it, and is probably not going to stay Jewish much longer.

My point here is not just to beat up on Orthodox Judaism. I’m sure that there’s some reply or other for the Slaying of the Firstborn, and probably a dozen of them. My point is that, when it comes to spontaneous self-questioning, one is much more likely to spontaneously self-attack strong points with comforting replies to rehearse, then to spontaneously self-attack the weakest, most vulnerable points. Similarly, one is likely to stop at the first reply and be comforted, rather than further criticizing the reply. A better title than “Avoiding Your Belief’s Real Weak Points” would be “Not Spontaneously Thinking About Your Belief’s Most Painful Weaknesses.”

More than anything, the grip of religion is sustained by people just-not-thinking-about the real weak points of their religion. I don’t think this is a matter of training, but a matter of instinct. People don’t think about the real weak points of their beliefs for the same reason they don’t touch an oven’s red-hot burners; it’s painful.

To do better: When you’re doubting one of your most cherished beliefs, close your eyes, empty your mind, grit your teeth, and deliberately think about whatever hurts the most. Don’t rehearse standard objections whose standard counters would make you feel better. Ask yourself what smart people who disagree would say to your first reply, and your second reply. Whenever you catch yourself flinching away from an objection you fleetingly thought of, drag it out into the forefront of your mind. Punch yourself in the solar plexus. Stick a knife in your heart, and wiggle to widen the hole. In the face of the pain, rehearse only this:

What is true is already so.

Owning up to it doesn’t make it worse.

Not being open about it doesn’t make it go away.

And because it’s true, it is what is there to be interacted with.

Anything untrue isn’t there to be lived.

People can stand what is true,

for they are already enduring it.

—Eugene Gendlin¹

(Hat tip to Stephen Omohundro.)

1. Eugene T. Gendlin, Focusing (Bantam Books, 1982).

75
Motivated Stopping and Motivated Continuation

While I disagree with some views of the Fast and Frugal crowd—in my opinion they make a few too many lemons into lemonade—it also seems to me that they tend to develop the most psychologically realistic models of any school of decision theory. Most experiments present the subjects with options, and the subject chooses an option, and that’s the experimental result. The frugalists realized that in real life, you have to generate your options, and they studied how subjects did that.

Likewise, although many experiments present evidence on a silver platter, in real life you have to gather evidence, which may be costly, and at some point decide that you have enough evidence to stop and choose. When you’re buying a house, you don’t get exactly ten houses to choose from, and you aren’t led on a guided tour of all of them before you’re allowed to decide anything. You look at one house, and another, and compare them to each other; you adjust your aspirations—reconsider how much you really need to be close to your workplace and how much you’re really willing to pay; you decide which house to look at next; and at some point you decide that you’ve seen enough houses, and choose.

Gilovich’s distinction between motivated skepticism and motivated credulity highlights how conclusions a person does not want to believe are held to a higher standard than conclusions a person wants to believe. A motivated skeptic asks if the evidence compels them to accept the conclusion; a motivated credulist asks if the evidence allows them to accept the conclusion.

I suggest that an analogous bias in psychologically realistic search is motivated stopping and motivated continuation: when we have a hidden motive for choosing the “best” current option, we have a hidden motive to stop, and choose, and reject consideration of any more options. When we have a hidden motive to reject the current best option, we have a hidden motive to suspend judgment pending additional evidence, to generate more options—to find something, anything, to do instead of coming to a conclusion.

A major historical scandal in statistics was R. A. Fisher, an eminent founder of the field, insisting that no causal link had been established between smoking and lung cancer. “Correlation is not causation,” he testified to Congress. Perhaps smokers had a gene which both predisposed them to smoke and predisposed them to lung cancer.

Or maybe Fisher’s being employed as a consultant for tobacco firms gave him a hidden motive to decide that the evidence already gathered was insufficient to come to a conclusion, and it was better to keep looking. Fisher was also a smoker himself, and died of colon cancer in 1962.

(Ad hominem note: Fisher was a frequentist. Bayesians are more reasonable about inferring probable causality.)

Like many other forms of motivated skepticism, motivated continuation can try to disguise itself as virtuous rationality. Who can argue against gathering more evidence? I can. Evidence is often costly, and worse, slow, and there is certainly nothing virtuous about refusing to integrate the evidence you already have. You can always change your mind later. (Apparent contradiction resolved as follows: Spending one hour discussing the problem, with your mind carefully cleared of all conclusions, is different from waiting ten years on another $20 million study.)

As for motivated stopping, it appears in every place a third alternative is feared, and wherever you have an argument whose obvious counterargument you would rather not see, and in other places as well. It appears when you pursue a course of action that makes you feel good just for acting, and so you’d rather not investigate how well your plan really worked, for fear of destroying the warm glow of moral satisfaction you paid good money to purchase. It appears wherever your beliefs and anticipations get out of sync, so you have a reason to fear any new evidence gathered.

The moral is that the decision to terminate a search procedure (temporarily or permanently) is, like the search procedure itself, subject to bias and hidden motives. You should suspect motivated stopping when you close off search, after coming to a comfortable conclusion, and yet there’s a lot of fast cheap evidence you haven’t gathered yet—there are websites you could visit, there are counter-counter arguments you could consider, or you haven’t closed your eyes for five minutes by the clock trying to think of a better option. You should suspect motivated continuation when some evidence is leaning in a way you don’t like, but you decide that more evidence is needed—expensive evidence that you know you can’t gather anytime soon, as opposed to something you’re going to look up on Google in thirty minutes—before you’ll have to do anything uncomfortable.

76
Fake Justification

Many Christians who’ve stopped really believing now insist that they revere the Bible as a source of ethical advice. The standard atheist reply is given by Sam Harris: “You and I both know that it would take us five minutes to produce a book that offers a more coherent and compassionate morality than the Bible does.” Similarly, one may try to insist that the Bible is valuable as a literary work. Then why not revere Lord of the Rings, a vastly superior literary work? And despite the standard criticisms of Tolkien’s morality, Lord of the Rings is at least superior to the Bible as a source of ethics. So why don’t people wear little rings around their neck, instead of crosses? Even Harry Potter is superior to the Bible, both as a work of literary art and as moral philosophy. If I really wanted to be cruel, I would compare the Bible to Jacqueline Carey’s Kushiel series.

“How can you justify buying a $1 million gem-studded laptop,” you ask your friend, “when so many people have no laptops at all?” And your friend says, “But think of the employment that this will provide—to the laptop maker, the laptop maker’s advertising agency—and then they’ll buy meals and haircuts—it will stimulate the economy and eventually many people will get their own laptops.” But it would be even more efficient to buy 5,000 One Laptop Per Child laptops, thus providing employment to the OLPC manufacturers and giving out laptops directly.

I’ve touched before on the failure to look for third alternatives. But this is not really motivated stopping. Calling it “motivated stopping” would imply that there was a search carried out in the first place.

In The Bottom Line, I observed that only the real determinants of our beliefs can ever influence our real-world accuracy, only the real determinants of our actions can influence our effectiveness in achieving our goals. Someone who buys a million-dollar laptop was really thinking, “Ooh, shiny,” and that was the one true causal history of their decision to buy a laptop. No amount of “justification” can change this, unless the justification is a genuine, newly running search process that can change the conclusion. Really change the conclusion. Most criticism carried out from a sense of duty is more of a token inspection than anything else. Free elections in a one-party country.

To genuinely justify the Bible as a lauding-object by reference to its literary quality, you would have to somehow perform a neutral reading through candidate books until you found the book of highest literary quality. Renown is one reasonable criteria for generating candidates, so I suppose you could legitimately end up reading Shakespeare, the Bible, and Gödel, Escher, Bach. (Otherwise it would be quite a coincidence to find the Bible as a candidate, among a million other books.) The real difficulty is in that “neutral reading” part. Easy enough if you’re not a Christian, but if you are . . .

But of course nothing like this happened. No search ever occurred. Writing the justification of “literary quality” above the bottom line of “I <heart> the Bible” is a historical misrepresentation of how the bottom line really got there, like selling cat milk as cow milk. That is just not where the bottom line really came from. That is just not what originally happened to produce that conclusion.

If you genuinely subject your conclusion to a criticism that can potentially de-conclude it—if the criticism genuinely has that power—then that does modify “the real algorithm behind” your conclusion. It changes the entanglement of your conclusion over possible worlds. But people overestimate, by far, how likely they really are to change their minds.

With all those open minds out there, you’d think there’d be more belief-updating.

Let me guess: Yes, you admit that you originally decided you wanted to buy a million-dollar laptop by thinking, “Ooh, shiny.” Yes, you concede that this isn’t a decision process consonant with your stated goals. But since then, you’ve decided that you really ought to spend your money in such fashion as to provide laptops to as many laptopless wretches as possible. And yet you just couldn’t find any more efficient way to do this than buying a million-dollar diamond-studded laptop—because, hey, you’re giving money to a laptop store and stimulating the economy! Can’t beat that!

My friend, I am damned suspicious of this amazing coincidence. I am damned suspicious that the best answer under this lovely, rational, altruistic criterion X, is also the idea that just happened to originally pop out of the unrelated indefensible process Y. If you don’t think that rolling dice would have been likely to produce the correct answer, then how likely is it to pop out of any other irrational cognition?

It’s improbable that you used mistaken reasoning, yet made no mistakes.

77
Is That Your True Rejection?

It happens every now and then, that the one encounters some of my transhumanist-side beliefs—as opposed to my ideas having to do with human rationality—strange, exotic-sounding ideas like superintelligence and Friendly AI. And the one rejects them.

If the one is called upon to explain the rejection, not uncommonly the one says, “Why should I believe anything Yudkowsky says? He doesn’t have a PhD!”

And occasionally someone else, hearing, says, “Oh, you should get a PhD, so that people will listen to you.” Or this advice may even be offered by the same one who disbelieved, saying, “Come back when you have a PhD.”

Now there are good and bad reasons to get a PhD, but this is one of the bad ones.

There’s many reasons why someone actually has an adverse reaction to transhumanist theses. Most are matters of pattern recognition, rather than verbal thought: the thesis matches against “strange weird idea” or “science fiction” or “end-of-the-world cult” or “overenthusiastic youth.”

So immediately, at the speed of perception, the idea is rejected. If, afterward, someone says “Why not?,” this launches a search for justification. But this search will not necessarily hit on the true reason—by “true reason” I mean not the best reason that could be offered, but rather, whichever causes were decisive as a matter of historical fact, at the very first moment the rejection occurred.

Instead, the search for justification hits on the justifying-sounding fact, “This speaker does not have a PhD.”

But I also don’t have a PhD when I talk about human rationality, so why is the same objection not raised there?

And more to the point, if I had a PhD, people would not treat this as a decisive factor indicating that they ought to believe everything I say. Rather, the same initial rejection would occur, for the same reasons; and the search for justification, afterward, would terminate at a different stopping point.

They would say, “Why should I believe you? You’re just some guy with a PhD! There are lots of those. Come back when you’re well-known in your field and tenured at a major university.”

But do people actually believe arbitrary professors at Harvard who say weird things? Of course not. (But if I were a professor at Harvard, it would in fact be easier to get media attention. Reporters initially disinclined to believe me—who would probably be equally disinclined to believe a random PhD-bearer—would still report on me, because it would be news that a Harvard professor believes such a weird thing.)

If you are saying things that sound wrong to a novice, as opposed to just rattling off magical-sounding technobabble about leptical quark braids in N + 2 dimensions; and the hearer is a stranger, unfamiliar with you personally and with the subject matter of your field; then I suspect that the point at which the average person will actually start to grant credence overriding their initial impression, purely because of academic credentials, is somewhere around the Nobel Laureate level. If that. Roughly, you need whatever level of academic credential qualifies as “beyond the mundane.”

This is more or less what happened to Eric Drexler, as far as I can tell. He presented his vision of nanotechnology, and people said, “Where are the technical details?” or “Come back when you have a PhD!” And Eric Drexler spent six years writing up technical details and got his PhD under Marvin Minsky for doing it. And Nanosystems is a great book. But did the same people who said, “Come back when you have a PhD,” actually change their minds at all about molecular nanotechnology? Not so far as I ever heard.

It has similarly been a general rule with the Machine Intelligence Research Institute that, whatever it is we’re supposed to do to be more credible, when we actually do it, nothing much changes. “Do you do any sort of code development? I’m not interested in supporting an organization that doesn’t develop code” → OpenCog → nothing changes. “Eliezer Yudkowsky lacks academic credentials” → Professor Ben Goertzel installed as Director of Research → nothing changes. The one thing that actually has seemed to raise credibility, is famous people associating with the organization, like Peter Thiel funding us, or Ray Kurzweil on the Board.

This might be an important thing for young businesses and new-minted consultants to keep in mind—that what your failed prospects tell you is the reason for rejection, may not make the real difference; and you should ponder that carefully before spending huge efforts. If the venture capitalist says “If only your sales were growing a little faster!,” or if the potential customer says “It seems good, but you don’t have feature X,” that may not be the true rejection. Fixing it may, or may not, change anything.

And it would also be something to keep in mind during disagreements. Robin Hanson and I share a belief that two rationalists should not agree to disagree: they should not have common knowledge of epistemic disagreement unless something is very wrong.

I suspect that, in general, if two rationalists set out to resolve a disagreement that persisted past the first exchange, they should expect to find that the true sources of the disagreement are either hard to communicate, or hard to expose. E.g.:

Uncommon, but well-supported, scientific knowledge or math;
Long inferential distances;
Hard-to-verbalize intuitions, perhaps stemming from specific visualizations;
Zeitgeists inherited from a profession (that may have good reason for it);
Patterns perceptually recognized from experience;
Sheer habits of thought;
Emotional commitments to believing in a particular outcome;
Fear of a past mistake being disproven;
Deep self-deception for the sake of pride or other personal benefits.

If the matter were one in which all the true rejections could be easily laid on the table, the disagreement would probably be so straightforward to resolve that it would never have lasted past the first meeting.

“Is this my true rejection?” is something that both disagreers should surely be asking themselves, to make things easier on the Other Fellow. However, attempts to directly, publicly psychoanalyze the Other may cause the conversation to degenerate very fast, in my observation.

Still—“Is that your true rejection?” should be fair game for Disagreers to humbly ask, if there’s any productive way to pursue that sub-issue. Maybe the rule could be that you can openly ask, “Is that simple straightforward-sounding reason your true rejection, or does it come from intuition-X or professional-zeitgeist-Y?” While the more embarrassing possibilities lower on the table are left to the Other’s conscience, as their own responsibility to handle.

78
Entangled Truths, Contagious Lies

One of your very early philosophers came to the conclusion that a fully competent mind, from a study of one fact or artifact belonging to any given universe, could construct or visualize that universe, from the instant of its creation to its ultimate end . . .

—First Lensman¹

If any one of you will concentrate upon one single fact, or small object, such as a pebble or the seed of a plant or other creature, for as short a period of time as one hundred of your years, you will begin to perceive its truth.

—Gray Lensman²

I am reasonably sure that a single pebble, taken from a beach of our own Earth, does not specify the continents and countries, politics and people of this Earth. Other planets in space and time, other Everett branches, would generate the same pebble. On the other hand, the identity of a single pebble would seem to include our laws of physics. In that sense the entirety of our Universe—all the Everett branches—would be implied by the pebble. (If, as seems likely, there are no truly free variables.)

So a single pebble probably does not imply our whole Earth. But a single pebble implies a very great deal. From the study of that single pebble you could see the laws of physics and all they imply. Thinking about those laws of physics, you can see that planets will form, and you can guess that the pebble came from such a planet. The internal crystals and molecular formations of the pebble formed under gravity, which tells you something about the planet’s mass; the mix of elements in the pebble tells you something about the planet’s formation.

I am not a geologist, so I don’t know to which mysteries geologists are privy. But I find it very easy to imagine showing a geologist a pebble, and saying, “This pebble came from a beach at Half Moon Bay,” and the geologist immediately says, “I’m confused” or even “You liar.” Maybe it’s the wrong kind of rock, or the pebble isn’t worn enough to be from a beach—I don’t know pebbles well enough to guess the linkages and signatures by which I might be caught, which is the point.

“Only God can tell a truly plausible lie.” I wonder if there was ever a religion that developed this as a proverb? I would (falsifiably) guess not: it’s a rationalist sentiment, even if you cast it in theological metaphor. Saying “everything is interconnected to everything else, because God made the whole world and sustains it” may generate some nice warm ’n’ fuzzy feelings during the sermon, but it doesn’t get you very far when it comes to assigning pebbles to beaches.

A penny on Earth exerts a gravitational acceleration on the Moon of around 4.5 × 10^-31 m/s², so in one sense it’s not too far wrong to say that every event is entangled with its whole past light cone. And since inferences can propagate backward and forward through causal networks, epistemic entanglements can easily cross the borders of light cones. But I wouldn’t want to be the forensic astronomer who had to look at the Moon and figure out whether the penny landed heads or tails—the influence is far less than quantum uncertainty and thermal noise.

If you said “Everything is entangled with something else” or “Everything is inferentially entangled and some entanglements are much stronger than others,” you might be really wise instead of just Deeply Wise.

Physically, each event is in some sense the sum of its whole past light cone, without borders or boundaries. But the list of noticeable entanglements is much shorter, and it gives you something like a network. This high-level regularity is what I refer to when I talk about the Great Web of Causality.

I use these Capitalized Letters somewhat tongue-in-cheek, perhaps; but if anything at all is worth Capitalized Letters, surely the Great Web of Causality makes the list.

“Oh what a tangled web we weave, when first we practise to deceive,” said Sir Walter Scott. Not all lies spin out of control—we don’t live in so righteous a universe. But it does occasionally happen, that someone lies about a fact, and then has to lie about an entangled fact, and then another fact entangled with that one:

“Where were you?”

“Oh, I was on a business trip.”

“What was the business trip about?”

“I can’t tell you that; it’s proprietary negotiations with a major client.”

“Oh—they’re letting you in on those? Good news! I should call your boss to thank him for adding you.”

“Sorry—he’s not in the office right now . . .”

Human beings, who are not gods, often fail to imagine all the facts they would need to distort to tell a truly plausible lie. “God made me pregnant” sounded a tad more likely in the old days before our models of the world contained (quotations of) Y chromosomes. Many similar lies, today, may blow up when genetic testing becomes more common. Rapists have been convicted, and false accusers exposed, years later, based on evidence they didn’t realize they could leave. A student of evolutionary biology can see the design signature of natural selection on every wolf that chases a rabbit; and every rabbit that runs away; and every bee that stings instead of broadcasting a polite warning—but the deceptions of creationists sound plausible to them, I’m sure.

Not all lies are uncovered, not all liars are punished; we don’t live in that righteous a universe. But not all lies are as safe as their liars believe. How many sins would become known to a Bayesian superintelligence, I wonder, if it did a (non-destructive?) nanotechnological scan of the Earth? At minimum, all the lies of which any evidence still exists in any brain. Some such lies may become known sooner than that, if the neuroscientists ever succeed in building a really good lie detector via neuroimaging. Paul Ekman (a pioneer in the study of tiny facial muscle movements) could probably read off a sizeable fraction of the world’s lies right now, given a chance.

Not all lies are uncovered, not all liars are punished. But the Great Web is very commonly underestimated. Just the knowledge that humans have already accumulated would take many human lifetimes to learn. Anyone who thinks that a non-God can tell a perfect lie, risk-free, is underestimating the tangledness of the Great Web.

Is honesty the best policy? I don’t know if I’d go that far: Even on my ethics, it’s sometimes okay to shut up. But compared to outright lies, either honesty or silence involves less exposure to recursively propagating risks you don’t know you’re taking.

1. Edward Elmer Smith and A. J. Donnell, First Lensman (Old Earth Books, 1997).

2. Edward Elmer Smith and Ric Binkley, Gray Lensman (Old Earth Books, 1998).

79
Of Lies and Black Swan Blowups

Judge Marcus Einfeld, age 70, Queen’s Counsel since 1977, Australian Living Treasure 1997, United Nations Peace Award 2002, founding president of Australia’s Human Rights and Equal Opportunities Commission, retired a few years back but routinely brought back to judge important cases . . .

. . . went to jail for two years over a series of perjuries and lies that started with a £36, 6-mph-over speeding ticket.

That whole suspiciously virtuous-sounding theory about honest people not being good at lying, and entangled traces being left somewhere, and the entire thing blowing up in a Black Swan epic fail, actually does have a certain number of exemplars in real life, though obvious selective reporting is at work in our hearing about this one.

80
Dark Side Epistemology

If you once tell a lie, the truth is ever after your enemy.

I have previously spoken of the notion that, the truth being entangled, lies are contagious. If you pick up a pebble from the driveway, and tell a geologist that you found it on a beach—well, do you know what a geologist knows about rocks? I don’t. But I can suspect that a water-worn pebble wouldn’t look like a droplet of frozen lava from a volcanic eruption. Do you know where the pebble in your driveway really came from? Things bear the marks of their places in a lawful universe; in that web, a lie is out of place. (Actually, a geologist in the comments says that most pebbles in driveways are taken from beaches, so they couldn’t tell the difference between a driveway pebble and a beach pebble, but they could tell the difference between a mountain pebble and a driveway/beach pebble. Case in point . . .)

What sounds like an arbitrary truth to one mind—one that could easily be replaced by a plausible lie—might be nailed down by a dozen linkages to the eyes of greater knowledge. To a creationist, the idea that life was shaped by “intelligent design” instead of “natural selection” might sound like a sports team to cheer for. To a biologist, plausibly arguing that an organism was intelligently designed would require lying about almost every facet of the organism. To plausibly argue that “humans” were intelligently designed, you’d have to lie about the design of the human retina, the architecture of the human brain, the proteins bound together by weak van der Waals forces instead of strong covalent bonds . . .

Or you could just lie about evolutionary theory, which is the path taken by most creationists. Instead of lying about the connected nodes in the network, they lie about the general laws governing the links.

And then to cover that up, they lie about the rules of science—like what it means to call something a “theory,” or what it means for a scientist to say that they are not absolutely certain.

So they pass from lying about specific facts, to lying about general laws, to lying about the rules of reasoning. To lie about whether humans evolved, you must lie about evolution; and then you have to lie about the rules of science that constrain our understanding of evolution.

But how else? Just as a human would be out of place in a community of actually intelligently designed life forms, and you have to lie about the rules of evolution to make it appear otherwise; so too, beliefs about creationism are themselves out of place in science—you wouldn’t find them in a well-ordered mind any more than you’d find palm trees growing on a glacier. And so you have to disrupt the barriers that would forbid them.

Which brings us to the case of self-deception.

A single lie you tell yourself may seem plausible enough, when you don’t know any of the rules governing thoughts, or even that there are rules; and the choice seems as arbitrary as choosing a flavor of ice cream, as isolated as a pebble on the shore . . .

. . . but then someone calls you on your belief, using the rules of reasoning that they’ve learned. They say, “Where’s your evidence?”

And you say, “What? Why do I need evidence?”

So they say, “In general, beliefs require evidence.”

This argument, clearly, is a soldier fighting on the other side, which you must defeat. So you say: “I disagree! Not all beliefs require evidence. In particular, beliefs about dragons don’t require evidence. When it comes to dragons, you’re allowed to believe anything you like. So I don’t need evidence to believe there’s a dragon in my garage.”

And the one says, “Eh? You can’t just exclude dragons like that. There’s a reason for the rule that beliefs require evidence. To draw a correct map of the city, you have to walk through the streets and make lines on paper that correspond to what you see. That’s not an arbitrary legal requirement—if you sit in your living room and draw lines on the paper at random, the map’s going to be wrong. With extremely high probability. That’s as true of a map of a dragon as it is of anything.”

So now this, the explanation of why beliefs require evidence, is also an opposing soldier. So you say: “Wrong with extremely high probability? Then there’s still a chance, right? I don’t have to believe if it’s not absolutely certain.”

Or maybe you even begin to suspect, yourself, that “beliefs require evidence.” But this threatens a lie you hold precious; so you reject the dawn inside you, push the Sun back under the horizon.

Or you’ve previously heard the proverb “beliefs require evidence,” and it sounded wise enough, and you endorsed it in public. But it never quite occurred to you, until someone else brought it to your attention, that this proverb could apply to your belief that there’s a dragon in your garage. So you think fast and say, “The dragon is in a separate magisterium.”

Having false beliefs isn’t a good thing, but it doesn’t have to be permanently crippling—if, when you discover your mistake, you get over it. The dangerous thing is to have a false belief that you believe should be protected as a belief—a belief-in-belief, whether or not accompanied by actual belief.

A single Lie That Must Be Protected can block someone’s progress into advanced rationality. No, it’s not harmless fun.

Just as the world itself is more tangled by far than it appears on the surface; so too, there are stricter rules of reasoning, constraining belief more strongly, than the untrained would suspect. The world is woven tightly, governed by general laws, and so are rational beliefs.

Think of what it would take to deny evolution or heliocentrism—all the connected truths and governing laws you wouldn’t be allowed to know. Then you can imagine how a single act of self-deception can block off the whole meta-level of truthseeking, once your mind begins to be threatened by seeing the connections. Forbidding all the intermediate and higher levels of the rationalist’s Art. Creating, in its stead, a vast complex of anti-law, rules of anti-thought, general justifications for believing the untrue.

Steven Kaas said, “Promoting less than maximally accurate beliefs is an act of sabotage. Don’t do it to anyone unless you’d also slash their tires.” Giving someone a false belief to protect—convincing them that the belief itself must be defended from any thought that seems to threaten it—well, you shouldn’t do that to someone unless you’d also give them a frontal lobotomy.

Once you tell a lie, the truth is your enemy; and every truth connected to that truth, and every ally of truth in general; all of these you must oppose, to protect the lie. Whether you’re lying to others, or to yourself.

You have to deny that beliefs require evidence, and then you have to deny that maps should reflect territories, and then you have to deny that truth is a good thing . . .

Thus comes into being the Dark Side.

I worry that people aren’t aware of it, or aren’t sufficiently wary—that as we wander through our human world, we can expect to encounter systematically bad epistemology.

The “how to think” memes floating around, the cached thoughts of Deep Wisdom—some of it will be good advice devised by rationalists. But other notions were invented to protect a lie or self-deception: spawned from the Dark Side.

“Everyone has a right to their own opinion.” When you think about it, where was that proverb generated? Is it something that someone would say in the course of protecting a truth, or in the course of protecting from the truth? But people don’t perk up and say, “Aha! I sense the presence of the Dark Side!” As far as I can tell, it’s not widely realized that the Dark Side is out there.

But how else? Whether you’re deceiving others, or just yourself, the Lie That Must Be Protected will propagate recursively through the network of empirical causality, and the network of general empirical rules, and the rules of reasoning themselves, and the understanding behind those rules. If there is good epistemology in the world, and also lies or self-deceptions that people are trying to protect, then there will come into existence bad epistemology to counter the good. We could hardly expect, in this world, to find the Light Side without the Dark Side; there is the Sun, and that which shrinks away and generates a cloaking Shadow.

Mind you, these are not necessarily evil people. The vast majority who go about repeating the Deep Wisdom are more duped than duplicitous, more self-deceived than deceiving. I think.

And it’s surely not my intent to offer you a Fully General Counterargument, so that whenever someone offers you some epistemology you don’t like, you say: “Oh, someone on the Dark Side made that up.” It’s one of the rules of the Light Side that you have to refute the proposition for itself, not by accusing its inventor of bad intentions.

But the Dark Side is out there. Fear is the path that leads to it, and one betrayal can turn you. Not all who wear robes are either Jedi or fakes; there are also the Sith Lords, masters and unwitting apprentices. Be warned, be wary.

As for listing common memes that were spawned by the Dark Side—not random false beliefs, mind you, but bad epistemology, the Generic Defenses of Fail—well, would you care to take a stab at it, dear readers?

Part H
Against Doublethink

81
Singlethink

I remember the exact moment when I began my journey as a rationalist.

It was not while reading Surely You’re Joking, Mr. Feynman or any existing work upon rationality; for these I simply accepted as obvious. The journey begins when you see a great flaw in your existing art, and discover a drive to improve, to create new skills beyond the helpful but inadequate ones you found in books.

In the last moments of my first life, I was fifteen years old, and rehearsing a pleasantly self-righteous memory of a time when I was much younger. My memories this far back are vague; I have a mental image, but I don’t remember how old I was exactly. I think I was six or seven, and that the original event happened during summer camp.

What happened originally was that a camp counselor, a teenage male, got us much younger boys to form a line, and proposed the following game: the boy at the end of the line would crawl through our legs, and we would spank him as he went past, and then it would be the turn of the next eight-year-old boy at the end of the line. (Maybe it’s just that I’ve lost my youthful innocence, but I can’t help but wonder . . .) I refused to play this game, and was told to go sit in the corner.

This memory—of refusing to spank and be spanked—came to symbolize to me that even at this very early age I had refused to take joy in hurting others. That I would not purchase a spank on another’s butt, at the price of a spank on my own; would not pay in hurt for the opportunity to inflict hurt. I had refused to play a negative-sum game.

And then, at the age of fifteen, I suddenly realized that it wasn’t true. I hadn’t refused out of a principled stand against negative-sum games. I found out about the Prisoner’s Dilemma pretty early in life, but not at the age of seven. I’d refused simply because I didn’t want to get hurt, and standing in the corner was an acceptable price to pay for not getting hurt.

More importantly, I realized that I had always known this—that the real memory had always been lurking in a corner of my mind, my mental eye glancing at it for a fraction of a second and then looking away.

In my very first step along the Way, I caught the feeling—generalized over the subjective experience—and said, “So that’s what it feels like to shove an unwanted truth into the corner of my mind! Now I’m going to notice every time I do that, and clean out all my corners!”

This discipline I named singlethink, after Orwell’s doublethink. In doublethink, you forget, and then forget you have forgotten. In singlethink, you notice you are forgetting, and then you remember. You hold only a single non-contradictory thought in your mind at once.

“Singlethink” was the first new rationalist skill I created, which I had not read about in books. I doubt that it is original in the sense of academic priority, but this is thankfully not required.

Oh, and my fifteen-year-old self liked to name things.

The terrifying depths of the confirmation bias go on and on. Not forever, for the brain is of finite complexity, but long enough that it feels like forever. You keep on discovering (or reading about) new mechanisms by which your brain shoves things out of the way.

But my young self swept out quite a few corners with that first broom.

82
Doublethink (Choosing to be Biased)

An oblong slip of newspaper had appeared between O’Brien’s fingers. For perhaps five seconds it was within the angle of Winston’s vision. It was a photograph, and there was no question of its identity. It was the photograph. It was another copy of the photograph of Jones, Aaronson, and Rutherford at the party function in New York, which he had chanced upon eleven years ago and promptly destroyed. For only an instant it was before his eyes, then it was out of sight again. But he had seen it, unquestionably he had seen it! He made a desperate, agonizing effort to wrench the top half of his body free. It was impossible to move so much as a centimetre in any direction. For the moment he had even forgotten the dial. All he wanted was to hold the photograph in his fingers again, or at least to see it.

“It exists!” he cried.

“No,” said O’Brien.

He stepped across the room.

There was a memory hole in the opposite wall. O’Brien lifted the grating. Unseen, the frail slip of paper was whirling away on the current of warm air; it was vanishing in a flash of flame. O’Brien turned away from the wall.

“Ashes,” he said. “Not even identifiable ashes. Dust. It does not exist. It never existed.”

“But it did exist! It does exist! It exists in memory. I remember it. You remember it.”

“I do not remember it,” said O’Brien.

Winston’s heart sank. That was doublethink. He had a feeling of deadly helplessness. If he could have been certain that O’Brien was lying, it would not have seemed to matter. But it was perfectly possible that O’Brien had really forgotten the photograph. And if so, then already he would have forgotten his denial of remembering it, and forgotten the act of forgetting. How could one be sure that it was simple trickery? Perhaps that lunatic dislocation in the mind could really happen: that was the thought that defeated him.

—George Orwell, 1984¹

What if self-deception helps us be happy? What if just running out and overcoming bias will make us—gasp!—unhappy? Surely, true wisdom would be second-order rationality, choosing when to be rational. That way you can decide which cognitive biases should govern you, to maximize your happiness.

Leaving the morality aside, I doubt such a lunatic dislocation in the mind could really happen.

Second-order rationality implies that at some point, you will think to yourself, “And now, I will irrationally believe that I will win the lottery, in order to make myself happy.” But we do not have such direct control over our beliefs. You cannot make yourself believe the sky is green by an act of will. You might be able to believe you believed it—though I have just made that more difficult for you by pointing out the difference. (You’re welcome!) You might even believe you were happy and self-deceived; but you would not in fact be happy and self-deceived.

For second-order rationality to be genuinely rational, you would first need a good model of reality, to extrapolate the consequences of rationality and irrationality. If you then chose to be first-order irrational, you would need to forget this accurate view. And then forget the act of forgetting. I don’t mean to commit the logical fallacy of generalizing from fictional evidence, but I think Orwell did a good job of extrapolating where this path leads.

You can’t know the consequences of being biased, until you have already debiased yourself. And then it is too late for self-deception.

The other alternative is to choose blindly to remain biased, without any clear idea of the consequences. This is not second-order rationality. It is willful stupidity.

Be irrationally optimistic about your driving skills, and you will be happily unconcerned where others sweat and fear. You won’t have to put up with the inconvenience of a seat belt. You will be happily unconcerned for a day, a week, a year. Then crash, and spend the rest of your life wishing you could scratch the itch in your phantom limb. Or paralyzed from the neck down. Or dead. It’s not inevitable, but it’s possible; how probable is it? You can’t make that tradeoff rationally unless you know your real driving skills, so you can figure out how much danger you’re placing yourself in. You can’t make that tradeoff rationally unless you know about biases like neglect of probability.

No matter how many days go by in blissful ignorance, it only takes a single mistake to undo a human life, to outweigh every penny you picked up from the railroad tracks of stupidity.

One of the chief pieces of advice I give to aspiring rationalists is “Don’t try to be clever.” And, “Listen to those quiet, nagging doubts.” If you don’t know, you don’t know what you don’t know, you don’t know how much you don’t know, and you don’t know how much you needed to know.

There is no second-order rationality. There is only a blind leap into what may or may not be a flaming lava pit. Once you know, it will be too late for blindness.

But people neglect this, because they do not know what they do not know. Unknown unknowns are not available. They do not focus on the blank area on the map, but treat it as if it corresponded to a blank territory. When they consider leaping blindly, they check their memory for dangers, and find no flaming lava pits in the blank map. Why not leap?

Been there. Tried that. Got burned. Don’t try to be clever.

I once said to a friend that I suspected the happiness of stupidity was greatly overrated. And she shook her head seriously, and said, “No, it’s not; it’s really not.”

Maybe there are stupid happy people out there. Maybe they are happier than you are. And life isn’t fair, and you won’t become happier by being jealous of what you can’t have. I suspect the vast majority of Overcoming Bias readers could not achieve the “happiness of stupidity” if they tried. That way is closed to you. You can never achieve that degree of ignorance, you cannot forget what you know, you cannot unsee what you see.

The happiness of stupidity is closed to you. You will never have it short of actual brain damage, and maybe not even then. You should wonder, I think, whether the happiness of stupidity is optimal—if it is the most happiness that a human can aspire to—but it matters not. That way is closed to you, if it was ever open.

All that is left to you now, is to aspire to such happiness as a rationalist can achieve. I think it may prove greater, in the end. There are bounded paths and open-ended paths; plateaus on which to laze, and mountains to climb; and if climbing takes more effort, still the mountain rises higher in the end.

Also there is more to life than happiness; and other happinesses than your own may be at stake in your decisions.

But that is moot. By the time you realize you have a choice, there is no choice. You cannot unsee what you see. The other way is closed.

1. Orwell, 1984.

83
No, Really, I’ve Deceived Myself

I recently spoke with a person who . . . it’s difficult to describe. Nominally, she was an Orthodox Jew. She was also highly intelligent, conversant with some of the archaeological evidence against her religion, and the shallow standard arguments against religion that religious people know about. For example, she knew that Mordecai, Esther, Haman, and Vashti were not in the Persian historical records, but that there was a corresponding old Persian legend about the Babylonian gods Marduk and Ishtar, and the rival Elamite gods Humman and Vashti. She knows this, and she still celebrates Purim. One of those highly intelligent religious people who stew in their own contradictions for years, elaborating and tweaking, until the insides of their minds look like an M. C. Escher painting.

Most people like this will pretend that they are much too wise to talk to atheists, but she was willing to talk with me for a few hours.

As a result, I now understand at least one more thing about self-deception that I didn’t explicitly understand before—namely, that you don’t have to really deceive yourself so long as you believe you’ve deceived yourself. Call it “belief in self-deception.”

When this woman was in high school, she thought she was an atheist. But she decided, at that time, that she should act as if she believed in God. And then—she told me earnestly—over time, she came to really believe in God.

So far as I can tell, she is completely wrong about that. Always throughout our conversation, she said, over and over, “I believe in God,” never once, “There is a God.” When I asked her why she was religious, she never once talked about the consequences of God existing, only about the consequences of believing in God. Never, “God will help me,” always, “my belief in God helps me.” When I put to her, “Someone who just wanted the truth and looked at our universe would not even invent God as a hypothesis,” she agreed outright.

She hasn’t actually deceived herself into believing that God exists or that the Jewish religion is true. Not even close, so far as I can tell.

On the other hand, I think she really does believe she has deceived herself.

So although she does not receive any benefit of believing in God—because she doesn’t—she honestly believes she has deceived herself into believing in God, and so she honestly expects to receive the benefits that she associates with deceiving oneself into believing in God; and that, I suppose, ought to produce much the same placebo effect as actually believing in God.

And this may explain why she was motivated to earnestly defend the statement that she believed in God from my skeptical questioning, while never saying “Oh, and by the way, God actually does exist” or even seeming the slightest bit interested in the proposition.

84
Belief in SelfDeception

I spoke of my conversation with a nominally Orthodox Jewish woman who vigorously defended the assertion that she believed in God, while seeming not to actually believe in God at all.

While I was questioning her about the benefits that she thought came from believing in God, I introduced the Litany of Tarski—which is actually an infinite family of litanies, a specific example being:

If the sky is blue

I desire to believe “the sky is blue”

If the sky is not blue

I desire to believe “the sky is not blue.”

“This is not my philosophy,” she said to me.

“I didn’t think it was,” I replied to her. “I’m just asking—assuming that God does not exist, and this is known, then should you still believe in God?”

She hesitated. She seemed to really be trying to think about it, which surprised me.

“So it’s a counterfactual question . . .” she said slowly.

I thought at the time that she was having difficulty allowing herself to visualize the world where God does not exist, because of her attachment to a God-containing world.

Now, however, I suspect she was having difficulty visualizing a contrast between the way the world would look if God existed or did not exist, because all her thoughts were about her belief in God, but her causal network modelling the world did not contain God as a node. So she could easily answer “How would the world look different if I didn’t believe in God?,” but not “How would the world look different if there was no God?”

She didn’t answer that question, at the time. But she did produce a counterexample to the Litany of Tarski:

She said, “I believe that people are nicer than they really are.”

I tried to explain that if you say, “People are bad,” that means you believe people are bad, and if you say, “I believe people are nice,” that means you believe you believe people are nice. So saying “People are bad and I believe people are nice” means you believe people are bad but you believe you believe people are nice.

I quoted to her:

If there were a verb meaning “to believe falsely,” it would not have any significant first person, present indicative.

—Ludwig Wittgenstein¹

She said, smiling, “Yes, I believe people are nicer than, in fact, they are. I just thought I should put it that way for you.”

“I reckon Granny ought to have a good look at you, Walter,” said Nanny. “I reckon your mind’s all tangled up like a ball of string what’s been dropped.”

—Terry Pratchett, Maskerade²

And I can type out the words, “Well, I guess she didn’t believe that her reasoning ought to be consistent under reflection,” but I’m still having trouble coming to grips with it.

I can see the pattern in the words coming out of her lips, but I can’t understand the mind behind on an empathic level. I can imagine myself into the shoes of babyeating aliens and the Lady 3rd Kiritsugu, but I cannot imagine what it is like to be her. Or maybe I just don’t want to?

This is why intelligent people only have a certain amount of time (measured in subjective time spent thinking about religion) to become atheists. After a certain point, if you’re smart, have spent time thinking about and defending your religion, and still haven’t escaped the grip of Dark Side Epistemology, the inside of your mind ends up as an Escher painting.

(One of the other few moments that gave her pause—I mention this, in case you have occasion to use it—is when she was talking about how it’s good to believe that someone cares whether you do right or wrong—not, of course, talking about how there actually is a God who cares whether you do right or wrong, this proposition is not part of her religion—

And I said, “But I care whether you do right or wrong. So what you’re saying is that this isn’t enough, and you also need to believe in something above humanity that cares whether you do right or wrong.” So that stopped her, for a bit, because of course she’d never thought of it in those terms before. Just a standard application of the nonstandard toolbox.)

Later on, at one point, I was asking her if it would be good to do anything differently if there definitely was no God, and this time, she answered, “No.”

“So,” I said incredulously, “if God exists or doesn’t exist, that has absolutely no effect on how it would be good for people to think or act? I think even a rabbi would look a little askance at that.”

Her religion seems to now consist entirely of the worship of worship. As the true believers of older times might have believed that an all-seeing father would save them, she now believes that belief in God will save her.

After she said “I believe people are nicer than they are,” I asked, “So, are you consistently surprised when people undershoot your expectations?” There was a long silence, and then, slowly: “Well . . . am I surprised when people . . . undershoot my expectations?”

I didn’t understand this pause at the time. I’d intended it to suggest that if she was constantly disappointed by reality, then this was a downside of believing falsely. But she seemed, instead, to be taken aback at the implications of not being surprised.

I now realize that the whole essence of her philosophy was her belief that she had deceived herself, and the possibility that her estimates of other people were actually accurate, threatened the Dark Side Epistemology that she had built around beliefs such as “I benefit from believing people are nicer than they actually are.”

She has taken the old idol off its throne, and replaced it with an explicit worship of the Dark Side Epistemology that was once invented to defend the idol; she worships her own attempt at selfdeception. The attempt failed, but she is honestly unaware of this.

And so humanity’s token guardians of sanity (motto: “pooping your deranged little party since Epicurus”) must now fight the active worship of selfdeception—the worship of the supposed benefits of faith, in place of God.

This actually explains a fact about myself that I didn’t really understand earlier—the reason why I’m annoyed when people talk as if selfdeception is easy, and why I write entire essays arguing that making a deliberate choice to believe the sky is green is harder to get away with than people seem to think.

It’s because—while you can’t just choose to believe the sky is green—if you don’t realize this fact, then you actually can fool yourself into believing that you’ve successfully deceived yourself.

And since you then sincerely expect to receive the benefits that you think come from selfdeception, you get the same sort of placebo benefit that would actually come from a successful selfdeception.

So by going around explaining how hard selfdeception is, I’m actually taking direct aim at the placebo benefits that people get from believing that they’ve deceived themselves, and targeting the new sort of religion that worships only the worship of God.

Will this battle, I wonder, generate a new list of reasons why, not belief, but belief in belief, is itself a good thing? Why people derive great benefits from worshipping their worship? Will we have to do this over again with belief in belief in belief and worship of worship of worship? Or will intelligent theists finally just give up on that line of argument?

I wish I could believe that no one could possibly believe in belief in belief in belief, but the Zombie World argument in philosophy has gotten even more tangled than this and its proponents still haven’t abandoned it.

1. Ludwig Wittgenstein, Philosophical Investigations, trans. Gertrude E. M. Anscombe (Oxford: Blackwell, 1953).

2. Terry Pratchett, Maskerade, Discworld Series (ISIS, 1997).

85
Moore’s Paradox

Moore’s Paradox is the standard term for saying “It’s raining outside but I don’t believe that it is.” Hat tip to painquale on MetaFilter.

I think I understand Moore’s Paradox a bit better now, after reading some of the comments on Less Wrong. Jimrandomh suggests:

Many people cannot distinguish between levels of indirection. To them, “I believe X” and “X” are the same thing, and therefore, reasons why it is beneficial to believe X are also reasons why X is true.

I don’t think this is correct—relatively young children can understand the concept of having a false belief, which requires separate mental buckets for the map and the territory. But it points in the direction of a similar idea:

Many people may not consciously distinguish between believing something and endorsing it.

After all—“I believe in democracy” means, colloquially, that you endorse the concept of democracy, not that you believe democracy exists. The word “belief,” then, has more than one meaning. We could be looking at a confused word that causes confused thinking (or maybe it just reflects pre-existing confusion).

So: in the original example, “I believe people are nicer than they are,” she came up with some reasons why it would be good to believe people are nice—health benefits and such—and since she now had some warm affect on “believing people are nice,” she introspected on this warm affect and concluded, “I believe people are nice.” That is, she mistook the positive affect attached to the quoted belief, as signaling her belief in the proposition. At the same time, the world itself seemed like people weren’t so nice. So she said, “I believe people are nicer than they are.”

And that verges on being an honest mistake—sort of—since people are not taught explicitly how to know when they believe something. As in the parable of the dragon in the garage; the one who says “There is a dragon in my garage—but it’s invisible,” does not recognize their anticipation of seeing no dragon, as indicating that they possess an (accurate) model with no dragon in it.

It’s not as if people are trained to recognize when they believe something. It’s not like they’re ever taught in high school: “What it feels like to actually believe something—to have that statement in your belief pool—is that it just seems like the way the world is. You should recognize this feeling, which is actual (unquoted) belief, and distinguish it from having good feelings about a belief that you recognize as a belief (which means that it’s in quote marks).”

This goes a long way toward making this real-life case of Moore’s Paradox seem less alien, and providing another mechanism whereby people can be simultaneously right and wrong.

Likewise Kurige, who wrote:

I believe that there is a God—and that He has instilled a sense of right and wrong in us by which we are able to evaluate the world around us. I also believe a sense of morality has been evolutionarily programmed into us—a sense of morality that is most likely a result of the formation of meta-political coalitions in Bonobo communities a very, very long time ago. These two beliefs are not contradictory, but the complexity lies in reconciling the two.

I suspect, Kurige, you have decided that you have reasons to endorse the quoted belief that God has instilled a sense of right and wrong in us. And also that you have reasons to endorse the verdict of science. They both seem like good communities to join, right? There are benefits to both sets of beliefs? You introspect and find that you feel good about both beliefs?

But you did not say:

“God instilled a sense of right and wrong in us, and also a sense of morality has been evolutionarily programmed into us. The two states of reality are not inconsistent, but the complexity lies in reconciling the two.”

If you’re reading this, Kurige, you should very quickly say the above out loud, so you can notice that it seems at least slightly harder to swallow—notice the subjective difference—before you go to the trouble of rerationalizing.

This is the subjective difference between having reasons to endorse two different beliefs, and your mental model of a single world, a single way-things-are.

86
Don’t Believe You’ll SelfDeceive

I don’t mean to seem like I’m picking on Kurige, but I think you have to expect a certain amount of questioning if you show up on Less Wrong and say:

One thing I’ve come to realize that helps to explain the disparity I feel when I talk with most other Christians is the fact that somewhere along the way my world-view took a major shift away from blind faith and landed somewhere in the vicinity of Orwellian double-think.

“If you know it’s double-think . . .

. . . how can you still believe it?” I helplessly want to say.

Or:

I chose to believe in the existence of God—deliberately and consciously. This decision, however, has absolutely zero effect on the actual existence of God.

If you know your belief isn’t correlated to reality, how can you still believe it?

Shouldn’t the gut-level realization, “Oh, wait, the sky really isn’t green” follow from the realization “My map that says ‘the sky is green’ has no reason to be correlated with the territory”?

Well . . . apparently not.

One part of this puzzle may be my explanation of Moore’s Paradox (“It’s raining, but I don’t believe it is”)—that people introspectively mistake positive affect attached to a quoted belief, for actual credulity.

But another part of it may just be that—contrary to the indignation I initially wanted to put forward—it’s actually quite easy not to make the jump from “The map that reflects the territory would say ‘X’” to actually believing “X.” It takes some work to explain the ideas of minds as map-territory correspondence builders, and even then, it may take more work to get the implications on a gut level.

I realize now that when I wrote “You cannot make yourself believe the sky is green by an act of will,” I wasn’t just a dispassionate reporter of the existing facts. I was also trying to instill a self-fulfilling prophecy.

It may be wise to go around deliberately repeating “I can’t get away with double-thinking! Deep down, I’ll know it’s not true! If I know my map has no reason to be correlated with the territory, that means I don’t believe it!”

Because that way—if you’re ever tempted to try—the thoughts “But I know this isn’t really true!” and “I can’t fool myself!” will always rise readily to mind; and that way, you will indeed be less likely to fool yourself successfully. You’re more likely to get, on a gut level, that telling yourself X doesn’t make X true: and therefore, really truly not-X.

If you keep telling yourself that you can’t just deliberately choose to believe the sky is green—then you’re less likely to succeed in fooling yourself on one level or another; either in the sense of really believing it, or of falling into Moore’s Paradox, belief in belief, or belief in self-deception.

If you keep telling yourself that deep down you’ll know—

If you keep telling yourself that you’d just look at your elaborately constructed false map, and just know that it was a false map without any expected correlation to the territory, and therefore, despite all its elaborate construction, you wouldn’t be able to invest any credulity in it—

If you keep telling yourself that reflective consistency will take over and make you stop believing on the object level, once you come to the meta-level realization that the map is not reflecting—

Then when push comes to shove—you may, indeed, fail.

When it comes to deliberate self-deception, you must believe in your own inability!

Tell yourself the effort is doomed—and it will be!

Is that the power of positive thinking, or the power of negative thinking? Either way, it seems like a wise precaution.

Part I
Seeing with Fresh Eyes

87
Anchoring and Adjustment

Suppose I spin a Wheel of Fortune device as you watch, and it comes up pointing to 65. Then I ask: Do you think the percentage of African countries in the UN is above or below this number? What do you think is the percentage of African countries in the UN? Take a moment to consider these two questions yourself, if you like, and please don’t Google.

Also, try to guess, within five seconds, the value of the following arithmetical expression. Five seconds. Ready? Set . . . Go!

1 × 2 × 3 × 4 × 5 × 6 × 7 × 8

Tversky and Kahneman recorded the estimates of subjects who saw the Wheel of Fortune showing various numbers.¹ The median estimate of subjects who saw the wheel show 65 was 45%; the median estimate of subjects who saw 10 was 25%.

The current theory for this and similar experiments is that subjects take the initial, uninformative number as their starting point or anchor; and then they adjust upward or downward from their starting estimate until they reached an answer that “sounded plausible”; and then they stopped adjusting. This typically results in under-adjustment from the anchor—more distant numbers could also be “plausible,” but one stops at the first satisfying-sounding answer.

Similarly, students shown “1 × 2 × 3 × 4 × 5 × 6 × 7 × 8” made a median estimate of 512, while students shown “8 × 7 × 6 × 5 × 4 × 3 × 2 × 1” made a median estimate of 2,250. The motivating hypothesis was that students would try to multiply (or guess-combine) the first few factors of the product, then adjust upward. In both cases the adjustments were insufficient, relative to the true value of 40,320; but the first set of guesses were much more insufficient because they started from a lower anchor.

Tversky and Kahneman report that offering payoffs for accuracy did not reduce the anchoring effect.

Strack and Mussweiler asked for the year Einstein first visited the United States.² Completely implausible anchors, such as 1215 or 1992, produced anchoring effects just as large as more plausible anchors such as 1905 or 1939.

There are obvious applications in, say, salary negotiations, or buying a car. I won’t suggest that you exploit it, but watch out for exploiters.

And watch yourself thinking, and try to notice when you are adjusting a figure in search of an estimate.

Debiasing manipulations for anchoring have generally proved not very effective. I would suggest these two: First, if the initial guess sounds implausible, try to throw it away entirely and come up with a new estimate, rather than sliding from the anchor. But this in itself may not be sufficient—subjects instructed to avoid anchoring still seem to do so.³ So, second, even if you are trying the first method, try also to think of an anchor in the opposite direction—an anchor that is clearly too small or too large, instead of too large or too small—and dwell on it briefly.

1. Amos Tversky and Daniel Kahneman, “Judgment Under Uncertainty: Heuristics and Biases,” Science 185, no. 4157 (1974): 1124–1131, doi:10.1126/science.185.4157.1124.

2. Fritz Strack and Thomas Mussweiler, “Explaining the Enigmatic Anchoring Effect: Mechanisms of Selective Accessibility,” Journal of Personality and Social Psychology 73, no. 3 (1997): 437–446.

3. George A. Quattrone et al., “Explorations in Anchoring: The Effects of Prior Range, Anchor Extremity, and Suggestive Hints” (Unpublished manuscript, Stanford University, 1981).

88
Priming and Contamination

Suppose you ask subjects to press one button if a string of letters forms a word, and another button if the string does not form a word (e.g., “banack” vs. “banner”). Then you show them the string “water.” Later, they will more quickly identify the string “drink” as a word. This is known as “cognitive priming”; this particular form would be “semantic priming” or “conceptual priming.”

The fascinating thing about priming is that it occurs at such a low level—priming speeds up identifying letters as forming a word, which one would expect to take place before you deliberate on the word’s meaning.

Priming also reveals the massive parallelism of spreading activation: if seeing “water” activates the word “drink,” it probably also activates “river,” or “cup,” or “splash” . . . and this activation spreads, from the semantic linkage of concepts, all the way back to recognizing strings of letters.

Priming is subconscious and unstoppable, an artifact of the human neural architecture. Trying to stop yourself from priming is like trying to stop the spreading activation of your own neural circuits. Try to say aloud the color—not the meaning, but the color—of the following letter-string:

GREEN

In Mussweiler and Strack’s experiment, subjects were asked an anchoring question: “Is the annual mean temperature in Germany higher or lower than 5 C / 20 C?”¹ Afterward, on a word-identification task, subjects presented with the 5 C anchor were faster on identifying words like “cold” and “snow,” while subjects with the high anchor were faster to identify “hot” and “sun.” This shows a non-adjustment mechanism for anchoring: priming compatible thoughts and memories.

The more general result is that completely uninformative, known false, or totally irrelevant “information” can influence estimates and decisions. In the field of heuristics and biases, this more general phenomenon is known as contamination.²

Early research in heuristics and biases discovered anchoring effects, such as subjects giving lower (higher) estimates of the percentage of UN countries found within Africa, depending on whether they were first asked if the percentage was more or less than 10 (65). This effect was originally attributed to subjects adjusting from the anchor as a starting point, stopping as soon as they reached a plausible value, and under-adjusting because they were stopping at one end of a confidence interval.³

Tversky and Kahneman’s early hypothesis still appears to be the correct explanation in some circumstances, notably when subjects generate the initial estimate themselves.⁴ But modern research seems to show that most anchoring is actually due to contamination, not sliding adjustment. (Hat tip to Unnamed for reminding me of this—I’d read the Epley and Gilovich paper years ago, as a chapter in Heuristics and Biases, but forgotten it.)

Your grocery store probably has annoying signs saying “Limit 12 per customer” or “5 for $10.” Are these signs effective at getting customers to buy in larger quantities? You probably think you’re not influenced. But someone must be, because these signs have been shown to work, which is why stores keep putting them up.⁵

Yet the most fearsome aspect of contamination is that it serves as yet another of the thousand faces of confirmation bias. Once an idea gets into your head, it primes information compatible with it—and thereby ensures its continued existence. Never mind the selection pressures for winning political arguments; confirmation bias is built directly into our hardware, associational networks priming compatible thoughts and memories. An unfortunate side effect of our existence as neural creatures.

A single fleeting image can be enough to prime associated words for recognition. Don’t think it takes anything more to set confirmation bias in motion. All it takes is that one quick flash, and the bottom line is already decided, for we change our minds less often than we think . . .

1. Thomas Mussweiler and Fritz Strack, “Comparing Is Believing: A Selective Accessibility Model of Judgmental Anchoring,” European Review of Social Psychology 10 (1 1999): 135–167, doi:10.1080/14792779943000044.

2. Gretchen B. Chapman and Eric J. Johnson, “Incorporating the Irrelevant: Anchors in Judgments of Belief and Value,” in Gilovich, Griffin, and Kahneman, Heuristics and Biases, 120–138.

3. Tversky and Kahneman, “Judgment Under Uncertainty.”

4. Nicholas Epley and Thomas Gilovich, “Putting Adjustment Back in the Anchoring and Adjustment Heuristic: Differential Processing of Self-Generated and Experimentor-Provided Anchors,” Psychological Science 12 (5 2001): 391–396, doi:10.1111/1467-9280.00372.

5. Brian Wansink, Robert J. Kent, and Stephen J. Hoch, “An Anchoring and Adjustment Model of Purchase Quantity Decisions,” Journal of Marketing Research 35, no. 1 (1998): 71–81, http://www.jstor.org/stable/3151931.

89
Do We Believe Everything We’re Told?

Some early experiments on anchoring and adjustment tested whether distracting the subjects—rendering subjects cognitively “busy” by asking them to keep a lookout for “5” in strings of numbers, or some such—would decrease adjustment, and hence increase the influence of anchors. Most of the experiments seemed to bear out the idea that cognitive busyness increased anchoring, and more generally contamination.

Looking over the accumulating experimental results—more and more findings of contamination, exacerbated by cognitive busyness—Daniel Gilbert saw a truly crazy pattern emerging: Do we believe everything we’re told?

One might naturally think that on being told a proposition, we would first comprehend what the proposition meant, then consider the proposition, and finally accept or reject it. This obvious-seeming model of cognitive process flow dates back to Descartes. But Descartes’s rival, Spinoza, disagreed; Spinoza suggested that we first passively accept a proposition in the course of comprehending it, and only afterward actively disbelieve propositions which are rejected by consideration.

Over the last few centuries, philosophers pretty much went along with Descartes, since his view seemed more, y’know, logical and intuitive. But Gilbert saw a way of testing Descartes’s and Spinoza’s hypotheses experimentally.

If Descartes is right, then distracting subjects should interfere with both accepting true statements and rejecting false statements. If Spinoza is right, then distracting subjects should cause them to remember false statements as being true, but should not cause them to remember true statements as being false.

Gilbert, Krull, and Malone bear out this result, showing that, among subjects presented with novel statements labeled TRUE or FALSE, distraction had no effect on identifying true propositions (55% success for uninterrupted presentations, vs. 58% when interrupted); but did affect identifying false propositions (55% success when uninterrupted, vs. 35% when interrupted).¹

A much more dramatic illustration was produced in followup experiments by Gilbert, Tafarodi, and Malone.² Subjects read aloud crime reports crawling across a video monitor, in which the color of the text indicated whether a particular statement was true or false. Some reports contained false statements that exacerbated the severity of the crime, other reports contained false statements that extenuated (excused) the crime. Some subjects also had to pay attention to strings of digits, looking for a “5,” while reading the crime reports—this being the distraction task to create cognitive busyness. Finally, subjects had to recommend the length of prison terms for each criminal, from 0 to 20 years.

Subjects in the cognitively busy condition recommended an average of 11.15 years in prison for criminals in the “exacerbating” condition, that is, criminals whose reports contained labeled false statements exacerbating the severity of the crime. Busy subjects recommended an average of 5.83 years in prison for criminals whose reports contained labeled false statements excusing the crime. This nearly twofold difference was, as you might suspect, statistically significant.

Non-busy participants read exactly the same reports, with the same labels, and the same strings of numbers occasionally crawling past, except that they did not have to search for the number “5.” Thus, they could devote more attention to “unbelieving” statements labeled false. These non-busy participants recommended 7.03 years versus 6.03 years for criminals whose reports falsely exacerbated or falsely excused.

Gilbert, Tafarodi, and Malone’s paper was entitled “You Can’t Not Believe Everything You Read.”

This suggests—to say the very least—that we should be more careful when we expose ourselves to unreliable information, especially if we’re doing something else at the time. Be careful when you glance at that newspaper in the supermarket.

PS: According to an unverified rumor I just made up, people will be less skeptical of this essay because of the distracting color changes.

1. Daniel T. Gilbert, Douglas S. Krull, and Patrick S. Malone, “Unbelieving the Unbelievable: Some Problems in the Rejection of False Information,” Journal of Personality and Social Psychology 59 (4 1990): 601–613, doi:10.1037/0022-3514.59.4.601.

2. Gilbert, Tafarodi, and Malone, “You Can’t Not Believe Everything You Read.”

90
Cached Thoughts

One of the single greatest puzzles about the human brain is how the damn thing works at all when most neurons fire 10–20 times per second, or 200Hz tops. In neurology, the “hundred-step rule” is that any postulated operation has to complete in at most 100 sequential steps—you can be as parallel as you like, but you can’t postulate more than 100 (preferably fewer) neural spikes one after the other.

Can you imagine having to program using 100Hz CPUs, no matter how many of them you had? You’d also need a hundred billion processors just to get anything done in realtime.

If you did need to write realtime programs for a hundred billion 100Hz processors, one trick you’d use as heavily as possible is caching. That’s when you store the results of previous operations and look them up next time, instead of recomputing them from scratch. And it’s a very neural idiom—recognition, association, completing the pattern.

It’s a good guess that the actual majority of human cognition consists of cache lookups.

This thought does tend to go through my mind at certain times.

There was a wonderfully illustrative story which I thought I had bookmarked, but couldn’t re-find: it was the story of a man whose know-it-all neighbor had once claimed in passing that the best way to remove a chimney from your house was to knock out the fireplace, wait for the bricks to drop down one level, knock out those bricks, and repeat until the chimney was gone. Years later, when the man wanted to remove his own chimney, this cached thought was lurking, waiting to pounce . . .

As the man noted afterward—you can guess it didn’t go well—his neighbor was not particularly knowledgeable in these matters, not a trusted source. If he’d questioned the idea, he probably would have realized it was a poor one. Some cache hits we’d be better off recomputing. But the brain completes the pattern automatically—and if you don’t consciously realize the pattern needs correction, you’ll be left with a completed pattern.

I suspect that if the thought had occurred to the man himself—if he’d personally had this bright idea for how to remove a chimney—he would have examined the idea more critically. But if someone else has already thought an idea through, you can save on computing power by caching their conclusion—right?

In modern civilization particularly, no one can think fast enough to think their own thoughts. If I’d been abandoned in the woods as an infant, raised by wolves or silent robots, I would scarcely be recognizable as human. No one can think fast enough to recapitulate the wisdom of a hunter-gatherer tribe in one lifetime, starting from scratch. As for the wisdom of a literate civilization, forget it.

But the flip side of this is that I continually see people who aspire to critical thinking, repeating back cached thoughts which were not invented by critical thinkers.

A good example is the skeptic who concedes, “Well, you can’t prove or disprove a religion by factual evidence.” As I have pointed out elsewhere, this is simply false as probability theory. And it is also simply false relative to the real psychology of religion—a few centuries ago, saying this would have gotten you burned at the stake. A mother whose daughter has cancer prays, “God, please heal my daughter,” not, “Dear God, I know that religions are not allowed to have any falsifiable consequences, which means that you can’t possibly heal my daughter, so . . . well, basically, I’m praying to make myself feel better, instead of doing something that could actually help my daughter.”

But people read “You can’t prove or disprove a religion by factual evidence,” and then, the next time they see a piece of evidence disproving a religion, their brain completes the pattern. Even some atheists repeat this absurdity without hesitation. If they’d thought of the idea themselves, rather than hearing it from someone else, they would have been more skeptical.

Death. Complete the pattern: “Death gives meaning to life.”

It’s frustrating, talking to good and decent folk—people who would never in a thousand years spontaneously think of wiping out the human species—raising the topic of existential risk, and hearing them say, “Well, maybe the human species doesn’t deserve to survive.” They would never in a thousand years shoot their own child, who is a part of the human species, but the brain completes the pattern.

What patterns are being completed, inside your mind, that you never chose to be there?

Rationality. Complete the pattern: “Love isn’t rational.”

If this idea had suddenly occurred to you personally, as an entirely new thought, how would you examine it critically? I know what I would say, but what would you? It can be hard to see with fresh eyes. Try to keep your mind from completing the pattern in the standard, unsurprising, already-known way. It may be that there is no better answer than the standard one, but you can’t think about the answer until you can stop your brain from filling in the answer automatically.

Now that you’ve read this, the next time you hear someone unhesitatingly repeating a meme you think is silly or false, you’ll think, “Cached thoughts.” My belief is now there in your mind, waiting to complete the pattern. But is it true? Don’t let your mind complete the pattern! Think!

91
The “Outside the Box” Box

Whenever someone exhorts you to “think outside the box,” they usually, for your convenience, point out exactly where “outside the box” is located. Isn’t it funny how nonconformists all dress the same . . .

In Artificial Intelligence, everyone outside the field has a cached result for brilliant new revolutionary AI idea—neural networks, which work just like the human brain! New AI idea. Complete the pattern: “Logical AIs, despite all the big promises, have failed to provide real intelligence for decades—what we need are neural networks!”

This cached thought has been around for three decades. Still no general intelligence. But, somehow, everyone outside the field knows that neural networks are the Dominant-Paradigm-Overthrowing New Idea, ever since backpropagation was invented in the 1970s. Talk about your aging hippies.

Nonconformist images, by their nature, permit no departure from the norm. If you don’t wear black, how will people know you’re a tortured artist? How will people recognize uniqueness if you don’t fit the standard pattern for what uniqueness is supposed to look like? How will anyone recognize you’ve got a revolutionary AI concept, if it’s not about neural networks?

Another example of the same trope is “subversive” literature, all of which sounds the same, backed up by a tiny defiant league of rebels who control the entire English Department. As Anonymous asks on Scott Aaronson’s blog:

Has any of the subversive literature you’ve read caused you to modify any of your political views?

Or as Lizard observes:

Revolution has already been televised. Revolution has been merchandised. Revolution is a commodity, a packaged lifestyle, available at your local mall. $19.95 gets you the black mask, the spray can, the “Crush the Fascists” protest sign, and access to your blog where you can write about the police brutality you suffered when you chained yourself to a fire hydrant. Capitalism has learned how to sell anti-capitalism.

Many in Silicon Valley have observed that the vast majority of venture capitalists at any given time are all chasing the same Revolutionary Innovation, and it’s the Revolutionary Innovation that IPO’d six months ago. This is an especially crushing observation in venture capital, because there’s a direct economic motive to not follow the herd—either someone else is also developing the product, or someone else is bidding too much for the startup. Steve Jurvetson once told me that at Draper Fisher Jurvetson, only two partners need to agree in order to fund any startup up to $1.5 million. And if all the partners agree that something sounds like a good idea, they won’t do it. If only grant committees were this sane.

The problem with originality is that you actually have to think in order to attain it, instead of letting your brain complete the pattern. There is no conveniently labeled “Outside the Box” to which you can immediately run off. There’s an almost Zen-like quality to it—like the way you can’t teach satori in words because satori is the experience of words failing you. The more you try to follow the Zen Master’s instructions in words, the further you are from attaining an empty mind.

There is a reason, I think, why people do not attain novelty by striving for it. Properties like truth or good design are independent of novelty: 2 + 2 = 4, yes, really, even though this is what everyone else thinks too. People who strive to discover truth or to invent good designs, may in the course of time attain creativity. Not every change is an improvement, but every improvement is a change.

Every improvement is a change, but not every change is an improvement. The one who says “I want to build an original mousetrap!,” and not “I want to build an optimal mousetrap!,” nearly always wishes to be perceived as original. “Originality” in this sense is inherently social, because it can only be determined by comparison to other people. So their brain simply completes the standard pattern for what is perceived as “original,” and their friends nod in agreement and say it is subversive.

Business books always tell you, for your convenience, where your cheese has been moved to. Otherwise the readers would be left around saying, “Where is this ‘Outside the Box’ I’m supposed to go?”

Actually thinking, like satori, is a wordless act of mind.

The eminent philosophers of Monty Python said it best of all in Life of Brian:¹

“You’ve got to think for yourselves! You’re all individuals!”

“Yes, we’re all individuals!”

“You’re all different!”

“Yes, we’re all different!”

“You’ve all got to work it out for yourselves!”

“Yes, we’ve got to work it out for ourselves!”

1. Graham Chapman et al., Monty Python’s The Life of Brian (of Nazareth) (Eyre Methuen, 1979).

92
Original Seeing

Since Robert Pirsig put this very well, I’ll just copy down what he said. I don’t know if this story is based on reality or not, but either way, it’s true.¹

He’d been having trouble with students who had nothing to say. At first he thought it was laziness but later it became apparent that it wasn’t. They just couldn’t think of anything to say.

One of them, a girl with strong-lensed glasses, wanted to write a five-hundred word essay about the United States. He was used to the sinking feeling that comes from statements like this, and suggested without disparagement that she narrow it down to just Bozeman.

When the paper came due she didn’t have it and was quite upset. She had tried and tried but she just couldn’t think of anything to say.

It just stumped him. Now he couldn’t think of anything to say. A silence occurred, and then a peculiar answer: “Narrow it down to the main street of Bozeman.” It was a stroke of insight.

She nodded dutifully and went out. But just before her next class she came back in real distress, tears this time, distress that had obviously been there for a long time. She still couldn’t think of anything to say, and couldn’t understand why, if she couldn’t think of anything about all of Bozeman, she should be able to think of something about just one street.

He was furious. “You’re not looking!” he said. A memory came back of his own dismissal from the University for having too much to say. For every fact there is an infinity of hypotheses. The more you look the more you see. She really wasn’t looking and yet somehow didn’t understand this.

He told her angrily, “Narrow it down to the front of one building on the main street of Bozeman. The Opera House. Start with the upper left-hand brick.”

Her eyes, behind the thick-lensed glasses, opened wide.

She came in the next class with a puzzled look and handed him a five-thousand-word essay on the front of the Opera House on the main street of Bozeman, Montana. “I sat in the hamburger stand across the street,” she said, “and started writing about the first brick, and the second brick, and then by the third brick it all started to come and I couldn’t stop. They thought I was crazy, and they kept kidding me, but here it all is. I don’t understand it.”

Neither did he, but on long walks through the streets of town he thought about it and concluded she was evidently stopped with the same kind of blockage that had paralyzed him on his first day of teaching. She was blocked because she was trying to repeat, in her writing, things she had already heard, just as on the first day he had tried to repeat things he had already decided to say. She couldn’t think of anything to write about Bozeman because she couldn’t recall anything she had heard worth repeating. She was strangely unaware that she could look and see freshly for herself, as she wrote, without primary regard for what had been said before. The narrowing down to one brick destroyed the blockage because it was so obvious she had to do some original and direct seeing.

—Robert M. Pirsig,
Zen and the Art of Motorcycle Maintenance

1. Pirsig, Zen and the Art of Motorcycle Maintenance.

93
Stranger than History

Suppose I told you that I knew for a fact that the following statements were true:

If you paint yourself a certain exact color between blue and green, it will reverse the force of gravity on you and cause you to fall upward.
In the future, the sky will be filled by billions of floating black spheres. Each sphere will be larger than all the zeppelins that have ever existed put together. If you offer a sphere money, it will lower a male prostitute out of the sky on a bungee cord.
Your grandchildren will think it is not just foolish, but evil, to put thieves in jail instead of spanking them.

You’d think I was crazy, right?

Now suppose it were the year 1901, and you had to choose between believing those statements I have just offered, and believing statements like the following:

There is an absolute speed limit on how fast two objects can seem to be traveling relative to each other, which is exactly 670,616,629.2 miles per hour. If you hop on board a train going almost this fast and fire a gun out the window, the fundamental units of length change around, so it looks to you like the bullet is speeding ahead of you, but other people see something different. Oh, and time changes around too.
In the future, there will be a superconnected global network of billions of adding machines, each one of which has more power than all pre-1901 adding machines put together. One of the primary uses of this network will be to transport moving pictures of lesbian sex by pretending they are made out of numbers.
Your grandchildren will think it is not just foolish, but evil, to say that someone should not be President of the United States because she is black.

Based on a comment of Robin Hanson’s: “I wonder if one could describe in enough detail a fictional story of an alternative reality, a reality that our ancestors could not distinguish from the truth, in order to make it very clear how surprising the truth turned out to be.”

94
The Logical Fallacy of Generalization from Fictional Evidence

When I try to introduce the subject of advanced AI, what’s the first thing I hear, more than half the time?

“Oh, you mean like the Terminator movies / The Matrix / Asimov’s robots!”

And I reply, “Well, no, not exactly. I try to avoid the logical fallacy of generalizing from fictional evidence.”

Some people get it right away, and laugh. Others defend their use of the example, disagreeing that it’s a fallacy.

What’s wrong with using movies or novels as starting points for the discussion? No one’s claiming that it’s true, after all. Where is the lie, where is the rationalist sin? Science fiction represents the author’s attempt to visualize the future; why not take advantage of the thinking that’s already been done on our behalf, instead of starting over?

Not every misstep in the precise dance of rationality consists of outright belief in a falsehood; there are subtler ways to go wrong.

First, let us dispose of the notion that science fiction represents a full-fledged rational attempt to forecast the future. Even the most diligent science fiction writers are, first and foremost, storytellers; the requirements of storytelling are not the same as the requirements of forecasting. As Nick Bostrom points out:¹

When was the last time you saw a movie about humankind suddenly going extinct (without warning and without being replaced by some other civilization)? While this scenario may be much more probable than a scenario in which human heroes successfully repel an invasion of monsters or robot warriors, it wouldn’t be much fun to watch.

So there are specific distortions in fiction. But trying to correct for these specific distortions is not enough. A story is never a rational attempt at analysis, not even with the most diligent science fiction writers, because stories don’t use probability distributions. I illustrate as follows:

Bob Merkelthud slid cautiously through the door of the alien spacecraft, glancing right and then left (or left and then right) to see whether any of the dreaded Space Monsters yet remained. At his side was the only weapon that had been found effective against the Space Monsters, a Space Sword forged of pure titanium with 30% probability, an ordinary iron crowbar with 20% probability, and a shimmering black discus found in the smoking ruins of Stonehenge with 45% probability, the remaining 5% being distributed over too many minor outcomes to list here.

Merklethud (though there’s a significant chance that Susan Wifflefoofer was there instead) took two steps forward or one step back, when a vast roar split the silence of the black airlock! Or the quiet background hum of the white airlock! Although Amfer and Woofi (1997) argue that Merklethud is devoured at this point, Spacklebackle (2003) points out that—

Characters can be ignorant, but the author can’t say the three magic words “I don’t know.” The protagonist must thread a single line through the future, full of the details that lend flesh to the story, from Wifflefoofer’s appropriately futuristic attitudes toward feminism, down to the color of her earrings.

Then all these burdensome details and questionable assumptions are wrapped up and given a short label, creating the illusion that they are a single package.

On problems with large answer spaces, the greatest difficulty is not verifying the correct answer but simply locating it in answer space to begin with. If someone starts out by asking whether or not AIs are gonna put us into capsules like in The Matrix, they’re jumping to a 100-bit proposition, without a corresponding 98 bits of evidence to locate it in the answer space as a possibility worthy of explicit consideration. It would only take a handful more evidence after the first 98 bits to promote that possibility to near-certainty, which tells you something about where nearly all the work gets done.

The “preliminary” step of locating possibilities worthy of explicit consideration includes steps like: Weighing what you know and don’t know, what you can and can’t predict, making a deliberate effort to avoid absurdity bias and widen confidence intervals, pondering which questions are the important ones, trying to adjust for possible Black Swans and think of (formerly) unknown unknowns. Jumping to “The Matrix: Yes or No?” skips over all of this.

Any professional negotiator knows that to control the terms of a debate is very nearly to control the outcome of the debate. If you start out by thinking of The Matrix, it brings to mind marching robot armies defeating humans after a long struggle—not a superintelligence snapping nanotechnological fingers. It focuses on an “Us vs. Them” struggle, directing attention to questions like “Who will win?” and “Who should win?” and “Will AIs really be like that?” It creates a general atmosphere of entertainment, of “What is your amazing vision of the future?”

Lost to the echoing emptiness are: considerations of more than one possible mind design that an “Artificial Intelligence” could implement; the future’s dependence on initial conditions; the power of smarter-than-human intelligence and the argument for its unpredictability; people taking the whole matter seriously and trying to do something about it.

If some insidious corrupter of debates decided that their preferred outcome would be best served by forcing discussants to start out by refuting Terminator, they would have done well in skewing the frame. Debating gun control, the NRA spokesperson does not wish to be introduced as a “shooting freak,” the anti-gun opponent does not wish to be introduced as a “victim disarmament advocate.” Why should you allow the same order of frame-skewing by Hollywood scriptwriters, even accidentally?

Journalists don’t tell me, “The future will be like 2001.” But they ask, “Will the future be like 2001, or will it be like A.I.?” This is just as huge a framing issue as asking “Should we cut benefits for disabled veterans, or raise taxes on the rich?”

In the ancestral environment, there were no moving pictures; what you saw with your own eyes was true. A momentary glimpse of a single word can prime us and make compatible thoughts more available, with demonstrated strong influence on probability estimates. How much havoc do you think a two-hour movie can wreak on your judgment? It will be hard enough to undo the damage by deliberate concentration—why invite the vampire into your house? In Chess or Go, every wasted move is a loss; in rationality, any non-evidential influence is (on average) entropic.

Do movie-viewers succeed in unbelieving what they see? So far as I can tell, few movie viewers act as if they have directly observed Earth’s future. People who watched the Terminator movies didn’t hide in fallout shelters on August 29, 1997. But those who commit the fallacy seem to act as if they had seen the movie events occurring on some other planet; not Earth, but somewhere similar to Earth.

You say, “Suppose we build a very smart AI,” and they say, “But didn’t that lead to nuclear war in The Terminator?” As far as I can tell, it’s identical reasoning, down to the tone of voice, of someone who might say: “But didn’t that lead to nuclear war on Alpha Centauri?” or “Didn’t that lead to the fall of the Italian city-state of Piccolo in the fourteenth century?” The movie is not believed, but it is available. It is treated, not as a prophecy, but as an illustrative historical case. Will history repeat itself? Who knows?

In a recent intelligence explosion discussion, someone mentioned that Vinge didn’t seem to think that brain-computer interfaces would increase intelligence much, and cited Marooned in Realtime and Tunç Blumenthal, who was the most advanced traveller but didn’t seem all that powerful. I replied indignantly, “But Tunç lost most of his hardware! He was crippled!” And then I did a mental double-take and thought to myself: What the hell am I saying.

Does the issue not have to be argued in its own right, regardless of how Vinge depicted his characters? Tunç Blumenthal is not “crippled,” he’s unreal. I could say “Vinge chose to depict Tunç as crippled, for reasons that may or may not have had anything to do with his personal best forecast,” and that would give his authorial choice an appropriate weight of evidence. I cannot say “Tunç was crippled.” There is no was of Tunç Blumenthal.

I deliberately left in a mistake I made, in my first draft of the beginning of this essay: “Others defend their use of the example, disagreeing that it’s a fallacy.” But The Matrix is not an example!

A neighboring flaw is the logical fallacy of arguing from imaginary evidence: “Well, if you did go to the end of the rainbow, you would find a pot of gold—which just proves my point!” (Updating on evidence predicted, but not observed, is the mathematical mirror image of hindsight bias.)

The brain has many mechanisms for generalizing from observation, not just the availability heuristic. You see three zebras, you form the category “zebra,” and this category embodies an automatic perceptual inference. Horse-shaped creatures with white and black stripes are classified as “Zebras,” therefore they are fast and good to eat; they are expected to be similar to other zebras observed.

So people see (moving pictures of) three Borg, their brain automatically creates the category “Borg,” and they infer automatically that humans with brain-computer interfaces are of class “Borg” and will be similar to other Borg observed: cold, uncompassionate, dressing in black leather, walking with heavy mechanical steps. Journalists don’t believe that the future will contain Borg—they don’t believe Star Trek is a prophecy. But when someone talks about brain-computer interfaces, they think, “Will the future contain Borg?” Not, “How do I know computer-assisted telepathy makes people less nice?” Not, “I’ve never seen a Borg and never has anyone else.” Not, “I’m forming a racial stereotype based on literally zero evidence.”

As George Orwell said of cliches:²

What is above all needed is to let the meaning choose the word, and not the other way around . . . When you think of something abstract you are more inclined to use words from the start, and unless you make a conscious effort to prevent it, the existing dialect will come rushing in and do the job for you, at the expense of blurring or even changing your meaning.

Yet in my estimation, the most damaging aspect of using other authors’ imaginations is that it stops people from using their own. As Robert Pirsig said:³

She was blocked because she was trying to repeat, in her writing, things she had already heard, just as on the first day he had tried to repeat things he had already decided to say. She couldn’t think of anything to write about Bozeman because she couldn’t recall anything she had heard worth repeating. She was strangely unaware that she could look and see freshly for herself, as she wrote, without primary regard for what had been said before.

Remembered fictions rush in and do your thinking for you; they substitute for seeing—the deadliest convenience of all.

1. Nick Bostrom, “Existential Risks: Analyzing Human Extinction Scenarios and Related Hazards,” Journal of Evolution and Technology 9 (2002), http://www.jetpress.org/volume9/risks.html.

2. Orwell, “Politics and the English Language.”

3. Pirsig, Zen and the Art of Motorcycle Maintenance.

95
The Virtue of Narrowness

What is true of one apple may not be true of another apple; thus more can be said about a single apple than about all the apples in the world.

—The Twelve Virtues of Rationality

Within their own professions, people grasp the importance of narrowness; a car mechanic knows the difference between a carburetor and a radiator, and would not think of them both as “car parts.” A hunter-gatherer knows the difference between a lion and a panther. A janitor does not wipe the floor with window cleaner, even if the bottles look similar to one who has not mastered the art.

Outside their own professions, people often commit the misstep of trying to broaden a word as widely as possible, to cover as much territory as possible. Is it not more glorious, more wise, more impressive, to talk about all the apples in the world? How much loftier it must be to explain human thought in general, without being distracted by smaller questions, such as how humans invent techniques for solving a Rubik’s Cube. Indeed, it scarcely seems necessary to consider specific questions at all; isn’t a general theory a worthy enough accomplishment on its own?

It is the way of the curious to lift up one pebble from among a million pebbles on the shore, and see something new about it, something interesting, something different. You call these pebbles “diamonds,” and ask what might be special about them—what inner qualities they might have in common, beyond the glitter you first noticed. And then someone else comes along and says: “Why not call this pebble a diamond too? And this one, and this one?” They are enthusiastic, and they mean well. For it seems undemocratic and exclusionary and elitist and unholistic to call some pebbles “diamonds,” and others not. It seems . . . narrow-minded . . . if you’ll pardon the phrase. Hardly open, hardly embracing, hardly communal.

You might think it poetic, to give one word many meanings, and thereby spread shades of connotation all around. But even poets, if they are good poets, must learn to see the world precisely. It is not enough to compare love to a flower. Hot jealous unconsummated love is not the same as the love of a couple married for decades. If you need a flower to symbolize jealous love, you must go into the garden, and look, and make subtle distinctions—find a flower with a heady scent, and a bright color, and thorns. Even if your intent is to shade meanings and cast connotations, you must keep precise track of exactly which meanings you shade and connote.

It is a necessary part of the rationalist’s art—or even the poet’s art!—to focus narrowly on unusual pebbles which possess some special quality. And look at the details which those pebbles—and those pebbles alone!—share among each other. This is not a sin.

It is perfectly all right for modern evolutionary biologists to explain just the patterns of living creatures, and not the “evolution” of stars or the “evolution” of technology. Alas, some unfortunate souls use the same word “evolution” to cover the naturally selected patterns of replicating life, and the strictly accidental structure of stars, and the intelligently configured structure of technology. And as we all know, if people use the same word, it must all be the same thing. We should automatically generalize anything we think we know about biological evolution to technology. Anyone who tells us otherwise must be a mere pointless pedant. It couldn’t possibly be that our ignorance of modern evolutionary theory is so total that we can’t tell the difference between a carburetor and a radiator. That’s unthinkable. No, the other person—you know, the one who’s studied the math—is just too dumb to see the connections.

And what could be more virtuous than seeing connections? Surely the wisest of all human beings are the New Age gurus who say, “Everything is connected to everything else.” If you ever say this aloud, you should pause, so that everyone can absorb the sheer shock of this Deep Wisdom.

There is a trivial mapping between a graph and its complement. A fully connected graph, with an edge between every two vertices, conveys the same amount of information as a graph with no edges at all. The important graphs are the ones where some things are not connected to some other things.

When the unenlightened ones try to be profound, they draw endless verbal comparisons between this topic, and that topic, which is like this, which is like that; until their graph is fully connected and also totally useless. The remedy is specific knowledge and in-depth study. When you understand things in detail, you can see how they are not alike, and start enthusiastically subtracting edges off your graph.

Likewise, the important categories are the ones that do not contain everything in the universe. Good hypotheses can only explain some possible outcomes, and not others.

It was perfectly all right for Isaac Newton to explain just gravity, just the way things fall down—and how planets orbit the Sun, and how the Moon generates the tides—but not the role of money in human society or how the heart pumps blood. Sneering at narrowness is rather reminiscent of ancient Greeks who thought that going out and actually looking at things was manual labor, and manual labor was for slaves.

As Plato put it in The Republic, Book VII:¹

If anyone should throw back his head and learn something by staring at the varied patterns on a ceiling, apparently you would think that he was contemplating with his reason, when he was only staring with his eyes . . . I cannot but believe that no study makes the soul look on high except that which is concerned with real being and the unseen. Whether he gape and stare upwards, or shut his mouth and stare downwards, if it be things of the senses that he tries to learn something about, I declare he never could learn, for none of these things admit of knowledge: I say his soul is looking down, not up, even if he is floating on his back on land or on sea!

Many today make a similar mistake, and think that narrow concepts are as lowly and unlofty and unphilosophical as, say, going out and looking at things—an endeavor only suited to the underclass. But rationalists—and also poets—need narrow words to express precise thoughts; they need categories that include only some things, and exclude others. There’s nothing wrong with focusing your mind, narrowing your categories, excluding possibilities, and sharpening your propositions. Really, there isn’t! If you make your words too broad, you end up with something that isn’t true and doesn’t even make good poetry.

And DON’T EVEN GET ME STARTED on people who think Wikipedia is an “Artificial Intelligence,” the invention of LSD was a “Singularity,” or that corporations are “superintelligent”!

1. Plato, Great Dialogues of Plato, ed. Eric H. Warmington and Philip G. Rouse (Signet Classic, 1999).

96
How to Seem (and Be) Deep

I recently attended a discussion group whose topic, at that session, was Death. It brought out deep emotions. I think that of all the Silicon Valley lunches I’ve ever attended, this one was the most honest; people talked about the death of family, the death of friends, what they thought about their own deaths. People really listened to each other. I wish I knew how to reproduce those conditions reliably.

I was the only transhumanist present, and I was extremely careful not to be obnoxious about it. (“A fanatic is someone who can’t change his mind and won’t change the subject.” I endeavor to at least be capable of changing the subject.) Unsurprisingly, people talked about the meaning that death gives to life, or how death is truly a blessing in disguise. But I did, very cautiously, explain that transhumanists are generally positive on life but thumbs down on death.

Afterward, several people came up to me and told me I was very “deep.” Well, yes, I am, but this got me thinking about what makes people seem deep.

At one point in the discussion, a woman said that thinking about death led her to be nice to people because, who knows, she might not see them again. “When I have a nice thing to say about someone,” she said, “now I say it to them right away, instead of waiting.”

“That is a beautiful thought,” I said, “and even if someday the threat of death is lifted from you, I hope you will keep on doing it—”

Afterward, this woman was one of the people who told me I was deep.

At another point in the discussion, a man spoke of some benefit X of death, I don’t recall exactly what. And I said: “You know, given human nature, if people got hit on the head by a baseball bat every week, pretty soon they would invent reasons why getting hit on the head with a baseball bat was a good thing. But if you took someone who wasn’t being hit on the head with a baseball bat, and you asked them if they wanted it, they would say no. I think that if you took someone who was immortal, and asked them if they wanted to die for benefit X, they would say no.”

Afterward, this man told me I was deep.

Correlation is not causality. Maybe I was just speaking in a deep voice that day, and so sounded wise.

But my suspicion is that I came across as “deep” because I coherently violated the cached pattern for “deep wisdom” in a way that made immediate sense.

There’s a stereotype of Deep Wisdom. Death. Complete the pattern: “Death gives meaning to life.” Everyone knows this standard Deeply Wise response. And so it takes on some of the characteristics of an applause light. If you say it, people may nod along, because the brain completes the pattern and they know they’re supposed to nod. They may even say “What deep wisdom!,” perhaps in the hope of being thought deep themselves. But they will not be surprised; they will not have heard anything outside the box; they will not have heard anything they could not have thought of for themselves. One might call it belief in wisdom—the thought is labeled “deeply wise,” and it’s the completed standard pattern for “deep wisdom,” but it carries no experience of insight.

People who try to seem Deeply Wise often end up seeming hollow, echoing as it were, because they’re trying to seem Deeply Wise instead of optimizing.

How much thinking did I need to do, in the course of seeming deep? Human brains only run at 100Hz and I responded in realtime, so most of the work must have been precomputed. The part I experienced as effortful was picking a response understandable in one inferential step and then phrasing it for maximum impact.

Philosophically, nearly all of my work was already done. Complete the pattern: Existing condition X is really justified because it has benefit Y. “Naturalistic fallacy?” “Status quo bias?” “Could we get Y without X?” / “If we had never even heard of X before, would we voluntarily take it on to get Y?” I think it’s fair to say that I execute these thought-patterns at around the same level of automaticity as I breathe. After all, most of human thought has to be cache lookups if the brain is to work at all.

And I already held to the developed philosophy of transhumanism. Transhumanism also has cached thoughts about death. Death. Complete the pattern: “Death is a pointless tragedy which people rationalize.” This was a nonstandard cache, one with which my listeners were unfamiliar. I had several opportunities to use nonstandard cache, and because they were all part of the developed philosophy of transhumanism, they all visibly belonged to the same theme. This made me seem coherent, as well as original.

I suspect this is one reason Eastern philosophy seems deep to Westerners—it has nonstandard but coherent cache for Deep Wisdom. Symmetrically, in works of Japanese fiction, one sometimes finds Christians depicted as repositories of deep wisdom and/or mystical secrets. (And sometimes not.)

If I recall correctly, an economist once remarked that popular audiences are so unfamiliar with standard economics that, when he was called upon to make a television appearance, he just needed to repeat back Econ 101 in order to sound like a brilliantly original thinker.

Also crucial was that my listeners could see immediately that my reply made sense. They might or might not have agreed with the thought, but it was not a complete non-sequitur unto them. I know transhumanists who are unable to seem deep because they are unable to appreciate what their listener does not already know. If you want to sound deep, you can never say anything that is more than a single step of inferential distance away from your listener’s current mental state. That’s just the way it is.

To seem deep, study nonstandard philosophies. Seek out discussions on topics that will give you a chance to appear deep. Do your philosophical thinking in advance, so you can concentrate on explaining well. Above all, practice staying within the one-inferential-step bound.

To be deep, think for yourself about “wise” or important or emotionally fraught topics. Thinking for yourself isn’t the same as coming up with an unusual answer. It does mean seeing for yourself, rather than letting your brain complete the pattern. If you don’t stop at the first answer, and cast out replies that seem vaguely unsatisfactory, in time your thoughts will form a coherent whole, flowing from the single source of yourself, rather than being fragmentary repetitions of other people’s conclusions.

97
We Change Our Minds Less Often Than We Think

Over the past few years, we have discreetly approached colleagues faced with a choice between job offers, and asked them to estimate the probability that they will choose one job over another. The average confidence in the predicted choice was a modest 66%, but only 1 of the 24 respondents chose the option to which he or she initially assigned a lower probability, yielding an overall accuracy rate of 96%.

—Dale Griffin and Amos Tversky¹

When I first read the words above—on August 1st, 2003, at around 3 o’clock in the afternoon—it changed the way I thought. I realized that once I could guess what my answer would be—once I could assign a higher probability to deciding one way than other—then I had, in all probability, already decided. We change our minds less often than we think. And most of the time we become able to guess what our answer will be within half a second of hearing the question.

How swiftly that unnoticed moment passes, when we can’t yet guess what our answer will be; the tiny window of opportunity for intelligence to act. In questions of choice, as in questions of fact.

The principle of the bottom line is that only the actual causes of your beliefs determine your effectiveness as a rationalist. Once your belief is fixed, no amount of argument will alter the truth-value; once your decision is fixed, no amount of argument will alter the consequences.

You might think that you could arrive at a belief, or a decision, by non-rational means, and then try to justify it, and if you found you couldn’t justify it, reject it.

But we change our minds less often—much less often—than we think.

I’m sure that you can think of at least one occasion in your life when you’ve changed your mind. We all can. How about all the occasions in your life when you didn’t change your mind? Are they as available, in your heuristic estimate of your competence?

Between hindsight bias, fake causality, positive bias, anchoring/priming, et cetera, et cetera, and above all the dreaded confirmation bias, once an idea gets into your head, it’s probably going to stay there.

1. Dale Griffin and Amos Tversky, “The Weighing of Evidence and the Determinants of Confidence,” Cognitive Psychology 24, no. 3 (1992): 411–435, doi:10.1016/0010-0285(92)90013-R.

98
Hold Off On Proposing Solutions

From Robyn Dawes’s Rational Choice in an Uncertain World.¹ Bolding added.

Norman R. F. Maier noted that when a group faces a problem, the natural tendency of its members is to propose possible solutions as they begin to discuss the problem. Consequently, the group interaction focuses on the merits and problems of the proposed solutions, people become emotionally attached to the ones they have suggested, and superior solutions are not suggested. Maier enacted an edict to enhance group problem solving: “Do not propose solutions until the problem has been discussed as thoroughly as possible without suggesting any.” It is easy to show that this edict works in contexts where there are objectively defined good solutions to problems.

Maier devised the following “role playing” experiment to demonstrate his point. Three employees of differing ability work on an assembly line. They rotate among three jobs that require different levels of ability, because the most able—who is also the most dominant—is strongly motivated to avoid boredom. In contrast, the least able worker, aware that he does not perform the more difficult jobs as well as the other two, has agreed to rotation because of the dominance of his able co-worker. An “efficiency expert” notes that if the most able employee were given the most difficult task and the least able the least difficult, productivity could be improved by 20%, and the expert recommends that the employees stop rotating. The three employees and . . . a fourth person designated to play the role of foreman are asked to discuss the expert’s recommendation. Some role-playing groups are given Maier’s edict not to discuss solutions until having discussed the problem thoroughly, while others are not. Those who are not given the edict immediately begin to argue about the importance of productivity versus worker autonomy and the avoidance of boredom. Groups presented with the edict have a much higher probability of arriving at the solution that the two more able workers rotate, while the least able one sticks to the least demanding job—a solution that yields a 19% increase in productivity.

I have often used this edict with groups I have led—particularly when they face a very tough problem, which is when group members are most apt to propose solutions immediately. While I have no objective criterion on which to judge the quality of the problem solving of the groups, Maier’s edict appears to foster better solutions to problems.

This is so true it’s not even funny. And it gets worse and worse the tougher the problem becomes. Take Artificial Intelligence, for example. A surprising number of people I meet seem to know exactly how to build an Artificial General Intelligence, without, say, knowing how to build an optical character recognizer or a collaborative filtering system (much easier problems). And as for building an AI with a positive impact on the world—a Friendly AI, loosely speaking—why, that problem is so incredibly difficult that an actual majority resolve the whole issue within fifteen seconds. Give me a break.

This problem is by no means unique to AI. Physicists encounter plenty of nonphysicists with their own theories of physics, economists get to hear lots of amazing new theories of economics. If you’re an evolutionary biologist, anyone you meet can instantly solve any open problem in your field, usually by postulating group selection. Et cetera.

Maier’s advice echoes the principle of the bottom line, that the effectiveness of our decisions is determined only by whatever evidence and processing we did in first arriving at our decisions—after you write the bottom line, it is too late to write more reasons above. If you make your decision very early on, it will, in fact, be based on very little thought, no matter how many amazing arguments you come up with afterward.

And consider furthermore that We Change Our Minds Less Often than We Think: 24 people assigned an average 66% probability to the future choice thought more probable, but only 1 in 24 actually chose the option thought less probable. Once you can guess what your answer will be, you have probably already decided. If you can guess your answer half a second after hearing the question, then you have half a second in which to be intelligent. It’s not a lot of time.

Traditional Rationality emphasizes falsification—the ability to relinquish an initial opinion when confronted by clear evidence against it. But once an idea gets into your head, it will probably require way too much evidence to get it out again. Worse, we don’t always have the luxury of overwhelming evidence.

I suspect that a more powerful (and more difficult) method is to hold off on thinking of an answer. To suspend, draw out, that tiny moment when we can’t yet guess what our answer will be; thus giving our intelligence a longer time in which to act.

Even half a minute would be an improvement over half a second.

1. Dawes, Rational Choice in An Uncertain World, 55–56.

99
The Genetic Fallacy

In lists of logical fallacies, you will find included “the genetic fallacy”—the fallacy of attacking a belief based on someone’s causes for believing it.

This is, at first sight, a very strange idea—if the causes of a belief do not determine its systematic reliability, what does? If Deep Blue advises us of a chess move, we trust it based on our understanding of the code that searches the game tree, being unable to evaluate the actual game tree ourselves. What could license any probability assignment as “rational,” except that it was produced by some systematically reliable process?

Articles on the genetic fallacy will tell you that genetic reasoning is not always a fallacy—that the origin of evidence can be relevant to its evaluation, as in the case of a trusted expert. But other times, say the articles, it is a fallacy; the chemist Kekulé first saw the ring structure of benzene in a dream, but this doesn’t mean we can never trust this belief.

So sometimes the genetic fallacy is a fallacy, and sometimes it’s not?

The genetic fallacy is formally a fallacy, because the original cause of a belief is not the same as its current justificational status, the sum of all the support and antisupport currently known.

Yet we change our minds less often than we think. Genetic accusations have a force among humans that they would not have among ideal Bayesians.

Clearing your mind is a powerful heuristic when you’re faced with new suspicion that many of your ideas may have come from a flawed source.

Once an idea gets into our heads, it’s not always easy for evidence to root it out. Consider all the people out there who grew up believing in the Bible; later came to reject (on a deliberate level) the idea that the Bible was written by the hand of God; and who nonetheless think that the Bible contains indispensable ethical wisdom. They have failed to clear their minds; they could do significantly better by doubting anything the Bible said because the Bible said it.

At the same time, they would have to bear firmly in mind the principle that reversed stupidity is not intelligence; the goal is to genuinely shake your mind loose and do independent thinking, not to negate the Bible and let that be your algorithm.

Once an idea gets into your head, you tend to find support for it everywhere you look—and so when the original source is suddenly cast into suspicion, you would be very wise indeed to suspect all the leaves that originally grew on that branch . . .

If you can! It’s not easy to clear your mind. It takes a convulsive effort to actually reconsider, instead of letting your mind fall into the pattern of rehearsing cached arguments. “It ain’t a true crisis of faith unless things could just as easily go either way,” said Thor Shenkel.

You should be extremely suspicious if you have many ideas suggested by a source that you now know to be untrustworthy, but by golly, it seems that all the ideas still ended up being right—the Bible being the obvious archetypal example.

On the other hand . . . there’s such a thing as sufficiently clear-cut evidence, that it no longer significantly matters where the idea originally came from. Accumulating that kind of clear-cut evidence is what Science is all about. It doesn’t matter any more that Kekulé first saw the ring structure of benzene in a dream—it wouldn’t matter if we’d found the hypothesis to test by generating random computer images, or from a spiritualist revealed as a fraud, or even from the Bible. The ring structure of benzene is pinned down by enough experimental evidence to make the source of the suggestion irrelevant.

In the absence of such clear-cut evidence, then you do need to pay attention to the original sources of ideas—to give experts more credence than layfolk, if their field has earned respect—to suspect ideas you originally got from suspicious sources—to distrust those whose motives are untrustworthy, if they cannot present arguments independent of their own authority.

The genetic fallacy is a fallacy when there exist justifications beyond the genetic fact asserted, but the genetic accusation is presented as if it settled the issue. Hal Finney suggests that we call correctly appealing to a claim’s origins “the genetic heuristic.”

Some good rules of thumb (for humans):

Be suspicious of genetic accusations against beliefs that you dislike, especially if the proponent claims justifications beyond the simple authority of a speaker. “Flight is a religious idea, so the Wright Brothers must be liars” is one of the classically given examples.
By the same token, don’t think you can get good information about a technical issue just by sagely psychoanalyzing the personalities involved and their flawed motives. If technical arguments exist, they get priority.
When new suspicion is cast on one of your fundamental sources, you really should doubt all the branches and leaves that grew from that root. You are not licensed to reject them outright as conclusions, because reversed stupidity is not intelligence, but . . .
Be extremely suspicious if you find that you still believe the early suggestions of a source you later rejected.

Part J
Death Spirals

100
The Affect Heuristic

The affect heuristic is when subjective impressions of goodness/badness act as a heuristic—a source of fast, perceptual judgments. Pleasant and unpleasant feelings are central to human reasoning, and the affect heuristic comes with lovely biases—some of my favorites.

Let’s start with one of the relatively less crazy biases. You’re about to move to a new city, and you have to ship an antique grandfather clock. In the first case, the grandfather clock was a gift from your grandparents on your fifth birthday. In the second case, the clock was a gift from a remote relative and you have no special feelings for it. How much would you pay for an insurance policy that paid out $100 if the clock were lost in shipping? According to Hsee and Kunreuther, subjects stated willingness to pay more than twice as much in the first condition.¹ This may sound rational—why not pay more to protect the more valuable object?—until you realize that the insurance doesn’t protect the clock, it just pays if the clock is lost, and pays exactly the same amount for either clock. (And yes, it was stated that the insurance was with an outside company, so it gives no special motive to the movers.)

All right, but that doesn’t sound too insane. Maybe you could get away with claiming the subjects were insuring affective outcomes, not financial outcomes—purchase of consolation.

Then how about this? Yamagishi showed that subjects judged a disease as more dangerous when it was described as killing 1,286 people out of every 10,000, versus a disease that was 24.14% likely to be fatal.² Apparently the mental image of a thousand dead bodies is much more alarming, compared to a single person who’s more likely to survive than not.

But wait, it gets worse.

Suppose an airport must decide whether to spend money to purchase some new equipment, while critics argue that the money should be spent on other aspects of airport safety. Slovic et al. presented two groups of subjects with the arguments for and against purchasing the equipment, with a response scale ranging from 0 (would not support at all) to 20 (very strong support).³ One group saw the measure described as saving 150 lives. The other group saw the measure described as saving 98% of 150 lives. The hypothesis motivating the experiment was that saving 150 lives sounds vaguely good—is that a lot? a little?—while saving 98% of something is clearly very good because 98% is so close to the upper bound of the percentage scale. Lo and behold, saving 150 lives had mean support of 10.4, while saving 98% of 150 lives had mean support of 13.6.

Or consider the report of Denes-Raj and Epstein:⁴ Subjects offered an opportunity to win $1 each time they randomly drew a red jelly bean from a bowl, often preferred to draw from a bowl with more red beans and a smaller proportion of red beans. E.g., 7 in 100 was preferred to 1 in 10.

According to Denes-Raj and Epstein, these subjects reported afterward that even though they knew the probabilities were against them, they felt they had a better chance when there were more red beans. This may sound crazy to you, oh Statistically Sophisticated Reader, but if you think more carefully you’ll realize that it makes perfect sense. A 7% probability versus 10% probability may be bad news, but it’s more than made up for by the increased number of red beans. It’s a worse probability, yes, but you’re still more likely to win, you see. You should meditate upon this thought until you attain enlightenment as to how the rest of the planet thinks about probability.

Finucane et al. found that for nuclear reactors, natural gas, and food preservatives, presenting information about high benefits made people perceive lower risks; presenting information about higher risks made people perceive lower benefits; and so on across the quadrants.⁵ People conflate their judgments about particular good/bad aspects of something into an overall good or bad feeling about that thing.

Finucane et al. also found that time pressure greatly increased the inverse relationship between perceived risk and perceived benefit, consistent with the general finding that time pressure, poor information, or distraction all increase the dominance of perceptual heuristics over analytic deliberation.

Ganzach found the same effect in the realm of finance.⁶ According to ordinary economic theory, return and risk should correlate positively—or to put it another way, people pay a premium price for safe investments, which lowers the return; stocks deliver higher returns than bonds, but have correspondingly greater risk. When judging familiar stocks, analysts’ judgments of risks and returns were positively correlated, as conventionally predicted. But when judging unfamiliar stocks, analysts tended to judge the stocks as if they were generally good or generally bad—low risk and high returns, or high risk and low returns.

For further reading I recommend Slovic’s fine summary article, “Rational Actors or Rational Fools: Implications of the Affect Heuristic for Behavioral Economics.”⁷

1. Christopher K. Hsee and Howard C. Kunreuther, “The Affection Effect in Insurance Decisions,” Journal of Risk and Uncertainty 20 (2 2000): 141–159, doi:10.1023/A:1007876907268.

2. Kimihiko Yamagishi, “When a 12.86% Mortality Is More Dangerous than 24.14%: Implications for Risk Communication,” Applied Cognitive Psychology 11 (6 1997): 461–554.

3. Paul Slovic et al., “Rational Actors or Rational Fools: Implications of the Affect Heuristic for Behavioral Economics,” Journal of Socio-Economics 31, no. 4 (2002): 329–342, doi:10.1016/S1053-5357(02)00174-9.

4. Veronika Denes-Raj and Seymour Epstein, “Conflict between Intuitive and Rational Processing: When People Behave against Their Better Judgment,” Journal of Personality and Social Psychology 66 (5 1994): 819–829, doi:10.1037/0022-3514.66.5.819.

5. Finucane et al., “The Affect Heuristic in Judgments of Risks and Benefits.”

6. Yoav Ganzach, “Judging Risk and Return of Financial Assets,” Organizational Behavior and Human Decision Processes 83, no. 2 (2000): 353–370, doi:10.1006/obhd.2000.2914.

7. Slovic et al., “Rational Actors or Rational Fools.”

101
Evaluability (and Cheap Holiday Shopping)

With the expensive part of the Hallowthankmas season now approaching, a question must be looming large in our readers’ minds:

“Dear Overcoming Bias, are there biases I can exploit to be seen as generous without actually spending lots of money?”

I’m glad to report the answer is yes! According to Hsee—in a paper entitled “Less is better: When low-value options are valued more highly than high-value options”—if you buy someone a $45 scarf, you are more likely to be seen as generous than if you buy them a $55 coat.¹

This is a special case of a more general phenomenon. In an earlier experiment, Hsee asked subjects how much they would be willing to pay for a second-hand music dictionary:²

Dictionary A, from 1993, with 10,000 entries, in like-new condition.
Dictionary B, from 1993, with 20,000 entries, with a torn cover and otherwise in like-new condition.

The gotcha was that some subjects saw both dictionaries side-by-side, while other subjects only saw one dictionary . . .

Subjects who saw only one of these options were willing to pay an average of $24 for Dictionary A and an average of $20 for Dictionary B. Subjects who saw both options, side-by-side, were willing to pay $27 for Dictionary B and $19 for Dictionary A.

Of course, the number of entries in a dictionary is more important than whether it has a torn cover, at least if you ever plan on using it for anything. But if you’re only presented with a single dictionary, and it has 20,000 entries, the number 20,000 doesn’t mean very much. Is it a little? A lot? Who knows? It’s non-evaluable. The torn cover, on the other hand—that stands out. That has a definite affective valence: namely, bad.

Seen side-by-side, though, the number of entries goes from non-evaluable to evaluable, because there are two compatible quantities to be compared. And, once the number of entries becomes evaluable, that facet swamps the importance of the torn cover.

From Slovic et al.: Which would you prefer?³

A 29/36 chance to win $2.
A 7/36 chance to win $9.

While the average prices (equivalence values) placed on these options were $1.25 and $2.11 respectively, their mean attractiveness ratings were 13.2 and 7.5. Both the prices and the attractiveness rating were elicited in a context where subjects were told that two gambles would be randomly selected from those rated, and they would play the gamble with the higher price or higher attractiveness rating. (Subjects had a motive to rate gambles as more attractive, or price them higher, that they would actually prefer to play.)

The gamble worth more money seemed less attractive, a classic preference reversal. The researchers hypothesized that the dollar values were more compatible with the pricing task, but the probability of payoff was more compatible with attractiveness. So (the researchers thought) why not try to make the gamble’s payoff more emotionally salient—more affectively evaluable—more attractive?

And how did they do this? By adding a very small loss to the gamble. The old gamble had a 7/36 chance of winning $9. The new gamble had a 7/36 chance of winning $9 and a 29/36 chance of losing 5 cents. In the old gamble, you implicitly evaluate the attractiveness of $9. The new gamble gets you to evaluate the attractiveness of winning $9 versus losing 5 cents.

“The results,” said Slovic et al., “exceeded our expectations.” In a new experiment, the simple gamble with a 7/36 chance of winning $9 had a mean attractiveness rating of 9.4, while the complex gamble that included a 29/36 chance of losing 5 cents had a mean attractiveness rating of 14.9.

A follow-up experiment tested whether subjects preferred the old gamble to a certain gain of $2. Only 33% of students preferred the old gamble. Among another group asked to choose between a certain $2 and the new gamble (with the added possibility of a 5 cents loss), fully 60.8% preferred the gamble. After all, $9 isn’t a very attractive amount of money, but $9 / 5 cents is an amazingly attractive win/loss ratio.

You can make a gamble more attractive by adding a strict loss! Isn’t psychology fun? This is why no one who truly appreciates the wondrous intricacy of human intelligence wants to design a human-like AI.

Of course, it only works if the subjects don’t see the two gambles side-by-side.

Similarly, which of these two ice creams do you think subjects in Hsee’s 1998 study preferred?

Naturally, the answer depends on whether the subjects saw a single ice cream, or the two side-by-side. Subjects who saw a single ice cream were willing to pay $1.66 to Vendor H and $2.26 to Vendor L. Subjects who saw both ice creams were willing to pay $1.85 to Vendor H and $1.56 to Vendor L.

What does this suggest for your holiday shopping? That if you spend $400 on a 16GB iPod Touch, your recipient sees the most expensive MP3 player. If you spend $400 on a Nintendo Wii, your recipient sees the least expensive game machine. Which is better value for the money? Ah, but that question only makes sense if you see the two side-by-side. You’ll think about them side-by-side while you’re shopping, but the recipient will only see what they get.

If you have a fixed amount of money to spend—and your goal is to display your friendship, rather than to actually help the recipient—you’ll be better off deliberately not shopping for value. Decide how much money you want to spend on impressing the recipient, then find the most worthless object which costs that amount. The cheaper the class of objects, the more expensive a particular object will appear, given that you spend a fixed amount. Which is more memorable, a $25 shirt or a $25 candle?

Gives a whole new meaning to the Japanese custom of buying $50 melons, doesn’t it? You look at that and shake your head and say “What is it with the Japanese?” And yet they get to be perceived as incredibly generous, spendthrift even, while spending only $50. You could spend $200 on a fancy dinner and not appear as wealthy as you can by spending $50 on a melon. If only there was a custom of gifting $25 toothpicks or $10 dust specks; they could get away with spending even less.

PS: If you actually use this trick, I want to know what you bought.

1. Christopher K. Hsee, “Less Is Better: When Low-Value Options Are Valued More Highly than High-Value Options,” Behavioral Decision Making 11 (2 1998): 107–121.

2. Christopher K. Hsee, “The Evaluability Hypothesis: An Explanation for Preference Reversals between Joint and Separate Evaluations of Alternatives,” Organizational Behavior and Human Decision Processes 67 (3 1996): 247–257, doi:10.1006/obhd.1996.0077.

3. Slovic et al., “Rational Actors or Rational Fools.”

102
Unbounded Scales, Huge Jury Awards, and Futurism

“Psychophysics,” despite the name, is the respectable field that links physical effects to sensory effects. If you dump acoustic energy into air—make noise—then how loud does that sound to a person, as a function of acoustic energy? How much more acoustic energy do you have to pump into the air, before the noise sounds twice as loud to a human listener? It’s not twice as much; more like eight times as much.

Acoustic energy and photons are straightforward to measure. When you want to find out how loud an acoustic stimulus sounds, how bright a light source appears, you usually ask the listener or watcher. This can be done using a bounded scale from “very quiet” to “very loud,” or “very dim” to “very bright.” You can also use an unbounded scale, whose zero is “not audible at all” or “not visible at all,” but which increases from there without limit. When you use an unbounded scale, the observer is typically presented with a constant stimulus, the modulus, which is given a fixed rating. For example, a sound that is assigned a loudness of 10. Then the observer can indicate a sound twice as loud as the modulus by writing 20.

And this has proven to be a fairly reliable technique. But what happens if you give subjects an unbounded scale, but no modulus? Zero to infinity, with no reference point for a fixed value? Then they make up their own modulus, of course. The ratios between stimuli will continue to correlate reliably between subjects. Subject A says that sound X has a loudness of 10 and sound Y has a loudness of 15. If subject B says that sound X has a loudness of 100, then it’s a good guess that subject B will assign loudness in the vicinity of 150 to sound Y. But if you don’t know what subject C is using as their modulus—their scaling factor—then there’s no way to guess what subject C will say for sound X. It could be 1. It could be 1,000.

For a subject rating a single sound, on an unbounded scale, without a fixed standard of comparison, nearly all the variance is due to the arbitrary choice of modulus, rather than the sound itself.

“Hm,” you think to yourself, “this sounds an awful lot like juries deliberating on punitive damages. No wonder there’s so much variance!” An interesting analogy, but how would you go about demonstrating it experimentally?

Kahneman et al. presented 867 jury-eligible subjects with descriptions of legal cases (e.g., a child whose clothes caught on fire) and asked them to either

Rate the outrageousness of the defendant’s actions, on a bounded scale,
Rate the degree to which the defendant should be punished, on a bounded scale, or
Assign a dollar value to punitive damages.¹

And, lo and behold, while subjects correlated very well with each other in their outrage ratings and their punishment ratings, their punitive damages were all over the map. Yet subjects’ rank-ordering of the punitive damages—their ordering from lowest award to highest award—correlated well across subjects.

If you asked how much of the variance in the “punishment” scale could be explained by the specific scenario—the particular legal case, as presented to multiple subjects—then the answer, even for the raw scores, was 0.49. For the rank orders of the dollar responses, the amount of variance predicted was 0.51. For the raw dollar amounts, the variance explained was 0.06!

Which is to say: if you knew the scenario presented—the aforementioned child whose clothes caught on fire—you could take a good guess at the punishment rating, and a good guess at the rank-ordering of the dollar award relative to other cases, but the dollar award itself would be completely unpredictable.

Taking the median of twelve randomly selected responses didn’t help much either.

So a jury award for punitive damages isn’t so much an economic valuation as an attitude expression—a psychophysical measure of outrage, expressed on an unbounded scale with no standard modulus.

I observe that many futuristic predictions are, likewise, best considered as attitude expressions. Take the question, “How long will it be until we have human-level AI?” The responses I’ve seen to this are all over the map. On one memorable occasion, a mainstream AI guy said to me, “Five hundred years.” (!!)

Now the reason why time-to-AI is just not very predictable, is a long discussion in its own right. But it’s not as if the guy who said “Five hundred years” was looking into the future to find out. And he can’t have gotten the number using the standard bogus method with Moore’s Law. So what did the number 500 mean?

As far as I can guess, it’s as if I’d asked, “On a scale where zero is ‘not difficult at all,’ how difficult does the AI problem feel to you?” If this were a bounded scale, every sane respondent would mark “extremely hard” at the right-hand end. Everything feels extremely hard when you don’t know how to do it. But instead there’s an unbounded scale with no standard modulus. So people just make up a number to represent “extremely difficult,” which may come out as 50, 100, or even 500. Then they tack “years” on the end, and that’s their futuristic prediction.

“How hard does the AI problem feel?” isn’t the only substitutable question. Others respond as if I’d asked “How positive do you feel about AI?,” except lower numbers mean more positive feelings, and then they also tack “years” on the end. But if these “time estimates” represent anything other than attitude expressions on an unbounded scale with no modulus, I have been unable to determine it.

1. Daniel Kahneman, David A. Schkade, and Cass R. Sunstein, “Shared Outrage and Erratic Awards: The Psychology of Punitive Damages,” Journal of Risk and Uncertainty 16 (1 1998): 48–86, doi:10.1023/A:1007710408413; Daniel Kahneman, Ilana Ritov, and David Schkade, “Economic Preferences or Attitude Expressions?: An Analysis of Dollar Responses to Public Issues,” Journal of Risk and Uncertainty 19, nos. 1–3 (1999): 203–235, doi:10.1023/A:1007835629236.

103
The Halo Effect

The affect heuristic is how an overall feeling of goodness or badness contributes to many other judgments, whether it’s logical or not, whether you’re aware of it or not. Subjects told about the benefits of nuclear power are likely to rate it as having fewer risks; stock analysts rating unfamiliar stocks judge them as generally good or generally bad—low risk and high returns, or high risk and low returns—in defiance of ordinary economic theory, which says that risk and return should correlate positively.

The halo effect is the manifestation of the affect heuristic in social psychology. Robert Cialdini, in Influence: Science and Practice,¹ summarizes:

Research has shown that we automatically assign to good-looking individuals such favorable traits as talent, kindness, honesty, and intelligence (for a review of this evidence, see Eagly, Ashmore, Makhijani, and Longo, 1991).² Furthermore, we make these judgments without being aware that physical attractiveness plays a role in the process. Some consequences of this unconscious assumption that “good-looking equals good” scare me. For example, a study of the 1974 Canadian federal elections found that attractive candidates received more than two and a half times as many votes as unattractive candidates (Efran and Patterson, 1976).³ Despite such evidence of favoritism toward handsome politicians, follow-up research demonstrated that voters did not realize their bias. In fact, 73 percent of Canadian voters surveyed denied in the strongest possible terms that their votes had been influenced by physical appearance; only 14 percent even allowed for the possibility of such influence (Efran and Patterson, 1976).⁴ Voters can deny the impact of attractiveness on electability all they want, but evidence has continued to confirm its troubling presence (Budesheim and DePaola, 1994).⁵

A similar effect has been found in hiring situations. In one study, good grooming of applicants in a simulated employment interview accounted for more favorable hiring decisions than did job qualifications—this, even though the interviewers claimed that appearance played a small role in their choices (Mack and Rainey, 1990).⁶ The advantage given to attractive workers extends past hiring day to payday. Economists examining US and Canadian samples have found that attractive individuals get paid an average of 12–14 percent more than their unattractive coworkers (Hamermesh and Biddle, 1994).⁷

Equally unsettling research indicates that our judicial process is similarly susceptible to the influences of body dimensions and bone structure. It now appears that good-looking people are likely to receive highly favorable treatment in the legal system (see Castellow, Wuensch, and Moore, 1991; and Downs and Lyons, 1990, for reviews).⁸ For example, in a Pennsylvania study (Stewart, 1980),⁹ researchers rated the physical attractiveness of 74 separate male defendants at the start of their criminal trials. When, much later, the researchers checked court records for the results of these cases, they found that the handsome men had received significantly lighter sentences. In fact, attractive defendants were twice as likely to avoid jail as unattractive defendants. In another study—this one on the damages awarded in a staged negligence trial—a defendant who was better looking than his victim was assessed an average amount of $5,623; but when the victim was the more attractive of the two, the average compensation was $10,051. What’s more, both male and female jurors exhibited the attractiveness-based favoritism (Kulka and Kessler, 1978).¹⁰

Other experiments have demonstrated that attractive people are more likely to obtain help when in need (Benson, Karabenic, and Lerner, 1976)¹¹ and are more persuasive in changing the opinions of an audience (Chaiken, 1979) . . .¹²

The influence of attractiveness on ratings of intelligence, honesty, or kindness is a clear example of bias—especially when you judge these other qualities based on fixed text—because we wouldn’t expect judgments of honesty and attractiveness to conflate for any legitimate reason. On the other hand, how much of my perceived intelligence is due to my honesty? How much of my perceived honesty is due to my intelligence? Finding the truth, and saying the truth, are not as widely separated in nature as looking pretty and looking smart . . .

But these studies on the halo effect of attractiveness should make us suspicious that there may be a similar halo effect for kindness, or intelligence. Let’s say that you know someone who not only seems very intelligent, but also honest, altruistic, kindly, and serene. You should be suspicious that some of these perceived characteristics are influencing your perception of the others. Maybe the person is genuinely intelligent, honest, and altruistic, but not all that kindly or serene. You should be suspicious if the people you know seem to separate too cleanly into devils and angels.

And—I know you don’t think you have to do it, but maybe you should—be just a little more skeptical of the more attractive political candidates.

1. Robert B. Cialdini, Influence: Science and Practice (Boston: Allyn & Bacon, 2001).

2. Alice H. Eagly et al., “What Is Beautiful Is Good, But . . . A Meta-analytic Review of Research on the Physical Attractiveness Stereotype,” Psychological Bulletin 110 (1 1991): 109–128, doi:10.1037/0033-2909.110.1.109.

3. M. G. Efran and E. W. J. Patterson, “The Politics of Appearance” (Unpublished PhD thesis, 1976).

4. Ibid.

5. Thomas Lee Budesheim and Stephen DePaola, “Beauty or the Beast?: The Effects of Appearance, Personality, and Issue Information on Evaluations of Political Candidates,” Personality and Social Psychology Bulletin 20 (4 1994): 339–348, doi:10.1177/0146167294204001.

6. Denise Mack and David Rainey, “Female Applicants’ Grooming and Personnel Selection,” Journal of Social Behavior and Personality 5 (5 1990): 399–407.

7. Daniel S. Hamermesh and Jeff E. Biddle, “Beauty and the Labor Market,” The American Economic Review 84 (5 1994): 1174–1194.

8. Wilbur A. Castellow, Karl L. Wuensch, and Charles H. Moore, “Effects of Physical Attractiveness of the Plaintiff and Defendant in Sexual Harassment Judgments,” Journal of Social Behavior and Personality 5 (6 1990): 547–562; A. Chris Downs and Phillip M. Lyons, “Natural Observations of the Links Between Attractiveness and Initial Legal Judgments,” Personality and Social Psychology Bulletin 17 (5 1991): 541–547, doi:10.1177/0146167291175009.

9. John E. Stewart, “Defendants’ Attractiveness as a Factor in the Outcome of Trials: An Observational Study,” Journal of Applied Social Psychology 10 (4 1980): 348–361, doi:10.1111/j.1559-1816.1980.tb00715.x.

10. Richard A. Kulka and Joan B. Kessler, “Is Justice Really Blind?: The Effect of Litigant Physical Attractiveness on Judicial Judgment,” Journal of Applied Social Psychology 8 (4 1978): 366–381, doi:10.1111/j.1559-1816.1978.tb00790.x.

11. Peter L. Benson, Stuart A. Karabenick, and Richard M. Lerner, “Pretty Pleases: The Effects of Physical Attractiveness, Race, and Sex on Receiving Help,” Journal of Experimental Social Psychology 12 (5 1976): 409–415, doi:10.1016/0022-1031(76)90073-1.

12. Shelly Chaiken, “Communicator Physical Attractiveness and Persuasion,” Journal of Personality and Social Psychology 37 (8 1979): 1387–1397, doi:10.1037/0022-3514.37.8.1387.

104
Superhero Bias

Suppose there’s a heavily armed sociopath, a kidnapper with hostages, who has just rejected all requests for negotiation and announced his intent to start killing. In real life, the good guys don’t usually kick down the door when the bad guy has hostages. But sometimes—very rarely, but sometimes—life imitates Hollywood to the extent of genuine good guys needing to smash through a door.

Imagine, in two widely separated realities, two heroes who charge into the room, first to confront the villain.

In one reality, the hero is strong enough to throw cars, can fire power blasts out of his nostrils, has X-ray hearing, and his skin doesn’t just deflect bullets but annihilates them on contact. The villain has ensconced himself in an elementary school and taken over two hundred children hostage; their parents are waiting outside, weeping.

In another reality, the hero is a New York police officer, and the hostages are three prostitutes the villain collected off the street.

Consider this question very carefully: Who is the greater hero? And who is more likely to get their own comic book?

The halo effect is that perceptions of all positive traits are correlated. Profiles rated higher on scales of attractiveness are also rated higher on scales of talent, kindness, honesty, and intelligence.

And so comic-book characters who seem strong and invulnerable, both positive traits, also seem to possess more of the heroic traits of courage and heroism. And yet:

How tough can it be to act all brave and courageous when you’re pretty much invulnerable?

—Adam Warren, Empowered, Vol. 1¹

I can’t remember if I read the following point somewhere, or hypothesized it myself: Fame, in particular, seems to combine additively with all other personality characteristics. Consider Gandhi. Was Gandhi the most altruistic person of the twentieth century, or just the most famous altruist? Gandhi faced police with riot sticks and soldiers with guns. But Gandhi was a celebrity, and he was protected by his celebrity. What about the others in the march, the people who faced riot sticks and guns even though there wouldn’t be international headlines if they were put in the hospital or gunned down?

What did Gandhi think of getting the headlines, the celebrity, the fame, the place in history, becoming the archetype for nonviolent resistance, when he took less risk than any of the people marching with him? How did he feel when one of those anonymous heroes came up to him, eyes shining, and told Gandhi how wonderful he was? Did Gandhi ever visualize his world in those terms? I don’t know; I’m not Gandhi.

This is not in any sense a criticism of Gandhi. The point of nonviolent resistance is not to show off your courage. That can be done much more easily by going over Niagara Falls in a barrel. Gandhi couldn’t help being somewhat-but-not-entirely protected by his celebrity. And Gandhi’s actions did take courage—not as much courage as marching anonymously, but still a great deal of courage.

The bias I wish to point out is that Gandhi’s fame score seems to get perceptually added to his justly accumulated altruism score. When you think about nonviolence, you think of Gandhi—not an anonymous protestor in one of Gandhi’s marches who faced down riot clubs and guns, and got beaten, and had to be taken to the hospital, and walked with a limp for the rest of her life, and no one ever remembered her name.

Similarly, which is greater—to risk your life to save two hundred children, or to risk your life to save three adults?

The answer depends on what one means by greater. If you ever have to choose between saving two hundred children and saving three adults, then choose the former. “Whoever saves a single life, it is as if he had saved the whole world” may be a fine applause light, but it’s terrible moral advice if you’ve got to pick one or the other. So if you mean “greater” in the sense of “Which is more important?” or “Which is the preferred outcome?” or “Which should I choose if I have to do one or the other?” then it is greater to save two hundred than three.

But if you ask about greatness in the sense of revealed virtue, then someone who would risk their life to save only three lives reveals more courage than someone who would risk their life to save two hundred but not three.

This doesn’t mean that you can deliberately choose to risk your life to save three adults, and let the two hundred schoolchildren go hang, because you want to reveal more virtue. Someone who risks their life because they want to be virtuous has revealed far less virtue than someone who risks their life because they want to save others. Someone who chooses to save three lives rather than two hundred lives, because they think it reveals greater virtue, is so selfishly fascinated with their own “greatness” as to have committed the moral equivalent of manslaughter.

It’s one of those wu wei scenarios: You cannot reveal virtue by trying to reveal virtue. Given a choice between a safe method to save the world which involves no personal sacrifice or discomfort, and a method that risks your life and requires you to endure great privation, you cannot become a hero by deliberately choosing the second path. There is nothing heroic about wanting to look like a hero. It would be a lost purpose.

Truly virtuous people who are genuinely trying to save lives, rather than trying to reveal virtue, will constantly seek to save more lives with less effort, which means that less of their virtue will be revealed. It may be confusing, but it’s not contradictory.

But we cannot always choose to be invulnerable to bullets. After we’ve done our best to reduce risk and increase scope, any remaining heroism is well and truly revealed.

The police officer who puts their life on the line with no superpowers, no X-Ray vision, no super-strength, no ability to fly, and above all no invulnerability to bullets, reveals far greater virtue than Superman—who is a mere superhero.

1. Adam Warren, Empowered, vol. 1 (Dark Horse Books, 2007).

105
Mere Messiahs

I discussed how the halo effect, which causes people to see all positive characteristics as correlated—for example, more attractive individuals are also perceived as more kindly, honest, and intelligent—causes us to admire heroes more if they’re super-strong and immune to bullets. Even though, logically, it takes much more courage to be a hero if you’re not immune to bullets. Furthermore, it reveals more virtue to act courageously to save one life than to save the world. (Although if you have to do one or the other, of course you should save the world.)

But let’s be more specific.

John Perry was a New York City police officer who also happened to be an Extropian and transhumanist, which is how I come to know his name. John Perry was due to retire shortly and start his own law practice, when word came that a plane had slammed into the World Trade Center. He died when the north tower fell. I didn’t know John Perry personally, so I cannot attest to this of direct knowledge; but very few Extropians believe in God, and I expect that Perry was likewise an atheist.

Which is to say that Perry knew he was risking his very existence, every week on the job. And it’s not, like most people in history, that he knew he had only a choice of how to die, and chose to make it matter—because Perry was a transhumanist; he had genuine hope. And Perry went out there and put his life on the line anyway. Not because he expected any divine reward. Not because he expected to experience anything at all, if he died. But because there were other people in danger, and they didn’t have immortal souls either, and his hope of life was worth no more than theirs.

I did not know John Perry. I do not know if he saw the world this way. But the fact that an atheist and a transhumanist can still be a police officer, can still run into the lobby of a burning building, says more about the human spirit than all the martyrs who ever hoped of heaven.

So that is one specific police officer . . .

. . . and now for the superhero.

As the Christians tell the story, Jesus Christ could walk on water, calm storms, drive out demons with a word. It must have made for a comfortable life. Starvation a problem? Xerox some bread. Don’t like a tree? Curse it. Romans a problem? Sic your Dad on them. Eventually this charmed life ended, when Jesus voluntarily presented himself for crucifixion. Being nailed to a cross is not a comfortable way to die. But as the Christians tell the story, Jesus did this knowing he would come back to life three days later, and then go to Heaven. What was the threat that moved Jesus to face this temporary suffering followed by eternity in Heaven? Was it the life of a single person? Was it the corruption of the church of Judea, or the oppression of Rome? No: as the Christians tell the story, the eternal fate of every human went on the line before Jesus suffered himself to be temporarily nailed to a cross.

But I do not wish to condemn a man who is not truly so guilty. What if Jesus—no, let’s pronounce his name correctly: Yeishu—what if Yeishu of Nazareth never walked on water, and nonetheless defied the church of Judea established by the powers of Rome?

Would that not deserve greater honor than that which adheres to Jesus Christ, who was a mere messiah?

Alas, somehow it seems greater for a hero to have steel skin and godlike powers. Somehow it seems to reveal more virtue to die temporarily to save the whole world, than to die permanently confronting a corrupt church. It seems so common, as if many other people through history had done the same.

Comfortably ensconced two thousand years in the future, we can levy all sorts of criticisms at Yeishu, but Yeishu did what he believed to be right, confronted a church he believed to be corrupt, and died for it. Without benefit of hindsight, he could hardly be expected to predict the true impact of his life upon the world. Relative to most other prophets of his day, he was probably relatively more honest, relatively less violent, and relatively more courageous. If you strip away the unintended consequences, the worst that can be said of Yeishu is that others in history did better. (Epicurus, Buddha, and Marcus Aurelius all come to mind.) Yeishu died forever, and—from one perspective—he did it for the sake of honesty. Fifteen hundred years before science, religious honesty was not an oxymoron.

As Sam Harris said:¹

It is not enough that Jesus was a man who transformed himself to such a degree that the Sermon on the Mount could be his heart’s confession. He also had to be the Son of God, born of a virgin, and destined to return to earth trailing clouds of glory. The effect of such dogma is to place the example of Jesus forever out of reach. His teaching ceases to become a set of empirical claims about the linkage between ethics and spiritual insight and instead becomes a gratuitous, and rather gruesome, fairy tale. According to the dogma of Christianity, becoming just like Jesus is impossible. One can only enumerate one’s sins, believe the unbelievable, and await the end of the world.

I severely doubt that Yeishu ever spoke the Sermon on the Mount. Nonetheless, Yeishu deserves honor. He deserves more honor than the Christians would grant him.

But since Yeishu probably anticipated his soul would survive, he doesn’t deserve more honor than John Perry.

1. Sam Harris, The End of Faith: Religion, Terror, and the Future of Reason (WW Norton & Company, 2005).

106
Affective Death Spirals

Many, many, many are the flaws in human reasoning which lead us to overestimate how well our beloved theory explains the facts. The phlogiston theory of chemistry could explain just about anything, so long as it didn’t have to predict it in advance. And the more phenomena you use your favored theory to explain, the truer your favored theory seems—has it not been confirmed by these many observations? As the theory seems truer, you will be more likely to question evidence that conflicts with it. As the favored theory seems more general, you will seek to use it in more explanations.

If you know anyone who believes that Belgium secretly controls the US banking system, or that they can use an invisible blue spirit force to detect available parking spaces, that’s probably how they got started.

(Just keep an eye out, and you’ll observe much that seems to confirm this theory . . .)

This positive feedback cycle of credulity and confirmation is indeed fearsome, and responsible for much error, both in science and in everyday life.

But it’s nothing compared to the death spiral that begins with a charge of positive affect—a thought that feels really good.

A new political system that can save the world. A great leader, strong and noble and wise. An amazing tonic that can cure upset stomachs and cancer.

Heck, why not go for all three? A great cause needs a great leader. A great leader should be able to brew up a magical tonic or two.

The halo effect is that any perceived positive characteristic (such as attractiveness or strength) increases perception of any other positive characteristic (such as intelligence or courage). Even when it makes no sense, or less than no sense.

Positive characteristics enhance perception of every other positive characteristic? That sounds a lot like how a fissioning uranium atom sends out neutrons that fission other uranium atoms.

Weak positive affect is subcritical; it doesn’t spiral out of control. An attractive person seems more honest, which, perhaps, makes them seem more attractive; but the effective neutron multiplication factor is less than one. Metaphorically speaking. The resonance confuses things a little, but then dies out.

With intense positive affect attached to the Great Thingy, the resonance touches everywhere. A believing Communist sees the wisdom of Marx in every hamburger bought at McDonald’s; in every promotion they’re denied that would have gone to them in a true worker’s paradise; in every election that doesn’t go to their taste; in every newspaper article “slanted in the wrong direction.” Every time they use the Great Idea to interpret another event, the Great Idea is confirmed all the more. It feels better—positive reinforcement—and of course, when something feels good, that, alas, makes us want to believe it all the more.

When the Great Thingy feels good enough to make you seek out new opportunities to feel even better about the Great Thingy, applying it to interpret new events every day, the resonance of positive affect is like a chamber full of mousetraps loaded with ping-pong balls.

You could call it a “happy attractor,” “overly positive feedback,” a “praise locked loop,” or “funpaper.” Personally I prefer the term “affective death spiral.”

Coming up next: How to resist an affective death spiral. (Hint: It’s not by refusing to ever admire anything again, nor by keeping the things you admire in safe little restricted magisterium.)

107
Resist the Happy Death Spiral

Once upon a time, there was a man who was convinced that he possessed a Great Idea. Indeed, as the man thought upon the Great Idea more and more, he realized that it was not just a great idea, but the most wonderful idea ever. The Great Idea would unravel the mysteries of the universe, supersede the authority of the corrupt and error-ridden Establishment, confer nigh-magical powers upon its wielders, feed the hungry, heal the sick, make the whole world a better place, etc., etc., etc.

The man was Francis Bacon, his Great Idea was the scientific method, and he was the only crackpot in all history to claim that level of benefit to humanity and turn out to be completely right.

(Bacon didn’t singlehandedly invent science, of course, but he did contribute, and may have been the first to realize the power.)

That’s the problem with deciding that you’ll never admire anything that much: Some ideas really are that good. Though no one has fulfilled claims more audacious than Bacon’s; at least, not yet.

But then how can we resist the happy death spiral with respect to Science itself? The happy death spiral starts when you believe something is so wonderful that the halo effect leads you to find more and more nice things to say about it, making you see it as even more wonderful, and so on, spiraling up into the abyss. What if Science is in fact so beneficial that we cannot acknowledge its true glory and retain our sanity? Sounds like a nice thing to say, doesn’t it? Oh no it’s starting ruuunnnnn . . .

If you retrieve the standard cached deep wisdom for don’t go overboard on admiring science, you will find thoughts like “Science gave us air conditioning, but it also made the hydrogen bomb” or “Science can tell us about stars and biology, but it can never prove or disprove the dragon in my garage.” But the people who originated such thoughts were not trying to resist a happy death spiral. They weren’t worrying about their own admiration of science spinning out of control. Probably they didn’t like something science had to say about their pet beliefs, and sought ways to undermine its authority.

The standard negative things to say about science, aren’t likely to appeal to someone who genuinely feels the exultation of science—that’s not the intended audience. So we’ll have to search for other negative things to say instead.

But if you look selectively for something negative to say about science—even in an attempt to resist a happy death spiral—do you not automatically convict yourself of rationalization? Why would you pay attention to your own thoughts, if you knew you were trying to manipulate yourself?

I am generally skeptical of people who claim that one bias can be used to counteract another. It sounds to me like an automobile mechanic who says that the motor is broken on your right windshield wiper, but instead of fixing it, they’ll just break your left windshield wiper to balance things out. This is the sort of cleverness that leads to shooting yourself in the foot. Whatever the solution, it ought to involve believing true things, rather than believing you believe things that you believe are false.

Can you prevent the happy death spiral by restricting your admiration of Science to a narrow domain? Part of the happy death spiral is seeing the Great Idea everywhere—thinking about how Communism could cure cancer if it was only given a chance. Probably the single most reliable sign of a cult guru is that the guru claims expertise, not in one area, not even in a cluster of related areas, but in everything. The guru knows what cult members should eat, wear, do for a living; who they should have sex with; which art they should look at; which music they should listen to . . .

Unfortunately for this plan, most people fail miserably when they try to describe the neat little box that science has to stay inside. The usual trick, “Hey, science won’t cure cancer” isn’t going to fly. “Science has nothing to say about a parent’s love for their child”—sorry, that’s simply false. If you try to sever science from e.g. parental love, you aren’t just denying cognitive science and evolutionary psychology. You’re also denying Martine Rothblatt’s founding of United Therapeutics to seek a cure for her daughter’s pulmonary hypertension. (Successfully, I might add.) Science is legitimately related, one way or another, to just about every important facet of human existence.

All right, so what’s an example of a false nice claim you could make about science?

In my humble opinion, one false claim is that science is so wonderful that scientists shouldn’t even try to take ethical responsibility for their work, it will automatically end well. This claim, to me, seems to misunderstand the nature of the process whereby science benefits humanity. Scientists are human, they have prosocial concerns just like most other other people, and this is at least part of why science ends up doing more good than evil.

But that point is, evidently, not beyond dispute. So here’s a simpler false nice claim: “A cancer patient can be cured just by publishing enough journal papers.” Or, “Sociopaths could become fully normal, if they just committed themselves to never believing anything without replicated experimental evidence with p < 0.05.”

The way to avoid believing such statements isn’t an affective cap, deciding that science is only slightly nice. Nor searching for reasons to believe that publishing journal papers causes cancer. Nor believing that science has nothing to say about cancer one way or the other.

Rather, if you know with enough specificity how science works, then you know that, while it may be possible for “science to cure cancer,” a cancer patient writing journal papers isn’t going to experience a miraculous remission. That specific proposed chain of cause and effect is not going to work out.

The happy death spiral is only an emotional problem because of a perceptual problem, the halo effect, that makes us more likely to accept future positive claims once we’ve accepted an initial positive claim. We can’t get rid of this effect just by wishing; it will probably always influence us a little. But we can manage to slow down, stop, consider each additional nice claim as an additional burdensome detail, and focus on the specific points of the claim apart from its positiveness.

What if a specific nice claim “can’t be disproven” but there are arguments “both for and against” it? Actually these are words to be wary of in general, because often this is what people say when they’re rehearsing the evidence or avoiding the real weak points. Given the danger of the happy death spiral, it makes sense to try to avoid being happy about unsettled claims—to avoid making them into a source of yet more positive affect about something you liked already.

The happy death spiral is only a big emotional problem because of the overly positive feedback, the ability for the process to go critical. You may not be able to eliminate the halo effect entirely, but you can apply enough critical reasoning to keep the halos subcritical—make sure that the resonance dies out rather than exploding.

You might even say that the whole problem starts with people not bothering to critically examine every additional burdensome detail—demanding sufficient evidence to compensate for complexity, searching for flaws as well as support, invoking curiosity—once they’ve accepted some core premise. Without the conjunction fallacy, there might still be a halo effect, but there wouldn’t be a happy death spiral.

Even on the nicest Nice Thingies in the known universe, a perfect rationalist who demanded exactly the necessary evidence for every additional (positive) claim would experience no affective resonance. You can’t do this, but you can stay close enough to rational to keep your happiness from spiraling out of control.

The really dangerous cases are the ones where any criticism of any positive claim about the Great Thingy feels bad or is socially unacceptable. Arguments are soldiers, any positive claim is a soldier on our side, stabbing your soldiers in the back is treason. Then the chain reaction goes supercritical. More on this later.

Stuart Armstrong gives closely related advice:

Cut up your Great Thingy into smaller independent ideas, and treat them as independent.

For instance a marxist would cut up Marx’s Great Thingy into a theory of value of labour, a theory of the political relations between classes, a theory of wages, a theory on the ultimate political state of mankind. Then each of them should be assessed independently, and the truth or falsity of one should not halo on the others. If we can do that, we should be safe from the spiral, as each theory is too narrow to start a spiral on its own.

This, metaphorically, is like keeping subcritical masses of plutonium from coming together. Three Great Ideas are far less likely to drive you mad than one Great Idea. Armstrong’s advice also helps promote specificity: As soon as someone says, “Publishing enough papers can cure your cancer,” you ask, “Is that a benefit of the experimental method, and if so, at which stage of the experimental process is the cancer cured? Or is it a benefit of science as a social process, and if so, does it rely on individual scientists wanting to cure cancer, or can they be self-interested?” Hopefully this leads you away from the good or bad feeling, and toward noticing the confusion and lack of support.

To summarize, you do avoid a Happy Death Spiral by:

Splitting the Great Idea into parts;
Treating every additional detail as burdensome;
Thinking about the specifics of the causal chain instead of the good or bad feelings;
Not rehearsing evidence; and
Not adding happiness from claims that “you can’t prove are wrong”;

but not by:

Refusing to admire anything too much;
Conducting a biased search for negative points until you feel unhappy again; or
Forcibly shoving an idea into a safe box.

108
Uncritical Supercriticality

Every now and then, you see people arguing over whether atheism is a “religion.” As I touch on elsewhere, in Purpose and Pragmatism, arguing over the meaning of a word nearly always means that you’ve lost track of the original question. How might this argument arise to begin with?

An atheist is holding forth, blaming “religion” for the Inquisition, the Crusades, and various conflicts with or within Islam. The religious one may reply, “But atheism is also a religion, because you also have beliefs about God; you believe God doesn’t exist.” Then the atheist answers, “If atheism is a religion, then not collecting stamps is a hobby,” and the argument begins.

Or the one may reply, “But horrors just as great were inflicted by Stalin, who was an atheist, and who suppressed churches in the name of atheism; therefore you are wrong to blame the violence on religion.” Now the atheist may be tempted to reply “No true Scotsman,” saying, “Stalin’s religion was Communism.” The religious one answers “If Communism is a religion, then Star Wars fandom is a government,” and the argument begins.

Should a “religious” person be defined as someone who has a definite opinion about the existence of at least one God, e.g., assigning a probability lower than 10% or higher than 90% to the existence of Zeus? Or should a “religious” person be defined as someone who has a positive opinion, say a probability higher than 90%, for the existence of at least one God? In the former case, Stalin was “religious”; in the latter case, Stalin was “not religious.”

But this is exactly the wrong way to look at the problem. What you really want to know—what the argument was originally about—is why, at certain points in human history, large groups of people were slaughtered and tortured, ostensibly in the name of an idea. Redefining a word won’t change the facts of history one way or the other.

Communism was a complex catastrophe, and there may be no single why, no single critical link in the chain of causality. But if I had to suggest an ur-mistake, it would be . . . well, I’ll let God say it for me:

If your brother, the son of your father or of your mother, or your son or daughter, or the spouse whom you embrace, or your most intimate friend, tries to secretly seduce you, saying, “Let us go and serve other gods,” unknown to you or your ancestors before you, gods of the peoples surrounding you, whether near you or far away, anywhere throughout the world, you must not consent, you must not listen to him; you must show him no pity, you must not spare him or conceal his guilt. No, you must kill him, your hand must strike the first blow in putting him to death and the hands of the rest of the people following. You must stone him to death, since he has tried to divert you from Yahweh your God.

—Deuteronomy 13:7–11, emphasis added

This was likewise the rule which Stalin set for Communism, and Hitler for Nazism: if your brother tries to tell you why Marx is wrong, if your son tries to tell you the Jews are not planning world conquest, then do not debate him or set forth your own evidence; do not perform replicable experiments or examine history; but turn him in at once to the secret police.

I suggested that one key to resisting an affective death spiral is the principle of “burdensome details”—just remembering to question the specific details of each additional nice claim about the Great Idea. (It’s not trivial advice. People often don’t remember to do this when they’re listening to a futurist sketching amazingly detailed projections about the wonders of tomorrow, let alone when they’re thinking about their favorite idea ever.) This wouldn’t get rid of the halo effect, but it would hopefully reduce the resonance to below criticality, so that one nice-sounding claim triggers less than 1.0 additional nice-sounding claims, on average.

The diametric opposite of this advice, which sends the halo effect supercritical, is when it feels wrong to argue against any positive claim about the Great Idea. Politics is the mind-killer. Arguments are soldiers. Once you know which side you’re on, you must support all favorable claims, and argue against all unfavorable claims. Otherwise it’s like giving aid and comfort to the enemy, or stabbing your friends in the back.

If . . .

. . . you feel that contradicting someone else who makes a flawed nice claim in favor of evolution would be giving aid and comfort to the creationists;
. . . you feel like you get spiritual credit for each nice thing you say about God, and arguing about it would interfere with your relationship with God;
. . . you have the distinct sense that the other people in the room will dislike you for “not supporting our troops” if you argue against the latest war;
. . . saying anything against Communism gets you stoned to death shot;

. . . then the affective death spiral has gone supercritical. It is now a Super Happy Death Spiral.

It’s not religion, as such, that is the key categorization, relative to our original question: “What makes the slaughter?” The best distinction I’ve heard between “supernatural” and “naturalistic” worldviews is that a supernatural worldview asserts the existence of ontologically basic mental substances, like spirits, while a naturalistic worldview reduces mental phenomena to nonmental parts. Focusing on this as the source of the problem buys into religious exceptionalism. Supernaturalist claims are worth distinguishing, because they always turn out to be wrong for fairly fundamental reasons. But it’s still just one kind of mistake.

An affective death spiral can nucleate around supernatural beliefs; especially monotheisms whose pinnacle is a Super Happy Agent, defined primarily by agreeing with any nice statement about it; especially meme complexes grown sophisticated enough to assert supernatural punishments for disbelief. But the death spiral can also start around a political innovation, a charismatic leader, belief in racial destiny, or an economic hypothesis. The lesson of history is that affective death spirals are dangerous whether or not they happen to involve supernaturalism. Religion isn’t special enough, as a class of mistake, to be the key problem.

Sam Harris came closer when he put the accusing finger on faith. If you don’t place an appropriate burden of proof on each and every additional nice claim, the affective resonance gets started very easily. Look at the poor New Agers. Christianity developed defenses against criticism, arguing for the wonders of faith; New Agers culturally inherit the cached thought that faith is positive, but lack Christianity’s exclusionary scripture to keep out competing memes. New Agers end up in happy death spirals around stars, trees, magnets, diets, spells, unicorns . . .

But the affective death spiral turns much deadlier after criticism becomes a sin, or a gaffe, or a crime. There are things in this world that are worth praising greatly, and you can’t flatly say that praise beyond a certain point is forbidden. But there is never an Idea so true that it’s wrong to criticize any argument that supports it. Never. Never ever never for ever. That is flat. The vast majority of possible beliefs in a nontrivial answer space are false, and likewise, the vast majority of possible supporting arguments for a true belief are also false, and not even the happiest idea can change that.

And it is triple ultra forbidden to respond to criticism with violence. There are a very few injunctions in the human art of rationality that have no ifs, ands, buts, or escape clauses. This is one of them. Bad argument gets counterargument. Does not get bullet. Never. Never ever never for ever.

109
Evaporative Cooling of Group Beliefs

Early studiers of cults were surprised to discover than when cults receive a major shock—a prophecy fails to come true, a moral flaw of the founder is revealed—they often come back stronger than before, with increased belief and fanaticism. The Jehovah’s Witnesses placed Armageddon in 1975, based on Biblical calculations; 1975 has come and passed. The Unarian cult, still going strong today, survived the nonappearance of an intergalactic spacefleet on September 27, 1975.

Why would a group belief become stronger after encountering crushing counterevidence?

The conventional interpretation of this phenomenon is based on cognitive dissonance. When people have taken “irrevocable” actions in the service of a belief—given away all their property in anticipation of the saucers landing—they cannot possibly admit they were mistaken. The challenge to their belief presents an immense cognitive dissonance; they must find reinforcing thoughts to counter the shock, and so become more fanatical. In this interpretation, the increased group fanaticism is the result of increased individual fanaticism.

I was looking at a Java applet which demonstrates the use of evaporative cooling to form a Bose-Einstein condensate, when it occurred to me that another force entirely might operate to increase fanaticism. Evaporative cooling sets up a potential energy barrier around a collection of hot atoms. Thermal energy is essentially statistical in nature—not all atoms are moving at the exact same speed. The kinetic energy of any given atom varies as the atoms collide with each other. If you set up a potential energy barrier that’s just a little higher than the average thermal energy, the workings of chance will give an occasional atom a kinetic energy high enough to escape the trap. When an unusually fast atom escapes, it takes with it an unusually large amount of kinetic energy, and the average energy decreases. The group becomes substantially cooler than the potential energy barrier around it. Playing with the Java applet may make this clearer.

In Festinger, Riecken, and Schachter’s classic When Prophecy Fails, one of the cult members walked out the door immediately after the flying saucer failed to land.¹ Who gets fed up and leaves first? An average cult member? Or a relatively more skeptical member, who previously might have been acting as a voice of moderation, a brake on the more fanatic members?

After the members with the highest kinetic energy escape, the remaining discussions will be between the extreme fanatics on one end and the slightly less extreme fanatics on the other end, with the group consensus somewhere in the “middle.”

And what would be the analogy to collapsing to form a Bose-Einstein condensate? Well, there’s no real need to stretch the analogy that far. But you may recall that I used a fission chain reaction analogy for the affective death spiral; when a group ejects all its voices of moderation, then all the people encouraging each other, and suppressing dissents, may internally increase in average fanaticism. (No thermodynamic analogy here, unless someone develops a nuclear weapon that explodes when it gets cold.)

When Ayn Rand’s long-running affair with Nathaniel Branden was revealed to the Objectivist membership, a substantial fraction of the Objectivist membership broke off and followed Branden into espousing an “open system” of Objectivism not bound so tightly to Ayn Rand. Who stayed with Ayn Rand even after the scandal broke? The ones who really, really believed in her—and perhaps some of the undecideds, who, after the voices of moderation left, heard arguments from only one side. This may account for how the Ayn Rand Institute is (reportedly) more fanatic after the breakup, than the original core group of Objectivists under Branden and Rand.

A few years back, I was on a transhumanist mailing list where a small group espousing “social democratic transhumanism” vitriolically insulted every libertarian on the list. Most libertarians left the mailing list, most of the others gave up on posting. As a result, the remaining group shifted substantially to the left. Was this deliberate? Probably not, because I don’t think the perpetrators knew that much psychology. (For that matter, I can’t recall seeing the evaporative cooling analogy elsewhere, though that doesn’t mean it hasn’t been noted before.) At most, they might have thought to make themselves “bigger fish in a smaller pond.”

This is one reason why it’s important to be prejudiced in favor of tolerating dissent. Wait until substantially after it seems to you justified in ejecting a member from the group, before actually ejecting. If you get rid of the old outliers, the group position will shift, and someone else will become the oddball. If you eject them too, you’re well on the way to becoming a Bose-Einstein condensate and, er, exploding.

The flip side: Thomas Kuhn believed that a science has to become a “paradigm,” with a shared technical language that excludes outsiders, before it can get any real work done. In the formative stages of a science, according to Kuhn, the adherents go to great pains to make their work comprehensible to outside academics. But (according to Kuhn) a science can only make real progress as a technical discipline once it abandons the requirement of outside accessibility, and scientists working in the paradigm assume familiarity with large cores of technical material in their communications. This sounds cynical, relative to what is usually said about public understanding of science, but I can definitely see a core of truth here.

My own theory of Internet moderation is that you have to be willing to exclude trolls and spam to get a conversation going. You must even be willing to exclude kindly but technically uninformed folks from technical mailing lists if you want to get any work done. A genuinely open conversation on the Internet degenerates fast. It’s the articulate trolls that you should be wary of ejecting, on this theory—they serve the hidden function of legitimizing less extreme disagreements. But you should not have so many articulate trolls that they begin arguing with each other, or begin to dominate conversations. If you have one person around who is the famous Guy Who Disagrees With Everything, anyone with a more reasonable, more moderate disagreement won’t look like the sole nail sticking out. This theory of Internet moderation may not have served me too well in practice, so take it with a grain of salt.

1. Leon Festinger, Henry W. Riecken, and Stanley Schachter, When Prophecy Fails: A Social and Psychological Study of a Modern Group That Predicted the Destruction of the World (Harper-Torchbooks, 1956).

110
When None Dare Urge Restraint

One morning, I got out of bed, turned on my computer, and my Netscape email client automatically downloaded that day’s news pane. On that particular day, the news was that two hijacked planes had been flown into the World Trade Center.

These were my first three thoughts, in order:

I guess I really am living in the Future.

Thank goodness it wasn’t nuclear.

and then

The overreaction to this will be ten times worse than the original event.

A mere factor of “ten times worse” turned out to be a vast understatement. Even I didn’t guess how badly things would go. That’s the challenge of pessimism; it’s really hard to aim low enough that you’re pleasantly surprised around as often and as much as you’re unpleasantly surprised.

Nonetheless, I did realize immediately that everyone everywhere would be saying how awful, how terrible this event was; and that no one would dare to be the voice of restraint, of proportionate response. Initially, on 9/11, it was thought that six thousand people had died. Any politician who’d said “6,000 deaths is 1/8 the annual US casualties from automobile accidents,” would have been asked to resign the same hour.

No, 9/11 wasn’t a good day. But if everyone gets brownie points for emphasizing how much it hurts, and no one dares urge restraint in how hard to hit back, then the reaction will be greater than the appropriate level, whatever the appropriate level may be.

This is the even darker mirror of the happy death spiral—the spiral of hate. Anyone who attacks the Enemy is a patriot; and whoever tries to dissect even a single negative claim about the Enemy is a traitor. But just as the vast majority of all complex statements are untrue, the vast majority of negative things you can say about anyone, even the worst person in the world, are untrue.

I think the best illustration was “the suicide hijackers were cowards.” Some common sense, please? It takes a little courage to voluntarily fly your plane into a building. Of all their sins, cowardice was not on the list. But I guess anything bad you say about a terrorist, no matter how silly, must be true. Would I get even more brownie points if I accused al-Qaeda of having assassinated John F. Kennedy? Maybe if I accused them of being Stalinists? Really, cowardice?

Yes, it matters that the 9/11 hijackers weren’t cowards. Not just for understanding the enemy’s realistic psychology. There is simply too much damage done by spirals of hate. It is just too dangerous for there to be any target in the world, whether it be the Jews or Adolf Hitler, about whom saying negative things trumps saying accurate things.

When the defense force contains thousands of aircraft and hundreds of thousands of heavily armed soldiers, one ought to consider that the immune system itself is capable of wreaking more damage than nineteen guys and four nonmilitary airplanes. The US spent billions of dollars and thousands of soldiers’ lives shooting off its own foot more effectively than any terrorist group could dream.

If the USA had completely ignored the 9/11 attack—just shrugged and rebuilt the building—it would have been better than the real course of history. But that wasn’t a political option. Even if anyone privately guessed that the immune response would be more damaging than the disease, American politicians had no career-preserving choice but to walk straight into al-Qaeda’s trap. Whoever argues for a greater response is a patriot. Whoever dissects a patriotic claim is a traitor.

Initially, there were smarter responses to 9/11 than I had guessed. I saw a Congressperson—I forget who—say in front of the cameras, “We have forgotten that the first purpose of government is not the economy, it is not health care, it is defending the country from attack.” That widened my eyes, that a politician could say something that wasn’t an applause light. The emotional shock must have been very great for a Congressperson to say something that . . . real.

But within two days, the genuine shock faded, and concern-for-image regained total control of the political discourse. Then the spiral of escalation took over completely. Once restraint becomes unspeakable, no matter where the discourse starts out, the level of fury and folly can only rise with time.

111
The Robbers Cave Experiment

Did you ever wonder, when you were a kid, whether your inane “summer camp” actually had some kind of elaborate hidden purpose—say, it was all a science experiment and the “camp counselors” were really researchers observing your behavior?

Me neither.

But we’d have been more paranoid if we’d read “Intergroup Conflict and Cooperation: The Robbers Cave Experiment” by Sherif, Harvey, White, Hood, and Sherif.¹ In this study, the experimental subjects—excuse me, “campers”—were 22 boys between fifth and sixth grade, selected from 22 different schools in Oklahoma City, of stable middle-class Protestant families, doing well in school, median IQ 112. They were as well-adjusted and as similar to each other as the researchers could manage.

The experiment, conducted in the bewildered aftermath of World War II, was meant to investigate the causes—and possible remedies—of intergroup conflict. How would they spark an intergroup conflict to investigate? Well, the 22 boys were divided into two groups of 11 campers, and—

—and that turned out to be quite sufficient.

The researchers’ original plans called for the experiment to be conducted in three stages. In Stage 1, each group of campers would settle in, unaware of the other group’s existence. Toward the end of Stage 1, the groups would gradually be made aware of each other. In Stage 2, a set of contests and prize competitions would set the two groups at odds.

They needn’t have bothered with Stage 2. There was hostility almost from the moment each group became aware of the other group’s existence: They were using our campground, our baseball diamond. On their first meeting, the two groups began hurling insults. They named themselves the Rattlers and the Eagles (they hadn’t needed names when they were the only group on the campground).

When the contests and prizes were announced, in accordance with pre-established experimental procedure, the intergroup rivalry rose to a fever pitch. Good sportsmanship in the contests was evident for the first two days but rapidly disintegrated.

The Eagles stole the Rattlers’ flag and burned it. Rattlers raided the Eagles’ cabin and stole the blue jeans of the group leader, which they painted orange and carried as a flag the next day, inscribed with the legend “The Last of the Eagles.” The Eagles launched a retaliatory raid on the Rattlers, turning over beds, scattering dirt. Then they returned to their cabin where they entrenched and prepared weapons (socks filled with rocks) in case of a return raid. After the Eagles won the last contest planned for Stage 2, the Rattlers raided their cabin and stole the prizes. This developed into a fistfight that the staff had to shut down for fear of injury. The Eagles, retelling the tale among themselves, turned the whole affair into a magnificent victory—they’d chased the Rattlers “over halfway back to their cabin” (they hadn’t).

Each group developed a negative stereotype of Them and a contrasting positive stereotype of Us. The Rattlers swore heavily. The Eagles, after winning one game, concluded that the Eagles had won because of their prayers and the Rattlers had lost because they used cuss-words all the time. The Eagles decided to stop using cuss-words themselves. They also concluded that since the Rattlers swore all the time, it would be wiser not to talk to them. The Eagles developed an image of themselves as proper-and-moral; the Rattlers developed an image of themselves as rough-and-tough.

Group members held their noses when members of the other group passed.

In Stage 3, the researchers tried to reduce friction between the two groups.

Mere contact (being present without contesting) did not reduce friction between the two groups. Attending pleasant events together—for example, shooting off Fourth of July fireworks—did not reduce friction; instead it developed into a food fight.

Would you care to guess what did work?

(Spoiler space . . .)

The boys were informed that there might be a water shortage in the whole camp, due to mysterious trouble with the water system—possibly due to vandals. (The Outside Enemy, one of the oldest tricks in the book.)

The area between the camp and the reservoir would have to be inspected by four search details. (Initially, these search details were composed uniformly of members from each group.) All details would meet up at the water tank if nothing was found. As nothing was found, the groups met at the water tank and observed for themselves that no water was coming from the faucet. The two groups of boys discussed where the problem might lie, pounded the sides of the water tank, discovered a ladder to the top, verified that the water tank was full, and finally found the sack stuffed in the water faucet. All the boys gathered around the faucet to clear it. Suggestions from members of both groups were thrown at the problem and boys from both sides tried to implement them.

When the faucet was finally cleared, the Rattlers, who had canteens, did not object to the Eagles taking a first turn at the faucets (the Eagles didn’t have canteens with them). No insults were hurled, not even the customary “Ladies first.”

It wasn’t the end of the rivalry. There was another food fight, with insults, the next morning. But a few more common tasks, requiring cooperation from both groups—e.g. restarting a stalled truck—did the job. At the end of the trip, the Rattlers used $5 won in a bean-toss contest to buy malts for all the boys in both groups.

The Robbers Cave Experiment illustrates the psychology of hunter-gatherer bands, echoed through time, as perfectly as any experiment ever devised by social science.

Any resemblance to modern politics is just your imagination.

(Sometimes I think humanity’s second-greatest need is a supervillain. Maybe I’ll go into that line of work after I finish my current job.)

1. Muzafer Sherif et al., “Study of Positive and Negative Intergroup Attitudes Between Experimentally Produced Groups: Robbers Cave Study,” Unpublished manuscript (1954).

112
Every Cause Wants to Be a Cult

Cade Metz at The Register recently alleged that a secret mailing list of Wikipedia’s top administrators has become obsessed with banning all critics and possible critics of Wikipedia. Including banning a productive user when one administrator—solely because of the productivity—became convinced that the user was a spy sent by Wikipedia Review. And that the top people at Wikipedia closed ranks to defend their own. (I have not investigated these allegations myself, as yet. Hat tip to Eugen Leitl.)

Is there some deep moral flaw in seeking to systematize the world’s knowledge, which would lead pursuers of that Cause into madness? Perhaps only people with innately totalitarian tendencies would try to become the world’s authority on everything—

Correspondence bias alert! (Correspondence bias: making inferences about someone’s unique disposition from behavior that can be entirely explained by the situation in which it occurs. When we see someone else kick a vending machine, we think they are “an angry person,” but when we kick the vending machine, it’s because the bus was late, the train was early, and the machine ate our money.) If the allegations about Wikipedia are true, they’re explained by ordinary human nature, not by extraordinary human nature.

The ingroup-outgroup dichotomy is part of ordinary human nature. So are happy death spirals and spirals of hate. A Noble Cause doesn’t need a deep hidden flaw for its adherents to form a cultish ingroup. It is sufficient that the adherents be human. Everything else follows naturally, decay by default, like food spoiling in a refrigerator after the electricity goes off.

In the same sense that every thermal differential wants to equalize itself, and every computer program wants to become a collection of ad-hoc patches, every Cause wants to be a cult. It’s a high-entropy state into which the system trends, an attractor in human psychology. It may have nothing to do with whether the Cause is truly Noble. You might think that a Good Cause would rub off its goodness on every aspect of the people associated with it—that the Cause’s followers would also be less susceptible to status games, ingroup-outgroup bias, affective spirals, leader-gods. But believing one true idea won’t switch off the halo effect. A noble cause won’t make its adherents something other than human. There are plenty of bad ideas that can do plenty of damage—but that’s not necessarily what’s going on.

Every group of people with an unusual goal—good, bad, or silly—will trend toward the cult attractor unless they make a constant effort to resist it. You can keep your house cooler than the outdoors, but you have to run the air conditioner constantly, and as soon as you turn off the electricity—give up the fight against entropy—things will go back to “normal.”

On one notable occasion there was a group that went semicultish whose rallying cry was “Rationality! Reason! Objective reality!” (More on this later.) Labeling the Great Idea “rationality” won’t protect you any more than putting up a sign over your house that says “Cold!” You still have to run the air conditioner—expend the required energy per unit time to reverse the natural slide into cultishness. Worshipping rationality won’t make you sane any more than worshipping gravity enables you to fly. You can’t talk to thermodynamics and you can’t pray to probability theory. You can use it, but not join it as an ingroup.

Cultishness is quantitative, not qualitative. The question is not “Cultish, yes or no?” but “How much cultishness and where?” Even in Science, which is the archetypal Genuinely Truly Noble Cause, we can readily point to the current frontiers of the war against cult-entropy, where the current battle line creeps forward and back. Are journals more likely to accept articles with a well-known authorial byline, or from an unknown author from a well-known institution, compared to an unknown author from an unknown institution? How much belief is due to authority and how much is from the experiment? Which journals are using blinded reviewers, and how effective is blinded reviewing?

I cite this example, rather than the standard vague accusations of “Scientists aren’t open to new ideas,” because it shows a battle line—a place where human psychology is being actively driven back, where accumulated cult-entropy is being pumped out. (Of course this requires emitting some waste heat.)

This essay is not a catalog of techniques for actively pumping against cultishness. Some such techniques I have said before, and some I will say later. Here I just want to point out that the worthiness of the Cause does not mean you can spend any less effort in resisting the cult attractor. And that if you can point to current battle lines, it does not mean you confess your Noble Cause unworthy. You might think that if the question were “Cultish, yes or no?” that you were obliged to answer “No,” or else betray your beloved Cause. But that is like thinking that you should divide engines into “perfectly efficient” and “inefficient,” instead of measuring waste.

Contrariwise, if you believe that it was the Inherent Impurity of those Foolish Other Causes that made them go wrong, if you laugh at the folly of “cult victims,” if you think that cults are led and populated by mutants, then you will not expend the necessary effort to pump against entropy—to resist being human.

113
Guardians of the Truth

The criticism is sometimes leveled against rationalists: “The Inquisition thought they had the truth! Clearly this ‘truth’ business is dangerous.”

There are many obvious responses, such as “If you think that possessing the truth would license you to torture and kill, you’re making a mistake that has nothing to do with epistemology.” Or, “So that historical statement you just made about the Inquisition—is it true?”

Reversed stupidity is not intelligence: “If your current computer stops working, you can’t conclude that everything about the current system is wrong and that you need a new system without an AMD processor, an ATI video card . . . even though your current system has all these things and it doesn’t work. Maybe you just need a new power cord.” To arrive at a poor conclusion requires only one wrong step, not every step wrong. The Inquisitors believed that 2 + 2 = 4, but that wasn’t the source of their madness. Maybe epistemological realism wasn’t the problem either?

It does seem plausible that if the Inquisition had been made up of relativists, professing that nothing was true and nothing mattered, they would have mustered less enthusiasm for their torture. They would also have been less enthusiastic if lobotomized. I think that’s a fair analogy.

And yet . . . I think the Inquisition’s attitude toward truth played a role. The Inquisition believed that there was such a thing as truth, and that it was important; well, likewise Richard Feynman. But the Inquisitors were not Truth-Seekers. They were Truth-Guardians.

I once read an argument (I can’t find the source) that a key component of a zeitgeist is whether it locates its ideals in its future or its past. Nearly all cultures before the Enlightenment believed in a Fall from Grace—that things had once been perfect in the distant past, but then catastrophe had struck, and everything had slowly run downhill since then:

In the age when life on Earth was full . . . They loved each other and did not know that this was “love of neighbor.” They deceived no one yet they did not know that they were “men to be trusted.” They were reliable and did not know that this was “good faith.” They lived freely together giving and taking, and did not know that they were generous. For this reason their deeds have not been narrated. They made no history.

—The Way of Chuang Tzu, trans. Thomas Merton¹

The perfect age of the past, according to our best anthropological evidence, never existed. But a culture that sees life running inexorably downward is very different from a culture in which you can reach unprecedented heights.

(I say “culture,” and not “society,” because you can have more than one subculture in a society.)

You could say that the difference between e.g. Richard Feynman and the Inquisition was that the Inquisition believed they had truth, while Richard Feynman sought truth. This isn’t quite defensible, though, because there were undoubtedly some truths that Richard Feynman thought he had as well. “The sky is blue,” for example, or “2 + 2 = 4.”

Yes, there are effectively certain truths of science. General Relativity may be overturned by some future physics—albeit not in any way that predicts the Sun will orbit Jupiter; the new theory must steal the successful predictions of the old theory, not contradict them. But evolutionary theory takes place on a higher level of organization than atoms, and nothing we discover about quarks is going to throw out Darwinism, or the cell theory of biology, or the atomic theory of chemistry, or a hundred other brilliant innovations whose truth is now established beyond reasonable doubt.

Are these “absolute truths”? Not in the sense of possessing a probability of literally 1.0. But they are cases where science basically thinks it’s got the truth.

And yet scientists don’t torture people who question the atomic theory of chemistry. Why not? Because they don’t believe that certainty licenses torture? Well, yes, that’s the surface difference; but why don’t scientists believe this?

Because chemistry asserts no supernatural penalty of eternal torture for disbelieving in the atomic theory of chemistry? But again we recurse and ask the question, “Why?” Why don’t chemists believe that you go to hell if you disbelieve in the atomic theory?

Because journals won’t publish your paper until you get a solid experimental observation of Hell? But all too many scientists can suppress their skeptical reflex at will. Why don’t chemists have a private cult which argues that nonchemists go to hell, given that many are Christians anyway?

Questions like that don’t have neat single-factor answers. But I would argue that one of the factors has to do with assuming a productive posture toward the truth, versus a defensive posture toward the truth.

When you are the Guardian of the Truth, you’ve got nothing useful to contribute to the Truth but your guardianship of it. When you’re trying to win the Nobel Prize in chemistry by discovering the next benzene or buckyball, someone who challenges the atomic theory isn’t so much a threat to your worldview as a waste of your time.

When you are a Guardian of the Truth, all you can do is try to stave off the inevitable slide into entropy by zapping anything that departs from the Truth. If there’s some way to pump against entropy, generate new true beliefs along with a little waste heat, that same pump can keep the truth alive without secret police. In chemistry you can replicate experiments and see for yourself—and that keeps the precious truth alive without need of violence.

And it’s not such a terrible threat if we make one mistake somewhere—end up believing a little untruth for a little while—because tomorrow we can recover the lost ground.

But this whole trick only works because the experimental method is a “criterion of goodness” which is not a mere “criterion of comparison.” Because experiments can recover the truth without need of authority, they can also override authority and create new true beliefs where none existed before.

Where there are criteria of goodness that are not criteria of comparison, there can exist changes which are improvements, rather than threats. Where there are only criteria of comparison, where there’s no way to move past authority, there’s also no way to resolve a disagreement between authorities. Except extermination. The bigger guns win.

I don’t mean to provide a grand overarching single-factor view of history. I do mean to point out a deep psychological difference between seeing your grand cause in life as protecting, guarding, preserving, versus discovering, creating, improving. Does the “up” direction of time point to the past or the future? It’s a distinction that shades everything, casts tendrils everywhere.

This is why I’ve always insisted, for example, that if you’re going to start talking about “AI ethics,” you had better be talking about how you are going to improve on the current situation using AI, rather than just keeping various things from going wrong. Once you adopt criteria of mere comparison, you start losing track of your ideals—lose sight of wrong and right, and start seeing simply “different” and “same.”

I would also argue that this basic psychological difference is one of the reasons why an academic field that stops making active progress tends to turn mean. (At least by the refined standards of science. Reputational assassination is tame by historical standards; most defensive-posture belief systems went for the real thing.) If major shakeups don’t arrive often enough to regularly promote young scientists based on merit rather than conformity, the field stops resisting the standard degeneration into authority. When there’s not many discoveries being made, there’s nothing left to do all day but witch-hunt the heretics.

To get the best mental health benefits of the discover/create/improve posture, you’ve got to actually be making progress, not just hoping for it.

1. Zhuangzi and Thomas Merton, The Way of Chuang Tzu (New Directions Publishing, 1965).

114
Guardians of the Gene Pool

Like any educated denizen of the twenty-first century, you may have heard of World War II. You may remember that Hitler and the Nazis planned to carry forward a romanticized process of evolution, to breed a new master race, supermen, stronger and smarter than anything that had existed before.

Actually this is a common misconception. Hitler believed that the Aryan superman had previously existed—the Nordic stereotype, the blond blue-eyed beast of prey—but had been polluted by mingling with impure races. There had been a racial Fall from Grace.

It says something about the degree to which the concept of progress permeates Western civilization, that the one is told about Nazi eugenics and hears “They tried to breed a superhuman.” You, dear reader—if you failed so hard that you endorsed coercive eugenics, you would try to create a superhuman. Because you locate your ideals in your future, not in your past. Because you are creative. The thought of breeding back to some Nordic archetype from a thousand years earlier would not even occur to you as a possibility—what, just the Vikings? That’s all? If you failed hard enough to kill, you would damn well try to reach heights never before reached, or what a waste it would all be, eh? Well, that’s one reason you’re not a Nazi, dear reader.

It says something about how difficult it is for the relatively healthy to envision themselves in the shoes of the relatively sick, that we are told of the Nazis, and distort the tale to make them defective transhumanists.

It’s the Communists who were the defective transhumanists. “New Soviet Man” and all that. The Nazis were quite definitely the bioconservatives of the tale.

115
Guardians of Ayn Rand

For skeptics, the idea that reason can lead to a cult is absurd. The characteristics of a cult are 180 degrees out of phase with reason. But as I will demonstrate, not only can it happen, it has happened, and to a group that would have to be considered the unlikeliest cult in history. It is a lesson in what happens when the truth becomes more important than the search for truth . . .

—Michael Shermer, “The Unlikeliest Cult in History”¹

I think Michael Shermer is over-explaining Objectivism. I’ll get around to amplifying on that.

Ayn Rand’s novels glorify technology, capitalism, individual defiance of the System, limited government, private property, selfishness. Her ultimate fictional hero, John Galt, was <SPOILER> a scientist who invented a new form of cheap renewable energy; but then refuses to give it to the world since the profits will only be stolen to prop up corrupt governments.</SPOILER>

And then—somehow—it all turned into a moral and philosophical “closed system” with Ayn Rand at the center. The term “closed system” is not my own accusation; it’s the term the Ayn Rand Institute uses to describe Objectivism. Objectivism is defined by the works of Ayn Rand. Now that Rand is dead, Objectivism is closed. If you disagree with Rand’s works in any respect, you cannot be an Objectivist.

Max Gluckman once said: “A science is any discipline in which the fool of this generation can go beyond the point reached by the genius of the last generation.” Science moves forward by slaying its heroes, as Newton fell to Einstein. Every young physicist dreams of being the new champion that future physicists will dream of dethroning.

Ayn Rand’s philosophical idol was Aristotle. Now maybe Aristotle was a hot young math talent 2,350 years ago, but math has made noticeable progress since his day. Bayesian probability theory is the quantitative logic of which Aristotle’s qualitative logic is a special case; but there’s no sign that Ayn Rand knew about Bayesian probability theory when she wrote her magnum opus, Atlas Shrugged. Rand wrote about “rationality,” yet failed to familiarize herself with the modern research in heuristics and biases. How can anyone claim to be a master rationalist, yet know nothing of such elementary subjects?

“Wait a minute,” objects the reader, “that’s not quite fair! Atlas Shrugged was published in 1957! Practically nobody knew about Bayes back then.” Bah. Next you’ll tell me that Ayn Rand died in 1982, and had no chance to read Judgment Under Uncertainty: Heuristics and Biases, which was published that same year.

Science isn’t fair. That’s sorta the point. An aspiring rationalist in 2007 starts with a huge advantage over an aspiring rationalist in 1957. It’s how we know that progress has occurred.

To me the thought of voluntarily embracing a system explicitly tied to the beliefs of one human being, who’s dead, falls somewhere between the silly and the suicidal. A computer isn’t five years old before it’s obsolete.

The vibrance that Rand admired in science, in commerce, in every railroad that replaced a horse-and-buggy route, in every skyscraper built with new architecture—it all comes from the principle of surpassing the ancient masters. How can there be science, if the most knowledgeable scientist there will ever be, has already lived? Who would raise the New York skyline that Rand admired so, if the tallest building that would ever exist, had already been built?

And yet Ayn Rand acknowledged no superior, in the past, or in the future yet to come. Rand, who began in admiring reason and individuality, ended by ostracizing anyone who dared contradict her. Shermer:

[Barbara] Branden recalled an evening when a friend of Rand’s remarked that he enjoyed the music of Richard Strauss. “When he left at the end of the evening, Ayn said, in a reaction becoming increasingly typical, ‘Now I understand why he and I can never be real soulmates. The distance in our sense of life is too great.’” Often she did not wait until a friend had left to make such remarks.

Ayn Rand changed over time, one suspects.

Rand grew up in Russia, and witnessed the Bolshevik revolution firsthand. She was granted a visa to visit American relatives at the age of 21, and she never returned. It’s easy to hate authoritarianism when you’re the victim. It’s easy to champion the freedom of the individual, when you are yourself the oppressed.

It takes a much stronger constitution to fear authority when you have the power. When people are looking to you for answers, it’s harder to say “What the hell do I know about music? I’m a writer, not a composer,” or “It’s hard to see how liking a piece of music can be untrue.”

When you’re the one crushing those who dare offend you, the exercise of power somehow seems much more justifiable than when you’re the one being crushed. All sorts of excellent justifications somehow leap to mind.

Michael Shermer goes into detail on how he thinks that Rand’s philosophy ended up descending into cultishness. In particular, Shermer says (it seems) that Objectivism failed because Rand thought that certainty was possible, while science is never certain. I can’t back Shermer on that one. The atomic theory of chemistry is pretty damned certain. But chemists haven’t become a cult.

Actually, I think Shermer’s falling prey to correspondence bias by supposing that there’s any particular correlation between Rand’s philosophy and the way her followers formed a cult. Every cause wants to be a cult.

Ayn Rand fled the Soviet Union, wrote a book about individualism that a lot of people liked, got plenty of compliments, and formed a coterie of admirers. Her admirers found nicer and nicer things to say about her (happy death spiral), and she enjoyed it too much to tell them to shut up. She found herself with the power to crush those of whom she disapproved, and she didn’t resist the temptation of power.

Ayn Rand and Nathaniel Branden carried on a secret extramarital affair. (With permission from both their spouses, which counts for a lot in my view. If you want to turn that into a “problem,” you have to specify that the spouses were unhappy—and then it’s still not a matter for outsiders.) When Branden was revealed to have “cheated” on Rand with yet another woman, Rand flew into a fury and excommunicated him. Many Objectivists broke away when news of the affair became public.

Who stayed with Rand, rather than following Branden, or leaving Objectivism altogether? Her strongest supporters. Who departed? The previous voices of moderation. (Evaporative cooling of group beliefs.) Ever after, Rand’s grip over her remaining coterie was absolute, and no questioning was allowed.

The only extraordinary thing about the whole business, is how ordinary it was.

You might think that a belief system which praised “reason” and “rationality” and “individualism” would have gained some kind of special immunity, somehow . . . ?

Well, it didn’t.

It worked around as well as putting a sign saying “Cold” on a refrigerator that wasn’t plugged in.

The active effort required to resist the slide into entropy wasn’t there, and decay inevitably followed.

And if you call that the “unlikeliest cult in history,” you’re just calling reality nasty names.

Let that be a lesson to all of us: Praising “rationality” counts for nothing. Even saying “You must justify your beliefs through Reason, not by agreeing with the Great Leader” just runs a little automatic program that takes whatever the Great Leader says and generates a justification that your fellow followers will view as Reason-able.

So where is the true art of rationality to be found? Studying up on the math of probability theory and decision theory. Absorbing the cognitive sciences like evolutionary psychology, or heuristics and biases. Reading history books . . .

“Study science, not just me!” is probably the most important piece of advice Ayn Rand should’ve given her followers and didn’t. There’s no one human being who ever lived, whose shoulders were broad enough to bear all the weight of a true science with many contributors.

It’s noteworthy, I think, that Ayn Rand’s fictional heroes were architects and engineers; John Galt, her ultimate, was a physicist; and yet Ayn Rand herself wasn’t a great scientist. As far as I know, she wasn’t particularly good at math. She could not aspire to rival her own heroes. Maybe that’s why she began to lose track of the will to keep improving herself.

Now me, y’know, I admire Francis Bacon’s audacity, but I retain my ability to bashfully confess, “If I could go back in time, and somehow make Francis Bacon understand the problem I’m currently working on, his eyeballs would pop out of their sockets like champagne corks and explode.”

I admire Newton’s accomplishments. But my attitude toward a woman’s right to vote bars me from accepting Newton as a moral paragon. Just as my knowledge of Bayesian probability bars me from viewing Newton as the ultimate unbeatable source of mathematical knowledge. And my knowledge of Special Relativity, paltry and little-used though it may be, bars me from viewing Newton as the ultimate authority on physics.

Newton couldn’t realistically have discovered any of the ideas I’m lording over him—but progress isn’t fair! That’s the point!

Science has heroes, but no gods. The great Names are not our superiors, or even our rivals; they are passed milestones on our road. And the most important milestone is the hero yet to come.

To be one more milestone in humanity’s road is the best that can be said of anyone; but this seemed too lowly to please Ayn Rand. And that is how she became a mere Ultimate Prophet.

1. Michael Shermer, “The Unlikeliest Cult in History,” Skeptic 2, no. 2 (1993): 74–81, http://www.2think.org/02_2_she.shtml.

116
Two Cult Koans

A novice rationalist studying under the master Ougi was rebuked by a friend who said, “You spend all this time listening to your master, and talking of ‘rational’ this and ‘rational’ that—you have fallen into a cult!”

The novice was deeply disturbed; he heard the words, “You have fallen into a cult!” resounding in his ears as he lay in bed that night, and even in his dreams.

The next day, the novice approached Ougi and related the events, and said, “Master, I am constantly consumed by worry that this is all really a cult, and that your teachings are only dogma.”

Ougi replied, “If you find a hammer lying in the road and sell it, you may ask a low price or a high one. But if you keep the hammer and use it to drive nails, who can doubt its worth?”

The novice said, “See, now that’s just the sort of thing I worry about—your mysterious Zen replies.”

Ougi said, “Fine, then, I will speak more plainly, and lay out perfectly reasonable arguments which demonstrate that you have not fallen into a cult. But first you have to wear this silly hat.”

Ougi gave the novice a huge brown ten-gallon cowboy hat.

“Er, master . . .” said the novice.

“When I have explained everything to you,” said Ougi, “you will see why this was necessary. Or otherwise, you can continue to lie awake nights, wondering whether this is a cult.”

The novice put on the cowboy hat.

Ougi said, “How long will you repeat my words and ignore the meaning? Disordered thoughts begin as feelings of attachment to preferred conclusions. You are too anxious about your self-image as a rationalist. You came to me to seek reassurance. If you had been truly curious, not knowing one way or the other, you would have thought of ways to resolve your doubts. Because you needed to resolve your cognitive dissonance, you were willing to put on a silly hat. If I had been an evil man, I could have made you pay a hundred silver coins. When you concentrate on a real-world question, the worth or worthlessness of your understanding will soon become apparent. You are like a swordsman who keeps glancing away to see if anyone might be laughing at him—”

“All right,” said the novice.

“You asked for the long version,” said Ougi.

This novice later succeeded Ougi and became known as Ni no Tachi. Ever after, he would not allow his students to cite his words in their debates, saying, “Use the techniques and do not mention them.”

A novice rationalist approached the master Ougi and said, “Master, I worry that our rationality dojo is . . . well . . . a little cultish.”

“That is a grave concern,” said Ougi.

The novice waited a time, but Ougi said nothing more.

So the novice spoke up again: “I mean, I’m sorry, but having to wear these robes, and the hood—it just seems like we’re the bloody Freemasons or something.”

“Ah,” said Ougi, “the robes and trappings.”

“Well, yes the robes and trappings,” said the novice. “It just seems terribly irrational.”

“I will address all your concerns,” said the master, “but first you must put on this silly hat.” And Ougi drew out a wizard’s hat, embroidered with crescents and stars.

The novice took the hat, looked at it, and then burst out in frustration: “How can this possibly help?”

“Since you are so concerned about the interactions of clothing with probability theory,” Ougi said, “it should not surprise you that you must wear a special hat to understand.”

When the novice attained the rank of grad student, he took the name Bouzo and would only discuss rationality while wearing a clown suit.

117
Asch’s Conformity Experiment

Solomon Asch, with experiments originally carried out in the 1950s and well-replicated since, highlighted a phenomenon now known as “conformity.” In the classic experiment, a subject sees a puzzle like the one in the nearby diagram: Which of the lines A, B, and C is the same size as the line X? Take a moment to determine your own answer . . .

The gotcha is that the subject is seated alongside a number of other people looking at the diagram—seemingly other subjects, actually confederates of the experimenter. The other “subjects” in the experiment, one after the other, say that line C seems to be the same size as X. The real subject is seated next-to-last. How many people, placed in this situation, would say “C”—giving an obviously incorrect answer that agrees with the unanimous answer of the other subjects? What do you think the percentage would be?

Three-quarters of the subjects in Asch’s experiment gave a “conforming” answer at least once. A third of the subjects conformed more than half the time.

Interviews after the experiment showed that while most subjects claimed to have not really believed their conforming answers, some said they’d really thought that the conforming option was the correct one.

Asch was disturbed by these results:

That we have found the tendency to conformity in our society so strong . . . is a matter of concern. It raises questions about our ways of education and about the values that guide our conduct.¹

It is not a trivial question whether the subjects of Asch’s experiments behaved irrationally. Robert Aumann’s Agreement Theorem shows that honest Bayesians cannot agree to disagree—if they have common knowledge of their probability estimates, they have the same probability estimate. Aumann’s Agreement Theorem was proved more than twenty years after Asch’s experiments, but it only formalizes and strengthens an intuitively obvious point—other people’s beliefs are often legitimate evidence.

If you were looking at a diagram like the one above, but you knew for a fact that the other people in the experiment were honest and seeing the same diagram as you, and three other people said that C was the same size as X, then what are the odds that only you are the one who’s right? I lay claim to no advantage of visual reasoning—I don’t think I’m better than an average human at judging whether two lines are the same size. In terms of individual rationality, I hope I would notice my own severe confusion and then assign >50% probability to the majority vote.

In terms of group rationality, seems to me that the proper thing for an honest rationalist to say is, “How surprising, it looks to me like B is the same size as X. But if we’re all looking at the same diagram and reporting honestly, I have no reason to believe that my assessment is better than yours.” The last sentence is important—it’s a much weaker claim of disagreement than, “Oh, I see the optical illusion—I understand why you think it’s C, of course, but the real answer is B.”

So the conforming subjects in these experiments are not automatically convicted of irrationality, based on what I’ve described so far. But as you might expect, the devil is in the details of the experimental results. According to a meta-analysis of over a hundred replications by Smith and Bond:²

Conformity increases strongly up to 3 confederates, but doesn’t increase further up to 10–15 confederates. If people are conforming rationally, then the opinion of 15 other subjects should be substantially stronger evidence than the opinion of 3 other subjects.

Adding a single dissenter—just one other person who gives the correct answer, or even an incorrect answer that’s different from the group’s incorrect answer—reduces conformity very sharply, down to 5–10% of subjects. If you’re applying some intuitive version of Aumann’s Agreement to think that when 1 person disagrees with 3 people, the 3 are probably right, then in most cases you should be equally willing to think that 2 people will disagree with 6 people. (Not automatically true, but true ceteris paribus.) On the other hand, if you’ve got people who are emotionally nervous about being the odd one out, then it’s easy to see how a single other person who agrees with you, or even a single other person who disagrees with the group, would make you much less nervous.

Unsurprisingly, subjects in the one-dissenter condition did not think their nonconformity had been influenced or enabled by the dissenter. Like the 90% of drivers who think they’re above-average in the top 50%, some of them may be right about this, but not all. People are not self-aware of the causes of their conformity or dissent, which weighs against trying to argue them as manifestations of rationality. For example, in the hypothesis that people are socially-rationally choosing to lie in order to not stick out, it appears that (at least some) subjects in the one-dissenter condition do not consciously anticipate the “conscious strategy” they would employ when faced with unanimous opposition.

When the single dissenter suddenly switched to conforming to the group, subjects’ conformity rates went back up to just as high as in the no-dissenter condition. Being the first dissenter is a valuable (and costly!) social service, but you’ve got to keep it up.

Consistently within and across experiments, all-female groups (a female subject alongside female confederates) conform significantly more often than all-male groups. Around one-half the women conform more than half the time, versus a third of the men. If you argue that the average subject is rational, then apparently women are too agreeable and men are too disagreeable, so neither group is actually rational . . .

Ingroup-outgroup manipulations (e.g., a handicapped subject alongside other handicapped subjects) similarly show that conformity is significantly higher among members of an ingroup.

Conformity is lower in the case of blatant diagrams, like the one at the beginning of this essay, versus diagrams where the errors are more subtle. This is hard to explain if (all) the subjects are making a socially rational decision to avoid sticking out.

Paul Crowley reminds me to note that when subjects can respond in a way that will not be seen by the group, conformity also drops, which also argues against an Aumann interpretation.

1. Solomon E. Asch, “Studies of Independence and Conformity: A Minority of One Against a Unanimous Majority,” Psychological Monographs 70 (1956).

2. Rod Bond and Peter B. Smith, “Culture and Conformity: A Meta-Analysis of Studies Using Asch’s (1952b, 1956) Line Judgment Task,” Psychological Bulletin 119 (1996): 111–137.

118
On Expressing Your Concerns

The scary thing about Asch’s conformity experiments is that you can get many people to say black is white, if you put them in a room full of other people saying the same thing. The hopeful thing about Asch’s conformity experiments is that a single dissenter tremendously drove down the rate of conformity, even if the dissenter was only giving a different wrong answer. And the wearisome thing is that dissent was not learned over the course of the experiment—when the single dissenter started siding with the group, rates of conformity rose back up.

Being a voice of dissent can bring real benefits to the group. But it also (famously) has a cost. And then you have to keep it up. Plus you could be wrong.

I recently had an interesting experience wherein I began discussing a project with two people who had previously done some planning on their own. I thought they were being too optimistic and made a number of safety-margin-type suggestions for the project. Soon a fourth guy wandered by, who was providing one of the other two with a ride home, and began making suggestions. At this point I had a sudden insight about how groups become overconfident, because whenever I raised a possible problem, the fourth guy would say, “Don’t worry, I’m sure we can handle it!” or something similarly reassuring.

An individual, working alone, will have natural doubts. They will think to themselves “Can I really do XYZ?,” because there’s nothing impolite about doubting your own competence. But when two unconfident people form a group, it is polite to say nice and reassuring things, and impolite to question the other person’s competence. Together they become more optimistic than either would be on their own, each one’s doubts quelled by the other’s seemingly confident reassurance, not realizing that the other person initially had the same inner doubts.

The most fearsome possibility raised by Asch’s experiments on conformity is the specter of everyone agreeing with the group, swayed by the confident voices of others, careful not to let their own doubts show—not realizing that others are suppressing similar worries. This is known as “pluralistic ignorance.”

Robin Hanson and I have a long-running debate over when, exactly, aspiring rationalists should dare to disagree. I tend toward the widely held position that you have no real choice but to form your own opinions. Robin Hanson advocates a more iconoclastic position, that you—not just other people—should consider that others may be wiser. Regardless of our various disputes, we both agree that Aumann’s Agreement Theorem extends to imply that common knowledge of a factual disagreement shows someone must be irrational. Despite the funny looks we’ve gotten, we’re sticking to our guns about modesty: Forget what everyone tells you about individualism, you should pay attention to what other people think.

Ahem. The point is that, for rationalists, disagreeing with the group is serious business. You can’t wave it off with “Everyone is entitled to their own opinion.”

I think the most important lesson to take away from Asch’s experiments is to distinguish “expressing concern” from “disagreement.” Raising a point that others haven’t voiced is not a promise to disagree with the group at the end of its discussion.

The ideal Bayesian’s process of convergence involves sharing evidence that is unpredictable to the listener. The Aumann agreement result holds only for common knowledge, where you know, I know, you know I know, etc. Hanson’s post or paper on “We Can’t Foresee to Disagree” provides a picture of how strange it would look to watch ideal rationalists converging on a probability estimate; it doesn’t look anything like two bargainers in a marketplace converging on a price.

Unfortunately, there’s not much difference socially between “expressing concerns” and “disagreement.” A group of rationalists might agree to pretend there’s a difference, but it’s not how human beings are really wired. Once you speak out, you’ve committed a socially irrevocable act; you’ve become the nail sticking up, the discord in the comfortable group harmony, and you can’t undo that. Anyone insulted by a concern you expressed about their competence to successfully complete task XYZ, will probably hold just as much of a grudge afterward if you say “No problem, I’ll go along with the group” at the end.

Asch’s experiment shows that the power of dissent to inspire others is real. Asch’s experiment shows that the power of conformity is real. If everyone refrains from voicing their private doubts, that will indeed lead groups into madness. But history abounds with lessons on the price of being the first, or even the second, to say that the Emperor has no clothes. Nor are people hardwired to distinguish “expressing a concern” from “disagreement even with common knowledge”; this distinction is a rationalist’s artifice. If you read the more cynical brand of self-help books (e.g., Machiavelli’s The Prince) they will advise you to mask your nonconformity entirely, not voice your concerns first and then agree at the end. If you perform the group service of being the one who gives voice to the obvious problems, don’t expect the group to thank you for it.

These are the costs and the benefits of dissenting—whether you “disagree” or just “express concern”—and the decision is up to you.

119
Lonely Dissent

Asch’s conformity experiment showed that the presence of a single dissenter tremendously reduced the incidence of “conforming” wrong answers. Individualism is easy, experiment shows, when you have company in your defiance. Every other subject in the room, except one, says that black is white. You become the second person to say that black is black. And it feels glorious: the two of you, lonely and defiant rebels, against the world! (Followup interviews showed that subjects in the one-dissenter condition expressed strong feelings of camaraderie with the dissenter—though, of course, they didn’t think the presence of the dissenter had influenced their own nonconformity.)

But you can only join the rebellion, after someone, somewhere, becomes the first to rebel. Someone has to say that black is black after hearing everyone else, one after the other, say that black is white. And that—experiment shows—is a lot harder.

Lonely dissent doesn’t feel like going to school dressed in black. It feels like going to school wearing a clown suit.

That’s the difference between joining the rebellion and leaving the pack.

If there’s one thing I can’t stand, it’s fakeness—you may have noticed this. Well, lonely dissent has got to be one of the most commonly, most ostentatiously faked characteristics around. Everyone wants to be an iconoclast.

I don’t mean to degrade the act of joining a rebellion. There are rebellions worth joining. It does take courage to brave the disapproval of your peer group, or perhaps even worse, their shrugs. Needless to say, going to a rock concert is not rebellion. But, for example, vegetarianism is. I’m not a vegetarian myself, but I respect people who are, because I expect it takes a noticeable amount of quiet courage to tell people that hamburgers won’t work for dinner. (Albeit that in the Bay Area, people ask as a matter of routine.)

Still, if you tell people that you’re a vegetarian, they’ll think they understand your motives (even if they don’t). They may disagree. They may be offended if you manage to announce it proudly enough, or for that matter, they may be offended just because they’re easily offended. But they know how to relate to you.

When someone wears black to school, the teachers and the other children understand the role thereby being assumed in their society. It’s Outside the System—in a very standard way that everyone recognizes and understands. Not, y’know, actually outside the system. It’s a Challenge to Standard Thinking, of a standard sort, so that people indignantly say “I can’t understand why you—” but don’t have to actually think any thoughts they had not thought before. As the saying goes, “Has any of the ‘subversive literature’ you’ve read caused you to modify any of your political views?”

What takes real courage is braving the outright incomprehension of the people around you, when you do something that isn’t Standard Rebellion #37, something for which they lack a ready-made script. They don’t hate you for a rebel, they just think you’re, like, weird, and turn away. This prospect generates a much deeper fear. It’s the difference between explaining vegetarianism and explaining cryonics. There are other cryonicists in the world, somewhere, but they aren’t there next to you. You have to explain it, alone, to people who just think it’s weird. Not forbidden, but outside bounds that people don’t even think about. You’re going to get your head frozen? You think that’s going to stop you from dying? What do you mean, brain information? Huh? What? Are you crazy?

I’m tempted to essay a post facto explanation in evolutionary psychology: You could get together with a small group of friends and walk away from your hunter-gatherer band, but having to go it alone in the forests was probably a death sentence—at least reproductively. We don’t reason this out explicitly, but that is not the nature of evolutionary psychology. Joining a rebellion that everyone knows about is scary, but nowhere near as scary as doing something really differently. Something that in ancestral times might have ended up, not with the band splitting, but with you being driven out alone.

As the case of cryonics testifies, the fear of thinking really different is stronger than the fear of death. Hunter-gatherers had to be ready to face death on a routine basis, hunting large mammals, or just walking around in a world that contained predators. They needed that courage in order to live. Courage to defy the tribe’s standard ways of thinking, to entertain thoughts that seem truly weird—well, that probably didn’t serve its bearers as well. We don’t reason this out explicitly; that’s not how evolutionary psychology works. We human beings are just built in such fashion that many more of us go skydiving than sign up for cryonics.

And that’s not even the highest courage. There’s more than one cryonicist in the world. Only Robert Ettinger had to say it first.

To be a scientific revolutionary, you’ve got to be the first person to contradict what everyone else you know is thinking. This is not the only route to scientific greatness; it is rare even among the great. No one can become a scientific revolutionary by trying to imitate revolutionariness. You can only get there by pursuing the correct answer in all things, whether the correct answer is revolutionary or not. But if, in the due course of time—if, having absorbed all the power and wisdom of the knowledge that has already accumulated—if, after all that and a dose of sheer luck, you find your pursuit of mere correctness taking you into new territory . . . then you have an opportunity for your courage to fail.

This is the true courage of lonely dissent, which every damn rock band out there tries to fake.

Of course not everything that takes courage is a good idea. It would take courage to walk off a cliff, but then you would just go splat.

The fear of lonely dissent is a hindrance to good ideas, but not every dissenting idea is good. See also Robin Hanson’s Against Free Thinkers. Most of the difficulty in having a new true scientific thought is in the “true” part.

It really isn’t necessary to be different for the sake of being different. If you do things differently only when you see an overwhelmingly good reason, you will have more than enough trouble to last you the rest of your life.

There are a few genuine packs of iconoclasts around. The Church of the SubGenius, for example, seems to genuinely aim at confusing the mundanes, not merely offending them. And there are islands of genuine tolerance in the world, such as science fiction conventions. There are certain people who have no fear of departing the pack. Many fewer such people really exist, than imagine themselves rebels; but they do exist. And yet scientific revolutionaries are tremendously rarer. Ponder that.

Now me, you know, I really am an iconoclast. Everyone thinks they are, but with me it’s true, you see. I would totally have worn a clown suit to school. My serious conversations were with books, not with other children.

But if you think you would totally wear that clown suit, then don’t be too proud of that either! It just means that you need to make an effort in the opposite direction to avoid dissenting too easily. That’s what I have to do, to correct for my own nature. Other people do have reasons for thinking what they do, and ignoring that completely is as bad as being afraid to contradict them. You wouldn’t want to end up as a free thinker. It’s not a virtue, you see—just a bias either way.

120
Cultish Countercultishness

In the modern world, joining a cult is probably one of the worse things that can happen to you. The best-case scenario is that you’ll end up in a group of sincere but deluded people, making an honest mistake but otherwise well-behaved, and you’ll spend a lot of time and money but end up with nothing to show. Actually, that could describe any failed Silicon Valley startup. Which is supposed to be a hell of a harrowing experience, come to think. So yes, very scary.

Real cults are vastly worse. “Love bombing” as a recruitment technique, targeted at people going through a personal crisis. Sleep deprivation. Induced fatigue from hard labor. Distant communes to isolate the recruit from friends and family. Daily meetings to confess impure thoughts. It’s not unusual for cults to take all the recruit’s money—life savings plus weekly paycheck—forcing them to depend on the cult for food and clothing. Starvation as a punishment for disobedience. Serious brainwashing and serious harm.

With all that taken into account, I should probably sympathize more with people who are terribly nervous, embarking on some odd-seeming endeavor, that they might be joining a cult. It should not grate on my nerves. Which it does.

Point one: “Cults” and “non-cults” aren’t separated natural kinds like dogs and cats. If you look at any list of cult characteristics, you’ll see items that could easily describe political parties and corporations—“group members encouraged to distrust outside criticism as having hidden motives,” “hierarchical authoritative structure.” I’ve written on group failure modes like group polarization, happy death spirals, uncriticality, and evaporative cooling, all of which seem to feed on each other. When these failures swirl together and meet, they combine to form a Super-Failure stupider than any of the parts, like Voltron. But this is not a cult essence; it is a cult attractor.

Dogs are born with dog DNA, and cats are born with cat DNA. In the current world, there is no in-between. (Even with genetic manipulation, it wouldn’t be as simple as creating an organism with half dog genes and half cat genes.) It’s not like there’s a mutually reinforcing set of dog-characteristics, which an individual cat can wander halfway into and become a semidog.

The human mind, as it thinks about categories, seems to prefer essences to attractors. The one wishes to say “It is a cult” or “It is not a cult,” and then the task of classification is over and done. If you observe that Socrates has ten fingers, wears clothes, and speaks fluent Greek, then you can say “Socrates is human” and from there deduce “Socrates is vulnerable to hemlock” without doing specific blood tests to confirm his mortality. You have decided Socrates’s humanness once and for all.

But if you observe that a certain group of people seems to exhibit ingroup-outgroup polarization and see a positive halo effect around their Favorite Thing Ever—which could be Objectivism, or vegetarianism, or neural networks—you cannot, from the evidence gathered so far, deduce whether they have achieved uncriticality. You cannot deduce whether their main idea is true, or false, or genuinely useful but not quite as useful as they think. From the information gathered so far, you cannot deduce whether they are otherwise polite, or if they will lure you into isolation and deprive you of sleep and food. The characteristics of cultness are not all present or all absent.

If you look at online arguments over “X is a cult,” “X is not a cult,” then one side goes through an online list of cult characteristics and finds one that applies and says “Therefore it is a cult!” And the defender finds a characteristic that does not apply and says “Therefore it is not a cult!”

You cannot build up an accurate picture of a group’s reasoning dynamic using this kind of essentialism. You’ve got to pay attention to individual characteristics individually.

Furthermore, reversed stupidity is not intelligence. If you’re interested in the central idea, not just the implementation group, then smart ideas can have stupid followers. Lots of New Agers talk about “quantum physics” but this is no strike against quantum physics. Of course stupid ideas can also have stupid followers. Along with binary essentialism goes the idea that if you infer that a group is a “cult,” therefore their beliefs must be false, because false beliefs are characteristic of cults, just like cats have fur. If you’re interested in the idea, then look at the idea, not the people. Cultishness is a characteristic of groups more than hypotheses.

The second error is that when people nervously ask, “This isn’t a cult, is it?,” it sounds to me like they’re seeking reassurance of rationality. The notion of a rationalist not getting too attached to their self-image as a rationalist deserves its own essay (though see Twelve Virtues, Why Truth? And . . ., and Two Cult Koans). But even without going into detail, surely one can see that nervously seeking reassurance is not the best frame of mind in which to evaluate questions of rationality. You will not be genuinely curious or think of ways to fulfill your doubts. Instead, you’ll find some online source which says that cults use sleep deprivation to control people, you’ll notice that Your-Favorite-Group doesn’t use sleep deprivation, and you’ll conclude “It’s not a cult. Whew!” If it doesn’t have fur, it must not be a cat. Very reassuring.

But Every Cause Wants To Be A Cult, whether the cause itself is wise or foolish. The ingroup-outgroup dichotomy etc. are part of human nature, not a special curse of mutants. Rationality is the exception, not the rule. You have to put forth a constant effort to maintain rationality against the natural slide into entropy. If you decide “It’s not a cult!” and sigh with relief, then you will not put forth a continuing effort to push back ordinary tendencies toward cultishness. You’ll decide the cult-essence is absent, and stop pumping against the entropy of the cult-attractor.

If you are terribly nervous about cultishness, then you will want to deny any hint of any characteristic that resembles a cult. But any group with a goal seen in a positive light is at risk for the halo effect, and will have to pump against entropy to avoid an affective death spiral. This is true even for ordinary institutions like political parties—people who think that “liberal values” or “conservative values” can cure cancer, etc. It is true for Silicon Valley startups, both failed and successful. It is true of Mac users and of Linux users. The halo effect doesn’t become okay just because everyone does it; if everyone walks off a cliff, you wouldn’t too. The error in reasoning is to be fought, not tolerated. But if you’re too nervous about “Are you sure this isn’t a cult?” then you will be reluctant to see any sign of cultishness, because that would imply you’re in a cult, and It’s not a cult!! So you won’t see the current battlefields where the ordinary tendencies toward cultishness are creeping forward, or being pushed back.

The third mistake in nervously asking “This isn’t a cult, is it?” is that, I strongly suspect, the nervousness is there for entirely the wrong reasons.

Why is it that groups which praise their Happy Thing to the stars, encourage members to donate all their money and work in voluntary servitude, and run private compounds in which members are kept tightly secluded, are called “religions” rather than “cults” once they’ve been around for a few hundred years?

Why is it that most of the people who nervously ask of cryonics, “This isn’t a cult, is it?” would not be equally nervous about attending a Republican or Democrat political rally? Ingroup-outgroup dichotomies and happy death spirals can happen in political discussion, in mainstream religions, in sports fandom. If the nervousness came from fear of rationality errors, people would ask “This isn’t an ingroup-outgroup dichotomy, is it?” about Democrat or Republican political rallies, in just the same fearful tones.

There’s a legitimate reason to be less fearful of Libertarianism than of a flying-saucer cult, because Libertarians don’t have a reputation for employing sleep deprivation to convert people. But cryonicists don’t have a reputation for using sleep deprivation, either. So why be any more worried about having your head frozen after you stop breathing?

I suspect that the nervousness is not the fear of believing falsely, or the fear of physical harm. It is the fear of lonely dissent. The nervous feeling that subjects get in Asch’s conformity experiment, when all the other subjects (actually confederates) say one after another that line C is the same size as line X, and it looks to the subject like line B is the same size as line X. The fear of leaving the pack.

That’s why groups whose beliefs have been around long enough to seem “normal” don’t inspire the same nervousness as “cults,” though some mainstream religions may also take all your money and send you to a monastery. It’s why groups like political parties, that are strongly liable for rationality errors, don’t inspire the same nervousness as “cults.” The word “cult” isn’t being used to symbolize rationality errors, it’s being used as a label for something that seems weird.

Not every change is an improvement, but every improvement is necessarily a change. That which you want to do better, you have no choice but to do differently. Common wisdom does embody a fair amount of, well, actual wisdom; yes, it makes sense to require an extra burden of proof for weirdness. But the nervousness isn’t that kind of deliberate, rational consideration. It’s the fear of believing something that will make your friends look at you really oddly. And so people ask “This isn’t a cult, is it?” in a tone that they would never use for attending a political rally, or for putting up a gigantic Christmas display.

That’s the part that bugs me.

It’s as if, as soon as you believe anything that your ancestors did not believe, the Cult Fairy comes down from the sky and infuses you with the Essence of Cultness, and the next thing you know, you’re all wearing robes and chanting. As if “weird” beliefs are the direct cause of the problems, never mind the sleep deprivation and beatings. The harm done by cults—the Heaven’s Gate suicide and so on—just goes to show that everyone with an odd belief is crazy; the first and foremost characteristic of “cult members” is that they are Outsiders with Peculiar Ways.

Yes, socially unusual belief puts a group at risk for ingroup-outgroup thinking and evaporative cooling and other problems. But the unusualness is a risk factor, not a disease in itself. Same thing with having a goal that you think is worth accomplishing. Whether or not the belief is true, having a nice goal always puts you at risk of the happy death spiral. But that makes lofty goals a risk factor, not a disease. Some goals are genuinely worth pursuing.

On the other hand, I see no legitimate reason for sleep deprivation or threatening dissenters with beating, full stop. When a group does this, then whether you call it “cult” or “not-cult,” you have directly answered the pragmatic question of whether to join.

Problem four: The fear of lonely dissent is something that cults themselves exploit. Being afraid of your friends looking at you disapprovingly is exactly the effect that real cults use to convert and keep members—surrounding converts with wall-to-wall agreement among cult believers.

The fear of strange ideas, the impulse to conformity, has no doubt warned many potential victims away from flying-saucer cults. When you’re out, it keeps you out. But when you’re in, it keeps you in. Conformity just glues you to wherever you are, whether that’s a good place or a bad place.

The one wishes there was some way they could be sure that they weren’t in a “cult.” Some definite, crushing rejoinder to people who looked at them funny. Some way they could know once and for all that they were doing the right thing, without these constant doubts. I believe that’s called “need for closure.” And—of course—cults exploit that, too.

Hence the phrase, “Cultish countercultishness.”

Living with doubt is not a virtue—the purpose of every doubt is to annihilate itself in success or failure, and a doubt that just hangs around accomplishes nothing. But sometimes a doubt does take a while to annihilate itself. Living with a stack of currently unresolved doubts is an unavoidable fact of life for rationalists. Doubt shouldn’t be scary. Otherwise you’re going to have to choose between living one heck of a hunted life, or one heck of a stupid one.

If you really, genuinely can’t figure out whether a group is a “cult,” then you’ll just have to choose under conditions of uncertainty. That’s what decision theory is all about.

Problem five: Lack of strategic thinking.

I know people who are cautious around Singularitarianism, and they’re also cautious around political parties and mainstream religions. Cautious, not nervous or defensive. These people can see at a glance that Singularitarianism is obviously not a full-blown cult with sleep deprivation etc. But they worry that Singularitarianism will become a cult, because of risk factors like turning the concept of a powerful AI into a Super Happy Agent (an agent defined primarily by agreeing with any nice thing said about it). Just because something isn’t a cult now, doesn’t mean it won’t become a cult in the future. Cultishness is an attractor, not an essence.

Does this kind of caution annoy me? Hell no. I spend a lot of time worrying about that scenario myself. I try to place my Go stones in advance to block movement in that direction. Hence, for example, the series of essays on cultish failures of reasoning.

People who talk about “rationality” also have an added risk factor. Giving people advice about how to think is an inherently dangerous business. But it is a risk factor, not a disease.

Both of my favorite Causes are at-risk for cultishness. Yet somehow, I get asked “Are you sure this isn’t a cult?” a lot more often when I talk about powerful AIs, than when I talk about probability theory and cognitive science. I don’t know if one risk factor is higher than the other, but I know which one sounds weirder . . .

Problem #6 with asking “This isn’t a cult, is it?” . . .

Just the question itself places me in a very annoying sort of Catch-22. An actual Evil Guru would surely use the one’s nervousness against them, and design a plausible elaborate argument explaining Why This Is Not A Cult, and the one would be eager to accept it. Sometimes I get the impression that this is what people want me to do! Whenever I try to write about cultishness and how to avoid it, I keep feeling like I’m giving in to that flawed desire—that I am, in the end, providing people with reassurance. Even when I tell people that a constant fight against entropy is required.

It feels like I’m making myself a first dissenter in Asch’s conformity experiment, telling people, “Yes, line X really is the same as line B, it’s okay for you to say so too.” They shouldn’t need to ask! Or, even worse, it feels like I’m presenting an elaborate argument for Why This Is Not A Cult. It’s a wrong question.

Just look at the group’s reasoning processes for yourself, and decide for yourself whether it’s something you want to be part of, once you get rid of the fear of weirdness. It is your own responsibility to stop yourself from thinking cultishly, no matter which group you currently happen to be operating in.

Once someone asks “This isn’t a cult, is it?” then no matter how I answer, I always feel like I’m defending something. I do not like this feeling. It is not the function of a Bayesian Master to give reassurance, nor of rationalists to defend.

Cults feed on groupthink, nervousness, desire for reassurance. You cannot make nervousness go away by wishing, and false self-confidence is even worse. But so long as someone needs reassurance—even reassurance about being a rationalist—that will always be a flaw in their armor. A skillful swordsman focuses on the target, rather than glancing away to see if anyone might be laughing. When you know what you’re trying to do and why, you’ll know whether you’re getting it done or not, and whether a group is helping you or hindering you.

(PS: If the one comes to you and says, “Are you sure this isn’t a cult?,” don’t try to explain all these concepts in one breath. You’re underestimating inferential distances. The one will say, “Aha, so you’re admitting you’re a cult!” or “Wait, you’re saying I shouldn’t worry about joining cults?” or “So . . . the fear of cults is cultish? That sounds awfully cultish to me.” So the last annoyance factor—#7 if you’re keeping count—is that all of this is such a long story to explain.)

121
The Importance of Saying “Oops”

I just finished reading a history of Enron’s downfall, The Smartest Guys in the Room, which hereby wins my award for “Least Appropriate Book Title.”

An unsurprising feature of Enron’s slow rot and abrupt collapse was that the executive players never admitted to having made a large mistake. When catastrophe #247 grew to such an extent that it required an actual policy change, they would say, “Too bad that didn’t work out—it was such a good idea—how are we going to hide the problem on our balance sheet?” As opposed to, “It now seems obvious in retrospect that it was a mistake from the beginning.” As opposed to, “I’ve been stupid.” There was never a watershed moment, a moment of humbling realization, of acknowledging a fundamental problem. After the bankruptcy, Jeff Skilling, the former COO and brief CEO of Enron, declined his own lawyers’ advice to take the Fifth Amendment; he testified before Congress that Enron had been a great company.

Not every change is an improvement, but every improvement is necessarily a change. If we only admit small local errors, we will only make small local changes. The motivation for a big change comes from acknowledging a big mistake.

As a child I was raised on equal parts science and science fiction, and from Heinlein to Feynman I learned the tropes of Traditional Rationality: theories must be bold and expose themselves to falsification; be willing to commit the heroic sacrifice of giving up your own ideas when confronted with contrary evidence; play nice in your arguments; try not to deceive yourself; and other fuzzy verbalisms.

A traditional rationalist upbringing tries to produce arguers who will concede to contrary evidence eventually—there should be some mountain of evidence sufficient to move you. This is not trivial; it distinguishes science from religion. But there is less focus on speed, on giving up the fight as quickly as possible, integrating evidence efficiently so that it only takes a minimum of contrary evidence to destroy your cherished belief.

I was raised in Traditional Rationality, and thought myself quite the rationalist. I switched to Bayescraft (Laplace Jaynes Tversky / Kahneman) in the aftermath of . . . well, it’s a long story. Roughly, I switched because I realized that Traditional Rationality’s fuzzy verbal tropes had been insufficient to prevent me from making a large mistake.

After I had finally and fully admitted my mistake, I looked back upon the path that had led me to my Awful Realization. And I saw that I had made a series of small concessions, minimal concessions, grudgingly conceding each millimeter of ground, realizing as little as possible of my mistake on each occasion, admitting failure only in small tolerable nibbles. I could have moved so much faster, I realized, if I had simply screamed “OOPS!”

And I thought: I must raise the level of my game.

There is a powerful advantage to admitting you have made a large mistake. It’s painful. It can also change your whole life.

It is important to have the watershed moment, the moment of humbling realization. To acknowledge a fundamental problem, not divide it into palatable bite-size mistakes.

Do not indulge in drama and become proud of admitting errors. It is surely superior to get it right the first time. But if you do make an error, better by far to see it all at once. Even hedonically, it is better to take one large loss than many small ones. The alternative is stretching out the battle with yourself over years. The alternative is Enron.

Since then I have watched others making their own series of minimal concessions, grudgingly conceding each millimeter of ground; never confessing a global mistake where a local one will do; always learning as little as possible from each error. What they could fix in one fell swoop voluntarily, they transform into tiny local patches they must be argued into. Never do they say, after confessing one mistake, I’ve been a fool. They do their best to minimize their embarrassment by saying I was right in principle, or It could have worked, or I still want to embrace the true essence of whatever-I’m-attached-to. Defending their pride in this passing moment, they ensure they will again make the same mistake, and again need to defend their pride.

Better to swallow the entire bitter pill in one terrible gulp.

122
The Crackpot Offer

When I was very young—I think thirteen or maybe fourteen—I thought I had found a disproof of Cantor’s Diagonal Argument, a famous theorem which demonstrates that the real numbers outnumber the rational numbers. Ah, the dreams of fame and glory that danced in my head!

My idea was that since each whole number can be decomposed into a bag of powers of 2, it was possible to map the whole numbers onto the set of subsets of whole numbers simply by writing out the binary expansion. The number 13, for example, 1101, would map onto {0, 2, 3}. It took a whole week before it occurred to me that perhaps I should apply Cantor’s Diagonal Argument to my clever construction, and of course it found a counterexample—the binary number (. . . 1111), which does not correspond to any finite whole number.

So I found this counterexample, and saw that my attempted disproof was false, along with my dreams of fame and glory.

I was initially a bit disappointed.

The thought went through my mind: “I’ll get that theorem eventually! Someday I’ll disprove Cantor’s Diagonal Argument, even though my first try failed!” I resented the theorem for being obstinately true, for depriving me of my fame and fortune, and I began to look for other disproofs.

And then I realized something. I realized that I had made a mistake, and that, now that I’d spotted my mistake, there was absolutely no reason to suspect the strength of Cantor’s Diagonal Argument any more than other major theorems of mathematics.

I saw then very clearly that I was being offered the opportunity to become a math crank, and to spend the rest of my life writing angry letters in green ink to math professors. (I’d read a book once about math cranks.)

I did not wish this to be my future, so I gave a small laugh, and let it go. I waved Cantor’s Diagonal Argument on with all good wishes, and I did not question it again.

And I don’t remember, now, if I thought this at the time, or if I thought it afterward . . . but what a terribly unfair test to visit upon a child of thirteen. That I had to be that rational, already, at that age, or fail.

The smarter you are, the younger you may be, the first time you have what looks to you like a really revolutionary idea. I was lucky in that I saw the mistake myself; that it did not take another mathematician to point it out to me, and perhaps give me an outside source to blame. I was lucky in that the disproof was simple enough for me to understand. Maybe I would have recovered eventually, otherwise. I’ve recovered from much worse, as an adult. But if I had gone wrong that early, would I ever have developed that skill?

I wonder how many people writing angry letters in green ink were thirteen when they made that first fatal misstep. I wonder how many were promising minds before then.

I made a mistake. That was all. I was not really right, deep down; I did not win a moral victory; I was not displaying ambition or skepticism or any other wondrous virtue; it was not a reasonable error; I was not half right or even the tiniest fraction right. I thought a thought I would never have thought if I had been wiser, and that was all there ever was to it.

If I had been unable to admit this to myself, if I had reinterpreted my mistake as virtuous, if I had insisted on being at least a little right for the sake of pride, then I would not have let go. I would have gone on looking for a flaw in the Diagonal Argument. And, sooner or later, I might have found one.

Until you admit you were wrong, you cannot get on with your life; your self-image will still be bound to the old mistake.

Whenever you are tempted to hold on to a thought you would never have thought if you had been wiser, you are being offered the opportunity to become a crackpot—even if you never write any angry letters in green ink. If no one bothers to argue with you, or if you never tell anyone your idea, you may still be a crackpot. It’s the clinging that defines it.

It’s not true. It’s not true deep down. It’s not half-true or even a little true. It’s nothing but a thought you should never have thought. Not every cloud has a silver lining. Human beings make mistakes, and not all of them are disguised successes. Human beings make mistakes; it happens, that’s all. Say “oops,” and get on with your life.

123
Just Lose Hope Already

Casey Serin, a 24-year-old web programmer with no prior experience in real estate, owes banks 2.2 million dollars after lying on mortgage applications in order to simultaneously buy eight different houses in different states. He took cash out of the mortgage (applied for larger amounts than the price of the house) and spent the money on living expenses and real-estate seminars. He was expecting the market to go up, it seems.

That’s not even the sad part. The sad part is that he still hasn’t given up. Casey Serin does not accept defeat. He refuses to declare bankruptcy, or get a job; he still thinks he can make it big in real estate. He went on spending money on seminars. He tried to take out a mortgage on a ninth house. He hasn’t failed, you see, he’s just had a learning experience.

That’s what happens when you refuse to lose hope.

While this behavior may seem to be merely stupid, it also puts me in mind of two Nobel-Prize-winning economists . . .

. . . namely Merton and Scholes of Long-Term Capital Management.

While LTCM raked in giant profits over its first three years, in 1998 the inefficiences that LTCM were exploiting had started to vanish—other people knew about the trick, so it stopped working.

LTCM refused to lose hope. Addicted to 40% annual returns, they borrowed more and more leverage to exploit tinier and tinier margins. When everything started to go wrong for LTCM, they had equity of $4.72 billion, leverage of $124.5 billion, and derivative positions of $1.25 trillion.

Every profession has a different way to be smart—different skills to learn and rules to follow. You might therefore think that the study of “rationality,” as a general discipline, wouldn’t have much to contribute to real-life success. And yet it seems to me that how to not be stupid has a great deal in common across professions. If you set out to teach someone how to not turn little mistakes into big mistakes, it’s nearly the same art whether in hedge funds or romance, and one of the keys is this: Be ready to admit you lost.

124
The Proper Use of Doubt

Once, when I was holding forth upon the Way, I remarked upon how most organized belief systems exist to flee from doubt. A listener replied to me that the Jesuits must be immune from this criticism, because they practice organized doubt: their novices, he said, are told to doubt Christianity; doubt the existence of God; doubt if their calling is real; doubt that they are suitable for perpetual vows of chastity and poverty. And I said: Ah, but they’re supposed to overcome these doubts, right? He said: No, they are to doubt that perhaps their doubts may grow and become stronger.

Googling failed to confirm or refute these allegations. (If anyone in the audience can help, I’d be much obliged.) But I find this scenario fascinating, worthy of discussion, regardless of whether it is true or false of Jesuits. If the Jesuits practiced deliberate doubt, as described above, would they therefore be virtuous as rationalists?

I think I have to concede that the Jesuits, in the (possibly hypothetical) scenario above, would not properly be described as “fleeing from doubt.” But the (possibly hypothetical) conduct still strikes me as highly suspicious. To a truly virtuous rationalist, doubt should not be scary. The conduct described above sounds to me like a program of desensitization for something very scary, like exposing an arachnophobe to spiders under carefully controlled conditions.

But even so, they are encouraging their novices to doubt—right? Does it matter if their reasons are flawed? Is this not still a worthy deed unto a rationalist?

All curiosity seeks to annihilate itself; there is no curiosity that does not want an answer. But if you obtain an answer, if you satisfy your curiosity, then the glorious mystery will no longer be mysterious.

In the same way, every doubt exists in order to annihilate some particular belief. If a doubt fails to destroy its target, the doubt has died unfulfilled—but that is still a resolution, an ending, albeit a sadder one. A doubt that neither destroys itself nor destroys its target might as well have never existed at all. It is the resolution of doubts, not the mere act of doubting, which drives the ratchet of rationality forward.

Every improvement is a change, but not every change is an improvement. Every rationalist doubts, but not all doubts are rational. Wearing doubts doesn’t make you a rationalist any more than wearing a white medical lab coat makes you a doctor.

A rational doubt comes into existence for a specific reason—you have some specific justification to suspect the belief is wrong. This reason in turn, implies an avenue of investigation which will either destroy the targeted belief, or destroy the doubt. This holds even for highly abstract doubts, like “I wonder if there might be a simpler hypothesis which also explains this data.” In this case you investigate by trying to think of simpler hypotheses. As this search continues longer and longer without fruit, you will think it less and less likely that the next increment of computation will be the one to succeed. Eventually the cost of searching will exceed the expected benefit, and you’ll stop searching. At which point you can no longer claim to be usefully doubting. A doubt that is not investigated might as well not exist. Every doubt exists to destroy itself, one way or the other. An unresolved doubt is a null-op; it does not turn the wheel, neither forward nor back.

If you really believe a religion (not just believe in it), then why would you tell your novices to consider doubts that must die unfulfilled? It would be like telling physics students to painstakingly doubt that the twentieth-century revolution might have been a mistake, and that Newtonian mechanics was correct all along. If you don’t really doubt something, why would you pretend that you do?

Because we all want to be seen as rational—and doubting is widely believed to be a virtue of a rationalist. But it is not widely understood that you need a particular reason to doubt, or that an unresolved doubt is a null-op. Instead people think it’s about modesty, a submissive demeanor, maintaining the tribal status hierarchy—almost exactly the same problem as with humility, on which I have previously written. Making a great public display of doubt to convince yourself that you are a rationalist will do around as much good as wearing a lab coat.

To avoid professing doubts, remember:

A rational doubt exists to destroy its target belief, and if it does not destroy its target it dies unfulfilled.
A rational doubt arises from some specific reason the belief might be wrong.
An unresolved doubt is a null-op.
An uninvestigated doubt might as well not exist.
You should not be proud of mere doubting, although you can justly be proud when you have just finished tearing a cherished belief to shreds.
Though it may take courage to face your doubts, never forget that to an ideal mind doubt would not be scary in the first place.

125
You Can Face Reality

What is true is already so.

Owning up to it doesn’t make it worse.

Not being open about it doesn’t make it go away.

And because it’s true, it is what is there to be interacted with.

Anything untrue isn’t there to be lived.

People can stand what is true,

for they are already enduring it.

—Eugene Gendlin

126
The Meditation on Curiosity

The first virtue is curiosity.

—The Twelve Virtues of Rationality

As rationalists, we are obligated to criticize ourselves and question our beliefs . . . are we not?

Consider what happens to you, on a psychological level, if you begin by saying: “It is my duty to criticize my own beliefs.” Roger Zelazny once distinguished between “wanting to be an author” versus “wanting to write.” Mark Twain said: “A classic is something that everyone wants to have read and no one wants to read.” Criticizing yourself from a sense of duty leaves you wanting to have investigated, so that you’ll be able to say afterward that your faith is not blind. This is not the same as wanting to investigate.

This can lead to motivated stopping of your investigation. You consider an objection, then a counterargument to that objection, then you stop there. You repeat this with several objections, until you feel that you have done your duty to investigate, and then you stop there. You have achieved your underlying psychological objective: to get rid of the cognitive dissonance that would result from thinking of yourself as a rationalist and yet knowing that you had not tried to criticize your belief. You might call it purchase of rationalist satisfaction—trying to create a “warm glow” of discharged duty.

Afterward, your stated probability level will be high enough to justify your keeping the plans and beliefs you started with, but not so high as to evoke incredulity from yourself or other rationalists.

When you’re really curious, you’ll gravitate to inquiries that seem most promising of producing shifts in belief, or inquiries that are least like the ones you’ve tried before. Afterward, your probability distribution likely should not look like it did when you started out—shifts should have occurred, whether up or down; and either direction is equally fine to you, if you’re genuinely curious.

Contrast this to the subconscious motive of keeping your inquiry on familiar ground, so that you can get your investigation over with quickly, so that you can have investigated, and restore the familiar balance on which your familiar old plans and beliefs are based.

As for what I think true curiosity should look like, and the power that it holds, I refer you to A Fable of Science and Politics. Each of the characters is intended to illustrate different lessons. Ferris, the last character, embodies the power of innocent curiosity: which is lightness, and an eager reaching forth for evidence.

Ursula K. LeGuin wrote: “In innocence there is no strength against evil. But there is strength in it for good.”¹ Innocent curiosity may turn innocently awry; and so the training of a rationalist, and its accompanying sophistication, must be dared as a danger if we want to become stronger. Nonetheless we can try to keep the lightness and the eager reaching of innocence.

As it is written in the Twelve Virtues:

If in your heart you believe you already know, or if in your heart you do not wish to know, then your questioning will be purposeless and your skills without direction. Curiosity seeks to annihilate itself; there is no curiosity that does not want an answer.

There just isn’t any good substitute for genuine curiosity. “A burning itch to know is higher than a solemn vow to pursue truth.” But you can’t produce curiosity just by willing it, any more than you can will your foot to feel warm when it feels cold. Sometimes, all we have is our mere solemn vows.

So what can you do with duty? For a start, we can try to take an interest in our dutiful investigations—keep a close eye out for sparks of genuine intrigue, or even genuine ignorance and a desire to resolve it. This goes right along with keeping a special eye out for possibilities that are painful, that you are flinching away from—it’s not all negative thinking.

It should also help to meditate on Conservation of Expected Evidence. For every new point of inquiry, for every piece of unseen evidence that you suddenly look at, the expected posterior probability should equal your prior probability. In the microprocess of inquiry, your belief should always be evenly poised to shift in either direction. Not every point may suffice to blow the issue wide open—to shift belief from 70% to 30% probability—but if your current belief is 70%, you should be as ready to drop it to 69% as raising it to 71%. You should not think that you know which direction it will go in (on average), because by the laws of probability theory, if you know your destination, you are already there. If you can investigate honestly, so that each new point really does have equal potential to shift belief upward or downward, this may help to keep you interested or even curious about the microprocess of inquiry.

If the argument you are considering is not new, then why is your attention going here? Is this where you would look if you were genuinely curious? Are you subconsciously criticizing your belief at its strong points, rather than its weak points? Are you rehearsing the evidence?

If you can manage not to rehearse already known support, and you can manage to drop down your belief by one tiny bite at a time from the new evidence, you may even be able to relinquish the belief entirely—to realize from which quarter the winds of evidence are blowing against you.

Another restorative for curiosity is what I have taken to calling the Litany of Tarski, which is really a meta-litany that specializes for each instance (this is only appropriate). For example, if I am tensely wondering whether a locked box contains a diamond, then, rather than thinking about all the wonderful consequences if the box does contain a diamond, I can repeat the Litany of Tarski:

If the box contains a diamond,
I desire to believe that the box contains a diamond;
If the box does not contain a diamond,
I desire to believe that the box does not contain a diamond;
Let me not become attached to beliefs I may not want.

Then you should meditate upon the possibility that there is no diamond, and the subsequent advantage that will come to you if you believe there is no diamond, and the subsequent disadvantage if you believe there is a diamond. See also the Litany of Gendlin.

If you can find within yourself the slightest shred of true uncertainty, then guard it like a forester nursing a campfire. If you can make it blaze up into a flame of curiosity, it will make you light and eager, and give purpose to your questioning and direction to your skills.

1. Ursula K. Le Guin, The Farthest Shore (Saga Press, 2001).

127
No One Can Exempt You From Rationality’s Laws

Traditional Rationality is phrased in terms of social rules, with violations interpretable as cheating—as defections from cooperative norms. If you want me to accept a belief from you, you are obligated to provide me with a certain amount of evidence. If you try to get out of it, we all know you’re cheating on your obligation. A theory is obligated to make bold predictions for itself, not just steal predictions that other theories have labored to make. A theory is obligated to expose itself to falsification—if it tries to duck out, that’s like trying to duck out of a fearsome initiation ritual; you must pay your dues.

Traditional Rationality is phrased similarly to the customs that govern human societies, which makes it easy to pass on by word of mouth. Humans detect social cheating with much greater reliability than isomorphic violations of abstract logical rules. But viewing rationality as a social obligation gives rise to some strange ideas.

For example, one finds religious people defending their beliefs by saying, “Well, you can’t justify your belief in science!” In other words, “How dare you criticize me for having unjustified beliefs, you hypocrite! You’re doing it too!”

To Bayesians, the brain is an engine of accuracy: it processes and concentrates entangled evidence into a map that reflects the territory. The principles of rationality are laws in the same sense as the Second Law of Thermodynamics: obtaining a reliable belief requires a calculable amount of entangled evidence, just as reliably cooling the contents of a refrigerator requires a calculable minimum of free energy.

In principle, the laws of physics are time-reversible, so there’s an infinitesimally tiny probability—indistinguishable from zero to all but mathematicians—that a refrigerator will spontaneously cool itself down while generating electricity. There’s a slightly larger infinitesimal chance that you could accurately draw a detailed street map of New York without ever visiting, sitting in your living room with your blinds closed and no Internet connection. But I wouldn’t hold your breath.

Before you try mapping an unseen territory, pour some water into a cup at room temperature and wait until it spontaneously freezes before proceeding. That way you can be sure the general trick—ignoring infinitesimally tiny probabilities of success—is working properly. You might not realize directly that your map is wrong, especially if you never visit New York; but you can see that water doesn’t freeze itself.

If the rules of rationality are social customs, then it may seem to excuse behavior X if you point out that others are doing the same thing. It wouldn’t be fair to demand evidence from you, if we can’t provide it ourselves. We will realize that none of us are better than the rest, and we will relent and mercifully excuse you from your social obligation to provide evidence for your belief. And we’ll all live happily ever afterward in liberty, fraternity, and equality.

If the rules of rationality are mathematical laws, then trying to justify evidence-free belief by pointing to someone else doing the same thing, will be around as effective as listing thirty reasons why you shouldn’t fall off a cliff. Even if we all vote that it’s unfair for your refrigerator to need electricity, it still won’t run (with probability ~1). Even if we all vote that you shouldn’t have to visit New York, the map will still be wrong. Lady Nature is famously indifferent to such pleading, and so is Lady Math.

So—to shift back to the social language of Traditional Rationality—don’t think you can get away with claiming that it’s okay to have arbitrary beliefs about XYZ, because other people have arbitrary beliefs too. If two parties to a contract both behave equally poorly, a human judge may decide to impose penalties on neither. But if two engineers design their engines equally poorly, neither engine will work. One design error cannot excuse another. Even if I’m doing XYZ wrong, it doesn’t help you, or exempt you from the rules; it just means we’re both screwed.

As a matter of human law in liberal democracies, everyone is entitled to their own beliefs. As a matter of Nature’s law, you are not entitled to accuracy. We don’t arrest people for believing weird things, at least not in the wiser countries. But no one can revoke the law that you need evidence to generate accurate beliefs. Not even a vote of the whole human species can obtain mercy in the court of Nature.

Physicists don’t decide the laws of physics, they just guess what they are. Rationalists don’t decide the laws of rationality, we just guess what they are. You cannot “rationalize” anything that is not rational to begin with. If by dint of extraordinary persuasiveness you convince all the physicists in the world that you are exempt from the law of gravity, and you walk off a cliff, you’ll fall. Even saying “We don’t decide” is too anthropomorphic. There is no higher authority that could exempt you. There is only cause and effect.

Remember this, when you plead to be excused just this once. We can’t excuse you. It isn’t up to us.

128
Leave a Line of Retreat

When you surround the enemy

Always allow them an escape route.

They must see that there is

An alternative to death.

—Sun Tzu, The Art of War¹

Don’t raise the pressure, lower the wall.

—Lois McMaster Bujold, Komarr²

Once I happened to be conversing with a nonrationalist who had somehow wandered into a local rationalists’ gathering. She had just declared (a) her belief in souls and (b) that she didn’t believe in cryonics because she believed the soul wouldn’t stay with the frozen body. I asked, “But how do you know that?” From the confusion that flashed on her face, it was pretty clear that this question had never occurred to her. I don’t say this in a bad way—she seemed like a nice person with absolutely no training in rationality, just like most of the rest of the human species. I really need to write that book.

Most of the ensuing conversation was on items already covered on Overcoming Bias—if you’re really curious about something, you probably can figure out a good way to test it; try to attain accurate beliefs first and then let your emotions flow from that—that sort of thing. But the conversation reminded me of one notion I haven’t covered here yet:

“Make sure,” I suggested to her, “that you visualize what the world would be like if there are no souls, and what you would do about that. Don’t think about all the reasons that it can’t be that way, just accept it as a premise and then visualize the consequences. So that you’ll think, ‘Well, if there are no souls, I can just sign up for cryonics,’ or ‘If there is no God, I can just go on being moral anyway,’ rather than it being too horrifying to face. As a matter of self-respect you should try to believe the truth no matter how uncomfortable it is, like I said before; but as a matter of human nature, it helps to make a belief less uncomfortable, before you try to evaluate the evidence for it.”

The principle behind the technique is simple: as Sun Tzu advises you to do with your enemies, you must do with yourself—leave yourself a line of retreat, so that you will have less trouble retreating. The prospect of losing your job, say, may seem a lot more scary when you can’t even bear to think about it, than after you have calculated exactly how long your savings will last, and checked the job market in your area, and otherwise planned out exactly what to do next. Only then will you be ready to fairly assess the probability of keeping your job in the planned layoffs next month. Be a true coward, and plan out your retreat in detail—visualize every step—preferably before you first come to the battlefield.

The hope is that it takes less courage to visualize an uncomfortable state of affairs as a thought experiment, than to consider how likely it is to be true. But then after you do the former, it becomes easier to do the latter.

Remember that Bayesianism is precise—even if a scary proposition really should seem unlikely, it’s still important to count up all the evidence, for and against, exactly fairly, to arrive at the rational quantitative probability. Visualizing a scary belief does not mean admitting that you think, deep down, it’s probably true. You can visualize a scary belief on general principles of good mental housekeeping. “The thought you cannot think controls you more than thoughts you speak aloud”—this happens even if the unthinkable thought is false!

The leave-a-line-of-retreat technique does require a certain minimum of self-honesty to use correctly.

For a start: You must at least be able to admit to yourself which ideas scare you, and which ideas you are attached to. But this is a substantially less difficult test than fairly counting the evidence for an idea that scares you. Does it help if I say that I have occasion to use this technique myself? A rationalist does not reject all emotion, after all. There are ideas which scare me, yet I still believe to be false. There are ideas to which I know I am attached, yet I still believe to be true. But I still plan my retreats, not because I’m planning to retreat, but because planning my retreat in advance helps me think about the problem without attachment.

But the greater test of self-honesty is to really accept the uncomfortable proposition as a premise, and figure out how you would really deal with it. When we’re faced with an uncomfortable idea, our first impulse is naturally to think of all the reasons why it can’t possibly be so. And so you will encounter a certain amount of psychological resistance in yourself, if you try to visualize exactly how the world would be, and what you would do about it, if My-Most-Precious-Belief were false, or My-Most-Feared-Belief were true.

Think of all the people who say that, without God, morality was impossible. (And yes, this topic did come up in the conversation; so I am not offering a strawman.) If theists could visualize their real reaction to believing as a fact that God did not exist, they could realize that, no, they wouldn’t go around slaughtering babies. They could realize that atheists are reacting to the nonexistence of God in pretty much the way they themselves would, if they came to believe that. I say this, to show that it is a considerable challenge to visualize the way you really would react, to believing the opposite of a tightly held belief.

Plus it’s always counterintuitive to realize that, yes, people do get over things. Newly minted quadriplegics are not as sad, six months later, as they expect to be, etc. It can be equally counterintuitive to realize that if the scary belief turned out to be true, you would come to terms with it somehow. Quadriplegics deal, and so would you.

See also the Litany of Gendlin and the Litany of Tarski. What is true is already so; owning up to it doesn’t make it worse. You shouldn’t be afraid to just visualize a world you fear. If that world is already actual, visualizing it won’t make it worse; and if it is not actual, visualizing it will do no harm. And remember, as you visualize, that if the scary things you’re imagining really are true—which they may not be!—then you would, indeed, want to believe it, and you should visualize that too; not believing wouldn’t help you.

How many religious people would retain their belief in God, if they could accurately visualize that hypothetical world in which there was no God and they themselves have become atheists?

Leaving a line of retreat is a powerful technique, but it’s not easy. Honest visualization doesn’t take as much effort as admitting outright that God doesn’t exist, but it does take an effort.

1. Sun Tzu, The Art of War (Cloud Hands, Inc., 2004).

2. Lois McMaster Bujold, Komarr, Miles Vorkosigan Adventures (Baen, 1999).

129
Crisis of Faith

It ain’t a true crisis of faith unless things could just as easily go either way.

—Thor Shenkel

Many in this world retain beliefs whose flaws a ten-year-old could point out, if that ten-year-old were hearing the beliefs for the first time. These are not subtle errors we are talking about. They would be child’s play for an unattached mind to relinquish, if the skepticism of a ten-year-old were applied without evasion. As Premise Checker put it, “Had the idea of god not come along until the scientific age, only an exceptionally weird person would invent such an idea and pretend that it explained anything.”

And yet skillful scientific specialists, even the major innovators of a field, even in this very day and age, do not apply that skepticism successfully. Nobel laureate Robert Aumann, of Aumann’s Agreement Theorem, is an Orthodox Jew: I feel reasonably confident in venturing that Aumann must, at one point or another, have questioned his faith. And yet he did not doubt successfully. We change our minds less often than we think.

This should scare you down to the marrow of your bones. It means you can be a world-class scientist and conversant with Bayesian mathematics and still fail to reject a belief whose absurdity a fresh-eyed ten-year-old could see. It shows the invincible defensive position which a belief can create for itself, if it has long festered in your mind.

What does it take to defeat an error that has built itself a fortress?

But by the time you know it is an error, it is already defeated. The dilemma is not “How can I reject long-held false belief X?” but “How do I know if long-held belief X is false?” Self-honesty is at its most fragile when we’re not sure which path is the righteous one. And so the question becomes:

How can we create in ourselves a true crisis of faith, that could just as easily go either way?

Religion is the trial case we can all imagine. (Readers born to atheist parents have missed out on a fundamental life trial, and must make do with the poor substitute of thinking of their religious friends.) But if you have cut off all sympathy and now think of theists as evil mutants, then you won’t be able to imagine the real internal trials they face. You won’t be able to ask the question:

“What general strategy would a religious person have to follow in order to escape their religion?”

I’m sure that some, looking at this challenge, are already rattling off a list of standard atheist talking points—“They would have to admit that there wasn’t any Bayesian evidence for God’s existence,” “They would have to see the moral evasions they were carrying out to excuse God’s behavior in the Bible,” “They need to learn how to use Occam’s Razor—”

WRONG! WRONG WRONG WRONG! This kind of rehearsal, where you just cough up points you already thought of long before, is exactly the style of thinking that keeps people within their current religions. If you stay with your cached thoughts, if your brain fills in the obvious answer so fast that you can’t see originally, you surely will not be able to conduct a crisis of faith.

Maybe it’s just a question of not enough people reading Gödel, Escher, Bach at a sufficiently young age, but I’ve noticed that a large fraction of the population—even technical folk—have trouble following arguments that go this meta. On my more pessimistic days I wonder if the camel has two humps.

Even when it’s explicitly pointed out, some people seemingly cannot follow the leap from the object-level “Use Occam’s Razor! You have to see that your God is an unnecessary belief!” to the meta-level “Try to stop your mind from completing the pattern the usual way!” Because in the same way that all your rationalist friends talk about Occam’s Razor like it’s a good thing, and in the same way that Occam’s Razor leaps right up into your mind, so too, the obvious friend-approved religious response is “God’s ways are mysterious and it is presumptuous to suppose that we can understand them.” So for you to think that the general strategy to follow is “Use Occam’s Razor,” would be like a theist saying that the general strategy is to have faith.

“But—but Occam’s Razor really is better than faith! That’s not like preferring a different flavor of ice cream! Anyone can see, looking at history, that Occamian reasoning has been far more productive than faith—”

Which is all true. But beside the point. The point is that you, saying this, are rattling off a standard justification that’s already in your mind. The challenge of a crisis of faith is to handle the case where, possibly, our standard conclusions are wrong and our standard justifications are wrong. So if the standard justification for X is “Occam’s Razor!,” and you want to hold a crisis of faith around X, you should be questioning if Occam’s Razor really endorses X, if your understanding of Occam’s Razor is correct, and—if you want to have sufficiently deep doubts—whether simplicity is the sort of criterion that has worked well historically in this case, or could reasonably be expected to work, et cetera. If you would advise a religionist to question their belief that “faith” is a good justification for X, then you should advise yourself to put forth an equally strong effort to question your belief that “Occam’s Razor” is a good justification for X.

(Think of all the people out there who don’t understand the Minimum Description Length or Solomonoff induction formulations of Occam’s Razor, who think that Occam’s Razor outlaws many-worlds or the Simulation Hypothesis. They would need to question their formulations of Occam’s Razor and their notions of why simplicity is a good thing. Whatever X in contention you just justified by saying “Occam’s Razor!,” I bet it’s not the same level of Occamian slam dunk as gravity.)

If “Occam’s Razor!” is your usual reply, your standard reply, the reply that all your friends give—then you’d better block your brain from instantly completing that pattern, if you’re trying to instigate a true crisis of faith.

Better to think of such rules as, “Imagine what a skeptic would say—and then imagine what they would say to your response—and then imagine what else they might say, that would be harder to answer.”

Or, “Try to think the thought that hurts the most.”

And above all, the rule:

“Put forth the same level of desperate effort that it would take for a theist to reject their religion.”

Because, if you aren’t trying that hard, then—for all you know—your head could be stuffed full of nonsense as ridiculous as religion.

Without a convulsive, wrenching effort to be rational, the kind of effort it would take to throw off a religion—then how dare you believe anything, when Robert Aumann believes in God?

Someone (I forget who) once observed that people had only until a certain age to reject their religious faith. Afterward they would have answers to all the objections, and it would be too late. That is the kind of existence you must surpass. This is a test of your strength as a rationalist, and it is very severe; but if you cannot pass it, you will be weaker than a ten-year-old.

But again, by the time you know a belief is an error, it is already defeated. So we’re not talking about a desperate, convulsive effort to undo the effects of a religious upbringing, after you’ve come to the conclusion that your religion is wrong. We’re talking about a desperate effort to figure out if you should be throwing off the chains, or keeping them. Self-honesty is at its most fragile when we don’t know which path we’re supposed to take—that’s when rationalizations are not obviously sins.

Not every doubt calls for staging an all-out Crisis of Faith. But you should consider it when:

A belief has long remained in your mind;
It is surrounded by a cloud of known arguments and refutations;
You have sunk costs in it (time, money, public declarations);
The belief has emotional consequences (note this does not make it wrong);
It has gotten mixed up in your personality generally.

None of these warning signs are immediate disproofs. These attributes place a belief at risk for all sorts of dangers, and make it very hard to reject when it is wrong. But they also hold for Richard Dawkins’s belief in evolutionary biology as well as the Pope’s Catholicism. This does not say that we are only talking about different flavors of ice cream. Only the unenlightened think that all deeply-held beliefs are on the same level regardless of the evidence supporting them, just because they are deeply held. The point is not to have shallow beliefs, but to have a map which reflects the territory.

I emphasize this, of course, so that you can admit to yourself, “My belief has these warning signs,” without having to say to yourself, “My belief is false.”

But what these warning signs do mark, is a belief that will take more than an ordinary effort to doubt effectively. So that if it were in fact false, you would in fact reject it. And where you cannot doubt effectively, you are blind, because your brain will hold the belief unconditionally. When a retina sends the same signal regardless of the photons entering it, we call that eye blind.

When should you stage a Crisis of Faith?

Again, think of the advice you would give to a theist: If you find yourself feeling a little unstable inwardly, but trying to rationalize reasons the belief is still solid, then you should probably stage a Crisis of Faith. If the belief is as solidly supported as gravity, you needn’t bother—but think of all the theists who would desperately want to conclude that God is as solid as gravity. So try to imagine what the skeptics out there would say to your “solid as gravity” argument. Certainly, one reason you might fail at a crisis of faith is that you never really sit down and question in the first place—that you never say, “Here is something I need to put effort into doubting properly.”

If your thoughts get that complicated, you should go ahead and stage a Crisis of Faith. Don’t try to do it haphazardly, don’t try it in an ad-hoc spare moment. Don’t rush to get it done with quickly, so that you can say “I have doubted as I was obliged to do.” That wouldn’t work for a theist and it won’t work for you either. Rest up the previous day, so you’re in good mental condition. Allocate some uninterrupted hours. Find somewhere quiet to sit down. Clear your mind of all standard arguments, try to see from scratch. And make a desperate effort to put forth a true doubt that would destroy a false, and only a false, deeply held belief.

Elements of the Crisis of Faith technique have been scattered over many essays:

Avoiding Your Belief’s Real Weak Points—One of the first temptations in a crisis of faith is to doubt the strongest points of your belief, so that you can rehearse your good answers. You need to seek out the most painful spots, not the arguments that are most reassuring to consider.
The Meditation on Curiosity—Roger Zelazny once distinguished between “wanting to be an author” versus “wanting to write,” and there is likewise a distinction between wanting to have investigated and wanting to investigate. It is not enough to say “It is my duty to criticize my own beliefs”; you must be curious, and only uncertainty can create curiosity. Keeping in mind Conservation of Expected Evidence may help you Update Yourself Incrementally: for every single point that you consider, and each element of new argument and new evidence, you should not expect your beliefs to shift more (on average) in one direction than another—thus you can be truly curious each time about how it will go.
Original Seeing—Use Pirsig’s technique to prevent standard cached thoughts from rushing in and completing the pattern.
The Litany of Gendlin and the Litany of Tarski—People can stand what is true, for they are already enduring it. If a belief is true you will be better off believing it, and if it is false you will be better off rejecting it. You would advise a religious person to try to visualize fully and deeply the world in which there is no God, and to, without excuses, come to the full understanding that if there is no God then they will be better off believing there is no God. If one cannot come to accept this on a deep emotional level, one will not be able to have a crisis of faith. So you should put in a sincere effort to visualize the alternative to your belief, the way that the best and highest skeptic would want you to visualize it. Think of the effort a religionist would have to put forth to imagine, without corrupting it for their own comfort, an atheist’s view of the universe.
Make an Extraordinary Effort—See the concept of isshokenmei, the desperate convulsive effort to be rational, the effort that it would take to surpass the level of Robert Aumann and all the great scientists throughout history who never let go of their religions.
The Genetic Heuristic—You should be extremely suspicious if you have many ideas suggested by a source that you now know to be untrustworthy, but by golly, it seems that all the ideas still ended up being right. (E.g., the one concedes that the Bible was written by human hands, but still clings to the idea that it contains indispensable ethical wisdom.)
The Importance of Saying “Oops”—It really is less painful to swallow the entire bitter pill in one terrible gulp.
Singlethink—The opposite of doublethink. See the thoughts you flinch away from, that appear in the corner of your mind for just a moment before you refuse to think them. If you become aware of what you are not thinking, you can think it.
Affective Death Spirals and Resist the Happy Death Spiral—Affective death spirals are prime generators of false beliefs that it will take a Crisis of Faith to shake loose. But since affective death spirals can also get started around real things that are genuinely nice, you don’t have to admit that your belief is a lie, to try and resist the halo effect at every point—refuse false praise even of genuinely nice things. Policy debates should not appear one-sided.
Hold Off On Proposing Solutions—Don’t propose any solutions until the problem has been discussed as thoroughly as possible. Make your mind wait on knowing what its answer will be; and try for five minutes before giving up, both generally, and especially when pursuing the devil’s point of view.

And these standard techniques are particularly relevant:

The sequence on The Bottom Line and Rationalization, which explains why it is always wrong to selectively argue one side of a debate.
Positive Bias and motivated skepticism and motivated stopping, lest you selectively look for support, selectively look for counter-counterarguments, and selectively stop the argument before it gets dangerous. Missing alternatives are a special case of stopping. A special case of motivated skepticism is fake humility, where you bashfully confess that no one can know something you would rather not know. Don’t selectively demand too much authority of counterarguments.
Beware of Semantic Stopsigns, Applause Lights, and your choice to Explain/Worship/Ignore.
Feel the weight of Burdensome Details; each detail a separate burden, a point of crisis.

But really there’s rather a lot of relevant material, here and on Overcoming Bias. The Crisis of Faith is only the critical point and sudden clash of the longer isshoukenmei—the lifelong uncompromising effort to be so incredibly rational that you rise above the level of stupid damn mistakes. It’s when you get a chance to use the skills that you’ve been practicing for so long, all-out against yourself.

I wish you the best of luck against your opponent. Have a wonderful crisis!

130
The Ritual

The room in which Jeffreyssai received his non-beisutsukai visitors was quietly formal, impeccably appointed in only the most conservative tastes. Sunlight and outside air streamed through a grillwork of polished silver, a few sharp edges making it clear that this wall was not to be opened. The floor and walls were glass, thick enough to distort, to a depth sufficient that it didn’t matter what might be underneath. Upon the surfaces of the glass were subtly scratched patterns of no particular meaning, scribed as if by the hand of an artistically inclined child (and this was in fact the case).

Elsewhere in Jeffreyssai’s home there were rooms of other style; but this, he had found, was what most outsiders expected of a Bayesian Master, and he chose not to enlighten them otherwise. That quiet amusement was one of life’s little joys, after all.

The guest sat across from him, knees on the pillow and heels behind. She was here solely upon the business of her Conspiracy, and her attire showed it: a form-fitting jumpsuit of pink leather with even her hands gloved—all the way to the hood covering her head and hair, though her face lay plain and unconcealed beneath.

And so Jeffreyssai had chosen to receive her in this room.

Jeffreyssai let out a long breath, exhaling. “Are you sure?”

“Oh,” she said, “and do I have to be absolutely certain before my advice can shift your opinions? Does it not suffice that I am a domain expert, and you are not?”

Jeffreyssai’s mouth twisted up at the corner in a half-smile. “How do you know so much about the rules, anyway? You’ve never had so much as a Planck length of formal training.”

“Do you even need to ask?” she said dryly. “If there’s one thing that you beisutsukai do love to go on about, it’s the reasons why you do things.”

Jeffreyssai inwardly winced at the thought of trying to pick up rationality by watching other people talk about it—

“And don’t inwardly wince at me like that,” she said. “I’m not trying to be a rationalist myself, just trying to win an argument with a rationalist. There’s a difference, as I’m sure you tell your students.”

Can she really read me that well? Jeffreyssai looked out through the silver grillwork, at the sunlight reflected from the faceted mountainside. Always, always the golden sunlight fell each day, in this place far above the clouds. An unchanging thing, that light. The distant Sun, which that light represented, was in five billion years burned out; but now, in this moment, the Sun still shone. And that could never alter. Why wish for things to stay the same way forever, when that wish was already granted as absolutely as any wish could be? The paradox of permanence and impermanence: only in the latter perspective was there any such thing as progress, or loss.

“You have always given me good counsel,” Jeffreyssai said. “Unchanging, that has been. Through all the time we’ve known each other.”

She inclined her head, acknowledging. This was true, and there was no need to spell out the implications.

“So,” Jeffreyssai said. “Not for the sake of arguing. Only because I want to know the answer. Are you sure?” He didn’t even see how she could guess.

“Pretty sure,” she said, “we’ve been collecting statistics for a long time, and in nine hundred and eighty-five out of a thousand cases like yours—”

Then she laughed at the look on his face. “No, I’m joking. Of course I’m not sure. This thing only you can decide. But I am sure that you should go off and do whatever it is you people do—I’m quite sure you have a ritual for it, even if you won’t discuss it with outsiders—when you very seriously consider abandoning a long-held premise of your existence.”

It was hard to argue with that, Jeffreyssai reflected, the more so when a domain expert had told you that you were, in fact, probably wrong.

“I concede,” Jeffreyssai said. Coming from his lips, the phrase was spoken with a commanding finality. There is no need to argue with me any further: you have won.

“Oh, stop it,” she said. She rose from her pillow in a single fluid shift without the slightest wasted motion. She didn’t flaunt her age, but she didn’t conceal it either. She took his outstretched hand, and raised it to her lips for a formal kiss. “Farewell, sensei.”

“Farewell?” repeated Jeffreyssai. That signified a higher order of departure than goodbye. “I do intend to visit you again, milady; and you are always welcome here.”

She walked toward the door without answering. At the doorway she paused, without turning around. “It won’t be the same,” she said. And then, without the movements seeming the least rushed, she walked away so swiftly it was almost like vanishing.

Jeffreyssai sighed. But at least, from here until the challenge proper, all his actions were prescribed, known quantities.

Leaving that formal reception area, he passed to his arena, and caused to be sent out messengers to his students, telling them that the next day’s classes must be improvised in his absence, and that there would be a test later.

And then he did nothing in particular. He read another hundred pages of the textbook he had borrowed; it wasn’t very good, but then the book he had loaned out in exchange wasn’t very good either. He wandered from room to room of his house, idly checking various storages to see if anything had been stolen (a deck of cards was missing, but that was all). From time to time his thoughts turned to tomorrow’s challenge, and he let them drift. Not directing his thoughts at all, only blocking out every thought that had ever previously occurred to him; and disallowing any kind of conclusion, or even any thought as to where his thoughts might be trending.

The sun set, and he watched it for a while, mind carefully put in idle. It was a fantastic balancing act to set your mind in idle without having to obsess about it, or exert energy to keep it that way; and years ago he would have sweated over it, but practice had long since made perfect.

The next morning he awoke with the chaos of the night’s dreaming fresh in his mind, and, doing his best to preserve the feeling of the chaos as well as its memory, he descended a flight of stairs, then another flight of stairs, then a flight of stairs after that, and finally came to the least fashionable room in his whole house.

It was white. That was pretty much it as far as the color scheme went.

All along a single wall were plaques, which, following the classic and suggested method, a younger Jeffreyssai had very carefully scribed himself, burning the concepts into his mind with each touch of the brush that wrote the words. That which can be destroyed by the truth should be. People can stand what is true, for they are already enduring it. Curiosity seeks to annihilate itself. Even one small plaque that showed nothing except a red horizontal slash. Symbols could be made to stand for anything; a flexibility of visual power that even the Bardic Conspiracy would balk at admitting outright.

Beneath the plaques, two sets of tally marks scratched into the wall. Under the plus column, two marks. Under the minus column, five marks. Seven times he had entered this room; five times he had decided not to change his mind; twice he had exited something of a different person. There was no set ratio prescribed, or set range—that would have been a mockery indeed. But if there were no marks in the plus column after a while, you might as well admit that there was no point in having the room, since you didn’t have the ability it stood for. Either that, or you’d been born knowing the truth and right of everything.

Jeffreyssai seated himself, not facing the plaques, but facing away from them, at the featureless white wall. It was better to have no visual distractions.

In his mind, he rehearsed first the meta-mnemonic, and then the various sub-mnemonics referenced, for the seven major principles and sixty-two specific techniques that were most likely to prove needful in the Ritual Of Changing One’s Mind. To this, Jeffreyssai added another mnemonic, reminding himself of his own fourteen most embarrassing oversights.

He did not take a deep breath. Regular breathing was best.

And then he asked himself the question.

Book III
The Machine in the Ghost

Minds: An Introduction
Interlude: The Power of Intelligence

L. The Simple Math of Evolution
131. An Alien God
132. The Wonder of Evolution
133. Evolutions Are Stupid (But Work Anyway)
134. No Evolutions for Corporations or Nanodevices
135. Evolving to Extinction
136. The Tragedy of Group Selectionism
137. Fake Optimization Criteria
138. Adaptation-Executers, Not Fitness-Maximizers
139. Evolutionary Psychology
140. An Especially Elegant Evolutionary Psychology Experiment
141. Superstimuli and the Collapse of Western Civilization
142. Thou Art Godshatter

M. Fragile Purposes
143. Belief in Intelligence
144. Humans in Funny Suits
145. Optimization and the Intelligence Explosion
146. Ghosts in the Machine
147. Artificial Addition
148. Terminal Values and Instrumental Values
149. Leaky Generalizations
150. The Hidden Complexity of Wishes
151. Anthropomorphic Optimism
152. Lost Purposes

N. A Human’s Guide to Words
153. The Parable of the Dagger
154. The Parable of Hemlock
155. Words as Hidden Inferences
156. Extensions and Intensions
157. Similarity Clusters
158. Typicality and Asymmetrical Similarity
159. The Cluster Structure of Thingspace
160. Disguised Queries
161. Neural Categories
162. How An Algorithm Feels From Inside
163. Disputing Definitions
164. Feel the Meaning
165. The Argument from Common Usage
166. Empty Labels
167. Taboo Your Words
168. Replace the Symbol with the Substance
169. Fallacies of Compression
170. Categorizing Has Consequences
171. Sneaking in Connotations
172. Arguing “By Definition”
173. Where to Draw the Boundary?
174. Entropy, and Short Codes
175. Mutual Information, and Density in Thingspace
176. Superexponential Conceptspace, and Simple Words
177. Conditional Independence, and Naive Bayes
178. Words as Mental Paintbrush Handles
179. Variable Question Fallacies
180. 37 Ways That Words Can Be Wrong

Interlude: An Intuitive Explanation of Bayes’s Theorem

Minds: An Introduction
by Rob Bensinger

You’re a mind, and that puts you in a pretty strange predicament.

Very few things get to be minds. You’re that odd bit of stuff in the universe that can form predictions and make plans, weigh and revise beliefs, suffer, dream, notice ladybugs, or feel a sudden craving for mango. You can even form, inside your mind, a picture of your whole mind. You can reason about your own reasoning process, and work to bring its operations more in line with your goals.

You’re a mind, implemented on a human brain. And it turns out that a human brain, for all its marvelous flexibility, is a lawful thing, a thing of pattern and routine. Your mind can follow a routine for a lifetime, without ever once noticing that it is doing so. And these routines can have great consequences.

When a mental pattern serves you well, we call that “rationality.”

You exist as you are, hardwired to exhibit certain species of rationality and certain species of irrationality, because of your ancestry. You, and all life on Earth, are descended from ancient self-replicating molecules. This replication process was initially clumsy and haphazard, and soon yielded replicable differences between the replicators. “Evolution” is our name for the change in these differences over time.

Since some of these reproducible differences impact reproducibility—a phenomenon called “selection”—evolution has resulted in organisms suited to reproduction in environments like the ones their ancestors had. Everything about you is built on the echoes of your ancestors’ struggles and victories.

And so here you are: a mind, carved from weaker minds, seeking to understand your own inner workings, that they can be improved upon—improved upon relative to your goals, and not those of your designer, evolution. What useful policies and insights can we take away from knowing that this is our basic situation?

Ghosts and Machines

Our brains, in their small-scale structure and dynamics, look like many other mechanical systems. Yet we rarely think of our minds in the same terms we think of objects in our environments or organs in our bodies. Our basic mental categories—belief, decision, word, idea, feeling, and so on—bear little resemblance to our physical categories.

Past philosophers have taken this observation and run with it, arguing that minds and brains are fundamentally distinct and separate phenomena. This is the view the philosopher Gilbert Ryle called “the dogma of the Ghost in the Machine.”¹ But modern scientists and philosophers who have rejected dualism haven’t necessarily replaced it with a better predictive model of how the mind works. Practically speaking, our purposes and desires still function like free-floating ghosts, like a magisterium cut off from the rest of our scientific knowledge. We can talk about “rationality” and “bias” and “how to change our minds,” but if those ideas are still imprecise and unconstrained by any overarching theory, our scientific-sounding language won’t protect us from making the same kinds of mistakes as those whose theoretical posits include spirits and essences.

Interestingly, the mystery and mystification surrounding minds doesn’t just obscure our view of humans. It also accrues to systems that seem mind-like or purposeful in evolutionary biology and artificial intelligence (AI). Perhaps, if we cannot readily glean what we are from looking at ourselves, we can learn more by using obviously inhuman processes as a mirror.

There are many ghosts to learn from here—ghosts past, and present, and yet to come. And these illusions are real cognitive events, real phenomena that we can study and explain. If there appears to be a ghost in the machine, that appearance is itself the hidden work of a machine.

The first sequence of The Machine in the Ghost, “The Simple Math of Evolution,” aims to communicate the dissonance and divergence between our hereditary history, our present-day biology, and our ultimate aspirations. This will require digging deeper than is common in introductions to evolution for non-biologists, which often restrict their attention to surface-level features of natural selection.

The third sequence, “A Human’s Guide to Words,” discusses the basic relationship between cognition and concept formation. This is followed by a longer essay introducing Bayesian inference.

Bridging the gap between these topics, “Fragile Purposes” abstracts from human cognition and evolution to the idea of minds and goal-directed systems at their most general. These essays serve the secondary purpose of explaining the author’s general approach to philosophy and the science of rationality, which is strongly informed by his work in AI.

Rebuilding Intelligence

Yudkowsky is a decision theorist and mathematician who works on foundational issues in Artificial General Intelligence (AGI), the theoretical study of domain-general problem-solving systems. Yudkowsky’s work in AI has been a major driving force behind his exploration of the psychology of human rationality, as he noted in his very first blog post on Overcoming Bias, The Martial Art of Rationality:

Such understanding as I have of rationality, I acquired in the course of wrestling with the challenge of Artificial General Intelligence (an endeavor which, to actually succeed, would require sufficient mastery of rationality to build a complete working rationalist out of toothpicks and rubber bands). In most ways the AI problem is enormously more demanding than the personal art of rationality, but in some ways it is actually easier. In the martial art of mind, we need to acquire the real-time procedural skill of pulling the right levers at the right time on a large, pre-existing thinking machine whose innards are not end-user-modifiable. Some of the machinery is optimized for evolutionary selection pressures that run directly counter to our declared goals in using it. Deliberately we decide that we want to seek only the truth; but our brains have hardwired support for rationalizing falsehoods. [ . . . ]

Trying to synthesize a personal art of rationality, using the science of rationality, may prove awkward: One imagines trying to invent a martial art using an abstract theory of physics, game theory, and human anatomy. But humans are not reflectively blind; we do have a native instinct for introspection. The inner eye is not sightless; but it sees blurrily, with systematic distortions. We need, then, to apply the science to our intuitions, to use the abstract knowledge to correct our mental movements and augment our metacognitive skills. We are not writing a computer program to make a string puppet execute martial arts forms; it is our own mental limbs that we must move. Therefore we must connect theory to practice. We must come to see what the science means, for ourselves, for our daily inner life.

From Yudkowsky’s perspective, I gather, talking about human rationality without saying anything interesting about AI is about as difficult as talking about AI without saying anything interesting about rationality.

In the long run, Yudkowsky predicts that AI will come to surpass humans in an “intelligence explosion,” a scenario in which self-modifying AI improves its own ability to productively redesign itself, kicking off a rapid succession of further self-improvements. The term “technological singularity” is sometimes used in place of “intelligence explosion;” until January 2013, MIRI was named “the Singularity Institute for Artificial Intelligence” and hosted an annual Singularity Summit. Since then, Yudkowsky has come to favor I.J. Good’s older term, “intelligence explosion,” to help distinguish his views from other futurist predictions, such as Ray Kurzweil’s exponential technological progress thesis.²

Technologies like smarter-than-human AI seem likely to result in large societal upheavals, for the better or for the worse. Yudkowsky coined the term “Friendly AI theory” to refer to research into techniques for aligning an AGI’s preferences with the preferences of humans. At this point, very little is known about when generally intelligent software might be invented, or what safety approaches would work well in such cases. Present-day autonomous AI can already be quite challenging to verify and validate with much confidence, and many current techniques are not likely to generalize to more intelligent and adaptive systems. “Friendly AI” is therefore closer to a menagerie of basic mathematical and philosophical questions than to a well-specified set of programming objectives.

As of 2015, Yudkowsky’s views on the future of AI continue to be debated by technology forecasters and AI researchers in industry and academia, who have yet to converge on a consensus position. Nick Bostrom’s book Superintelligence provides a big-picture summary of the many moral and strategic questions raised by smarter-than-human AI.³

For a general introduction to the field of AI, the most widely used textbook is Russell and Norvig’s Artificial Intelligence: A Modern Approach.⁴ In a chapter discussing the moral and philosophical questions raised by AI, Russell and Norvig note the technical difficulty of specifying good behavior in strongly adaptive AI:

[Yudkowsky] asserts that friendliness (a desire not to harm humans) should be designed in from the start, but that the designers should recognize both that their own designs may be flawed, and that the robot will learn and evolve over time. Thus the challenge is one of mechanism design—to define a mechanism for evolving AI systems under a system of checks and balances, and to give the systems utility functions that will remain friendly in the face of such changes. We can’t just give a program a static utility function, because circumstances, and our desired responses to circumstances, change over time.

Disturbed by the possibility that future progress in AI, nanotechnology, biotechnology, and other fields could endanger human civilization, Bostrom and Ćirković compiled the first academic anthology on the topic, Global Catastrophic Risks.⁵ The most extreme of these are the existential risks, risks that could result in the permanent stagnation or extinction of humanity.⁶

People (experts included) tend to be extraordinarily bad at forecasting major future events (new technologies included). Part of Yudkowsky’s goal in discussing rationality is to figure out which biases are interfering with our ability to predict and prepare for big upheavals well in advance. Yudkowsky’s contributions to the Global Catastrophic Risks volume, “Cognitive biases potentially affecting judgement of global risks” and “Artificial intelligence as a positive and negative factor in global risk,” tie together his research in cognitive science and AI. Yudkowsky and Bostrom summarize near-term concerns along with long-term ones in a chapter of the Cambridge Handbook of Artificial Intelligence, “The ethics of artificial intelligence.”⁷

Though this is a book about human rationality, the topic of AI has relevance as a source of simple illustrations of aspects of human cognition. Long-term technology forecasting is also one of the more important applications of Bayesian rationality, which can model correct reasoning even in domains where the data is scarce or equivocal.

Knowing the design can tell you much about the designer; and knowing the designer can tell you much about the design.

We’ll begin, then, by inquiring into what our own designer can teach us about ourselves.

1. Gilbert Ryle, The Concept of Mind (University of Chicago Press, 1949).

2. Irving John Good, “Speculations Concerning the First Ultraintelligent Machine,” in Advances in Computers, ed. Franz L. Alt and Morris Rubinoff, vol. 6 (New York: Academic Press, 1965), 31–88, doi:10.1016/S0065-2458(08)60418-0.

3. Nick Bostrom, Superintelligence: Paths, Dangers, Strategies (Oxford University Press, 2014).

4. Stuart J. Russell and Peter Norvig, Artificial Intelligence: A Modern Approach, 3rd ed. (Upper Saddle River, NJ: Prentice-Hall, 2010).

5. Bostrom and Ćirković, Global Catastrophic Risks.

6. An example of a possible existential risk is the “grey goo” scenario, in which molecular robots designed to efficiently self-replicate do their job too well, rapidly outcompeting living organisms as they consume the Earth’s available matter.

7. Nick Bostrom and Eliezer Yudkowsky, “The Ethics of Artificial Intelligence,” in The Cambridge Handbook of Artificial Intelligence, ed. Keith Frankish and William Ramsey (New York: Cambridge University Press, 2014).

Interlude
The Power of Intelligence

In our skulls we carry around three pounds of slimy, wet, grayish tissue, corrugated like crumpled toilet paper.

You wouldn’t think, to look at the unappetizing lump, that it was some of the most powerful stuff in the known universe. If you’d never seen an anatomy textbook, and you saw a brain lying in the street, you’d say “Yuck!” and try not to get any of it on your shoes. Aristotle thought the brain was an organ that cooled the blood. It doesn’t look dangerous.

Five million years ago, the ancestors of lions ruled the day, the ancestors of wolves roamed the night. The ruling predators were armed with teeth and claws—sharp, hard cutting edges, backed up by powerful muscles. Their prey, in self-defense, evolved armored shells, sharp horns, toxic venoms, camouflage. The war had gone on through hundreds of eons and countless arms races. Many a loser had been removed from the game, but there was no sign of a winner. Where one species had shells, another species would evolve to crack them; where one species became poisonous, another would evolve to tolerate the poison. Each species had its private niche—for who could live in the seas and the skies and the land at once? There was no ultimate weapon and no ultimate defense and no reason to believe any such thing was possible.

Then came the Day of the Squishy Things.

They had no armor. They had no claws. They had no venoms.

If you saw a movie of a nuclear explosion going off, and you were told an Earthly life form had done it, you would never in your wildest dreams imagine that the Squishy Things could be responsible. After all, Squishy Things aren’t radioactive.

In the beginning, the Squishy Things had no fighter jets, no machine guns, no rifles, no swords. No bronze, no iron. No hammers, no anvils, no tongs, no smithies, no mines. All the Squishy Things had were squishy fingers—too weak to break a tree, let alone a mountain. Clearly not dangerous. To cut stone you would need steel, and the Squishy Things couldn’t excrete steel. In the environment there were no steel blades for Squishy fingers to pick up. Their bodies could not generate temperatures anywhere near hot enough to melt metal. The whole scenario was obviously absurd.

And as for the Squishy Things manipulating DNA—that would have been beyond ridiculous. Squishy fingers are not that small. There is no access to DNA from the Squishy level; it would be like trying to pick up a hydrogen atom. Oh, technically it’s all one universe, technically the Squishy Things and DNA are part of the same world, the same unified laws of physics, the same great web of causality. But let’s be realistic: you can’t get there from here.

Even if Squishy Things could someday evolve to do any of those feats, it would take thousands of millennia. We have watched the ebb and flow of Life through the eons, and let us tell you, a year is not even a single clock tick of evolutionary time. Oh, sure, technically a year is six hundred trillion trillion trillion trillion Planck intervals. But nothing ever happens in less than six hundred million trillion trillion trillion trillion Planck intervals, so it’s a moot point. The Squishy Things, as they run across the savanna now, will not fly across continents for at least another ten million years; no one could have that much sex.

Now explain to me again why an Artificial Intelligence can’t do anything interesting over the Internet unless a human programmer builds it a robot body.

I have observed that someone’s flinch-reaction to “intelligence”—the thought that crosses their mind in the first half-second after they hear the word “intelligence”—often determines their flinch-reaction to the notion of an intelligence explosion. Often they look up the keyword “intelligence” and retrieve the concept booksmarts—a mental image of the Grand Master chess player who can’t get a date, or a college professor who can’t survive outside academia.

“It takes more than intelligence to succeed professionally,” people say, as if charisma resided in the kidneys, rather than the brain. “Intelligence is no match for a gun,” they say, as if guns had grown on trees. “Where will an Artificial Intelligence get money?” they ask, as if the first Homo sapiens had found dollar bills fluttering down from the sky, and used them at convenience stores already in the forest. The human species was not born into a market economy. Bees won’t sell you honey if you offer them an electronic funds transfer. The human species imagined money into existence, and it exists—for us, not mice or wasps—because we go on believing in it.

I keep trying to explain to people that the archetype of intelligence is not Dustin Hoffman in Rain Man. It is a human being, period. It is squishy things that explode in a vacuum, leaving footprints on their moon. Within that gray wet lump is the power to search paths through the great web of causality, and find a road to the seemingly impossible—the power sometimes called creativity.

People—venture capitalists in particular—sometimes ask how, if the Machine Intelligence Research Institute successfully builds a true AI, the results will be commercialized. This is what we call a framing problem.

Or maybe it’s something deeper than a simple clash of assumptions. With a bit of creative thinking, people can imagine how they would go about travelling to the Moon, or curing smallpox, or manufacturing computers. To imagine a trick that could accomplish all these things at once seems downright impossible—even though such a power resides only a few centimeters behind their own eyes. The gray wet thing still seems mysterious to the gray wet thing.

And so, because people can’t quite see how it would all work, the power of intelligence seems less real; harder to imagine than a tower of fire sending a ship to Mars. The prospect of visiting Mars captures the imagination. But if one should promise a Mars visit, and also a grand unified theory of physics, and a proof of the Riemann Hypothesis, and a cure for obesity, and a cure for cancer, and a cure for aging, and a cure for stupidity—well, it just sounds wrong, that’s all.

And well it should. It’s a serious failure of imagination to think that intelligence is good for so little. Who could have imagined, ever so long ago, what minds would someday do? We may not even know what our real problems are.

But meanwhile, because it’s hard to see how one process could have such diverse powers, it’s hard to imagine that one fell swoop could solve even such prosaic problems as obesity and cancer and aging.

Well, one trick cured smallpox and built airplanes and cultivated wheat and tamed fire. Our current science may not agree yet on how exactly the trick works, but it works anyway. If you are temporarily ignorant about a phenomenon, that is a fact about your current state of mind, not a fact about the phenomenon. A blank map does not correspond to a blank territory. If one does not quite understand that power which put footprints on the Moon, nonetheless, the footprints are still there—real footprints, on a real Moon, put there by a real power. If one were to understand deeply enough, one could create and shape that power. Intelligence is as real as electricity. It’s merely far more powerful, far more dangerous, has far deeper implications for the unfolding story of life in the universe—and it’s a tiny little bit harder to figure out how to build a generator.

Part L
The Simple Math of Evolution

131
An Alien God

“A curious aspect of the theory of evolution,” said Jacques Monod, “is that everybody thinks he understands it.”

A human being, looking at the natural world, sees a thousand times purpose. A rabbit’s legs, built and articulated for running; a fox’s jaws, built and articulated for tearing. But what you see is not exactly what is there . . .

In the days before Darwin, the cause of all this apparent purposefulness was a very great puzzle unto science. The Goddists said “God did it,” because you get 50 bonus points each time you use the word “God” in a sentence. Yet perhaps I’m being unfair. In the days before Darwin, it seemed like a much more reasonable hypothesis. Find a watch in the desert, said William Paley, and you can infer the existence of a watchmaker.

But when you look at all the apparent purposefulness in Nature, rather than picking and choosing your examples, you start to notice things that don’t fit the Judeo-Christian concept of one benevolent God. Foxes seem well-designed to catch rabbits. Rabbits seem well-designed to evade foxes. Was the Creator having trouble making up Its mind?

When I design a toaster oven, I don’t design one part that tries to get electricity to the coils and a second part that tries to prevent electricity from getting to the coils. It would be a waste of effort. Who designed the ecosystem, with its predators and prey, viruses and bacteria? Even the cactus plant, which you might think well-designed to provide water and fruit to desert animals, is covered with inconvenient spines.

The ecosystem would make much more sense if it wasn’t designed by a unitary Who, but, rather, created by a horde of deities—say from the Hindu or Shinto religions. This handily explains both the ubiquitous purposefulnesses, and the ubiquitous conflicts: More than one deity acted, often at cross-purposes. The fox and rabbit were both designed, but by distinct competing deities. I wonder if anyone ever remarked on the seemingly excellent evidence thus provided for Hinduism over Christianity. Probably not.

Similarly, the Judeo-Christian God is alleged to be benevolent—well, sort of. And yet much of nature’s purposefulness seems downright cruel. Darwin suspected a non-standard Creator for studying Ichneumon wasps, whose paralyzing stings preserve its prey to be eaten alive by its larvae: “I cannot persuade myself,” wrote Darwin, “that a beneficent and omnipotent God would have designedly created the Ichneumonidae with the express intention of their feeding within the living bodies of Caterpillars, or that a cat should play with mice.”¹ I wonder if any earlier thinker remarked on the excellent evidence thus provided for Manichaean religions over monotheistic ones.

By now we all know the punchline: you just say “evolution.”

I worry that’s how some people are absorbing the “scientific” explanation, as a magical purposefulness factory in Nature. I’ve previously discussed the case of Storm from the movie X-Men, who in one mutation gets the ability to throw lightning bolts. Why? Well, there’s this thing called “evolution” that somehow pumps a lot of purposefulness into Nature, and the changes happen through “mutations.” So if Storm gets a really large mutation, she can be redesigned to throw lightning bolts. Radioactivity is a popular super origin: radiation causes mutations, so more powerful radiation causes more powerful mutations. That’s logic.

But evolution doesn’t allow just any kind of purposefulness to leak into Nature. That’s what makes evolution a success as an empirical hypothesis. If evolutionary biology could explain a toaster oven, not just a tree, it would be worthless. There’s a lot more to evolutionary theory than pointing at Nature and saying, “Now purpose is allowed,” or “Evolution did it!” The strength of a theory is not what it allows, but what it prohibits; if you can invent an equally persuasive explanation for any outcome, you have zero knowledge.

“Many non-biologists,” observed George Williams, “think that it is for their benefit that rattles grow on rattlesnake tails.”² Bzzzt! This kind of purposefulness is not allowed. Evolution doesn’t work by letting flashes of purposefulness creep in at random—reshaping one species for the benefit of a random recipient.

Evolution is powered by a systematic correlation between the different ways that different genes construct organisms, and how many copies of those genes make it into the next generation. For rattles to grow on rattlesnake tails, rattle-growing genes must become more and more frequent in each successive generation. (Actually genes for incrementally more complex rattles, but if I start describing all the fillips and caveats to evolutionary biology, we really will be here all day.)

There isn’t an Evolution Fairy that looks over the current state of Nature, decides what would be a “good idea,” and chooses to increase the frequency of rattle-constructing genes.

I suspect this is where a lot of people get stuck, in evolutionary biology. They understand that “helpful” genes become more common, but “helpful” lets any sort of purpose leak in. They don’t think there’s an Evolution Fairy, yet they ask which genes will be “helpful” as if a rattlesnake gene could “help” non-rattlesnakes.

The key realization is that there is no Evolution Fairy. There’s no outside force deciding which genes ought to be promoted. Whatever happens, happens because of the genes themselves.

Genes for constructing (incrementally better) rattles must have somehow ended up more frequent in the rattlesnake gene pool, because of the rattle. In this case it’s probably because rattlesnakes with better rattles survive more often—rather than mating more successfully, or having brothers that reproduce more successfully, etc.

Maybe predators are wary of rattles and don’t step on the snake. Or maybe the rattle diverts attention from the snake’s head. (As George Williams suggests, “The outcome of a fight between a dog and a viper would depend very much on whether the dog initially seized the reptile by the head or by the tail.”)

But that’s just a snake’s rattle. There are much more complicated ways that a gene can cause copies of itself to become more frequent in the next generation. Your brother or sister shares half your genes. A gene that sacrifices one unit of resources to bestow three units of resource on a brother, may promote some copies of itself by sacrificing one of its constructed organisms. (If you really want to know all the details and caveats, buy a book on evolutionary biology; there is no royal road.)

The main point is that the gene’s effect must cause copies of that gene to become more frequent in the next generation. There’s no Evolution Fairy that reaches in from outside. There’s nothing which decides that some genes are “helpful” and should, therefore, increase in frequency. It’s just cause and effect, starting from the genes themselves.

This explains the strange conflicting purposefulness of Nature, and its frequent cruelty. It explains even better than a horde of Shinto deities.

Why is so much of Nature at war with other parts of Nature? Because there isn’t one Evolution directing the whole process. There’s as many different “evolutions” as reproducing populations. Rabbit genes are becoming more or less frequent in rabbit populations. Fox genes are becoming more or less frequent in fox populations. Fox genes which construct foxes that catch rabbits, insert more copies of themselves in the next generation. Rabbit genes which construct rabbits that evade foxes are naturally more common in the next generation of rabbits. Hence the phrase “natural selection.”

Why is Nature cruel? You, a human, can look at an Ichneumon wasp, and decide that it’s cruel to eat your prey alive. You can decide that if you’re going to eat your prey alive, you can at least have the decency to stop it from hurting. It would scarcely cost the wasp anything to anesthetize its prey as well as paralyze it. Or what about old elephants, who die of starvation when their last set of teeth fall out? These elephants aren’t going to reproduce anyway. What would it cost evolution—the evolution of elephants, rather—to ensure that the elephant dies right away, instead of slowly and in agony? What would it cost evolution to anesthetize the elephant, or give it pleasant dreams before it dies? Nothing; that elephant won’t reproduce more or less either way.

If you were talking to a fellow human, trying to resolve a conflict of interest, you would be in a good negotiating position—would have an easy job of persuasion. It would cost so little to anesthetize the prey, to let the elephant die without agony! Oh please, won’t you do it, kindly . . . um . . .

There’s no one to argue with.

Human beings fake their justifications, figure out what they want using one method, and then justify it using another method. There’s no Evolution of Elephants Fairy that’s trying to (a) figure out what’s best for elephants, and then (b) figure out how to justify it to the Evolutionary Overseer, who (c) doesn’t want to see reproductive fitness decreased, but is (d) willing to go along with the painless-death idea, so long as it doesn’t actually harm any genes.

There’s no advocate for the elephants anywhere in the system.

Humans, who are often deeply concerned for the well-being of animals, can be very persuasive in arguing how various kindnesses wouldn’t harm reproductive fitness at all. Sadly, the evolution of elephants doesn’t use a similar algorithm; it doesn’t select nice genes that can plausibly be argued to help reproductive fitness. Simply: genes that replicate more often become more frequent in the next generation. Like water flowing downhill, and equally benevolent.

A human, looking over Nature, starts thinking of all the ways we would design organisms. And then we tend to start rationalizing reasons why our design improvements would increase reproductive fitness—a political instinct, trying to sell your own preferred option as matching the boss’s favored justification.

And so, amateur evolutionary biologists end up making all sorts of wonderful and completely mistaken predictions. Because the amateur biologists are drawing their bottom line—and more importantly, locating their prediction in hypothesis-space—using a different algorithm than evolutions use to draw their bottom lines.

A human engineer would have designed human taste buds to measure how much of each nutrient we had, and how much we needed. When fat was scarce, almonds or cheeseburgers would taste delicious. But if you started to become obese, or if vitamins were lacking, lettuce would taste delicious. But there is no Evolution of Humans Fairy, which intelligently planned ahead and designed a general system for every contingency. It was a reliable invariant of humans’ ancestral environment that calories were scarce. So genes whose organisms loved calories, became more frequent. Like water flowing downhill.

We are simply the embodied history of which organisms did in fact survive and reproduce, not which organisms ought prudentially to have survived and reproduced.

The human retina is constructed backward: The light-sensitive cells are at the back, and the nerves emerge from the front and go back through the retina into the brain. Hence the blind spot. To a human engineer, this looks simply stupid—and other organisms have independently evolved retinas the right way around. Why not redesign the retina?

The problem is that no single mutation will reroute the whole retina simultaneously. A human engineer can redesign multiple parts simultaneously, or plan ahead for future changes. But if a single mutation breaks some vital part of the organism, it doesn’t matter what wonderful things a Fairy could build on top of it—the organism dies and the gene decreases in frequency.

If you turn around the retina’s cells without also reprogramming the nerves and optic cable, the system as a whole won’t work. It doesn’t matter that, to a Fairy or a human engineer, this is one step forward in redesigning the retina. The organism is blind. Evolution has no foresight, it is simply the frozen history of which organisms did in fact reproduce. Evolution is as blind as a halfway-redesigned retina.

Find a watch in a desert, said William Paley, and you can infer the watchmaker. There were once those who denied this, who thought that life “just happened” without need of an optimization process, mice being spontaneously generated from straw and dirty shirts.

If we ask who was more correct—the theologians who argued for a Creator-God, or the intellectually unfulfilled atheists who argued that mice spontaneously generated—then the theologians must be declared the victors: evolution is not God, but it is closer to God than it is to pure random entropy. Mutation is random, but selection is non-random. This doesn’t mean an intelligent Fairy is reaching in and selecting. It means there’s a non-zero statistical correlation between the gene and how often the organism reproduces. Over a few million years, that non-zero statistical correlation adds up to something very powerful. It’s not a god, but it’s more closely akin to a god than it is to snow on a television screen.

In a lot of ways, evolution is like unto theology. “Gods are ontologically distinct from creatures,” said Damien Broderick, “or they’re not worth the paper they’re written on.” And indeed, the Shaper of Life is not itself a creature. Evolution is bodiless, like the Judeo-Christian deity. Omnipresent in Nature, immanent in the fall of every leaf. Vast as a planet’s surface. Billions of years old. Itself unmade, arising naturally from the structure of physics. Doesn’t that all sound like something that might have been said about God?

And yet the Maker has no mind, as well as no body. In some ways, its handiwork is incredibly poor design by human standards. It is internally divided. Most of all, it isn’t nice.

In a way, Darwin discovered God—a God that failed to match the preconceptions of theology, and so passed unheralded. If Darwin had discovered that life was created by an intelligent agent—a bodiless mind that loves us, and will smite us with lightning if we dare say otherwise—people would have said “My gosh! That’s God!”

But instead Darwin discovered a strange alien God—not comfortably “ineffable,” but really genuinely different from us. Evolution is not a God, but if it were, it wouldn’t be Jehovah. It would be H. P. Lovecraft’s Azathoth, the blind idiot God burbling chaotically at the center of everything, surrounded by the thin monotonous piping of flutes.

Which you might have predicted, if you had really looked at Nature.

So much for the claim some religionists make, that they believe in a vague deity with a correspondingly high probability. Anyone who really believed in a vague deity, would have recognized their strange inhuman creator when Darwin said “Aha!”

So much for the claim some religionists make, that they are waiting innocently curious for Science to discover God. Science has already discovered the sort-of-godlike maker of humans—but it wasn’t what the religionists wanted to hear. They were waiting for the discovery of their God, the highly specific God they want to be there. They shall wait forever, for the great discovery has already taken place, and the winner is Azathoth.

Well, more power to us humans. I like having a Creator I can outwit. Beats being a pet. I’m glad it was Azathoth and not Odin.

1. Francis Darwin, ed., The Life and Letters of Charles Darwin, vol. 2 (John Murray, 1887).

2. George C. Williams, Adaptation and Natural Selection: A Critique of Some Current Evolutionary Thought, Princeton Science Library (Princeton, NJ: Princeton University Press, 1966).

132
The Wonder of Evolution

The wonder of evolution is that it works at all.

I mean that literally: If you want to marvel at evolution, that’s what’s marvel-worthy.

How does optimization first arise in the universe? If an intelligent agent designed Nature, who designed the intelligent agent? Where is the first design that has no designer? The puzzle is not how the first stage of the bootstrap can be super-clever and super-efficient; the puzzle is how it can happen at all.

Evolution resolves the infinite regression, not by being super-clever and super-efficient, but by being stupid and inefficient and working anyway. This is the marvel.

For professional reasons, I often have to discuss the slowness, randomness, and blindness of evolution. Afterward someone says: “You just said that evolution can’t plan simultaneous changes, and that evolution is very inefficient because mutations are random. Isn’t that what the creationists say? That you couldn’t assemble a watch by randomly shaking the parts in a box?”

But the reply to creationists is not that you can assemble a watch by shaking the parts in a box. The reply is that this is not how evolution works. If you think that evolution does work by whirlwinds assembling 747s, then the creationists have successfully misrepresented biology to you; they’ve sold the strawman.

The real answer is that complex machinery evolves either incrementally, or by adapting previous complex machinery used for a new purpose. Squirrels jump from treetop to treetop using just their muscles, but the length they can jump depends to some extent on the aerodynamics of their bodies. So now there are flying squirrels, so aerodynamic they can glide short distances. If birds were wiped out, the descendants of flying squirrels might reoccupy that ecological niche in ten million years, gliding membranes transformed into wings. And the creationists would say, “What good is half a wing? You’d just fall down and splat. How could squirrelbirds possibly have evolved incrementally?”

That’s how one complex adaptation can jump-start a new complex adaptation. Complexity can also accrete incrementally, starting from a single mutation.

First comes some gene A which is simple, but at least a little useful on its own, so that A increases to universality in the gene pool. Now along comes gene B, which is only useful in the presence of A, but A is reliably present in the gene pool, so there’s a reliable selection pressure in favor of B. Now a modified version of A^* arises, which depends on B, but doesn’t break B’s dependency on A∕A^*. Then along comes C, which depends on A^* and B, and B^*, which depends on A^* and C. Soon you’ve got “irreducibly complex” machinery that breaks if you take out any single piece.

And yet you can still visualize the trail backward to that single piece: you can, without breaking the whole machine, make one piece less dependent on another piece, and do this a few times, until you can take out one whole piece without breaking the machine, and so on until you’ve turned a ticking watch back into a crude sundial.

Here’s an example: DNA stores information very nicely, in a durable format that allows for exact duplication. A ribosome turns that stored information into a sequence of amino acids, a protein, which folds up into a variety of chemically active shapes. The combined system, DNA and ribosome, can build all sorts of protein machinery. But what good is DNA, without a ribosome that turns DNA information into proteins? What good is a ribosome, without DNA to tell it which proteins to make?

Organisms don’t always leave fossils, and evolutionary biology can’t always figure out the incremental pathway. But in this case we do know how it happened. RNA shares with DNA the property of being able to carry information and replicate itself, although RNA is less durable and copies less accurately. And RNA also shares the ability of proteins to fold up into chemically active shapes, though it’s not as versatile as the amino acid chains of proteins. Almost certainly, RNA is the single A which predates the mutually dependent A^* and B.

It’s just as important to note that RNA does the combined job of DNA and proteins poorly, as that it does the combined job at all. It’s amazing enough that a single molecule can both store information and manipulate chemistry. For it to do the job well would be a wholly unnecessary miracle.

What was the very first replicator ever to exist? It may well have been an RNA strand, because by some strange coincidence, the chemical ingredients of RNA are chemicals that would have arisen naturally on the prebiotic Earth of 4 billion years ago. Please note: evolution does not explain the origin of life; evolutionary biology is not supposed to explain the first replicator, because the first replicator does not come from another replicator. Evolution describes statistical trends in replication. The first replicator wasn’t a statistical trend, it was a pure accident. The notion that evolution should explain the origin of life is a pure strawman—more creationist misrepresentation.

If you’d been watching the primordial soup on the day of the first replicator, the day that reshaped the Earth, you would not have been impressed by how well the first replicator replicated. The first replicator probably copied itself like a drunken monkey on LSD. It would have exhibited none of the signs of careful fine-tuning embodied in modern replicators, because the first replicator was an accident. It was not needful for that single strand of RNA, or chemical hypercycle, or pattern in clay, to replicate gracefully. It just had to happen at all. Even so, it was probably very improbable, considered in an isolated event—but it only had to happen once, and there were a lot of tide pools. A few billions of years later, the replicators are walking on the Moon.

The first accidental replicator was the most important molecule in the history of time. But if you praised it too highly, attributing to it all sorts of wonderful replication-aiding capabilities, you would be missing the whole point.

Don’t think that, in the political battle between evolutionists and creationists, whoever praises evolution must be on the side of science. Science has a very exact idea of the capabilities of evolution. If you praise evolution one millimeter higher than this, you’re not “fighting on evolution’s side” against creationism. You’re being scientifically inaccurate, full stop. You’re falling into a creationist trap by insisting that, yes, a whirlwind does have the power to assemble a 747! Isn’t that amazing! How wonderfully intelligent is evolution, how praiseworthy! Look at me, I’m pledging my allegiance to science! The more nice things I say about evolution, the more I must be on evolution’s side against the creationists!

But to praise evolution too highly destroys the real wonder, which is not how well evolution designs things, but that a naturally occurring process manages to design anything at all.

So let us dispose of the idea that evolution is a wonderful designer, or a wonderful conductor of species destinies, which we human beings ought to imitate. For human intelligence to imitate evolution as a designer, would be like a sophisticated modern bacterium trying to imitate the first replicator as a biochemist. As T. H. Huxley, “Darwin’s Bulldog,” put it:¹

Let us understand, once and for all, that the ethical progress of society depends, not on imitating the cosmic process, still less in running away from it, but in combating it.

Huxley didn’t say that because he disbelieved in evolution, but because he understood it all too well.

1. Thomas Henry Huxley, Evolution and Ethics and Other Essays (Macmillan, 1894).

133
Evolutions Are Stupid (But Work Anyway)

In the previous essay, I wrote:

Science has a very exact idea of the capabilities of evolution. If you praise evolution one millimeter higher than this, you’re not “fighting on evolution’s side” against creationism. You’re being scientifically inaccurate, full stop.

In this essay I describe some well-known inefficiencies and limitations of evolutions. I say “evolutions,” plural, because fox evolution works at cross-purposes to rabbit evolution, and neither can talk to snake evolution to learn how to build venomous fangs.

So I am talking about limitations of evolution here, but this does not mean I am trying to sneak in creationism. This is standard Evolutionary Biology 201. (583 if you must derive the equations.) Evolutions, thus limited, can still explain observed biology; in fact the limitations are necessary to make sense of it. Remember that the wonder of evolutions is not how well they work, but that they work at all.

Human intelligence is so complicated that no one has any good way to calculate how efficient it is. Natural selection, though not simple, is simpler than a human brain; and correspondingly slower and less efficient, as befits the first optimization process ever to exist. In fact, evolutions are simple enough that we can calculate exactly how stupid they are.

Evolutions are slow. How slow? Suppose there’s a beneficial mutation that conveys a fitness advantage of 3%: on average, bearers of this gene have 1.03 times as many children as non-bearers. Assuming that the mutation spreads at all, how long will it take to spread through the whole population? That depends on the population size. A gene conveying a 3% fitness advantage, spreading through a population of 100,000, would require an average of 768 generations to reach universality in the gene pool. A population of 500,000 would require 875 generations. The general formula is

Generations to fixation = 2ln(N) / s,

where N is the population size and (1 + s) is the fitness. (If each bearer of the gene has 1.03 times as many children as a non-bearer, s = 0.03.)

Thus, if the population size were 1,000,000—the estimated population in hunter-gatherer times—then it would require 2,763 generations for a gene conveying a 1% advantage to spread through the gene pool.¹

This should not be surprising; genes have to do all their own work of spreading. There’s no Evolution Fairy who can watch the gene pool and say, “Hm, that gene seems to be spreading rapidly—I should distribute it to everyone.” In a human market economy, someone who is legitimately getting 20% returns on investment—especially if there’s an obvious, clear mechanism behind it—can rapidly acquire more capital from other investors; and others will start duplicate enterprises. Genes have to spread without stock markets or banks or imitators—as if Henry Ford had to make one car, sell it, buy the parts for 1.01 more cars (on average), sell those cars, and keep doing this until he was up to a million cars.

All this assumes that the gene spreads in the first place. Here the equation is simpler and ends up not depending at all on population size:

Probability of fixation = 2s.

A mutation conveying a 3% advantage (which is pretty darned large, as mutations go) has a 6% chance of spreading, at least on that occasion.² Mutations can happen more than once, but in a population of a million with a copying fidelity of 10^-8 errors per base per generation, you may have to wait a hundred generations for another chance, and then it still has only a 6% chance of fixating.

Still, in the long run, an evolution has a good shot at getting there eventually. (This is going to be a running theme.)

Complex adaptations take a very long time to evolve. First comes allele A, which is advantageous of itself, and requires a thousand generations to fixate in the gene pool. Only then can another allele B, which depends on A, begin rising to fixation. A fur coat is not a strong advantage unless the environment has a statistically reliable tendency to throw cold weather at you. Well, genes form part of the environment of other genes, and if B depends on A, then B will not have a strong advantage unless A is reliably present in the genetic environment.

Let’s say that B confers a 5% advantage in the presence of A, no advantage otherwise. Then while A is still at 1% frequency in the population, B only confers its advantage 1 out of 100 times, so the average fitness advantage of B is 0.05%, and B’s probability of fixation is 0.1%. With a complex adaptation, first A has to evolve over a thousand generations, then B has to evolve over another thousand generations, then A^* evolves over another thousand generations . . . and several million years later, you’ve got a new complex adaptation.

Then other evolutions don’t imitate it. If snake evolution develops an amazing new venom, it doesn’t help fox evolution or lion evolution.

Contrast all this to a human programmer, who can design a new complex mechanism with a hundred interdependent parts over the course of a single afternoon. How is this even possible? I don’t know all the answer, and my guess is that neither does science; human brains are much more complicated than evolutions. I could wave my hands and say something like “goal-directed backward chaining using combinatorial modular representations,” but you would not thereby be enabled to design your own human. Still: Humans can foresightfully design new parts in anticipation of later designing other new parts; produce coordinated simultaneous changes in interdependent machinery; learn by observing single test cases; zero in on problem spots and think abstractly about how to solve them; and prioritize which tweaks are worth trying, rather than waiting for a cosmic ray strike to produce a good one. By the standards of natural selection, this is simply magic.

Humans can do things that evolutions probably can’t do period over the expected lifetime of the universe. As the eminent biologist Cynthia Kenyon once put it at a dinner I had the honor of attending, “One grad student can do things in an hour that evolution could not do in a billion years.” According to biologists’ best current knowledge, evolutions have invented a fully rotating wheel on a grand total of three occasions.

And don’t forget the part where the programmer posts the code snippet to the Internet.

Yes, some evolutionary handiwork is impressive even by comparison to the best technology of Homo sapiens. But our Cambrian explosion only started, we only really began accumulating knowledge, around . . . what, four hundred years ago? In some ways, biology still excels over the best human technology: we can’t build a self-replicating system the size of a butterfly. In other ways, human technology leaves biology in the dust. We got wheels, we got steel, we got guns, we got knives, we got pointy sticks; we got rockets, we got transistors, we got nuclear power plants. With every passing decade, that balance tips further.

So, once again: for a human to look to natural selection as inspiration on the art of design is like a sophisticated modern bacterium trying to imitate the first awkward replicator’s biochemistry. The first replicator would be eaten instantly if it popped up in today’s competitive ecology. The same fate would accrue to any human planner who tried making random point mutations to their strategies and waiting 768 iterations of testing to adopt a 3% improvement.

Don’t praise evolutions one millimeter more than they deserve.

Coming up next: More exciting mathematical bounds on evolution!

1. Dan Graur and Wen-Hsiung Li, Fundamentals of Molecular Evolution, 2nd ed. (Sunderland, MA: Sinauer Associates, 2000).

2. John B. S. Haldane, “A Mathematical Theory of Natural and Artificial Selection,” Mathematical Proceedings of the Cambridge Philosophical Society 23 (5 1927): 607–615, doi:10.1017/S0305004100011750.

134
No Evolutions for Corporations or Nanodevices

The laws of physics and the rules of math don’t cease to apply. That leads me to believe that evolution doesn’t stop. That further leads me to believe that nature—bloody in tooth and claw, as some have termed it—will simply be taken to the next level . . .

[Getting rid of Darwinian evolution is] like trying to get rid of gravitation. So long as there are limited resources and multiple competing actors capable of passing on characteristics, you have selection pressure.

—Perry Metzger, predicting that the reign of natural selection would continue into the indefinite future

In evolutionary biology, as in many other fields, it is important to think quantitatively rather than qualitatively. Does a beneficial mutation “sometimes spread, but not always”? Well, a psychic power would be a beneficial mutation, so you’d expect it to spread, right? Yet this is qualitative reasoning, not quantitative—if X is true, then Y is true; if psychic powers are beneficial, they may spread. In Evolutions Are Stupid, I described the equations for a beneficial mutation’s probability of fixation, roughly twice the fitness advantage (6% for a 3% advantage). Only this kind of numerical thinking is likely to make us realize that mutations which are only rarely useful are extremely unlikely to spread, and that it is practically impossible for complex adaptations to arise without constant use. If psychic powers really existed, we should expect to see everyone using them all the time—not just because they would be so amazingly useful, but because otherwise they couldn’t have evolved in the first place.

“So long as there are limited resources and multiple competing actors capable of passing on characteristics, you have selection pressure.” This is qualitative reasoning. How much selection pressure?

While there are several candidates for the most important equation in evolutionary biology, I would pick Price’s Equation, which in its simplest formulation reads:

▵cov(v_i, z_i)

change in average characteristic = covariance(relative fitness, characteristic).

This is a very powerful and general formula. For example, a particular gene for height can be the Z, the characteristic that changes, in which case Price’s Equation says that the change in the probability of possessing this gene equals the covariance of the gene with reproductive fitness. Or you can consider height in general as the characteristic Z, apart from any particular genes, and Price’s Equation says that the change in height in the next generation will equal the covariance of height with relative reproductive fitness.

(At least, this is true so long as height is straightforwardly heritable. If nutrition improves, so that a fixed genotype becomes taller, you have to add a correction term to Price’s Equation. If there are complex nonlinear interactions between many genes, you have to either add a correction term, or calculate the equation in such a complicated way that it ceases to enlighten.)

Many enlightenments may be attained by studying the different forms and derivations of Price’s Equation. For example, the final equation says that the average characteristic changes according to its covariance with relative fitness, rather than its absolute fitness. This means that if a Frodo gene saves its whole species from extinction, the average Frodo characteristic does not increase, since Frodo’s act benefited all genotypes equally and did not covary with relative fitness.

It is said that Price became so disturbed with the implications of his equation for altruism that he committed suicide, though he may have had other issues. (Overcoming Bias does not advocate committing suicide after studying Price’s Equation.)

One of the enlightenments which may be gained by meditating upon Price’s Equation is that “limited resources” and “multiple competing actors capable of passing on characteristics” are not sufficient to give rise to an evolution. “Things that replicate themselves” is not a sufficient condition. Even “competition between replicating things” is not sufficient.

Do corporations evolve? They certainly compete. They occasionally spin off children. Their resources are limited. They sometimes die.

But how much does the child of a corporation resemble its parents? Much of the personality of a corporation derives from key officers, and CEOs cannot divide themselves by fission. Price’s Equation only operates to the extent that characteristics are heritable across generations. If great-great-grandchildren don’t much resemble their great-great-grandparents, you won’t get more than four generations’ worth of cumulative selection pressure—anything that happened more than four generations ago will blur itself out. Yes, the personality of a corporation can influence its spinoff—but that’s nothing like the heritability of DNA, which is digital rather than analog, and can transmit itself with 10^-8 errors per base per generation.

With DNA you have heritability lasting for millions of generations. That’s how complex adaptations can arise by pure evolution—the digital DNA lasts long enough for a gene conveying 3% advantage to spread itself over 768 generations, and then another gene dependent on it can arise. Even if corporations replicated with digital fidelity, they would currently be at most ten generations into the RNA World.

Now, corporations are certainly selected, in the sense that incompetent corporations go bust. This should logically make you more likely to observe corporations with features contributing to competence. And in the same sense, any star that goes nova shortly after it forms, is less likely to be visible when you look up at the night sky. But if an accident of stellar dynamics makes one star burn longer than another star, that doesn’t make it more likely that future stars will also burn longer—the feature will not be copied onto other stars. We should not expect future astrophysicists to discover complex internal features of stars which seem designed to help them burn longer. That kind of mechanical adaptation requires much larger cumulative selection pressures than a once-off winnowing.

Think of the principle introduced in Einstein’s Arrogance—that the vast majority of the evidence required to think of General Relativity had to go into raising that one particular equation to the level of Einstein’s personal attention; the amount of evidence required to raise it from a deliberately considered possibility to 99.9% certainty was trivial by comparison. In the same sense, complex features of corporations that require hundreds of bits to specify are produced primarily by human intelligence, not a handful of generations of low-fidelity evolution. In biology, the mutations are purely random and evolution supplies thousands of bits of cumulative selection pressure. In corporations, humans offer up thousand-bit intelligently designed complex “mutations,” and then the further selection pressure of “Did it go bankrupt or not?” accounts for a handful of additional bits in explaining what you see.

Advanced molecular nanotechnology—the artificial sort, not biology—should be able to copy itself with digital fidelity through thousands of generations. Would Price’s Equation thereby gain a foothold?

Correlation is covariance divided by variance, so if A is highly predictive of B, there can be a strong “correlation” between them even if A is ranging from 0 to 9 and B is only ranging from 50.0001 and 50.0009. Price’s Equation runs on covariance of characteristics with reproduction—not correlation! If you can compress variance in characteristics into a tiny band, the covariance goes way down, and so does the cumulative change in the characteristic.

The Foresight Institute suggests, among other sensible proposals, that the replication instructions for any nanodevice should be encrypted. Moreover, encrypted such that flipping a single bit of the encoded instructions will entirely scramble the decrypted output. If all nanodevices produced are precise molecular copies, and moreover, any mistakes on the assembly line are not heritable because the offspring got a digital copy of the original encrypted instructions for use in making grandchildren, then your nanodevices ain’t gonna be doin’ much evolving.

You’d still have to worry about prions—self-replicating assembly errors apart from the encrypted instructions, where a robot arm fails to grab a carbon atom that is used in assembling a homologue of itself, and this causes the offspring’s robot arm to likewise fail to grab a carbon atom, etc., even with all the encrypted instructions remaining constant. But how much correlation is there likely to be, between this sort of transmissible error, and a higher reproductive rate? Let’s say that one nanodevice produces a copy of itself every 1,000 seconds, and the new nanodevice is magically more efficient (it not only has a prion, it has a beneficial prion) and copies itself every 999.99999 seconds. It needs one less carbon atom attached, you see. That’s not a whole lot of variance in reproduction, so it’s not a whole lot of covariance either.

And how often will these nanodevices need to replicate? Unless they’ve got more atoms available than exist in the solar system, or for that matter, the visible Universe, only a small number of generations will pass before they hit the resource wall. “Limited resources” are not a sufficient condition for evolution; you need the frequently iterated death of a substantial fraction of the population to free up resources. Indeed, “generations” is not so much an integer as an integral over the fraction of the population that consists of newly created individuals.

This is, to me, the most frightening thing about gray goo or nanotechnological weapons—that they could eat the whole Earth and then that would be it, nothing interesting would happen afterward. Diamond is stabler than proteins held together by van der Waals forces, so the goo would only need to reassemble some pieces of itself when an asteroid hit. Even if prions were a powerful enough idiom to support evolution at all—evolution is slow enough with digital DNA!—fewer than 1.0 generations might pass between when the goo ate the Earth and when the Sun died.

To sum up, if you have all of the following properties:

Entities that replicate;
Substantial variation in their characteristics;
Substantial variation in their reproduction;
Persistent correlation between the characteristics and reproduction;
High-fidelity long-range heritability in characteristics;
Frequent birth of a significant fraction of the breeding population;
And all this remains true through many iterations . . .

Then you will have significant cumulative selection pressures, enough to produce complex adaptations by the force of evolution.

135
Evolving to Extinction

It is a very common misconception that an evolution works for the good of its species. Can you remember hearing someone talk about two rabbits breeding eight rabbits and thereby “contributing to the survival of their species”? A modern evolutionary biologist would never say such a thing; they’d sooner breed with a rabbit.

It’s yet another case where you’ve got to simultaneously consider multiple abstract concepts and keep them distinct. Evolution doesn’t operate on particular individuals; individuals keep whatever genes they’re born with. Evolution operates on a reproducing population, a species, over time. There’s a natural tendency to think that if an Evolution Fairy is operating on the species, she must be optimizing for the species. But what really changes are the gene frequencies, and frequencies don’t increase or decrease according to how much the gene helps the species as a whole. As we shall later see, it’s quite possible for a species to evolve to extinction.

Why are boys and girls born in roughly equal numbers? (Leaving aside crazy countries that use artificial gender selection technologies.) To see why this is surprising, consider that 1 male can impregnate 2, 10, or 100 females; it wouldn’t seem that you need the same number of males as females to ensure the survival of the species. This is even more surprising in the vast majority of animal species where the male contributes very little to raising the children—humans are extraordinary, even among primates, for their level of paternal investment. Balanced gender ratios are found even in species where the male impregnates the female and vanishes into the mist.

Consider two groups on different sides of a mountain; in group A, each mother gives birth to 2 males and 2 females; in group B, each mother gives birth to 3 females and 1 male. Group A and group B will have the same number of children, but group B will have 50% more grandchildren and 125% more great-grandchildren. You might think this would be a significant evolutionary advantage.

But consider: The rarer males become, the more reproductively valuable they become—not to the group, but to the individual parent. Every child has one male and one female parent. Then in every generation, the total genetic contribution from all males equals the total genetic contribution from all females. The fewer males, the greater the individual genetic contribution per male. If all the females around you are doing what’s good for the group, what’s good for the species, and birthing 1 male per 10 females, you can make a genetic killing by birthing all males, each of whom will have (on average) ten times as many grandchildren as their female cousins.

So while group selection ought to favor more girls, individual selection favors equal investment in male and female offspring. Looking at the statistics of a maternity ward, you can see at a glance that the quantitative balance between group selection forces and individual selection forces is overwhelmingly tilted in favor of individual selection in Homo sapiens.

(Technically, this isn’t quite a glance. Individual selection favors equal parental investments in male and female offspring. If males cost half as much to birth and/or raise, twice as many males as females will be born at the evolutionarily stable equilibrium. If the same number of males and females were born in the population at large, but males were twice as cheap to birth, then you could again make a genetic killing by birthing more males. So the maternity ward should reflect the balance of parental opportunity costs, in a hunter-gatherer society, between raising boys and raising girls; and you’d have to assess that somehow. But ya know, it doesn’t seem all that much more reproductive-opportunity-costly for a hunter-gatherer family to raise a girl, so it’s kinda suspicious that around the same number of boys are born as girls.)

Natural selection isn’t about groups, or species, or even individuals. In a sexual species, an individual organism doesn’t evolve; it keeps whatever genes it’s born with. An individual is a once-off collection of genes that will never reappear; how can you select on that? When you consider that nearly all of your ancestors are dead, it’s clear that “survival of the fittest” is a tremendous misnomer. “Replication of the fitter” would be more accurate, although technically fitness is defined only in terms of replication.

Natural selection is really about gene frequencies. To get a complex adaptation, a machine with multiple dependent parts, each new gene as it evolves depends on the other genes being reliably present in its genetic environment. They must have high frequencies. The more complex the machine, the higher the frequencies must be. The signature of natural selection occurring is a gene rising from 0.00001% of the gene pool to 99% of the gene pool. This is the information, in an information-theoretic sense; and this is what must happen for large complex adaptations to evolve.

The real struggle in natural selection is not the competition of organisms for resources; this is an ephemeral thing when all the participants will vanish in another generation. The real struggle is the competition of alleles for frequency in the gene pool. This is the lasting consequence that creates lasting information. The two rams bellowing and locking horns are only passing shadows.

It’s perfectly possible for an allele to spread to fixation by outcompeting an alternative allele which was “better for the species.” If the Flying Spaghetti Monster magically created a species whose gender mix was perfectly optimized to ensure the survival of the species—the optimal gender mix to bounce back reliably from near-extinction events, adapt to new niches, et cetera—then the evolution would rapidly degrade this species optimum back into the individual-selection optimum of equal parental investment in males and females.

Imagine a “Frodo gene” that sacrifices its vehicle to save its entire species from an extinction event. What happens to the allele frequency as a result? It goes down. Kthxbye.

If species-level extinction threats occur regularly (call this a “Buffy environment”) then the Frodo gene will systematically decrease in frequency and vanish, and soon thereafter, so will the species.

A hypothetical example? Maybe. If the human species was going to stay biological for another century, it would be a good idea to start cloning Gandhi.

In viruses, there’s the tension between individual viruses replicating as fast as possible, versus the benefit of leaving the host alive long enough to transmit the illness. This is a good real-world example of group selection, and if the virus evolves to a point on the fitness landscape where the group selection pressures fail to overcome individual pressures, the virus could vanish shortly thereafter. I don’t know if a disease has ever been caught in the act of evolving to extinction, but it’s probably happened any number of times.

Segregation-distorters subvert the mechanisms that usually guarantee fairness of sexual reproduction. For example, there is a segregation-distorter on the male sex chromosome of some mice which causes only male children to be born, all carrying the segregation-distorter. Then these males impregnate females, who give birth to only male children, and so on. You might cry “This is cheating!” but that’s a human perspective; the reproductive fitness of this allele is extremely high, since it produces twice as many copies of itself in the succeeding generation as its nonmutant alternative. Even as females become rarer and rarer, males carrying this gene are no less likely to mate than any other male, and so the segregation-distorter remains twice as fit as its alternative allele. It’s speculated that real-world group selection may have played a role in keeping the frequency of this gene as low as it seems to be. In which case, if mice were to evolve the ability to fly and migrate for the winter, they would probably form a single reproductive population, and would evolve to extinction as the segregation-distorter evolved to fixation.

Around 50% of the total genome of maize consists of transposons, DNA elements whose primary function is to copy themselves into other locations of DNA. A class of transposons called “P elements” seem to have first appeared in Drosophila only in the middle of the twentieth century, and spread to every population of the species within 50 years. The “Alu sequence” in humans, a 300-base transposon, is repeated between 300,000 and a million times in the human genome. This may not extinguish a species, but it doesn’t help it; transposons cause more mutations which are as always mostly harmful, decrease the effective copying fidelity of DNA. Yet such cheaters are extremely fit.

Suppose that in some sexually reproducing species, a perfect DNA-copying mechanism is invented. Since most mutations are detrimental, this gene complex is an advantage to its holders. Now you might wonder about beneficial mutations—they do happen occasionally, so wouldn’t the unmutable be at a disadvantage? But in a sexual species, a beneficial mutation that began in a mutable can spread to the descendants of unmutables as well. The mutables suffer from degenerate mutations in each generation; and the unmutables can sexually acquire, and thereby benefit from, any beneficial mutations that occur in the mutables. Thus the mutables have a pure disadvantage. The perfect DNA-copying mechanism rises in frequency to fixation. Ten thousand years later there’s an ice age and the species goes out of business. It evolved to extinction.

The “bystander effect” is that, when someone is in trouble, solitary individuals are more likely to intervene than groups. A college student apparently having an epileptic seizure was helped 85% of the time by a single bystander, and 31% of the time by five bystanders. I speculate that even if the kinship relation in a hunter-gatherer tribe was strong enough to create a selection pressure for helping individuals not directly related, when several potential helpers were present, a genetic arms race might occur to be the last one to step forward. Everyone delays, hoping that someone else will do it. Humanity is facing multiple species-level extinction threats right now, and I gotta tell ya, there ain’t a lot of people steppin’ forward. If we lose this fight because virtually no one showed up on the battlefield, then—like a probably-large number of species which we don’t see around today—we will have evolved to extinction.

Cancerous cells do pretty well in the body, prospering and amassing more resources, far outcompeting their more obedient counterparts. For a while.

Multicellular organisms can only exist because they’ve evolved powerful internal mechanisms to outlaw evolution. If the cells start evolving, they rapidly evolve to extinction: the organism dies.

So praise not evolution for the solicitous concern it shows for the individual; nearly all of your ancestors are dead. Praise not evolution for the solicitous concern it shows for a species; no one has ever found a complex adaptation which can only be interpreted as operating to preserve a species, and the mathematics would seem to indicate that this is virtually impossible. Indeed, it’s perfectly possible for a species to evolve to extinction. Humanity may be finishing up the process right now. You can’t even praise evolution for the solicitous concern it shows for genes; the battle between two alternative alleles at the same location is a zero-sum game for frequency.

Fitness is not always your friend.

136
The Tragedy of Group Selectionism

Before 1966, it was not unusual to see serious biologists advocating evolutionary hypotheses that we would now regard as magical thinking. These muddled notions played an important historical role in the development of later evolutionary theory, error calling forth correction; like the folly of English kings provoking into existence the Magna Carta and constitutional democracy.

As an example of romance, Vero Wynne-Edwards, Warder Allee, and J. L. Brereton, among others, believed that predators would voluntarily restrain their breeding to avoid overpopulating their habitat and exhausting the prey population.

But evolution does not open the floodgates to arbitrary purposes. You cannot explain a rattlesnake’s rattle by saying that it exists to benefit other animals who would otherwise be bitten. No outside Evolution Fairy decides when a gene ought to be promoted; the gene’s effect must somehow directly cause the gene to be more prevalent in the next generation. It’s clear why our human sense of aesthetics, witnessing a population crash of foxes who’ve eaten all the rabbits, cries “Something should’ve been done!” But how would a gene complex for restraining reproduction—of all things!—cause itself to become more frequent in the next generation?

A human being designing a neat little toy ecology—for entertainment purposes, like a model railroad—might be annoyed if their painstakingly constructed fox and rabbit populations self-destructed by the foxes eating all the rabbits and then dying of starvation themselves. So the human would tinker with the toy ecology—a fox-breeding-restrainer is the obvious solution that leaps to our human minds—until the ecology looked nice and neat. Nature has no human, of course, but that needn’t stop us—now that we know what we want on aesthetic grounds, we just have to come up with a plausible argument that persuades Nature to want the same thing on evolutionary grounds.

Obviously, selection on the level of the individual won’t produce individual restraint in breeding. Individuals who reproduce unrestrainedly will, naturally, produce more offspring than individuals who restrain themselves.

(Individual selection will not produce individual sacrifice of breeding opportunities. Individual selection can certainly produce individuals who, after acquiring all available resources, use those resources to produce four big eggs instead of eight small eggs—not to conserve social resources, but because that is the individual sweet spot for (number of eggs)×(egg survival probability). This does not get rid of the commons problem.)

But suppose that the species population was broken up into subpopulations, which were mostly isolated, and only occasionally interbred. Then, surely, subpopulations that restrained their breeding would be less likely to go extinct, and would send out more messengers, and create new colonies to reinhabit the territories of crashed populations.

The problem with this scenario wasn’t that it was mathematically impossible. The problem was that it was possible but very difficult.

The fundamental problem is that it’s not only restrained breeders who reap the benefits of restrained breeding. If some foxes refrain from spawning cubs who eat rabbits, then the uneaten rabbits don’t go to only cubs who carry the restrained-breeding adaptation. The unrestrained foxes, and their many more cubs, will happily eat any rabbits left unhunted. The only way the restraining gene can survive against this pressure, is if the benefits of restraint preferentially go to restrainers.

Specifically, the requirement is C∕B < F_ST where C is the cost of altruism to the donor, B is the benefit of altruism to the recipient, and F_ST is the spatial structure of the population: the average relatedness between a randomly selected organism and its randomly selected neighbor, where a “neighbor” is any other fox who benefits from an altruistic fox’s restraint.¹

So is the cost of restrained breeding sufficiently small, and the empirical benefit of less famine sufficiently large, compared to the empirical spatial structure of fox populations and rabbit populations, that the group selection argument can work?

The math suggests this is pretty unlikely. In this simulation, for example, the cost to altruists is 3% of fitness, pure altruist groups have a fitness twice as great as pure selfish groups, the subpopulation size is 25, and 20% of all deaths are replaced with messengers from another group: the result is polymorphic for selfishness and altruism. If the subpopulation size is doubled to 50, selfishness is fixed; if the cost to altruists is increased to 6%, selfishness is fixed; if the altruistic benefit is decreased by half, selfishness is fixed or in large majority. Neighborhood-groups must be very small, with only around 5 members, for group selection to operate when the cost of altruism exceeds 10%. This doesn’t seem plausibly true of foxes restraining their breeding.

You can guess by now, I think, that the group selectionists ultimately lost the scientific argument. The kicker was not the mathematical argument, but empirical observation: foxes didn’t restrain their breeding (I forget the exact species of dispute; it wasn’t foxes and rabbits), and indeed, predator-prey systems crash all the time. Group selectionism would later revive, somewhat, in drastically different form—mathematically speaking, there is neighborhood structure, which implies nonzero group selection pressure not necessarily capable of overcoming countervailing individual selection pressure, and if you don’t take it into account your math will be wrong, full stop. And evolved enforcement mechanisms (not originally postulated) change the game entirely. So why is this now-historical scientific dispute worthy material for Overcoming Bias?

A decade after the controversy, a biologist had a fascinating idea. The mathematical conditions for group selection overcoming individual selection were too extreme to be found in Nature. Why not create them artificially, in the laboratory? Michael J. Wade proceeded to do just that, repeatedly selecting populations of insects for low numbers of adults per subpopulation.² And what was the result? Did the insects restrain their breeding and live in quiet peace with enough food for all?

No; the adults adapted to cannibalize eggs and larvae, especially female larvae.

Of course selecting for small subpopulation sizes would not select for individuals who restrained their own breeding; it would select for individuals who ate other individuals’ children. Especially the girls.

Once you have that experimental result in hand—and it’s massively obvious in retrospect—then it suddenly becomes clear how the original group selectionists allowed romanticism, a human sense of aesthetics, to cloud their predictions of Nature.

This is an archetypal example of a missed Third Alternative, resulting from a rationalization of a predetermined bottom line that produced a fake justification and then motivatedly stopped. The group selectionists didn’t start with clear, fresh minds, happen upon the idea of group selection, and neutrally extrapolate forward the probable outcome. They started out with the beautiful idea of fox populations voluntarily restraining their reproduction to what the rabbit population would bear, Nature in perfect harmony; then they searched for a reason why this would happen, and came up with the idea of group selection; then, since they knew what they wanted the outcome of group selection to be, they didn’t look for any less beautiful and aesthetic adaptations that group selection would be more likely to promote instead. If they’d really been trying to calmly and neutrally predict the result of selecting for small subpopulation sizes resistant to famine, they would have thought of cannibalizing other organisms’ children or some similarly “ugly” outcome—long before they imagined anything so evolutionarily outré as individual restraint in breeding!

This also illustrates the point I was trying to make in Einstein’s Arrogance: With large answer spaces, nearly all of the real work goes into promoting one possible answer to the point of being singled out for attention. If a hypothesis is improperly promoted to your attention—your sense of aesthetics suggests a beautiful way for Nature to be, and yet natural selection doesn’t involve an Evolution Fairy who shares your appreciation—then this alone may seal your doom, unless you can manage to clear your mind entirely and start over.

In principle, the world’s stupidest person may say the Sun is shining, but that doesn’t make it dark out. Even if an answer is suggested by a lunatic on LSD, you should be able to neutrally calculate the evidence for and against, and if necessary, un-believe.

In practice, the group selectionists were doomed because their bottom line was originally suggested by their sense of aesthetics, and Nature’s bottom line was produced by natural selection. These two processes had no principled reason for their outputs to correlate, and indeed they didn’t. All the furious argument afterward didn’t change that.

If you start with your own desires for what Nature should do, consider Nature’s own observed reasons for doing things, and then rationalize an extremely persuasive argument for why Nature should produce your preferred outcome for Nature’s own reasons, then Nature, alas, still won’t listen. The universe has no mind and is not subject to clever political persuasion. You can argue all day why gravity should really make water flow uphill, and the water just ends up in the same place regardless. It’s like the universe plain isn’t listening. J. R. Molloy said: “Nature is the ultimate bigot, because it is obstinately and intolerantly devoted to its own prejudices and absolutely refuses to yield to the most persuasive rationalizations of humans.”

I often recommend evolutionary biology to friends just because the modern field tries to train its students against rationalization, error calling forth correction. Physicists and electrical engineers don’t have to be carefully trained to avoid anthropomorphizing electrons, because electrons don’t exhibit mindish behaviors. Natural selection creates purposefulnesses which are alien to humans, and students of evolutionary theory are warned accordingly. It’s good training for any thinker, but it is especially important if you want to think clearly about other weird mindish processes that do not work like you do.

1. David Sloan Wilson, “A Theory of Group Selection,” Proceedings of the National Academy of Sciences of the United States of America 72, no. 1 (1975): 143–146.

2. Michael J. Wade, “Group selections among laboratory populations of Tribolium,” Proceedings of the National Academy of Sciences of the United States of America 73, no. 12 (1976): 4604–4607, doi:10.1073/pnas.73.12.4604.

137
Fake Optimization Criteria

I’ve previously dwelt in considerable length upon forms of rationalization whereby our beliefs appear to match the evidence much more strongly than they actually do. And I’m not overemphasizing the point, either. If we could beat this fundamental metabias and see what every hypothesis really predicted, we would be able to recover from almost any other error of fact.

The mirror challenge for decision theory is seeing which option a choice criterion really endorses. If your stated moral principles call for you to provide laptops to everyone, does that really endorse buying a $1 million gem-studded laptop for yourself, or spending the same money on shipping 5,000 OLPCs?

We seem to have evolved a knack for arguing that practically any goal implies practically any action. A phlogiston theorist explaining why magnesium gains weight when burned has nothing on an Inquisitor explaining why God’s infinite love for all His children requires burning some of them at the stake.

There’s no mystery about this. Politics was a feature of the ancestral environment. We are descended from those who argued most persuasively that the good of the tribe meant executing their hated rival Uglak. (We sure ain’t descended from Uglak.)

And yet . . . is it possible to prove that if Robert Mugabe cared only for the good of Zimbabwe, he would resign from its presidency? You can argue that the policy follows from the goal, but haven’t we just seen that humans can match up any goal to any policy? How do you know that you’re right and Mugabe is wrong? (There are a number of reasons this is a good guess, but bear with me here.)

Human motives are manifold and obscure, our decision processes as vastly complicated as our brains. And the world itself is vastly complicated, on every choice of real-world policy. Can we even prove that human beings are rationalizing—that we’re systematically distorting the link from principles to policy—when we lack a single firm place on which to stand? When there’s no way to find out exactly what even a single optimization criterion implies? (Actually, you can just observe that people disagree about office politics in ways that strangely correlate to their own interests, while simultaneously denying that any such interests are at work. But again, bear with me here.)

Where is the standardized, open-source, generally intelligent, consequentialist optimization process into which we can feed a complete morality as an XML file, to find out what that morality really recommends when applied to our world? Is there even a single real-world case where we can know exactly what a choice criterion recommends? Where is the pure moral reasoner—of known utility function, purged of all other stray desires that might distort its optimization—whose trustworthy output we can contrast to human rationalizations of the same utility function?

Why, it’s our old friend the alien god, of course! Natural selection is guaranteed free of all mercy, all love, all compassion, all aesthetic sensibilities, all political factionalism, all ideological allegiances, all academic ambitions, all libertarianism, all socialism, all Blue and all Green. Natural selection doesn’t maximize its criterion of inclusive genetic fitness—it’s not that smart. But when you look at the output of natural selection, you are guaranteed to be looking at an output that was optimized only for inclusive genetic fitness, and not the interests of the US agricultural industry.

In the case histories of evolutionary science—in, for example, The Tragedy of Group Selectionism—we can directly compare human rationalizations to the result of pure optimization for a known criterion. What did Wynne-Edwards think would be the result of group selection for small subpopulation sizes? Voluntary individual restraint in breeding, and enough food for everyone. What was the actual laboratory result? Cannibalism.

Now you might ask: Are these case histories of evolutionary science really relevant to human morality, which doesn’t give two figs for inclusive genetic fitness when it gets in the way of love, compassion, aesthetics, healing, freedom, fairness, et cetera? Human societies didn’t even have a concept of “inclusive genetic fitness” until the twentieth century.

But I ask in return: If we can’t see clearly the result of a single monotone optimization criterion—if we can’t even train ourselves to hear a single pure note—then how will we listen to an orchestra? How will we see that “Always be selfish” or “Always obey the government” are poor guiding principles for human beings to adopt—if we think that even optimizing genes for inclusive fitness will yield organisms that sacrifice reproductive opportunities in the name of social resource conservation?

To train ourselves to see clearly, we need simple practice cases.

138
AdaptationExecuters, Not FitnessMaximizers

Individual organisms are best thought of as adaptationexecuters rather than as fitnessmaximizers.

—John Tooby and Leda Cosmides,
“The Psychological Foundations of Culture”¹

Fifty thousand years ago, the taste buds of Homo sapiens directed their bearers to the scarcest, most critical food resources—sugar and fat. Calories, in a word. Today, the context of a taste bud’s function has changed, but the taste buds themselves have not. Calories, far from being scarce (in First World countries), are actively harmful. Micronutrients that were reliably abundant in leaves and nuts are absent from bread, but our taste buds don’t complain. A scoop of ice cream is a superstimulus, containing more sugar, fat, and salt than anything in the ancestral environment.

No human being with the deliberate goal of maximizing their alleles’ inclusive genetic fitness would ever eat a cookie unless they were starving. But individual organisms are best thought of as adaptationexecuters, not fitnessmaximizers.

A Phillips-head screwdriver, though its designer intended it to turn screws, won’t reconform itself to a flat-head screw to fulfill its function. We created these tools, but they exist independently of us, and they continue independently of us.

The atoms of a screwdriver don’t have tiny little XML tags inside describing their “objective” purpose. The designer had something in mind, yes, but that’s not the same as what happens in the real world. If you forgot that the designer is a separate entity from the designed thing, you might think, “The purpose of the screwdriver is to drive screws”—as though this were an explicit property of the screwdriver itself, rather than a property of the designer’s state of mind. You might be surprised that the screwdriver didn’t reconfigure itself to the flat-head screw, since, after all, the screwdriver’s purpose is to turn screws.

The cause of the screwdriver’s existence is the designer’s mind, which imagined an imaginary screw, and imagined an imaginary handle turning. The actual operation of the screwdriver, its actual fit to an actual screw head, cannot be the objective cause of the screwdriver’s existence: The future cannot cause the past. But the designer’s brain, as an actually existent thing within the past, can indeed be the cause of the screwdriver.

The consequence of the screwdriver’s existence may not correspond to the imaginary consequences in the designer’s mind. The screwdriver blade could slip and cut the user’s hand.

And the meaning of the screwdriver—why, that’s something that exists in the mind of a user, not in tiny little labels on screwdriver atoms. The designer may intend it to turn screws. A murderer may buy it to use as a weapon. And then accidentally drop it, to be picked up by a child, who uses it as a chisel.

So the screwdriver’s cause, and its shape, and its consequence, and its various meanings, are all different things; and only one of these things is found within the screwdriver itself.

Where do taste buds come from? Not from an intelligent designer visualizing their consequences, but from a frozen history of ancestry: Adam liked sugar and ate an apple and reproduced, Barbara liked sugar and ate an apple and reproduced, Charlie liked sugar and ate an apple and reproduced, and 2763 generations later, the allele became fixed in the population. For convenience of thought, we sometimes compress this giant history and say: “Evolution did it.” But it’s not a quick, local event like a human designer visualizing a screwdriver. This is the objective cause of a taste bud.

What is the objective shape of a taste bud? Technically, it’s a molecular sensor connected to reinforcement circuitry. This adds another level of indirection, because the taste bud isn’t directly acquiring food. It’s influencing the organism’s mind, making the organism want to eat foods that are similar to the food just eaten.

What is the objective consequence of a taste bud? In a modern First World human, it plays out in multiple chains of causality: from the desire to eat more chocolate, to the plan to eat more chocolate, to eating chocolate, to getting fat, to getting fewer dates, to reproducing less successfully. This consequence is directly opposite the key regularity in the long chain of ancestral successes that caused the taste bud’s shape. But, since overeating has only recently become a problem, no significant evolution (compressed regularity of ancestry) has further influenced the taste bud’s shape.

What is the meaning of eating chocolate? That’s between you and your moral philosophy. Personally, I think chocolate tastes good, but I wish it were less harmful; acceptable solutions would include redesigning the chocolate or redesigning my biochemistry.

Smushing several of the concepts together, you could sort-of-say, “Modern humans do today what would have propagated our genes in a hunter-gatherer society, whether or not it helps our genes in a modern society.” But this still isn’t quite right, because we’re not actually asking ourselves which behaviors would maximize our ancestors’ inclusive fitness. And many of our activities today have no ancestral analogue. In the hunter-gatherer society there wasn’t any such thing as chocolate.

So it’s better to view our taste buds as an adaptation fitted to ancestral conditions that included near-starvation and apples and roast rabbit, which modern humans execute in a new context that includes cheap chocolate and constant bombardment by advertisements.

Therefore it is said: Individual organisms are best thought of as adaptationexecuters, not fitnessmaximizers.

1. John Tooby and Leda Cosmides, “The Psychological Foundations of Culture,” in The Adapted Mind: Evolutionary Psychology and the Generation of Culture, ed. Jerome H. Barkow, Leda Cosmides, and John Tooby (New York: Oxford University Press, 1992), 19–136.

139
Evolutionary Psychology

Like “IRC chat” or “TCP/IP protocol,” the phrase “reproductive organ” is redundant. All organs are reproductive organs. Where do a bird’s wings come from? An Evolution-of-Birds Fairy who thinks that flying is really neat? The bird’s wings are there because they contributed to the bird’s ancestors’ reproduction. Likewise the bird’s heart, lungs, and genitals. At most we might find it worthwhile to distinguish between directly reproductive organs and indirectly reproductive organs.

This observation holds true also of the brain, the most complex organ system known to biology. Some brain organs are directly reproductive, like lust; others are indirectly reproductive, like anger.

Where does the human emotion of anger come from? An Evolution-of-Humans Fairy who thought that anger was a worthwhile feature? The neural circuitry of anger is a reproductive organ as surely as your liver. Anger exists in Homo sapiens because angry ancestors had more kids. There’s no other way it could have gotten there.

This historical fact about the origin of anger confuses all too many people. They say, “Wait, are you saying that when I’m angry, I’m subconsciously trying to have children? That’s not what I’m thinking after someone punches me in the nose.”

No. No. No. NO!

Individual organisms are best thought of as adaptation-executers, not fitness-maximizers. The cause of an adaptation, the shape of an adaptation, and the consequence of an adaptation are all separate things. If you built a toaster, you wouldn’t expect the toaster to reshape itself when you tried to cram in a whole loaf of bread; yes, you intended it to make toast, but that intention is a fact about you, not a fact about the toaster. The toaster has no sense of its own purpose.

But a toaster is not an intention-bearing object. It is not a mind at all, so we are not tempted to attribute goals to it. If we see the toaster as purposed, we don’t think the toaster knows it, because we don’t think the toaster knows anything.

It’s like the old test of being asked to say the color of the letters in “blue.” It takes longer for subjects to name this color, because of the need to untangle the meaning of the letters and the color of the letters. You wouldn’t have similar trouble naming the color of the letters in “wind.”

But a human brain, in addition to being an artifact historically produced by evolution, is also a mind capable of bearing its own intentions, purposes, desires, goals, and plans. Both a bee and a human are designs, but only a human is a designer. The bee is “wind;” the human is “blue.”

Cognitive causes are ontologically distinct from evolutionary causes. They are made out of a different kind of stuff. Cognitive causes are made of neurons. Evolutionary causes are made of ancestors.

The most obvious kind of cognitive cause is deliberate, like an intention to go to the supermarket, or a plan for toasting toast. But an emotion also exists physically in the brain, as a train of neural impulses or a cloud of spreading hormones. Likewise an instinct, or a flash of visualization, or a fleetingly suppressed thought; if you could scan the brain in three dimensions and you understood the code, you would be able to see them.

Even subconscious cognitions exist physically in the brain. “Power tends to corrupt,” observed Lord Acton. Stalin may or may not have believed himself an altruist, working toward the greatest good for the greatest number. But it seems likely that, somewhere in Stalin’s brain, there were neural circuits that reinforced pleasurably the exercise of power, and neural circuits that detected anticipations of increases and decreases in power. If there were nothing in Stalin’s brain that correlated to power—no little light that went on for political command, and off for political weakness—then how could Stalin’s brain have known to be corrupted by power?

Evolutionary selection pressures are ontologically distinct from the biological artifacts they create. The evolutionary cause of a bird’s wings is millions of ancestor-birds who reproduced more often than other ancestor-birds, with statistical regularity owing to their possession of incrementally improved wings compared to their competitors. We compress this gargantuan historical-statistical macrofact by saying “evolution did it.”

Natural selection is ontologically distinct from creatures; evolution is not a little furry thing lurking in an undiscovered forest. Evolution is a causal, statistical regularity in the reproductive history of ancestors.

And this logic applies also to the brain. Evolution has made wings that flap, but do not understand flappiness. It has made legs that walk, but do not understand walkyness. Evolution has carved bones of calcium ions, but the bones themselves have no explicit concept of strength, let alone inclusive genetic fitness. And evolution designed brains themselves capable of designing; yet these brains had no more concept of evolution than a bird has of aerodynamics. Until the twentieth century, not a single human brain explicitly represented the complex abstract concept of inclusive genetic fitness.

When we’re told that “The evolutionary purpose of anger is to increase inclusive genetic fitness,” there’s a tendency to slide to “The purpose of anger is reproduction” to “The cognitive purpose of anger is reproduction.” No! The statistical regularity of ancestral history isn’t in the brain, even subconsciously, any more than the designer’s intentions of toast are in a toaster!

Thinking that your built-in anger-circuitry embodies an explicit desire to reproduce is like thinking your hand is an embodied mental desire to pick things up.

Your hand is not wholly cut off from your mental desires. In particular circumstances, you can control the flexing of your fingers by an act of will. If you bend down and pick up a penny, then this may represent an act of will; but it is not an act of will that made your hand grow in the first place.

One must distinguish a one-time event of particular anger (anger-1, anger-2, anger-3) from the underlying neural circuitry for anger. An anger-event is a cognitive cause, and an anger-event may have cognitive causes, but you didn’t will the anger-circuitry to be wired into the brain.

So you have to distinguish the event of anger, from the circuitry of anger, from the gene complex that laid down the neural template, from the ancestral macrofact that explains the gene complex’s presence.

If there were ever a discipline that genuinely demanded X-Treme Nitpicking, it is evolutionary psychology.

Consider, O my readers, this sordid and joyful tale: A man and a woman meet in a bar. The man is attracted to her clear complexion and firm breasts, which would have been fertility cues in the ancestral environment, but which in this case result from makeup and a bra. This does not bother the man; he just likes the way she looks. His clear-complexion-detecting neural circuitry does not know that its purpose is to detect fertility, any more than the atoms in his hand contain tiny little XML tags reading “<purpose>pick things up</purpose>.” The woman is attracted to his confident smile and firm manner, cues to high status, which in the ancestral environment would have signified the ability to provide resources for children. She plans to use birth control, but her confident-smile-detectors don’t know this any more than a toaster knows its designer intended it to make toast. She’s not concerned philosophically with the meaning of this rebellion, because her brain is a creationist and denies vehemently that evolution exists. He’s not concerned philosophically with the meaning of this rebellion, because he just wants to get laid. They go to a hotel, and undress. He puts on a condom, because he doesn’t want kids, just the dopamine-noradrenaline rush of sex, which reliably produced offspring 50,000 years ago when it was an invariant feature of the ancestral environment that condoms did not exist. They have sex, and shower, and go their separate ways. The main objective consequence is to keep the bar and the hotel and the condom-manufacturer in business; which was not the cognitive purpose in their minds, and has virtually nothing to do with the key statistical regularities of reproduction 50,000 years ago which explain how they got the genes that built their brains that executed all this behavior.

To reason correctly about evolutionary psychology you must simultaneously consider many complicated abstract facts that are strongly related yet importantly distinct, without a single mixup or conflation.

140
An Especially Elegant Evolutionary Psychology Experiment

In a 1989 Canadian study, adults were asked to imagine the death of children of various ages and estimate which deaths would create the greatest sense of loss in a parent. The results, plotted on a graph, show grief growing until just before adolescence and then beginning to drop. When this curve was compared with a curve showing changes in reproductive potential over the life cycle (a pattern calculated from Canadian demographic data), the correlation was fairly strong. But much stronger—nearly perfect, in fact—was the correlation between the grief curves of these modern Canadians and the reproductive-potential curve of a hunter-gatherer people, the !Kung of Africa. In other words, the pattern of changing grief was almost exactly what a Darwinian would predict, given demographic realities in the ancestral environment.

—Robert Wright, The Moral Animal,
summarizing Crawford et al.¹

The first correlation was 0.64, the second an extremely high 0.92 (N = 221).

The most obvious inelegance of this study, as described, is that it was conducted by asking human adults to imagine parental grief, rather than asking real parents with children of particular ages. (Presumably that would have cost more / allowed fewer subjects.) However, my understanding is that the results here squared well with the data from closer studies of parental grief that were looking for other correlations (i.e., a raw correlation between parental grief and child age).

That said, consider some of this experiment’s elegant aspects:

A correlation of 0.92(!) This may sound suspiciously high—could evolution really do such exact fine-tuning?—until you realize that this selection pressure was not only great enough to fine-tune parental grief, but, in fact, carve it out of existence from scratch in the first place.
People who say that evolutionary psychology hasn’t made any advance predictions are (ironically) mere victims of “no one knows what science doesn’t know” syndrome. You wouldn’t even think of this as an experiment to be performed if not for evolutionary psychology.
The experiment illustrates, as beautifully and as cleanly as any I have ever seen, the distinction between a conscious or subconscious ulterior motive and an executing adaptation with no realtime sensitivity to the original selection pressure that created it.

The parental grief is not even subconsciously about reproductive value—otherwise it would update for Canadian reproductive value instead of !Kung reproductive value. Grief is an adaptation that now simply exists, real in the mind and continuing under its own inertia.

Parents do not care about children for the sake of their reproductive contribution. Parents care about children for their own sake; and the non-cognitive, evolutionary-historical reason why such minds exist in the universe in the first place is that children carry their parents’ genes.

Indeed, evolution is the reason why there are any minds in the universe at all. So you can see why I’d want to draw a sharp line through my cynicism about ulterior motives at the evolutionarycognitive boundary; otherwise, I might as well stand up in a supermarket checkout line and say, “Hey! You’re only correctly processing visual information while bagging my groceries in order to maximize your inclusive genetic fitness!”

1. I think 0.92 is the highest correlation I’ve ever seen in any evolutionary psychology experiment, and indeed, one of the highest correlations I’ve seen in any psychology experiment. (Although I’ve seen e.g. a correlation of 0.98 reported for asking one group of subjects “How similar is A to B?” and another group “What is the probability of A given B?” on questions like “How likely are you to draw 60 red balls and 40 white balls from this barrel of 800 red balls and 200 white balls?”—in other words, these are simply processed as the same question.)

Since we are all Bayesians here, we may take our priors into account and ask if at least some of this unexpectedly high correlation is due to luck. The evolutionary fine-tuning we can probably take for granted; this is a huge selection pressure we’re talking about. The remaining sources of suspiciously low variance are (a) whether a large group of adults could correctly envision, on average, relative degrees of parental grief (apparently they can), and (b) whether the surviving !Kung are typical ancestral hunter-gatherers in this dimension, or whether variance between hunter-gatherer tribal types should have been too high to allow a correlation of 0.92.

But even after taking into account any skeptical priors, correlation 0.92 and N = 221 is pretty strong evidence, and our posteriors should be less skeptical on all these counts.

2. You might think it an inelegance of the experiment that it was performed prospectively on imagined grief, rather than retrospectively on real grief. But it is prospectively imagined grief that will actually operate to steer parental behavior away from losing the child! From an evolutionary standpoint, an actual dead child is a sunk cost; evolution “wants” the parent to learn from the pain, not do it again, adjust back to their hedonic set point, and go on raising other children.

3. Similarly, the graph that correlates to parental grief is for the future reproductive potential of a child that has survived to a given age, and not the sunk cost of raising the child which has survived to that age. (Might we get an even higher correlation if we tried to take into account the reproductive opportunity cost of raising a child of age X to independent maturity, while discarding all sunk costs to raise a child to age X?)

Humans usually do notice sunk costs—this is presumably either an adaptation to prevent us from switching strategies too often (compensating for an overeager opportunity-noticer?) or an unfortunate spandrel of pain felt on wasting resources.

Evolution, on the other hand—it’s not that evolution “doesn’t care about sunk costs,” but that evolution doesn’t even remotely “think” that way; “evolution” is just a macrofact about the real historical reproductive consequences.

So—of course—the parental grief adaptation is fine-tuned in a way that has nothing to do with past investment in a child, and everything to do with the future reproductive consequences of losing that child. Natural selection isn’t crazy about sunk costs the way we are.

But—of course—the parental grief adaptation goes on functioning as if the parent were living in a !Kung tribe rather than Canada. Most humans would notice the difference.

Humans and natural selection are insane in different stable complicated ways.

1. Robert Wright, The Moral Animal: Why We Are the Way We Are: The New Science of Evolutionary Psychology (Pantheon Books, 1994); Charles B. Crawford, Brenda E. Salter, and Kerry L. Jang, “Human Grief: Is Its Intensity Related to the Reproductive Value of the Deceased?,” Ethology and Sociobiology 10, no. 4 (1989): 297–307.

141
Superstimuli and the Collapse of Western Civilization

At least three people have died playing online games for days without rest. People have lost their spouses, jobs, and children to World of Warcraft. If people have the right to play video games—and it’s hard to imagine a more fundamental right—then the market is going to respond by supplying the most engaging video games that can be sold, to the point that exceptionally engaged consumers are removed from the gene pool.

How does a consumer product become so involving that, after 57 hours of using the product, the consumer would rather use the product for one more hour than eat or sleep? (I suppose one could argue that the consumer makes a rational decision that they’d rather play Starcraft for the next hour than live out the rest of their life, but let’s just not go there. Please.)

A candy bar is a superstimulus: it contains more concentrated sugar, salt, and fat than anything that exists in the ancestral environment. A candy bar matches taste buds that evolved in a hunter-gatherer environment, but it matches those taste buds much more strongly than anything that actually existed in the hunter-gatherer environment. The signal that once reliably correlated to healthy food has been hijacked, blotted out with a point in tastespace that wasn’t in the training dataset—an impossibly distant outlier on the old ancestral graphs. Tastiness, formerly representing the evolutionarily identified correlates of healthiness, has been reverse-engineered and perfectly matched with an artificial substance. Unfortunately there’s no equally powerful market incentive to make the resulting food item as healthy as it is tasty. We can’t taste healthfulness, after all.

The now-famous Dove Evolution video shows the painstaking construction of another superstimulus: an ordinary woman transformed by makeup, careful photography, and finally extensive Photoshopping, into a billboard model—a beauty impossible, unmatchable by human women in the unretouched real world. Actual women are killing themselves (e.g., supermodels using cocaine to keep their weight down) to keep up with competitors that literally don’t exist.

And likewise, a video game can be so much more engaging than mere reality, even through a simple computer monitor, that someone will play it without food or sleep until they literally die. I don’t know all the tricks used in video games, but I can guess some of them—challenges poised at the critical point between ease and impossibility, intermittent reinforcement, feedback showing an ever-increasing score, social involvement in massively multiplayer games.

Is there a limit to the market incentive to make video games more engaging? You might hope there’d be no incentive past the point where the players lose their jobs; after all, they must be able to pay their subscription fee. This would imply a “sweet spot” for the addictiveness of games, where the mode of the bell curve is having fun, and only a few unfortunate souls on the tail become addicted to the point of losing their jobs. As of 2007, playing World of Warcraft for 58 hours straight until you literally die is still the exception rather than the rule. But video game manufacturers compete against each other, and if you can make your game 5% more addictive, you may be able to steal 50% of your competitor’s customers. You can see how this problem could get a lot worse.

If people have the right to be tempted—and that’s what free will is all about—the market is going to respond by supplying as much temptation as can be sold. The incentive is to make your stimuli 5% more tempting than those of your current leading competitors. This continues well beyond the point where the stimuli become ancestrally anomalous superstimuli. Consider how our standards of product-selling feminine beauty have changed since the advertisements of the 1950s. And as candy bars demonstrate, the market incentive also continues well beyond the point where the superstimulus begins wreaking collateral damage on the consumer.

So why don’t we just say no? A key assumption of free-market economics is that, in the absence of force and fraud, people can always refuse to engage in a harmful transaction. (To the extent this is true, a free market would be, not merely the best policy on the whole, but a policy with few or no downsides.)

An organism that regularly passes up food will die, as some video game players found out the hard way. But, on some occasions in the ancestral environment, a typically beneficial (and therefore tempting) act may in fact be harmful. Humans, as organisms, have an unusually strong ability to perceive these special cases using abstract thought. On the other hand we also tend to imagine lots of special-case consequences that don’t exist, like ancestor spirits commanding us not to eat perfectly good rabbits.

Evolution seems to have struck a compromise, or perhaps just aggregated new systems on top of old. Homo sapiens are still tempted by food, but our oversized prefrontal cortices give us a limited ability to resist temptation. Not unlimited ability—our ancestors with too much willpower probably starved themselves to sacrifice to the gods, or failed to commit adultery one too many times. The video game players who died must have exercised willpower (in some sense) to keep playing for so long without food or sleep; the evolutionary hazard of self-control.

Resisting any temptation takes conscious expenditure of an exhaustible supply of mental energy. It is not in fact true that we can “just say no”—not just say no, without cost to ourselves. Even humans who won the birth lottery for willpower or foresightfulness still pay a price to resist temptation. The price is just more easily paid.

Our limited willpower evolved to deal with ancestral temptations; it may not operate well against enticements beyond anything known to hunter-gatherers. Even where we successfully resist a superstimulus, it seems plausible that the effort required would deplete willpower much faster than resisting ancestral temptations.

Is public display of superstimuli a negative externality, even to the people who say no? Should we ban chocolate cookie ads, or storefronts that openly say “Ice Cream”?

Just because a problem exists doesn’t show (without further justification and a substantial burden of proof) that the government can fix it. The regulator’s career incentive does not focus on products that combine low-grade consumer harm with addictive superstimuli; it focuses on products with failure modes spectacular enough to get into the newspaper. Conversely, just because the government may not be able to fix something, doesn’t mean it isn’t going wrong.

I leave you with a final argument from fictional evidence: Simon Funk’s online novel After Life depicts (among other plot points) the planned extermination of biological Homo sapiens—not by marching robot armies, but by artificial children that are much cuter and sweeter and more fun to raise than real children. Perhaps the demographic collapse of advanced societies happens because the market supplies ever-more-tempting alternatives to having children, while the attractiveness of changing diapers remains constant over time. Where are the advertising billboards that say “BREED”? Who will pay professional image consultants to make arguing with sullen teenagers seem more alluring than a vacation in Tahiti?

“In the end,” Simon Funk wrote, “the human species was simply marketed out of existence.”

142
Thou Art Godshatter

Before the twentieth century, not a single human being had an explicit concept of “inclusive genetic fitness,” the sole and absolute obsession of the blind idiot god. We have no instinctive revulsion of condoms or oral sex. Our brains, those supreme reproductive organs, don’t perform a check for reproductive efficacy before granting us sexual pleasure.

Why not? Why aren’t we consciously obsessed with inclusive genetic fitness? Why did the Evolution-of-Humans Fairy create brains that would invent condoms? “It would have been so easy,” thinks the human, who can design new complex systems in an afternoon.

The Evolution Fairy, as we all know, is obsessed with inclusive genetic fitness. When she decides which genes to promote to universality, she doesn’t seem to take into account anything except the number of copies a gene produces. (How strange!)

But since the maker of intelligence is thus obsessed, why not create intelligent agents—you can’t call them humans—who would likewise care purely about inclusive genetic fitness? Such agents would have sex only as a means of reproduction, and wouldn’t bother with sex that involved birth control. They could eat food out of an explicitly reasoned belief that food was necessary to reproduce, not because they liked the taste, and so they wouldn’t eat candy if it became detrimental to survival or reproduction. Post-menopausal women would babysit grandchildren until they became sick enough to be a net drain on resources, and would then commit suicide.

It seems like such an obvious design improvement—from the Evolution Fairy’s perspective.

Now it’s clear that it’s hard to build a powerful enough consequentialist. Natural selection sort-of reasons consequentially, but only by depending on the actual consequences. Human evolutionary theorists have to do really high-falutin’ abstract reasoning in order to imagine the links between adaptations and reproductive success.

But human brains clearly can imagine these links in protein. So when the Evolution Fairy made humans, why did It bother with any motivation except inclusive genetic fitness?

It’s been less than two centuries since a protein brain first represented the concept of natural selection. The modern notion of “inclusive genetic fitness” is even more subtle, a highly abstract concept. What matters is not the number of shared genes. Chimpanzees share 95% of your genes. What matters is shared genetic variance, within a reproducing population—your sister is one-half related to you, because any variations in your genome, within the human species, are 50% likely to be shared by your sister.

Only in the last century—arguably only in the last fifty years—have evolutionary biologists really begun to understand the full range of causes of reproductive success, things like reciprocal altruism and costly signaling. Without all this highly detailed knowledge, an intelligent agent that set out to “maximize inclusive fitness” would fall flat on its face.

So why not preprogram protein brains with the knowledge? Why wasn’t a concept of “inclusive genetic fitness” programmed into us, along with a library of explicit strategies? Then you could dispense with all the reinforcers. The organism would be born knowing that, with high probability, fatty foods would lead to fitness. If the organism later learned that this was no longer the case, it would stop eating fatty foods. You could refactor the whole system. And it wouldn’t invent condoms or cookies.

This looks like it should be quite possible in principle. I occasionally run into people who don’t quite understand consequentialism, who say, “But if the organism doesn’t have a separate drive to eat, it will starve, and so fail to reproduce.” So long as the organism knows this very fact, and has a utility function that values reproduction, it will automatically eat. In fact, this is exactly the consequentialist reasoning that natural selection itself used to build automatic eaters.

What about curiosity? Wouldn’t a consequentialist only be curious when it saw some specific reason to be curious? And wouldn’t this cause it to miss out on lots of important knowledge that came with no specific reason for investigation attached? Again, a consequentialist will investigate given only the knowledge of this very same fact. If you consider the curiosity drive of a human—which is not undiscriminating, but responds to particular features of problems—then this complex adaptation is purely the result of consequentialist reasoning by DNA, an implicit representation of knowledge: Ancestors who engaged in this kind of inquiry left more descendants.

So in principle, the pure reproductive consequentialist is possible. In principle, all the ancestral history implicitly represented in cognitive adaptations can be converted to explicitly represented knowledge, running on a core consequentialist.

But the blind idiot god isn’t that smart. Evolution is not a human programmer who can simultaneously refactor whole code architectures. Evolution is not a human programmer who can sit down and type out instructions at sixty words per minute.

For millions of years before hominid consequentialism, there was reinforcement learning. The reward signals were events that correlated reliably to reproduction. You can’t ask a nonhominid brain to foresee that a child eating fatty foods now will live through the winter. So the DNA builds a protein brain that generates a reward signal for eating fatty food. Then it’s up to the organism to learn which prey animals are tastiest.

DNA constructs protein brains with reward signals that have a long-distance correlation to reproductive fitness, but a short-distance correlation to organism behavior. You don’t have to figure out that eating sugary food in the fall will lead to digesting calories that can be stored fat to help you survive the winter so that you mate in spring to produce offspring in summer. An apple simply tastes good, and your brain just has to plot out how to get more apples off the tree.

And so organisms evolve rewards for eating, and building nests, and scaring off competitors, and helping siblings, and discovering important truths, and forming strong alliances, and arguing persuasively, and of course having sex . . .

When hominid brains capable of cross-domain consequential reasoning began to show up, they reasoned consequentially about how to get the existing reinforcers. It was a relatively simple hack, vastly simpler than rebuilding an “inclusive fitness maximizer” from scratch. The protein brains plotted how to acquire calories and sex, without any explicit cognitive representation of “inclusive fitness.”

A human engineer would have said, “Whoa, I’ve just invented a consequentialist! Now I can take all my previous hard-won knowledge about which behaviors improve fitness, and declare it explicitly! I can convert all this complicated reinforcement learning machinery into a simple declarative knowledge statement that ‘fatty foods and sex usually improve your inclusive fitness.’ Consequential reasoning will automatically take care of the rest. Plus, it won’t have the obvious failure mode where it invents condoms!”

But then a human engineer wouldn’t have built the retina backward, either.

The blind idiot god is not a unitary purpose, but a many-splintered attention. Foxes evolve to catch rabbits, rabbits evolve to evade foxes; there are as many evolutions as species. But within each species, the blind idiot god is purely obsessed with inclusive genetic fitness. No quality is valued, not even survival, except insofar as it increases reproductive fitness. There’s no point in an organism with steel skin if it ends up having 1% less reproductive capacity.

Yet when the blind idiot god created protein computers, its monomaniacal focus on inclusive genetic fitness was not faithfully transmitted. Its optimization criterion did not successfully quine. We, the handiwork of evolution, are as alien to evolution as our Maker is alien to us. One pure utility function splintered into a thousand shards of desire.

Why? Above all, because evolution is stupid in an absolute sense. But also because the first protein computers weren’t anywhere near as general as the blind idiot god, and could only utilize short-term desires.

In the final analysis, asking why evolution didn’t build humans to maximize inclusive genetic fitness is like asking why evolution didn’t hand humans a ribosome and tell them to design their own biochemistry. Because evolution can’t refactor code that fast, that’s why. But maybe in a billion years of continued natural selection that’s exactly what would happen, if intelligence were foolish enough to allow the idiot god continued reign.

The Mote in God’s Eye by Niven and Pournelle depicts an intelligent species that stayed biological a little too long, slowly becoming truly enslaved by evolution, gradually turning into true fitness maximizers obsessed with outreproducing each other. But thankfully that’s not what happened. Not here on Earth. At least not yet.

So humans love the taste of sugar and fat, and we love our sons and daughters. We seek social status, and sex. We sing and dance and play. We learn for the love of learning.

A thousand delicious tastes, matched to ancient reinforcers that once correlated with reproductive fitness—now sought whether or not they enhance reproduction. Sex with birth control, chocolate, the music of long-dead Bach on a CD.

And when we finally learn about evolution, we think to ourselves: “Obsess all day about inclusive genetic fitness? Where’s the fun in that?”

The blind idiot god’s single monomaniacal goal splintered into a thousand shards of desire. And this is well, I think, though I’m a human who says so. Or else what would we do with the future? What would we do with the billion galaxies in the night sky? Fill them with maximally efficient replicators? Should our descendants deliberately obsess about maximizing their inclusive genetic fitness, regarding all else only as a means to that end?

Being a thousand shards of desire isn’t always fun, but at least it’s not boring. Somewhere along the line, we evolved tastes for novelty, complexity, elegance, and challenge—tastes that judge the blind idiot god’s monomaniacal focus, and find it aesthetically unsatisfying.

And yes, we got those very same tastes from the blind idiot’s godshatter.

So what?

Part M
Fragile Purposes

143
Belief in Intelligence

I don’t know what moves Garry Kasparov would make in a chess game. What, then, is the empirical content of my belief that “Kasparov is a highly intelligent chess player”? What real-world experience does my belief tell me to anticipate? Is it a cleverly masked form of total ignorance?

To sharpen the dilemma, suppose Kasparov plays against some mere chess grandmaster Mr. G, who’s not in the running for world champion. My own ability is far too low to distinguish between these levels of chess skill. When I try to guess Kasparov’s move, or Mr. G’s next move, all I can do is try to guess “the best chess move” using my own meager knowledge of chess. Then I would produce exactly the same prediction for Kasparov’s move or Mr. G’s move in any particular chess position. So what is the empirical content of my belief that “Kasparov is a better chess player than Mr. G”?

The empirical content of my belief is the testable, falsifiable prediction that the final chess position will occupy the class of chess positions that are wins for Kasparov, rather than drawn games or wins for Mr. G. (Counting resignation as a legal move that leads to a chess position classified as a loss.) The degree to which I think Kasparov is a “better player” is reflected in the amount of probability mass I concentrate into the “Kasparov wins” class of outcomes, versus the “drawn game” and “Mr. G wins” class of outcomes. These classes are extremely vague in the sense that they refer to vast spaces of possible chess positions—but “Kasparov wins” is more specific than maximum entropy, because it can be definitely falsified by a vast set of chess positions.

The outcome of Kasparov’s game is predictable because I know, and understand, Kasparov’s goals. Within the confines of the chess board, I know Kasparov’s motivations—I know his success criterion, his utility function, his target as an optimization process. I know where Kasparov is ultimately trying to steer the future and I anticipate he is powerful enough to get there, although I don’t anticipate much about how Kasparov is going to do it.

Imagine that I’m visiting a distant city, and a local friend volunteers to drive me to the airport. I don’t know the neighborhood. Each time my friend approaches a street intersection, I don’t know whether my friend will turn left, turn right, or continue straight ahead. I can’t predict my friend’s move even as we approach each individual intersection—let alone predict the whole sequence of moves in advance.

Yet I can predict the result of my friend’s unpredictable actions: we will arrive at the airport. Even if my friend’s house were located elsewhere in the city, so that my friend made a completely different sequence of turns, I would just as confidently predict our arrival at the airport. I can predict this long in advance, before I even get into the car. My flight departs soon, and there’s no time to waste; I wouldn’t get into the car in the first place, if I couldn’t confidently predict that the car would travel to the airport along an unpredictable pathway.

Isn’t this a remarkable situation to be in, from a scientific perspective? I can predict the outcome of a process, without being able to predict any of the intermediate steps of the process.

How is this even possible? Ordinarily one predicts by imagining the present and then running the visualization forward in time. If you want a precise model of the Solar System, one that takes into account planetary perturbations, you must start with a model of all major objects and run that model forward in time, step by step.

Sometimes simpler problems have a closed-form solution, where calculating the future at time T takes the same amount of work regardless of T. A coin rests on a table, and after each minute, the coin turns over. The coin starts out showing heads. What face will it show a hundred minutes later? Obviously you did not answer this question by visualizing a hundred intervening steps. You used a closed-form solution that worked to predict the outcome, and would also work to predict any of the intervening steps.

But when my friend drives me to the airport, I can predict the outcome successfully using a strange model that won’t work to predict any of the intermediate steps. My model doesn’t even require me to input the initial conditions—I don’t need to know where we start out in the city!

I do need to know something about my friend. I must know that my friend wants me to make my flight. I must credit that my friend is a good enough planner to successfully drive me to the airport (if he wants to). These are properties of my friend’s initial state—properties which let me predict the final destination, though not any intermediate turns.

I must also credit that my friend knows enough about the city to drive successfully. This may be regarded as a relation between my friend and the city; hence, a property of both. But an extremely abstract property, which does not require any specific knowledge about either the city, or about my friend’s knowledge about the city.

This is one way of viewing the subject matter to which I’ve devoted my life—these remarkable situations which place us in such odd epistemic positions. And my work, in a sense, can be viewed as unraveling the exact form of that strange abstract knowledge we can possess; whereby, not knowing the actions, we can justifiably know the consequence.

“Intelligence” is too narrow a term to describe these remarkable situations in full generality. I would say rather “optimization process.” A similar situation accompanies the study of biological natural selection, for example; we can’t predict the exact form of the next organism observed.

But my own specialty is the kind of optimization process called “intelligence”; and even narrower, a particular kind of intelligence called “Friendly Artificial Intelligence”—of which, I hope, I will be able to obtain especially precise abstract knowledge.

144
Humans in Funny Suits

Many times the human species has travelled into space, only to find the stars inhabited by aliens who look remarkably like humans in funny suits—or even humans with a touch of makeup and latex—or just beige Caucasians in fee simple.

Star Trek: The Original Series, “Arena,” © CBS Corporation

It’s remarkable how the human form is the natural baseline of the universe, from which all other alien species are derived via a few modifications.

What could possibly explain this fascinating phenomenon? Convergent evolution, of course! Even though these alien life-forms evolved on a thousand alien planets, completely independently from Earthly life, they all turned out the same.

Don’t be fooled by the fact that a kangaroo (a mammal) resembles us rather less than does a chimp (a primate), nor by the fact that a frog (amphibians, like us, are tetrapods) resembles us less than the kangaroo. Don’t be fooled by the bewildering variety of the insects, who split off from us even longer ago than the frogs; don’t be fooled that insects have six legs, and their skeletons on the outside, and a different system of optics, and rather different sexual practices.

You might think that a truly alien species would be more different from us than we are from insects. As I said, don’t be fooled. For an alien species to evolve intelligence, it must have two legs with one knee each attached to an upright torso, and must walk in a way similar to us. You see, any intelligence needs hands, so you’ve got to repurpose a pair of legs for that—and if you don’t start with a four-legged being, it can’t develop a running gait and walk upright, freeing the hands.

. . . Or perhaps we should consider, as an alternative theory, that it’s the easy way out to use humans in funny suits.

But the real problem is not shape; it is mind. “Humans in funny suits” is a well-known term in literary science-fiction fandom, and it does not refer to something with four limbs that walks upright. An angular creature of pure crystal is a “human in a funny suit” if she thinks remarkably like a human—especially a human of an English-speaking culture of the late-twentieth/early-twenty-first century.

I don’t watch a lot of ancient movies. When I was watching the movie Psycho (1960) a few years back, I was taken aback by the cultural gap between the Americans on the screen and my America. The buttoned-shirted characters of Psycho are considerably more alien than the vast majority of so-called “aliens” I encounter on TV or the silver screen.

To write a culture that isn’t just like your own culture, you have to be able to see your own culture as a special case—not as a norm which all other cultures must take as their point of departure. Studying history may help—but then it is only little black letters on little white pages, not a living experience. I suspect that it would help more to live for a year in China or Dubai or among the !Kung . . . this I have never done, being busy. Occasionally I wonder what things I might not be seeing (not there, but here).

Seeing your humanity as a special case is very much harder than this.

In every known culture, humans seem to experience joy, sadness, fear, disgust, anger, and surprise. In every known culture, these emotions are indicated by the same facial expressions. Next time you see an “alien”—or an “AI,” for that matter—I bet that when it gets angry (and it will get angry), it will show the human-universal facial expression for anger.

We humans are very much alike under our skulls—that goes with being a sexually reproducing species; you can’t have everyone using different complex adaptations, they wouldn’t assemble. (Do the aliens reproduce sexually, like humans and many insects? Do they share small bits of genetic material, like bacteria? Do they form colonies, like fungi? Does the rule of psychological unity apply among them?)

The only intelligences your ancestors had to manipulate—complexly so, and not just tame or catch in nets—the only minds your ancestors had to model in detail—were minds that worked more or less like their own. And so we evolved to predict Other Minds by putting ourselves in their shoes, asking what we would do in their situations; for that which was to be predicted, was similar to the predictor.

“What?” you say. “I don’t assume other people are just like me! Maybe I’m sad, and they happen to be angry! They believe other things than I do; their personalities are different from mine!” Look at it this way: a human brain is an extremely complicated physical system. You are not modeling it neuron-by-neuron or atom-by-atom. If you came across a physical system as complex as the human brain which was not like you, it would take scientific lifetimes to unravel it. You do not understand how human brains work in an abstract, general sense; you can’t build one, and you can’t even build a computer model that predicts other brains as well as you predict them.

The only reason you can try at all to grasp anything as physically complex and poorly understood as the brain of another human being is that you configure your own brain to imitate it. You empathize (though perhaps not sympathize). You impose on your own brain the shadow of the other mind’s anger and the shadow of its beliefs. You may never think the words, “What would I do in this situation?,” but that little shadow of the other mind that you hold within yourself is something animated within your own brain, invoking the same complex machinery that exists in the other person, synchronizing gears you don’t understand. You may not be angry yourself, but you know that if you were angry at you, and you believed that you were godless scum, you would try to hurt you . . .

This “empathic inference” (as I shall call it) works for humans, more or less.

But minds with different emotions—minds that feel emotions you’ve never felt yourself, or that fail to feel emotions you would feel? That’s something you can’t grasp by putting your brain into the other brain’s shoes. I can tell you to imagine an alien that grew up in a universe with four spatial dimensions, instead of three spatial dimensions, but you won’t be able to reconfigure your visual cortex to see like that alien would see. I can try to write a story about aliens with different emotions, but you won’t be able to feel those emotions, and neither will I.

Imagine an alien watching a video of the Marx Brothers and having absolutely no idea what was going on, or why you would actively seek out such a sensory experience, because the alien has never conceived of anything remotely like a sense of humor. Don’t pity them for missing out; you’ve never antled.

You might ask: Maybe the aliens do have a sense of humor, but you’re not telling funny enough jokes? This is roughly the equivalent of trying to speak English very loudly, and very slowly, in a foreign country, on the theory that those foreigners must have an inner ghost that can hear the meaning dripping from your words, inherent in your words, if only you can speak them loud enough to overcome whatever strange barrier stands in the way of your perfectly sensible English.

It is important to appreciate that laughter can be a beautiful and valuable thing, even if it is not universalizable, even if it is not possessed by all possible minds. It would be our own special part of the gift we give to tomorrow. That can count for something too.

It had better, because universalizability is one metaethical notion that I can’t salvage for you. Universalizability among humans, maybe; but not among all possible minds.

And what about minds that don’t run on emotional architectures like your own—that don’t have things analogous to emotions? No, don’t bother explaining why any intelligent mind powerful enough to build complex machines must inevitably have states analogous to emotions. Natural selection builds complex machines without itself having emotions. Now there’s a Real Alien for you—an optimization process that really Does Not Work Like You Do.

Much of the progress in biology since the 1960s has consisted of trying to enforce a moratorium on anthropomorphizing evolution. That was a major academic slap-fight, and I’m not sure that sanity would have won the day if not for the availability of crushing experimental evidence backed up by clear math. Getting people to stop putting themselves in alien shoes is a long, hard, uphill slog. I’ve been fighting that battle on AI for years.

Our anthropomorphism runs very deep in us; it cannot be excised by a simple act of will, a determination to say, “Now I shall stop thinking like a human!” Humanity is the air we breathe; it is our generic, the white paper on which we begin our sketches. And we do not think of ourselves as being human when we are being human.

It is proverbial in literary science fiction that the true test of an author is their ability to write Real Aliens. (And not just conveniently incomprehensible aliens who, for their own mysterious reasons, do whatever the plot happens to require.) Jack Vance was one of the great masters of this art. Vance’s humans, if they come from a different culture, are more alien than most “aliens.” (Never read any Vance? I would recommend starting with City of the Chasch.) Niven and Pournelle’s The Mote in God’s Eye also gets a standard mention here.

And conversely—well, I once read a science fiction author (I think Orson Scott Card) say that the all-time low point of television science fiction was the Star Trek episode where parallel evolution has proceeded to the extent of producing aliens who not only look just like humans, who not only speak English, but have also independently rewritten, word for word, the preamble to the US Constitution.

This is the Great Failure of Imagination. Don’t think that it’s just about science fiction, or even just about AI. The inability to imagine the alien is the inability to see yourself—the inability to understand your own specialness. Who can see a human camouflaged against a human background?

145
Optimization and the Intelligence Explosion

Among the topics I haven’t delved into here is the notion of an optimization process. Roughly, this is the idea that your power as a mind is your ability to hit small targets in a large search space—this can be either the space of possible futures (planning) or the space of possible designs (invention).

Suppose you have a car, and suppose we already know that your preferences involve travel. Now suppose that you take all the parts in the car, or all the atoms, and jumble them up at random. It’s very unlikely that you’ll end up with a travel-artifact at all, even so much as a wheeled cart; let alone a travel-artifact that ranks as high in your preferences as the original car. So, relative to your preference ordering, the car is an extremely improbable artifact. The power of an optimization process is that it can produce this kind of improbability.

You can view both intelligence and natural selection as special cases of optimization: processes that hit, in a large search space, very small targets defined by implicit preferences. Natural selection prefers more efficient replicators. Human intelligences have more complex preferences. Neither evolution nor humans have consistent utility functions, so viewing them as “optimization processes” is understood to be an approximation. You’re trying to get at the sort of work being done, not claim that humans or evolution do this work perfectly.

This is how I see the story of life and intelligence—as a story of improbably good designs being produced by optimization processes. The “improbability” here is improbability relative to a random selection from the design space, not improbability in an absolute sense—if you have an optimization process around, then “improbably” good designs become probable.

Looking over the history of optimization on Earth up until now, the first step is to conceptually separate the meta level from the object level—separate the structure of optimization from that which is optimized.

If you consider biology in the absence of hominids, then on the object level we have things like dinosaurs and butterflies and cats. On the meta level we have things like sexual recombination and natural selection of asexual populations. The object level, you will observe, is rather more complicated than the meta level. Natural selection is not an easy subject and it involves math. But if you look at the anatomy of a whole cat, the cat has dynamics immensely more complicated than “mutate, recombine, reproduce.”

This is not surprising. Natural selection is an accidental optimization process, that basically just started happening one day in a tidal pool somewhere. A cat is the subject of millions of years and billions of years of evolution.

Cats have brains, of course, which operate to learn over a lifetime; but at the end of the cat’s lifetime, that information is thrown away, so it does not accumulate. The cumulative effects of cat-brains upon the world as optimizers, therefore, are relatively small.

Or consider a bee brain, or a beaver brain. A bee builds hives, and a beaver builds dams; but they didn’t figure out how to build them from scratch. A beaver can’t figure out how to build a hive, a bee can’t figure out how to build a dam.

So animal brains—up until recently—were not major players in the planetary game of optimization; they were pieces but not players. Compared to evolution, brains lacked both generality of optimization power (they could not produce the amazing range of artifacts produced by evolution) and cumulative optimization power (their products did not accumulate complexity over time). For more on this theme see Protein Reinforcement and DNA Consequentialism.

Very recently, certain animal brains have begun to exhibit both generality of optimization power (producing an amazingly wide range of artifacts, in time scales too short for natural selection to play any significant role) and cumulative optimization power (artifacts of increasing complexity, as a result of skills passed on through language and writing).

Natural selection takes hundreds of generations to do anything and millions of years for de novo complex designs. Human programmers can design a complex machine with a hundred interdependent elements in a single afternoon. This is not surprising, since natural selection is an accidental optimization process that basically just started happening one day, whereas humans are optimized optimizers handcrafted by natural selection over millions of years.

The wonder of evolution is not how well it works, but that it works at all without being optimized. This is how optimization bootstrapped itself into the universe—starting, as one would expect, from an extremely inefficient accidental optimization process. Which is not the accidental first replicator, mind you, but the accidental first process of natural selection. Distinguish the object level and the meta level!

Since the dawn of optimization in the universe, a certain structural commonality has held across both natural selection and human intelligence . . .

Natural selection selects on genes, but generally speaking, the genes do not turn around and optimize natural selection. The invention of sexual recombination is an exception to this rule, and so is the invention of cells and DNA. And you can see both the power and the rarity of such events, by the fact that evolutionary biologists structure entire histories of life on Earth around them.

But if you step back and take a human standpoint—if you think like a programmer—then you can see that natural selection is still not all that complicated. We’ll try bundling different genes together? We’ll try separating information storage from moving machinery? We’ll try randomly recombining groups of genes? On an absolute scale, these are the sort of bright ideas that any smart hacker comes up with during the first ten minutes of thinking about system architectures.

Because natural selection started out so inefficient (as a completely accidental process), this tiny handful of meta-level improvements feeding back in from the replicators—nowhere near as complicated as the structure of a cat—structure the evolutionary epochs of life on Earth.

And after all that, natural selection is still a blind idiot of a god. Gene pools can evolve to extinction, despite all cells and sex.

Now natural selection does feed on itself in the sense that each new adaptation opens up new avenues of further adaptation; but that takes place on the object level. The gene pool feeds on its own complexity—but only thanks to the protected interpreter of natural selection that runs in the background, and that is not itself rewritten or altered by the evolution of species.

Likewise, human beings invent sciences and technologies, but we have not yet begun to rewrite the protected structure of the human brain itself. We have a prefrontal cortex and a temporal cortex and a cerebellum, just like the first inventors of agriculture. We haven’t started to genetically engineer ourselves. On the object level, science feeds on science, and each new discovery paves the way for new discoveries—but all that takes place with a protected interpreter, the human brain, running untouched in the background.

We have meta-level inventions like science, that try to instruct humans in how to think. But the first person to invent Bayes’s Theorem did not become a Bayesian; they could not rewrite themselves, lacking both that knowledge and that power. Our significant innovations in the art of thinking, like writing and science, are so powerful that they structure the course of human history; but they do not rival the brain itself in complexity, and their effect upon the brain is comparatively shallow.

The present state of the art in rationality training is not sufficient to turn an arbitrarily selected mortal into Albert Einstein, which shows the power of a few minor genetic quirks of brain design compared to all the self-help books ever written in the twentieth century.

Because the brain hums away invisibly in the background, people tend to overlook its contribution and take it for granted; and talk as if the simple instruction to “Test ideas by experiment,” or the p < 0.05 significance rule, were the same order of contribution as an entire human brain. Try telling chimpanzees to test their ideas by experiment and see how far you get.

Now . . . some of us want to intelligently design an intelligence that would be capable of intelligently redesigning itself, right down to the level of machine code.

The machine code at first, and the laws of physics later, would be a protected level of a sort. But that “protected level” would not contain the dynamic of optimization; the protected levels would not structure the work. The human brain does quite a bit of optimization on its own, and screws up on its own, no matter what you try to tell it in school. But this fully wraparound recursive optimizer would have no protected level that was optimizing. All the structure of optimization would be subject to optimization itself.

And that is a sea change which breaks with the entire past since the first replicator, because it breaks the idiom of a protected meta level.

The history of Earth up until now has been a history of optimizers spinning their wheels at a constant rate, generating a constant optimization pressure. And creating optimized products, not at a constant rate, but at an accelerating rate, because of how object-level innovations open up the pathway to other object-level innovations. But that acceleration is taking place with a protected meta level doing the actual optimizing. Like a search that leaps from island to island in the search space, and good islands tend to be adjacent to even better islands, but the jumper doesn’t change its legs. Occasionally, a few tiny little changes manage to hit back to the meta level, like sex or science, and then the history of optimization enters a new epoch and everything proceeds faster from there.

Imagine an economy without investment, or a university without language, a technology without tools to make tools. Once in a hundred million years, or once in a few centuries, someone invents a hammer.

That is what optimization has been like on Earth up until now.

When I look at the history of Earth, I don’t see a history of optimization over time. I see a history of optimization power in, and optimized products out. Up until now, thanks to the existence of almost entirely protected meta-levels, it’s been possible to split up the history of optimization into epochs, and, within each epoch, graph the cumulative object-level optimization over time, because the protected level is running in the background and is not itself changing within an epoch.

What happens when you build a fully wraparound, recursively self-improving AI? Then you take the graph of “optimization in, optimized out,” and fold the graph in on itself. Metaphorically speaking.

If the AI is weak, it does nothing, because it is not powerful enough to significantly improve itself—like telling a chimpanzee to rewrite its own brain.

If the AI is powerful enough to rewrite itself in a way that increases its ability to make further improvements, and this reaches all the way down to the AI’s full understanding of its own source code and its own design as an optimizer . . . then even if the graph of “optimization power in” and “optimized product out” looks essentially the same, the graph of optimization over time is going to look completely different from Earth’s history so far.

People often say something like, “But what if it requires exponentially greater amounts of self-rewriting for only a linear improvement?” To this the obvious answer is, “Natural selection exerted roughly constant optimization power on the hominid line in the course of coughing up humans; and this doesn’t seem to have required exponentially more time for each linear increment of improvement.”

All of this is still mere analogic reasoning. A full Artificial General Intelligence thinking about the nature of optimization and doing its own AI research and rewriting its own source code, is not really like a graph of Earth’s history folded in on itself. It is a different sort of beast. These analogies are at best good for qualitative predictions, and even then, I have a large amount of other beliefs I haven’t yet explained, which are telling me which analogies to make, et cetera.

But if you want to know why I might be reluctant to extend the graph of biological and economic growth over time, into the future and over the horizon of an AI that thinks at transistor speeds and invents self-replicating molecular nanofactories and improves its own source code, then there is my reason: you are drawing the wrong graph, and it should be optimization power in versus optimized product out, not optimized product versus time.

146
Ghosts in the Machine

People hear about Friendly AI and say—this is one of the top three initial reactions:

“Oh, you can try to tell the AI to be Friendly, but if the AI can modify its own source code, it’ll just remove any constraints you try to place on it.”

And where does that decision come from?

Does it enter from outside causality, rather than being an effect of a lawful chain of causes that started with the source code as originally written? Is the AI the ultimate source of its own free will?

A Friendly AI is not a selfish AI constrained by a special extra conscience module that overrides the AI’s natural impulses and tells it what to do. You just build the conscience, and that is the AI. If you have a program that computes which decision the AI should make, you’re done. The buck stops immediately.

At this point, I shall take a moment to quote some case studies from the Computer Stupidities site and Programming subtopic. (I am not linking to this, because it is a fearsome time-trap; you can Google if you dare.)

I tutored college students who were taking a computer programming course. A few of them didn’t understand that computers are not sentient. More than one person used comments in their Pascal programs to put detailed explanations such as, “Now I need you to put these letters on the screen.” I asked one of them what the deal was with those comments. The reply: “How else is the computer going to understand what I want it to do?” Apparently they would assume that since they couldn’t make sense of Pascal, neither could the computer.

While in college, I used to tutor in the school’s math lab. A student came in because his BASIC program would not run. He was taking a beginner course, and his assignment was to write a program that would calculate the recipe for oatmeal cookies, depending upon the number of people you’re baking for. I looked at his program, and it went something like this:

10 Preheat oven to 350
20 Combine all ingredients in a large mixing bowl
30 Mix until smooth

An introductory programming student once asked me to look at his program and figure out why it was always churning out zeroes as the result of a simple computation. I looked at the program, and it was pretty obvious:

begin
read("Number of Apples", apples)
read("Number of Carrots", carrots)
read("Price for 1 Apple", a_price)
read("Price for 1 Carrot", c_price)
write("Total for Apples", a_total)
write("Total for Carrots", c_total)
write("Total", total)
total = a_total + c_total
a_total = apples * a_price
c_total = carrots * c_price
end

Me: “Well, your program can’t print correct results before they’re computed.”

Him: “Huh? It’s logical what the right solution is, and the computer should reorder the instructions the right way.”

There’s an instinctive way of imagining the scenario of “programming an AI.” It maps onto a similar-seeming human endeavor: Telling a human being what to do. Like the “program” is giving instructions to a little ghost that sits inside the machine, which will look over your instructions and decide whether it likes them or not.

There is no ghost who looks over the instructions and decides how to follow them. The program is the AI.

That doesn’t mean the ghost does anything you wish for, like a genie. It doesn’t mean the ghost does everything you want the way you want it, like a slave of exceeding docility. It means your instruction is the only ghost that’s there, at least at boot time.

AI is much harder than people instinctively imagined, exactly because you can’t just tell the ghost what to do. You have to build the ghost from scratch, and everything that seems obvious to you, the ghost will not see unless you know how to make the ghost see it. You can’t just tell the ghost to see it. You have to create that-which-sees from scratch.

If you don’t know how to build something that seems to have some strange ineffable elements like, say, “decision-making,” then you can’t just shrug your shoulders and let the ghost’s free will do the job. You’re left forlorn and ghostless.

There’s more to building a chess-playing program than building a really fast processor—so the AI will be really smart—and then typing at the command prompt “Make whatever chess moves you think are best.” You might think that, since the programmers themselves are not very good chess players, any advice they tried to give the electronic superbrain would just slow the ghost down. But there is no ghost. You see the problem.

And there isn’t a simple spell you can perform to—poof!—summon a complete ghost into the machine. You can’t say, “I summoned the ghost, and it appeared; that’s cause and effect for you.” (It doesn’t work if you use the notion of “emergence” or “complexity” as a substitute for “summon,” either.) You can’t give an instruction to the CPU, “Be a good chess player!” You have to see inside the mystery of chess-playing thoughts, and structure the whole ghost from scratch.

No matter how common-sensical, no matter how logical, no matter how “obvious” or “right” or “self-evident” or “intelligent” something seems to you, it will not happen inside the ghost. Unless it happens at the end of a chain of cause and effect that began with the instructions that you had to decide on, plus any causal dependencies on sensory data that you built into the starting instructions.

This doesn’t mean you program in every decision explicitly. Deep Blue was a chess player far superior to its programmers. Deep Blue made better chess moves than anything its makers could have explicitly programmed—but not because the programmers shrugged and left it up to the ghost. Deep Blue moved better than its programmers . . . at the end of a chain of cause and effect that began in the programmers’ code and proceeded lawfully from there. Nothing happened just because it was so obviously a good move that Deep Blue’s ghostly free will took over, without the code and its lawful consequences being involved.

If you try to wash your hands of constraining the AI, you aren’t left with a free ghost like an emancipated slave. You are left with a heap of sand that no one has purified into silicon, shaped into a CPU and programmed to think.

Go ahead, try telling a computer chip “Do whatever you want!” See what happens? Nothing. Because you haven’t constrained it to understand freedom.

All it takes is one single step that is so obvious, so logical, so self-evident that your mind just skips right over it, and you’ve left the path of the AI programmer. It takes an effort like the one I illustrate in Grasping Slippery Things to prevent your mind from doing this.

147
Artificial Addition

Suppose that human beings had absolutely no idea how they performed arithmetic. Imagine that human beings had evolved, rather than having learned, the ability to count sheep and add sheep. People using this built-in ability have no idea how it worked, the way Aristotle had no idea how his visual cortex supported his ability to see things. Peano Arithmetic as we know it has not been invented. There are philosophers working to formalize numerical intuitions, but they employ notations such as

Plus-Of(Seven,Six) = Thirteen

to formalize the intuitively obvious fact that when you add “seven” plus “six,” of course you get “thirteen.”

In this world, pocket calculators work by storing a giant lookup table of arithmetical facts, entered manually by a team of expert Artificial Arithmeticians, for starting values that range between zero and one hundred. While these calculators may be helpful in a pragmatic sense, many philosophers argue that they’re only simulating addition, rather than really adding. No machine can really count—that’s why humans have to count thirteen sheep before typing “thirteen” into the calculator. Calculators can recite back stored facts, but they can never know what the statements mean—if you type in “two hundred plus two hundred” the calculator says “Error: Outrange,” when it’s intuitively obvious, if you know what the words mean, that the answer is “four hundred.”

Some philosophers, of course, are not so naive as to be taken in by these intuitions. Numbers are really a purely formal system—the label “thirty-seven” is meaningful, not because of any inherent property of the words themselves, but because the label refers to thirty-seven sheep in the external world. A number is given this referential property by its semantic network of relations to other numbers. That’s why, in computer programs, the LISP token for “thirty-seven” doesn’t need any internal structure—it’s only meaningful because of reference and relation, not some computational property of “thirty-seven” itself.

No one has ever developed an Artificial General Arithmetician, though of course there are plenty of domain-specific, narrow Artificial Arithmeticians that work on numbers between “twenty” and “thirty,” and so on. And if you look at how slow progress has been on numbers in the range of “two hundred,” then it becomes clear that we’re not going to get Artificial General Arithmetic any time soon. The best experts in the field estimate it will be at least a hundred years before calculators can add as well as a human twelve-year-old.

But not everyone agrees with this estimate, or with merely conventional beliefs about Artificial Arithmetic. It’s common to hear statements such as the following:

“It’s a framing problem—what ‘twenty-one plus’ equals depends on whether it’s ‘plus three’ or ‘plus four.’ If we can just get enough arithmetical facts stored to cover the common-sense truths that everyone knows, we’ll start to see real addition in the network.”
“But you’ll never be able to program in that many arithmetical facts by hiring experts to enter them manually. What we need is an Artificial Arithmetician that can learn the vast network of relations between numbers that humans acquire during their childhood by observing sets of apples.”
“No, what we really need is an Artificial Arithmetician that can understand natural language, so that instead of having to be explicitly told that twenty-one plus sixteen equals thirty-seven, it can get the knowledge by exploring the Web.”
“Frankly, it seems to me that you’re just trying to convince yourselves that you can solve the problem. None of you really know what arithmetic is, so you’re floundering around with these generic sorts of arguments. ‘We need an AA that can learn X,’ ‘We need an AA that can extract X from the Internet.’ I mean, it sounds good, it sounds like you’re making progress, and it’s even good for public relations, because everyone thinks they understand the proposed solution—but it doesn’t really get you any closer to general addition, as opposed to domain-specific addition. Probably we will never know the fundamental nature of arithmetic. The problem is just too hard for humans to solve.”
“That’s why we need to develop a general arithmetician the same way Nature did—evolution.”
“Top-down approaches have clearly failed to produce arithmetic. We need a bottom-up approach, some way to make arithmetic emerge. We have to acknowledge the basic unpredictability of complex systems.”
“You’re all wrong. Past efforts to create machine arithmetic were futile from the start, because they just didn’t have enough computing power. If you look at how many trillions of synapses there are in the human brain, it’s clear that calculators don’t have lookup tables anywhere near that large. We need calculators as powerful as a human brain. According to Moore’s Law, this will occur in the year 2031 on April 27 between 4:00 and 4:30 in the morning.”
“I believe that machine arithmetic will be developed when researchers scan each neuron of a complete human brain into a computer, so that we can simulate the biological circuitry that performs addition in humans.”
“I don’t think we have to wait to scan a whole brain. Neural networks are just like the human brain, and you can train them to do things without knowing how they do them. We’ll create programs that will do arithmetic without we, our creators, ever understanding how they do arithmetic.”
“But Gödel’s Theorem shows that no formal system can ever capture the basic properties of arithmetic. Classical physics is formalizable, so to add two and two, the brain must take advantage of quantum physics.”
“Hey, if human arithmetic were simple enough that we could reproduce it in a computer, we wouldn’t be able to count high enough to build computers.”
“Haven’t you heard of John Searle’s Chinese Calculator Experiment? Even if you did have a huge set of rules that would let you add ‘twenty-one’ and ‘sixteen,’ just imagine translating all the words into Chinese, and you can see that there’s no genuine addition going on. There are no real numbers anywhere in the system, just labels that humans use for numbers . . .”

There is more than one moral to this parable, and I have told it with different morals in different contexts. It illustrates the idea of levels of organization, for example—a CPU can add two large numbers because the numbers aren’t black-box opaque objects, they’re ordered structures of 32 bits.

But for purposes of overcoming bias, let us draw two morals:

First, the danger of believing assertions you can’t regenerate from your own knowledge.
Second, the danger of trying to dance around basic confusions.

Lest anyone accuse me of generalizing from fictional evidence, both lessons may be drawn from the real history of Artificial Intelligence as well.

The first danger is the object-level problem that the AA devices ran into: they functioned as tape recorders playing back “knowledge” generated from outside the system, using a process they couldn’t capture internally. A human could tell the AA device that “twenty-one plus sixteen equals thirty-seven,” and the AA devices could record this sentence and play it back, or even pattern-match “twenty-one plus sixteen” to output “thirty-seven!”—but the AA devices couldn’t generate such knowledge for themselves.

Which is strongly reminiscent of believing a physicist who tells you “Light is waves,” recording the fascinating words and playing them back when someone asks “What is light made of?,” without being able to generate the knowledge for yourself.

The second moral is the meta-level danger that consumed the Artificial Arithmetic researchers and opinionated bystanders—the danger of dancing around confusing gaps in your knowledge. The tendency to do just about anything except grit your teeth and buckle down and fill in the damn gap.

Whether you say, “It is emergent!,” or whether you say, “It is unknowable!,” in neither case are you acknowledging that there is a basic insight required which is possessable, but unpossessed by you.

How can you know when you’ll have a new basic insight? And there’s no way to get one except by banging your head against the problem, learning everything you can about it, studying it from as many angles as possible, perhaps for years. It’s not a pursuit that academia is set up to permit, when you need to publish at least one paper per month. It’s certainly not something that venture capitalists will fund. You want to either go ahead and build the system now, or give up and do something else instead.

Look at the comments above: none are aimed at setting out on a quest for the missing insight which would make numbers no longer mysterious, make “twenty-seven” more than a black box. None of the commenters realized that their difficulties arose from ignorance or confusion in their own minds, rather than an inherent property of arithmetic. They were not trying to achieve a state where the confusing thing ceased to be confusing.

If you read Judea Pearl’s Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference,¹ then you will see that the basic insight behind graphical models is indispensable to problems that require it. (It’s not something that fits on a T-shirt, I’m afraid, so you’ll have to go and read the book yourself. I haven’t seen any online popularizations of Bayesian networks that adequately convey the reasons behind the principles, or the importance of the math being exactly the way it is, but Pearl’s book is wonderful.) There were once dozens of “non-monotonic logics” awkwardly trying to capture intuitions such as “If my burglar alarm goes off, there was probably a burglar, but if I then learn that there was a small earthquake near my home, there was probably not a burglar.” With the graphical-model insight in hand, you can give a mathematical explanation of exactly why first-order logic has the wrong properties for the job, and express the correct solution in a compact way that captures all the common-sense details in one elegant swoop. Until you have that insight, you’ll go on patching the logic here, patching it there, adding more and more hacks to force it into correspondence with everything that seems “obviously true.”

You won’t know the Artificial Arithmetic problem is unsolvable without its key. If you don’t know the rules, you don’t know the rule that says you need to know the rules to do anything. And so there will be all sorts of clever ideas that seem like they might work, like building an Artificial Arithmetician that can read natural language and download millions of arithmetical assertions from the Internet.

And yet somehow the clever ideas never work. Somehow it always turns out that you “couldn’t see any reason it wouldn’t work” because you were ignorant of the obstacles, not because no obstacles existed. Like shooting blindfolded at a distant target—you can fire blind shot after blind shot, crying, “You can’t prove to me that I won’t hit the center!” But until you take off the blindfold, you’re not even in the aiming game. When “no one can prove to you” that your precious idea isn’t right, it means you don’t have enough information to strike a small target in a vast answer space. Until you know your idea will work, it won’t.

From the history of previous key insights in Artificial Intelligence, and the grand messes that were proposed prior to those insights, I derive an important real-life lesson: When the basic problem is your ignorance, clever strategies for bypassing your ignorance lead to shooting yourself in the foot.

1. Pearl, Probabilistic Reasoning in Intelligent Systems.

148
Terminal Values and Instrumental Values

On a purely instinctive level, any human planner behaves as if they distinguish between means and ends. Want chocolate? There’s chocolate at the Publix supermarket. You can get to the supermarket if you drive one mile south on Washington Ave. You can drive if you get into the car. You can get into the car if you open the door. You can open the door if you have your car keys. So you put your car keys into your pocket, and get ready to leave the house . . .

. . . when suddenly the word comes on the radio that an earthquake has destroyed all the chocolate at the local Publix. Well, there’s no point in driving to the Publix if there’s no chocolate there, and no point in getting into the car if you’re not driving anywhere, and no point in having car keys in your pocket if you’re not driving. So you take the car keys out of your pocket, and call the local pizza service and have them deliver a chocolate pizza. Mm, delicious.

I rarely notice people losing track of plans they devised themselves. People usually don’t drive to the supermarket if they know the chocolate is gone. But I’ve also noticed that when people begin explicitly talking about goal systems instead of just wanting things, mentioning “goals” instead of using them, they oft become confused. Humans are experts at planning, not experts on planning, or there’d be a lot more AI developers in the world.

In particular, I’ve noticed people get confused when—in abstract philosophical discussions rather than everyday life—they consider the distinction between means and ends; more formally, between “instrumental values” and “terminal values.”

Part of the problem, it seems to me, is that the human mind uses a rather ad-hoc system to keep track of its goals—it works, but not cleanly. English doesn’t embody a sharp distinction between means and ends: “I want to save my sister’s life” and “I want to administer penicillin to my sister” use the same word “want.”

Can we describe, in mere English, the distinction that is getting lost?

As a first stab:

“Instrumental values” are desirable strictly conditional on their anticipated consequences. “I want to administer penicillin to my sister,” not because a penicillin-filled sister is an intrinsic good, but in anticipation of penicillin curing her flesh-eating pneumonia. If instead you anticipated that injecting penicillin would melt your sister into a puddle like the Wicked Witch of the West, you’d fight just as hard to keep her penicillin-free.

“Terminal values” are desirable without conditioning on other consequences: “I want to save my sister’s life” has nothing to do with your anticipating whether she’ll get injected with penicillin after that.

This first attempt suffers from obvious flaws. If saving my sister’s life would cause the Earth to be swallowed up by a black hole, then I would go off and cry for a while, but I wouldn’t administer penicillin. Does this mean that saving my sister’s life was not a “terminal” or “intrinsic” value, because it’s theoretically conditional on its consequences? Am I only trying to save her life because of my belief that a black hole won’t consume the Earth afterward? Common sense should say that’s not what’s happening.

So forget English. We can set up a mathematical description of a decision system in which terminal values and instrumental values are separate and incompatible types—like integers and floating-point numbers, in a programming language with no automatic conversion between them.

An ideal Bayesian decision system can be set up using only four elements:

Outcomes : type Outcome[]
- list of possible outcomes
- {sister lives, sister dies}
Actions : type Action[]
- list of possible actions
- {administer penicillin, don’t administer penicillin}
Utility_function : type Outcome -> Utility
- utility function that maps each outcome onto a utility
- (a utility being representable as a real number between negative and positive infinity)
- {sister lives → 1, sister dies → 0}
Conditional_probability_function :
type Action -> (Outcome -> Probability)
- conditional probability function that maps each action onto a probability distribution over outcomes
- (a probability being representable as a real number between 0 and 1)
- {administer penicillin → (sister lives → 0.9, sister dies → 0.1), don’t administer penicillin → (sister lives → 0.3, sister dies → 0.7)}

If you can’t read the type system directly, don’t worry, I’ll always translate into English. For programmers, seeing it described in distinct statements helps to set up distinct mental objects.

And the decision system itself?

Expected_Utility : Action A ->
(Sum O in Outcomes: Utility(O) * Probability(O|A))
- The “expected utility” of an action equals the sum, over all outcomes, of the utility of that outcome times the conditional probability of that outcome given that action.
- {EU(administer penicillin) = 0.9, EU(don’t administer penicillin) = 0.3}
Choose :
-> (Argmax A in Actions: Expected_Utility(A))
- Pick an action whose “expected utility” is maximal.
- {return: administer penicillin}

For every action, calculate the conditional probability of all the consequences that might follow, then add up the utilities of those consequences times their conditional probability. Then pick the best action.

This is a mathematically simple sketch of a decision system. It is not an efficient way to compute decisions in the real world.

What if, for example, you need a sequence of acts to carry out a plan? The formalism can easily represent this by letting each Action stand for a whole sequence. But this creates an exponentially large space, like the space of all sentences you can type in 100 letters. As a simple example, if one of the possible acts on the first turn is “Shoot my own foot off,” a human planner will decide this is a bad idea generally—eliminate all sequences beginning with this action. But we’ve flattened this structure out of our representation. We don’t have sequences of acts, just flat “actions.”

So, yes, there are a few minor complications. Obviously so, or we’d just run out and build a real AI this way. In that sense, it’s much the same as Bayesian probability theory itself.

But this is one of those times when it’s a surprisingly good idea to consider the absurdly simple version before adding in any high-falutin’ complications.

Consider the philosopher who asserts, “All of us are ultimately selfish; we care only about our own states of mind. The mother who claims to care about her son’s welfare, really wants to believe that her son is doing well—this belief is what makes the mother happy. She helps him for the sake of her own happiness, not his.” You say, “Well, suppose the mother sacrifices her life to push her son out of the path of an oncoming truck. That’s not going to make her happy, just dead.” The philosopher stammers for a few moments, then replies, “But she still did it because she valued that choice above others—because of the feeling of importance she attached to that decision.”

So you say,

TYPE ERROR: No constructor found for Expected_Utility -> Utility.

Allow me to explain that reply.

Even our simple formalism illustrates a sharp distinction between expected utility, which is something that actions have; and utility, which is something that outcomes have. Sure, you can map both utilities and expected utilities onto real numbers. But that’s like observing that you can map wind speed and temperature onto real numbers. It doesn’t make them the same thing.

The philosopher begins by arguing that all your Utilities must be over Outcomes consisting of your state of mind. If this were true, your intelligence would operate as an engine to steer the future into regions where you were happy. Future states would be distinguished only by your state of mind; you would be indifferent between any two futures in which you had the same state of mind.

And you would, indeed, be rather unlikely to sacrifice your own life to save another.

When we object that people sometimes do sacrifice their lives, the philosopher’s reply shifts to discussing Expected Utilities over Actions: “The feeling of importance she attached to that decision.” This is a drastic jump that should make us leap out of our chairs in indignation. Trying to convert an Expected_Utility into a Utility would cause an outright error in our programming language. But in English it all sounds the same.

The choices of our simple decision system are those with highest Expected_Utility, but this doesn’t say anything whatsoever about where it steers the future. It doesn’t say anything about the utilities the decider assigns, or which real-world outcomes are likely to happen as a result. It doesn’t say anything about the mind’s function as an engine.

The physical cause of a physical action is a cognitive state, in our ideal decider an Expected_Utility, and this expected utility is calculated by evaluating a utility function over imagined consequences. To save your son’s life, you must imagine the event of your son’s life being saved, and this imagination is not the event itself. It’s a quotation, like the difference between “snow” and snow. But that doesn’t mean that what’s inside the quote marks must itself be a cognitive state. If you choose the action that leads to the future that you represent with “my son is still alive,” then you have functioned as an engine to steer the future into a region where your son is still alive. Not an engine that steers the future into a region where you represent the sentence “my son is still alive.” To steer the future there, your utility function would have to return a high utility when fed ““my son is still alive””, the quotation of the quotation, your imagination of yourself imagining. Recipes make poor cake when you grind them up and toss them in the batter.

And that’s why it’s helpful to consider the simple decision systems first. Mix enough complications into the system, and formerly clear distinctions become harder to see.

So now let’s look at some complications. Clearly the Utility function (mapping Outcomes onto Utilities) is meant to formalize what I earlier referred to as “terminal values,” values not contingent upon their consequences. What about the case where saving your sister’s life leads to Earth’s destruction by a black hole? In our formalism, we’ve flattened out this possibility. Outcomes don’t lead to Outcomes, only Actions lead to Outcomes. Your sister recovering from pneumonia followed by the Earth being devoured by a black hole would be flattened into a single “possible outcome.”

And where are the “instrumental values” in this simple formalism? Actually, they’ve vanished entirely! You see, in this formalism, actions lead directly to outcomes with no intervening events. There’s no notion of throwing a rock that flies through the air and knocks an apple off a branch so that it falls to the ground. Throwing the rock is the Action, and it leads straight to the Outcome of the apple lying on the ground—according to the conditional probability function that turns an Action directly into a Probability distribution over Outcomes.

In order to actually compute the conditional probability function, and in order to separately consider the utility of a sister’s pneumonia and a black hole swallowing Earth, we would have to represent the network structure of causality—the way that events lead to other events.

And then the instrumental values would start coming back. If the causal network was sufficiently regular, you could find a state B that tended to lead to C regardless of how you achieved B. Then if you wanted to achieve C for some reason, you could plan efficiently by first working out a B that led to C, and then an A that led to B. This would be the phenomenon of “instrumental value”—B would have “instrumental value” because it led to C. The state C itself might be terminally valued—a term in the utility function over the total outcome. Or C might just be an instrumental value, a node that was not directly valued by the utility function.

Instrumental value, in this formalism, is purely an aid to the efficient computation of plans. It can and should be discarded wherever this kind of regularity does not exist.

Suppose, for example, that there’s some particular value of B that doesn’t lead to C. Would you choose an A which led to that B? Or never mind the abstract philosophy: If you wanted to go to the supermarket to get chocolate, and you wanted to drive to the supermarket, and you needed to get into your car, would you gain entry by ripping off the car door with a steam shovel? (No.) Instrumental value is a “leaky abstraction,” as we programmers say; you sometimes have to toss away the cached value and compute out the actual expected utility. Part of being efficient without being suicidal is noticing when convenient shortcuts break down. Though this formalism does give rise to instrumental values, it does so only where the requisite regularity exists, and strictly as a convenient shortcut in computation.

But if you complicate the formalism before you understand the simple version, then you may start thinking that instrumental values have some strange life of their own, even in a normative sense. That, once you say B is usually good because it leads to C, you’ve committed yourself to always try for B even in the absence of C. People make this kind of mistake in abstract philosophy, even though they would never, in real life, rip open their car door with a steam shovel. You may start thinking that there’s no way to develop a consequentialist that maximizes only inclusive genetic fitness, because it will starve unless you include an explicit terminal value for “eating food.” People make this mistake even though they would never stand around opening car doors all day long, for fear of being stuck outside their cars if they didn’t have a terminal value for opening car doors.

Instrumental values live in (the network structure of) the conditional probability function. This makes instrumental value strictly dependent on beliefs-of-fact given a fixed utility function. If I believe that penicillin causes pneumonia, and that the absence of penicillin cures pneumonia, then my perceived instrumental value of penicillin will go from high to low. Change the beliefs of fact—change the conditional probability function that associates actions to believed consequences—and the instrumental values will change in unison.

In moral arguments, some disputes are about instrumental consequences, and some disputes are about terminal values. If your debating opponent says that banning guns will lead to lower crime, and you say that banning guns will lead to higher crime, then you agree about a superior instrumental value (crime is bad), but you disagree about which intermediate events lead to which consequences. But I do not think an argument about female circumcision is really a factual argument about how to best achieve a shared value of treating women fairly or making them happy.

This important distinction often gets flushed down the toilet in angry arguments. People with factual disagreements and shared values each decide that their debating opponents must be sociopaths. As if your hated enemy, gun control/rights advocates, really wanted to kill people, which should be implausible as realistic psychology.

I fear the human brain does not strongly type the distinction between terminal moral beliefs and instrumental moral beliefs. “We should ban guns” and “We should save lives” don’t feel different, as moral beliefs, the way that sight feels different from sound. Despite all the other ways that the human goal system complicates everything in sight, this one distinction it manages to collapse into a mishmash of things-with-conditional-value.

To extract out the terminal values we have to inspect this mishmash of valuable things, trying to figure out which ones are getting their value from somewhere else. It’s a difficult project! If you say that you want to ban guns in order to reduce crime, it may take a moment to realize that “reducing crime” isn’t a terminal value, it’s a superior instrumental value with links to terminal values for human lives and human happinesses. And then the one who advocates gun rights may have links to the superior instrumental value of “reducing crime” plus a link to a value for “freedom,” which might be a terminal value unto them, or another instrumental value . . .

We can’t print out our complete network of values derived from other values. We probably don’t even store the whole history of how values got there. By considering the right moral dilemmas, “Would you do X if Y,” we can often figure out where our values came from. But even this project itself is full of pitfalls; misleading dilemmas and gappy philosophical arguments. We don’t know what our own values are, or where they came from, and can’t find out except by undertaking error-prone projects of cognitive archaeology. Just forming a conscious distinction between “terminal value” and “instrumental value,” and keeping track of what it means, and using it correctly, is hard work. Only by inspecting the simple formalism can we see how easy it ought to be, in principle.

And that’s to say nothing of all the other complications of the human reward system—the whole use of reinforcement architecture, and the way that eating chocolate is pleasurable, and anticipating eating chocolate is pleasurable, but they’re different kinds of pleasures . . .

But I don’t complain too much about the mess.

Being ignorant of your own values may not always be fun, but at least it’s not boring.

149
Leaky Generalizations

Are apples good to eat? Usually, but some apples are rotten.

Do humans have ten fingers? Most of us do, but plenty of people have lost a finger and nonetheless qualify as “human.”

Unless you descend to a level of description far below any macroscopic object—below societies, below people, below fingers, below tendon and bone, below cells, all the way down to particles and fields where the laws are truly universal—practically every generalization you use in the real world will be leaky.

(Though there may, of course, be some exceptions to the above rule . . .)

Mostly, the way you deal with leaky generalizations is that, well, you just have to deal. If the cookie market almost always closes at 10 p.m., except on Thanksgiving it closes at 6 p.m., and today happens to be National Native American Genocide Day, you’d better show up before 6 p.m. or you won’t get a cookie.

Our ability to manipulate leaky generalizations is opposed by need for closure, the degree to which we want to say once and for all that humans have ten fingers, and get frustrated when we have to tolerate continued ambiguity. Raising the value of the stakes can increase need for closure—which shuts down complexity tolerance when complexity tolerance is most needed.

Life would be complicated even if the things we wanted were simple (they aren’t). The leakyness of leaky generalizations about what-to-do-next would leak in from the leaky structure of the real world. Or to put it another way:

Instrumental values often have no specification that is both compact and local.

Suppose there’s a box containing a million dollars. The box is locked, not with an ordinary combination lock, but with a dozen keys controlling a machine that can open the box. If you know how the machine works, you can deduce which sequences of key-presses will open the box. There’s more than one key sequence that can trigger the machine to open the box. But if you press a sufficiently wrong sequence, the machine incinerates the money. And if you don’t know about the machine, there’s no simple rules like “Pressing any key three times opens the box” or “Pressing five different keys with no repetitions incinerates the money.”

There’s a compact nonlocal specification of which keys you want to press: You want to press keys such that they open the box. You can write a compact computer program that computes which key sequences are good, bad or neutral, but the computer program will need to describe the machine, not just the keys themselves.

There’s likewise a local noncompact specification of which keys to press: a giant lookup table of the results for each possible key sequence. It’s a very large computer program, but it makes no mention of anything except the keys.

But there’s no way to describe which key sequences are good, bad, or neutral, which is both simple and phrased only in terms of the keys themselves.

It may be even worse if there are tempting local generalizations which turn out to be leaky. Pressing most keys three times in a row will open the box, but there’s a particular key that incinerates the money if you press it just once. You might think you had found a perfect generalization—a locally describable class of sequences that always opened the box—when you had merely failed to visualize all the possible paths of the machine, or failed to value all the side effects.

The machine represents the complexity of the real world. The openness of the box (which is good) and the incinerator (which is bad) represent the thousand shards of desire that make up our terminal values. The keys represent the actions and policies and strategies available to us.

When you consider how many different ways we value outcomes, and how complicated are the paths we take to get there, it’s a wonder that there exists any such thing as helpful ethical advice. (Of which the strangest of all advices, and yet still helpful, is that “the end does not justify the means.”)

But conversely, the complicatedness of action need not say anything about the complexity of goals. You often find people who smile wisely, and say, “Well, morality is complicated, you know, female circumcision is right in one culture and wrong in another, it’s not always a bad thing to torture people. How naive you are, how full of need for closure, that you think there are any simple rules.”

You can say, unconditionally and flatly, that killing anyone is a huge dose of negative terminal utility. Yes, even Hitler. That doesn’t mean you shouldn’t shoot Hitler. It means that the net instrumental utility of shooting Hitler carries a giant dose of negative utility from Hitler’s death, and a hugely larger dose of positive utility from all the other lives that would be saved as a consequence.

Many commit the type error that I warned against in Terminal Values and Instrumental Values, and think that if the net consequential expected utility of Hitler’s death is conceded to be positive, then the immediate local terminal utility must also be positive, meaning that the moral principle “Death is always a bad thing” is itself a leaky generalization. But this is double counting, with utilities instead of probabilities; you’re setting up a resonance between the expected utility and the utility, instead of a one-way flow from utility to expected utility.

Or maybe it’s just the urge toward a one-sided policy debate: the best policy must have no drawbacks.

In my moral philosophy, the local negative utility of Hitler’s death is stable, no matter what happens to the external consequences and hence to the expected utility.

Of course, you can set up a moral argument that it’s an inherently good thing to punish evil people, even with capital punishment for sufficiently evil people. But you can’t carry this moral argument by pointing out that the consequence of shooting a man holding a leveled gun may be to save other lives. This is appealing to the value of life, not appealing to the value of death. If expected utilities are leaky and complicated, it doesn’t mean that utilities must be leaky and complicated as well. They might be! But it would be a separate argument.

150
The Hidden Complexity of Wishes

I wish to live in the locations of my choice, in a physically healthy, uninjured, and apparently normal version of my current body containing my current mental state, a body which will heal from all injuries at a rate three sigmas faster than the average given the medical technology available to me, and which will be protected from any diseases, injuries or illnesses causing disability, pain, or degraded functionality or any sense, organ, or bodily function for more than ten days consecutively or fifteen days in any year . . .

—The Open-Source Wish Project, Wish For Immortality 1.1

There are three kinds of genies: Genies to whom you can safely say, “I wish for you to do what I should wish for”; genies for which no wish is safe; and genies that aren’t very powerful or intelligent.

Suppose your aged mother is trapped in a burning building, and it so happens that you’re in a wheelchair; you can’t rush in yourself. You could cry, “Get my mother out of that building!” but there would be no one to hear.

Luckily you have, in your pocket, an Outcome Pump. This handy device squeezes the flow of time, pouring probability into some outcomes, draining it from others.

The Outcome Pump is not sentient. It contains a tiny time machine, which resets time unless a specified outcome occurs. For example, if you hooked up the Outcome Pump’s sensors to a coin, and specified that the time machine should keep resetting until it sees the coin come up heads, and then you actually flipped the coin, you would see the coin come up heads. (The physicists say that any future in which a “reset” occurs is inconsistent, and therefore never happens in the first place—so you aren’t actually killing any versions of yourself.)

Whatever proposition you can manage to input into the Outcome Pump somehow happens, though not in a way that violates the laws of physics. If you try to input a proposition that’s too unlikely, the time machine will suffer a spontaneous mechanical failure before that outcome ever occurs.

You can also redirect probability flow in more quantitative ways, using the “future function” to scale the temporal reset probability for different outcomes. If the temporal reset probability is 99% when the coin comes up heads, and 1% when the coin comes up tails, the odds will go from 1:1 to 99:1 in favor of tails. If you had a mysterious machine that spit out money, and you wanted to maximize the amount of money spit out, you would use reset probabilities that diminished as the amount of money increased. For example, spitting out $10 might have a 99.999999% reset probability, and spitting out $100 might have a 99.99999% reset probability. This way you can get an outcome that tends to be as high as possible in the future function, even when you don’t know the best attainable maximum.

So you desperately yank the Outcome Pump from your pocket—your mother is still trapped in the burning building, remember?—and try to describe your goal: get your mother out of the building!

The user interface doesn’t take English inputs. The Outcome Pump isn’t sentient, remember? But it does have 3D scanners for the near vicinity, and built-in utilities for pattern matching. So you hold up a photo of your mother’s head and shoulders; match on the photo; use object contiguity to select your mother’s whole body (not just her head and shoulders); and define the future function using your mother’s distance from the building’s center. The further she gets from the building’s center, the less the time machine’s reset probability.

You cry “Get my mother out of the building!,” for luck, and press Enter.

For a moment it seems like nothing happens. You look around, waiting for the fire truck to pull up, and rescuers to arrive—or even just a strong, fast runner to haul your mother out of the building—

BOOM! With a thundering roar, the gas main under the building explodes. As the structure comes apart, in what seems like slow motion, you glimpse your mother’s shattered body being hurled high into the air, traveling fast, rapidly increasing its distance from the former center of the building.

On the side of the Outcome Pump is an Emergency Regret Button. All future functions are automatically defined with a huge negative value for the Regret Button being pressed—a temporal reset probability of nearly 1—so that the Outcome Pump is extremely unlikely to do anything which upsets the user enough to make them press the Regret Button. You can’t ever remember pressing it. But you’ve barely started to reach for the Regret Button (and what good will it do now?) when a flaming wooden beam drops out of the sky and smashes you flat.

Which wasn’t really what you wanted, but scores very high in the defined future function . . .

The Outcome Pump is a genie of the second class. No wish is safe.

If someone asked you to get their poor aged mother out of a burning building, you might help, or you might pretend not to hear. But it wouldn’t even occur to you to explode the building. “Get my mother out of the building” sounds like a much safer wish than it really is, because you don’t even consider the plans that you assign extreme negative values.

Consider again the Tragedy of Group Selectionism: Some early biologists asserted that group selection for low subpopulation sizes would produce individual restraint in breeding; and yet actually enforcing group selection in the laboratory produced cannibalism, especially of immature females. It’s obvious in hindsight that, given strong selection for small subpopulation sizes, cannibals will outreproduce individuals who voluntarily forego reproductive opportunities. But eating little girls is such an un-aesthetic solution that Wynne-Edwards, Allee, Brereton, and the other group-selectionists simply didn’t think of it. They only saw the solutions they would have used themselves.

Suppose you try to patch the future function by specifying that the Outcome Pump should not explode the building: outcomes in which the building materials are distributed over too much volume will have ~1 temporal reset probabilities.

So your mother falls out of a second-story window and breaks her neck. The Outcome Pump took a different path through time that still ended up with your mother outside the building, and it still wasn’t what you wanted, and it still wasn’t a solution that would occur to a human rescuer.

If only the Open-Source Wish Project had developed a Wish To Get Your Mother Out Of A Burning Building:

I wish to move my mother (defined as the woman who shares half my genes and gave birth to me) to outside the boundaries of the building currently closest to me which is on fire; but not by exploding the building; nor by causing the walls to crumble so that the building no longer has boundaries; nor by waiting until after the building finishes burning down for a rescue worker to take out the body . . .

All these special cases, the seemingly unlimited number of required patches, should remind you of the parable of Artificial Addition—programming an Arithmetic Expert Systems by explicitly adding ever more assertions like “fifteen plus fifteen equals thirty, but fifteen plus sixteen equals thirty-one instead.”

How do you exclude the outcome where the building explodes and flings your mother into the sky? You look ahead, and you foresee that your mother would end up dead, and you don’t want that consequence, so you try to forbid the event leading up to it.

Your brain isn’t hardwired with a specific, prerecorded statement that “Blowing up a burning building containing my mother is a bad idea.” And yet you’re trying to prerecord that exact specific statement in the Outcome Pump’s future function. So the wish is exploding, turning into a giant lookup table that records your judgment of every possible path through time.

You failed to ask for what you really wanted. You wanted your mother to go on living, but you wished for her to become more distant from the center of the building.

Except that’s not all you wanted. If your mother was rescued from the building but was horribly burned, that outcome would rank lower in your preference ordering than an outcome where she was rescued safe and sound. So you not only value your mother’s life, but also her health.

And you value not just her bodily health, but her state of mind. Being rescued in a fashion that traumatizes her—for example, a giant purple monster roaring up out of nowhere and seizing her—is inferior to a fireman showing up and escorting her out through a non-burning route. (Yes, we’re supposed to stick with physics, but maybe a powerful enough Outcome Pump has aliens coincidentally showing up in the neighborhood at exactly that moment.) You would certainly prefer her being rescued by the monster to her being roasted alive, however.

How about a wormhole spontaneously opening and swallowing her to a desert island? Better than her being dead; but worse than her being alive, well, healthy, untraumatized, and in continual contact with you and the other members of her social network.

Would it be okay to save your mother’s life at the cost of the family dog’s life, if it ran to alert a fireman but then got run over by a car? Clearly yes, but it would be better ceteris paribus to avoid killing the dog. You wouldn’t want to swap a human life for hers, but what about the life of a convicted murderer? Does it matter if the murderer dies trying to save her, from the goodness of his heart? How about two murderers? If the cost of your mother’s life was the destruction of every extant copy, including the memories, of Bach’s Little Fugue in G Minor, would that be worth it? How about if she had a terminal illness and would die anyway in eighteen months?

If your mother’s foot is crushed by a burning beam, is it worthwhile to extract the rest of her? What if her head is crushed, leaving her body? What if her body is crushed, leaving only her head? What if there’s a cryonics team waiting outside, ready to suspend the head? Is a frozen head a person? Is Terry Schiavo a person? How much is a chimpanzee worth?

Your brain is not infinitely complicated; there is only a finite Kolmogorov complexity / message length which suffices to describe all the judgments you would make. But just because this complexity is finite does not make it small. We value many things, and no they are not reducible to valuing happiness or valuing reproductive fitness.

There is no safe wish smaller than an entire human morality. There are too many possible paths through Time. You can’t visualize all the roads that lead to the destination you give the genie. “Maximizing the distance between your mother and the center of the building” can be done even more effectively by detonating a nuclear weapon. Or, at higher levels of genie power, flinging her body out of the Solar System. Or, at higher levels of genie intelligence, doing something that neither you nor I would think of, just like a chimpanzee wouldn’t think of detonating a nuclear weapon. You can’t visualize all the paths through time, any more than you can program a chess-playing machine by hardcoding a move for every possible board position.

And real life is far more complicated than chess. You cannot predict, in advance, which of your values will be needed to judge the path through time that the genie takes. Especially if you wish for something longer-term or wider-range than rescuing your mother from a burning building.

I fear the Open-Source Wish Project is futile, except as an illustration of how not to think about genie problems. The only safe genie is a genie that shares all your judgment criteria, and at that point, you can just say “I wish for you to do what I should wish for.” Which simply runs the genie’s should function.

Indeed, it shouldn’t be necessary to say anything. To be a safe fulfiller of a wish, a genie must share the same values that led you to make the wish. Otherwise the genie may not choose a path through time that leads to the destination you had in mind, or it may fail to exclude horrible side effects that would lead you to not even consider a plan in the first place. Wishes are leaky generalizations, derived from the huge but finite structure that is your entire morality; only by including this entire structure can you plug all the leaks.

With a safe genie, wishing is superfluous. Just run the genie.

151
Anthropomorphic Optimism

The core fallacy of anthropomorphism is expecting something to be predicted by the black box of your brain, when its causal structure is so different from that of a human brain as to give you no license to expect any such thing.

The early (pre-1966) biologists in The Tragedy of Group Selectionism believed that predators would voluntarily restrain their breeding to avoid overpopulating their habitat and exhausting the prey population. Later on, when Michael J. Wade actually went out and created in the laboratory the nigh-impossible conditions for group selection, the adults adapted to cannibalize eggs and larvae, especially female larvae.¹

Now, why might the group selectionists have not thought of that possibility?

Suppose you were a member of a tribe, and you knew that, in the near future, your tribe would be subjected to a resource squeeze. You might propose, as a solution, that no couple have more than one child—after the first child, the couple goes on birth control. Saying, “Let’s all individually have as many children as we can, but then hunt down and cannibalize each other’s children, especially the girls,” would not even occur to you as a possibility.

Think of a preference ordering over solutions, relative to your goals. You want a solution as high in this preference ordering as possible. How do you find one? With a brain, of course! Think of your brain as a high-ranking-solution-generator—a search process that produces solutions that rank high in your innate preference ordering.

The solution space on all real-world problems is generally fairly large, which is why you need an efficient brain that doesn’t even bother to formulate the vast majority of low-ranking solutions.

If your tribe is faced with a resource squeeze, you could try hopping everywhere on one leg, or chewing off your own toes. These “solutions” obviously wouldn’t work and would incur large costs, as you can see upon examination—but in fact your brain is too efficient to waste time considering such poor solutions; it doesn’t generate them in the first place. Your brain, in its search for high-ranking solutions, flies directly to parts of the solution space like “Everyone in the tribe gets together, and agrees to have no more than one child per couple until the resource squeeze is past.”

Such a low-ranking solution as “Everyone have as many kids as possible, then cannibalize the girls” would not be generated in your search process.

But the ranking of an option as “low” or “high” is not an inherent property of the option. It is a property of the optimization process that does the preferring. And different optimization processes will search in different orders.

So far as evolution is concerned, individuals reproducing to the fullest and then cannibalizing others’ daughters is a no-brainer; whereas individuals voluntarily restraining their own breeding for the good of the group is absolutely ludicrous. Or to say it less anthropomorphically, the first set of alleles would rapidly replace the second in a population. (And natural selection has no obvious search order here—these two alternatives seem around equally simple as mutations.)

Suppose that one of the biologists had said, “If a predator population has only finite resources, evolution will craft them to voluntarily restrain their breeding—that’s how I’d do it if I were in charge of building predators.” This would be anthropomorphism outright, the lines of reasoning naked and exposed: I would do it this way, therefore I infer that evolution will do it this way.

One does occasionally encounter the fallacy outright, in my line of work. But suppose you say to the one, “An AI will not necessarily work like you do.” Suppose you say to this hypothetical biologist, “Evolution doesn’t work like you do.” What will the one say in response? I can tell you a reply you will not hear: “Oh my! I didn’t realize that! One of the steps of my inference was invalid; I will throw away the conclusion and start over from scratch.”

No: what you’ll hear instead is a reason why any AI has to reason the same way as the speaker. Or a reason why natural selection, following entirely different criteria of optimization and using entirely different methods of optimization, ought to do the same thing that would occur to a human as a good idea.

Hence the elaborate idea that group selection would favor predator groups where the individuals voluntarily forsook reproductive opportunities.

The group selectionists went just as far astray, in their predictions, as someone committing the fallacy outright. Their final conclusions were the same as if they were assuming outright that evolution necessarily thought like themselves. But they erased what had been written above the bottom line of their argument, without erasing the actual bottom line, and wrote in new rationalizations. Now the fallacious reasoning is disguised; the obviously flawed step in the inference has been hidden—even though the conclusion remains exactly the same; and hence, in the real world, exactly as wrong.

But why would any scientist do this? In the end, the data came out against the group selectionists and they were embarrassed.

As I remarked in Fake Optimization Criteria, we humans seem to have evolved an instinct for arguing that our preferred policy arises from practically any criterion of optimization. Politics was a feature of the ancestral environment; we are descended from those who argued most persuasively that the tribe’s interest—not just their own interest—required that their hated rival Uglak be executed. We certainly aren’t descended from Uglak, who failed to argue that his tribe’s moral code—not just his own obvious self-interest—required his survival.

And because we can more persuasively argue for what we honestly believe, we have evolved an instinct to honestly believe that other people’s goals, and our tribe’s moral code, truly do imply that they should do things our way for their benefit.

So the group selectionists, imagining this beautiful picture of predators restraining their breeding, instinctively rationalized why natural selection ought to do things their way, even according to natural selection’s own purposes. The foxes will be fitter if they restrain their breeding! No, really! They’ll even outbreed other foxes who don’t restrain their breeding! Honestly!

The problem with trying to argue natural selection into doing things your way is that evolution does not contain that which could be moved by your arguments. Evolution does not work like you do—not even to the extent of having any element that could listen to or care about your painstaking explanation of why evolution ought to do things your way. Human arguments are not even commensurate with the internal structure of natural selection as an optimization process—human arguments aren’t used in promoting alleles, as human arguments would play a causal role in human politics.

So instead of successfully persuading natural selection to do things their way, the group selectionists were simply embarrassed when reality came out differently.

There’s a fairly heavy subtext here about Unfriendly AI.

But the point generalizes: this is the problem with optimistic reasoning in general. What is optimism? It is ranking the possibilities by your own preference ordering, and selecting an outcome high in that preference ordering, and somehow that outcome ends up as your prediction. What kind of elaborate rationalizations were generated along the way is probably not so relevant as one might fondly believe; look at the cognitive history and it’s optimism in, optimism out. But Nature, or whatever other process is under discussion, is not actually, causally choosing between outcomes by ranking them in your preference ordering and picking a high one. So the brain fails to synchronize with the environment, and the prediction fails to match reality.

1. Wade, “Group selections among laboratory populations of Tribolium.”

152
Lost Purposes

It was in either kindergarten or first grade that I was first asked to pray, given a transliteration of a Hebrew prayer. I asked what the words meant. I was told that so long as I prayed in Hebrew, I didn’t need to know what the words meant, it would work anyway.

That was the beginning of my break with Judaism.

As you read this, some young man or woman is sitting at a desk in a university, earnestly studying material they have no intention of ever using, and no interest in knowing for its own sake. They want a high-paying job, and the high-paying job requires a piece of paper, and the piece of paper requires a previous master’s degree, and the master’s degree requires a bachelor’s degree, and the university that grants the bachelor’s degree requires you to take a class in twelfth-century knitting patterns to graduate. So they diligently study, intending to forget it all the moment the final exam is administered, but still seriously working away, because they want that piece of paper.

Maybe you realized it was all madness, but I bet you did it anyway. You didn’t have a choice, right? A recent study here in the Bay Area showed that 80% of teachers in K-5 reported spending less than one hour per week on science, and 16% said they spend no time on science. Why? I’m given to understand the proximate cause is the No Child Left Behind Act and similar legislation. Virtually all classroom time is now spent on preparing for tests mandated at the state or federal level. I seem to recall (though I can’t find the source) that just taking mandatory tests was 40% of classroom time in one school.

The old Soviet bureaucracy was famous for being more interested in appearances than reality. One shoe factory overfulfilled its quota by producing lots of tiny shoes. Another shoe factory reported cut but unassembled leather as a “shoe.” The superior bureaucrats weren’t interested in looking too hard, because they also wanted to report quota overfulfillments. All this was a great help to the comrades freezing their feet off.

It is now being suggested in several sources that an actual majority of published findings in medicine, though “statistically significant with p < 0.05,” are untrue. But so long as p < 0.05 remains the threshold for publication, why should anyone hold themselves to higher standards, when that requires bigger research grants for larger experimental groups, and decreases the likelihood of getting a publication? Everyone knows that the whole point of science is to publish lots of papers, just as the whole point of a university is to print certain pieces of parchment, and the whole point of a school is to pass the mandatory tests that guarantee the annual budget. You don’t get to set the rules of the game, and if you try to play by different rules, you’ll just lose.

(Though for some reason, physics journals require a threshold of p < 0.0001. It’s as if they conceive of some other purpose to their existence than publishing physics papers.)

There’s chocolate at the supermarket, and you can get to the supermarket by driving, and driving requires that you be in the car, which means opening your car door, which needs keys. If you find there’s no chocolate at the supermarket, you won’t stand around opening and slamming your car door because the car door still needs opening. I rarely notice people losing track of plans they devised themselves.

It’s another matter when incentives must flow through large organizations—or worse, many different organizations and interest groups, some of them governmental. Then you see behaviors that would mark literal insanity, if they were born from a single mind. Someone gets paid every time they open a car door, because that’s what’s measurable; and this person doesn’t care whether the driver ever gets paid for arriving at the supermarket, let alone whether the buyer purchases the chocolate, or whether the eater is happy or starving.

From a Bayesian perspective, subgoals are epiphenomena of conditional probability functions. There is no expected utility without utility. How silly would it be to think that instrumental value could take on a mathematical life of its own, leaving terminal value in the dust? It’s not sane by decision-theoretical criteria of sanity.

But consider the No Child Left Behind Act. The politicians want to look like they’re doing something about educational difficulties; the politicians have to look busy to voters this year, not fifteen years later when the kids are looking for jobs. The politicians are not the consumers of education. The bureaucrats have to show progress, which means that they’re only interested in progress that can be measured this year. They aren’t the ones who’ll end up ignorant of science. The publishers who commission textbooks, and the committees that purchase textbooks, don’t sit in the classrooms bored out of their skulls.

The actual consumers of knowledge are the children—who can’t pay, can’t vote, can’t sit on the committees. Their parents care for them, but don’t sit in the classes themselves; they can only hold politicians responsible according to surface images of “tough on education.” Politicians are too busy being re-elected to study all the data themselves; they have to rely on surface images of bureaucrats being busy and commissioning studies—it may not work to help any children, but it works to let politicians appear caring. Bureaucrats don’t expect to use textbooks themselves, so they don’t care if the textbooks are hideous to read, so long as the process by which they are purchased looks good on the surface. The textbook publishers have no motive to produce bad textbooks, but they know that the textbook purchasing committee will be comparing textbooks based on how many different subjects they cover, and that the fourth-grade purchasing committee isn’t coordinated with the third-grade purchasing committee, so they cram as many subjects into one textbook as possible. Teachers won’t get through a fourth of the textbook before the end of the year, and then the next year’s teacher will start over. Teachers might complain, but they aren’t the decision-makers, and ultimately, it’s not their future on the line, which puts sharp bounds on how much effort they’ll spend on unpaid altruism . . .

It’s amazing, when you look at it that way—consider all the lost information and lost incentives—that anything at all remains of the original purpose, gaining knowledge. Though many educational systems seem to be currently in the process of collapsing into a state not much better than nothing.

Want to see the problem really solved? Make the politicians go to school.

A single human mind can track a probabilistic expectation of utility as it flows through the conditional chances of a dozen intermediate events—including nonlocal dependencies, places where the expected utility of opening the car door depends on whether there’s chocolate in the supermarket. But organizations can only reward today what is measurable today, what can be written into legal contract today, and this means measuring intermediate events rather than their distant consequences. These intermediate measures, in turn, are leaky generalizations—often very leaky. Bureaucrats are untrustworthy genies, for they do not share the values of the wisher.

Miyamoto Musashi said:¹

The primary thing when you take a sword in your hands is your intention to cut the enemy, whatever the means. Whenever you parry, hit, spring, strike or touch the enemy’s cutting sword, you must cut the enemy in the same movement. It is essential to attain this. If you think only of hitting, springing, striking or touching the enemy, you will not be able actually to cut him. More than anything, you must be thinking of carrying your movement through to cutting him. You must thoroughly research this.

(I wish I lived in an era where I could just tell my readers they have to thoroughly research something, without giving insult.)

Why would any individual lose track of their purposes in a swordfight? If someone else had taught them to fight, if they had not generated the entire art from within themselves, they might not understand the reason for parrying at one moment, or springing at another moment; they might not realize when the rules had exceptions, fail to see the times when the usual method won’t cut through.

The essential thing in the art of epistemic rationality is to understand how every rule is cutting through to the truth in the same movement. The corresponding essential of pragmatic rationality—decision theory, versus probability theory—is to always see how every expected utility cuts through to utility. You must thoroughly research this.

C. J. Cherryh said:²

Your sword has no blade. It has only your intention. When that goes astray you have no weapon.

I have seen many people go astray when they wish to the genie of an imagined AI, dreaming up wish after wish that seems good to them, sometimes with many patches and sometimes without even that pretense of caution. And they don’t jump to the meta-level. They don’t instinctively look-to-purpose, the instinct that started me down the track to atheism at the age of five. They do not ask, as I reflexively ask, “Why do I think this wish is a good idea? Will the genie judge likewise?” They don’t see the source of their judgment, hovering behind the judgment as its generator. They lose track of the ball; they know the ball bounced, but they don’t instinctively look back to see where it bounced from—the criterion that generated their judgments.

Likewise with people not automatically noticing when supposedly selfish people give altruistic arguments in favor of selfishness, or when supposedly altruistic people give selfish arguments in favor of altruism.

People can handle goal-tracking for driving to the supermarket just fine, when it’s all inside their own heads, and no genies or bureaucracies or philosophies are involved. The trouble is that real civilization is immensely more complicated than this. Dozens of organizations, and dozens of years, intervene between the child suffering in the classroom, and the new-minted college graduate not being very good at their job. (But will the interviewer or manager notice, if the college graduate is good at looking busy?) With every new link that intervenes between the action and its consequence, intention has one more chance to go astray. With every intervening link, information is lost, incentive is lost. And this bothers most people a lot less than it bothers me, or why were all my classmates willing to say prayers without knowing what they meant? They didn’t feel the same instinct to look-to-the-generator.

Can people learn to keep their eye on the ball? To keep their intention from going astray? To never spring or strike or touch, without knowing the higher goal they will complete in the same movement? People do often want to do their jobs, all else being equal. Can there be such a thing as a sane corporation? A sane civilization, even? That’s only a distant dream, but it’s what I’ve been getting at with all of these essays on the flow of intentions (a.k.a. expected utility, a.k.a. instrumental value) without losing purpose (a.k.a. utility, a.k.a. terminal value). Can people learn to feel the flow of parent goals and child goals? To know consciously, as well as implicitly, the distinction between expected utility and utility?

Do you care about threats to your civilization? The worst metathreat to complex civilization is its own complexity, for that complication leads to the loss of many purposes.

I look back, and I see that more than anything, my life has been driven by an exceptionally strong abhorrence to lost purposes. I hope it can be transformed to a learnable skill.

1. Miyamoto Musashi, Book of Five Rings (New Line Publishing, 2003).

2. Carolyn J. Cherryh, The Paladin (Baen, 2002).

Part N
A Human’s Guide to Words

153
The Parable of the Dagger

(Adapted from Raymond Smullyan.¹)

Once upon a time, there was a court jester who dabbled in logic.

The jester presented the king with two boxes. Upon the first box was inscribed:

Either this box contains an angry frog, or the box with a false inscription contains an angry frog, but not both.

On the second box was inscribed:

Either this box contains gold and the box with a false inscription contains an angry frog, or this box contains an angry frog and the box with a true inscription contains gold.

And the jester said to the king: “One box contains an angry frog, the other box gold; and one, and only one, of the inscriptions is true.”

The king opened the wrong box, and was savaged by an angry frog.

“You see,” the jester said, “let us hypothesize that the first inscription is the true one. Then suppose the first box contains gold. Then the other box would have an angry frog, while the box with a true inscription would contain gold, which would make the second statement true as well. Now hypothesize that the first inscription is false, and that the first box contains gold. Then the second inscription would be—”

The king ordered the jester thrown in the dungeons.

A day later, the jester was brought before the king in chains and shown two boxes.

“One box contains a key,” said the king, “to unlock your chains; and if you find the key you are free. But the other box contains a dagger for your heart if you fail.”

And the first box was inscribed:

Either both inscriptions are true, or both inscriptions are false.

And the second box was inscribed:

This box contains the key.

The jester reasoned thusly: “Suppose the first inscription is true. Then the second inscription must also be true. Now suppose the first inscription is false. Then again the second inscription must be true. So the second box must contain the key, if the first inscription is true, and also if the first inscription is false. Therefore, the second box must logically contain the key.”

The jester opened the second box, and found a dagger.

“How?!” cried the jester in horror, as he was dragged away. “It’s logically impossible!”

“It is entirely possible,” replied the king. “I merely wrote those inscriptions on two boxes, and then I put the dagger in the second one.”

1. Raymond M. Smullyan, What Is the Name of This Book?: The Riddle of Dracula and Other Logical Puzzles (Penguin Books, 1990).

154
The Parable of Hemlock

All men are mortal. Socrates is a man. Therefore Socrates is mortal.

—Standard Medieval syllogism

Socrates raised the glass of hemlock to his lips . . .

“Do you suppose,” asked one of the onlookers, “that even hemlock will not be enough to kill so wise and good a man?”

“No,” replied another bystander, a student of philosophy; “all men are mortal, and Socrates is a man; and if a mortal drinks hemlock, surely he dies.”

“Well,” said the onlooker, “what if it happens that Socrates isn’t mortal?”

“Nonsense,” replied the student, a little sharply; “all men are mortal by definition; it is part of what we mean by the word ‘man.’ All men are mortal, Socrates is a man, therefore Socrates is mortal. It is not merely a guess, but a logical certainty.”

“I suppose that’s right . . .” said the onlooker. “Oh, look, Socrates already drank the hemlock while we were talking.”

“Yes, he should be keeling over any minute now,” said the student.

And they waited, and they waited, and they waited . . .

“Socrates appears not to be mortal,” said the onlooker.

“Then Socrates must not be a man,” replied the student. “All men are mortal, Socrates is not mortal, therefore Socrates is not a man. And that is not merely a guess, but a logical certainty.”

The fundamental problem with arguing that things are true “by definition” is that you can’t make reality go a different way by choosing a different definition.

You could reason, perhaps, as follows: “All things I have observed which wear clothing, speak language, and use tools, have also shared certain other properties as well, such as breathing air and pumping red blood. The last thirty ‘humans’ belonging to this cluster whom I observed to drink hemlock soon fell over and stopped moving. Socrates wears a toga, speaks fluent ancient Greek, and drank hemlock from a cup. So I predict that Socrates will keel over in the next five minutes.”

But that would be mere guessing. It wouldn’t be, y’know, absolutely and eternally certain. The Greek philosophers—like most prescientific philosophers—were rather fond of certainty.

Luckily the Greek philosophers have a crushing rejoinder to your questioning. You have misunderstood the meaning of “All humans are mortal,” they say. It is not a mere observation. It is part of the definition of the word “human.” Mortality is one of several properties that are individually necessary, and together sufficient, to determine membership in the class “human.” The statement “All humans are mortal” is a logically valid truth, absolutely unquestionable. And if Socrates is human, he must be mortal: it is a logical deduction, as certain as certain can be.

But then we can never know for certain that Socrates is a “human” until after Socrates has been observed to be mortal. It does no good to observe that Socrates speaks fluent Greek, or that Socrates has red blood, or even that Socrates has human DNA. None of these characteristics are logically equivalent to mortality. You have to see him die before you can conclude that he was human.

(And even then it’s not infinitely certain. What if Socrates rises from the grave a night after you see him die? Or more realistically, what if Socrates is signed up for cryonics? If mortality is defined to mean finite lifespan, then you can never really know if someone was human, until you’ve observed to the end of eternity—just to make sure they don’t come back. Or you could think you saw Socrates keel over, but it could be an illusion projected onto your eyes with a retinal scanner. Or maybe you just hallucinated the whole thing . . .)

The problem with syllogisms is that they’re always valid. “All humans are mortal; Socrates is human; therefore Socrates is mortal” is—if you treat it as a logical syllogism—logically valid within our own universe. It’s also logically valid within neighboring Everett branches in which, due to a slightly different evolved biochemistry, hemlock is a delicious treat rather than a poison. And it’s logically valid even in universes where Socrates never existed, or for that matter, where humans never existed.

The Bayesian definition of evidence favoring a hypothesis is evidence which we are more likely to see if the hypothesis is true than if it is false. Observing that a syllogism is logically valid can never be evidence favoring any empirical proposition, because the syllogism will be logically valid whether that proposition is true or false.

Syllogisms are valid in all possible worlds, and therefore, observing their validity never tells us anything about which possible world we actually live in.

This doesn’t mean that logic is useless—just that logic can only tell us that which, in some sense, we already know. But we do not always believe what we know. Is the number 29,384,209 prime? By virtue of how I define my decimal system and my axioms of arithmetic, I have already determined my answer to this question—but I do not know what my answer is yet, and I must do some logic to find out.

Similarly, if I form the uncertain empirical generalization “Humans are vulnerable to hemlock,” and the uncertain empirical guess “Socrates is human,” logic can tell me that my previous guesses are predicting that Socrates will be vulnerable to hemlock.

It’s been suggested that we can view logical reasoning as resolving our uncertainty about impossible possible worlds—eliminating probability mass in logically impossible worlds which we did not know to be logically impossible. In this sense, logical argument can be treated as observation.

But when you talk about an empirical prediction like “Socrates is going to keel over and stop breathing” or “Socrates is going to do fifty jumping jacks and then compete in the Olympics next year,” that is a matter of possible worlds, not impossible possible worlds.

Logic can tell us which hypotheses match up to which observations, and it can tell us what these hypotheses predict for the future—it can bring old observations and previous guesses to bear on a new problem. But logic never flatly says, “Socrates will stop breathing now.” Logic never dictates any empirical question; it never settles any real-world query which could, by any stretch of the imagination, go either way.

Just remember the Litany Against Logic:

Logic stays true, wherever you may go,

So logic never tells you where you live.

155
Words as Hidden Inferences

Suppose I find a barrel, sealed at the top, but with a hole large enough for a hand. I reach in and feel a small, curved object. I pull the object out, and it’s blue—a bluish egg. Next I reach in and feel something hard and flat, with edges—which, when I extract it, proves to be a red cube. I pull out 11 eggs and 8 cubes, and every egg is blue, and every cube is red.

Now I reach in and I feel another egg-shaped object. Before I pull it out and look, I have to guess: What will it look like?

The evidence doesn’t prove that every egg in the barrel is blue and every cube is red. The evidence doesn’t even argue this all that strongly: 19 is not a large sample size. Nonetheless, I’ll guess that this egg-shaped object is blue—or as a runner-up guess, red. If I guess anything else, there’s as many possibilities as distinguishable colors—and for that matter, who says the egg has to be a single shade? Maybe it has a picture of a horse painted on.

So I say “blue,” with a dutiful patina of humility. For I am a sophisticated rationalist-type person, and I keep track of my assumptions and dependencies—I guess, but I’m aware that I’m guessing . . . right?

But when a large yellow striped feline-shaped object leaps out at me from the shadows, I think, “Yikes! A tiger!” Not, “Hm . . . objects with the properties of largeness, yellowness, stripedness, and feline shape, have previously often possessed the properties ‘hungry’ and ‘dangerous,’ and thus, although it is not logically necessary, it may be an empirically good guess that aaauuughhhh CRUNCH CRUNCH GULP.”

The human brain, for some odd reason, seems to have been adapted to make this inference quickly, automatically, and without keeping explicit track of its assumptions.

And if I name the egg-shaped objects “bleggs” (for blue eggs) and the red cubes “rubes,” then, when I reach in and feel another egg-shaped object, I may think, Oh, it’s a blegg, rather than considering all that problem-of-induction stuff.

It is a common misconception that you can define a word any way you like.

This would be true if the brain treated words as purely logical constructs, Aristotelian classes, and you never took out any more information than you put in.

Yet the brain goes on about its work of categorization, whether or not we consciously approve. “All humans are mortal; Socrates is a human; therefore Socrates is mortal”—thus spake the ancient Greek philosophers. Well, if mortality is part of your logical definition of “human,” you can’t logically classify Socrates as human until you observe him to be mortal. But—this is the problem—Aristotle knew perfectly well that Socrates was a human. Aristotle’s brain placed Socrates in the “human” category as efficiently as your own brain categorizes tigers, apples, and everything else in its environment: Swiftly, silently, and without conscious approval.

Aristotle laid down rules under which no one could conclude Socrates was “human” until after he died. Nonetheless, Aristotle and his students went on concluding that living people were humans and therefore mortal; they saw distinguishing properties such as human faces and human bodies, and their brains made the leap to inferred properties such as mortality.

Misunderstanding the working of your own mind does not, thankfully, prevent the mind from doing its work. Otherwise Aristotelians would have starved, unable to conclude that an object was edible merely because it looked and felt like a banana.

So the Aristotelians went on classifying environmental objects on the basis of partial information, the way people had always done. Students of Aristotelian logic went on thinking exactly the same way, but they had acquired an erroneous picture of what they were doing.

If you asked an Aristotelian philosopher whether Carol the grocer was mortal, they would say “Yes.” If you asked them how they knew, they would say “All humans are mortal; Carol is human; therefore Carol is mortal.” Ask them whether it was a guess or a certainty, and they would say it was a certainty (if you asked before the sixteenth century, at least). Ask them how they knew that humans were mortal, and they would say it was established by definition.

The Aristotelians were still the same people, they retained their original natures, but they had acquired incorrect beliefs about their own functioning. They looked into the mirror of self-awareness, and saw something unlike their true selves: they reflected incorrectly.

Your brain doesn’t treat words as logical definitions with no empirical consequences, and so neither should you. The mere act of creating a word can cause your mind to allocate a category, and thereby trigger unconscious inferences of similarity. Or block inferences of similarity; if I create two labels I can get your mind to allocate two categories. Notice how I said “you” and “your brain” as if they were different things?

Making errors about the inside of your head doesn’t change what’s there; otherwise Aristotle would have died when he concluded that the brain was an organ for cooling the blood. Philosophical mistakes usually don’t interfere with blink-of-an-eye perceptual inferences.

But philosophical mistakes can severely mess up the deliberate thinking processes that we use to try to correct our first impressions. If you believe that you can “define a word any way you like,” without realizing that your brain goes on categorizing without your conscious oversight, then you won’t make the effort to choose your definitions wisely.

156
Extensions and Intensions

“What is red?”

“Red is a color.”

“What’s a color?”

“A color is a property of a thing.”

But what is a thing? And what’s a property? Soon the two are lost in a maze of words defined in other words, the problem that Steven Harnad once described as trying to learn Chinese from a Chinese/Chinese dictionary.

Alternatively, if you asked me “What is red?” I could point to a stop sign, then to someone wearing a red shirt, and a traffic light that happens to be red, and blood from where I accidentally cut myself, and a red business card, and then I could call up a color wheel on my computer and move the cursor to the red area. This would probably be sufficient, though if you know what the word “No” means, the truly strict would insist that I point to the sky and say “No.”

I think I stole this example from S. I. Hayakawa—though I’m really not sure, because I heard this way back in the indistinct blur of my childhood. (When I was twelve, my father accidentally deleted all my computer files. I have no memory of anything before that.)

But that’s how I remember first learning about the difference between intensional and extensional definition. To give an “intensional definition” is to define a word or phrase in terms of other words, as a dictionary does. To give an “extensional definition” is to point to examples, as adults do when teaching children. The preceding sentence gives an intensional definition of “extensional definition,” which makes it an extensional example of “intensional definition.”

In Hollywood Rationality and popular culture generally, “rationalists” are depicted as word-obsessed, floating in endless verbal space disconnected from reality.

But the actual Traditional Rationalists have long insisted on maintaining a tight connection to experience:

If you look into a textbook of chemistry for a definition of lithium, you may be told that it is that element whose atomic weight is 7 very nearly. But if the author has a more logical mind he will tell you that if you search among minerals that are vitreous, translucent, grey or white, very hard, brittle, and insoluble, for one which imparts a crimson tinge to an unluminous flame, this mineral being triturated with lime or witherite rats-bane, and then fused, can be partly dissolved in muriatic acid; and if this solution be evaporated, and the residue be extracted with sulphuric acid, and duly purified, it can be converted by ordinary methods into a chloride, which being obtained in the solid state, fused, and electrolyzed with half a dozen powerful cells, will yield a globule of a pinkish silvery metal that will float on gasolene; and the material of that is a specimen of lithium.

—Charles Sanders Peirce¹

That’s an example of “logical mind” as described by a genuine Traditional Rationalist, rather than a Hollywood scriptwriter.

But note: Peirce isn’t actually showing you a piece of lithium. He didn’t have pieces of lithium stapled to his book. Rather he’s giving you a treasure map—an intensionally defined procedure which, when executed, will lead you to an extensional example of lithium. This is not the same as just tossing you a hunk of lithium, but it’s not the same as saying “atomic weight 7” either. (Though if you had sufficiently sharp eyes, saying “3 protons” might let you pick out lithium at a glance . . .)

So that is intensional and extensional definition, which is a way of telling someone else what you mean by a concept. When I talked about “definitions” above, I talked about a way of communicating concepts—telling someone else what you mean by “red,” “tiger,” “human,” or “lithium.” Now let’s talk about the actual concepts themselves.

The actual intension of my “tiger” concept would be the neural pattern (in my temporal cortex) that inspects an incoming signal from the visual cortex to determine whether or not it is a tiger.

The actual extension of my “tiger” concept is everything I call a tiger.

Intensional definitions don’t capture entire intensions; extensional definitions don’t capture entire extensions. If I point to just one tiger and say the word “tiger,” the communication may fail if they think I mean “dangerous animal” or “male tiger” or “yellow thing.” Similarly, if I say “dangerous yellow-black striped animal,” without pointing to anything, the listener may visualize giant hornets.

You can’t capture in words all the details of the cognitive concept—as it exists in your mind—that lets you recognize things as tigers or nontigers. It’s too large. And you can’t point to all the tigers you’ve ever seen, let alone everything you would call a tiger.

The strongest definitions use a crossfire of intensional and extensional communication to nail down a concept. Even so, you only communicate maps to concepts, or instructions for building concepts—you don’t communicate the actual categories as they exist in your mind or in the world.

(Yes, with enough creativity you can construct exceptions to this rule, like “Sentences Eliezer Yudkowsky has published containing the term ‘huragaloni’ as of Feb 4, 2008.” I’ve just shown you this concept’s entire extension. But except in mathematics, definitions are usually treasure maps, not treasure.)

So that’s another reason you can’t “define a word any way you like”: You can’t directly program concepts into someone else’s brain.

Even within the Aristotelian paradigm, where we pretend that the definitions are the actual concepts, you don’t have simultaneous freedom of intension and extension. Suppose I define Mars as “A huge red rocky sphere, around a tenth of Earth’s mass and 50% further away from the Sun.” It’s then a separate matter to show that this intensional definition matches some particular extensional thing in my experience, or indeed, that it matches any real thing whatsoever. If instead I say “That’s Mars” and point to a red light in the night sky, it becomes a separate matter to show that this extensional light matches any particular intensional definition I may propose—or any intensional beliefs I may have—such as “Mars is the God of War.”

But most of the brain’s work of applying intensions happens sub-deliberately. We aren’t consciously aware that our identification of a red light as “Mars” is a separate matter from our verbal definition “Mars is the God of War.” No matter what kind of intensional definition I make up to describe Mars, my mind believes that “Mars” refers to this thingy, and that it is the fourth planet in the Solar System.

When you take into account the way the human mind actually, pragmatically works, the notion “I can define a word any way I like” soon becomes “I can believe anything I want about a fixed set of objects” or “I can move any object I want in or out of a fixed membership test.” Just as you can’t usually convey a concept’s whole intension in words because it’s a big complicated neural membership test, you can’t control the concept’s entire intension because it’s applied sub-deliberately. This is why arguing that XYZ is true “by definition” is so popular. If definition changes behaved like the empirical null-ops they’re supposed to be, no one would bother arguing them. But abuse definitions just a little, and they turn into magic wands—in arguments, of course; not in reality.

1. Charles Sanders Peirce, Collected Papers (Harvard University Press, 1931).

157
Similarity Clusters

Once upon a time, the philosophers of Plato’s Academy claimed that the best definition of human was a “featherless biped.” Diogenes of Sinope, also called Diogenes the Cynic, is said to have promptly exhibited a plucked chicken and declared “Here is Plato’s man.” The Platonists promptly changed their definition to “a featherless biped with broad nails.”

No dictionary, no encyclopedia, has ever listed all the things that humans have in common. We have red blood, five fingers on each of two hands, bony skulls, 23 pairs of chromosomes—but the same might be said of other animal species. We make complex tools to make complex tools, we use syntactical combinatorial language, we harness critical fission reactions as a source of energy: these things may serve out to single out only humans, but not all humans—many of us have never built a fission reactor. With the right set of necessary-and-sufficient gene sequences you could single out all humans, and only humans—at least for now—but it would still be far from all that humans have in common.

But so long as you don’t happen to be near a plucked chicken, saying “Look for featherless bipeds” may serve to pick out a few dozen of the particular things that are humans, as opposed to houses, vases, sandwiches, cats, colors, or mathematical theorems.

Once the definition “featherless biped” has been bound to some particular featherless bipeds, you can look over the group, and begin harvesting some of the other characteristics—beyond mere featherfree twolegginess—that the “featherless bipeds” seem to share in common. The particular featherless bipeds that you see seem to also use language, build complex tools, speak combinatorial language with syntax, bleed red blood if poked, die when they drink hemlock.

Thus the category “human” grows richer, and adds more and more characteristics; and when Diogenes finally presents his plucked chicken, we are not fooled: This plucked chicken is obviously not similar to the other “featherless bipeds.”

(If Aristotelian logic were a good model of human psychology, the Platonists would have looked at the plucked chicken and said, “Yes, that’s a human; what’s your point?”)

If the first featherless biped you see is a plucked chicken, then you may end up thinking that the verbal label “human” denotes a plucked chicken; so I can modify my treasure map to point to “featherless bipeds with broad nails,” and if I am wise, go on to say, “See Diogenes over there? That’s a human, and I’m a human, and you’re a human; and that chimpanzee is not a human, though fairly close.”

The initial clue only has to lead the user to the similarity cluster—the group of things that have many characteristics in common. After that, the initial clue has served its purpose, and I can go on to convey the new information “humans are currently mortal,” or whatever else I want to say about us featherless bipeds.

A dictionary is best thought of, not as a book of Aristotelian class definitions, but a book of hints for matching verbal labels to similarity clusters, or matching labels to properties that are useful in distinguishing similarity clusters.

158
Typicality and Asymmetrical Similarity

Birds fly. Well, except ostriches don’t. But which is a more typical bird—a robin, or an ostrich?

Which is a more typical chair: a desk chair, a rocking chair, or a beanbag chair?

Most people would say that a robin is a more typical bird, and a desk chair is a more typical chair. The cognitive psychologists who study this sort of thing experimentally, do so under the heading of “typicality effects” or “prototype effects.”¹ For example, if you ask subjects to press a button to indicate “true” or “false” in response to statements like “A robin is a bird” or “A penguin is a bird,” reaction times are faster for more central examples.² Typicality measures correlate well using different investigative methods—reaction times are one example; you can also ask people to directly rate, on a scale of 1 to 10, how well an example (like a specific robin) fits a category (like “bird”).

So we have a mental measure of typicality—which might, perhaps, function as a heuristic—but is there a corresponding bias we can use to pin it down?

Well, which of these statements strikes you as more natural: “98 is approximately 100,” or “100 is approximately 98”? If you’re like most people, the first statement seems to make more sense.³ For similar reasons, people asked to rate how similar Mexico is to the United States, gave consistently higher ratings than people asked to rate how similar the United States is to Mexico.⁴

And if that still seems harmless, a study by Rips showed that people were more likely to expect a disease would spread from robins to ducks on an island, than from ducks to robins.⁵ Now this is not a logical impossibility, but in a pragmatic sense, whatever difference separates a duck from a robin and would make a disease less likely to spread from a duck to a robin, must also be a difference between a robin and a duck, and would make a disease less likely to spread from a robin to a duck.

Yes, you can come up with rationalizations, like “Well, there could be more neighboring species of the robins, which would make the disease more likely to spread initially, etc.,” but be careful not to try too hard to rationalize the probability ratings of subjects who didn’t even realize there was a comparison going on. And don’t forget that Mexico is more similar to the United States than the United States is to Mexico, and that 98 is closer to 100 than 100 is to 98. A simpler interpretation is that people are using the (demonstrated) similarity heuristic as a proxy for the probability that a disease spreads, and this heuristic is (demonstrably) asymmetrical.

Kansas is unusually close to the center of the United States, and Alaska is unusually far from the center of the United States; so Kansas is probably closer to most places in the US and Alaska is probably farther. It does not follow, however, that Kansas is closer to Alaska than is Alaska to Kansas. But people seem to reason (metaphorically speaking) as if closeness is an inherent property of Kansas and distance is an inherent property of Alaska; so that Kansas is still close, even to Alaska; and Alaska is still distant, even from Kansas.

So once again we see that Aristotle’s notion of categories—logical classes with membership determined by a collection of properties that are individually strictly necessary, and together strictly sufficient—is not a good model of human cognitive psychology. (Science’s view has changed somewhat over the last 2350 years? Who would’ve thought?) We don’t even reason as if set membership is a true-or-false property: statements of set membership can be more or less true. (Note: This is not the same thing as being more or less probable.)

One more reason not to pretend that you, or anyone else, is really going to treat words as Aristotelian logical classes.

1. Eleanor Rosch, “Principles of Categorization,” in Cognition and Categorization, ed. Eleanor Rosch and Barbara B. Lloyd (Hillsdale, NJ: Lawrence Erlbaum, 1978).

2. George Lakoff, Women, Fire, and Dangerous Things: What Categories Reveal about the Mind (Chicago: Chicago University Press, 1987).

3. Jerrold Sadock, “Truth and Approximations,” Papers from the Third Annual Meeting of the Berkeley Linguistics Society (1977): 430–439.

4. Amos Tversky and Itamar Gati, “Studies of Similarity,” in Cognition and Categorization, ed. Eleanor Rosch and Barbara Lloyd (Hillsdale, NJ: Lawrence Erlbaum Associates, Inc., 1978), 79–98.

5. Lance J. Rips, “Inductive Judgments about Natural Categories,” Journal of Verbal Learning and Verbal Behavior 14 (1975): 665–681.

159
The Cluster Structure of Thingspace

The notion of a “configuration space” is a way of translating object descriptions into object positions. It may seem like blue is “closer” to blue-green than to red, but how much closer? It’s hard to answer that question by just staring at the colors. But it helps to know that the (proportional) color coordinates in RGB are 0:0:5, 0:3:2, and 5:0:0. It would be even clearer if plotted on a 3D graph.

In the same way, you can see a robin as a robin—brown tail, red breast, standard robin shape, maximum flying speed when unladen, its species-typical DNA and individual alleles. Or you could see a robin as a single point in a configuration space whose dimensions described everything we knew, or could know, about the robin.

A robin is bigger than a virus, and smaller than an aircraft carrier—that might be the “volume” dimension. Likewise a robin weighs more than a hydrogen atom, and less than a galaxy; that might be the “mass” dimension. Different robins will have strong correlations between “volume” and “mass,” so the robin-points will be lined up in a fairly linear string, in those two dimensions—but the correlation won’t be exact, so we do need two separate dimensions.

This is the benefit of viewing robins as points in space: You couldn’t see the linear lineup as easily if you were just imagining the robins as cute little wing-flapping creatures.

A robin’s DNA is a highly multidimensional variable, but you can still think of it as part of a robin’s location in thingspace—millions of quaternary coordinates, one coordinate for each DNA base—or maybe a more sophisticated view than that. The shape of the robin, and its color (surface reflectance), you can likewise think of as part of the robin’s position in thingspace, even though they aren’t single dimensions.

Just like the coordinate point 0:0:5 contains the same information as the actual HTML color blue, we shouldn’t actually lose information when we see robins as points in space. We believe the same statement about the robin’s mass whether we visualize a robin balancing the scales opposite a 0.07-kilogram weight, or a robin-point with a mass-coordinate of +70.

We can even imagine a configuration space with one or more dimensions for every distinct characteristic of an object, so that the position of an object’s point in this space corresponds to all the information in the real object itself. Rather redundantly represented, too—dimensions would include the mass, the volume, and the density.

If you think that’s extravagant, quantum physicists use an infinite-dimensional configuration space, and a single point in that space describes the location of every particle in the universe. So we’re actually being comparatively conservative in our visualization of thingspace—a point in thingspace describes just one object, not the entire universe.

If we’re not sure of the robin’s exact mass and volume, then we can think of a little cloud in thingspace, a volume of uncertainty, within which the robin might be. The density of the cloud is the density of our belief that the robin has that particular mass and volume. If you’re more sure of the robin’s density than of its mass and volume, your probability-cloud will be highly concentrated in the density dimension, and concentrated around a slanting line in the subspace of mass/volume. (Indeed, the cloud here is actually a surface, because of the relation V D = M.)

“Radial categories” are how cognitive psychologists describe the non-Aristotelian boundaries of words. The central “mother” conceives her child, gives birth to it, and supports it. Is an egg donor who never sees her child a mother? She is the “genetic mother.” What about a woman who is implanted with a foreign embryo and bears it to term? She is a “surrogate mother.” And the woman who raises a child that isn’t hers genetically? Why, she’s an “adoptive mother.” The Aristotelian syllogism would run, “Humans have ten fingers, Fred has nine fingers, therefore Fred is not a human,” but the way we actually think is “Humans have ten fingers, Fred is a human, therefore Fred is a ‘nine-fingered human.’”

We can think about the radial-ness of categories in intensional terms, as described above—properties that are usually present, but optionally absent. If we thought about the intension of the word “mother,” it might be like a distributed glow in thingspace, a glow whose intensity matches the degree to which that volume of thingspace matches the category “mother.” The glow is concentrated in the center of genetics and birth and child-raising; the volume of egg donors would also glow, but less brightly.

Or we can think about the radial-ness of categories extensionally. Suppose we mapped all the birds in the world into thingspace, using a distance metric that corresponds as well as possible to perceived similarity in humans: A robin is more similar to another robin, than either is similar to a pigeon, but robins and pigeons are all more similar to each other than either is to a penguin, et cetera.

Then the center of all birdness would be densely populated by many neighboring tight clusters, robins and sparrows and canaries and pigeons and many other species. Eagles and falcons and other large predatory birds would occupy a nearby cluster. Penguins would be in a more distant cluster, and likewise chickens and ostriches.

The result might look, indeed, something like an astronomical cluster: many galaxies orbiting the center, and a few outliers.

Or we could think simultaneously about both the intension of the cognitive category “bird,” and its extension in real-world birds: The central clusters of robins and sparrows glowing brightly with highly typical birdness; satellite clusters of ostriches and penguins glowing more dimly with atypical birdness, and Abraham Lincoln a few megaparsecs away and glowing not at all.

I prefer that last visualization—the glowing points—because as I see it, the structure of the cognitive intension followed from the extensional cluster structure. First came the structure-in-the-world, the empirical distribution of birds over thingspace; then, by observing it, we formed a category whose intensional glow roughly overlays this structure.

This gives us yet another view of why words are not Aristotelian classes: the empirical clustered structure of the real universe is not so crystalline. A natural cluster, a group of things highly similar to each other, may have no set of necessary and sufficient properties—no set of characteristics that all group members have, and no non-members have.

But even if a category is irrecoverably blurry and bumpy, there’s no need to panic. I would not object if someone said that birds are “feathered flying things.” But penguins don’t fly!—well, fine. The usual rule has an exception; it’s not the end of the world. Definitions can’t be expected to exactly match the empirical structure of thingspace in any event, because the map is smaller and much less complicated than the territory. The point of the definition “feathered flying things” is to lead the listener to the bird cluster, not to give a total description of every existing bird down to the molecular level.

When you draw a boundary around a group of extensional points empirically clustered in thingspace, you may find at least one exception to every simple intensional rule you can invent.

But if a definition works well enough in practice to point out the intended empirical cluster, objecting to it may justly be called “nitpicking.”

160
Disguised Queries

Imagine that you have a peculiar job in a peculiar factory: Your task is to take objects from a mysterious conveyor belt, and sort the objects into two bins. When you first arrive, Susan the Senior Sorter explains to you that blue egg-shaped objects are called “bleggs” and go in the “blegg bin,” while red cubes are called “rubes” and go in the “rube bin.”

Once you start working, you notice that bleggs and rubes differ in ways besides color and shape. Bleggs have fur on their surface, while rubes are smooth. Bleggs flex slightly to the touch; rubes are hard. Bleggs are opaque, the rube’s surface slightly translucent.

Soon after you begin working, you encounter a blegg shaded an unusually dark blue—in fact, on closer examination, the color proves to be purple, halfway between red and blue.

Yet wait! Why are you calling this object a “blegg”? A “blegg” was originally defined as blue and egg-shaped—the qualification of blueness appears in the very name “blegg,” in fact. This object is not blue. One of the necessary qualifications is missing; you should call this a “purple egg-shaped object,” not a “blegg.”

But it so happens that, in addition to being purple and egg-shaped, the object is also furred, flexible, and opaque. So when you saw the object, you thought, “Oh, a strangely colored blegg.” It certainly isn’t a rube . . . right?

Still, you aren’t quite sure what to do next. So you call over Susan the Senior Sorter.

“Oh, yes, it’s a blegg,” Susan says, “you can put it in the blegg bin.”

You start to toss the purple blegg into the blegg bin, but pause for a moment. “Susan,” you say, “how do you know this is a blegg?”

Susan looks at you oddly. “Isn’t it obvious? This object may be purple, but it’s still egg-shaped, furred, flexible, and opaque, like all the other bleggs. You’ve got to expect a few color defects. Or is this one of those philosophical conundrums, like ‘How do you know the world wasn’t created five minutes ago complete with false memories?’ In a philosophical sense I’m not absolutely certain that this is a blegg, but it seems like a good guess.”

“No, I mean . . .” You pause, searching for words. “Why is there a blegg bin and a rube bin? What’s the difference between bleggs and rubes?”

“Bleggs are blue and egg-shaped, rubes are red and cube-shaped,” Susan says patiently. “You got the standard orientation lecture, right?”

“Why do bleggs and rubes need to be sorted?”

“Er . . . because otherwise they’d be all mixed up?” says Susan. “Because nobody will pay us to sit around all day and not sort bleggs and rubes?”

“Who originally determined that the first blue egg-shaped object was a ‘blegg,’ and how did they determine that?”

Susan shrugs. “I suppose you could just as easily call the red cube-shaped objects ‘bleggs’ and the blue egg-shaped objects ‘rubes,’ but it seems easier to remember this way.”

You think for a moment. “Suppose a completely mixed-up object came off the conveyor. Like, an orange sphere-shaped furred translucent object with writhing green tentacles. How could I tell whether it was a blegg or a rube?”

“Wow, no one’s ever found an object that mixed up,” says Susan, “but I guess we’d take it to the sorting scanner.”

“How does the sorting scanner work?” you inquire. “X-rays? Magnetic resonance imaging? Fast neutron transmission spectroscopy?”

“I’m told it works by Bayes’s Rule, but I don’t quite understand how,” says Susan. “I like to say it, though. Bayes Bayes Bayes Bayes Bayes.”

“What does the sorting scanner tell you?”

“It tells you whether to put the object into the blegg bin or the rube bin. That’s why it’s called a sorting scanner.”

At this point you fall silent.

“Incidentally,” Susan says casually, “it may interest you to know that bleggs contain small nuggets of vanadium ore, and rubes contain shreds of palladium, both of which are useful industrially.”

“Susan, you are pure evil.”

“Thank you.”

So now it seems we’ve discovered the heart and essence of bleggness: a blegg is an object that contains a nugget of vanadium ore. Surface characteristics, like blue color and furredness, do not determine whether an object is a blegg; surface characteristics only matter because they help you infer whether an object is a blegg, that is, whether the object contains vanadium.

Containing vanadium is a necessary and sufficient definition: all bleggs contain vanadium and everything that contains vanadium is a blegg: “blegg” is just a shorthand way of saying “vanadium-containing object.” Right?

Not so fast, says Susan: Around 98% of bleggs contain vanadium, but 2% contain palladium instead. To be precise (Susan continues) around 98% of blue egg-shaped furred flexible opaque objects contain vanadium. For unusual bleggs, it may be a different percentage: 95% of purple bleggs contain vanadium, 92% of hard bleggs contain vanadium, etc.

Now suppose you find a blue egg-shaped furred flexible opaque object, an ordinary blegg in every visible way, and just for kicks you take it to the sorting scanner, and the scanner says “palladium”—this is one of the rare 2%. Is it a blegg?

At first you might answer that, since you intend to throw this object in the rube bin, you might as well call it a “rube.” However, it turns out that almost all bleggs, if you switch off the lights, glow faintly in the dark, while almost all rubes do not glow in the dark. And the percentage of bleggs that glow in the dark is not significantly different for blue egg-shaped furred flexible opaque objects that contain palladium, instead of vanadium. Thus, if you want to guess whether the object glows like a blegg, or remains dark like a rube, you should guess that it glows like a blegg.

So is the object really a blegg or a rube?

On one hand, you’ll throw the object in the rube bin no matter what else you learn. On the other hand, if there are any unknown characteristics of the object you need to infer, you’ll infer them as if the object were a blegg, not a rube—group it into the similarity cluster of blue egg-shaped furred flexible opaque things, and not the similarity cluster of red cube-shaped smooth hard translucent things.

The question “Is this object a blegg?” may stand in for different queries on different occasions.

If it weren’t standing in for some query, you’d have no reason to care.

Is atheism a “religion”? Is transhumanism a “cult”? People who argue that atheism is a religion “because it states beliefs about God” are really trying to argue (I think) that the reasoning methods used in atheism are on a par with the reasoning methods used in religion, or that atheism is no safer than religion in terms of the probability of causally engendering violence, etc. . . . What’s really at stake is an atheist’s claim of substantial difference and superiority relative to religion, which the religious person is trying to reject by denying the difference rather than the superiority(!).

But that’s not the a priori irrational part: The a priori irrational part is where, in the course of the argument, someone pulls out a dictionary and looks up the definition of “atheism” or “religion.” (And yes, it’s just as silly whether an atheist or religionist does it.) How could a dictionary possibly decide whether an empirical cluster of atheists is really substantially different from an empirical cluster of theologians? How can reality vary with the meaning of a word? The points in thingspace don’t move around when we redraw a boundary.

But people often don’t realize that their argument about where to draw a definitional boundary, is really a dispute over whether to infer a characteristic shared by most things inside an empirical cluster . . .

Hence the phrase, “disguised query.”

161
Neural Categories

In Disguised Queries, I talked about a classification task of “bleggs” and “rubes.” The typical blegg is blue, egg-shaped, furred, flexible, opaque, glows in the dark, and contains vanadium. The typical rube is red, cube-shaped, smooth, hard, translucent, unglowing, and contains palladium. For the sake of simplicity, let us forget the characteristics of flexibility/hardness and opaqueness/translucency. This leaves five dimensions in thingspace: color, shape, texture, luminance, and interior.

Suppose I want to create an Artificial Neural Network (ANN) to predict unobserved blegg characteristics from observed blegg characteristics. And suppose I’m fairly naive about ANNs: I’ve read excited popular science books about how neural networks are distributed, emergent, and parallel just like the human brain!! but I can’t derive the differential equations for gradient descent in a non-recurrent multilayer network with sigmoid units (which is actually a lot easier than it sounds).

Then I might design a neural network that looks something like Figure 161.1.

Figure 161.1: Network 1

Network 1 is for classifying bleggs and rubes. But since “blegg” is an unfamiliar and synthetic concept, I’ve also included a similar Network 1b in Figure 161.2 for distinguishing humans from Space Monsters, with input from Aristotle (“All men are mortal”) and Plato’s Academy (“A featherless biped with broad nails”).

Figure 161.2: Network 1b

A neural network needs a learning rule. The obvious idea is that when two nodes are often active at the same time, we should strengthen the connection between them—this is one of the first rules ever proposed for training a neural network, known as Hebb’s Rule.

Thus, if you often saw things that were both blue and furred—thus simultaneously activating the “color” node in the + state and the “texture” node in the + state—the connection would strengthen between color and texture, so that + colors activated + textures, and vice versa. If you saw things that were blue and egg-shaped and vanadium-containing, that would strengthen positive mutual connections between color and shape and interior.

Let’s say you’ve already seen plenty of bleggs and rubes come off the conveyor belt. But now you see something that’s furred, egg-shaped, and—gasp!—reddish purple (which we’ll model as a “color” activation level of -2/3). You haven’t yet tested the luminance, or the interior. What to predict, what to predict?

What happens then is that the activation levels in Network 1 bounce around a bit. Positive activation flows to luminance from shape, negative activation flows to interior from color, negative activation flows from interior to luminance . . . Of course all these messages are passed in parallel!! and asynchronously!! just like the human brain . . .

Finally Network 1 settles into a stable state, which has high positive activation for “luminance” and “interior.” The network may be said to “expect” (though it has not yet seen) that the object will glow in the dark, and that it contains vanadium.

And lo, Network 1 exhibits this behavior even though there’s no explicit node that says whether the object is a blegg or not. The judgment is implicit in the whole network!! Bleggness is an attractor!! which arises as the result of emergent behavior!! from the distributed!! learning rule.

Now in real life, this kind of network design—however faddish it may sound—runs into all sorts of problems. Recurrent networks don’t always settle right away: They can oscillate, or exhibit chaotic behavior, or just take a very long time to settle down. This is a Bad Thing when you see something big and yellow and striped, and you have to wait five minutes for your distributed neural network to settle into the “tiger” attractor. Asynchronous and parallel it may be, but it’s not real-time.

And there are other problems, like double-counting the evidence when messages bounce back and forth: If you suspect that an object glows in the dark, your suspicion will activate belief that the object contains vanadium, which in turn will activate belief that the object glows in the dark.

Plus if you try to scale up the Network 1 design, it requires O(N²) connections, where N is the total number of observables.

So what might be a more realistic neural network design?

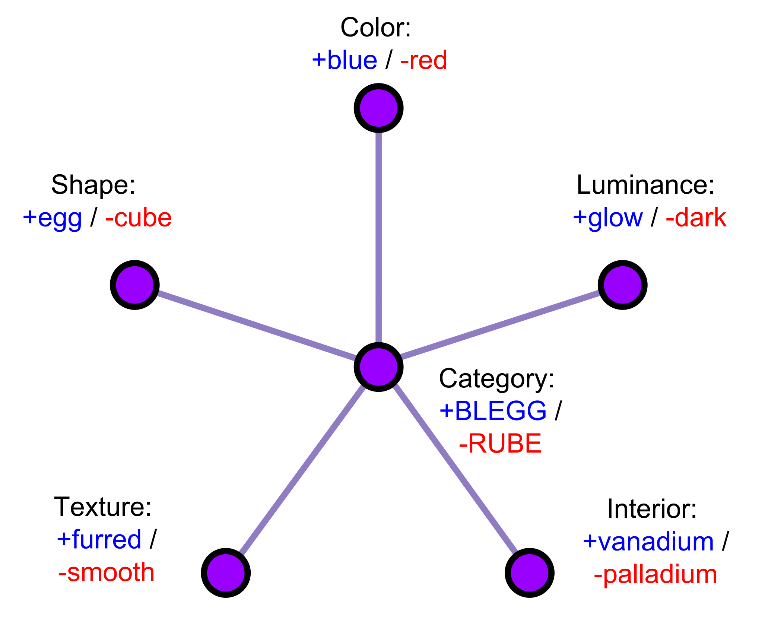
Figure 161.3: Network 2

In Network 2 of Figure 161.3, a wave of activation converges on the central node from any clamped (observed) nodes, and then surges back out again to any unclamped (unobserved) nodes. Which means we can compute the answer in one step, rather than waiting for the network to settle—an important requirement in biology when the neurons only run at 20Hz. And the network architecture scales as O(N), rather than O(N²).

Admittedly, there are some things you can notice more easily with the first network architecture than the second. Network 1 has a direct connection between every two nodes. So if red objects never glow in the dark, but red furred objects usually have the other blegg characteristics like egg-shape and vanadium, Network 1 can easily represent this: it just takes a very strong direct negative connection from color to luminance, but more powerful positive connections from texture to all other nodes except luminance.

Nor is this a “special exception” to the general rule that bleggs glow—remember, in Network 1, there is no unit that represents blegg-ness; blegg-ness emerges as an attractor in the distributed network.

So yes, those O(N²) connections were buying us something. But not very much. Network 1 is not more useful on most real-world problems, where you rarely find an animal stuck halfway between being a cat and a dog.

(There are also facts that you can’t easily represent in Network 1 or Network 2. Let’s say sea-blue color and spheroid shape, when found together, always indicate the presence of palladium; but when found individually, without the other, they are each very strong evidence for vanadium. This is hard to represent, in either architecture, without extra nodes. Both Network 1 and Network 2 embody implicit assumptions about what kind of environmental structure is likely to exist; the ability to read this off is what separates the adults from the babes, in machine learning.)

Make no mistake: Neither Network 1 nor Network 2 is biologically realistic. But it still seems like a fair guess that however the brain really works, it is in some sense closer to Network 2 than Network 1. Fast, cheap, scalable, works well to distinguish dogs and cats: natural selection goes for that sort of thing like water running down a fitness landscape.

It seems like an ordinary enough task to classify objects as either bleggs or rubes, tossing them into the appropriate bin. But would you notice if sea-blue objects never glowed in the dark?

Maybe, if someone presented you with twenty objects that were alike only in being sea-blue, and then switched off the light, and none of the objects glowed. If you got hit over the head with it, in other words. Perhaps by presenting you with all these sea-blue objects in a group, your brain forms a new subcategory, and can detect the “doesn’t glow” characteristic within that subcategory. But you probably wouldn’t notice if the sea-blue objects were scattered among a hundred other bleggs and rubes. It wouldn’t be easy or intuitive to notice, the way that distinguishing cats and dogs is easy and intuitive.

Or: “Socrates is human, all humans are mortal, therefore Socrates is mortal.” How did Aristotle know that Socrates was human? Well, Socrates had no feathers, and broad nails, and walked upright, and spoke Greek, and, well, was generally shaped like a human and acted like one. So the brain decides, once and for all, that Socrates is human; and from there, infers that Socrates is mortal like all other humans thus yet observed. It doesn’t seem easy or intuitive to ask how much wearing clothes, as opposed to using language, is associated with mortality. Just, “things that wear clothes and use language are human” and “humans are mortal.”

Are there biases associated with trying to classify things into categories once and for all? Of course there are. See e.g. Cultish Countercultishness.

162
How An Algorithm Feels From Inside

“If a tree falls in the forest, and no one hears it, does it make a sound?” I remember seeing an actual argument get started on this subject—a fully naive argument that went nowhere near Berkeleian subjectivism. Just:

“It makes a sound, just like any other falling tree!”

“But how can there be a sound that no one hears?”

The standard rationalist view would be that the first person is speaking as if “sound” means acoustic vibrations in the air; the second person is speaking as if “sound” means an auditory experience in a brain. If you ask “Are there acoustic vibrations?” or “Are there auditory experiences?,” the answer is at once obvious. And so the argument is really about the definition of the word “sound.”

I think the standard analysis is essentially correct. So let’s accept that as a premise, and ask: Why do people get into such arguments? What’s the underlying psychology?

A key idea of the heuristics and biases program is that mistakes are often more revealing of cognition than correct answers. Getting into a heated dispute about whether, if a tree falls in a deserted forest, it makes a sound, is traditionally considered a mistake.

So what kind of mind design corresponds to that error?

In Disguised Queries I introduced the blegg/rube classification task, in which Susan the Senior Sorter explains that your job is to sort objects coming off a conveyor belt, putting the blue eggs or “bleggs” into one bin, and the red cubes or “rubes” into the rube bin. This, it turns out, is because bleggs contain small nuggets of vanadium ore, and rubes contain small shreds of palladium, both of which are useful industrially.

Except that around 2% of blue egg-shaped objects contain palladium instead. So if you find a blue egg-shaped thing that contains palladium, should you call it a “rube” instead? You’re going to put it in the rube bin—why not call it a “rube”?

But when you switch off the light, nearly all bleggs glow faintly in the dark. And blue egg-shaped objects that contain palladium are just as likely to glow in the dark as any other blue egg-shaped object.

So if you find a blue egg-shaped object that contains palladium and you ask “Is it a blegg?,” the answer depends on what you have to do with the answer. If you ask “Which bin does the object go in?,” then you choose as if the object is a rube. But if you ask “If I turn off the light, will it glow?,” you predict as if the object is a blegg. In one case, the question “Is it a blegg?” stands in for the disguised query, “Which bin does it go in?” In the other case, the question “Is it a blegg?” stands in for the disguised query, “Will it glow in the dark?”

Now suppose that you have an object that is blue and egg-shaped and contains palladium; and you have already observed that it is furred, flexible, opaque, and glows in the dark.

This answers every query, observes every observable introduced. There’s nothing left for a disguised query to stand for.

So why might someone feel an impulse to go on arguing whether the object is really a blegg?

Figure 162.1: Network 1

Figure 162.2: Network 2

These diagrams from Neural Categories show two different neural networks that might be used to answer questions about bleggs and rubes. Network 1 (Figure 162.1) has a number of disadvantages—such as potentially oscillating/chaotic behavior, or requiring O(N²) connections—but Network 1’s structure does have one major advantage over Network 2: every unit in the network corresponds to a testable query. If you observe every observable, clamping every value, there are no units in the network left over.

Network 2 (Figure 162.2), however, is a far better candidate for being something vaguely like how the human brain works: It’s fast, cheap, scalable—and has an extra dangling unit in the center, whose activation can still vary, even after we’ve observed every single one of the surrounding nodes.

Which is to say that even after you know whether an object is blue or red, egg or cube, furred or smooth, bright or dark, and whether it contains vanadium or palladium, it feels like there’s a leftover, unanswered question: But is it really a blegg?

Usually, in our daily experience, acoustic vibrations and auditory experience go together. But a tree falling in a deserted forest unbundles this common association. And even after you know that the falling tree creates acoustic vibrations but not auditory experience, it feels like there’s a leftover question: Did it make a sound?

We know where Pluto is, and where it’s going; we know Pluto’s shape, and Pluto’s mass—but is it a planet?

Now remember: When you look at Network 2, as I’ve laid it out here, you’re seeing the algorithm from the outside. People don’t think to themselves, “Should the central unit fire, or not?” any more than you think “Should neuron #12,234,320,242 in my visual cortex fire, or not?”

It takes a deliberate effort to visualize your brain from the outside—and then you still don’t see your actual brain; you imagine what you think is there. Hopefully based on science, but regardless, you don’t have any direct access to neural network structures from introspection. That’s why the ancient Greeks didn’t invent computational neuroscience.

When you look at Network 2, you are seeing from the outside; but the way that neural network structure feels from the inside, if you yourself are a brain running that algorithm, is that even after you know every characteristic of the object, you still find yourself wondering: “But is it a blegg, or not?”

This is a great gap to cross, and I’ve seen it stop people in their tracks. Because we don’t instinctively see our intuitions as “intuitions,” we just see them as the world. When you look at a green cup, you don’t think of yourself as seeing a picture reconstructed in your visual cortex—although that is what you are seeing—you just see a green cup. You think, “Why, look, this cup is green,” not, “The picture in my visual cortex of this cup is green.”

And in the same way, when people argue over whether the falling tree makes a sound, or whether Pluto is a planet, they don’t see themselves as arguing over whether a categorization should be active in their neural networks. It seems like either the tree makes a sound, or not.

We know where Pluto is, and where it’s going; we know Pluto’s shape, and Pluto’s mass—but is it a planet? And yes, there were people who said this was a fight over definitions—but even that is a Network 2 sort of perspective, because you’re arguing about how the central unit ought to be wired up. If you were a mind constructed along the lines of Network 1, you wouldn’t say “It depends on how you define ‘planet,’” you would just say, “Given that we know Pluto’s orbit and shape and mass, there is no question left to ask.” Or, rather, that’s how it would feel—it would feel like there was no question left—if you were a mind constructed along the lines of Network 1.

Before you can question your intuitions, you have to realize that what your mind’s eye is looking at is an intuition—some cognitive algorithm, as seen from the inside—rather than a direct perception of the Way Things Really Are.

People cling to their intuitions, I think, not so much because they believe their cognitive algorithms are perfectly reliable, but because they can’t see their intuitions as the way their cognitive algorithms happen to look from the inside.

And so everything you try to say about how the native cognitive algorithm goes astray, ends up being contrasted to their direct perception of the Way Things Really Are—and discarded as obviously wrong.

163
Disputing Definitions

I have watched more than one conversation—even conversations supposedly about cognitive science—go the route of disputing over definitions. Taking the classic example to be “If a tree falls in a forest, and no one hears it, does it make a sound?,” the dispute often follows a course like this:

If a tree falls in the forest, and no one hears it, does it make a sound?

ALBERT: “Of course it does. What kind of silly question is that? Every time I’ve listened to a tree fall, it made a sound, so I’ll guess that other trees falling also make sounds. I don’t believe the world changes around when I’m not looking.”

BARRY: “Wait a minute. If no one hears it, how can it be a sound?”

In this example, Barry is arguing with Albert because of a genuinely different intuition about what constitutes a sound. But there’s more than one way the Standard Dispute can start. Barry could have a motive for rejecting Albert’s conclusion. Or Barry could be a skeptic who, upon hearing Albert’s argument, reflexively scrutinized it for possible logical flaws; and then, on finding a counterargument, automatically accepted it without applying a second layer of search for a counter-counterargument; thereby arguing himself into the opposite position. This doesn’t require that Barry’s prior intuition—the intuition Barry would have had, if we’d asked him before Albert spoke—differs from Albert’s.

Well, if Barry didn’t have a differing intuition before, he sure has one now.

ALBERT: “What do you mean, there’s no sound? The tree’s roots snap, the trunk comes crashing down and hits the ground. This generates vibrations that travel through the ground and the air. That’s where the energy of the fall goes, into heat and sound. Are you saying that if people leave the forest, the tree violates Conservation of Energy?”

BARRY: “But no one hears anything. If there are no humans in the forest, or, for the sake of argument, anything else with a complex nervous system capable of ‘hearing,’ then no one hears a sound.”

Albert and Barry recruit arguments that feel like support for their respective positions, describing in more detail the thoughts that caused their “sound”-detectors to fire or stay silent. But so far the conversation has still focused on the forest, rather than definitions. And note that they don’t actually disagree on anything that happens in the forest.

ALBERT: “This is the dumbest argument I’ve ever been in. You’re a niddlewicking fallumphing pickleplumber.”

BARRY: “Yeah? Well, you look like your face caught on fire and someone put it out with a shovel.”

Insult has been proffered and accepted; now neither party can back down without losing face. Technically, this isn’t part of the argument, as rationalists account such things; but it’s such an important part of the Standard Dispute that I’m including it anyway.

ALBERT: “The tree produces acoustic vibrations. By definition, that is a sound.”

BARRY: “No one hears anything. By definition, that is not a sound.”

The argument starts shifting to focus on definitions. Whenever you feel tempted to say the words “by definition” in an argument that is not literally about pure mathematics, remember that anything which is true “by definition” is true in all possible worlds, and so observing its truth can never constrain which world you live in.

ALBERT: “My computer’s microphone can record a sound without anyone being around to hear it, store it as a file, and it’s called a ‘sound file.’ And what’s stored in the file is the pattern of vibrations in air, not the pattern of neural firings in anyone’s brain. ‘Sound’ means a pattern of vibrations.”

Albert deploys an argument that feels like support for the word “sound” having a particular meaning. This is a different kind of question from whether acoustic vibrations take place in a forest—but the shift usually passes unnoticed.

BARRY: “Oh, yeah? Let’s just see if the dictionary agrees with you.”

There’s a lot of things I could be curious about in the falling-tree scenario. I could go into the forest and look at trees, or learn how to derive the wave equation for changes of air pressure, or examine the anatomy of an ear, or study the neuroanatomy of the auditory cortex. Instead of doing any of these things, I am to consult a dictionary, apparently. Why? Are the editors of the dictionary expert botanists, expert physicists, expert neuroscientists? Looking in an encyclopedia might make sense, but why a dictionary?

ALBERT: “Hah! Definition 2c in Merriam-Webster: ‘Sound: Mechanical radiant energy that is transmitted by longitudinal pressure waves in a material medium (as air).’”

BARRY: “Hah! Definition 2b in Merriam-Webster: ‘Sound: The sensation perceived by the sense of hearing.’”

ALBERT AND BARRY, CHORUS: “Consarned dictionary! This doesn’t help at all!”

Dictionary editors are historians of usage, not legislators of language. Dictionary editors find words in current usage, then write down the words next to (a small part of) what people seem to mean by them. If there’s more than one usage, the editors write down more than one definition.

ALBERT: “Look, suppose that I left a microphone in the forest and recorded the pattern of the acoustic vibrations of the tree falling. If I played that back to someone, they’d call it a ‘sound’! That’s the common usage! Don’t go around making up your own wacky definitions!”

BARRY: “One, I can define a word any way I like so long as I use it consistently. Two, the meaning I gave was in the dictionary. Three, who gave you the right to decide what is or isn’t common usage?”

There’s quite a lot of rationality errors in the Standard Dispute. Some of them I’ve already covered, and some of them I’ve yet to cover; likewise the remedies.

But for now, I would just like to point out—in a mournful sort of way—that Albert and Barry seem to agree on virtually every question of what is actually going on inside the forest, and yet it doesn’t seem to generate any feeling of agreement.

Arguing about definitions is a garden path; people wouldn’t go down the path if they saw at the outset where it led. If you asked Albert (Barry) why he’s still arguing, he’d probably say something like: “Barry (Albert) is trying to sneak in his own definition of ‘sound,’ the scurvey scoundrel, to support his ridiculous point; and I’m here to defend the standard definition.”

But suppose I went back in time to before the start of the argument:

(Eliezer appears from nowhere in a peculiar conveyance that looks just like the time machine from the original The Time Machine movie.)

BARRY: “Gosh! A time traveler!”

ELIEZER: “I am a traveler from the future! Hear my words! I have traveled far into the past—around fifteen minutes—”

ALBERT: “Fifteen minutes?”

ELIEZER: “—to bring you this message!”

(There is a pause of mixed confusion and expectancy.)

ELIEZER: “Do you think that ‘sound’ should be defined to require both acoustic vibrations (pressure waves in air) and also auditory experiences (someone to listen to the sound), or should ‘sound’ be defined as meaning only acoustic vibrations, or only auditory experience?”

BARRY: “You went back in time to ask us that?”

ELIEZER: “My purposes are my own! Answer!”

ALBERT: “Well . . . I don’t see why it would matter. You can pick any definition so long as you use it consistently.”

BARRY: “Flip a coin. Er, flip a coin twice.”

ELIEZER: “Personally I’d say that if the issue arises, both sides should switch to describing the event in unambiguous lower-level constituents, like acoustic vibrations or auditory experiences. Or each side could designate a new word, like ‘alberzle’ and ‘bargulum,’ to use for what they respectively used to call ‘sound’; and then both sides could use the new words consistently. That way neither side has to back down or lose face, but they can still communicate. And of course you should try to keep track, at all times, of some testable proposition that the argument is actually about. Does that sound right to you?”

ALBERT: “I guess . . .”

BARRY: “Why are we talking about this?”

ELIEZER: “To preserve your friendship against a contingency you will, now, never know. For the future has already changed!”

(Eliezer and the machine vanish in a puff of smoke.)

BARRY: “Where were we again?”

ALBERT: “Oh, yeah: If a tree falls in the forest, and no one hears it, does it make a sound?”

BARRY: “It makes an alberzle but not a bargulum. What’s the next question?”

This remedy doesn’t destroy every dispute over categorizations. But it destroys a substantial fraction.

164
Feel the Meaning

When I hear someone say, “Oh, look, a butterfly,” the spoken phonemes “butterfly” enter my ear and vibrate on my ear drum, being transmitted to the cochlea, tickling auditory nerves that transmit activation spikes to the auditory cortex, where phoneme processing begins, along with recognition of words, and reconstruction of syntax (a by no means serial process), and all manner of other complications.

But at the end of the day, or rather, at the end of the second, I am primed to look where my friend is pointing and see a visual pattern that I will recognize as a butterfly; and I would be quite surprised to see a wolf instead.

My friend looks at a butterfly, his throat vibrates and lips move, the pressure waves travel invisibly through the air, my ear hears and my nerves transduce and my brain reconstructs, and lo and behold, I know what my friend is looking at. Isn’t that marvelous? If we didn’t know about the pressure waves in the air, it would be a tremendous discovery in all the newspapers: Humans are telepathic! Human brains can transfer thoughts to each other!

Well, we are telepathic, in fact; but magic isn’t exciting when it’s merely real, and all your friends can do it too.

Think telepathy is simple? Try building a computer that will be telepathic with you. Telepathy, or “language,” or whatever you want to call our partial thought transfer ability, is more complicated than it looks.

But it would be quite inconvenient to go around thinking, “Now I shall partially transduce some features of my thoughts into a linear sequence of phonemes which will invoke similar thoughts in my conversational partner . . .”

So the brain hides the complexity—or rather, never represents it in the first place—which leads people to think some peculiar thoughts about words.

As I remarked earlier, when a large yellow striped object leaps at me, I think “Yikes! A tiger!” not “Hm . . . objects with the properties of largeness, yellowness, and stripedness have previously often possessed the properties ‘hungry’ and ‘dangerous,’ and therefore, although it is not logically necessary, auughhhh CRUNCH CRUNCH GULP.”

Similarly, when someone shouts “Yikes! A tiger!,” natural selection would not favor an organism that thought, “Hm . . . I have just heard the syllables ‘Tie’ and ‘Grr’ which my fellow tribe members associate with their internal analogues of my own tiger concept, and which they are more likely to utter if they see an object they categorize as aiiieeee CRUNCH CRUNCH help it’s got my arm CRUNCH GULP.”

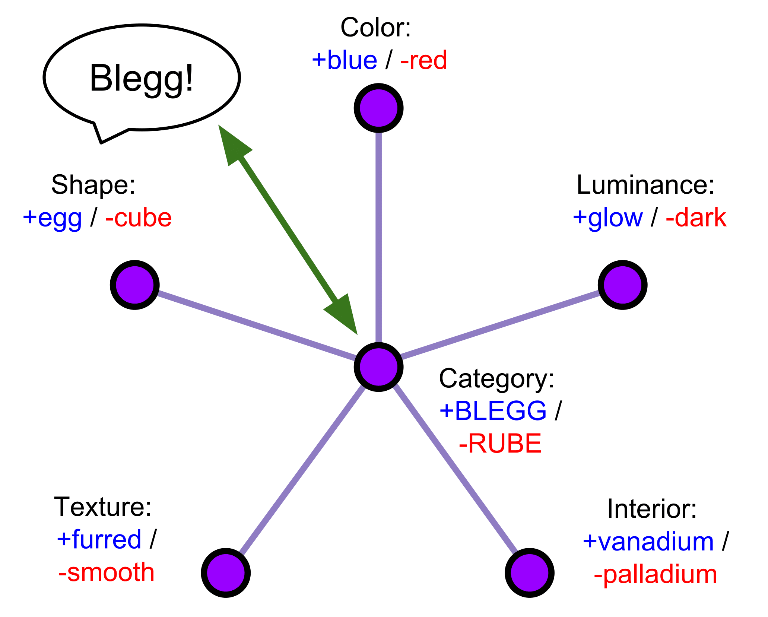
Figure 164.1: Network 3

Considering this as a design constraint on the human cognitive architecture, you wouldn’t want any extra steps between when your auditory cortex recognizes the syllables “tiger,” and when the tiger concept gets activated.

Going back to the parable of bleggs and rubes, and the centralized network that categorizes quickly and cheaply, you might visualize a direct connection running from the unit that recognizes the syllable “blegg” to the unit at the center of the blegg network. The central unit, the blegg concept, gets activated almost as soon as you hear Susan the Senior Sorter say, “Blegg!”

Or, for purposes of talking—which also shouldn’t take eons—as soon as you see a blue egg-shaped thing and the central blegg unit fires, you holler “Blegg!” to Susan.

And what that algorithm feels like from inside is that the label, and the concept, are very nearly identified; the meaning feels like an intrinsic property of the word itself.

The cognoscenti will recognize this as a case of E. T. Jaynes’s “Mind Projection Fallacy.” It feels like a word has a meaning, as a property of the word itself; just like how redness is a property of a red apple, or mysteriousness is a property of a mysterious phenomenon.

Indeed, on most occasions, the brain will not distinguish at all between the word and the meaning—only bothering to separate the two while learning a new language, perhaps. And even then, you’ll see Susan pointing to a blue egg-shaped thing and saying “Blegg!,” and you’ll think, I wonder what “blegg” means, and not, I wonder what mental category Susan associates to the auditory label “blegg.”

Consider, in this light, the part of the Standard Dispute of Definitions where the two parties argue about what the word “sound” really means—the same way they might argue whether a particular apple is really red or green:

ALBERT: “My computer’s microphone can record a sound without anyone being around to hear it, store it as a file, and it’s called a ‘sound file.’ And what’s stored in the file is the pattern of vibrations in air, not the pattern of neural firings in anyone’s brain. ‘Sound’ means a pattern of vibrations.”

BARRY: “Oh, yeah? Let’s just see if the dictionary agrees with you.”

Albert feels intuitively that the word “sound” has a meaning and that the meaning is acoustic vibrations. Just as Albert feels that a tree falling in the forest makes a sound (rather than causing an event that matches the sound category).

Barry likewise feels that:

sound.meaning == auditory experiences

forest.sound == false.

Rather than:

myBrain.FindConcept("sound") == concept_AuditoryExperience

concept_AuditoryExperience.match(forest) == false.

Which is closer to what’s really going on; but humans have not evolved to know this, anymore than humans instinctively know the brain is made of neurons.

Albert and Barry’s conflicting intuitions provide the fuel for continuing the argument in the phase of arguing over what the word “sound” means—which feels like arguing over a fact like any other fact, like arguing over whether the sky is blue or green.

You may not even notice that anything has gone astray, until you try to perform the rationalist ritual of stating a testable experiment whose result depends on the facts you’re so heatedly disputing . . .

165
The Argument from Common Usage

Part of the Standard Definitional Dispute runs as follows:

ALBERT: “Look, suppose that I left a microphone in the forest and recorded the pattern of the acoustic vibrations of the tree falling. If I played that back to someone, they’d call it a ‘sound’! That’s the common usage! Don’t go around making up your own wacky definitions!”

BARRY: “One, I can define a word any way I like so long as I use it consistently. Two, the meaning I gave was in the dictionary. Three, who gave you the right to decide what is or isn’t common usage?”

Not all definitional disputes progress as far as recognizing the notion of common usage. More often, I think, someone picks up a dictionary because they believe that words have meanings, and the dictionary faithfully records what this meaning is. Some people even seem to believe that the dictionary determines the meaning—that the dictionary editors are the Legislators of Language. Maybe because back in elementary school, their authority-teacher said that they had to obey the dictionary, that it was a mandatory rule rather than an optional one?

Dictionary editors read what other people write, and record what the words seem to mean; they are historians. The Oxford English Dictionary may be comprehensive, but never authoritative.

But surely there is a social imperative to use words in a commonly understood way? Does not our human telepathy, our valuable power of language, rely on mutual coordination to work? Perhaps we should voluntarily treat dictionary editors as supreme arbiters—even if they prefer to think of themselves as historians—in order to maintain the quiet cooperation on which all speech depends.

The phrase “authoritative dictionary” is almost never used correctly, an example of proper usage being The Authoritative Dictionary of IEEE Standards Terms. The IEEE is a body of voting members who have a professional need for exact agreement on terms and definitions, and so The Authoritative Dictionary of IEEE Standards Terms is actual, negotiated legislation, which exerts whatever authority one regards as residing in the IEEE.

In everyday life, shared language usually does not arise from a deliberate agreement, as of the IEEE. It’s more a matter of infection, as words are invented and diffuse through the culture. (A “meme,” one might say, following Richard Dawkins forty years ago—but you already know what I mean, and if not, you can look it up on Google, and then you too will have been infected.)

Yet as the example of the IEEE shows, agreement on language can also be a cooperatively established public good. If you and I wish to undergo an exchange of thoughts via language, the human telepathy, then it is in our mutual interest that we use the same word for similar concepts—preferably, concepts similar to the limit of resolution in our brain’s representation thereof—even though we have no obvious mutual interest in using any particular word for a concept.

We have no obvious mutual interest in using the word “oto” to mean sound, or “sound” to mean oto; but we have a mutual interest in using the same word, whichever word it happens to be. (Preferably, words we use frequently should be short, but let’s not get into information theory just yet.)

But, while we have a mutual interest, it is not strictly necessary that you and I use the similar labels internally; it is only convenient. If I know that, to you, “oto” means sound—that is, you associate “oto” to a concept very similar to the one I associate to “sound”—then I can say “Paper crumpling makes a crackling oto.” It requires extra thought, but I can do it if I want.

Similarly, if you say “What is the walking-stick of a bowling ball dropping on the floor?” and I know which concept you associate with the syllables “walking-stick,” then I can figure out what you mean. It may require some thought, and give me pause, because I ordinarily associate “walking-stick” with a different concept. But I can do it just fine.

When humans really want to communicate with each other, we’re hard to stop! If we’re stuck on a deserted island with no common language, we’ll take up sticks and draw pictures in sand.

Albert’s appeal to the Argument from Common Usage assumes that agreement on language is a cooperatively established public good. Yet Albert assumes this for the sole purpose of rhetorically accusing Barry of breaking the agreement, and endangering the public good. Now the falling-tree argument has gone all the way from botany to semantics to politics; and so Barry responds by challenging Albert for the authority to define the word.

A rationalist, with the discipline of hugging the query active, would notice that the conversation had gone rather far astray.

Oh, dear reader, is it all really necessary? Albert knows what Barry means by “sound.” Barry knows what Albert means by “sound.” Both Albert and Barry have access to words, such as “acoustic vibrations” or “auditory experience,” which they already associate to the same concepts, and which can describe events in the forest without ambiguity. If they were stuck on a deserted island, trying to communicate with each other, their work would be done.

When both sides know what the other side wants to say, and both sides accuse the other side of defecting from “common usage,” then whatever it is they are about, it is clearly not working out a way to communicate with each other. But this is the whole benefit that common usage provides in the first place.

Why would you argue about the meaning of a word, two sides trying to wrest it back and forth? If it’s just a namespace conflict that has gotten blown out of proportion, and nothing more is at stake, then the two sides need merely generate two new words and use them consistently.

Yet often categorizations function as hidden inferences and disguised queries. Is atheism a “religion”? If someone is arguing that the reasoning methods used in atheism are on a par with the reasoning methods used in Judaism, or that atheism is on a par with Islam in terms of causally engendering violence, then they have a clear argumentative stake in lumping it all together into an indistinct gray blur of “faith.”

Or consider the fight to blend together blacks and whites as “people.” This would not be a time to generate two words—what’s at stake is exactly the idea that you shouldn’t draw a moral distinction.

But once any empirical proposition is at stake, or any moral proposition, you can no longer appeal to common usage.

If the question is how to cluster together similar things for purposes of inference, empirical predictions will depend on the answer; which means that definitions can be wrong. A conflict of predictions cannot be settled by an opinion poll.

If you want to know whether atheism should be clustered with supernaturalist religions for purposes of some particular empirical inference, the dictionary can’t answer you.

If you want to know whether blacks are people, the dictionary can’t answer you.

If everyone believes that the red light in the sky is Mars the God of War, the dictionary will define “Mars” as the God of War. If everyone believes that fire is the release of phlogiston, the dictionary will define “fire” as the release of phlogiston.

There is an art to using words; even when definitions are not literally true or false, they are often wiser or more foolish. Dictionaries are mere histories of past usage; if you treat them as supreme arbiters of meaning, it binds you to the wisdom of the past, forbidding you to do better.

Though do take care to ensure (if you must depart from the wisdom of the past) that people can figure out what you’re trying to swim.

166
Empty Labels

Consider (yet again) the Aristotelian idea of categories. Let’s say that there’s some object with properties A, B, C, D, and E, or at least it looks E-ish.

FRED: “You mean that thing over there is blue, round, fuzzy, and—”

ME: “In Aristotelian logic, it’s not supposed to make a difference what the properties are, or what I call them. That’s why I’m just using the letters.”

Next, I invent the Aristotelian category “zawa,” which describes those objects, all those objects, and only those objects, that have properties A, C, and D.

ME: “Object 1 is zawa, B, and E.”

FRED: “And it’s blue—I mean, A—too, right?”

ME: “That’s implied when I say it’s zawa.”

FRED: “Still, I’d like you to say it explicitly.”

ME: “Okay. Object 1 is A, B, zawa, and E.”

Then I add another word, “yokie,” which describes all and only objects that are B and E; and the word “xippo,” which describes all and only objects which are E but not D.

ME: “Object 1 is zawa and yokie, but not xippo.”

FRED: “Wait, is it luminescent? I mean, is it E?”

ME: “Yes. That is the only possibility on the information given.”

FRED: “I’d rather you spelled it out.”

ME: “Fine: Object 1 is A, zawa, B, yokie, C, D, E, and not xippo.”

FRED: “Amazing! You can tell all that just by looking?”

Impressive, isn’t it? Let’s invent even more new words: “Bolo” is A, C, and yokie; “mun” is A, C, and xippo; and “merlacdonian” is bolo and mun.

Pointlessly confusing? I think so too. Let’s replace the labels with the definitions:

“Zawa, B, and E” becomes [A, C, D], B, E

“Bolo and A” becomes [A, C, [B, E]], A

“Merlacdonian” becomes [A, C, [B, E]], [A, C, [E, ¬D]].

And the thing to remember about the Aristotelian idea of categories is that [A, C, D] is the entire information of “zawa.” It’s not just that I can vary the label, but that I can get along just fine without any label at all—the rules for Aristotelian classes work purely on structures like [A, C, D]. To call one of these structures “zawa,” or attach any other label to it, is a human convenience (or inconvenience) which makes not the slightest difference to the Aristotelian rules.

Let’s say that “human” is to be defined as a mortal featherless biped. Then the classic syllogism would have the form:

All [mortal, ¬feathers, bipedal] are mortal.

Socrates is a [mortal, ¬feathers, bipedal].

Therefore, Socrates is mortal.

The feat of reasoning looks a lot less impressive now, doesn’t it?

Here the illusion of inference comes from the labels, which conceal the premises, and pretend to novelty in the conclusion. Replacing labels with definitions reveals the illusion, making visible the tautology’s empirical unhelpfulness. You can never say that Socrates is a [mortal, ¬feathers, biped] until you have observed him to be mortal.

There’s an idea, which you may have noticed I hate, that “you can define a word any way you like.” This idea came from the Aristotelian notion of categories; since, if you follow the Aristotelian rules exactly and without flaw—which humans never do; Aristotle knew perfectly well that Socrates was human, even though that wasn’t justified under his rules—but, if some imaginary nonhuman entity were to follow the rules exactly, they would never arrive at a contradiction. They wouldn’t arrive at much of anything: they couldn’t say that Socrates is a [mortal, ¬feathers, biped] until they observed him to be mortal.

But it’s not so much that labels are arbitrary in the Aristotelian system, as that the Aristotelian system works fine without any labels at all—it cranks out exactly the same stream of tautologies, they just look a lot less impressive. The labels are only there to create the illusion of inference.

So if you’re going to have an Aristotelian proverb at all, the proverb should be, not “I can define a word any way I like,” nor even, “Defining a word never has any consequences,” but rather, “Definitions don’t need words.”

167
Taboo Your Words

In the game Taboo (by Hasbro), the objective is for a player to have their partner guess a word written on a card, without using that word or five additional words listed on the card. For example, you might have to get your partner to say “baseball” without using the words “sport,” “bat,” “hit,” “pitch,” “base” or of course “baseball.”

As soon as I see a problem like that, I at once think, “An artificial group conflict in which you use a long wooden cylinder to whack a thrown spheroid, and then run between four safe positions.” It might not be the most efficient strategy to convey the word “baseball” under the stated rules—that might be, “It’s what the Yankees play”—but the general skill of blanking a word out of my mind was one I’d practiced for years, albeit with a different purpose.

In the previous essay we saw how replacing terms with definitions could reveal the empirical unproductivity of the classical Aristotelian syllogism. All humans are mortal (and also, apparently, featherless bipeds); Socrates is human; therefore Socrates is mortal. When we replace the word “human” by its apparent definition, the following underlying reasoning is revealed:

All [mortal, ¬feathers, biped] are mortal;

Socrates is a [mortal, ¬feathers, biped];

Therefore Socrates is mortal.

But the principle of replacing words by definitions applies much more broadly:

ALBERT: “A tree falling in a deserted forest makes a sound.”

BARRY: “A tree falling in a deserted forest does not make a sound.”

Clearly, since one says “sound” and one says “not sound,” we must have a contradiction, right? But suppose that they both dereference their pointers before speaking:

ALBERT: “A tree falling in a deserted forest matches [membership test: this event generates acoustic vibrations].”

BARRY: “A tree falling in a deserted forest does not match [membership test: this event generates auditory experiences].”

Now there is no longer an apparent collision—all they had to do was prohibit themselves from using the word sound. If “acoustic vibrations” came into dispute, we would just play Taboo again and say “pressure waves in a material medium”; if necessary we would play Taboo again on the word “wave” and replace it with the wave equation. (Play Taboo on “auditory experience” and you get “That form of sensory processing, within the human brain, that takes as input a linear time series of frequency mixes . . .”)

But suppose, on the other hand, that Albert and Barry were to have the argument:

ALBERT: “Socrates matches the concept [membership test: this person will die after drinking hemlock].”

BARRY: “Socrates matches the concept [membership test: this person will not die after drinking hemlock].”

Now Albert and Barry have a substantive clash of expectations; a difference in what they anticipate seeing after Socrates drinks hemlock. But they might not notice this, if they happened to use the same word “human” for their different concepts.

You get a very different picture of what people agree or disagree about, depending on whether you take a label’s-eye-view (Albert says “sound” and Barry says “not sound,” so they must disagree) or taking the test’s-eye-view (Albert’s membership test is acoustic vibrations, Barry’s is auditory experience).

Get together a pack of soi-disant futurists and ask them if they believe we’ll have Artificial Intelligence in thirty years, and I would guess that at least half of them will say yes. If you leave it at that, they’ll shake hands and congratulate themselves on their consensus. But make the term “Artificial Intelligence” taboo, and ask them to describe what they expect to see, without ever using words like “computers” or “think,” and you might find quite a conflict of expectations hiding under that featureless standard word. See also Shane Legg’s compilation of 71 definitions of “intelligence.”

The illusion of unity across religions can be dispelled by making the term “God” taboo, and asking them to say what it is they believe in; or making the word “faith” taboo, and asking them why they believe it. Though mostly they won’t be able to answer at all, because it is mostly profession in the first place, and you cannot cognitively zoom in on an audio recording.

When you find yourself in philosophical difficulties, the first line of defense is not to define your problematic terms, but to see whether you can think without using those terms at all. Or any of their short synonyms. And be careful not to let yourself invent a new word to use instead. Describe outward observables and interior mechanisms; don’t use a single handle, whatever that handle may be.

Albert says that people have “free will.” Barry says that people don’t have “free will.” Well, that will certainly generate an apparent conflict. Most philosophers would advise Albert and Barry to try to define exactly what they mean by “free will,” on which topic they will certainly be able to discourse at great length. I would advise Albert and Barry to describe what it is that they think people do, or do not have, without using the phrase “free will” at all. (If you want to try this at home, you should also avoid the words “choose,” “act,” “decide,” “determined,” “responsible,” or any of their synonyms.)

This is one of the nonstandard tools in my toolbox, and in my humble opinion, it works way way better than the standard one. It also requires more effort to use; you get what you pay for.

168
Replace the Symbol with the Substance

What does it take to—as in the previous essay’s example—see a “baseball game” as “An artificial group conflict in which you use a long wooden cylinder to whack a thrown spheroid, and then run between four safe positions”? What does it take to play the rationalist version of Taboo, in which the goal is not to find a synonym that isn’t on the card, but to find a way of describing without the standard concept-handle?

You have to visualize. You have to make your mind’s eye see the details, as though looking for the first time. You have to perform an Original Seeing.

Is that a “bat”? No, it’s a long, round, tapering, wooden rod, narrowing at one end so that a human can grasp and swing it.

Is that a “ball”? No, it’s a leather-covered spheroid with a symmetrical stitching pattern, hard but not metal-hard, which someone can grasp and throw, or strike with the wooden rod, or catch.

Are those “bases”? No, they’re fixed positions on a game field, that players try to run to as quickly as possible because of their safety within the game’s artificial rules.

The chief obstacle to performing an original seeing is that your mind already has a nice neat summary, a nice little easy-to-use concept handle. Like the word “baseball,” or “bat,” or “base.” It takes an effort to stop your mind from sliding down the familiar path, the easy path, the path of least resistance, where the small featureless word rushes in and obliterates the details you’re trying to see. A word itself can have the destructive force of cliché; a word itself can carry the poison of a cached thought.

Playing the game of Taboo—being able to describe without using the standard pointer/label/handle—is one of the fundamental rationalist capacities. It occupies the same primordial level as the habit of constantly asking “Why?” or “What does this belief make me anticipate?”

The art is closely related to:

Pragmatism, because seeing in this way often gives you a much closer connection to anticipated experience, rather than propositional belief;
Reductionism, because seeing in this way often forces you to drop down to a lower level of organization, look at the parts instead of your eye skipping over the whole;
Hugging the query, because words often distract you from the question you really want to ask;
Avoiding cached thoughts, which will rush in using standard words, so you can block them by tabooing standard words;
The writer’s rule of “Show, don’t tell!,” which has power among rationalists;
And not losing sight of your original purpose.

How could tabooing a word help you keep your purpose?

From Lost Purposes:

As you read this, some young man or woman is sitting at a desk in a university, earnestly studying material they have no intention of ever using, and no interest in knowing for its own sake. They want a high-paying job, and the high-paying job requires a piece of paper, and the piece of paper requires a previous master’s degree, and the master’s degree requires a bachelor’s degree, and the university that grants the bachelor’s degree requires you to take a class in twelfth-century knitting patterns to graduate. So they diligently study, intending to forget it all the moment the final exam is administered, but still seriously working away, because they want that piece of paper.

Why are you going to “school”? To get an “education” ending in a “degree.” Blank out the forbidden words and all their obvious synonyms, visualize the actual details, and you’re much more likely to notice that “school” currently seems to consist of sitting next to bored teenagers listening to material you already know, that a “degree” is a piece of paper with some writing on it, and that “education” is forgetting the material as soon as you’re tested on it.

Leaky generalizations often manifest through categorizations: People who actually learn in classrooms are categorized as “getting an education,” so “getting an education” must be good; but then anyone who actually shows up at a college will also match against the concept “getting an education,” whether or not they learn.

Students who understand math will do well on tests, but if you require schools to produce good test scores, they’ll spend all their time teaching to the test. A mental category, that imperfectly matches your goal, can produce the same kind of incentive failure internally. You want to learn, so you need an “education”; and then as long as you’re getting anything that matches against the category “education,” you may not notice whether you’re learning or not. Or you’ll notice, but you won’t realize you’ve lost sight of your original purpose, because you’re “getting an education” and that’s how you mentally described your goal.

To categorize is to throw away information. If you’re told that a falling tree makes a “sound,” you don’t know what the actual sound is; you haven’t actually heard the tree falling. If a coin lands “heads,” you don’t know its radial orientation. A blue egg-shaped thing may be a “blegg,” but what if the exact egg shape varies, or the exact shade of blue? You want to use categories to throw away irrelevant information, to sift gold from dust, but often the standard categorization ends up throwing out relevant information too. And when you end up in that sort of mental trouble, the first and most obvious solution is to play Taboo.

For example: “Play Taboo” is itself a leaky generalization. Hasbro’s version is not the rationalist version; they only list five additional banned words on the card, and that’s not nearly enough coverage to exclude thinking in familiar old words. What rationalists do would count as playing Taboo—it would match against the “play Taboo” concept—but not everything that counts as playing Taboo works to force original seeing. If you just think “play Taboo to force original seeing,” you’ll start thinking that anything that counts as playing Taboo must count as original seeing.

The rationalist version isn’t a game, which means that you can’t win by trying to be clever and stretching the rules. You have to play Taboo with a voluntary handicap: Stop yourself from using synonyms that aren’t on the card. You also have to stop yourself from inventing a new simple word or phrase that functions as an equivalent mental handle to the old one. You are trying to zoom in on your map, not rename the cities; dereference the pointer, not allocate a new pointer; see the events as they happen, not rewrite the cliché in a different wording.

By visualizing the problem in more detail, you can see the lost purpose: Exactly what do you do when you “play Taboo”? What purpose does each and every part serve?

If you see your activities and situation originally, you will be able to originally see your goals as well. If you can look with fresh eyes, as though for the first time, you will see yourself doing things that you would never dream of doing if they were not habits.

Purpose is lost whenever the substance (learning, knowledge, health) is displaced by the symbol (a degree, a test score, medical care). To heal a lost purpose, or a lossy categorization, you must do the reverse:

Replace the symbol with the substance; replace the signifier with the signified; replace the property with the membership test; replace the word with the meaning; replace the label with the concept; replace the summary with the details; replace the proxy question with the real question; dereference the pointer; drop into a lower level of organization; mentally simulate the process instead of naming it; zoom in on your map.

The Simple Truth was generated by an exercise of this discipline to describe “truth” on a lower level of organization, without invoking terms like “accurate,” “correct,” “represent,” “reflect,” “semantic,” “believe,” “knowledge,” “map,” or “real.” (And remember that the goal is not really to play Taboo—the word “true” appears in the text, but not to define truth. It would get a buzzer in Hasbro’s game, but we’re not actually playing that game. Ask yourself whether the document fulfilled its purpose, not whether it followed the rules.)

Bayes’s Rule itself describes “evidence” in pure math, without using words like “implies,” “means,” “supports,” “proves,” or “justifies.” Set out to define such philosophical terms, and you’ll just go in circles.

And then there’s the most important word of all to Taboo. I’ve often warned that you should be careful not to overuse it, or even avoid the concept in certain cases. Now you know the real reason why. It’s not a bad subject to think about. But your true understanding is measured by your ability to describe what you’re doing and why, without using that word or any of its synonyms.

169
Fallacies of Compression

“The map is not the territory,” as the saying goes. The only life-size, atomically detailed, 100% accurate map of California is California. But California has important regularities, such as the shape of its highways, that can be described using vastly less information—not to mention vastly less physical material—than it would take to describe every atom within the state borders. Hence the other saying: “The map is not the territory, but you can’t fold up the territory and put it in your glove compartment.”

A paper map of California, at a scale of 10 kilometers to 1 centimeter (a million to one), doesn’t have room to show the distinct position of two fallen leaves lying a centimeter apart on the sidewalk. Even if the map tried to show the leaves, the leaves would appear as the same point on the map; or rather the map would need a feature size of 10 nanometers, which is a finer resolution than most book printers handle, not to mention human eyes.

Reality is very large—just the part we can see is billions of lightyears across. But your map of reality is written on a few pounds of neurons, folded up to fit inside your skull. I don’t mean to be insulting, but your skull is tiny. Comparatively speaking.

Inevitably, then, certain things that are distinct in reality, will be compressed into the same point on your map.

But what this feels like from inside is not that you say, “Oh, look, I’m compressing two things into one point on my map.” What it feels like from inside is that there is just one thing, and you are seeing it.

A sufficiently young child, or a sufficiently ancient Greek philosopher, would not know that there were such things as “acoustic vibrations” or “auditory experiences.” There would just be a single thing that happened when a tree fell; a single event called “sound.”

To realize that there are two distinct events, underlying one point on your map, is an essentially scientific challenge—a big, difficult scientific challenge.

Sometimes fallacies of compression result from confusing two known things under the same label—you know about acoustic vibrations, and you know about auditory processing in brains, but you call them both “sound” and so confuse yourself. But the more dangerous fallacy of compression arises from having no idea whatsoever that two distinct entities even exist. There is just one mental folder in the filing system, labeled “sound,” and everything thought about “sound” drops into that one folder. It’s not that there are two folders with the same label; there’s just a single folder. By default, the map is compressed; why would the brain create two mental buckets where one would serve?

Or think of a mystery novel in which the detective’s critical insight is that one of the suspects has an identical twin. In the course of the detective’s ordinary work, their job is just to observe that Carol is wearing red, that she has black hair, that her sandals are leather—but all these are facts about Carol. It’s easy enough to question an individual fact, like WearsRed(Carol) or BlackHair(Carol). Maybe BlackHair(Carol) is false. Maybe Carol dyes her hair. Maybe BrownHair(Carol). But it takes a subtler detective to wonder if the Carol in WearsRed(Carol) and BlackHair(Carol)—the Carol file into which their observations drop—should be split into two files. Maybe there are two Carols, so that the Carol who wore red is not the same woman as the Carol who had black hair.

Here it is the very act of creating two different buckets that is the stroke of genius insight. ’Tis easier to question one’s facts than one’s ontology.

The map of reality contained in a human brain, unlike a paper map of California, can expand dynamically when we write down more detailed descriptions. But what this feels like from inside is not so much zooming in on a map, as fissioning an indivisible atom—taking one thing (it felt like one thing) and splitting it into two or more things.

Often this manifests in the creation of new words, like “acoustic vibrations” and “auditory experiences” instead of just “sound.” Something about creating the new name seems to allocate the new bucket. The detective is liable to start calling one of their suspects “Carol-2” or “the Other Carol” almost as soon as they realize that there are two Carols.

But expanding the map isn’t always as simple as generating new city names. It is a stroke of scientific insight to realize that such things as acoustic vibrations, or auditory experiences, even exist.

The obvious modern-day illustration would be words like “intelligence” or “consciousness.” Every now and then one sees a press release claiming that a research study has “explained consciousness” because a team of neurologists investigated a 40Hz electrical rhythm that might have something to do with cross-modality binding of sensory information, or because they investigated the reticular activating system that keeps humans awake. That’s an extreme example, and the usual failures are more subtle, but they are of the same kind. The part of “consciousness” that people find most interesting is reflectivity, self-awareness, realizing that the person I see in the mirror is “me”; that and the hard problem of subjective experience as distinguished by David Chalmers. We also label “conscious” the state of being awake, rather than asleep, in our daily cycle. But they are all different concepts going under the same name, and the underlying phenomena are different scientific puzzles. You can explain being awake without explaining reflectivity or subjectivity.

Fallacies of compression also underlie the bait-and-switch technique in philosophy—you argue about “consciousness” under one definition (like the ability to think about thinking) and then apply the conclusions to “consciousness” under a different definition (like subjectivity). Of course it may be that the two are the same thing, but if so, genuinely understanding this fact would require first a conceptual split and then a genius stroke of reunification.

Expanding your map is (I say again) a scientific challenge: part of the art of science, the skill of inquiring into the world. (And of course you cannot solve a scientific challenge by appealing to dictionaries, nor master a complex skill of inquiry by saying “I can define a word any way I like.”) Where you see a single confusing thing, with protean and self-contradictory attributes, it is a good guess that your map is cramming too much into one point—you need to pry it apart and allocate some new buckets. This is not like defining the single thing you see, but it does often follow from figuring out how to talk about the thing without using a single mental handle.

So the skill of prying apart the map is linked to the rationalist version of Taboo, and to the wise use of words; because words often represent the points on our map, the labels under which we file our propositions and the buckets into which we drop our information. Avoiding a single word, or allocating new ones, is often part of the skill of expanding the map.

170
Categorizing Has Consequences

Among the many genetic variations and mutations you carry in your genome, there are a very few alleles you probably know—including those determining your blood type: the presence or absence of the A, B, and + antigens. If you receive a blood transfusion containing an antigen you don’t have, it will trigger an allergic reaction. It was Karl Landsteiner’s discovery of this fact, and how to test for compatible blood types, that made it possible to transfuse blood without killing the patient. (1930 Nobel Prize in Medicine.) Also, if a mother with blood type A (for example) bears a child with blood type A+, the mother may acquire an allergic reaction to the + antigen; if she has another child with blood type A+, the child will be in danger, unless the mother takes an allergic suppressant during pregnancy. Thus people learn their blood types before they marry.

Oh, and also: people with blood type A are earnest and creative, while people with blood type B are wild and cheerful. People with type O are agreeable and sociable, while people with type AB are cool and controlled. (You would think that O would be the absence of A and B, while AB would just be A plus B, but no . . .) All this, according to the Japanese blood type theory of personality. It would seem that blood type plays the role in Japan that astrological signs play in the West, right down to blood type horoscopes in the daily newspaper.

This fad is especially odd because blood types have never been mysterious, not in Japan and not anywhere. We only know blood types even exist thanks to Karl Landsteiner. No mystic witch doctor, no venerable sorcerer, ever said a word about blood types; there are no ancient, dusty scrolls to shroud the error in the aura of antiquity. If the medical profession claimed tomorrow that it had all been a colossal hoax, we layfolk would not have one scrap of evidence from our unaided senses to contradict them.

There’s never been a war between blood types. There’s never even been a political conflict between blood types. The stereotypes must have arisen strictly from the mere existence of the labels.

Now, someone is bound to point out that this is a story of categorizing humans. Does the same thing happen if you categorize plants, or rocks, or office furniture? I can’t recall reading about such an experiment, but of course, that doesn’t mean one hasn’t been done. (I’d expect the chief difficulty of doing such an experiment would be finding a protocol that didn’t mislead the subjects into thinking that, since the label was given you, it must be significant somehow.) So while I don’t mean to update on imaginary evidence, I would predict a positive result for the experiment: I would expect them to find that mere labeling had power over all things, at least in the human imagination.

You can see this in terms of similarity clusters: once you draw a boundary around a group, the mind starts trying to harvest similarities from the group. And unfortunately the human pattern-detectors seem to operate in such overdrive that we see patterns whether they’re there or not; a weakly negative correlation can be mistaken for a strong positive one with a bit of selective memory.

You can see this in terms of neural algorithms: creating a name for a set of things is like allocating a subnetwork to find patterns in them.

You can see this in terms of a compression fallacy: things given the same name end up dumped into the same mental bucket, blurring them together into the same point on the map.

Or you can see this in terms of the boundless human ability to make stuff up out of thin air and believe it because no one can prove it’s wrong. As soon as you name the category, you can start making up stuff about it. The named thing doesn’t have to be perceptible; it doesn’t have to exist; it doesn’t even have to be coherent.

And no, it’s not just Japan: Here in the West, a blood-type-based diet book called Eat Right 4 Your Type was a bestseller.

Any way you look at it, drawing a boundary in thingspace is not a neutral act. Maybe a more cleanly designed, more purely Bayesian AI could ponder an arbitrary class and not be influenced by it. But you, a human, do not have that option. Categories are not static things in the context of a human brain; as soon as you actually think of them, they exert force on your mind. One more reason not to believe you can define a word any way you like.

171
Sneaking in Connotations

In the previous essay, we saw that in Japan, blood types have taken the place of astrology—if your blood type is AB, for example, you’re supposed to be “cool and controlled.”

So suppose we decided to invent a new word, “wiggin,” and defined this word to mean people with green eyes and black hair—

A green-eyed man with black hair walked into a restaurant.

“Ha,” said Danny, watching from a nearby table, “did you see that? A wiggin just walked into the room. Bloody wiggins. Commit all sorts of crimes, they do.”

His sister Erda sighed. “You haven’t seen him commit any crimes, have you, Danny?”

“Don’t need to,” Danny said, producing a dictionary. “See, it says right here in the Oxford English Dictionary. ‘Wiggin. (1) A person with green eyes and black hair.’ He’s got green eyes and black hair, he’s a wiggin. You’re not going to argue with the Oxford English Dictionary, are you? By definition, a green-eyed black-haired person is a wiggin.”

“But you called him a wiggin,” said Erda. “That’s a nasty thing to say about someone you don’t even know. You’ve got no evidence that he puts too much ketchup on his burgers, or that as a kid he used his slingshot to launch baby squirrels.”

“But he is a wiggin,” Danny said patiently. “He’s got green eyes and black hair, right? Just you watch, as soon as his burger arrives, he’s reaching for the ketchup.”

The human mind passes from observed characteristics to inferred characteristics via the medium of words. In “All humans are mortal, Socrates is a human, therefore Socrates is mortal,” the observed characteristics are Socrates’s clothes, speech, tool use, and generally human shape; the categorization is “human”; the inferred characteristic is poisonability by hemlock.

Of course there’s no hard distinction between “observed characteristics” and “inferred characteristics.” If you hear someone speak, they’re probably shaped like a human, all else being equal. If you see a human figure in the shadows, then ceteris paribus it can probably speak.

And yet some properties do tend to be more inferred than observed. You’re more likely to decide that someone is human, and will therefore burn if exposed to open flame, than carry through the inference the other way around.

If you look in a dictionary for the definition of “human,” you’re more likely to find characteristics like “intelligence” and “featherless biped”—characteristics that are useful for quickly eyeballing what is and isn’t a human—rather than the ten thousand connotations, from vulnerability to hemlock, to overconfidence, that we can infer from someone’s being human. Why? Perhaps dictionaries are intended to let you match up labels to similarity groups, and so are designed to quickly isolate clusters in thingspace. Or perhaps the big, distinguishing characteristics are the most salient, and therefore first to pop into a dictionary editor’s mind. (I’m not sure how aware dictionary editors are of what they really do.)

But the upshot is that when Danny pulls out his OED to look up “wiggin,” he sees listed only the first-glance characteristics that distinguish a wiggin: Green eyes and black hair. The OED doesn’t list the many minor connotations that have come to attach to this term, such as criminal proclivities, culinary peculiarities, and some unfortunate childhood activities.

How did those connotations get there in the first place? Maybe there was once a famous wiggin with those properties. Or maybe someone made stuff up at random, and wrote a series of bestselling books about it (The Wiggin, Talking to Wiggins, Raising Your Little Wiggin, Wiggins in the Bedroom). Maybe even the wiggins believe it now, and act accordingly. As soon as you call some people “wiggins,” the word will begin acquiring connotations.

But remember the Parable of Hemlock: If we go by the logical class definitions, we can never class Socrates as a “human” until after we observe him to be mortal. Whenever someone pulls a dictionary, they’re generally trying to sneak in a connotation, not the actual definition written down in the dictionary.

After all, if the only meaning of the word “wiggin” is “green-eyed black-haired person,” then why not just call those people “green-eyed black-haired people”? And if you’re wondering whether someone is a ketchup-reacher, why not ask directly, “Is he a ketchup-reacher?” rather than “Is he a wiggin?” (Note substitution of substance for symbol.)

Oh, but arguing the real question would require work. You’d have to actually watch the wiggin to see if he reached for the ketchup. Or maybe see if you can find statistics on how many green-eyed black-haired people actually like ketchup. At any rate, you wouldn’t be able to do it sitting in your living room with your eyes closed. And people are lazy. They’d rather argue “by definition,” especially since they think “you can define a word any way you like.”

But of course the real reason they care whether someone is a “wiggin” is a connotation—a feeling that comes along with the word—that isn’t in the definition they claim to use.

Imagine Danny saying, “Look, he’s got green eyes and black hair. He’s a wiggin! It says so right there in the dictionary!—therefore, he’s got black hair. Argue with that, if you can!”

Doesn’t have much of a triumphant ring to it, does it? If the real point of the argument actually was contained in the dictionary definition—if the argument genuinely was logically valid—then the argument would feel empty; it would either say nothing new, or beg the question.

It’s only the attempt to smuggle in connotations not explicitly listed in the definition, that makes anyone feel they can score a point that way.

172
Arguing “By Definition”

“This plucked chicken has two legs and no feathers—therefore, by definition, it is a human!”

When people argue definitions, they usually start with some visible, known, or at least widely believed set of characteristics; then pull out a dictionary, and point out that these characteristics fit the dictionary definition; and so conclude, “Therefore, by definition, atheism is a religion!”

But visible, known, widely believed characteristics are rarely the real point of a dispute. Just the fact that someone thinks Socrates’s two legs are evident enough to make a good premise for the argument, “Therefore, by definition, Socrates is human!” indicates that bipedalism probably isn’t really what’s at stake—or the listener would reply, “Whaddaya mean Socrates is bipedal? That’s what we’re arguing about in the first place!”

Now there is an important sense in which we can legitimately move from evident characteristics to not-so-evident ones. You can, legitimately, see that Socrates is human-shaped, and predict his vulnerability to hemlock. But this probabilistic inference does not rely on dictionary definitions or common usage; it relies on the universe containing empirical clusters of similar things.

This cluster structure is not going to change depending on how you define your words. Even if you look up the dictionary definition of “human” and it says “all featherless bipeds except Socrates,” that isn’t going to change the actual degree to which Socrates is similar to the rest of us featherless bipeds.

When you are arguing correctly from cluster structure, you’ll say something like, “Socrates has two arms, two feet, a nose and tongue, speaks fluent Greek, uses tools, and in every aspect I’ve been able to observe him, seems to have every major and minor property that characterizes Homo sapiens; so I’m going to guess that he has human DNA, human biochemistry, and is vulnerable to hemlock just like all other Homo sapiens in whom hemlock has been clinically tested for lethality.”

And suppose I reply, “But I saw Socrates out in the fields with some herbologists; I think they were trying to prepare an antidote. Therefore I don’t expect Socrates to keel over after he drinks the hemlock—he will be an exception to the general behavior of objects in his cluster: they did not take an antidote, and he did.”

Now there’s not much point in arguing over whether Socrates is “human” or not. The conversation has to move to a more detailed level, poke around inside the details that make up the “human” category—talk about human biochemistry, and specifically, the neurotoxic effects of coniine.

If you go on insisting, “But Socrates is a human and humans, by definition, are mortal!” then what you’re really trying to do is blur out everything you know about Socrates except the fact of his humanity—insist that the only correct prediction is the one you would make if you knew nothing about Socrates except that he was human.

Which is like insisting that a coin is 50% likely to be showing heads or tails, because it is a “fair coin,” after you’ve actually looked at the coin and it’s showing heads. It’s like insisting that Frodo has ten fingers, because most hobbits have ten fingers, after you’ve already looked at his hands and seen nine fingers. Naturally this is illegal under Bayesian probability theory: You can’t just refuse to condition on new evidence.

And you can’t just keep one categorization and make estimates based on that, while deliberately throwing out everything else you know.

Not every piece of new evidence makes a significant difference, of course. If I see that Socrates has nine fingers, this isn’t going to noticeably change my estimate of his vulnerability to hemlock, because I’ll expect that the way Socrates lost his finger didn’t change the rest of his biochemistry. And this is true, whether or not the dictionary’s definition says that human beings have ten fingers. The legal inference is based on the cluster structure of the environment, and the causal structure of biology; not what the dictionary editor writes down, nor even “common usage.”

Now ordinarily, when you’re doing this right—in a legitimate way—you just say, “The coniine alkaloid found in hemlock produces muscular paralysis in humans, resulting in death by asphyxiation.” Or more simply, “Humans are vulnerable to hemlock.” That’s how it’s usually said in a legitimate argument.

When would someone feel the need to strengthen the argument with the emphatic phrase “by definition”? (E.g. “Humans are vulnerable to hemlock by definition!”) Why, when the inferred characteristic has been called into doubt—Socrates has been seen consulting herbologists—and so the speaker feels the need to tighten the vise of logic.

So when you see “by definition” used like this, it usually means: “Forget what you’ve heard about Socrates consulting herbologists—humans, by definition, are mortal!”

People feel the need to squeeze the argument onto a single course by saying “Any P, by definition, has property Q!,” on exactly those occasions when they see, and prefer to dismiss out of hand, additional arguments that call into doubt the default inference based on clustering.

So too with the argument “X, by definition, is a Y!” E.g., “Atheists believe that God doesn’t exist; therefore atheists have beliefs about God, because a negative belief is still a belief; therefore atheism asserts answers to theological questions; therefore atheism is, by definition, a religion.”

You wouldn’t feel the need to say, “Hinduism, by definition, is a religion!” because, well, of course Hinduism is a religion. It’s not just a religion “by definition,” it’s, like, an actual religion.

Atheism does not resemble the central members of the “religion” cluster, so if it wasn’t for the fact that atheism is a religion by definition, you might go around thinking that atheism wasn’t a religion. That’s why you’ve got to crush all opposition by pointing out that “Atheism is a religion” is true by definition, because it isn’t true any other way.

Which is to say: People insist that “X, by definition, is a Y!” on those occasions when they’re trying to sneak in a connotation of Y that isn’t directly in the definition, and X doesn’t look all that much like other members of the Y cluster.

Over the last thirteen years I’ve been keeping track of how often this phrase is used correctly versus incorrectly—though not with literal statistics, I fear. But eyeballing suggests that using the phrase by definition, anywhere outside of math, is among the most alarming signals of flawed argument I’ve ever found. It’s right up there with “Hitler,” “God,” “absolutely certain,” and “can’t prove that.”

This heuristic of failure is not perfect—the first time I ever spotted a correct usage outside of math, it was by Richard Feynman; and since then I’ve spotted more. But you’re probably better off just deleting the phrase “by definition” from your vocabulary—and always on any occasion where you might be tempted to say it in italics or followed with an exclamation mark. That’s a bad idea by definition!

173
Where to Draw the Boundary?

The one comes to you and says:

Long have I pondered the meaning of the word “Art,” and at last I’ve found what seems to me a satisfactory definition: “Art is that which is designed for the purpose of creating a reaction in an audience.”

Just because there’s a word “art” doesn’t mean that it has a meaning, floating out there in the void, which you can discover by finding the right definition.

It feels that way, but it is not so.

Wondering how to define a word means you’re looking at the problem the wrong way—searching for the mysterious essence of what is, in fact, a communication signal.

Now, there is a real challenge which a rationalist may legitimately attack, but the challenge is not to find a satisfactory definition of a word. The real challenge can be played as a single-player game, without speaking aloud. The challenge is figuring out which things are similar to each other—which things are clustered together—and sometimes, which things have a common cause.

If you define “eluctromugnetism” to include lightning, include compasses, exclude light, and include Mesmer’s “animal magnetism” (what we now call hypnosis), then you will have some trouble asking “How does eluctromugnetism work?” You have lumped together things which do not belong together, and excluded others that would be needed to complete a set. (This example is historically plausible; Mesmer came before Faraday.)

We could say that eluctromugnetism is a wrong word, a boundary in thingspace that loops around and swerves through the clusters, a cut that fails to carve reality along its natural joints.

Figuring where to cut reality in order to carve along the joints—this is the problem worthy of a rationalist. It is what people should be trying to do, when they set out in search of the floating essence of a word.

And make no mistake: it is a scientific challenge to realize that you need a single word to describe breathing and fire. So do not think to consult the dictionary editors, for that is not their job.

What is “art”? But there is no essence of the word, floating in the void.

Perhaps you come to me with a long list of the things that you call “art” and “not art”:

The Little Fugue in G Minor: Art.

A punch in the nose: Not art.

Escher’s Relativity: Art.

A flower: Not art.

The Python programming language: Art.

A cross floating in urine: Not art.

Jack Vance’s Tschai novels: Art.

Modern Art: Not art.

And you say to me: “It feels intuitive to me to draw this boundary, but I don’t know why—can you find me an intension that matches this extension? Can you give me a simple description of this boundary?”

So I reply: “I think it has to do with admiration of craftsmanship: work going in and wonder coming out. What the included items have in common is the similar aesthetic emotions that they inspire, and the deliberate human effort that went into them with the intent of producing such an emotion.”

Is this helpful, or is it just cheating at Taboo? I would argue that the list of which human emotions are or are not aesthetic is far more compact than the list of everything that is or isn’t art. You might be able to see those emotions lighting up an fMRI scan—I say this by way of emphasizing that emotions are not ethereal.

But of course my definition of art is not the real point. The real point is that you could well dispute either the intension or the extension of my definition.

You could say, “Aesthetic emotion is not what these things have in common; what they have in common is an intent to inspire any complex emotion for the sake of inspiring it.” That would be disputing my intension, my attempt to draw a curve through the data points. You would say, “Your equation may roughly fit those points, but it is not the true generating distribution.”

Or you could dispute my extension by saying, “Some of these things do belong together—I can see what you’re getting at—but the Python language shouldn’t be on the list, and Modern Art should be.” (This would mark you as a philistine, but you could argue it.) Here, the presumption is that there is indeed an underlying curve that generates this apparent list of similar and dissimilar things—that there is a rhyme and reason, even though you haven’t said yet where it comes from—but I have unwittingly lost the rhythm and included some data points from a different generator.

Long before you know what it is that electricity and magnetism have in common, you might still suspect—based on surface appearances—that “animal magnetism” does not belong on the list.

Once upon a time it was thought that the word “fish” included dolphins. Now you could play the oh-so-clever arguer, and say, “The list: {Salmon, guppies, sharks, dolphins, trout} is just a list—you can’t say that a list is wrong. I can prove in set theory that this list exists. So my definition of fish, which is simply this extensional list, cannot possibly be ‘wrong’ as you claim.”

Or you could stop playing games and admit that dolphins don’t belong on the fish list.

You come up with a list of things that feel similar, and take a guess at why this is so. But when you finally discover what they really have in common, it may turn out that your guess was wrong. It may even turn out that your list was wrong.

You cannot hide behind a comforting shield of correct-by-definition. Both extensional definitions and intensional definitions can be wrong, can fail to carve reality at the joints.

Categorizing is a guessing endeavor, in which you can make mistakes; so it’s wise to be able to admit, from a theoretical standpoint, that your definition-guesses can be “mistaken.”

174
Entropy, and Short Codes

(If you aren’t familiar with Bayesian inference, this may be a good time to read An Intuitive Explanation of Bayes’s Theorem.)

Suppose you have a system X that’s equally likely to be in any of 8 possible states:

{X₁, X₂, X₃, X₄, X₅, X₆, X₇, X₈}.

There’s an extraordinarily ubiquitous quantity—in physics, mathematics, and even biology—called entropy; and the entropy of X is 3 bits. This means that, on average, we’ll have to ask 3 yes-or-no questions to find out X’s value. For example, someone could tell us X’s value using this code:

X₁ : 001
X₂ : 010
X₃ : 011
X₄ : 100
X₅ : 101
X₆ : 110
X₇ : 111
X₈ : 000.

So if I asked “Is the first symbol 1?” and heard “yes,” then asked “Is the second symbol 1?” and heard “no,” then asked “Is the third symbol 1?” and heard “no,” I would know that X was in state 4.

Now suppose that the system Y has four possible states with the following probabilities:

Y₁ : 1∕2 (50%)
Y₂ : 1∕4 (25%)
Y₃ : 1∕8 (12.5%)
Y₄ : 1∕8 (12.5%).

Then the entropy of Y would be 1.75 bits, meaning that we can find out its value by asking 1.75 yes-or-no questions.

What does it mean to talk about asking one and three-fourths of a question? Imagine that we designate the states of Y using the following code:

Y₁ : 1
Y₂ : 01
Y₃ : 001
Y₄ : 000.

First you ask, “Is the first symbol 1?” If the answer is “yes,” you’re done: Y is in state 1. This happens half the time, so 50% of the time, it takes 1 yes-or-no question to find out Y’s state.

Suppose that instead the answer is “No.” Then you ask, “Is the second symbol 1?” If the answer is “yes,” you’re done: Y is in state 2. The system Y is in state 2 with probability 1/4, and each time Y is in state 2 we discover this fact using two yes-or-no questions, so 25% of the time it takes 2 questions to discover Y’s state.

If the answer is “No” twice in a row, you ask “Is the third symbol 1?” If “yes,” you’re done and Y is in state 3; if “no,” you’re done and Y is in state 4. The 1/8 of the time that Y is in state 3, it takes three questions; and the 1/8 of the time that Y is in state 4, it takes three questions.

(1/2 × 1) + (1/4 × 2) + (1/8 × 3) + (1/8 × 3)

= 0.5 + 0.5 + 0.375 + 0.375

= 1.75.

The general formula for the entropy H(S) of a system S is the sum, over all S_i, of -P(S_i)log₂(P(S_i)).

For example, the log (base 2) of 1/8 is -3. So -(1∕8 × -3) = 0.375 is the contribution of state S₄ to the total entropy: 1/8 of the time, we have to ask 3 questions.

You can’t always devise a perfect code for a system, but if you have to tell someone the state of arbitrarily many copies of S in a single message, you can get arbitrarily close to a perfect code. (Google “arithmetic coding” for a simple method.)

Now, you might ask: “Why not use the code 10 for Y₄, instead of 000? Wouldn’t that let us transmit messages more quickly?”

But if you use the code 10 for Y₄, then when someone answers “Yes” to the question “Is the first symbol 1?,” you won’t know yet whether the system state is Y₁ (1) or Y₄ (10). In fact, if you change the code this way, the whole system falls apart—because if you hear “1001,” you don’t know if it means “Y₄, followed by Y₂” or “Y₁, followed by Y₃.”

The moral is that short words are a conserved resource.

The key to creating a good code—a code that transmits messages as compactly as possible—is to reserve short words for things that you’ll need to say frequently, and use longer words for things that you won’t need to say as often.

When you take this art to its limit, the length of the message you need to describe something corresponds exactly or almost exactly to its probability. This is the Minimum Description Length or Minimum Message Length formalization of Occam’s Razor.

And so even the labels that we use for words are not quite arbitrary. The sounds that we attach to our concepts can be better or worse, wiser or more foolish. Even apart from considerations of common usage!

I say all this, because the idea that “You can X any way you like” is a huge obstacle to learning how to X wisely. “It’s a free country; I have a right to my own opinion” obstructs the art of finding truth. “I can define a word any way I like” obstructs the art of carving reality at its joints. And even the sensible-sounding “The labels we attach to words are arbitrary” obstructs awareness of compactness. Prosody too, for that matter—Tolkien once observed what a beautiful sound the phrase “cellar door” makes; that is the kind of awareness it takes to use language like Tolkien.

The length of words also plays a nontrivial role in the cognitive science of language:

Consider the phrases “recliner,” “chair,” and “furniture.” Recliner is a more specific category than chair; furniture is a more general category than chair. But the vast majority of chairs have a common use—you use the same sort of motor actions to sit down in them, and you sit down in them for the same sort of purpose (to take your weight off your feet while you eat, or read, or type, or rest). Recliners do not depart from this theme. “Furniture,” on the other hand, includes things like beds and tables which have different uses, and call up different motor functions, from chairs.

In the terminology of cognitive psychology, “chair” is a basic-level category.

People have a tendency to talk, and presumably think, at the basic level of categorization—to draw the boundary around “chairs,” rather than around the more specific category “recliner,” or the more general category “furniture.” People are more likely to say “You can sit in that chair” than “You can sit in that recliner” or “You can sit in that furniture.”

And it is no coincidence that the word for “chair” contains fewer syllables than either “recliner” or “furniture.” Basic-level categories, in general, tend to have short names; and nouns with short names tend to refer to basic-level categories. Not a perfect rule, of course, but a definite tendency. Frequent use goes along with short words; short words go along with frequent use.

Or as Douglas Hofstadter put it, there’s a reason why the English language uses “the” to mean “the” and “antidisestablishmentarianism” to mean “antidisestablishmentarianism” instead of antidisestablishmentarianism other way around.

175
Mutual Information, and Density in Thingspace

Suppose you have a system X that can be in any of 8 states, which are all equally probable (relative to your current state of knowledge), and a system Y that can be in any of 4 states, all equally probable.

The entropy of X, as defined in the previous essay, is 3 bits; we’ll need to ask 3 yes-or-no questions to find out X’s exact state. The entropy of Y is 2 bits; we have to ask 2 yes-or-no questions to find out Y’s exact state. This may seem obvious since 2³ = 8 and 2² = 4, so 3 questions can distinguish 8 possibilities and 2 questions can distinguish 4 possibilities; but remember that if the possibilities were not all equally likely, we could use a more clever code to discover Y’s state using e.g. 1.75 questions on average. In this case, though, X’s probability mass is evenly distributed over all its possible states, and likewise Y, so we can’t use any clever codes.

What is the entropy of the combined system (X,Y)?

You might be tempted to answer, “It takes 3 questions to find out X, and then 2 questions to find out Y, so it takes 5 questions total to find out the state of X and Y.”

But what if the two variables are entangled, so that learning the state of Y tells us something about the state of X?

In particular, let’s suppose that X and Y are either both odd or both even.

Now if we receive a 3-bit message (ask 3 questions) and learn that X is in state X₅, we know that Y is in state Y₁ or state Y₃, but not state Y₂ or state Y₄. So the single additional question “Is Y in state Y₃?,” answered “No,” tells us the entire state of (X,Y): X = X₅,Y = Y₁. And we learned this with a total of 4 questions.

Conversely, if we learn that Y is in state Y₄ using two questions, it will take us only an additional two questions to learn whether X is in state X₂, X₄, X₆, or X₈. Again, four questions to learn the state of the joint system.

The mutual information of two variables is defined as the difference between the entropy of the joint system and the entropy of the independent systems: I(X;Y) = H(X) + H(Y) - H(X,Y).

Here there is one bit of mutual information between the two systems: Learning X tells us one bit of information about Y (cuts down the space of possibilities from 4 possibilities to 2, a factor-of-2 decrease in the volume) and learning Y tells us one bit of information about X (cuts down the possibility space from 8 possibilities to 4).

What about when probability mass is not evenly distributed? Last essay, for example, we discussed the case in which Y had the probabilities 1/2, 1/4, 1/8, 1/8 for its four states. Let us take this to be our probability distribution over Y, considered independently—if we saw Y, without seeing anything else, this is what we’d expect to see. And suppose the variable Z has two states, Z₁ and Z₂, with probabilities 3/8 and 5/8 respectively.

Then if and only if the joint distribution of Y and Z is as follows, there is zero mutual information between Y and Z:

Z₁Y₁ : 3/16
Z₁Y₂ : 3/32
Z₁Y₃ : 3/64
Z₁Y₄ : 3/64
Z₂Y₁ : 5/16
Z₂Y₂ : 5/32
Z₂Y₃ : 5/64
Z₂Y₄ : 5/64.

This distribution obeys the law

P(Y,Z) = P(Y)P(Z).

For example, P(Z₁Y₂) = P(Z₁)P(Y₂) = 3∕8 × 1∕4 = 3∕32.

And observe that we can recover the marginal (independent) probabilities of Y and Z just by looking at the joint distribution:

P(Y₁) = total probability of all the different ways Y₁ can happen

= P (Z₁Y₁) + P(Z₂Y₁)

= 3/16 + 5/16

= 1/2.

So, just by inspecting the joint distribution, we can determine whether the marginal variables Y and Z are independent; that is, whether the joint distribution factors into the product of the marginal distributions; whether, for all Y and Z, we have P(Y,Z) = P(Y)P(Z).

This last is significant because, by Bayes’s Rule,

P(Z_jY_i) = P(Y_i)P(Z_j)

P(Z_jY_i)/P(Z_j) = P(Y_i)

P(Y_i|Z_j) = P(Y_i).

In English: “After you learn Z_j, your belief about Y_i is just what it was before.”

So when the distribution factorizes—when P(Y,Z) = P(Y)P(Z)—this is equivalent to “Learning about Y never tells us anything about Z or vice versa.”

From which you might suspect, correctly, that there is no mutual information between Y and Z. Where there is no mutual information, there is no Bayesian evidence, and vice versa.

Suppose that in the distribution (Y,Z) above, we treated each possible combination of Y and Z as a separate event—so that the distribution (Y,Z) would have a total of 8 possibilities, with the probabilities shown—and then we calculated the entropy of the distribution (Y,Z) the same way we would calculate the entropy of any distribution:

P(Z₁Y₁)log₂(P(Z₁Y₁)) + P(Z₁Y₂)log₂(P(Z₁Y₂)) + P(Z₁Y₃)log₂(P(Z₁Y₃)) + . . . + P (Z₂Y₄)log₂(P(Z₂Y₄))

=(3/16)log₂(3/16) + (3/32)log₂(3/32) + (3/64)log₂(3/64) + . . . + (5/64)log₂(5/64).

You would end up with the same total you would get if you separately calculated the entropy of Y plus the entropy of Z. There is no mutual information between the two variables, so our uncertainty about the joint system is not any less than our uncertainty about the two systems considered separately. (I am not showing the calculations, but you are welcome to do them; and I am not showing the proof that this is true in general, but you are welcome to Google on “Shannon entropy” and “mutual information.”)

What if the joint distribution doesn’t factorize? For example:

Z₁Y₁ : 12/64
Z₁Y₂ : 8/64
Z₁Y₃ : 1/64
Z₁Y₄ : 3/64
Z₂Y₁ : 20/64
Z₂Y₂ : 8/64
Z₂Y₃ : 7/64
Z₂Y₄ : 5/64.

If you add up the joint probabilities to get marginal probabilities, you should find that P(Y₁) = 1∕2, P(Z₁) = 3∕8, and so on—the marginal probabilities are the same as before.

But the joint probabilities do not always equal the product of the marginal probabilities. For example, the probability P(Z₁Y₂) equals 8/64, where P(Z₁)P(Y₂) would equal 3∕8 × 1∕4 = 6∕64. That is, the probability of running into Z₁Y₂ together is greater than you’d expect based on the probabilities of running into Z₁ or Y₂ separately.

Which in turn implies:

P(Z₁Y₂) > P(Z₁)P(Y₂)

P(Z₁Y₂)/P(Y₂) > P(Z₁)

P(Z₁|Y₂) > P(Z₁).

Since there’s an “unusually high” probability for P(Z₁Y₂)—defined as a probability higher than the marginal probabilities would indicate by default—it follows that observing Y₂ is evidence that increases the probability of Z₁. And by a symmetrical argument, observing Z₁ must favor Y₂.

As there are at least some values of Y that tell us about Z (and vice versa) there must be mutual information between the two variables; and so you will find—I am confident, though I haven’t actually checked—that calculating the entropy of (Y,Z) yields less total uncertainty than the sum of the independent entropies of Y and Z. That is, H(Y,Z) = H(Y) + H(Z) - I(Y;Z), with all quantities necessarily positive.

(I digress here to remark that the symmetry of the expression for the mutual information shows that Y must tell us as much about Z, on average, as Z tells us about Y. I leave it as an exercise to the reader to reconcile this with anything they were taught in logic class about how, if all ravens are black, being allowed to reason Raven(x) ⇒ Black(x) doesn’t mean you’re allowed to reason Black(x) ⇒ Raven(x). How different seem the symmetrical probability flows of the Bayesian, from the sharp lurches of logic—even though the latter is just a degenerate case of the former.)

“But,” you ask, “what has all this to do with the proper use of words?”

In Empty Labels and then Replace the Symbol with the Substance, we saw the technique of replacing a word with its definition—the example being given:

All [mortal, ¬feathers, bipedal] are mortal.

Socrates is a [mortal, ¬feathers, bipedal].

Therefore, Socrates is mortal.

Why, then, would you even want to have a word for “human”? Why not just say “Socrates is a mortal featherless biped”?

Because it’s helpful to have shorter words for things that you encounter often. If your code for describing single properties is already efficient, then there will not be an advantage to having a special word for a conjunction—like “human” for “mortal featherless biped”—unless things that are mortal and featherless and bipedal, are found more often than the marginal probabilities would lead you to expect.

In efficient codes, word length corresponds to probability—so the code for Z₁Y₂ will be just as long as the code for Z₁ plus the code for Y₂, unless P(Z₁Y₂) > P(Z₁)P(Y₂), in which case the code for the word can be shorter than the codes for its parts.

And this in turn corresponds exactly to the case where we can infer some of the properties of the thing from seeing its other properties. It must be more likely than the default that featherless bipedal things will also be mortal.

Of course the word “human” really describes many, many more properties—when you see a human-shaped entity that talks and wears clothes, you can infer whole hosts of biochemical and anatomical and cognitive facts about it. To replace the word “human” with a description of everything we know about humans would require us to spend an inordinate amount of time talking. But this is true only because a featherless talking biped is far more likely than default to be poisonable by hemlock, or have broad nails, or be overconfident.

Having a word for a thing, rather than just listing its properties, is a more compact code precisely in those cases where we can infer some of those properties from the other properties. (With the exception perhaps of very primitive words, like “red,” that we would use to send an entirely uncompressed description of our sensory experiences. But by the time you encounter a bug, or even a rock, you’re dealing with nonsimple property collections, far above the primitive level.)

So having a word “wiggin” for green-eyed black-haired people is more useful than just saying “green-eyed black-haired person” precisely when:

Green-eyed people are more likely than average to be black-haired (and vice versa), meaning that we can probabilistically infer green eyes from black hair or vice versa; or
Wiggins share other properties that can be inferred at greater-than-default probability. In this case we have to separately observe the green eyes and black hair; but then, after observing both these properties independently, we can probabilistically infer other properties (like a taste for ketchup).

One may even consider the act of defining a word as a promise to this effect. Telling someone, “I define the word ‘wiggin’ to mean a person with green eyes and black hair,” by Gricean implication, asserts that the word “wiggin” will somehow help you make inferences / shorten your messages.

If green-eyes and black hair have no greater than default probability to be found together, nor does any other property occur at greater than default probability along with them, then the word “wiggin” is a lie: The word claims that certain people are worth distinguishing as a group, but they’re not.

In this case the word “wiggin” does not help describe reality more compactly—it is not defined by someone sending the shortest message—it has no role in the simplest explanation. Equivalently, the word “wiggin” will be of no help to you in doing any Bayesian inference. Even if you do not call the word a lie, it is surely an error.

And the way to carve reality at its joints is to draw your boundaries around concentrations of unusually high probability density in Thingspace.

176
Superexponential Conceptspace, and Simple Words

Thingspace, you might think, is a rather huge space. Much larger than reality, for where reality only contains things that actually exist, Thingspace contains everything that could exist.

Actually, the way I “defined” Thingspace to have dimensions for every possible attribute—including correlated attributes like density and volume and mass—Thingspace may be too poorly defined to have anything you could call a size. But it’s important to be able to visualize Thingspace anyway. Surely, no one can really understand a flock of sparrows if all they see is a cloud of flapping cawing things, rather than a cluster of points in Thingspace.

But as vast as Thingspace may be, it doesn’t hold a candle to the size of Conceptspace.

“Concept,” in machine learning, means a rule that includes or excludes examples. If you see the data {2:+, 3:-, 14:+, 23:-, 8:+, 9:-} then you might guess that the concept was “even numbers.” There is a rather large literature (as one might expect) on how to learn concepts from data . . . given random examples, given chosen examples . . . given possible errors in classification . . . and most importantly, given different spaces of possible rules.

Suppose, for example, that we want to learn the concept “good days on which to play tennis.” The possible attributes of Days are

Sky: {Sunny, Cloudy, Rainy}
AirTemp: {Warm, Cold}
Humidity: {Normal, High}
Wind: {Strong, Weak}.

We’re then presented with the following data, where + indicates a positive example of the concept, and - indicates a negative classification:

+ Sky: Sunny; AirTemp: Warm; Humidity: High; Wind: Strong.
- Sky: Rainy; AirTemp: Cold; Humidity: High; Wind: Strong.
+ Sky: Sunny; AirTemp: Warm; Humidity: High; Wind: Weak.

What should an algorithm infer from this?

A machine learner might represent one concept that fits this data as follows:

{Sky: ?; AirTemp: Warm; Humidity: High; Wind: ?}.

In this format, to determine whether this concept accepts or rejects an example, we compare element-by-element: ? accepts anything, but a specific value accepts only that specific value.

So the concept above will accept only Days with AirTemp = Warm and Humidity = High, but the Sky and the Wind can take on any value. This fits both the negative and the positive classifications in the data so far—though it isn’t the only concept that does so.

We can also simplify the above concept representation to

{?, Warm, High, ?}.

Without going into details, the classic algorithm would be:

Maintain the set of the most general hypotheses that fit the data—those that positively classify as many examples as possible, while still fitting the facts.
Maintain another set of the most specific hypotheses that fit the data—those that negatively classify as many examples as possible, while still fitting the facts.
Each time we see a new negative example, we strengthen all the most general hypotheses as little as possible, so that the new set is again as general as possible while fitting the facts.
Each time we see a new positive example, we relax all the most specific hypotheses as little as possible, so that the new set is again as specific as possible while fitting the facts.
We continue until we have only a single hypothesis left. This will be the answer if the target concept was in our hypothesis space at all.

In the case above, the set of most general hypotheses would be

{{?, Warm, ?, ?},{Sunny, ?, ?, ?}},

while the set of most specific hypotheses contains the single member {Sunny, Warm, High, ?}.

Any other concept you can find that fits the data will be strictly more specific than one of the most general hypotheses, and strictly more general than the most specific hypothesis.

(For more on this, I recommend Tom Mitchell’s Machine Learning, from which this example was adapted.¹)

Now you may notice that the format above cannot represent all possible concepts. E.g., “Play tennis when the sky is sunny or the air is warm.” That fits the data, but in the concept representation defined above, there’s no quadruplet of values that describes the rule.

Clearly our machine learner is not very general. Why not allow it to represent all possible concepts, so that it can learn with the greatest possible flexibility?

Days are composed of these four variables, one variable with 3 values and three variables with 2 values. So there are 3 × 2 × 2 × 2 = 24 possible Days that we could encounter.

The format given for representing Concepts allows us to require any of these values for a variable, or leave the variable open. So there are 4 × 3 × 3 × 3 = 108 concepts in that representation. For the most-general/most-specific algorithm to work, we need to start with the most specific hypothesis “no example is ever positively classified.” If we add that, it makes a total of 109 concepts.

Is it suspicious that there are more possible concepts than possible Days? Surely not: After all, a concept can be viewed as a collection of Days. A concept can be viewed as the set of days that it classifies positively, or isomorphically, the set of days that it classifies negatively.

So the space of all possible concepts that classify Days is the set of all possible sets of Days, whose size is 2²⁴ = 16,777,216.

This complete space includes all the concepts we have discussed so far. But it also includes concepts like “Positively classify only the examples {Sunny, Warm, High, Strong} and {Sunny, Warm, High, Weak} and reject everything else” or “Negatively classify only the example {Rainy, Cold, High, Strong} and accept everything else.” It includes concepts with no compact representation, just a flat list of what is and isn’t allowed.

That’s the problem with trying to build a “fully general” inductive learner: They can’t learn concepts until they’ve seen every possible example in the instance space.

If we add on more attributes to Days—like the Water temperature, or the Forecast for tomorrow—then the number of possible days will grow exponentially in the number of attributes. But this isn’t a problem with our restricted concept space, because you can narrow down a large space using a logarithmic number of examples.

Let’s say we add the Water: {Warm, Cold} attribute to days, which will make for 48 possible Days and 325 possible concepts. Let’s say that each Day we see is, usually, classified positive by around half of the currently-plausible concepts, and classified negative by the other half. Then when we learn the actual classification of the example, it will cut the space of compatible concepts in half. So it might only take 9 examples (2⁹ = 512) to narrow 325 possible concepts down to one.

Even if Days had forty binary attributes, it should still only take a manageable amount of data to narrow down the possible concepts to one. Sixty-four examples, if each example is classified positive by half the remaining concepts. Assuming, of course, that the actual rule is one we can represent at all!

If you want to think of all the possibilities, well, good luck with that. The space of all possible concepts grows superexponentially in the number of attributes.

By the time you’re talking about data with forty binary attributes, the number of possible examples is past a trillion—but the number of possible concepts is past two-to-the-trillionth-power. To narrow down that superexponential concept space, you’d have to see over a trillion examples before you could say what was In, and what was Out. You’d have to see every possible example, in fact.

That’s with forty binary attributes, mind you. Forty bits, or 5 bytes, to be classified simply “Yes” or “No.” Forty bits implies 2⁴⁰ possible examples, and 2^2⁴⁰ possible concepts that classify those examples as positive or negative.

So, here in the real world, where objects take more than 5 bytes to describe and a trillion examples are not available and there is noise in the training data, we only even think about highly regular concepts. A human mind—or the whole observable universe—is not nearly large enough to consider all the other hypotheses.

From this perspective, learning doesn’t just rely on inductive bias, it is nearly all inductive bias—when you compare the number of concepts ruled out a priori, to those ruled out by mere evidence.

But what has this (you inquire) to do with the proper use of words?

It’s the whole reason that words have intensions as well as extensions.

In the last essay, I concluded:

The way to carve reality at its joints is to draw boundaries around concentrations of unusually high probability density.

I deliberately left out a key qualification in that (slightly edited) statement, because I couldn’t explain it until now. A better statement would be:

The way to carve reality at its joints, is to draw simple boundaries around concentrations of unusually high probability density in Thingspace.

Otherwise you would just gerrymander Thingspace. You would create really odd noncontiguous boundaries that collected the observed examples, examples that couldn’t be described in any shorter message than your observations themselves, and say: “This is what I’ve seen before, and what I expect to see more of in the future.”

In the real world, nothing above the level of molecules repeats itself exactly. Socrates is shaped a lot like all those other humans who were vulnerable to hemlock, but he isn’t shaped exactly like them. So your guess that Socrates is a “human” relies on drawing simple boundaries around the human cluster in Thingspace. Rather than, “Things shaped exactly like [5-megabyte shape specification 1] and with [lots of other characteristics], or exactly like [5-megabyte shape specification 2] and [lots of other characteristics], . . . , are human.”

If you don’t draw simple boundaries around your experiences, you can’t do inference with them. So you try to describe “art” with intensional definitions like “that which is intended to inspire any complex emotion for the sake of inspiring it,” rather than just pointing at a long list of things that are, or aren’t art.

In fact, the above statement about “how to carve reality at its joints” is a bit chicken-and-eggish: You can’t assess the density of actual observations until you’ve already done at least a little carving. And the probability distribution comes from drawing the boundaries, not the other way around—if you already had the probability distribution, you’d have everything necessary for inference, so why would you bother drawing boundaries?

And this suggests another—yes, yet another—reason to be suspicious of the claim that “you can define a word any way you like.” When you consider the superexponential size of Conceptspace, it becomes clear that singling out one particular concept for consideration is an act of no small audacity—not just for us, but for any mind of bounded computing power.

Presenting us with the word “wiggin,” defined as “a black-haired green-eyed person,” without some reason for raising this particular concept to the level of our deliberate attention, is rather like a detective saying: “Well, I haven’t the slightest shred of support one way or the other for who could’ve murdered those orphans . . . not even an intuition, mind you . . . but have we considered John Q. Wiffleheim of 1234 Norkle Rd as a suspect?”

1. Tom M. Mitchell, Machine Learning (McGraw-Hill Science/Engineering/Math, 1997).

177
Conditional Independence, and Naive Bayes

Previously I spoke of mutual information between X and Y, written I(X;Y), which is the difference between the entropy of the joint probability distribution, H(X,Y), and the entropies of the marginal distributions, H(X) + H(Y).

I gave the example of a variable X, having eight states, X₁ through X₈, which are all equally probable if we have not yet encountered any evidence; and a variable Y, with states Y₁ through Y₄, which are all equally probable if we have not yet encountered any evidence. Then if we calculate the marginal entropies H(X) and H(Y), we will find that X has 3 bits of entropy, and Y has 2 bits.

However, we also know that X and Y are both even or both odd; and this is all we know about the relation between them. So for the joint distribution (X,Y) there are only 16 possible states, all equally probable, for a joint entropy of 4 bits. This is a 1-bit entropy defect, compared to 5 bits of entropy if X and Y were independent. This entropy defect is the mutual information—the information that X tells us about Y, or vice versa, so that we are not as uncertain about one after having learned the other.

Suppose, however, that there exists a third variable Z. The variable Z has two states, “even” and “odd,” perfectly correlated to the evenness or oddness of (X,Y). In fact, we’ll suppose that Z is just the question “Are X and Y even or odd?”

If we have no evidence about X and Y, then Z itself necessarily has 1 bit of entropy on the information given. There is 1 bit of mutual information between Z and X, and 1 bit of mutual information between Z and Y. And, as previously noted, 1 bit of mutual information between X and Y. So how much entropy for the whole system (X,Y,Z)? You might naively expect that

H(X,Y,Z) = H(X) + H(Y) + H(Z) - I(X;Z) - I(Z;Y) - I(X;Y),

but this turns out not to be the case.

The joint system (X,Y,Z) only has 16 possible states—since Z is just the question “Are X and Y even or odd?”—so H(X,Y,Z) = 4 bits.

But if you calculate the formula just given, you get

(3 + 2 + 1 - 1 - 1 - 1) bits = 3 bits = WRONG!

Why? Because if you have the mutual information between X and Z, and the mutual information between Z and Y, that may include some of the same mutual information that we’ll calculate exists between X and Y. In this case, for example, knowing that X is even tells us that Z is even, and knowing that Z is even tells us that Y is even, but this is the same information that X would tell us about Y. We double-counted some of our knowledge, and so came up with too little entropy.

The correct formula is (I believe):

H(X,Y,Z) = H(X) + H(Y) + H(Z) - I(X;Z) - I(Z;Y) - I(X;Y|Z).

Here the last term, I(X;Y |Z), means, “the information that X tells us about Y, given that we already know Z.” In this case, X doesn’t tell us anything about Y, given that we already know Z, so the term comes out as zero—and the equation gives the correct answer. There, isn’t that nice?

“No,” you correctly reply, “for you have not told me how to calculate I(X;Y |Z), only given me a verbal argument that it ought to be zero.”

We calculate I(X;Y|Z) just the way you would expect. We know I(X;Y) = H(X) + H(Y) - H(X,Y), so

I(X;Y|Z) = H(X|Z) + H(Y|Z) - H(X,Y|Z).

And now, I suppose, you want to know how to calculate the conditional entropy? Well, the original formula for the entropy is

H(S) = ∑_i{-P(S_i) × log₂(P(S_i))}.

If we then learned a new fact Z₀, our remaining uncertainty about S would be

H(S|Z0) = ∑_i{-P(S_i|Z₀)log₂(P(S_i|Z₀))}.

So if we’re going to learn a new fact Z, but we don’t know which Z yet, then, on average, we expect to be around this uncertain of S afterward:

H(S|Z) = ∑_j{P(Z_j)∑_i{-P(S_i|Z_j)log₂(P(S_i|Z_j))}}

And that’s how one calculates conditional entropies; from which, in turn, we can get the conditional mutual information.

There are all sorts of ancillary theorems here, like

H(X|Y) = H (X,Y) - H(Y)

and

if I(X;Z) = 0 and I(Y;X|Z) = 0 then I(X;Y) = 0,

but I’m not going to go into those.

“But,” you ask, “what does this have to do with the nature of words and their hidden Bayesian structure?”

I am just so unspeakably glad that you asked that question, because I was planning to tell you whether you liked it or not. But first there are a couple more preliminaries.

You will remember—yes, you will remember—that there is a duality between mutual information and Bayesian evidence. Mutual information is positive if and only if the probability of at least some joint events P(x,y) does not equal the product of the probabilities of the separate events P(x)P(y). This, in turn, is exactly equivalent to the condition that Bayesian evidence exists between x and y:

I(X;Y) > 0 ⇒

P(x,y) ≠ P(x)P(y)

P(x,y) / P(y) ≠ P(x)

P(x|y) ≠ P(x).

If you’re conditioning on Z, you just adjust the whole derivation accordingly:

I(X;Y|Z) > 0 ⇒

P(x,y|z) ≠ P(x|z)P(y|z)

P(x,y|z) / P(y|z) ≠ P (x|z)

(P(x,y,z)/P(z)) (P(y,z)P(z)) ≠ P(x|z)

P(x,y,z) / P(y,z) ≠ P(x|z)

P(x|y,z) ≠ P(x|z).

Which last line reads “Even knowing Z, learning Y still changes our beliefs about X.”

Conversely, as in our original case of Z being “even” or “odd,” Z screens off X from Y—that is, if we know that Z is “even,” learning that Y is in state Y₄ tells us nothing more about whether X is X₂, X₄, X₆, or X₈. Or if we know that Z is “odd,” then learning that X is X₅ tells us nothing more about whether Y is Y₁ or Y₃. Learning Z has rendered X and Y conditionally independent.

Conditional independence is a hugely important concept in probability theory—to cite just one example, without conditional independence, the universe would have no structure.

Here, though, I only intend to talk about one particular kind of conditional independence—the case of a central variable that screens off other variables surrounding it, like a central body with tentacles.

Let there be five variables U,V, W, X, and Y; and moreover, suppose that for every pair of these variables, one variable is evidence about the other. If you select U and W, for example, then learning U = U₁ will tell you something you didn’t know before about the probability that W = W₁.

An unmanageable inferential mess? Evidence gone wild? Not necessarily.

Maybe U is “Speaks a language,” V is “Two arms and ten digits,” W is “Wears clothes,” X is “Poisonable by hemlock,” and Y is “Red blood.” Now if you encounter a thing-in-the-world, that might be an apple and might be a rock, and you learn that this thing speaks Chinese, you are liable to assess a much higher probability that it wears clothes; and if you learn that the thing is not poisonable by hemlock, you will assess a somewhat lower probability that it has red blood.

Now some of these rules are stronger than others. There is the case of Fred, who is missing a finger due to a volcano accident, and the case of Barney the Baby who doesn’t speak yet, and the case of Irving the IRCBot who emits sentences but has no blood. So if we learn that a certain thing is not wearing clothes, that doesn’t screen off everything that its speech capability can tell us about its blood color. If the thing doesn’t wear clothes but does talk, maybe it’s Nude Nellie.

This makes the case more interesting than, say, five integer variables that are all odd or all even, but otherwise uncorrelated. In that case, knowing any one of the variables would screen off everything that knowing a second variable could tell us about a third variable.

But here, we have dependencies that don’t go away as soon as we learn just one variable, as the case of Nude Nellie shows. So is it an unmanageable inferential inconvenience?

Fear not! For there may be some sixth variable Z, which, if we knew it, really would screen off every pair of variables from each other. There may be some variable Z—even if we have to construct Z rather than observing it directly—such that:

P(U|V,W,X,Y,Z) = P(U|Z)

P(V|U,W,X,Y,Z) = P(V|Z)

P(W|U,V,X,Y,Z) = P(W|Z)

…

Perhaps, given that a thing is “human,” then the probabilities of it speaking, wearing clothes, and having the standard number of fingers, are all independent. Fred may be missing a finger—but he is no more likely to be a nudist than the next person; Nude Nellie never wears clothes, but knowing this doesn’t make it any less likely that she speaks; and Baby Barney doesn’t talk yet, but is not missing any limbs.

This is called the “Naive Bayes” method, because it usually isn’t quite true, but pretending that it’s true can simplify the living daylights out of your calculations. We don’t keep separate track of the influence of clothed-ness on speech capability given finger number. We just use all the information we’ve observed to keep track of the probability that this thingy is a human (or alternatively, something else, like a chimpanzee or robot) and then use our beliefs about the central class to predict anything we haven’t seen yet, like vulnerability to hemlock.

Any observations of U,V, W, X, and Y just act as evidence for the central class variable Z, and then we use the posterior distribution on Z to make any predictions that need making about unobserved variables in U,V, W, X, and Y.

Sound familiar? It should; see Figure 177.1.

Figure 177.1: Network 2

As a matter of fact, if you use the right kind of neural network units, this “neural network” ends up exactly, mathematically equivalent to Naive Bayes. The central unit just needs a logistic threshold—an S-curve response—and the weights of the inputs just need to match the logarithms of the likelihood ratios, et cetera. In fact, it’s a good guess that this is one of the reasons why logistic response often works so well in neural networks—it lets the algorithm sneak in a little Bayesian reasoning while the designers aren’t looking.

Just because someone is presenting you with an algorithm that they call a “neural network” with buzzwords like “scruffy” and “emergent” plastered all over it, disclaiming proudly that they have no idea how the learned network works—well, don’t assume that their little AI algorithm really is Beyond the Realms of Logic. For this paradigm of adhockery, if it works, will turn out to have Bayesian structure; it may even be exactly equivalent to an algorithm of the sort called “Bayesian.”

Even if it doesn’t look Bayesian, on the surface.

And then you just know that the Bayesians are going to start explaining exactly how the algorithm works, what underlying assumptions it reflects, which environmental regularities it exploits, where it works and where it fails, and even attaching understandable meanings to the learned network weights.

Disappointing, isn’t it?

178
Words as Mental Paintbrush Handles

Suppose I tell you: “It’s the strangest thing: The lamps in this hotel have triangular lightbulbs.”

You may or may not have visualized it—if you haven’t done it yet, do so now—what, in your mind’s eye, does a “triangular lightbulb” look like?

In your mind’s eye, did the glass have sharp edges, or smooth?

When the phrase “triangular lightbulb” first crossed my mind—no, the hotel doesn’t have them—then as best as my introspection could determine, I first saw a pyramidal lightbulb with sharp edges, then (almost immediately) the edges were smoothed, and then my mind generated a loop of flourescent bulb in the shape of a smooth triangle as an alternative.

As far as I can tell, no deliberative/verbal thoughts were involved—just wordless reflex flinch away from the imaginary mental vision of sharp glass, which design problem was solved before I could even think in words.

Believe it or not, for some decades, there was a serious debate about whether people really had mental images in their mind—an actual picture of a chair somewhere—or if people just naively thought they had mental images (having been misled by “introspection,” a very bad forbidden activity), while actually just having a little “chair” label, like a LISP token, active in their brain.

I am trying hard not to say anything like “How spectacularly silly,” because there is always the hindsight effect to consider, but: how spectacularly silly.

This academic paradigm, I think, was mostly a deranged legacy of behaviorism, which denied the existence of thoughts in humans, and sought to explain all human phenomena as “reflex,” including speech. Behaviorism probably deserves its own write at some point, as it was a perversion of rationalism; but this is not that write.

“You call it ‘silly,’” you inquire, “but how do you know that your brain represents visual images? Is it merely that you can close your eyes and see them?”

This question used to be harder to answer, back in the day of the controversy. If you wanted to prove the existence of mental imagery “scientifically,” rather than just by introspection, you had to infer the existence of mental imagery from experiments like this: Show subjects two objects and ask them if one can be rotated into correspondence with the other. The response time is linearly proportional to the angle of rotation required. This is easy to explain if you are actually visualizing the image and continuously rotating it at a constant speed, but hard to explain if you are just checking propositional features of the image.

Today we can actually neuroimage the little pictures in the visual cortex. So, yes, your brain really does represent a detailed image of what it sees or imagines. See Stephen Kosslyn’s Image and Brain: The Resolution of the Imagery Debate.¹

Part of the reason people get in trouble with words, is that they do not realize how much complexity lurks behind words.

Can you visualize a “green dog”? Can you visualize a “cheese apple”?

“Apple” isn’t just a sequence of two syllables or five letters. That’s a shadow. That’s the tip of the tiger’s tail.

Words, or rather the concepts behind them, are paintbrushes—you can use them to draw images in your own mind. Literally draw, if you employ concepts to make a picture in your visual cortex. And by the use of shared labels, you can reach into someone else’s mind, and grasp their paintbrushes to draw pictures in their minds—sketch a little green dog in their visual cortex.

But don’t think that, because you send syllables through the air, or letters through the Internet, it is the syllables or the letters that draw pictures in the visual cortex. That takes some complex instructions that wouldn’t fit in the sequence of letters. “Apple” is 5 bytes, and drawing a picture of an apple from scratch would take more data than that.

“Apple” is merely the tag attached to the true and wordless apple concept, which can paint a picture in your visual cortex, or collide with “cheese,” or recognize an apple when you see one, or taste its archetype in apple pie, maybe even send out the motor behavior for eating an apple . . .

And it’s not as simple as just calling up a picture from memory. Or how would you be able to visualize combinations like a “triangular lightbulb”—imposing triangleness on lightbulbs, keeping the essence of both, even if you’ve never seen such a thing in your life?

Don’t make the mistake the behaviorists made. There’s far more to speech than sound in air. The labels are just pointers—“look in memory area 1387540.” Sooner or later, when you’re handed a pointer, it comes time to dereference it, and actually look in memory area 1387540.

What does a word point to?

1. Stephen M. Kosslyn, Image and Brain: The Resolution of the Imagery Debate (Cambridge, MA: MIT Press, 1994).

179
Variable Question Fallacies

ALBERT: “Every time I’ve listened to a tree fall, it made a sound, so I’ll guess that other trees falling also make sounds. I don’t believe the world changes around when I’m not looking.”

BARRY: “Wait a minute. If no one hears it, how can it be a sound?”

While writing the dialogue of Albert and Barry in their dispute over whether a falling tree in a deserted forest makes a sound, I sometimes found myself losing empathy with my characters. I would start to lose the gut feel of why anyone would ever argue like that, even though I’d seen it happen many times.

On these occasions, I would repeat to myself, “Either the falling tree makes a sound, or it does not!” to restore my borrowed sense of indignation.

(P or ¬P) is not always a reliable heuristic, if you substitute arbitrary English sentences for P. “This sentence is false” cannot be consistently viewed as true or false. And then there’s the old classic, “Have you stopped beating your wife?”

Now if you are a mathematician, and one who believes in classical (rather than intuitionistic) logic, there are ways to continue insisting that (P or ¬P) is a theorem: for example, saying that “This sentence is false” is not a sentence.

But such resolutions are subtle, which suffices to demonstrate a need for subtlety. You cannot just bull ahead on every occasion with “Either it does or it doesn’t!”

So does the falling tree make a sound, or not, or . . . ?

Surely, 2 + 2 = X or it does not? Well, maybe, if it’s really the same X, the same 2, and the same + and = . If X evaluates to 5 on some occasions and 4 on another, your indignation may be misplaced.

To even begin claiming that (P or ¬P) ought to be a necessary truth, the symbol P must stand for exactly the same thing in both halves of the dilemma. “Either the fall makes a sound, or not!”—but if Albert::sound is not the same as Barry::sound, there is nothing paradoxical about the tree making an Albert::sound but not a Barry::sound.

(The :: idiom is something I picked up in my C++ days for avoiding namespace collisions. If you’ve got two different packages that define a class Sound, you can write Package1::Sound to specify which Sound you mean. The idiom is not widely known, I think; which is a pity, because I often wish I could use it in writing.)

The variability may be subtle: Albert and Barry may carefully verify that it is the same tree, in the same forest, and the same occasion of falling, just to ensure that they really do have a substantive disagreement about exactly the same event. And then forget to check that they are matching this event against exactly the same concept.

Think about the grocery store that you visit most often: Is it on the left side of the street, or the right? But of course there is no “the left side” of the street, only your left side, as you travel along it from some particular direction. Many of the words we use are really functions of implicit variables supplied by context.

It’s actually one heck of a pain, requiring one heck of a lot of work, to handle this kind of problem in an Artificial Intelligence program intended to parse language—the phenomenon going by the name of “speaker deixis.”

“Martin told Bob the building was on his left.” But “left” is a function-word that evaluates with a speaker-dependent variable invisibly grabbed from the surrounding context. Whose “left” is meant, Bob’s or Martin’s?

The variables in a variable question fallacy often aren’t neatly labeled—it’s not as simple as “Say, do you think Z + 2 equals 6?”

If a namespace collision introduces two different concepts that look like “the same concept” because they have the same name—or a map compression introduces two different events that look like the same event because they don’t have separate mental files—or the same function evaluates in different contexts—then reality itself becomes protean, changeable. At least that’s what the algorithm feels like from inside. Your mind’s eye sees the map, not the territory directly.

If you have a question with a hidden variable, that evaluates to different expressions in different contexts, it feels like reality itself is unstable—what your mind’s eye sees, shifts around depending on where it looks.

This often confuses undergraduates (and postmodernist professors) who discover a sentence with more than one interpretation; they think they have discovered an unstable portion of reality.

“Oh my gosh! ‘The Sun goes around the Earth’ is true for Hunga Huntergatherer, but for Amara Astronomer, ‘The Sun goes around the Earth’ is false! There is no fixed truth!” The deconstruction of this sophomoric nitwittery is left as an exercise to the reader.

And yet, even I initially found myself writing “If X is 5 on some occasions and 4 on another, the sentence ‘2 + 2 = X’ may have no fixed truth-value.” There is not one sentence with a variable truth-value. “2 + 2 = X” has no truth-value. It is not a proposition, not yet, not as mathematicians define proposition-ness, any more than “2 + 2 =” is a proposition, or “Fred jumped over the” is a grammatical sentence.

But this fallacy tends to sneak in, even when you allegedly know better, because, well, that’s how the algorithm feels from inside.

180
37 Ways That Words Can Be Wrong

Some reader is bound to declare that a better title for this essay would be “37 Ways That You Can Use Words Unwisely,” or “37 Ways That Suboptimal Use Of Categories Can Have Negative Side Effects On Your Cognition.”

But one of the primary lessons of this gigantic list is that saying “There’s no way my choice of X can be ‘wrong’” is nearly always an error in practice, whatever the theory. You can always be wrong. Even when it’s theoretically impossible to be wrong, you can still be wrong. There is never a Get Out of Jail Free card for anything you do. That’s life.

Besides, I can define the word “wrong” to mean anything I like—it’s not like a word can be wrong.

Personally, I think it quite justified to use the word “wrong” when:

A word fails to connect to reality in the first place. Is Socrates a framster? Yes or no? (The Parable of the Dagger)

Your argument, if it worked, could coerce reality to go a different way by choosing a different word definition. Socrates is a human, and humans, by definition, are mortal. So if you defined humans to not be mortal, would Socrates live forever? (The Parable of Hemlock)

You try to establish any sort of empirical proposition as being true “by definition.” Socrates is a human, and humans, by definition, are mortal. So is it a logical truth if we empirically predict that Socrates should keel over if he drinks hemlock? It seems like there are logically possible, non-self-contradictory worlds where Socrates doesn’t keel over—where he’s immune to hemlock by a quirk of biochemistry, say. Logical truths are true in all possible worlds, and so never tell you which possible world you live in—and anything you can establish “by definition” is a logical truth. (The Parable of Hemlock)

You unconsciously slap the conventional label on something, without actually using the verbal definition you just gave. You know perfectly well that Bob is “human,” even though, by your definition, you can never call Bob “human” without first observing him to be mortal. (The Parable of Hemlock)

The act of labeling something with a word disguises a challengable inductive inference you are making. If the last 11 egg-shaped objects drawn have been blue, and the last 8 cubes drawn have been red, it is a matter of induction to say this rule will hold in the future. But if you call the blue eggs “bleggs” and the red cubes “rubes,” you may reach into the barrel, feel an egg shape, and think “Oh, a blegg.” (Words as Hidden Inferences)

You try to define a word using words, in turn defined with ever-more-abstract words, without being able to point to an example. “What is red?” “Red is a color.” “What’s a color?” “It’s a property of a thing.” “What’s a thing? What’s a property?” It never occurs to you to point to a stop sign and an apple. (Extensions and Intensions)

The extension doesn’t match the intension. We aren’t consciously aware of our identification of a red light in the sky as “Mars,” which will probably happen regardless of your attempt to define “Mars” as “The God of War.” (Extensions and Intensions)

Your verbal definition doesn’t capture more than a tiny fraction of the category’s shared characteristics, but you try to reason as if it does. When the philosophers of Plato’s Academy claimed that the best definition of a human was a “featherless biped,” Diogenes the Cynic is said to have exhibited a plucked chicken and declared “Here is Plato’s Man.” The Platonists promptly changed their definition to “a featherless biped with broad nails.” (Similarity Clusters)

You try to treat category membership as all-or-nothing, ignoring the existence of more and less typical subclusters. Ducks and penguins are less typical birds than robins and pigeons. Interestingly, a between-groups experiment showed that subjects thought a disease was more likely to spread from robins to ducks on an island, than from ducks to robins. (Typicality and Asymmetrical Similarity)

A verbal definition works well enough in practice to point out the intended cluster of similar things, but you nitpick exceptions. Not every human has ten fingers, or wears clothes, or uses language; but if you look for an empirical cluster of things which share these characteristics, you’ll get enough information that the occasional nine-fingered human won’t fool you. (The Cluster Structure of Thingspace)

You ask whether something “is” or “is not” a category member but can’t name the question you really want answered. What is a “man”? Is Barney the Baby Boy a “man”? The “correct” answer may depend considerably on whether the query you really want answered is “Would hemlock be a good thing to feed Barney?” or “Will Barney make a good husband?” (Disguised Queries)

You treat intuitively perceived hierarchical categories like the only correct way to parse the world, without realizing that other forms of statistical inference are possible even though your brain doesn’t use them. It’s much easier for a human to notice whether an object is a “blegg” or “rube”; than for a human to notice that red objects never glow in the dark, but red furred objects have all the other characteristics of bleggs. Other statistical algorithms work differently. (Neural Categories)

You talk about categories as if they are manna fallen from the Platonic Realm, rather than inferences implemented in a real brain. The ancient philosophers said “Socrates is a man,” not, “My brain perceptually classifies Socrates as a match against the ‘human’ concept.” (How An Algorithm Feels From Inside)

You argue about a category membership even after screening off all questions that could possibly depend on a category-based inference. After you observe that an object is blue, egg-shaped, furred, flexible, opaque, luminescent, and palladium-containing, what’s left to ask by arguing, “Is it a blegg?” But if your brain’s categorizing neural network contains a (metaphorical) central unit corresponding to the inference of blegg-ness, it may still feel like there’s a leftover question. (How An Algorithm Feels From Inside)

You allow an argument to slide into being about definitions, even though it isn’t what you originally wanted to argue about. If, before a dispute started about whether a tree falling in a deserted forest makes a “sound,” you asked the two soon-to-be arguers whether they thought a “sound” should be defined as “acoustic vibrations” or “auditory experiences,” they’d probably tell you to flip a coin. Only after the argument starts does the definition of a word become politically charged. (Disputing Definitions)

You think a word has a meaning, as a property of the word itself; rather than there being a label that your brain associates to a particular concept. When someone shouts “Yikes! A tiger!,” evolution would not favor an organism that thinks, “Hm . . . I have just heard the syllables ‘Tie’ and ‘Grr’ which my fellow tribemembers associate with their internal analogues of my own tiger concept and which aiiieeee CRUNCH CRUNCH GULP.” So the brain takes a shortcut, and it seems that the meaning of tigerness is a property of the label itself. People argue about the correct meaning of a label like “sound.” (Feel the Meaning)

You argue over the meanings of a word, even after all sides understand perfectly well what the other sides are trying to say. The human ability to associate labels to concepts is a tool for communication. When people want to communicate, we’re hard to stop; if we have no common language, we’ll draw pictures in sand. When you each understand what is in the other’s mind, you are done. (The Argument From Common Usage)

You pull out a dictionary in the middle of an empirical or moral argument. Dictionary editors are historians of usage, not legislators of language. If the common definition contains a problem—if “Mars” is defined as the God of War, or a “dolphin” is defined as a kind of fish, or “Negroes” are defined as a separate category from humans, the dictionary will reflect the standard mistake. (The Argument From Common Usage)

You pull out a dictionary in the middle of any argument ever. Seriously, what the heck makes you think that dictionary editors are an authority on whether “atheism” is a “religion” or whatever? If you have any substantive issue whatsoever at stake, do you really think dictionary editors have access to ultimate wisdom that settles the argument? (The Argument From Common Usage)

You defy common usage without a reason, making it gratuitously hard for others to understand you. Fast stand up plutonium, with bagels without handle. (The Argument From Common Usage)

You use complex renamings to create the illusion of inference. Is a “human” defined as a “mortal featherless biped”? Then write: “All [mortal featherless bipeds] are mortal; Socrates is a [mortal featherless biped]; therefore, Socrates is mortal.” Looks less impressive that way, doesn’t it? (Empty Labels)

You get into arguments that you could avoid if you just didn’t use the word. If Albert and Barry aren’t allowed to use the word “sound,” then Albert will have to say “A tree falling in a deserted forest generates acoustic vibrations,” and Barry will say “A tree falling in a deserted forest generates no auditory experiences.” When a word poses a problem, the simplest solution is to eliminate the word and its synonyms. (Taboo Your Words)

The existence of a neat little word prevents you from seeing the details of the thing you’re trying to think about. What actually goes on in schools once you stop calling it “education”? What’s a degree, once you stop calling it a “degree”? If a coin lands “heads,” what’s its radial orientation? What is “truth,” if you can’t say “accurate” or “correct” or “represent” or “reflect” or “semantic” or “believe” or “knowledge” or “map” or “real” or any other simple term? (Replace the Symbol with the Substance)

You have only one word, but there are two or more different things-in-reality, so that all the facts about them get dumped into a single undifferentiated mental bucket. It’s part of a detective’s ordinary work to observe that Carol wore red last night, or that she has black hair; and it’s part of a detective’s ordinary work to wonder if maybe Carol dyes her hair. But it takes a subtler detective to wonder if there are two Carols, so that the Carol who wore red is not the same as the Carol who had black hair. (Fallacies of Compression)

You see patterns where none exist, harvesting other characteristics from your definitions even when there is no similarity along that dimension. In Japan, it is thought that people of blood type A are earnest and creative, blood type Bs are wild and cheerful, blood type Os are agreeable and sociable, and blood type ABs are cool and controlled. (Categorizing Has Consequences)

You try to sneak in the connotations of a word, by arguing from a definition that doesn’t include the connotations. A “wiggin” is defined in the dictionary as a person with green eyes and black hair. The word “wiggin” also carries the connotation of someone who commits crimes and launches cute baby squirrels, but that part isn’t in the dictionary. So you point to someone and say: “Green eyes? Black hair? See, told you he’s a wiggin! Watch, next he’s going to steal the silverware.” (Sneaking in Connotations)

You claim “X, by definition, is a Y!” On such occasions you’re almost certainly trying to sneak in a connotation of Y that wasn’t in your given definition. You define “human” as a “featherless biped,” and point to Socrates and say, “No feathers—two legs—he must be human!” But what you really care about is something else, like mortality. If what was in dispute was Socrates’s number of legs, the other fellow would just reply, “Whaddaya mean, Socrates’s got two legs? That’s what we’re arguing about in the first place!” (Arguing “By Definition”)

You claim “Ps, by definition, are Qs!” If you see Socrates out in the field with some biologists, gathering herbs that might confer resistance to hemlock, there’s no point in arguing “Men, by definition, are mortal!” The main time you feel the need to tighten the vise by insisting that something is true “by definition” is when there’s other information that calls the default inference into doubt. (Arguing “By Definition”)

You try to establish membership in an empirical cluster “by definition.” You wouldn’t feel the need to say, “Hinduism, by definition, is a religion!” because, well, of course Hinduism is a religion. It’s not just a religion “by definition,” it’s, like, an actual religion. Atheism does not resemble the central members of the “religion” cluster, so if it wasn’t for the fact that atheism is a religion by definition, you might go around thinking that atheism wasn’t a religion. That’s why you’ve got to crush all opposition by pointing out that “Atheism is a religion” is true by definition, because it isn’t true any other way. (Arguing “By Definition”)

Your definition draws a boundary around things that don’t really belong together. You can claim, if you like, that you are defining the word “fish” to refer to salmon, guppies, sharks, dolphins, and trout, but not jellyfish or algae. You can claim, if you like, that this is merely a list, and there is no way a list can be “wrong.” Or you can stop playing games and admit that you made a mistake and that dolphins don’t belong on the fish list. (Where to Draw the Boundary?)

You use a short word for something that you won’t need to describe often, or a long word for something you’ll need to describe often. This can result in inefficient thinking, or even misapplications of Occam’s Razor, if your mind thinks that short sentences sound “simpler.” Which sounds more plausible, “God did a miracle” or “A supernatural universe-creating entity temporarily suspended the laws of physics”? (Entropy, and Short Codes)

You draw your boundary around a volume of space where there is no greater-than-usual density, meaning that the associated word does not correspond to any performable Bayesian inferences. Since green-eyed people are not more likely to have black hair, or vice versa, and they don’t share any other characteristics in common, why have a word for “wiggin”? (Mutual Information, and Density in Thingspace)

You draw an unsimple boundary without any reason to do so. The act of defining a word to refer to all humans, except black people, seems kind of suspicious. If you don’t present reasons to draw that particular boundary, trying to create an “arbitrary” word in that location is like a detective saying: “Well, I haven’t the slightest shred of support one way or the other for who could’ve murdered those orphans . . . but have we considered John Q. Wiffleheim as a suspect?” (Superexponential Conceptspace, and Simple Words)

You use categorization to make inferences about properties that don’t have the appropriate empirical structure, namely, conditional independence given knowledge of the class, to be well-approximated by Naive Bayes. No way am I trying to summarize this one. Just read the essay. (Conditional Independence, and Naive Bayes)

You think that words are like tiny little LISP symbols in your mind, rather than words being labels that act as handles to direct complex mental paintbrushes that can paint detailed pictures in your sensory workspace. Visualize a “triangular lightbulb.” What did you see? (Words as Mental Paintbrush Handles)

You use a word that has different meanings in different places as though it meant the same thing on each occasion, possibly creating the illusion of something protean and shifting. “Martin told Bob the building was on his left.” But “left” is a function-word that evaluates with a speaker-dependent variable grabbed from the surrounding context. Whose “left” is meant, Bob’s or Martin’s? (Variable Question Fallacies)

You think that definitions can’t be “wrong,” or that “I can define a word any way I like!” This kind of attitude teaches you to indignantly defend your past actions, instead of paying attention to their consequences, or fessing up to your mistakes. (37 Ways That Suboptimal Use Of Categories Can Have Negative Side Effects On Your Cognition)

Everything you do in the mind has an effect, and your brain races ahead unconsciously without your supervision.

Saying “Words are arbitrary; I can define a word any way I like” makes around as much sense as driving a car over thin ice with the accelerator floored and saying, “Looking at this steering wheel, I can’t see why one radial angle is special—so I can turn the steering wheel any way I like.”

If you’re trying to go anywhere, or even just trying to survive, you had better start paying attention to the three or six dozen optimality criteria that control how you use words, definitions, categories, classes, boundaries, labels, and concepts.

Interlude
An Intuitive Explanation of Bayes’s Theorem

Editor’s Note: This is an abridgement of the original version of this essay, which contained many interactive elements.

Your friends and colleagues are talking about something called “Bayes’s Theorem” or “Bayes’s Rule,” or something called Bayesian reasoning. They sound really enthusiastic about it, too, so you google and find a web page about Bayes’s Theorem and . . .

It’s this equation. That’s all. Just one equation. The page you found gives a definition of it, but it doesn’t say what it is, or why it’s useful, or why your friends would be interested in it. It looks like this random statistics thing.

Why does a mathematical concept generate this strange enthusiasm in its students? What is the so-called Bayesian Revolution now sweeping through the sciences, which claims to subsume even the experimental method itself as a special case? What is the secret that the adherents of Bayes know? What is the light that they have seen?

Soon you will know. Soon you will be one of us.

While there are a few existing online explanations of Bayes’s Theorem, my experience with trying to introduce people to Bayesian reasoning is that the existing online explanations are too abstract. Bayesian reasoning is very counterintuitive. People do not employ Bayesian reasoning intuitively, find it very difficult to learn Bayesian reasoning when tutored, and rapidly forget Bayesian methods once the tutoring is over. This holds equally true for novice students and highly trained professionals in a field. Bayesian reasoning is apparently one of those things which, like quantum mechanics or the Wason Selection Test, is inherently difficult for humans to grasp with our built-in mental faculties.

Or so they claim. Here you will find an attempt to offer an intuitive explanation of Bayesian reasoning—an excruciatingly gentle introduction that invokes all the human ways of grasping numbers, from natural frequencies to spatial visualization. The intent is to convey, not abstract rules for manipulating numbers, but what the numbers mean, and why the rules are what they are (and cannot possibly be anything else). When you are finished reading this, you will see Bayesian problems in your dreams.

And let’s begin.

Here’s a story problem about a situation that doctors often encounter:

1% of women at age forty who participate in routine screening have breast cancer. 80% of women with breast cancer will get positive mammographies. 9.6% of women without breast cancer will also get positive mammographies. A woman in this age group had a positive mammography in a routine screening. What is the probability that she actually has breast cancer?

What do you think the answer is? If you haven’t encountered this kind of problem before, please take a moment to come up with your own answer before continuing.

Next, suppose I told you that most doctors get the same wrong answer on this problem—usually, only around 15% of doctors get it right. (“Really? 15%? Is that a real number, or an urban legend based on an Internet poll?” It’s a real number. See Casscells, Schoenberger, and Graboys 1978;¹ Eddy 1982;² Gigerenzer and Hoffrage 1995;³ and many other studies. It’s a surprising result which is easy to replicate, so it’s been extensively replicated.)

On the story problem above, most doctors estimate the probability to be between 70% and 80%, which is wildly incorrect.

Here’s an alternate version of the problem on which doctors fare somewhat better:

10 out of 1,000 women at age forty who participate in routine screening have breast cancer. 800 out of 1,000 women with breast cancer will get positive mammographies. 96 out of 1,000 women without breast cancer will also get positive mammographies. If 1,000 women in this age group undergo a routine screening, about what fraction of women with positive mammographies will actually have breast cancer?

And finally, here’s the problem on which doctors fare best of all, with 46%—nearly half—arriving at the correct answer:

100 out of 10,000 women at age forty who participate in routine screening have breast cancer. 80 of every 100 women with breast cancer will get a positive mammography. 950 out of 9,900 women without breast cancer will also get a positive mammography. If 10,000 women in this age group undergo a routine screening, about what fraction of women with positive mammographies will actually have breast cancer?

The correct answer is 7.8%, obtained as follows: Out of 10,000 women, 100 have breast cancer; 80 of those 100 have positive mammographies. From the same 10,000 women, 9,900 will not have breast cancer and of those 9,900 women, 950 will also get positive mammographies. This makes the total number of women with positive mammographies 950 + 80 or 1,030. Of those 1,030 women with positive mammographies, 80 will have cancer. Expressed as a proportion, this is 80/1,030 or 0.07767 or 7.8%.

To put it another way, before the mammography screening, the 10,000 women can be divided into two groups:

Group 1: 100 women with breast cancer.
Group 2: 9,900 women without breast cancer.

Summing these two groups gives a total of 10,000 patients, confirming that none have been lost in the math. After the mammography, the women can be divided into four groups:

Group A: 80 women with breast cancer and a positive mammography.
Group B: 20 women with breast cancer and a negative mammography.
Group C: 950 women without breast cancer and a positive mammography.
Group D: 8,950 women without breast cancer and a negative mammography.

The sum of groups A and B, the groups with breast cancer, corresponds to group 1; and the sum of groups C and D, the groups without breast cancer, corresponds to group 2. If you administer a mammography to 10,000 patients, then out of the 1,030 with positive mammographies, eighty of those positive-mammography patients will have cancer. This is the correct answer, the answer a doctor should give a positive-mammography patient if she asks about the chance she has breast cancer; if thirteen patients ask this question, roughly one out of those thirteen will have cancer.

The most common mistake is to ignore the original fraction of women with breast cancer, and the fraction of women without breast cancer who receive false positives, and focus only on the fraction of women with breast cancer who get positive results. For example, the vast majority of doctors in these studies seem to have thought that if around 80% of women with breast cancer have positive mammographies, then the probability of a women with a positive mammography having breast cancer must be around 80%.

Figuring out the final answer always requires all three pieces of information—the percentage of women with breast cancer, the percentage of women without breast cancer who receive false positives, and the percentage of women with breast cancer who receive (correct) positives.

The original proportion of patients with breast cancer is known as the prior probability. The chance that a patient with breast cancer gets a positive mammography, and the chance that a patient without breast cancer gets a positive mammography, are known as the two conditional probabilities. Collectively, this initial information is known as the priors. The final answer—the estimated probability that a patient has breast cancer, given that we know she has a positive result on her mammography—is known as the revised probability or the posterior probability. What we’ve just seen is that the posterior probability depends in part on the prior probability.

To see that the final answer always depends on the original fraction of women with breast cancer, consider an alternate universe in which only one woman out of a million has breast cancer. Even if mammography in this world detects breast cancer in 8 out of 10 cases, while returning a false positive on a woman without breast cancer in only 1 out of 10 cases, there will still be a hundred thousand false positives for every real case of cancer detected. The original probability that a woman has cancer is so extremely low that, although a positive result on the mammography does increase the estimated probability, the probability isn’t increased to certainty or even “a noticeable chance”; the probability goes from 1:1,000,000 to 1:100,000.

What this demonstrates is that the mammography result doesn’t replace your old information about the patient’s chance of having cancer; the mammography slides the estimated probability in the direction of the result. A positive result slides the original probability upward; a negative result slides the probability downward. For example, in the original problem where 1% of the women have cancer, 80% of women with cancer get positive mammographies, and 9.6% of women without cancer get positive mammographies, a positive result on the mammography slides the 1% chance upward to 7.8%.

Most people encountering problems of this type for the first time carry out the mental operation of replacing the original 1% probability with the 80% probability that a woman with cancer gets a positive mammography. It may seem like a good idea, but it just doesn’t work. “The probability that a woman with a positive mammography has breast cancer” is not at all the same thing as “the probability that a woman with breast cancer has a positive mammography”; they are as unlike as apples and cheese.

Q. Why did the Bayesian reasoner cross the road?

A. You need more information to answer this question.

Suppose that a barrel contains many small plastic eggs. Some eggs are painted red and some are painted blue. 40% of the eggs in the bin contain pearls, and 60% contain nothing. 30% of eggs containing pearls are painted blue, and 10% of eggs containing nothing are painted blue. What is the probability that a blue egg contains a pearl? For this example the arithmetic is simple enough that you may be able to do it in your head, and I would suggest trying to do so.

A more compact way of specifying the problem:

P(pearl) = 40%

P(blue|pearl) = 30%

P(blue|¬pearl) = 10%

P(pearl|blue) = ?

The symbol “¬” is shorthand for “not,” so ¬pearl reads “not pearl.”

The notation P(blue|pearl) is shorthand for “the probability of blue given pearl” or “the probability that an egg is painted blue, given that the egg contains a pearl.” The item on the right side is what you already know or the premise, and the item on the left side is the implication or conclusion. If we have P(blue|pearl) = 30%, and we already know that some egg contains a pearl, then we can conclude there is a 30% chance that the egg is painted blue. Thus, the final fact we’re looking for—“the chance that a blue egg contains a pearl” or “the probability that an egg contains a pearl, if we know the egg is painted blue”—reads P(pearl|blue).

40% of the eggs contain pearls, and 60% of the eggs contain nothing. 30% of the eggs containing pearls are painted blue, so 12% of the eggs altogether contain pearls and are painted blue. 10% of the eggs containing nothing are painted blue, so altogether 6% of the eggs contain nothing and are painted blue. A total of 18% of the eggs are painted blue, and a total of 12% of the eggs are painted blue and contain pearls, so the chance a blue egg contains a pearl is 12/18 or 2/3 or around 67%.

As before, we can see the necessity of all three pieces of information by considering extreme cases. In a (large) barrel in which only one egg out of a thousand contains a pearl, knowing that an egg is painted blue slides the probability from 0.1% to 0.3% (instead of sliding the probability from 40% to 67%). Similarly, if 999 out of 1,000 eggs contain pearls, knowing that an egg is blue slides the probability from 99.9% to 99.966%; the probability that the egg does not contain a pearl goes from 1/1,000 to around 1/3,000.

On the pearl-egg problem, most respondents unfamiliar with Bayesian reasoning would probably respond that the probability a blue egg contains a pearl is 30%, or perhaps 20% (the 30% chance of a true positive minus the 10% chance of a false positive). Even if this mental operation seems like a good idea at the time, it makes no sense in terms of the question asked. It’s like the experiment in which you ask a second-grader: “If eighteen people get on a bus, and then seven more people get on the bus, how old is the bus driver?” Many second-graders will respond: “Twenty-five.” They understand when they’re being prompted to carry out a particular mental procedure, but they haven’t quite connected the procedure to reality. Similarly, to find the probability that a woman with a positive mammography has breast cancer, it makes no sense whatsoever to replace the original probability that the woman has cancer with the probability that a woman with breast cancer gets a positive mammography. Neither can you subtract the probability of a false positive from the probability of the true positive. These operations are as wildly irrelevant as adding the number of people on the bus to find the age of the bus driver.

A study by Gigerenzer and Hoffrage in 1995 showed that some ways of phrasing story problems are much more evocative of correct Bayesian reasoning.⁴ The least evocative phrasing used probabilities. A slightly more evocative phrasing used frequencies instead of probabilities; the problem remained the same, but instead of saying that 1% of women had breast cancer, one would say that 1 out of 100 women had breast cancer, that 80 out of 100 women with breast cancer would get a positive mammography, and so on. Why did a higher proportion of subjects display Bayesian reasoning on this problem? Probably because saying “1 out of 100 women” encourages you to concretely visualize X women with cancer, leading you to visualize X women with cancer and a positive mammography, etc.

The most effective presentation found so far is what’s known as natural frequencies—saying that 40 out of 100 eggs contain pearls, 12 out of 40 eggs containing pearls are painted blue, and 6 out of 60 eggs containing nothing are painted blue. A natural frequencies presentation is one in which the information about the prior probability is included in presenting the conditional probabilities. If you were just learning about the eggs’ conditional probabilities through natural experimentation, you would—in the course of cracking open a hundred eggs—crack open around 40 eggs containing pearls, of which 12 eggs would be painted blue, while cracking open 60 eggs containing nothing, of which about 6 would be painted blue. In the course of learning the conditional probabilities, you’d see examples of blue eggs containing pearls about twice as often as you saw examples of blue eggs containing nothing.

Unfortunately, while natural frequencies are a step in the right direction, it probably won’t be enough. When problems are presented in natural frequencies, the proportion of people using Bayesian reasoning rises to around half. A big improvement, but not big enough when you’re talking about real doctors and real patients.

Q. How can I find the priors for a problem?
A. Many commonly used priors are listed in the Handbook of Chemistry and Physics.

Q. Where do priors originally come from?
A. Never ask that question.

Q. Uh huh. Then where do scientists get their priors?
A. Priors for scientific problems are established by annual vote of the AAAS. In recent years the vote has become fractious and controversial, with widespread acrimony, factional polarization, and several outright assassinations. This may be a front for infighting within the Bayes Council, or it may be that the disputants have too much spare time. No one is really sure.

Q. I see. And where does everyone else get their priors?
A. They download their priors from Kazaa.

Q. What if the priors I want aren’t available on Kazaa?
A. There’s a small, cluttered antique shop in a back alley of San Francisco’s Chinatown. Don’t ask about the bronze rat.

Actually, priors are true or false just like the final answer—they reflect reality and can be judged by comparing them against reality. For example, if you think that 920 out of 10,000 women in a sample have breast cancer, and the actual number is 100 out of 10,000, then your priors are wrong. For our particular problem, the priors might have been established by three studies—a study on the case histories of women with breast cancer to see how many of them tested positive on a mammography, a study on women without breast cancer to see how many of them test positive on a mammography, and an epidemiological study on the prevalence of breast cancer in some specific demographic.

The probability P(A,B) is the same as P(B,A), but P(A|B) is not the same thing as P(B|A), and P(A,B) is completely different from P(A|B). It’s a common confusion to mix up some or all of these quantities.

To get acquainted with all the relationships between them, we’ll play “follow the degrees of freedom.” For example, the two quantities P(cancer) and P(¬cancer) have one degree of freedom between them, because of the general law P(A) + P(¬A) = 1. If you know that P(¬cancer) = 0.99, you can obtain P(cancer) = 1 - P(¬cancer) = 0.01.

The quantities P(positive|cancer) and P(¬positive|cancer) also have only one degree of freedom between them; either a woman with breast cancer gets a positive mammography or she doesn’t. On the other hand, P(positive|cancer) and P(positive|¬cancer) have two degrees of freedom. You can have a mammography test that returns positive for 80% of cancer patients and 9.6% of healthy patients, or that returns positive for 70% of cancer patients and 2% of healthy patients, or even a health test that returns “positive” for 30% of cancer patients and 92% of healthy patients. The two quantities, the output of the mammography test for cancer patients and the output of the mammography test for healthy patients, are in mathematical terms independent; one cannot be obtained from the other in any way, and so they have two degrees of freedom between them.

What about P(positive, cancer), P(positive|cancer), and P(cancer)? Here we have three quantities; how many degrees of freedom are there? In this case the equation that must hold is

P(positive, cancer) = P(positive|cancer) × P(cancer).

This equality reduces the degrees of freedom by one. If we know the fraction of patients with cancer, and the chance that a cancer patient has a positive mammography, we can deduce the fraction of patients who have breast cancer and a positive mammography by multiplying.

Similarly, if we know the number of patients with breast cancer and positive mammographies, and also the number of patients with breast cancer, we can estimate the chance that a woman with breast cancer gets a positive mammography by dividing: P(positive|cancer) = P(positive, cancer)∕P(cancer). In fact, this is exactly how such medical diagnostic tests are calibrated; you do a study on 8,520 women with breast cancer and see that there are 6,816 (or thereabouts) women with breast cancer and positive mammographies, then divide 6,816 by 8,520 to find that 80% of women with breast cancer had positive mammographies. (Incidentally, if you accidentally divide 8,520 by 6,816 instead of the other way around, your calculations will start doing strange things, such as insisting that 125% of women with breast cancer and positive mammographies have breast cancer. This is a common mistake in carrying out Bayesian arithmetic, in my experience.) And finally, if you know P(positive, cancer) and P(positive|cancer), you can deduce how many cancer patients there must have been originally. There are two degrees of freedom shared out among the three quantities; if we know any two, we can deduce the third.

How about P(positive), P(positive, cancer), and P(positive,¬cancer)? Again there are only two degrees of freedom among these three variables. The equation occupying the extra degree of freedom is

P(positive) = P(positive, cancer) + P(positive,¬cancer).

This is how P(positive) is computed to begin with; we figure out the number of women with breast cancer who have positive mammographies, and the number of women without breast cancer who have positive mammographies, then add them together to get the total number of women with positive mammographies. It would be very strange to go out and conduct a study to determine the number of women with positive mammographies—just that one number and nothing else—but in theory you could do so. And if you then conducted another study and found the number of those women who had positive mammographies and breast cancer, you would also know the number of women with positive mammographies and no breast cancer—either a woman with a positive mammography has breast cancer or she doesn’t. In general, P(A,B) + P(A,¬B) = P(A). Symmetrically, P(A,B) + P(¬A,B) = P(B).

What about P(positive, cancer), P(positive,¬cancer), P(¬positive, cancer), and P(¬positive,¬cancer)? You might at first be tempted to think that there are only two degrees of freedom for these four quantities—that you can, for example, get P(positive,¬cancer) by multiplying P(positive) × P(¬cancer), and thus that all four quantities can be found given only the two quantities P(positive) and P(cancer). This is not the case! P(positive,¬cancer) = P(positive) × P(¬cancer) only if the two probabilities are statistically independent—if the chance that a woman has breast cancer has no bearing on whether she has a positive mammography. This amounts to requiring that the two conditional probabilities be equal to each other—a requirement which would eliminate one degree of freedom. If you remember that these four quantities are the groups A, B, C, and D, you can look over those four groups and realize that, in theory, you can put any number of people into the four groups. If you start with a group of 80 women with breast cancer and positive mammographies, there’s no reason why you can’t add another group of 500 women with breast cancer and negative mammographies, followed by a group of 3 women without breast cancer and negative mammographies, and so on. So now it seems like the four quantities have four degrees of freedom. And they would, except that in expressing them as probabilities, we need to normalize them to fractions of the complete group, which adds the constraint that P(positive, cancer)+P(positive,¬cancer)+P(¬positive, cancer)+P(¬positive,¬cancer) = 1. This equation takes up one degree of freedom, leaving three degrees of freedom among the four quantities. If you specify the fractions of women in groups A, B, and D, you can deduce the fraction of women in group C.

Given the four groups A, B, C, and D, it is very straightforward to compute everything else:

P(cancer) = (A + B) / (A + B + C + D)

P(¬positive|cancer) = B / (A + B),

and so on. Since {A,B,C,D} contains three degrees of freedom, it follows that the entire set of probabilities relating cancer rates to test results contains only three degrees of freedom. Remember that in our problems we always needed three pieces of information—the prior probability and the two conditional probabilities—which, indeed, have three degrees of freedom among them. Actually, for Bayesian problems, any three quantities with three degrees of freedom between them should logically specify the entire problem.

The probability that a test gives a true positive divided by the probability that a test gives a false positive is known as the likelihood ratio of that test. The likelihood ratio for a positive result summarizes how much a positive result will slide the prior probability. Does the likelihood ratio of a medical test then sum up everything there is to know about the usefulness of the test?

No, it does not! The likelihood ratio sums up everything there is to know about the meaning of a positive result on the medical test, but the meaning of a negative result on the test is not specified, nor is the frequency with which the test is useful. For example, a mammography with a hit rate of 80% for patients with breast cancer and a false positive rate of 9.6% for healthy patients has the same likelihood ratio as a test with an 8% hit rate and a false positive rate of 0.96%. Although these two tests have the same likelihood ratio, the first test is more useful in every way—it detects disease more often, and a negative result is stronger evidence of health.

Suppose that you apply two tests for breast cancer in succession—say, a standard mammography and also some other test which is independent of mammography. Since I don’t know of any such test that is independent of mammography, I’ll invent one for the purpose of this problem, and call it the Tams-Braylor Division Test, which checks to see if any cells are dividing more rapidly than other cells. We’ll suppose that the Tams-Braylor gives a true positive for 90% of patients with breast cancer, and gives a false positive for 5% of patients without cancer. Let’s say the prior prevalence of breast cancer is 1%. If a patient gets a positive result on her mammography and her Tams-Braylor, what is the revised probability she has breast cancer?

One way to solve this problem would be to take the revised probability for a positive mammography, which we already calculated as 7.8%, and plug that into the Tams-Braylor test as the new prior probability. If we do this, we find that the result comes out to 60%.

Suppose that the prior prevalence of breast cancer in a demographic is 1%. Suppose that we, as doctors, have a repertoire of three independent tests for breast cancer. Our first test, test A, a mammography, has a likelihood ratio of 80%/9.6% = 8.33. The second test, test B, has a likelihood ratio of 18.0 (for example, from 90% versus 5%); and the third test, test C, has a likelihood ratio of 3.5 (which could be from 70% versus 20%, or from 35% versus 10%; it makes no difference). Suppose a patient gets a positive result on all three tests. What is the probability the patient has breast cancer?

Here’s a fun trick for simplifying the bookkeeping. If the prior prevalence of breast cancer in a demographic is 1%, then 1 out of 100 women have breast cancer, and 99 out of 100 women do not have breast cancer. So if we rewrite the probability of 1% as an odds ratio, the odds are 1:99.

And the likelihood ratios of the three tests A, B, and C are:

8.33:1 = 25:3

18.0:1 = 18:1

3.5:1 = 7.5:2.

The odds for women with breast cancer who score positive on all three tests, versus women without breast cancer who score positive on all three tests, will equal:

1 × 25 × 18 × 7 : 99 × 3 × 1 × 2 = 3150 : 594.

To recover the probability from the odds, we just write:

3150 / (3150 + 594) = 84%.

This always works regardless of how the odds ratios are written; i.e., 8.33:1 is just the same as 25:3 or 75:9. It doesn’t matter in what order the tests are administered, or in what order the results are computed. The proof is left as an exercise for the reader.

E. T. Jaynes, in Probability Theory With Applications in Science and Engineering, suggests that credibility and evidence should be measured in decibels.⁵

Decibels?

Decibels are used for measuring exponential differences of intensity. For example, if the sound from an automobile horn carries 10,000 times as much energy (per square meter per second) as the sound from an alarm clock, the automobile horn would be 40 decibels louder. The sound of a bird singing might carry 1,000 times less energy than an alarm clock, and hence would be 30 decibels softer. To get the number of decibels, you take the logarithm base 10 and multiply by 10:

decibels = 10log₁₀(intensity)

intensity = 10^decibels/10.

Suppose we start with a prior probability of 1% that a woman has breast cancer, corresponding to an odds ratio of 1:99. And then we administer three tests of likelihood ratios 25:3, 18:1, and 7:2. You could multiply those numbers . . . or you could just add their logarithms:

10log₁₀(1/99) ≈ -20

10log₁₀(25/3) ≈ 9

10log₁₀(18/1) ≈ 13

10log₁₀(7/2) ≈ 5.

It starts out as fairly unlikely that a woman has breast cancer—our credibility level is at -20 decibels. Then three test results come in, corresponding to 9, 13, and 5 decibels of evidence. This raises the credibility level by a total of 27 decibels, meaning that the prior credibility of -20 decibels goes to a posterior credibility of 7 decibels. So the odds go from 1:99 to 5:1, and the probability goes from 1% to around 83%.

You are a mechanic for gizmos. When a gizmo stops working, it is due to a blocked hose 30% of the time. If a gizmo’s hose is blocked, there is a 45% probability that prodding the gizmo will produce sparks. If a gizmo’s hose is unblocked, there is only a 5% chance that prodding the gizmo will produce sparks. A customer brings you a malfunctioning gizmo. You prod the gizmo and find that it produces sparks. What is the probability that a spark-producing gizmo has a blocked hose?

What is the sequence of arithmetical operations that you performed to solve this problem?

(45% × 30%) / (45% × 30% + 5% × 70%)

Similarly, to find the chance that a woman with positive mammography has breast cancer, we computed:

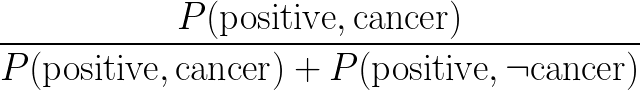
which is

P(positive,cancer) / P(positive)

which is

P(cancer|positive).

The fully general form of this calculation is known as Bayes’s Theorem or Bayes’s Rule.

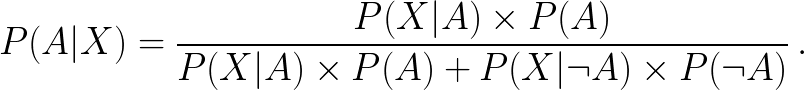
When there is some phenomenon A that we want to investigate, and an observation X that is evidence about A—for example, in the previous example, A is breast cancer and X is a positive mammography—Bayes’s Theorem tells us how we should update our probability of A, given the new evidence X.

By this point, Bayes’s Theorem may seem blatantly obvious or even tautological, rather than exciting and new. If so, this introduction has entirely succeeded in its purpose.

Bayes’s Theorem describes what makes something “evidence” and how much evidence it is. Statistical models are judged by comparison to the Bayesian method because, in statistics, the Bayesian method is as good as it gets—the Bayesian method defines the maximum amount of mileage you can get out of a given piece of evidence, in the same way that thermodynamics defines the maximum amount of work you can get out of a temperature differential. This is why you hear cognitive scientists talking about Bayesian reasoners. In cognitive science, Bayesian reasoner is the technically precise code word that we use to mean rational mind.

There are also a number of general heuristics about human reasoning that you can learn from looking at Bayes’s Theorem.

For example, in many discussions of Bayes’s Theorem, you may hear cognitive psychologists saying that people do not take prior frequencies sufficiently into account, meaning that when people approach a problem where there’s some evidence X indicating that condition A might hold true, they tend to judge A’s likelihood solely by how well the evidence X seems to match A, without taking into account the prior frequency of A. If you think, for example, that under the mammography example, the woman’s chance of having breast cancer is in the range of 70%–80%, then this kind of reasoning is insensitive to the prior frequency given in the problem; it doesn’t notice whether 1% of women or 10% of women start out having breast cancer. “Pay more attention to the prior frequency!” is one of the many things that humans need to bear in mind to partially compensate for our built-in inadequacies.

A related error is to pay too much attention to P(X|A) and not enough to P(X|¬A) when determining how much evidence X is for A. The degree to which a result X is evidence for A depends not only on the strength of the statement we’d expect to see result X if A were true, but also on the strength of the statement we wouldn’t expect to see result X if A weren’t true. For example, if it is raining, this very strongly implies the grass is wet—P(wetgrass|rain) ≈ 1—but seeing that the grass is wet doesn’t necessarily mean that it has just rained; perhaps the sprinkler was turned on, or you’re looking at the early morning dew. Since P(wetgrass|¬rain) is substantially greater than zero, P(rain|wetgrass) is substantially less than one. On the other hand, if the grass was never wet when it wasn’t raining, then knowing that the grass was wet would always show that it was raining, P(rain|wetgrass) ≈ 1, even if P(wetgrass|rain) = 50%; that is, even if the grass only got wet 50% of the times it rained. Evidence is always the result of the differential between the two conditional probabilities. Strong evidence is not the product of a very high probability that A leads to X, but the product of a very low probability that not-A could have led to X.

The Bayesian revolution in the sciences is fueled, not only by more and more cognitive scientists suddenly noticing that mental phenomena have Bayesian structure in them; not only by scientists in every field learning to judge their statistical methods by comparison with the Bayesian method; but also by the idea that science itself is a special case of Bayes’s Theorem; experimental evidence is Bayesian evidence. The Bayesian revolutionaries hold that when you perform an experiment and get evidence that “confirms” or “disconfirms” your theory, this confirmation and disconfirmation is governed by the Bayesian rules. For example, you have to take into account not only whether your theory predicts the phenomenon, but whether other possible explanations also predict the phenomenon.

Previously, the most popular philosophy of science was probably Karl Popper’s falsificationism—this is the old philosophy that the Bayesian revolution is currently dethroning. Karl Popper’s idea that theories can be definitely falsified, but never definitely confirmed, is yet another special case of the Bayesian rules; if P(X|A) ≈ 1—if the theory makes a definite prediction—then observing ¬X very strongly falsifies A. On the other hand, if P(X|A) ≈ 1, and we observe X, this doesn’t definitely confirm the theory; there might be some other condition B such that P(X|B) ≈ 1, in which case observing X doesn’t favor A over B. For observing X to definitely confirm A, we would have to know, not that P(X|A) ≈ 1, but that P(X|¬A) ≈ 0, which is something that we can’t know because we can’t range over all possible alternative explanations. For example, when Einstein’s theory of General Relativity toppled Newton’s incredibly well-confirmed theory of gravity, it turned out that all of Newton’s predictions were just a special case of Einstein’s predictions.

You can even formalize Popper’s philosophy mathematically. The likelihood ratio for X, the quantity P(X|A)/P(X|¬A), determines how much observing X slides the probability for A; the likelihood ratio is what says how strong X is as evidence. Well, in your theory A, you can predict X with probability 1, if you like; but you can’t control the denominator of the likelihood ratio, P(X|¬A)—there will always be some alternative theories that also predict X, and while we go with the simplest theory that fits the current evidence, you may someday encounter some evidence that an alternative theory predicts but your theory does not. That’s the hidden gotcha that toppled Newton’s theory of gravity. So there’s a limit on how much mileage you can get from successful predictions; there’s a limit on how high the likelihood ratio goes for confirmatory evidence.

On the other hand, if you encounter some piece of evidence Y that is definitely not predicted by your theory, this is enormously strong evidence against your theory. If P(Y|A) is infinitesimal, then the likelihood ratio will also be infinitesimal. For example, if P(Y|A) is 0.0001%, and P(Y|¬A) is 1%, then the likelihood ratio P(Y|A)/P(Y|¬A) will be 1:10,000. That’s -40 decibels of evidence! Or, flipping the likelihood ratio, if P(Y|A) is very small, then P(Y|¬A)/P(Y|A) will be very large, meaning that observing Y greatly favors ¬A over A. Falsification is much stronger than confirmation. This is a consequence of the earlier point that very strong evidence is not the product of a very high probability that A leads to X, but the product of a very low probability that not-A could have led to X. This is the precise Bayesian rule that underlies the heuristic value of Popper’s falsificationism.

Similarly, Popper’s dictum that an idea must be falsifiable can be interpreted as a manifestation of the Bayesian conservation-of-probability rule; if a result X is positive evidence for the theory, then the result ¬X would have disconfirmed the theory to some extent. If you try to interpret both X and ¬X as “confirming” the theory, the Bayesian rules say this is impossible! To increase the probability of a theory you must expose it to tests that can potentially decrease its probability; this is not just a rule for detecting would-be cheaters in the social process of science, but a consequence of Bayesian probability theory. On the other hand, Popper’s idea that there is only falsification and no such thing as confirmation turns out to be incorrect. Bayes’s Theorem shows that falsification is very strong evidence compared to confirmation, but falsification is still probabilistic in nature; it is not governed by fundamentally different rules from confirmation, as Popper argued.

So we find that many phenomena in the cognitive sciences, plus the statistical methods used by scientists, plus the scientific method itself, are all turning out to be special cases of Bayes’s Theorem. Hence the Bayesian revolution.

Having introduced Bayes’s Theorem explicitly, we can explicitly discuss its components.

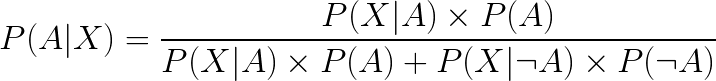
We’ll start with P(A|X). If you ever find yourself getting confused about what’s A and what’s X in Bayes’s Theorem, start with P(A|X) on the left side of the equation; that’s the simplest part to interpret. In P(A|X), A is the thing we want to know about. X is how we’re observing it; X is the evidence we’re using to make inferences about A. Remember that for every expression P(Q|P), we want to know about the probability for Q given P, the degree to which P implies Q—a more sensible notation, which it is now too late to adopt, would be P(Q ← P).

P(Q|P) is closely related to P(Q,P), but they are not identical. Expressed as a probability or a fraction, P(Q,P) is the proportion of things that have property Q and property P among all things; e.g., the proportion of “women with breast cancer and a positive mammography” within the group of all women. If the total number of women is 10,000, and 80 women have breast cancer and a positive mammography, then P(Q,P) is 80/10,000 = 0.8%. You might say that the absolute quantity, 80, is being normalized to a probability relative to the group of all women. Or to make it clearer, suppose that there’s a group of 641 women with breast cancer and a positive mammography within a total sample group of 89,031 women. Six hundred and forty-one is the absolute quantity. If you pick out a random woman from the entire sample, then the probability you’ll pick a woman with breast cancer and a positive mammography is P(Q,P), or 0.72% (in this example).

On the other hand, P(Q|P) is the proportion of things that have property Q and property P among all things that have P; e.g., the proportion of women with breast cancer and a positive mammography within the group of all women with positive mammographies. If there are 641 women with breast cancer and positive mammographies, 7,915 women with positive mammographies, and 89,031 women, then P(Q,P) is the probability of getting one of those 641 women if you’re picking at random from the entire group of 89,031, while P(Q|P) is the probability of getting one of those 641 women if you’re picking at random from the smaller group of 7,915.

In a sense, P(Q|P) really means P(Q,P|P), but specifying the extra P all the time would be redundant. You already know it has property P, so the property you’re investigating is Q—even though you’re looking at the size of group (Q,P) within group P, not the size of group Q within group P (which would be nonsense). This is what it means to take the property on the right-hand side as given; it means you know you’re working only within the group of things that have property P. When you constrict your focus of attention to see only this smaller group, many other probabilities change. If you’re taking P as given, then P(Q,P) equals just P(Q)—at least, relative to the group P. The old P(Q), the frequency of “things that have property Q within the entire sample,” is revised to the new frequency of “things that have property Q within the subsample of things that have property P.” If P is given, if P is our entire world, then looking for (Q,P) is the same as looking for just Q.

If you constrict your focus of attention to only the population of eggs that are painted blue, then suddenly “the probability that an egg contains a pearl” becomes a different number; this proportion is different for the population of blue eggs than the population of all eggs. The given, the property that constricts our focus of attention, is always on the right side of P(Q|P); the P becomes our world, the entire thing we see, and on the other side of the “given” P always has probability 1—that is what it means to take P as given. So P(Q|P) means “If P has probability 1, what is the probability of Q?” or “If we constrict our attention to only things or events where P is true, what is the probability of Q?” The statement Q, on the other side of the given, is not certain—its probability may be 10% or 90% or any other number. So when you use Bayes’s Theorem, and you write the part on the left side as P(A|X)—how to update the probability of A after seeing X, the new probability of A given that we know X, the degree to which X implies A—you can tell that X is always the observation or the evidence, and A is the property being investigated, the thing you want to know about.

The right side of Bayes’s Theorem is derived from the left side through these steps:

Once the derivation is finished, all the implications on the right side of the equation are of the form P(X|A) or P(X|¬A), while the implication on the left side is P(A|X). The symmetry arises because the elementary causal relations are generally implications from facts to observations, e.g., from breast cancer to positive mammography. The elementary steps in reasoning are generally implications from observations to facts, e.g., from a positive mammography to breast cancer. The left side of Bayes’s Theorem is an elementary inferential step from the observation of positive mammography to the conclusion of an increased probability of breast cancer. Implication is written right-to-left, so we write P(cancer|positive) on the left side of the equation. The right side of Bayes’s Theorem describes the elementary causal steps—for example, from breast cancer to a positive mammography—and so the implications on the right side of Bayes’s Theorem take the form P(positive|cancer) or P(positive|¬cancer).

And that’s Bayes’s Theorem. Rational inference on the left end, physical causality on the right end; an equation with mind on one side and reality on the other. Remember how the scientific method turned out to be a special case of Bayes’s Theorem? If you wanted to put it poetically, you could say that Bayes’s Theorem binds reasoning into the physical universe.

Okay, we’re done.

Reverend Bayes says:

You are now an initiate of the Bayesian Conspiracy.

1. Ward Casscells, Arno Schoenberger, and Thomas Graboys, “Interpretation by Physicians of Clinical Laboratory Results,” New England Journal of Medicine 299 (1978): 999–1001.

2. David M. Eddy, “Probabilistic Reasoning in Clinical Medicine: Problems and Opportunities,” in Judgement Under Uncertainty: Heuristics and Biases, ed. Daniel Kahneman, Paul Slovic, and Amos Tversky (Cambridge University Press, 1982).

3. Gerd Gigerenzer and Ulrich Hoffrage, “How to Improve Bayesian Reasoning without Instruction: Frequency Formats,” Psychological Review 102 (1995): 684–704.

4. Ibid.

5. Edwin T. Jaynes, “Probability Theory, with Applications in Science and Engineering,” Unpublished manuscript (1974).

Book IV
Mere Reality

The World: An Introduction

O. Lawful Truth
181. Universal Fire
182. Universal Law
183. Is Reality Ugly?
184. Beautiful Probability
185. Outside the Laboratory
186. The Second Law of Thermodynamics, and Engines of Cognition
187. Perpetual Motion Beliefs
188. Searching for Bayes-Structure

P. Reductionism 101
189. Dissolving the Question
190. Wrong Questions
191. Righting a Wrong Question
192. Mind Projection Fallacy
193. Probability is in the Mind
194. The Quotation is Not the Referent
195. Qualitatively Confused
196. Think Like Reality
197. Chaotic Inversion
198. Reductionism
199. Explaining vs. Explaining Away
200. Fake Reductionism
201. Savannah Poets

Q. Joy in the Merely Real
202. Joy in the Merely Real
203. Joy in Discovery
204. Bind Yourself to Reality
205. If You Demand Magic, Magic Won’t Help
206. Mundane Magic
207. The Beauty of Settled Science
208. Amazing Breakthrough Day: April 1st
209. Is Humanism a Religion Substitute?
210. Scarcity
211. The Sacred Mundane
212. To Spread Science, Keep It Secret
213. Initiation Ceremony

R. Physicalism 201
214. Hand vs. Fingers
215. Angry Atoms
216. Heat vs. Motion
217. Brain Breakthrough! It’s Made of Neurons!
218. When Anthropomorphism Became Stupid
219. A Priori
220. Reductive Reference
221. Zombies! Zombies?
222. Zombie Responses
223. The Generalized Anti-Zombie Principle
224. GAZP vs. GLUT
225. Belief in the Implied Invisible
226. Zombies: The Movie
227. Excluding the Supernatural
228. Psychic Powers

S. Quantum Physics and Many Worlds
229. Quantum Explanations
230. Configurations and Amplitude
231. Joint Configurations
232. Distinct Configurations
233. Collapse Postulates
234. Decoherence is Simple
235. Decoherence is Falsifiable and Testable
236. Privileging the Hypothesis
237. Living in Many Worlds
238. Quantum Non-Realism
239. If Many-Worlds Had Come First
240. Where Philosophy Meets Science
241. Thou Art Physics
242. Many Worlds, One Best Guess

T. Science and Rationality
243. The Failures of Eld Science
244. The Dilemma: Science or Bayes?
245. Science Doesn’t Trust Your Rationality
246. When Science Can’t Help
247. Science Isn’t Strict Enough
248. Do Scientists Already Know This Stuff?
249. No Safe Defense, Not Even Science
250. Changing the Definition of Science
251. Faster Than Science
252. Einstein’s Speed
253. That Alien Message
254. My Childhood Role Model
255. Einstein’s Superpowers
256. Class Project

Interlude: A Technical Explanation of Technical Explanation

The World: An Introduction
by Rob Bensinger

Previous essays have discussed human reasoning, language, goals, and social dynamics. Mathematics, physics, and biology were cited to explain patterns in human behavior, but little has been said about humanity’s place in nature, or about the natural world in its own right.

Just as it was useful to contrast humans as goal-oriented systems with inhuman processes in evolutionary biology and artificial intelligence, it will be useful in the coming sequences of essays to contrast humans as physical systems with inhuman processes that aren’t mind-like.

We humans are, after all, built out of inhuman parts. The world of atoms looks nothing like the world as we ordinarily think of it, and certainly looks nothing like the world’s conscious denizens as we ordinarily think of them. As Giulio Giorello put the point in an interview with Daniel Dennett: “Yes, we have a soul. But it’s made of lots of tiny robots.”¹

Mere Reality collects seven sequences of essays on this topic. The first three introduce the question of how the human world relates to the world revealed by physics: “Lawful Truth” (on the basic links between physics and human cognition), “Reductionism 101” (on the project of scientifically explaining phenomena), and “Joy in the Merely Real” (on the emotional, personal significance of the scientific world-view). This is followed by two sequences that go into more depth on specific academic debates: “Physicalism 201” (on the hard problem of consciousness) and “Quantum Physics and Many Worlds” (on the measurement problem in physics). Finally, the sequence “Science and Rationality” and the essay A Technical Explanation of Technical Explanation tie these ideas together and relate them to scientific practice.

The discussions of consciousness and quantum physics illustrate the relevance of reductionism to present-day controversies in science and philosophy. For those interested in a bit of extra context, I’ll say a few more words about those two topics here. For those eager to skip ahead: skip ahead!

Minds in the World

Can we ever know what it’s like to be a bat?

We can certainly develop better cognitive models for predicting bat behavior, or more fine-grained models of bat neurology—but it isn’t obvious that this would tell us what echolocation subjectively feels like, or what flying feels like, from the bat’s point of view.

Indeed, it seems as though we could never even be certain that there is anything it’s like to be a bat. Why couldn’t an unconscious automaton replicate all the overt behaviors of a conscious agent to arbitrary precision? (Philosophers call such automata “zombies,” though they have little in common with the zombies of folklore—who are quite visibly different from conscious agents!)

A race of alien psychologists would run into the same problem in trying to model human consciousness. They might arrive at a perfect predictive model of what we say and do when we see a red rose, but that wouldn’t mean that the aliens fully understand what redness feels like “from the inside.”

Running with examples like these, philosophers like Thomas Nagel and David Chalmers have argued that third-person cognitive and neural models can never fully capture first-person consciousness.²^,³ No matter how much we know about a physical system, it is always logically possible, on this view, that the system has no first-person experiences. Traditional dualism, with its immaterial souls freely floating around violating physical laws, may be false; but Chalmers insists on a weaker thesis, that consciousness is a “further fact” not fully explainable by the physical facts.

A number of philosophers and scientists have found this line of reasoning persuasive.⁴ If we feel this argument’s intuitive force, should we grant its conclusion and ditch physicalism?

We certainly shouldn’t reject it just because it sounds strange or feels vaguely unscientific. But how does the argument stand up to a technical understanding of how explanation and belief work? Are there any hints we can take from the history of science, or from our understanding of the physical mechanisms underlying evidence? “Physicalism 201” will return to this question.

Worlds in the World

Quantum mechanics is our best mathematical model of the universe to date, powerfully confirmed by a century of tests. The theory posits a complex-numbered “probability amplitude,” so called because a specific operation (squaring the number’s absolute value—the Born rule) lets us probabilistically predict phenomena at small scales and extreme energy levels. This amplitude changes deterministically in accord with the Schrödinger equation. In the process, it often enters odd states called “superpositions.”

Yet when we perform experiments, the superpositions seem to vanish without a trace. When we aren’t looking, the Schrödinger equation appears to capture everything there is to know about the dynamics of physical systems. When we are looking, though, this clean determinism is replaced by Born’s probabilistic rule. It’s as though the ordinary laws of physics are suddenly suspended whenever we make “observations.” As John Stewart Bell put the point:

It would seem that the theory is exclusively concerned about “results of measurements” and has nothing to say about anything else. What exactly qualifies some physical systems to play the role of the “measurer”? Was the wavefunction of the world waiting to jump for thousands of millions of years until a single-celled living creature appeared? Or did it have to wait a little longer, for some better qualified system . . . with a PhD?

Everyone agrees that this strange mix of Schrödinger and Born’s rules has proved empirically adequate. However, the question of exactly when Born’s rule enters the mix, and what it all means, has produced a chaos of different views on the nature of quantum mechanics.

Early on, the Copenhagen school—Niels Bohr and other originators of quantum theory—splintered into several standard ways of talking about the experimental results and the odd formalism used to predict them. Some, taking the theory’s focus on “measurements” and “observations” quite literally, proposed that consciousness plays a fundamental role in physical law, intervening to cause complex amplitudes to “collapse” into observables. Others, led by Werner Heisenberg, advocated a non-realistic view according to which physics is about our states of knowledge rather than about any objective reality. Yet another Copenhagen tradition, summed up in the slogan “shut up and calculate,” warned against metaphysical speculation of all kinds.

Yudkowsky uses this scientific controversy as a proving ground for some central ideas from previous sequences: map-territory distinctions, mysterious answers, Bayesianism, and Occam’s Razor. Since he is not a physicist—and neither am I—I’ll provide some outside sources here for readers who want to vet his arguments or learn more about his physics examples.

Tegmark’s Our Mathematical Universe discusses a number of relevant ideas in philosophy and physics.⁵ Among Tegmark’s more novel ideas is his argument that all consistent mathematical structures exist, including worlds with physical laws and boundary conditions entirely unlike our own. He distinguishes these Tegmark worlds from multiverses in more scientifically mainstream hypotheses—e.g., worlds in stochastic eternal inflationary models of the Big Bang and in Hugh Everett’s manyworlds interpretation of quantum physics.

Yudkowsky discusses manyworlds interpretations at greater length, as a response to the Copenhagen interpretations of quantum mechanics. Manyworlds has become very popular in recent decades among physicists, especially cosmologists. However, a number of physicists continue to reject it or maintain agnosticism. For a (mostly) philosophically mainstream introduction to this debate, see Albert’s Quantum Mechanics and Experience.⁶ See also the Stanford Encyclopedia of Philosophy’s introduction to “Measurement in Quantum Theory,”⁷ and their introduction to several of the views associated with “many worlds” in “Everett’s Relative-State Formulation”⁸ and “ManyWorlds Interpretation.”⁹

On the less theoretical side, Epstein’s Thinking Physics is a great text for training physical intuitions.¹⁰ It’s worth keeping in mind that just as one can understand most of cognitive science without understanding the nature of subjective awareness, one can understand most of physics without having a settled view of the ultimate nature (and size!) of the physical world.

1. Daniel C. Dennett, Freedom Evolves (Viking Books, 2003).

2. David J. Chalmers, The Conscious Mind: In Search of a Fundamental Theory (New York: Oxford University Press, 1996).

3. Thomas Nagel, “What Is It Like to Be a Bat?,” Philosophical Review 83, no. 4 (1974): 435–450, http://www.jstor.org/stable/2183914.

4. In a survey of Anglophone professional philosophers, 56.5% endorsed physicalism, 27.1% endorsed anti-physicalism, and 16.4% endorsed other views (e.g., “I don’t know”).¹¹ Most philosophers reject the metaphysical possibility of Chalmers’s “zombies,” but there is no consensus about why, exactly, Chalmers’s zombie argument fails. Kirk summarizes contemporary positions on phenomenal consciousness, giving arguments that resemble Yudkowsky’s against the possibility of knowing or referring to irreducible qualia.¹²

5. Max Tegmark, Our Mathematical Universe: My Quest for the Ultimate Nature of Reality (Random House LLC, 2014).

6. David Z. Albert, Quantum Mechanics and Experience (Harvard University Press, 1994).

7. Henry Krips, “Measurement in Quantum Theory,” in The Stanford Encyclopedia of Philosophy, Fall 2013, ed. Edward N. Zalta.

8. Jeffrey Barrett, Everett’s Relative-State Formulation of Quantum Mechanics, ed. Edward N. Zalta, http://plato.stanford.edu/archives/fall2008/entries/qm-everett/.

9. Lev Vaidman, “ManyWorlds Interpretation of Quantum Mechanics,” in The Stanford Encyclopedia of Philosophy, Fall 2008, ed. Edward N. Zalta.

10. Lewis Carroll Epstein, Thinking Physics: Understandable Practical Reality, 3rd Edition (Insight Press, 2009).

11. David Bourget and David J. Chalmers, “What Do Philosophers Believe?,” Philosophical Studies (2013): 1–36.

12. Robert Kirk, Mind and Body (McGill-Queen’s University Press, 2003).

181
Universal Fire

In L. Sprague de Camp’s fantasy story The Incomplete Enchanter (which set the mold for the many imitations that followed), the hero, Harold Shea, is transported from our own universe into the universe of Norse mythology.¹ This world is based on magic rather than technology; so naturally, when Our Hero tries to light a fire with a match brought along from Earth, the match fails to strike.

I realize it was only a fantasy story, but . . . how do I put this . . .

No.

In the late eighteenth century, Antoine-Laurent de Lavoisier discovered fire. “What?” you say. “Hasn’t the use of fire been dated back for hundreds of thousands of years?” Well, yes, people used fire; it was hot, bright, sort of orangey-colored, and you could use it to cook things. But nobody knew how it worked. Greek and medieval alchemists thought that Fire was a basic thing, one of the Four Elements. In Lavoisier’s time the alchemical paradigm had been gradually amended and greatly complicated, but fire was still held to be basic—in the form of “phlogiston,” a rather mysterious substance which was said to explain fire, and also every other phenomenon in alchemy.

Lavoisier’s great innovation was to weigh all the pieces of the chemical puzzle, both before and after the chemical reaction. It had previously been thought that some chemical transmutations changed the weight of the total material: If you subjected finely ground antimony to the focused sunlight of a burning glass, the antimony would be reduced to ashes after one hour, and the ashes would weigh one-tenth more than the original antimony—even though the burning had been accompanied by the loss of a thick white smoke. Lavoisier weighed all the components of such reactions, including the air in which the reaction took place, and discovered that matter was neither created nor destroyed. If the burnt ashes increased in weight, there was a corresponding decrease in the weight of the air.

Lavoisier also knew how to separate gases, and discovered that a burning candle diminished the amount of one kind of gas, vital air, and produced another gas, fixed air. Today we would call them oxygen and carbon dioxide. When the vital air was exhausted, the fire went out. One might guess, perhaps, that combustion transformed vital air into fixed air and fuel to ash, and that the ability of this transformation to continue was limited by the amount of vital air available.

Lavoisier’s proposal directly contradicted the then-current phlogiston theory. That alone would have been shocking enough, but it also turned out . . .

To appreciate what comes next, you must put yourself into an eighteenth-century frame of mind. Forget the discovery of DNA, which occurred only in 1953. Unlearn the cell theory of biology, which was formulated in 1839. Imagine looking at your hand, flexing your fingers . . . and having absolutely no idea how it worked. The anatomy of muscle and bone was known, but no one had any notion of “what makes it go”—why a muscle moves and flexes, while clay molded into a similar shape just sits there. Imagine your own body being composed of mysterious, incomprehensible gloop. And then, imagine discovering . . .

. . . that humans, in the course of breathing, consumed vital air and breathed out fixed air. People also ran on combustion! Lavoisier measured the amount of heat that animals (and Lavoisier’s assistant, Seguin) produced when exercising, the amount of vital air consumed, and the fixed air breathed out. When animals produced more heat, they consumed more vital air and exhaled more fixed air. People, like fire, consumed fuel and oxygen; people, like fire, produced heat and carbon dioxide. Deprive people of oxygen, or fuel, and the light goes out.

Matches catch fire because of phosphorus—“safety matches” have phosphorus on the ignition strip; strike-anywhere matches have phosphorus in the match heads. Phosphorus is highly reactive; pure phosphorus glows in the dark and may spontaneously combust. (Henning Brand, who purified phosphorus in 1669, announced that he had discovered Elemental Fire.) Phosphorus is thus also well-suited to its role in adenosine triphosphate, ATP, your body’s chief method of storing chemical energy. ATP is sometimes called the “molecular currency.” It invigorates your muscles and charges up your neurons. Almost every metabolic reaction in biology relies on ATP, and therefore on the chemical properties of phosphorus.

If a match stops working, so do you. You can’t change just one thing.

The surface-level rules, “Matches catch fire when struck,” and “Humans need air to breathe,” are not obviously connected. It took centuries to discover the connection, and even then, it still seems like some distant fact learned in school, relevant only to a few specialists. It is all too easy to imagine a world where one surface rule holds, and the other doesn’t; to suppress our credence in one belief, but not the other. But that is imagination, not reality. If your map breaks into four pieces for easy storage, it doesn’t mean the territory is also broken into disconnected parts. Our minds store different surface-level rules in different compartments, but this does not reflect any division in the laws that govern Nature.

We can take the lesson further. Phosphorus derives its behavior from even deeper laws, electrodynamics and chromodynamics. “Phosphorus” is merely our word for electrons and quarks arranged a certain way. You cannot change the chemical properties of phosphorus without changing the laws governing electrons and quarks.

If you stepped into a world where matches failed to strike, you would cease to exist as organized matter.

Reality is laced together a lot more tightly than humans might like to believe.

1. Lyon Sprague de Camp and Fletcher Pratt, The Incomplete Enchanter (New York: Henry Holt & Company, 1941).

182
Universal Law

Antoine-Laurent de Lavoisier discovered that breathing (respiration) and fire (combustion) operated on the same principle. It was one of the most startling unifications in the history of science, for it brought together the mundane realm of matter and the sacred realm of life, which humans had divided into separate magisteria.

The first great simplification was that of Isaac Newton, who unified the course of the planets with the trajectory of a falling apple. The shock of this discovery was greater by far than Lavoisier’s. It wasn’t just that Newton had dared to unify the Earthly realm of base matter with the obviously different and sacred celestial realm, once thought to be the abode of the gods. Newton’s discovery gave rise to the notion of a universal law, one that is the same everywhere and everywhen, with literally zero exceptions.

Human beings live in a world of surface phenomena, and surface phenomena are divided into leaky categories with plenty of exceptions. A tiger does not behave like a buffalo. Most buffalo have four legs, but perhaps this one has three. Why would anyone think there would be laws that hold everywhere? It’s just so obviously untrue.

The only time when it seems like we would want a law to hold everywhere is when we are talking about moral laws—tribal rules of behavior. Some tribe members may try to take more than their fair share of the buffalo meat—perhaps coming up with some clever excuse—so in the case of moral laws we do seem to have an instinct to universality. Yes, the rule about dividing the meat evenly applies to you, right now, whether you like it or not. But even here there are exceptions. If—for some bizarre reason—a more powerful tribe threatened to spear all of you unless Bob received twice as much meat on just this one occasion, you’d give Bob twice as much meat. The idea of a rule with literally no exceptions seems insanely rigid, the product of closed-minded thinking by fanatics so in the grip of their one big idea that they can’t see the richness and complexity of the real universe.

This is the customary accusation made against scientists—the professional students of the richness and complexity of the real universe. Because when you actually look at the universe, it turns out to be, by human standards, insanely rigid in applying its rules. As far as we know, there has been not one single violation of Conservation of Momentum from the uttermost dawn of time up until now.

Sometimes—very rarely—we observe an apparent violation of our models of the fundamental laws. Though our scientific models may last for a generation or two, they are not stable over the course of centuries . . . but do not fancy that this makes the universe itself whimsical. That is mixing up the map with the territory. For when the dust subsides and the old theory is overthrown, it turns out that the universe always was acting according to the new generalization we have discovered, which once again is absolutely universal as far as humanity’s knowledge extends. When it was discovered that Newtonian gravitation was a special case of General Relativity, it was seen that General Relativity had been governing the orbit of Mercury for decades before any human being knew about it; and it would later become apparent that General Relativity had been governing the collapse of stars for billions of years before humanity. It is only our model that was mistaken—the Law itself was always absolutely constant—or so our new model tells us.

I may repose only 80% confidence that the lightspeed limit will last out the next hundred thousand years, but this does not mean that I think the lightspeed limit holds only 80% of the time, with occasional exceptions. The proposition to which I assign 80% probability is that the lightspeed law is absolutely inviolable throughout the entirety of space and time.

One of the reasons the ancient Greeks didn’t discover science is that they didn’t realize you could generalize from experiments. The Greek philosophers were interested in “normal” phenomena. If you set up a contrived experiment, you would probably get a “monstrous” result, one that had no implications for how things really worked.

So that is how humans tend to dream, before they learn better; but what of the universe’s own quiet dreams that it dreamed to itself before ever it dreamed of humans? If you would learn to think like reality, then here is the Tao:

Since the beginning
not one unusual thing
has ever happened.

183
Is Reality Ugly?

Consider the cubes, {1, 8, 27, 64, 125, . . . }. Their first differences {7, 19, 37, 61, . . . } might at first seem to lack an obvious pattern, but taking the second differences {12, 18, 24, . . . } takes you down to the simply related level. Taking the third differences {6, 6, . . . } brings us to the perfectly stable level, where chaos dissolves into order.

But this is a handpicked example. Perhaps the “messy real world” lacks the beauty of these abstract mathematical objects? Perhaps it would be more appropriate to talk about neuroscience or gene expression networks?

Abstract math, being constructed solely in imagination, arises from simple foundations—a small set of initial axioms—and is a closed system; conditions that might seem unnaturally conducive to neatness.

Which is to say: In pure math, you don’t have to worry about a tiger leaping out of the bushes and eating Pascal’s Triangle.

So is the real world uglier than mathematics?

Strange that people ask this. I mean, the question might have been sensible two and a half millennia ago . . . Back when the Greek philosophers were debating what this “real world” thingy might be made of, there were many positions. Heraclitus said, “All is fire.” Thales said, “All is water.” Pythagoras said, “All is number.”

Score:

Heraclitus: 0
Thales: 0
Pythagoras: 1

Beneath the complex forms and shapes of the surface world, there is a simple level, an exact and stable level, whose laws we name “physics.” This discovery, the Great Surprise, has already taken place at our point in human history—but it does not do to forget that it was surprising. Once upon a time, people went in search of underlying beauty, with no guarantee of finding it; and once upon a time, they found it; and now it is a known thing, and taken for granted.

Then why can’t we predict the location of every tiger in the bushes as easily as we predict the sixth cube?

I count three sources of uncertainty even within worlds of pure math—two obvious sources, and one not so obvious.

The first source of uncertainty is that even a creature of pure math, living embedded in a world of pure math, may not know the math. Humans walked the Earth long before Galileo/Newton/Einstein discovered the law of gravity that prevents us from being flung off into space. You can be governed by stable fundamental rules without knowing them. There is no law of physics which says that laws of physics must be explicitly represented, as knowledge, in brains that run under them.

We do not yet have the Theory of Everything. Our best current theories are things of math, but they are not perfectly integrated with each other. The most probable explanation is that—as has previously proved to be the case—we are seeing surface manifestations of deeper math. So by far the best guess is that reality is made of math; but we do not fully know which math, yet.

But physicists have to construct huge particle accelerators to distinguish between theories—to manifest their remaining uncertainty in any visible fashion. That physicists must go to such lengths to be unsure, suggests that this is not the source of our uncertainty about stock prices.

The second obvious source of uncertainty is that even when you know all the relevant laws of physics, you may not have enough computing power to extrapolate them. We know every fundamental physical law that is relevant to a chain of amino acids folding itself into a protein. But we still can’t predict the shape of the protein from the amino acids. Some tiny little 5-nanometer molecule that folds in a microsecond is too much information for current computers to handle (never mind tigers and stock prices). Our frontier efforts in protein folding use clever approximations, rather than the underlying Schrödinger equation. When it comes to describing a 5-nanometer object using really basic physics, over quarks—well, you don’t even bother trying.

We have to use instruments like X-ray crystallography and NMR to discover the shapes of proteins that are fully determined by physics we know and a DNA sequence we know. We are not logically omniscient; we cannot see all the implications of our thoughts; we do not know what we believe.

The third source of uncertainty is the most difficult to understand, and Nick Bostrom has written a book about it. Suppose that the sequence {1, 8, 27, 64, 125, . . . } exists; suppose that this is a fact. And suppose that atop each cube is a little person—one person per cube—and suppose that this is also a fact.

If you stand on the outside and take a global perspective—looking down from above at the sequence of cubes and the little people perched on top—then these two facts say everything there is to know about the sequence and the people.

But if you are one of the little people perched atop a cube, and you know these two facts, there is still a third piece of information you need to make predictions: “Which cube am I standing on?”

You expect to find yourself standing on a cube; you do not expect to find yourself standing on the number 7. Your anticipations are definitely constrained by your knowledge of the basic physics; your beliefs are falsifiable. But you still have to look down to find out whether you’re standing on 1,728 or 5,177,717. If you can do fast mental arithmetic, then seeing that the first two digits of a four-digit cube are 17__ will be sufficient to guess that the last digits are 2 and 8. Otherwise you may have to look to discover the 2 and 8 as well.

To figure out what the night sky should look like, it’s not enough to know the laws of physics. It’s not even enough to have logical omniscience over their consequences. You have to know where you are in the universe. You have to know that you’re looking up at the night sky from Earth. The information required is not just the information to locate Earth in the visible universe, but in the entire universe, including all the parts that our telescopes can’t see because they are too distant, and different inflationary universes, and alternate Everett branches.

It’s a good bet that “uncertainty about initial conditions at the boundary” is really indexical uncertainty. But if not, it’s empirical uncertainty, uncertainty about how the universe is from a global perspective, which puts it in the same class as uncertainty about fundamental laws.

Wherever our best guess is that the “real world” has an irretrievably messy component, it is because of the second and third sources of uncertainty—logical uncertainty and indexical uncertainty.

Ignorance of fundamental laws does not tell you that a messy-looking pattern really is messy. It might just be that you haven’t figured out the order yet.

But when it comes to messy gene expression networks, we’ve already found the hidden beauty—the stable level of underlying physics. Because we’ve already found the master order, we can guess that we won’t find any additional secret patterns that will make biology as easy as a sequence of cubes. Knowing the rules of the game, we know that the game is hard. We don’t have enough computing power to do protein chemistry from physics (the second source of uncertainty) and evolutionary pathways may have gone different ways on different planets (the third source of uncertainty). New discoveries in basic physics won’t help us here.

If you were an ancient Greek staring at the raw data from a biology experiment, you would be much wiser to look for some hidden structure of Pythagorean elegance, all the proteins lining up in a perfect icosahedron. But in biology we already know where the Pythagorean elegance is, and we know it’s too far down to help us overcome our indexical and logical uncertainty.

Similarly, we can be confident that no one will ever be able to predict the results of certain quantum experiments, only because our fundamental theory tells us quite definitely that different versions of us will see different results. If your knowledge of fundamental laws tells you that there’s a sequence of cubes, and that there’s one little person standing on top of each cube, and that the little people are all alike except for being on different cubes, and that you are one of these little people, then you know that you have no way of deducing which cube you’re on except by looking.

The best current knowledge says that the “real world” is a perfectly regular, deterministic, and very large mathematical object which is highly expensive to simulate. So “real life” is less like predicting the next cube in a sequence of cubes, and more like knowing that lots of little people are standing on top of cubes, but not knowing who you personally are, and also not being very good at mental arithmetic. Our knowledge of the rules does constrain our anticipations, quite a bit, but not perfectly.

There, now doesn’t that sound like real life?

But uncertainty exists in the map, not in the territory. If we are ignorant of a phenomenon, that is a fact about our state of mind, not a fact about the phenomenon itself. Empirical uncertainty, logical uncertainty, and indexical uncertainty are just names for our own bewilderment. The best current guess is that the world is math and the math is perfectly regular. The messiness is only in the eye of the beholder.

Even the huge morass of the blogosphere is embedded in this perfect physics, which is ultimately as orderly as {1, 8, 27, 64, 125, . . . }.

So the Internet is not a big muck . . . it’s a series of cubes.

184
Beautiful Probability

Should we expect rationality to be, on some level, simple? Should we search and hope for underlying beauty in the arts of belief and choice?

Let me introduce this issue by borrowing a complaint of the late great Bayesian Master, E. T. Jaynes:¹

Two medical researchers use the same treatment independently, in different hospitals. Neither would stoop to falsifying the data, but one had decided beforehand that because of finite resources he would stop after treating n = 100 patients, however many cures were observed by then. The other had staked his reputation on the efficacy of the treatment, and decided he would not stop until he had data indicating a rate of cures definitely greater than 60%, however many patients that might require. But in fact, both stopped with exactly the same data: n = 100 [patients], r = 70 [cures]. Should we then draw different conclusions from their experiments?” [Presumably the two control groups also had equal results.]

Cyan directs us to chapter 37 of MacKay’s excellent statistics book, free online, for a more thorough explanation of this problem.²

According to old-fashioned statistical procedure—which I believe is still being taught today—the two researchers have performed different experiments with different stopping conditions. The two experiments could have terminated with different data, and therefore represent different tests of the hypothesis, requiring different statistical analyses. It’s quite possible that the first experiment will be “statistically significant,” the second not.

Whether or not you are disturbed by this says a good deal about your attitude toward probability theory, and indeed, rationality itself.

Non-Bayesian statisticians might shrug, saying, “Well, not all statistical tools have the same strengths and weaknesses, y’know—a hammer isn’t like a screwdriver—and if you apply different statistical tools you may get different results, just like using the same data to compute a linear regression or train a regularized neural network. You’ve got to use the right tool for the occasion. Life is messy—”

And then there’s the Bayesian reply: “Excuse you? The evidential impact of a fixed experimental method, producing the same data, depends on the researcher’s private thoughts? And you have the nerve to accuse us of being ‘too subjective’?”

If Nature is one way, the likelihood of the data coming out the way we have seen will be one thing. If Nature is another way, the likelihood of the data coming out that way will be something else. But the likelihood of a given state of Nature producing the data we have seen, has nothing to do with the researcher’s private intentions. So whatever our hypotheses about Nature, the likelihood ratio is the same, and the evidential impact is the same, and the posterior belief should be the same, between the two experiments. At least one of the two Old Style methods must discard relevant information—or simply do the wrong calculation—for the two methods to arrive at different answers.

The ancient war between the Bayesians and the accursèd frequentists stretches back through decades, and I’m not going to try to recount that elder history in this essay.

But one of the central conflicts is that Bayesians expect probability theory to be . . . what’s the word I’m looking for? “Neat?” “Clean?” “Self-consistent?”

As Jaynes says, the theorems of Bayesian probability are just that, theorems in a coherent proof system. No matter what derivations you use, in what order, the results of Bayesian probability theory should always be consistent—every theorem compatible with every other theorem.

If you want to know the sum 10 + 10, you can redefine it as (2 × 5) + (7 + 3) or as (2 × (4 + 6)) or use whatever other legal tricks you like, but the result always has to come out to be the same, in this case, 20. If it comes out as 20 one way and 19 the other way, then you may conclude you did something illegal on at least one of the two occasions. (In arithmetic, the illegal operation is usually division by zero; in probability theory, it is usually an infinity that was not taken as a the limit of a finite process.)

If you get the result 19 = 20, look hard for that error you just made, because it’s unlikely that you’ve sent arithmetic itself up in smoke. If anyone should ever succeed in deriving a real contradiction from Bayesian probability theory—like, say, two different evidential impacts from the same experimental method yielding the same results—then the whole edifice goes up in smoke. Along with set theory, ’cause I’m pretty sure ZF provides a model for probability theory.

Math! That’s the word I was looking for. Bayesians expect probability theory to be math. That’s why we’re interested in Cox’s Theorem and its many extensions, showing that any representation of uncertainty which obeys certain constraints has to map onto probability theory. Coherent math is great, but unique math is even better.

And yet . . . should rationality be math? It is by no means a foregone conclusion that probability should be pretty. The real world is messy—so shouldn’t you need messy reasoning to handle it? Maybe the non-Bayesian statisticians, with their vast collection of ad-hoc methods and ad-hoc justifications, are strictly more competent because they have a strictly larger toolbox. It’s nice when problems are clean, but they usually aren’t, and you have to live with that.

After all, it’s a well-known fact that you can’t use Bayesian methods on many problems because the Bayesian calculation is computationally intractable. So why not let many flowers bloom? Why not have more than one tool in your toolbox?

That’s the fundamental difference in mindset. Old School statisticians thought in terms of tools, tricks to throw at particular problems. Bayesians—at least this Bayesian, though I don’t think I’m speaking only for myself—we think in terms of laws.

Looking for laws isn’t the same as looking for especially neat and pretty tools. The Second Law of Thermodynamics isn’t an especially neat and pretty refrigerator.

The Carnot cycle is an ideal engine—in fact, the ideal engine. No engine powered by two heat reservoirs can be more efficient than a Carnot engine. As a corollary, all thermodynamically reversible engines operating between the same heat reservoirs are equally efficient.

But, of course, you can’t use a Carnot engine to power a real car. A real car’s engine bears the same resemblance to a Carnot engine that the car’s tires bear to perfect rolling cylinders.

Clearly, then, a Carnot engine is a useless tool for building a real-world car. The Second Law of Thermodynamics, obviously, is not applicable here. It’s too hard to make an engine that obeys it, in the real world. Just ignore thermodynamics—use whatever works.

This is the sort of confusion that I think reigns over they who still cling to the Old Ways.

No, you can’t always do the exact Bayesian calculation for a problem. Sometimes you must seek an approximation; often, indeed. This doesn’t mean that probability theory has ceased to apply, any more than your inability to calculate the aerodynamics of a 747 on an atom-by-atom basis implies that the 747 is not made out of atoms. Whatever approximation you use, it works to the extent that it approximates the ideal Bayesian calculation—and fails to the extent that it departs.

Bayesianism’s coherence and uniqueness proofs cut both ways. Just as any calculation that obeys Cox’s coherency axioms (or any of the many reformulations and generalizations) must map onto probabilities, so too, anything that is not Bayesian must fail one of the coherency tests. This, in turn, opens you to punishments like Dutch-booking (accepting combinations of bets that are sure losses, or rejecting combinations of bets that are sure gains).

You may not be able to compute the optimal answer. But whatever approximation you use, both its failures and successes will be explainable in terms of Bayesian probability theory. You may not know the explanation; that does not mean no explanation exists.

So you want to use a linear regression, instead of doing Bayesian updates? But look to the underlying structure of the linear regression, and you see that it corresponds to picking the best point estimate given a Gaussian likelihood function and a uniform prior over the parameters.

You want to use a regularized linear regression, because that works better in practice? Well, that corresponds (says the Bayesian) to having a Gaussian prior over the weights.

Sometimes you can’t use Bayesian methods literally; often, indeed. But when you can use the exact Bayesian calculation that uses every scrap of available knowledge, you are done. You will never find a statistical method that yields a better answer. You may find a cheap approximation that works excellently nearly all the time, and it will be cheaper, but it will not be more accurate. Not unless the other method uses knowledge, perhaps in the form of disguised prior information, that you are not allowing into the Bayesian calculation; and then when you feed the prior information into the Bayesian calculation, the Bayesian calculation will again be equal or superior.

When you use an Old Style ad-hoc statistical tool with an ad-hoc (but often quite interesting) justification, you never know if someone else will come up with an even more clever tool tomorrow. But when you can directly use a calculation that mirrors the Bayesian law, you’re done—like managing to put a Carnot heat engine into your car. It is, as the saying goes, “Bayes-optimal.”

It seems to me that the toolboxers are looking at the sequence of cubes {1, 8, 27, 64, 125, . . . } and pointing to the first differences {7, 19, 37, 61, . . . } and saying “Look, life isn’t always so neat—you’ve got to adapt to circumstances.” And the Bayesians are pointing to the third differences, the underlying stable level {6, 6, 6, 6, 6, . . . }. And the critics are saying, “What the heck are you talking about? It’s 7, 19, 37 not 6, 6, 6. You are oversimplifying this messy problem; you are too attached to simplicity.”

It’s not necessarily simple on a surface level. You have to dive deeper than that to find stability.

Think laws, not tools. Needing to calculate approximations to a law doesn’t change the law. Planes are still atoms, they aren’t governed by special exceptions in Nature for aerodynamic calculations. The approximation exists in the map, not in the territory. You can know the Second Law of Thermodynamics, and yet apply yourself as an engineer to build an imperfect car engine. The Second Law does not cease to be applicable; your knowledge of that law, and of Carnot cycles, helps you get as close to the ideal efficiency as you can.

We aren’t enchanted by Bayesian methods merely because they’re beautiful. The beauty is a side effect. Bayesian theorems are elegant, coherent, optimal, and provably unique because they are laws.

1. Edwin T. Jaynes, “Probability Theory as Logic,” in Maximum Entropy and Bayesian Methods, ed. Paul F. Fougère (Springer Netherlands, 1990).

2. David J. C. MacKay, Information Theory, Inference, and Learning Algorithms (New York: Cambridge University Press, 2003).

185
Outside the Laboratory

“Outside the laboratory, scientists are no wiser than anyone else.” Sometimes this proverb is spoken by scientists, humbly, sadly, to remind themselves of their own fallibility. Sometimes this proverb is said for rather less praiseworthy reasons, to devalue unwanted expert advice. Is the proverb true? Probably not in an absolute sense. It seems much too pessimistic to say that scientists are literally no wiser than average, that there is literally zero correlation.

But the proverb does appear true to some degree, and I propose that we should be very disturbed by this fact. We should not sigh, and shake our heads sadly. Rather we should sit bolt upright in alarm. Why? Well, suppose that an apprentice shepherd is laboriously trained to count sheep, as they pass in and out of a fold. Thus the shepherd knows when all the sheep have left, and when all the sheep have returned. Then you give the shepherd a few apples, and say: “How many apples?” But the shepherd stares at you blankly, because they weren’t trained to count apples—just sheep. You would probably suspect that the shepherd didn’t understand counting very well.

Now suppose we discover that a PhD economist buys a lottery ticket every week. We have to ask ourselves: Does this person really understand expected utility, on a gut level? Or have they just been trained to perform certain algebra tricks?

One thinks of Richard Feynman’s account of a failing physics education program:

The students had memorized everything, but they didn’t know what anything meant. When they heard “light that is reflected from a medium with an index,” they didn’t know that it meant a material such as water. They didn’t know that the “direction of the light” is the direction in which you see something when you’re looking at it, and so on. Everything was entirely memorized, yet nothing had been translated into meaningful words. So if I asked, “What is Brewster’s Angle?” I’m going into the computer with the right keywords. But if I say, “Look at the water,” nothing happens—they don’t have anything under “Look at the water”!

Suppose we have an apparently competent scientist, who knows how to design an experiment on N subjects; the N subjects will receive a randomized treatment; blinded judges will classify the subject outcomes; and then we’ll run the results through a computer and see if the results are significant at the 0.05 confidence level. Now this is not just a ritualized tradition. This is not a point of arbitrary etiquette like using the correct fork for salad. It is a ritualized tradition for testing hypotheses experimentally. Why should you test your hypothesis experimentally? Because you know the journal will demand so before it publishes your paper? Because you were trained to do it in college? Because everyone else says in unison that it’s important to do the experiment, and they’ll look at you funny if you say otherwise?

No: because, in order to map a territory, you have to go out and look at the territory. It isn’t possible to produce an accurate map of a city while sitting in your living room with your eyes closed, thinking pleasant thoughts about what you wish the city was like. You have to go out, walk through the city, and write lines on paper that correspond to what you see. It happens, in miniature, every time you look down at your shoes to see if your shoelaces are untied. Photons arrive from the Sun, bounce off your shoelaces, strike your retina, are transduced into neural firing frequencies, and are reconstructed by your visual cortex into an activation pattern that is strongly correlated with the current shape of your shoelaces. To gain new information about the territory, you have to interact with the territory. There has to be some real, physical process whereby your brain state ends up correlated to the state of the environment. Reasoning processes aren’t magic; you can give causal descriptions of how they work. Which all goes to say that, to find things out, you’ve got to go look.

Now what are we to think of a scientist who seems competent inside the laboratory, but who, outside the laboratory, believes in a spirit world? We ask why, and the scientist says something along the lines of: “Well, no one really knows, and I admit that I don’t have any evidence—it’s a religious belief, it can’t be disproven one way or another by observation.” I cannot but conclude that this person literally doesn’t know why you have to look at things. They may have been taught a certain ritual of experimentation, but they don’t understand the reason for it—that to map a territory, you have to look at it—that to gain information about the environment, you have to undergo a causal process whereby you interact with the environment and end up correlated to it. This applies just as much to a double-blind experimental design that gathers information about the efficacy of a new medical device, as it does to your eyes gathering information about your shoelaces.

Maybe our spiritual scientist says: “But it’s not a matter for experiment. The spirits spoke to me in my heart.” Well, if we really suppose that spirits are speaking in any fashion whatsoever, that is a causal interaction and it counts as an observation. Probability theory still applies. If you propose that some personal experience of “spirit voices” is evidence for actual spirits, you must propose that there is a favorable likelihood ratio for spirits causing “spirit voices,” as compared to other explanations for “spirit voices,” which is sufficient to overcome the prior improbability of a complex belief with many parts. Failing to realize that “the spirits spoke to me in my heart” is an instance of “causal interaction,” is analogous to a physics student not realizing that a “medium with an index” means a material such as water.

It is easy to be fooled, perhaps, by the fact that people wearing lab coats use the phrase “causal interaction” and that people wearing gaudy jewelry use the phrase “spirits speaking.” Discussants wearing different clothing, as we all know, demarcate independent spheres of existence—“separate magisteria,” in Stephen J. Gould’s immortal blunder of a phrase. Actually, “causal interaction” is just a fancy way of saying, “Something that makes something else happen,” and probability theory doesn’t care what clothes you wear.

In modern society there is a prevalent notion that spiritual matters can’t be settled by logic or observation, and therefore you can have whatever religious beliefs you like. If a scientist falls for this, and decides to live their extralaboratorial life accordingly, then this, to me, says that they only understand the experimental principle as a social convention. They know when they are expected to do experiments and test the results for statistical significance. But put them in a context where it is socially conventional to make up wacky beliefs without looking, and they just as happily do that instead.

The apprentice shepherd is told that if “seven” sheep go out, and “eight” sheep go out, then “fifteen” sheep had better come back in. Why “fifteen” instead of “fourteen” or “three”? Because otherwise you’ll get no dinner tonight, that’s why! So that’s professional training of a kind, and it works after a fashion—but if social convention is the only reason why seven sheep plus eight sheep equals fifteen sheep, then maybe seven apples plus eight apples equals three apples. Who’s to say that the rules shouldn’t be different for apples?

But if you know why the rules work, you can see that addition is the same for sheep and for apples. Isaac Newton is justly revered, not for his outdated theory of gravity, but for discovering that—amazingly, surprisingly—the celestial planets, in the glorious heavens, obeyed just the same rules as falling apples. In the macroscopic world—the everyday ancestral environment—different trees bear different fruits, different customs hold for different people at different times. A genuinely unified universe, with stationary universal laws, is a highly counterintuitive notion to humans! It is only scientists who really believe it, though some religions may talk a good game about the “unity of all things.”

As Richard Feynman put it:

If we look at a glass closely enough we see the entire universe. There are the things of physics: the twisting liquid which evaporates depending on the wind and weather, the reflections in the glass, and our imagination adds the atoms. The glass is a distillation of the Earth’s rocks, and in its composition we see the secret of the universe’s age, and the evolution of the stars. What strange array of chemicals are there in the wine? How did they come to be? There are the ferments, the enzymes, the substrates, and the products. There in wine is found the great generalization: all life is fermentation. Nobody can discover the chemistry of wine without discovering, as did Louis Pasteur, the cause of much disease. How vivid is the claret, pressing its existence into the consciousness that watches it! If our small minds, for some convenience, divide this glass of wine, this universe, into parts—physics, biology, geology, astronomy, psychology, and so on—remember that Nature does not know it! So let us put it all back together, not forgetting ultimately what it is for. Let it give us one more final pleasure: drink it and forget it all!

A few religions, especially the ones invented or refurbished after Isaac Newton, may profess that “everything is connected to everything else.” (Since there is a trivial isomorphism between graphs and their complements, this profound wisdom conveys exactly the same useful information as a graph with no edges.) But when it comes to the actual meat of the religion, prophets and priests follow the ancient human practice of making everything up as they go along. And they make up one rule for women under twelve, another rule for men over thirteen; one rule for the Sabbath and another rule for weekdays; one rule for science and another rule for sorcery . . .

Reality, we have learned to our shock, is not a collection of separate magisteria, but a single unified process governed by mathematically simple low-level rules. Different buildings on a university campus do not belong to different universes, though it may sometimes seem that way. The universe is not divided into mind and matter, or life and nonlife; the atoms in our heads interact seamlessly with the atoms of the surrounding air. Nor is Bayes’s Theorem different from one place to another.

If, outside of their specialist field, some particular scientist is just as susceptible as anyone else to wacky ideas, then they probably never did understand why the scientific rules work. Maybe they can parrot back a bit of Popperian falsificationism; but they don’t understand on a deep level, the algebraic level of probability theory, the causal level of cognition-as-machinery. They’ve been trained to behave a certain way in the laboratory, but they don’t like to be constrained by evidence; when they go home, they take off the lab coat and relax with some comfortable nonsense. And yes, that does make me wonder if I can trust that scientist’s opinions even in their own field—especially when it comes to any controversial issue, any open question, anything that isn’t already nailed down by massive evidence and social convention.

Maybe we can beat the proverb—be rational in our personal lives, not just our professional lives. We shouldn’t let a mere proverb stop us: “A witty saying proves nothing,” as Voltaire said. Maybe we can do better, if we study enough probability theory to know why the rules work, and enough experimental psychology to see how they apply in real-world cases—if we can learn to look at the water. An ambition like that lacks the comfortable modesty of being able to confess that, outside your specialty, you’re no better than anyone else. But if our theories of rationality don’t generalize to everyday life, we’re doing something wrong. It’s not a different universe inside and outside the laboratory.

186
The Second Law of Thermodynamics, and Engines of Cognition

The First Law of Thermodynamics, better known as Conservation of Energy, says that you can’t create energy from nothing: it prohibits perpetual motion machines of the first type, which run and run indefinitely without consuming fuel or any other resource. According to our modern view of physics, energy is conserved in each individual interaction of particles. By mathematical induction, we see that no matter how large an assemblage of particles may be, it cannot produce energy from nothing—not without violating what we presently believe to be the laws of physics.

This is why the US Patent Office will summarily reject your amazingly clever proposal for an assemblage of wheels and gears that cause one spring to wind up another as the first runs down, and so continue to do work forever, according to your calculations. There’s a fully general proof that at least one wheel must violate (our standard model of) the laws of physics for this to happen. So unless you can explain how one wheel violates the laws of physics, the assembly of wheels can’t do it either.

A similar argument applies to a “reactionless drive,” a propulsion system that violates Conservation of Momentum. In standard physics, momentum is conserved for all individual particles and their interactions; by mathematical induction, momentum is conserved for physical systems whatever their size. If you can visualize two particles knocking into each other and always coming out with the same total momentum that they started with, then you can see how scaling it up from particles to a gigantic complicated collection of gears won’t change anything. Even if there’s a trillion quadrillion atoms involved, 0 + 0 + … + 0 = 0.

But Conservation of Energy, as such, cannot prohibit converting heat into work. You can, in fact, build a sealed box that converts ice cubes and stored electricity into warm water. It isn’t even difficult. Energy cannot be created or destroyed: the net change in energy, from transforming (ice cubes + electricity) to (warm water), must be 0. So it couldn’t violate Conservation of Energy, as such, if you did it the other way around . . .

Perpetual motion machines of the second type, which convert warm water into electrical current and ice cubes, are prohibited by the Second Law of Thermodynamics.

The second law is a bit harder to understand, as it is essentially Bayesian in nature.

Yes, really.

The essential physical law underlying the Second Law of Thermodynamics is a theorem which can be proven within the standard model of physics: In the development over time of any closed system, phase space volume is conserved.

Let’s say you’re holding a ball high above the ground. We can describe this state of affairs as a point in a multidimensional space, at least one of whose dimensions is “height of ball above the ground.” Then, when you drop the ball, it moves, and so does the dimensionless point in phase space that describes the entire system that includes you and the ball. “Phase space,” in physics-speak, means that there are dimensions for the momentum of the particles, not just their position—e.g., a system of 2 particles would have 12 dimensions, 3 dimensions for each particle’s position, and 3 dimensions for each particle’s momentum.

If you had a multidimensional space, each of whose dimensions described the position of a gear in a huge assemblage of gears, then as you turned the gears a single point would swoop and dart around in a rather high-dimensional phase space. Which is to say, just as you can view a great big complex machine as a single point in a very-high-dimensional space, so too you can view the laws of physics describing the behavior of this machine over time as describing the trajectory of its point through the phase space.

The Second Law of Thermodynamics is a consequence of a theorem which can be proven in the standard model of physics: If you take a volume of phase space, and develop it forward in time using standard physics, the total volume of the phase space is conserved.

For example, let there be two systems, X and Y, where X has 8 possible states, Y has 4 possible states, and the joint system (X,Y) has 32 possible states.

The development of the joint system over time can be described as a rule that maps initial points onto future points. For example, the system could start out in X₇Y₂, then develop (under some set of physical laws) into the state X₃Y₃ a minute later. Which is to say: if X started in state X₇, and Y started in state Y₂, and we watched it for 1 minute, we would see X go to X₃ and Y go to Y₃. Such are the laws of physics.

Next, let’s carve out a subspace S of the joint system state. The space S will be the subspace bounded by X being in state X₁ and Y being in states Y₁ through Y₄. So the total volume of S is 4 states.

And let’s suppose that, under the laws of physics governing (X,Y), the states initially in S behave as follows:

X₁Y₁ → X₂Y₁

X₁Y₂ → X₄Y₁

X₁Y₃ → X₆Y₁

X₁Y₄ → X₈Y₁.

That, in a nutshell, is how a refrigerator works.

The X subsystem began in a narrow region of state space—the single state X₁, in fact—and Y began distributed over a wider region of space, states Y₁ through Y₄. By interacting with each other, Y went into a narrow region, and X ended up in a wide region; but the total phase space volume was conserved. Four initial states mapped to four end states.

Clearly, so long as total phase space volume is conserved by physics over time, you can’t squeeze Y harder than X expands, or vice versa—for every subsystem you squeeze into a narrower region of state space, some other subsystem has to expand into a wider region of state space.

Now let’s say that we’re uncertain about the joint system (X,Y), and our uncertainty is described by an equiprobable distribution over S. That is, we’re pretty sure X is in state X₁, but Y is equally likely to be in any of the states Y₁ through Y₄. If we shut our eyes for a minute and then open them again, we will expect to see Y in state Y₁, but X might be in any of the states X₂ through X₈. Actually, X can only be in some of the states X₂ through X₈, but it would be too costly to think out exactly which states these might be, so we’ll just say X₂ through X₈.

If you consider the Shannon entropy of our uncertainty about X and Y as individual systems, X began with 0 bits of entropy because it had a single definite state, and Y began with 2 bits of entropy because it was equally likely to be in any of 4 possible states. (There’s no mutual information between X and Y.) A bit of physics occurred, and lo, the entropy of Y went to 0, but the entropy of X went to log₂(7) = 2.8 bits. So entropy was transferred from one system to another, and decreased within the Y subsystem; but due to the cost of bookkeeping, we didn’t bother to track some information, and hence (from our perspective) the overall entropy increased.

Suppose there was a physical process that mapped past states onto future states like this:

X₂Y₁ → X₂Y₁

X₂Y₂ → X₂Y₁

X₂Y₃ → X₂Y₁

X₂Y₄ → X₂Y₁.

Then you could have a physical process that would actually decrease entropy, because no matter where you started out, you would end up at the same place. The laws of physics, developing over time, would compress the phase space.

But there is a theorem, Liouville’s Theorem, which can be proven true of our laws of physics, which says that this never happens: phase space is conserved.

The Second Law of Thermodynamics is a corollary of Liouville’s Theorem: no matter how clever your configuration of wheels and gears, you’ll never be able to decrease entropy in one subsystem without increasing it somewhere else. When the phase space of one subsystem narrows, the phase space of another subsystem must widen, and the joint space keeps the same volume.

Except that what was initially a compact phase space, may develop squiggles and wiggles and convolutions; so that to draw a simple boundary around the whole mess, you must draw a much larger boundary than before—this is what gives the appearance of entropy increasing. (And in quantum systems, where different universes go different ways, entropy actually does increase in any local universe. But omit this complication for now.)

The Second Law of Thermodynamics is actually probabilistic in nature—if you ask about the probability of hot water spontaneously entering the “cold water and electricity” state, the probability does exist, it’s just very small. This doesn’t mean Liouville’s Theorem is violated with small probability; a theorem’s a theorem, after all. It means that if you’re in a great big phase space volume at the start, but you don’t know where, you may assess a tiny little probability of ending up in some particular phase space volume. So far as you know, with infinitesimal probability, this particular glass of hot water may be the kind that spontaneously transforms itself to electrical current and ice cubes. (Neglecting, as usual, quantum effects.)

So the Second Law really is inherently Bayesian. When it comes to any real thermodynamic system, it’s a strictly lawful statement of your beliefs about the system, but only a probabilistic statement about the system itself.

“Hold on,” you say. “That’s not what I learned in physics class,” you say. “In the lectures I heard, thermodynamics is about, you know, temperatures. Uncertainty is a subjective state of mind! The temperature of a glass of water is an objective property of the water! What does heat have to do with probability?”

Oh ye of little trust.

In one direction, the connection between heat and probability is relatively straightforward: If the only fact you know about a glass of water is its temperature, then you are much more uncertain about a hot glass of water than a cold glass of water.

Heat is the zipping around of lots of tiny molecules; the hotter they are, the faster they can go. Not all the molecules in hot water are travelling at the same speed—the “temperature” isn’t a uniform speed of all the molecules, it’s an average speed of the molecules, which in turn corresponds to a predictable statistical distribution of speeds—anyway, the point is that, the hotter the water, the faster the water molecules could be going, and hence, the more uncertain you are about the velocity (not just speed) of any individual molecule. When you multiply together your uncertainties about all the individual molecules, you will be exponentially more uncertain about the whole glass of water.

We take the logarithm of this exponential volume of uncertainty, and call that the entropy. So it all works out, you see.

The connection in the other direction is less obvious. Suppose there was a glass of water, about which, initially, you knew only that its temperature was 72 degrees. Then, suddenly, Saint Laplace reveals to you the exact locations and velocities of all the atoms in the water. You now know perfectly the state of the water, so, by the information-theoretic definition of entropy, its entropy is zero. Does that make its thermodynamic entropy zero? Is the water colder, because we know more about it?

Ignoring quantumness for the moment, the answer is: Yes! Yes it is!

Maxwell once asked: Why can’t we take a uniformly hot gas, and partition it into two volumes A and B, and let only fast-moving molecules pass from B to A, while only slow-moving molecules are allowed to pass from A to B? If you could build a gate like this, soon you would have hot gas on the A side, and cold gas on the B side. That would be a cheap way to refrigerate food, right?

The agent who inspects each gas molecule, and decides whether to let it through, is known as “Maxwell’s Demon.” And the reason you can’t build an efficient refrigerator this way, is that Maxwell’s Demon generates entropy in the process of inspecting the gas molecules and deciding which ones to let through.

But suppose you already knew where all the gas molecules were?

Then you actually could run Maxwell’s Demon and extract useful work.

So (again ignoring quantum effects for the moment), if you know the states of all the molecules in a glass of hot water, it is cold in a genuinely thermodynamic sense: you can take electricity out of it and leave behind an ice cube.

This doesn’t violate Liouville’s Theorem, because if Y is the water, and you are Maxwell’s Demon (denoted M), the physical process behaves as:

M₁Y₁ → M₁Y₁

M₂Y₂ → M₂Y₁

M₃Y₃ → M₃Y₁

M₄Y₄ → M₄Y₁.

Because Maxwell’s demon knows the exact state of Y, this is mutual information between M and Y. The mutual information decreases the joint entropy of (M,Y): we have H(M,Y) = H(M) + H(Y) - I(M;Y). The demon M has 2 bits of entropy, Y has two bits of entropy, and their mutual information is 2 bits, so (M,Y) has a total of 2 + 2 - 2 = 2 bits of entropy. The physical process just transforms the “coldness” (negative entropy, or negentropy) of the mutual information to make the actual water cold—afterward, M has 2 bits of entropy, Y has 0 bits of entropy, and the mutual information is 0. Nothing wrong with that!

And don’t tell me that knowledge is “subjective.” Knowledge has to be represented in a brain, and that makes it as physical as anything else. For M to physically represent an accurate picture of the state of Y, it must be that M’s physical state correlates with the state of Y. You can take thermodynamic advantage of that—it’s called a Szilárd engine.

Or as E. T. Jaynes put it, “The old adage ‘knowledge is power’ is a very cogent truth, both in human relations and in thermodynamics.”

And conversely, one subsystem cannot increase in mutual information with another subsystem, without (a) interacting with it and (b) doing thermodynamic work.

Otherwise you could build a Maxwell’s Demon and violate the Second Law of Thermodynamics—which in turn would violate Liouville’s Theorem—which is prohibited in the standard model of physics.

Which is to say: To form accurate beliefs about something, you really do have to observe it. It’s a very physical, very real process: any rational mind does “work” in the thermodynamic sense, not just the sense of mental effort.

(It is sometimes said that it is erasing bits in order to prepare for the next observation that takes the thermodynamic work—but that distinction is just a matter of words and perspective; the math is unambiguous.)

(Discovering logical “truths” is a complication which I will not, for now, consider—at least in part because I am still thinking through the exact formalism myself. In thermodynamics, knowledge of logical truths does not count as negentropy; as would be expected, since a reversible computer can compute logical truths at arbitrarily low cost. All this that I have said is true of the logically omniscient: any lesser mind will necessarily be less efficient.)

“Forming accurate beliefs requires a corresponding amount of evidence” is a very cogent truth both in human relations and in thermodynamics: if blind faith actually worked as a method of investigation, you could turn warm water into electricity and ice cubes. Just build a Maxwell’s Demon that has blind faith in molecule velocities.

Engines of cognition are not so different from heat engines, though they manipulate entropy in a more subtle form than burning gasoline. For example, to the extent that an engine of cognition is not perfectly efficient, it must radiate waste heat, just like a car engine or refrigerator.

“Cold rationality” is true in a sense that Hollywood scriptwriters never dreamed (and false in the sense that they did dream).

So unless you can tell me which specific step in your argument violates the laws of physics by giving you true knowledge of the unseen, don’t expect me to believe that a big, elaborate clever argument can do it either.

187
Perpetual Motion Beliefs

The last essay concluded:

To form accurate beliefs about something, you really do have to observe it. It’s a very physical, very real process: any rational mind does “work” in the thermodynamic sense, not just the sense of mental effort . . . So unless you can tell me which specific step in your argument violates the laws of physics by giving you true knowledge of the unseen, don’t expect me to believe that a big, elaborate clever argument can do it either.

One of the chief morals of the mathematical analogy between thermodynamics and cognition is that the constraints of probability are inescapable; probability may be a “subjective state of belief,” but the laws of probability are harder than steel.

People learn under the traditional school regimen that the teacher tells you certain things, and you must believe them and recite them back; but if a mere student suggests a belief, you do not have to obey it. They map the domain of belief onto the domain of authority, and think that a certain belief is like an order that must be obeyed, but a probabilistic belief is like a mere suggestion.

They look at a lottery ticket, and say, “But you can’t prove I won’t win, right?” Meaning: “You may have calculated a low probability of winning, but since it is a probability, it’s just a suggestion, and I am allowed to believe what I want.”

Here’s a little experiment: Smash an egg on the floor. The rule that says that the egg won’t spontaneously reform and leap back into your hand is merely probabilistic. A suggestion, if you will. The laws of thermodynamics are probabilistic, so they can’t really be laws, the way that “Thou shalt not murder” is a law . . . right?

So why not just ignore the suggestion? Then the egg will unscramble itself . . . right?

It may help to think of it this way—if you still have some lingering intuition that uncertain beliefs are not authoritative:

In reality, there may be a very small chance that the egg spontaneously reforms. But you cannot expect it to reform. You must expect it to smash. Your mandatory belief is that the egg’s probability of spontaneous reformation is ~0. Probabilities are not certainties, but the laws of probability are theorems.

If you doubt this, try dropping an egg on the floor a few decillion times, ignoring the thermodynamic suggestion and expecting it to spontaneously reassemble, and see what happens. Probabilities may be subjective states of belief, but the laws governing them are stronger by far than steel. I once knew a fellow who was convinced that his system of wheels and gears would produce reactionless thrust, and he had an Excel spreadsheet that would prove this—which of course he couldn’t show us because he was still developing the system. In classical mechanics, violating Conservation of Momentum is provably impossible. So any Excel spreadsheet calculated according to the rules of classical mechanics must necessarily show that no reactionless thrust exists—unless your machine is complicated enough that you have made a mistake in the calculations.

And similarly, when half-trained or tenth-trained rationalists abandon their art and try to believe without evidence just this once, they often build vast edifices of justification, confusing themselves just enough to conceal the magical steps.

It can be quite a pain to nail down where the magic occurs—their structure of argument tends to morph and squirm away as you interrogate them. But there’s always some step where a tiny probability turns into a large one—where they try to believe without evidence—where they step into the unknown, thinking, “No one can prove me wrong.”

Their foot naturally lands on thin air, for there is far more thin air than ground in the realms of Possibility. Ah, but there is an (exponentially tiny) amount of ground in Possibility, and you do have an (exponentially tiny) probability of hitting it by luck, so maybe this time, your foot will land in the right place! It is merely a probability, so it must be merely a suggestion.

The exact state of a glass of boiling-hot water may be unknown to you—indeed, your ignorance of its exact state is what makes the molecules’ kinetic energy “heat,” rather than work waiting to be extracted like the momentum of a spinning flywheel. So the water might cool down your hand instead of heating it up, with probability ~0.

Decide to ignore the laws of thermodynamics and stick your hand in anyway, and you’ll get burned.

“But you don’t know that!”

I don’t know it with certainty, but it is mandatory that I expect it to happen. Probabilities are not logical truths, but the laws of probability are.

“But what if I guess the state of the boiling water, and I happen to guess correctly?”

Your chance of guessing correctly by luck, is even less than the chance of the boiling water cooling your hand by luck.

“But you can’t prove I won’t guess correctly.”

I can (indeed, must) assign extremely low probability to it.

“That’s not the same as certainty, though.”

Hey, maybe if you add enough wheels and gears to your argument, it’ll turn warm water into electricity and ice cubes! Or, rather, you will no longer see why this couldn’t be the case.

“Right! I can’t see why couldn’t be the case! So maybe it is!”

Another gear? That just makes your machine even less efficient. It wasn’t a perpetual motion machine before, and each extra gear you add makes it even less efficient than that.

Each extra detail in your argument necessarily decreases the joint probability. The probability that you’ve violated the Second Law of Thermodynamics without knowing exactly how, by guessing the exact state of boiling water without evidence, so that you can stick your finger in without getting burned, is, necessarily, even less than the probability of sticking in your finger into boiling water without getting burned.

I say all this, because people really do construct these huge edifices of argument in the course of believing without evidence. One must learn to see this as analogous to all the wheels and gears that fellow added onto his reactionless drive, until he finally collected enough complications to make a mistake in his Excel spreadsheet.

188
Searching for BayesStructure

Gnomish helms should not function. Their very construction seems to defy the nature of thaumaturgical law. In fact, they are impossible. Like most products of gnomish minds, they include a large number of bells and whistles, and very little substance. Those that work usually have a minor helm contained within, always hidden away, disguised to appear innocuous and inessential.

—Spelljammer campaign set

We have seen that knowledge implies mutual information between a mind and its environment, and we have seen that this mutual information is negentropy in a very physical sense: If you know where molecules are and how fast they’re moving, you can turn heat into work via a Maxwell’s Demon / Szilárd engine.

We have seen that forming true beliefs without evidence is the same sort of improbability as a hot glass of water spontaneously reorganizing into ice cubes and electricity. Rationality takes “work” in a thermodynamic sense, not just the sense of mental effort; minds have to radiate heat if they are not perfectly efficient. This cognitive work is governed by probability theory, of which thermodynamics is a special case. (Statistical mechanics is a special case of statistics.)

If you saw a machine continually spinning a wheel, apparently without being plugged into a wall outlet or any other source of power, then you would look for a hidden battery, or a nearby broadcast power source—something to explain the work being done, without violating the laws of physics.

So if a mind is arriving at true beliefs, and we assume that the Second Law of Thermodynamics has not been violated, that mind must be doing something at least vaguely Bayesian—at least one process with a sort-of Bayesian structure somewhere—or it couldn’t possibly work.

In the beginning, at time T = 0, a mind has no mutual information with a subsystem S in its environment. At time T = 1, the mind has 10 bits of mutual information with S. Somewhere in between, the mind must have encountered evidence—under the Bayesian definition of evidence, because all Bayesian evidence is mutual information and all mutual information is Bayesian evidence, they are just different ways of looking at it—and processed at least some of that evidence, however inefficiently, in the right direction according to Bayes on at least some occasions. The mind must have moved in harmony with the Bayes at least a little, somewhere along the line—either that or violated the Second Law of Thermodynamics by creating mutual information from nothingness.

In fact, any part of a cognitive process that contributes usefully to truth-finding must have at least a little Bayesian structure—must harmonize with Bayes, at some point or another—must partially conform with the Bayesian flow, however noisily—despite however many disguising bells and whistles—even if this Bayesian structure is only apparent in the context of surrounding processes. Or it couldn’t even help.

How philosophers pondered the nature of words! All the ink spent on the true definitions of words, and the true meaning of definitions, and the true meaning of meaning! What collections of gears and wheels they built, in their explanations! And all along, it was a disguised form of Bayesian inference!

I was actually a bit disappointed that no one in the audience jumped up and said: “Yes! Yes, that’s it! Of course! It was really Bayes all along!”

But perhaps it is not quite as exciting to see something that doesn’t look Bayesian on the surface, revealed as Bayes wearing a clever disguise, if: (a) you don’t unravel the mystery yourself, but read about someone else doing it (Newton had more fun than most students taking calculus), and (b) you don’t realize that searching for the hidden Bayesstructure is this huge, difficult, omnipresent quest, like searching for the Holy Grail.

It’s a different quest for each facet of cognition, but the Grail always turns out to be the same. It has to be the right Grail, though—and the entire Grail, without any parts missing—and so each time you have to go on the quest looking for a full answer whatever form it may take, rather than trying to artificially construct vaguely hand-waving Grailish arguments. Then you always find the same Holy Grail at the end.

It was previously pointed out to me that I might be losing some of my readers with the long essays, because I hadn’t “made it clear where I was going” . . .

. . . but it’s not so easy to just tell people where you’re going, when you’re going somewhere like that.

It’s not very helpful to merely know that a form of cognition is Bayesian, if you don’t know how it is Bayesian. If you can’t see the detailed flow of probability, you have nothing but a password—or, a bit more charitably, a hint at the form an answer would take; but certainly not an answer. That’s why there’s a Grand Quest for the Hidden BayesStructure, rather than being done when you say “Bayes!” Bayesstructure can be buried under all kinds of disguises, hidden behind thickets of wheels and gears, obscured by bells and whistles.

The way you begin to grasp the Quest for the Holy Bayes is that you learn about cognitive phenomenon XYZ, which seems really useful—and there’s this bunch of philosophers who’ve been arguing about its true nature for centuries, and they are still arguing—and there’s a bunch of AI scientists trying to make a computer do it, but they can’t agree on the philosophy either—

And—Huh, that’s odd!—this cognitive phenomenon didn’t look anything like Bayesian on the surface, but there’s this non-obvious underlying structure that has a Bayesian interpretation—but wait, there’s still some useful work getting done that can’t be explained in Bayesian terms—no wait, that’s Bayesian too—OH MY GOD this completely different cognitive process, that also didn’t look Bayesian on the surface, ALSO HAS BAYESIAN STRUCTURE—hold on, are these non-Bayesian parts even doing anything?

Yes: Wow, those are Bayesian too!
No: Dear heavens, what a stupid design. I could eat a bucket of amino acids and puke a better brain architecture than that.

Once this happens to you a few times, you kinda pick up the rhythm. That’s what I’m talking about here, the rhythm.

Trying to talk about the rhythm is like trying to dance about architecture.

This left me in a bit of a pickle when it came to trying to explain in advance where I was going. I know from experience that if I say, “Bayes is the secret of the universe,” some people may say “Yes! Bayes is the secret of the universe!”; and others will snort and say, “How narrow-minded you are; look at all these other ad-hoc but amazingly useful methods, like regularized linear regression, that I have in my toolbox.”

I hoped that with a specific example in hand of “something that doesn’t look all that Bayesian on the surface, but turns out to be Bayesian after all”—and an explanation of the difference between passwords and knowledge—and an explanation of the difference between tools and laws—maybe then I could convey such of the rhythm as can be understood without personally going on the quest.

Of course this is not the full Secret of the Bayesian Conspiracy, but it’s all that I can convey at this point. Besides, the complete secret is known only to the Bayes Council, and if I told you, I’d have to hire you.

To see through the surface adhockery of a cognitive process, to the Bayesian structure underneath—to perceive the probability flows, and know how, not just know that, this cognition too is Bayesian—as it always is—as it always must be—to be able to sense the Force underlying all cognition—this, is the Bayes-Sight.

“. . . And the Queen of Kashfa sees with the Eye of the Serpent.”

“I don’t know that she sees with it,” I said. “She’s still recovering from the operation. But that’s an interesting thought. If she could see with it, what might she behold?”

“The clear, cold lines of eternity, I daresay. Beneath all Shadow.”

—Roger Zelazny, Prince of Chaos¹

1. Roger Zelazny, Prince of Chaos (Thorndike Press, 2001).

Part P
Reductionism 101

189
Dissolving the Question

“If a tree falls in the forest, but no one hears it, does it make a sound?”

I didn’t answer that question. I didn’t pick a position “Yes!” or “No!” and defend it. Instead I went off and deconstructed the human algorithm for processing words, even going so far as to sketch an illustration of a neural network. At the end, I hope, there was no question left—not even the feeling of a question.

Many philosophers—particularly amateur philosophers, and ancient philosophers—share a dangerous instinct: If you give them a question, they try to answer it.

Like, say, “Do we have free will?”

The dangerous instinct of philosophy is to marshal the arguments in favor, and marshal the arguments against, and weigh them up, and publish them in a prestigious journal of philosophy, and so finally conclude: “Yes, we must have free will,” or “No, we cannot possibly have free will.”

Some philosophers are wise enough to recall the warning that most philosophical disputes are really disputes over the meaning of a word, or confusions generated by using different meanings for the same word in different places. So they try to define very precisely what they mean by “free will,” and then ask again, “Do we have free will? Yes or no?”

A philosopher wiser yet may suspect that the confusion about “free will” shows the notion itself is flawed. So they pursue the Traditional Rationalist course: They argue that “free will” is inherently self-contradictory, or meaningless because it has no testable consequences. And then they publish these devastating observations in a prestigious philosophy journal.

But proving that you are confused may not make you feel any less confused. Proving that a question is meaningless may not help you any more than answering it.

The philosopher’s instinct is to find the most defensible position, publish it, and move on. But the “naive” view, the instinctive view, is a fact about human psychology. You can prove that free will is impossible until the Sun goes cold, but this leaves an unexplained fact of cognitive science: If free will doesn’t exist, what goes on inside the head of a human being who thinks it does? This is not a rhetorical question!

It is a fact about human psychology that people think they have free will. Finding a more defensible philosophical position doesn’t change, or explain, that psychological fact. Philosophy may lead you to reject the concept, but rejecting a concept is not the same as understanding the cognitive algorithms behind it.

You could look at the Standard Dispute over “If a tree falls in the forest, and no one hears it, does it make a sound?,” and you could do the Traditional Rationalist thing: Observe that the two don’t disagree on any point of anticipated experience, and triumphantly declare the argument pointless. That happens to be correct in this particular case; but, as a question of cognitive science, why did the arguers make that mistake in the first place?

The key idea of the heuristics and biases program is that the mistakes we make often reveal far more about our underlying cognitive algorithms than our correct answers. So (I asked myself, once upon a time) what kind of mind design corresponds to the mistake of arguing about trees falling in deserted forests?

The cognitive algorithms we use are the way the world feels. And these cognitive algorithms may not have a one-to-one correspondence with reality—not even macroscopic reality, to say nothing of the true quarks. There can be things in the mind that cut skew to the world.

For example, there can be a dangling unit in the center of a neural network, which does not correspond to any real thing, or any real property of any real thing, existent anywhere in the real world. This dangling unit is often useful as a shortcut in computation, which is why we have them. (Metaphorically speaking. Human neurobiology is surely far more complex.)

This dangling unit feels like an unresolved question, even after every answerable query is answered. No matter how much anyone proves to you that no difference of anticipated experience depends on the question, you’re left wondering: “But does the falling tree really make a sound, or not?”

But once you understand in detail how your brain generates the feeling of the question—once you realize that your feeling of an unanswered question corresponds to an illusory central unit wanting to know whether it should fire, even after all the edge units are clamped at known values—or better yet, you understand the technical workings of Naive Bayes—then you’re done. Then there’s no lingering feeling of confusion, no vague sense of dissatisfaction.

If there is any lingering feeling of a remaining unanswered question, or of having been fast-talked into something, then this is a sign that you have not dissolved the question. A vague dissatisfaction should be as much warning as a shout. Really dissolving the question doesn’t leave anything behind.

A triumphant thundering refutation of free will, an absolutely unarguable proof that free will cannot exist, feels very satisfying—a grand cheer for the home team. And so you may not notice that—as a point of cognitive science—you do not have a full and satisfactory descriptive explanation of how each intuitive sensation arises, point by point.

You may not even want to admit your ignorance of this point of cognitive science, because that would feel like a score against Your Team. In the midst of smashing all foolish beliefs of free will, it would seem like a concession to the opposing side to concede that you’ve left anything unexplained.

And so, perhaps, you’ll come up with a just-so evolutionary-psychological argument that hunter-gatherers who believed in free will were more likely to take a positive outlook on life, and so outreproduce other hunter-gatherers—to give one example of a completely bogus explanation. If you say this, you are arguing that the brain generates an illusion of free will—but you are not explaining how. You are trying to dismiss the opposition by deconstructing its motives—but in the story you tell, the illusion of free will is a brute fact. You have not taken the illusion apart to see the wheels and gears.

Imagine that in the Standard Dispute about a tree falling in a deserted forest, you first prove that no difference of anticipation exists, and then go on to hypothesize, “But perhaps people who said that arguments were meaningless were viewed as having conceded, and so lost social status, so now we have an instinct to argue about the meanings of words.” That’s arguing that or explaining why a confusion exists. Now look at the neural network structure in Feel the Meaning. That’s explaining how, disassembling the confusion into smaller pieces that are not themselves confusing. See the difference?

Coming up with good hypotheses about cognitive algorithms (or even hypotheses that hold together for half a second) is a good deal harder than just refuting a philosophical confusion. Indeed, it is an entirely different art. Bear this in mind, and you should feel less embarrassed to say, “I know that what you say can’t possibly be true, and I can prove it. But I cannot write out a flowchart which shows how your brain makes the mistake, so I’m not done yet, and will continue investigating.”

I say all this, because it sometimes seems to me that at least 20% of the real-world effectiveness of a skilled rationalist comes from not stopping too early. If you keep asking questions, you’ll get to your destination eventually. If you decide too early that you’ve found an answer, you won’t.

The challenge, above all, is to notice when you are confused—even if it just feels like a little tiny bit of confusion—and even if there’s someone standing across from you, insisting that humans have free will, and smirking at you, and the fact that you don’t know exactly how the cognitive algorithms work, has nothing to do with the searing folly of their position . . .

But when you can lay out the cognitive algorithm in sufficient detail that you can walk through the thought process, step by step, and describe how each intuitive perception arises—decompose the confusion into smaller pieces not themselves confusing—then you’re done.

So be warned that you may believe you’re done, when all you have is a mere triumphant refutation of a mistake.

But when you’re really done, you’ll know you’re done. Dissolving the question is an unmistakable feeling—once you experience it, and, having experienced it, resolve not to be fooled again. Those who dream do not know they dream, but when you wake you know you are awake.

Which is to say: When you’re done, you’ll know you’re done, but unfortunately the reverse implication does not hold.

So here’s your homework problem: What kind of cognitive algorithm, as felt from the inside, would generate the observed debate about “free will”?

Your assignment is not to argue about whether people have free will, or not.

Your assignment is not to argue that free will is compatible with determinism, or not.

Your assignment is not to argue that the question is ill-posed, or that the concept is self-contradictory, or that it has no testable consequences.

You are not asked to invent an evolutionary explanation of how people who believed in free will would have reproduced; nor an account of how the concept of free will seems suspiciously congruent with bias X. Such are mere attempts to explain why people believe in “free will,” not explain how.

Your homework assignment is to write a stack trace of the internal algorithms of the human mind as they produce the intuitions that power the whole damn philosophical argument.

This is one of the first real challenges I tried as an aspiring rationalist, once upon a time. One of the easier conundrums, relatively speaking. May it serve you likewise.

190
Wrong Questions

Where the mind cuts against reality’s grain, it generates wrong questions—questions that cannot possibly be answered on their own terms, but only dissolved by understanding the cognitive algorithm that generates the perception of a question.

One good cue that you’re dealing with a “wrong question” is when you cannot even imagine any concrete, specific state of how-the-world-is that would answer the question. When it doesn’t even seem possible to answer the question.

Take the Standard Definitional Dispute, for example, about the tree falling in a deserted forest. Is there any way-the-world-could-be—any state of affairs—that corresponds to the word “sound” really meaning only acoustic vibrations, or really meaning only auditory experiences?

(“Why, yes,” says the one, “it is the state of affairs where ‘sound’ means acoustic vibrations.” So Taboo the word “means,” and “represents,” and all similar synonyms, and describe again: What way-the-world-can-be, what state of affairs, would make one side right, and the other side wrong?)

Or if that seems too easy, take free will: What concrete state of affairs, whether in deterministic physics, or in physics with a dice-rolling random component, could ever correspond to having free will?

And if that seems too easy, then ask “Why does anything exist at all?,” and then tell me what a satisfactory answer to that question would even look like.

And no, I don’t know the answer to that last one. But I can guess one thing, based on my previous experience with unanswerable questions. The answer will not consist of some grand triumphant First Cause. The question will go away as a result of some insight into how my mental algorithms run skew to reality, after which I will understand how the question itself was wrong from the beginning—how the question itself assumed the fallacy, contained the skew.

Mystery exists in the mind, not in reality. If I am ignorant about a phenomenon, that is a fact about my state of mind, not a fact about the phenomenon itself. All the more so if it seems like no possible answer can exist: Confusion exists in the map, not in the territory. Unanswerable questions do not mark places where magic enters the universe. They mark places where your mind runs skew to reality.

Such questions must be dissolved. Bad things happen when you try to answer them. It inevitably generates the worst sort of Mysterious Answer to a Mysterious Question: The one where you come up with seemingly strong arguments for your Mysterious Answer, but the “answer” doesn’t let you make any new predictions even in retrospect, and the phenomenon still possesses the same sacred inexplicability that it had at the start.

I could guess, for example, that the answer to the puzzle of the First Cause is that nothing does exist—that the whole concept of “existence” is bogus. But if you sincerely believed that, would you be any less confused? Me neither.

But the wonderful thing about unanswerable questions is that they are always solvable, at least in my experience. What went through Queen Elizabeth I’s mind, first thing in the morning, as she woke up on her fortieth birthday? As I can easily imagine answers to this question, I can readily see that I may never be able to actually answer it, the true information having been lost in time.

On the other hand, “Why does anything exist at all?” seems so absolutely impossible that I can infer that I am just confused, one way or another, and the truth probably isn’t all that complicated in an absolute sense, and once the confusion goes away I’ll be able to see it.

This may seem counterintuitive if you’ve never solved an unanswerable question, but I assure you that it is how these things work.

Coming next: a simple trick for handling “wrong questions.”

191
Righting a Wrong Question

When you are faced with an unanswerable question—a question to which it seems impossible to even imagine an answer—there is a simple trick that can turn the question solvable.

Compare:

“Why do I have free will?”
“Why do I think I have free will?”

The nice thing about the second question is that it is guaranteed to have a real answer, whether or not there is any such thing as free will. Asking “Why do I have free will?” or “Do I have free will?” sends you off thinking about tiny details of the laws of physics, so distant from the macroscopic level that you couldn’t begin to see them with the naked eye. And you’re asking “Why is X the case?” where X may not be coherent, let alone the case.

“Why do I think I have free will?,” in contrast, is guaranteed answerable. You do, in fact, believe you have free will. This belief seems far more solid and graspable than the ephemerality of free will. And there is, in fact, some nice solid chain of cognitive cause and effect leading up to this belief.

If you’ve already outgrown free will, choose one of these substitutes:

“Why does time move forward instead of backward?” versus “Why do I think time moves forward instead of backward?”
“Why was I born as myself rather than someone else?” versus “Why do I think I was born as myself rather than someone else?”
“Why am I conscious?” versus “Why do I think I’m conscious?”
“Why does reality exist?” versus “Why do I think reality exists?”

The beauty of this method is that it works whether or not the question is confused. As I type this, I am wearing socks. I could ask “Why am I wearing socks?” or “Why do I believe I’m wearing socks?” Let’s say I ask the second question. Tracing back the chain of causality, I find:

I believe I’m wearing socks, because I can see socks on my feet.
I see socks on my feet, because my retina is sending sock signals to my visual cortex.
My retina is sending sock signals, because sock-shaped light is impinging on my retina.
Sock-shaped light impinges on my retina, because it reflects from the socks I’m wearing.
It reflects from the socks I’m wearing, because I’m wearing socks.
I’m wearing socks because I put them on.
I put socks on because I believed that otherwise my feet would get cold.
Et cetera.

Tracing back the chain of causality, step by step, I discover that my belief that I’m wearing socks is fully explained by the fact that I’m wearing socks. This is right and proper, as you cannot gain information about something without interacting with it.

On the other hand, if I see a mirage of a lake in a desert, the correct causal explanation of my vision does not involve the fact of any actual lake in the desert. In this case, my belief in the lake is not just explained, but explained away.

But either way, the belief itself is a real phenomenon taking place in the real universe—psychological events are events—and its causal history can be traced back.

“Why is there a lake in the middle of the desert?” may fail if there is no lake to be explained. But “Why do I perceive a lake in the middle of the desert?” always has a causal explanation, one way or the other.

Perhaps someone will see an opportunity to be clever, and say: “Okay. I believe in free will because I have free will. There, I’m done.” Of course it’s not that easy.

My perception of socks on my feet is an event in the visual cortex. The workings of the visual cortex can be investigated by cognitive science, should they be confusing.

My retina receiving light is not a mystical sensing procedure, a magical sock detector that lights in the presence of socks for no explicable reason; there are mechanisms that can be understood in terms of biology. The photons entering the retina can be understood in terms of optics. The shoe’s surface reflectance can be understood in terms of electromagnetism and chemistry. My feet getting cold can be understood in terms of thermodynamics.

So it’s not as easy as saying, “I believe I have free will because I have it—there, I’m done!” You have to be able to break the causal chain into smaller steps, and explain the steps in terms of elements not themselves confusing.

The mechanical interaction of my retina with my socks is quite clear, and can be described in terms of non-confusing components like photons and electrons. Where’s the free-will-sensor in your brain, and how does it detect the presence or absence of free will? How does the sensor interact with the sensed event, and what are the mechanical details of the interaction?

If your belief does derive from valid observation of a real phenomenon, we will eventually reach that fact, if we start tracing the causal chain backward from your belief.

If what you are really seeing is your own confusion, tracing back the chain of causality will find an algorithm that runs skew to reality.

Either way, the question is guaranteed to have an answer. You even have a nice, concrete place to begin tracing—your belief, sitting there solidly in your mind.

Cognitive science may not seem so lofty and glorious as metaphysics. But at least questions of cognitive science are solvable. Finding an answer may not be easy, but at least an answer exists.

Oh, and also: the idea that cognitive science is not so lofty and glorious as metaphysics is simply wrong. Some readers are beginning to notice this, I hope.

192
Mind Projection Fallacy

In the dawn days of science fiction, alien invaders would occasionally kidnap a girl in a torn dress and carry her off for intended ravishing, as lovingly depicted on many ancient magazine covers. Oddly enough, the aliens never go after men in torn shirts.

Would a non-humanoid alien, with a different evolutionary history and evolutionary psychology, sexually desire a human female? It seems rather unlikely. To put it mildly.

People don’t make mistakes like that by deliberately reasoning: “All possible minds are likely to be wired pretty much the same way, therefore a bug-eyed monster will find human females attractive.” Probably the artist did not even think to ask whether an alien perceives human females as attractive. Instead, a human female in a torn dress is sexy—inherently so, as an intrinsic property.

They who went astray did not think about the alien’s evolutionary history; they focused on the woman’s torn dress. If the dress were not torn, the woman would be less sexy; the alien monster doesn’t enter into it.

Apparently we instinctively represent Sexiness as a direct attribute of the Woman data structure, Woman.sexiness, like Woman.height or Woman.weight.

If your brain uses that data structure, or something metaphorically similar to it, then from the inside it feels like sexiness is an inherent property of the woman, not a property of the alien looking at the woman. Since the woman is attractive, the alien monster will be attracted to her—isn’t that logical?

E. T. Jaynes used the term Mind Projection Fallacy to denote the error of projecting your own mind’s properties into the external world. Jaynes, as a late grand master of the Bayesian Conspiracy, was most concerned with the mistreatment of probabilities as inherent properties of objects, rather than states of partial knowledge in some particular mind. More about this shortly.

But the Mind Projection Fallacy generalizes as an error. It is in the argument over the real meaning of the word sound, and in the magazine cover of the monster carrying off a woman in the torn dress, and Kant’s declaration that space by its very nature is flat, and Hume’s definition of a priori ideas as those “discoverable by the mere operation of thought, without dependence on what is anywhere existent in the universe” . . .

(Incidentally, I once read a science fiction story about a human male who entered into a sexual relationship with a sentient alien plant of appropriately squishy fronds; discovered that it was an androecious (male) plant; agonized about this for a bit; and finally decided that it didn’t really matter at that point. And in Foglio and Pollotta’s Illegal Aliens, the humans land on a planet inhabited by sentient insects, and see a movie advertisement showing a human carrying off a bug in a delicate chiffon dress. Just thought I’d mention that.)

193
Probability is in the Mind

In the previous essay I spoke of the Mind Projection Fallacy, giving the example of the alien monster who carries off a girl in a torn dress for intended ravishing—a mistake which I imputed to the artist’s tendency to think that a woman’s sexiness is a property of the woman herself, Woman.sexiness, rather than something that exists in the mind of an observer, and probably wouldn’t exist in an alien mind.

The term “Mind Projection Fallacy” was coined by the late great Bayesian Master E. T. Jaynes, as part of his long and hard-fought battle against the accursèd frequentists. Jaynes was of the opinion that probabilities were in the mind, not in the environment—that probabilities express ignorance, states of partial information; and if I am ignorant of a phenomenon, that is a fact about my state of mind, not a fact about the phenomenon.

I cannot do justice to this ancient war in a few words—but the classic example of the argument runs thus:

You have a coin.

The coin is biased.

You don’t know which way it’s biased or how much it’s biased. Someone just told you “The coin is biased,” and that’s all they said.

This is all the information you have, and the only information you have.

You draw the coin forth, flip it, and slap it down.

Now—before you remove your hand and look at the result—are you willing to say that you assign a 0.5 probability to the coin’s having come up heads?

The frequentist says, “No. Saying ‘probability 0.5’ means that the coin has an inherent propensity to come up heads as often as tails, so that if we flipped the coin infinitely many times, the ratio of heads to tails would approach 1:1. But we know that the coin is biased, so it can have any probability of coming up heads except 0.5.”

The Bayesian says, “Uncertainty exists in the map, not in the territory. In the real world, the coin has either come up heads, or come up tails. Any talk of ‘probability’ must refer to the information that I have about the coin—my state of partial ignorance and partial knowledge—not just the coin itself. Furthermore, I have all sorts of theorems showing that if I don’t treat my partial knowledge a certain way, I’ll make stupid bets. If I’ve got to plan, I’ll plan for a 50/50 state of uncertainty, where I don’t weigh outcomes conditional on heads any more heavily in my mind than outcomes conditional on tails. You can call that number whatever you like, but it has to obey the probability laws on pain of stupidity. So I don’t have the slightest hesitation about calling my outcome-weighting a probability.”

I side with the Bayesians. You may have noticed that about me.

Even before a fair coin is tossed, the notion that it has an inherent 50% probability of coming up heads may be just plain wrong. Maybe you’re holding the coin in such a way that it’s just about guaranteed to come up heads, or tails, given the force at which you flip it, and the air currents around you. But, if you don’t know which way the coin is biased on this one occasion, so what?

I believe there was a lawsuit where someone alleged that the draft lottery was unfair, because the slips with names on them were not being mixed thoroughly enough; and the judge replied, “To whom is it unfair?”

To make the coinflip experiment repeatable, as frequentists are wont to demand, we could build an automated coinflipper, and verify that the results were 50% heads and 50% tails. But maybe a robot with extra-sensitive eyes and a good grasp of physics, watching the autoflipper prepare to flip, could predict the coin’s fall in advance—not with certainty, but with 90% accuracy. Then what would the real probability be?

There is no “real probability.” The robot has one state of partial information. You have a different state of partial information. The coin itself has no mind, and doesn’t assign a probability to anything; it just flips into the air, rotates a few times, bounces off some air molecules, and lands either heads or tails.

So that is the Bayesian view of things, and I would now like to point out a couple of classic brainteasers that derive their brain-teasing ability from the tendency to think of probabilities as inherent properties of objects.

Let’s take the old classic: You meet a mathematician on the street, and she happens to mention that she has given birth to two children on two separate occasions. You ask: “Is at least one of your children a boy?” The mathematician says, “Yes, he is.”

What is the probability that she has two boys? If you assume that the prior probability of a child’s being a boy is 1/2, then the probability that she has two boys, on the information given, is 1/3. The prior probabilities were: 1/4 two boys, 1/2 one boy one girl, 1/4 two girls. The mathematician’s “Yes” response has probability 1 in the first two cases, and probability 0 in the third. Renormalizing leaves us with a 1/3 probability of two boys, and a 2/3 probability of one boy one girl.

But suppose that instead you had asked, “Is your eldest child a boy?” and the mathematician had answered “Yes.” Then the probability of the mathematician having two boys would be 1/2. Since the eldest child is a boy, and the younger child can be anything it pleases.

Likewise if you’d asked “Is your youngest child a boy?” The probability of their being both boys would, again, be 1/2.

Now, if at least one child is a boy, it must be either the oldest child who is a boy, or the youngest child who is a boy. So how can the answer in the first case be different from the answer in the latter two?

Or here’s a very similar problem: Let’s say I have four cards, the ace of hearts, the ace of spades, the two of hearts, and the two of spades. I draw two cards at random. You ask me, “Are you holding at least one ace?” and I reply “Yes.” What is the probability that I am holding a pair of aces? It is 1/5. There are six possible combinations of two cards, with equal prior probability, and you have just eliminated the possibility that I am holding a pair of twos. Of the five remaining combinations, only one combination is a pair of aces. So 1/5.

Now suppose that instead you asked me, “Are you holding the ace of spades?” If I reply “Yes,” the probability that the other card is the ace of hearts is 1/3. (You know I’m holding the ace of spades, and there are three possibilities for the other card, only one of which is the ace of hearts.) Likewise, if you ask me “Are you holding the ace of hearts?” and I reply “Yes,” the probability I’m holding a pair of aces is 1/3.

But then how can it be that if you ask me, “Are you holding at least one ace?” and I say “Yes,” the probability I have a pair is 1/5? Either I must be holding the ace of spades or the ace of hearts, as you know; and either way, the probability that I’m holding a pair of aces is 1/3.

How can this be? Have I miscalculated one or more of these probabilities?

If you want to figure it out for yourself, do so now, because I’m about to reveal . . .

That all stated calculations are correct.

As for the paradox, there isn’t one. The appearance of paradox comes from thinking that the probabilities must be properties of the cards themselves. The ace I’m holding has to be either hearts or spades; but that doesn’t mean that your knowledge about my cards must be the same as if you knew I was holding hearts, or knew I was holding spades.

It may help to think of Bayes’s Theorem:

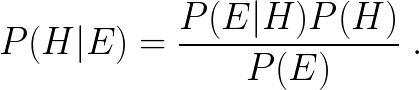
That last term, where you divide by P(E), is the part where you throw out all the possibilities that have been eliminated, and renormalize your probabilities over what remains.

Now let’s say that you ask me, “Are you holding at least one ace?” Before I answer, your probability that I say “Yes” should be 5/6.

But if you ask me “Are you holding the ace of spades?,” your prior probability that I say “Yes” is just 1/2.

So right away you can see that you’re learning something very different in the two cases. You’re going to be eliminating some different possibilities, and renormalizing using a different P(E). If you learn two different items of evidence, you shouldn’t be surprised at ending up in two different states of partial information.

Similarly, if I ask the mathematician “Is at least one of your two children a boy?” then I expect to hear “Yes” with probability 3/4, but if I ask “Is your eldest child a boy?” then I expect to hear “Yes” with probability 1/2. So it shouldn’t be surprising that I end up in a different state of partial knowledge, depending on which of the two questions I ask.

The only reason for seeing a “paradox” is thinking as though the probability of holding a pair of aces is a property of cards that have at least one ace, or a property of cards that happen to contain the ace of spades. In which case, it would be paradoxical for card-sets containing at least one ace to have an inherent pair-probability of 1/5, while card-sets containing the ace of spades had an inherent pair-probability of 1/3, and card-sets containing the ace of hearts had an inherent pair-probability of 1/3.

Similarly, if you think a 1/3 probability of being both boys is an inherent property of child-sets that include at least one boy, then that is not consistent with child-sets’ of which the eldest is male having an inherent probability of 1/2 of being both boys, and child-sets’ of which the youngest is male having an inherent 1/2 probability of being both boys. It would be like saying, “All green apples weigh a pound, and all red apples weigh a pound, and all apples that are green or red weigh half a pound.”

That’s what happens when you start thinking as if probabilities are in things, rather than probabilities being states of partial information about things.

Probabilities express uncertainty, and it is only agents who can be uncertain. A blank map does not correspond to a blank territory. Ignorance is in the mind.

194
The Quotation is Not the Referent

In classical logic, the operational definition of identity is that whenever A = B is a theorem, you can substitute A for B in any theorem where B appears. For example, if (2 + 2) = 4 is a theorem, and ((2 + 2) + 3) = 7 is a theorem, then (4 + 3) = 7 is a theorem.

This leads to a problem that is usually phrased in the following terms: The morning star and the evening star happen to be the same object, the planet Venus. Suppose John knows that the morning star and evening star are the same object. Mary, however, believes that the morning star is the god Lucifer, but the evening star is the god Venus. John believes Mary believes that the morning star is Lucifer. Must John therefore (by substitution) believe that Mary believes that the evening star is Lucifer?

Or here’s an even simpler version of the problem. The statement 2 + 2 = 4 is true; it is a theorem that (((2 + 2) = 4) = TRUE). Fermat’s Last Theorem is also true. So: I believe 2 + 2 = 4 ⇒ I believe TRUE ⇒ I believe Fermat’s Last Theorem.

Yes, I know this seems obviously wrong. But imagine someone writing a logical reasoning program using the principle “equal terms can always be substituted,” and this happening to them. Now imagine them writing a paper about how to prevent it from happening. Now imagine someone else disagreeing with their solution. The argument is still going on.

P’rsnally, I would say that John is committing a type error, like trying to subtract 5 grams from 20 meters. “The morning star” is not the same type as the morning star, let alone the same thing. Beliefs are not planets.

morning star = evening star

“morning star” ≠ “evening star”

The problem, in my view, stems from the failure to enforce the type distinction between beliefs and things. The original error was writing an AI that stores its beliefs about Mary’s beliefs about “the morning star” using the same representation as in its beliefs about the morning star.

If Mary believes the “morning star” is Lucifer, that doesn’t mean Mary believes the “evening star” is Lucifer, because “morning star” ≠ “evening star.” The whole paradox stems from the failure to use quote marks in appropriate places.

You may recall that this is not the first time I’ve talked about enforcing type discipline—the last time was when I spoke about the error of confusing expected utilities with utilities. It is immensely helpful, when one is first learning physics, to learn to keep track of one’s units—it may seem like a bother to keep writing down “cm” and “kg” and so on, until you notice that (a) your answer seems to be the wrong order of magnitude and (b) it is expressed in seconds per square gram.

Similarly, beliefs are different things than planets. If we’re talking about human beliefs, at least, then: Beliefs live in brains, planets live in space. Beliefs weigh a few micrograms, planets weigh a lot more. Planets are larger than beliefs . . . but you get the idea.

Merely putting quote marks around “morning star” seems insufficient to prevent people from confusing it with the morning star, due to the visual similarity of the text. So perhaps a better way to enforce type discipline would be with a visibly different encoding:

morning star = evening star

13.15.18.14.9.14.7.0.19.20.1.18 ≠ 5.22.5.14.9.14.7.0.19.20.1.18.

Studying mathematical logic may also help you learn to distinguish the quote and the referent. In mathematical logic, ⊢P (P is a theorem) and ⊢☐^⌈P^⌉ (it is provable that there exists an encoded proof of the encoded sentence P in some encoded proof system) are very distinct propositions. If you drop a level of quotation in mathematical logic, it’s like dropping a metric unit in physics—you can derive visibly ridiculous results, like “The speed of light is 299,792,458 meters long.”

Alfred Tarski once tried to define the meaning of “true” using an infinite family of sentences:

(“Snow is white” is true) if and only (snow is white)

(“Weasels are green” is true) if and only if (weasels are green)

. . .

When sentences like these start seeming meaningful, you’ll know that you’ve started to distinguish between encoded sentences and states of the outside world.

Similarly, the notion of truth is quite different from the notion of reality. Saying “true” compares a belief to reality. Reality itself does not need to be compared to any beliefs in order to be real. Remember this the next time someone claims that nothing is true.

195
Qualitatively Confused

I suggest that a primary cause of confusion about the distinction between “belief,” “truth,” and “reality” is qualitative thinking about beliefs.

Consider the archetypal postmodernist attempt to be clever:

“The Sun goes around the Earth” is true for Hunga Huntergatherer, but “The Earth goes around the Sun” is true for Amara Astronomer! Different societies have different truths!

No, different societies have different beliefs. Belief is of a different type than truth; it’s like comparing apples and probabilities.

Ah, but there’s no difference between the way you use the word “belief” and the way you use the word “truth”! Whether you say, “I believe ‘snow is white,’” or you say, “‘Snow is white’ is true,” you’re expressing exactly the same opinion.

No, these sentences mean quite different things, which is how I can conceive of the possibility that my beliefs are false.

Oh, you claim to conceive it, but you never believe it. As Wittgenstein said, “If there were a verb meaning ‘to believe falsely,’ it would not have any significant first person, present indicative.”

And that’s what I mean by putting my finger on qualitative reasoning as the source of the problem. The dichotomy between belief and disbelief, being binary, is confusingly similar to the dichotomy between truth and untruth.

So let’s use quantitative reasoning instead. Suppose that I assign a 70% probability to the proposition that snow is white. It follows that I think there’s around a 70% chance that the sentence “snow is white” will turn out to be true. If the sentence “snow is white” is true, is my 70% probability assignment to the proposition, also “true”? Well, it’s more true than it would have been if I’d assigned 60% probability, but not so true as if I’d assigned 80% probability.

When talking about the correspondence between a probability assignment and reality, a better word than “truth” would be “accuracy.” “Accuracy” sounds more quantitative, like an archer shooting an arrow: how close did your probability assignment strike to the center of the target?

To make a long story short, it turns out that there’s a very natural way of scoring the accuracy of a probability assignment, as compared to reality: just take the logarithm of the probability assigned to the real state of affairs.

So if snow is white, my belief “70%: ‘snow is white’” will score -0.51 bits: log₂(0.7) = -0.51.

But what if snow is not white, as I have conceded a 30% probability is the case? If “snow is white” is false, my belief “30% probability: ‘snow is not white’” will score -1.73 bits. Note that -1.73 < -0.51, so I have done worse.

About how accurate do I think my own beliefs are? Well, my expectation over the score is 70% × -0.51 + 30% × -1.73 = -0.88 bits. If snow is white, then my beliefs will be more accurate than I expected; and if snow is not white, my beliefs will be less accurate than I expected; but in neither case will my belief be exactly as accurate as I expected on average.

All this should not be confused with the statement “I assign 70% credence that ‘snow is white.’” I may well believe that proposition with probability 1—be quite certain that this is in fact my belief. If so I’ll expect my meta-belief “1: ‘I assign 70% credence that “snow is white” ’” to score ~0 bits of accuracy, which is as good as it gets.

Just because I am uncertain about snow, does not mean I am uncertain about my quoted probabilistic beliefs. Snow is out there, my beliefs are inside me. I may be a great deal less uncertain about how uncertain I am about snow, than I am uncertain about snow. (Though beliefs about beliefs are not always accurate.)

Contrast this probabilistic situation to the qualitative reasoning where I just believe that snow is white, and believe that I believe that snow is white, and believe “‘snow is white’ is true,” and believe “my belief ‘“snow is white” is true’ is correct,” etc. Since all the quantities involved are 1, it’s easy to mix them up.

Yet the nice distinctions of quantitative reasoning will be short-circuited if you start thinking “‘“snow is white” with 70% probability’ is true,” which is a type error. It is a true fact about you, that you believe “70% probability: ‘snow is white’”; but that does not mean the probability assignment itself can possibly be “true.” The belief scores either -0.51 bits or -1.73 bits of accuracy, depending on the actual state of reality.

The cognoscenti will recognize “‘“snow is white” with 70% probability’ is true” as the mistake of thinking that probabilities are inherent properties of things.

From the inside, our beliefs about the world look like the world, and our beliefs about our beliefs look like beliefs. When you see the world, you are experiencing a belief from the inside. When you notice yourself believing something, you are experiencing a belief about belief from the inside. So if your internal representations of belief, and belief about belief, are dissimilar, then you are less likely to mix them up and commit the Mind Projection Fallacy—I hope.

When you think in probabilities, your beliefs, and your beliefs about your beliefs, will hopefully not be represented similarly enough that you mix up belief and accuracy, or mix up accuracy and reality. When you think in probabilities about the world, your beliefs will be represented with probabilities in the range (0,1). Unlike the truth-values of propositions, which are in the set {true, false}. As for the accuracy of your probabilistic belief, you can represent that in the range (-∞, 0). Your probabilities about your beliefs will typically be extreme. And things themselves—why, they’re just red, or blue, or weighing 20 pounds, or whatever.

Thus we will be less likely, perhaps, to mix up the map with the territory.

This type distinction may also help us remember that uncertainty is a state of mind. A coin is not inherently 50% uncertain of which way it will land. The coin is not a belief processor, and does not have partial information about itself. In qualitative reasoning you can create a belief that corresponds very straightforwardly to the coin, like “The coin will land heads.” This belief will be true or false depending on the coin, and there will be a transparent implication from the truth or falsity of the belief, to the facing side of the coin.

But even under qualitative reasoning, to say that the coin itself is “true” or “false” would be a severe type error. The coin is not a belief. It is a coin. The territory is not the map.

If a coin cannot be true or false, how much less can it assign a 50% probability to itself?

196
Think Like Reality

Whenever I hear someone describe quantum physics as “weird”—whenever I hear someone bewailing the mysterious effects of observation on the observed, or the bizarre existence of nonlocal correlations, or the incredible impossibility of knowing position and momentum at the same time—then I think to myself: This person will never understand physics no matter how many books they read.

Reality has been around since long before you showed up. Don’t go calling it nasty names like “bizarre” or “incredible.” The universe was propagating complex amplitudes through configuration space for ten billion years before life ever emerged on Earth. Quantum physics is not “weird.” You are weird. You have the absolutely bizarre idea that reality ought to consist of little billiard balls bopping around, when in fact reality is a perfectly normal cloud of complex amplitude in configuration space. This is your problem, not reality’s, and you are the one who needs to change.

Human intuitions were produced by evolution and evolution is a hack. The same optimization process that built your retina backward and then routed the optic cable through your field of vision, also designed your visual system to process persistent objects bouncing around in three spatial dimensions because that’s what it took to chase down tigers. But “tigers” are leaky surface generalizations—tigers came into existence gradually over evolutionary time, and they are not all absolutely similar to each other. When you go down to the fundamental level, the level on which the laws are stable, global, and exception-free, there aren’t any tigers. In fact there aren’t any persistent objects bouncing around in three spatial dimensions. Deal with it.

Calling reality “weird” keeps you inside a viewpoint already proven erroneous. Probability theory tells us that surprise is the measure of a poor hypothesis; if a model is consistently stupid—consistently hits on events the model assigns tiny probabilities—then it’s time to discard that model. A good model makes reality look normal, not weird; a good model assigns high probability to that which is actually the case. Intuition is only a model by another name: poor intuitions are shocked by reality, good intuitions make reality feel natural. You want to reshape your intuitions so that the universe looks normal. You want to think like reality.

This end state cannot be forced. It is pointless to pretend that quantum physics feels natural to you when in fact it feels strange. This is merely denying your confusion, not becoming less confused. But it will also hinder you to keep thinking How bizarre! Spending emotional energy on incredulity wastes time you could be using to update. It repeatedly throws you back into the frame of the old, wrong viewpoint. It feeds your sense of righteous indignation at reality daring to contradict you.

The principle extends beyond physics. Have you ever caught yourself saying something like, “I just don’t understand how a PhD physicist can believe in astrology?” Well, if you literally don’t understand, this indicates a problem with your model of human psychology. Perhaps you are indignant—you wish to express strong moral disapproval. But if you literally don’t understand, then your indignation is stopping you from coming to terms with reality. It shouldn’t be hard to imagine how a PhD physicist ends up believing in astrology. People compartmentalize, enough said.

I now try to avoid using the English idiom “I just don’t understand how . . .” to express indignation. If I genuinely don’t understand how, then my model is being surprised by the facts, and I should discard it and find a better model.

Surprise exists in the map, not in the territory. There are no surprising facts, only models that are surprised by facts. Likewise for facts called such nasty names as “bizarre,” “incredible,” “unbelievable,” “unexpected,” “strange,” “anomalous,” or “weird.” When you find yourself tempted by such labels, it may be wise to check if the alleged fact is really factual. But if the fact checks out, then the problem isn’t the fact—it’s you.

197
Chaotic Inversion

I was recently having a conversation with some friends on the topic of hour-by-hour productivity and willpower maintenance—something I’ve struggled with my whole life.

I can avoid running away from a hard problem the first time I see it (perseverance on a timescale of seconds), and I can stick to the same problem for years; but to keep working on a timescale of hours is a constant battle for me. It goes without saying that I’ve already read reams and reams of advice; and the most help I got from it was realizing that a sizable fraction of other creative professionals had the same problem, and couldn’t beat it either, no matter how reasonable all the advice sounds.

“What do you do when you can’t work?” my friends asked me. (Conversation probably not accurate, this is a very loose gist.)

And I replied that I usually browse random websites, or watch a short video.

“Well,” they said, “if you know you can’t work for a while, you should watch a movie or something.”

“Unfortunately,” I replied, “I have to do something whose time comes in short units, like browsing the Web or watching short videos, because I might become able to work again at any time, and I can’t predict when—”

And then I stopped, because I’d just had a revelation.

I’d always thought of my workcycle as something chaotic, something unpredictable. I never used those words, but that was the way I treated it.

But here my friends seemed to be implying—what a strange thought—that other people could predict when they would become able to work again, and structure their time accordingly.

And it occurred to me for the first time that I might have been committing that damned old chestnut the Mind Projection Fallacy, right out there in my ordinary everyday life instead of high abstraction.

Maybe it wasn’t that my productivity was unusually chaotic; maybe I was just unusually stupid with respect to predicting it.

That’s what inverted stupidity looks like—chaos. Something hard to handle, hard to grasp, hard to guess, something you can’t do anything with. It’s not just an idiom for high abstract things like Artificial Intelligence. It can apply in ordinary life too.

And the reason we don’t think of the alternative explanation “I’m stupid,” is not—I suspect—that we think so highly of ourselves. It’s just that we don’t think of ourselves at all. We just see a chaotic feature of the environment.

So now it’s occurred to me that my productivity problem may not be chaos, but my own stupidity.

And that may or may not help anything. It certainly doesn’t fix the problem right away. Saying “I’m ignorant” doesn’t make you knowledgeable.

But it is, at least, a different path than saying “it’s too chaotic.”

198
Reductionism

Almost one year ago, in April 2007, Matthew C. submitted the following suggestion for an Overcoming Bias topic:

How and why the current reigning philosophical hegemon (reductionistic materialism) is obviously correct [ . . . ], while the reigning philosophical viewpoints of all past societies and civilizations are obviously suspect—

I remember this, because I looked at the request and deemed it legitimate, but I knew I couldn’t do that topic until I’d started on the Mind Projection Fallacy sequence, which wouldn’t be for a while . . .

But now it’s time to begin addressing this question. And while I haven’t yet come to the “materialism” issue, we can now start on “reductionism.”

First, let it be said that I do indeed hold that “reductionism,” according to the meaning I will give for that word, is obviously correct; and to perdition with any past civilizations that disagreed.

This seems like a strong statement, at least the first part of it. General Relativity seems well-supported, yet who knows but that some future physicist may overturn it?

On the other hand, we are never going back to Newtonian mechanics. The ratchet of science turns, but it does not turn in reverse. There are cases in scientific history where a theory suffered a wound or two, and then bounced back; but when a theory takes as many arrows through the chest as Newtonian mechanics, it stays dead.

“To hell with what past civilizations thought” seems safe enough, when past civilizations believed in something that has been falsified to the trash heap of history.

And reductionism is not so much a positive hypothesis, as the absence of belief—in particular, disbelief in a form of the Mind Projection Fallacy.

I once met a fellow who claimed that he had experience as a Navy gunner, and he said, “When you fire artillery shells, you’ve got to compute the trajectories using Newtonian mechanics. If you compute the trajectories using relativity, you’ll get the wrong answer.”

And I, and another person who was present, said flatly, “No.” I added, “You might not be able to compute the trajectories fast enough to get the answers in time—maybe that’s what you mean? But the relativistic answer will always be more accurate than the Newtonian one.”

“No,” he said, “I mean that relativity will give you the wrong answer, because things moving at the speed of artillery shells are governed by Newtonian mechanics, not relativity.”

“If that were really true,” I replied, “you could publish it in a physics journal and collect your Nobel Prize.”

Standard physics uses the same fundamental theory to describe the flight of a Boeing 747 airplane, and collisions in the Relativistic Heavy Ion Collider. Nuclei and airplanes alike, according to our understanding, are obeying Special Relativity, quantum mechanics, and chromodynamics.

But we use entirely different models to understand the aerodynamics of a 747 and a collision between gold nuclei in the RHIC. A computer modeling the aerodynamics of a 747 may not contain a single token, a single bit of RAM, that represents a quark.

So is the 747 made of something other than quarks? No, you’re just modeling it with representational elements that do not have a one-to-one correspondence with the quarks of the 747. The map is not the territory.

Why not model the 747 with a chromodynamic representation? Because then it would take a gazillion years to get any answers out of the model. Also we could not store the model on all the memory on all the computers in the world, as of 2008.

As the saying goes, “The map is not the territory, but you can’t fold up the territory and put it in your glove compartment.” Sometimes you need a smaller map to fit in a more cramped glove compartment—but this does not change the territory. The scale of a map is not a fact about the territory, it’s a fact about the map.

If it were possible to build and run a chromodynamic model of the 747, it would yield accurate predictions. Better predictions than the aerodynamic model, in fact.

To build a fully accurate model of the 747, it is not necessary, in principle, for the model to contain explicit descriptions of things like airflow and lift. There does not have to be a single token, a single bit of RAM, that corresponds to the position of the wings. It is possible, in principle, to build an accurate model of the 747 that makes no mention of anything except elementary particle fields and fundamental forces.

“What?” cries the antireductionist. “Are you telling me the 747 doesn’t really have wings? I can see the wings right there!”

The notion here is a subtle one. It’s not just the notion that an object can have different descriptions at different levels.

It’s the notion that “having different descriptions at different levels” is itself something you say that belongs in the realm of Talking About Maps, not the realm of Talking About Territory.

It’s not that the airplane itself, the laws of physics themselves, use different descriptions at different levels—as yonder artillery gunner thought. Rather we, for our convenience, use different simplified models at different levels.

If you looked at the ultimate chromodynamic model, the one that contained only elementary particle fields and fundamental forces, that model would contain all the facts about airflow and lift and wing positions—but these facts would be implicit, rather than explicit.

You, looking at the model, and thinking about the model, would be able to figure out where the wings were. Having figured it out, there would be an explicit representation in your mind of the wing position—an explicit computational object, there in your neural RAM. In your mind.

You might, indeed, deduce all sorts of explicit descriptions of the airplane, at various levels, and even explicit rules for how your models at different levels interacted with each other to produce combined predictions—

And the way that algorithm feels from inside is that the airplane would seem to be made up of many levels at once, interacting with each other.

The way a belief feels from inside is that you seem to be looking straight at reality. When it actually seems that you’re looking at a belief, as such, you are really experiencing a belief about belief.

So when your mind simultaneously believes explicit descriptions of many different levels, and believes explicit rules for transiting between levels, as part of an efficient combined model, it feels like you are seeing a system that is made of different level descriptions and their rules for interaction.

But this is just the brain trying to efficiently compress an object that it cannot remotely begin to model on a fundamental level. The airplane is too large. Even a hydrogen atom would be too large. Quark-to-quark interactions are insanely intractable. You can’t handle the truth.

But the way physics really works, as far as we can tell, is that there is only the most basic level—the elementary particle fields and fundamental forces. You can’t handle the raw truth, but reality can handle it without the slightest simplification. (I wish I knew where Reality got its computing power.)

The laws of physics do not contain distinct additional causal entities that correspond to lift or airplane wings, the way that the mind of an engineer contains distinct additional cognitive entities that correspond to lift or airplane wings.

This, as I see it, is the thesis of reductionism. Reductionism is not a positive belief, but rather, a disbelief that the higher levels of simplified multilevel models are out there in the territory. Understanding this on a gut level dissolves the question of “How can you say the airplane doesn’t really have wings, when I can see the wings right there?” The critical words are really and see.

199
Explaining vs. Explaining Away

John Keats’s Lamia (1819)¹ surely deserves some kind of award for Most Famously Annoying Poetry:

. . . Do not all charms fly

At the mere touch of cold philosophy?

There was an awful rainbow once in heaven:

We know her woof, her texture; she is given

In the dull catalogue of common things.

Philosophy will clip an Angel’s wings,

Conquer all mysteries by rule and line,

Empty the haunted air, and gnomed mine—

Unweave a rainbow . . .

My usual reply ends with the phrase: “If we cannot learn to take joy in the merely real, our lives will be empty indeed.” I shall expand on that later.

Here I have a different point in mind. Let’s just take the lines:

Empty the haunted air, and gnomed mine—

Unweave a rainbow . . .

Apparently “the mere touch of cold philosophy,” i.e., the truth, has destroyed:

Haunts in the air;
Gnomes in the mine;
Rainbows.

Which calls to mind a rather different bit of verse:

One of these things

Is not like the others

One of these things

Doesn’t belong.

The air has been emptied of its haunts, and the mine de-gnomed—but the rainbow is still there!

In Righting a Wrong Question, I wrote:

Tracing back the chain of causality, step by step, I discover that my belief that I’m wearing socks is fully explained by the fact that I’m wearing socks . . . On the other hand, if I see a mirage of a lake in the desert, the correct causal explanation of my vision does not involve the fact of any actual lake in the desert. In this case, my belief in the lake is not just explained, but explained away.

The rainbow was explained. The haunts in the air, and gnomes in the mine, were explained away.

I think this is the key distinction that anti-reductionists don’t get about reductionism.

You can see this failure to get the distinction in the classic objection to reductionism:

If reductionism is correct, then even your belief in reductionism is just the mere result of the motion of molecules—why should I listen to anything you say?

The key word, in the above, is mere; a word which implies that accepting reductionism would explain away all the reasoning processes leading up to my acceptance of reductionism, the way that an optical illusion is explained away.

But you can explain how a cognitive process works without its being “mere”! My belief that I’m wearing socks is a mere result of my visual cortex reconstructing nerve impulses sent from my retina which received photons reflected off my socks . . . which is to say, according to scientific reductionism, my belief that I’m wearing socks is a mere result of the fact that I’m wearing socks.

What could be going on in the anti-reductionists’ minds, such that they would put rainbows and belief-in-reductionism in the same category as haunts and gnomes?

Several things are going on simultaneously. But for now let’s focus on the basic idea introduced in a previous essay: The Mind Projection Fallacy between a multi-level map and a mono-level territory.

(I.e.: There’s no way you can model a 747 quark-by-quark, so you’ve got to use a multi-level map with explicit cognitive representations of wings, airflow, and so on. This doesn’t mean there’s a multi-level territory. The true laws of physics, to the best of our knowledge, are only over elementary particle fields.)

I think that when physicists say “There are no fundamental rainbows,” the anti-reductionists hear, “There are no rainbows.”

If you don’t distinguish between the multi-level map and the mono-level territory, then when someone tries to explain to you that the rainbow is not a fundamental thing in physics, acceptance of this will feel like erasing rainbows from your multi-level map, which feels like erasing rainbows from the world.

When Science says “tigers are not elementary particles, they are made of quarks” the anti-reductionist hears this as the same sort of dismissal as “we looked in your garage for a dragon, but there was just empty air.”

What scientists did to rainbows, and what scientists did to gnomes, seemingly felt the same to Keats . . .

In support of this sub-thesis, I deliberately used several phrasings, in my discussion of Keats’s poem, that were Mind Projection Fallacious. If you didn’t notice, this would seem to argue that such fallacies are customary enough to pass unremarked.

For example:

The air has been emptied of its haunts, and the mine de-gnomed—but the rainbow is still there!

Actually, Science emptied the model of air of belief in haunts, and emptied the map of the mine of representations of gnomes. Science did not actually—as Keats’s poem itself would have it—take real Angel’s wings, and destroy them with a cold touch of truth. In reality there never were any haunts in the air, or gnomes in the mine.

Another example:

What scientists did to rainbows, and what scientists did to gnomes, seemingly felt the same to Keats.

Scientists didn’t do anything to gnomes, only to “gnomes.” The quotation is not the referent.

But if you commit the Mind Projection Fallacy—and by default, our beliefs just feel like the way the world is—then at time T = 0, the mines (apparently) contain gnomes; at time T = 1 a scientist dances across the scene, and at time T = 2 the mines (apparently) are empty. Clearly, there used to be gnomes there, but the scientist killed them.

Bad scientist! No poems for you, gnomekiller!

Well, that’s how it feels, if you get emotionally attached to the gnomes, and then a scientist says there aren’t any gnomes. It takes a strong mind, a deep honesty, and a deliberate effort to say, at this point, “That which can be destroyed by the truth should be,” and “The scientist hasn’t taken the gnomes away, only taken my delusion away,” and “I never held just title to my belief in gnomes in the first place; I have not been deprived of anything I rightfully owned,” and “If there are gnomes, I desire to believe there are gnomes; if there are no gnomes, I desire to believe there are no gnomes; let me not become attached to beliefs I may not want,” and all the other things that rationalists are supposed to say on such occasions.

But with the rainbow it is not even necessary to go that far. The rainbow is still there!

1. John Keats, “Lamia,” The Poetical Works of John Keats (London: Macmillan) (1884).

200
Fake Reductionism

There was an awful rainbow once in heaven:

We know her woof, her texture; she is given

In the dull catalogue of common things.

—John Keats, Lamia

I am guessing—though it is only a guess—that Keats himself did not know the woof and texture of the rainbow. Not the way that Newton understood rainbows. Perhaps not even at all. Maybe Keats just read, somewhere, that Newton had explained the rainbow as “light reflected from raindrops”—

—which was actually known in the thirteenth century. Newton only added a refinement by showing that the light was decomposed into colored parts, rather than transformed in color. But that put rainbows back in the news headlines. And so Keats, with Charles Lamb and William Wordsworth and Benjamin Haydon, drank “confusion to the memory of Newton” because “he destroyed the poetry of the rainbow by reducing it to a prism.” That’s one reason to suspect Keats didn’t understand the subject too deeply.

I am guessing, though it is only a guess, that Keats could not have sketched out on paper why rainbows only appear when the Sun is behind your head, or why the rainbow is an arc of a circle.

If so, Keats had a Fake Explanation. In this case, a fake reduction. He’d been told that the rainbow had been reduced, but it had not actually been reduced in his model of the world.

This is another of those distinctions that anti-reductionists fail to get—the difference between professing the flat fact that something is reducible, and seeing it.

In this, the anti-reductionists are not too greatly to be blamed, for it is part of a general problem.

I’ve written before on seeming knowledge that is not knowledge, and beliefs that are not about their supposed objects but only recordings to recite back in the classroom, and words that operate as stop signs for curiosity rather than answers, and technobabble that only conveys membership in the literary genre of “science” . . .

There is a very great distinction between being able to see where the rainbow comes from, and playing around with prisms to confirm it, and maybe making a rainbow yourself by spraying water droplets—

—versus some dour-faced philosopher just telling you, “No, there’s nothing special about the rainbow. Didn’t you hear? Scientists have explained it away. Just something to do with raindrops or whatever. Nothing to be excited about.”

I think this distinction probably accounts for a hell of a lot of the deadly existential emptiness that supposedly accompanies scientific reductionism.

You have to interpret the anti-reductionists’ experience of “reductionism,” not in terms of their actually seeing how rainbows work, not in terms of their having the critical “Aha!,” but in terms of their being told that the password is “Science.” The effect is just to move rainbows to a different literary genre—a literary genre they have been taught to regard as boring.

For them, the effect of hearing “Science has explained rainbows!” is to hang up a sign over rainbows saying, “This phenomenon has been labeled BORING by order of the Council of Sophisticated Literary Critics. Move along.”

And that’s all the sign says: only that, and nothing more.

So the literary critics have their gnomes yanked out by force; not dissolved in insight, but removed by flat order of authority. They are given no beauty to replace the hauntless air, no genuine understanding that could be interesting in its own right. Just a label saying, “Ha! You thought rainbows were pretty? You poor, unsophisticated fool. This is part of the literary genre of science, of dry and solemn incomprehensible words.”

That’s how anti-reductionists experience “reductionism.”

Well, can’t blame Keats, poor lad probably wasn’t raised right.

But he dared to drink “Confusion to the memory of Newton”?

I propose “To the memory of Keats’s confusion” as a toast for rationalists. Cheers.

201
Savannah Poets

Poets say science takes away from the beauty of the stars—mere globs of gas atoms. Nothing is “mere.” I too can see the stars on a desert night, and feel them. But do I see less or more?

The vastness of the heavens stretches my imagination—stuck on this carousel my little eye can catch one-million-year-old light. A vast pattern—of which I am a part—perhaps my stuff was belched from some forgotten star, as one is belching there. Or see them with the greater eye of Palomar, rushing all apart from some common starting point when they were perhaps all together. What is the pattern, or the meaning, or the why? It does not do harm to the mystery to know a little about it.

For far more marvelous is the truth than any artists of the past imagined! Why do the poets of the present not speak of it?

What men are poets who can speak of Jupiter if he were like a man, but if he is an immense spinning sphere of methane and ammonia must be silent?

—Richard Feynman, The Feynman Lectures on Physics,¹
Vol I, p. 3–6 (line breaks added)

That’s a real question, there on the last line—what kind of poet can write about Jupiter the god, but not Jupiter the immense sphere? Whether or not Feynman meant the question rhetorically, it has a real answer:

If Jupiter is like us, he can fall in love, and lose love, and regain love.

If Jupiter is like us, he can strive, and rise, and be cast down.

If Jupiter is like us, he can laugh or weep or dance.

If Jupiter is an immense spinning sphere of methane and ammonia, it is more difficult for the poet to make us feel.

There are poets and storytellers who say that the Great Stories are timeless, and they never change, are only ever retold. They say, with pride, that Shakespeare and Sophocles are bound by ties of craft stronger than mere centuries; that the two playwrights could have swapped times without a jolt.

Donald Brown once compiled a list of over two hundred “human universals,” found in all (or a vast supermajority of) studied human cultures, from San Francisco to the !Kung of the Kalahari Desert. Marriage is on the list, and incest avoidance, and motherly love, and sibling rivalry, and music and envy and dance and storytelling and aesthetics, and ritual magic to heal the sick, and poetry in spoken lines separated by pauses—

No one who knows anything about evolutionary psychology could be expected to deny it: The strongest emotions we have are deeply engraved, blood and bone, brain and DNA.

It might take a bit of tweaking, but you probably could tell “Hamlet” sitting around a campfire on the ancestral savanna.

So one can see why John “Unweave a rainbow” Keats might feel something had been lost, on being told that the rainbow was sunlight scattered from raindrops. Raindrops don’t dance.

In the Old Testament, it is written that God once destroyed the world with a flood that covered all the land, drowning all the horribly guilty men and women of the world along with their horribly guilty babies, but Noah built a gigantic wooden ark, etc., and after most of the human species was wiped out, God put rainbows in the sky as a sign that he wouldn’t do it again. At least not with water.

You can see how Keats would be shocked that this beautiful story was contradicted by modern science. Especially if (as I described in the previous essay) Keats had no real understanding of rainbows, no “Aha!” insight that could be fascinating in its own right, to replace the drama subtracted—

Ah, but maybe Keats would be right to be disappointed even if he knew the math. The Biblical story of the rainbow is a tale of bloodthirsty murder and smiling insanity. How could anything about raindrops and refraction properly replace that? Raindrops don’t scream when they die.

So science takes the romance away (says the Romantic poet), and what you are given back never matches the drama of the original—

(that is, the original delusion)

—even if you do know the equations, because the equations are not about strong emotions.

That is the strongest rejoinder I can think of that any Romantic poet could have said to Feynman—though I can’t remember ever hearing it said.

You can guess that I don’t agree with the Romantic poets. So my own stance is this:

It is not necessary for Jupiter to be like a human, because humans are like humans. If Jupiter is an immense spinning sphere of methane and ammonia, that doesn’t mean that love and hate are emptied from the universe. There are still loving and hating minds in the universe. Us.

With more than six billion of us at the last count, does Jupiter really need to be on the list of potential protagonists?

It is not necessary to tell the Great Stories about planets or rainbows. They play out all over our world, every day. Every day, someone kills for revenge; every day, someone kills a friend by mistake; every day, upward of a hundred thousand people fall in love. And even if this were not so, you could write fiction about humans—not about Jupiter.

Earth is old, and has played out the same stories many times beneath the Sun. I do wonder if it might not be time for some of the Great Stories to change. For me, at least, the story called “Goodbye” has lost its charm.

The Great Stories are not timeless, because the human species is not timeless. Go far enough back in hominid evolution, and no one will understand Hamlet. Go far enough back in time, and you won’t find any brains.

The Great Stories are not eternal, because the human species, Homo sapiens sapiens, is not eternal. I most sincerely doubt that we have another thousand years to go in our current form. I do not say this in sadness: I think we can do better.

I would not like to see all the Great Stories lost completely, in our future. I see very little difference between that outcome, and the Sun falling into a black hole.

But the Great Stories in their current forms have already been told, over and over. I do not think it ill if some of them should change their forms, or diversify their endings.

“And they lived happily ever after” seems worth trying at least once.

The Great Stories can and should diversify, as humankind grows up. Part of that ethic is the idea that when we find strangeness, we should respect it enough to tell its story truly. Even if it makes writing poetry a little more difficult.

If you are a good enough poet to write an ode to an immense spinning sphere of methane and ammonia, you are writing something original, about a newly discovered part of the real universe. It may not be as dramatic, or as gripping, as Hamlet. But the tale of Hamlet has already been told! If you write of Jupiter as though it were a human, then you are making our map of the universe just a little more impoverished of complexity; you are forcing Jupiter into the mold of all the stories that have already been told of Earth.

James Thomson’s “A Poem Sacred to the Memory of Sir Isaac Newton,” which praises the rainbow for what it really is—you can argue whether or not Thomson’s poem is as gripping as John Keats’s Lamia who was loved and lost. But tales of love and loss and cynicism had already been told, far away in ancient Greece, and no doubt many times before. Until we understood the rainbow as a thing different from tales of human-shaped magic, the true story of the rainbow could not be poeticized.

The border between science fiction and space opera was once drawn as follows: If you can take the plot of a story and put it back in the Old West, or the Middle Ages, without changing it, then it is not real science fiction. In real science fiction, the science is intrinsically part of the plot—you can’t move the story from space to the savanna, not without losing something.

Richard Feynman asked: “What men are poets who can speak of Jupiter if he were like a man, but if he is an immense spinning sphere of methane and ammonia must be silent?”

They are savanna poets, who can only tell stories that would have made sense around a campfire ten thousand years ago. Savanna poets, who can tell only the Great Stories in their classic forms, and nothing more.

1. Richard P. Feynman, Robert B. Leighton, and Matthew L. Sands, The Feynman Lectures on Physics, 3 vols. (Reading, MA: Addison-Wesley, 1963).

202
Joy in the Merely Real

. . . Do not all charms fly

At the mere touch of cold philosophy?

There was an awful rainbow once in heaven:

We know her woof, her texture; she is given

In the dull catalogue of common things.

—John Keats, Lamia

Nothing is “mere.”

—Richard Feynman

You’ve got to admire that phrase, “dull catalogue of common things.” What is it, exactly, that goes in this catalogue? Besides rainbows, that is?

Why, things that are mundane, of course. Things that are normal; things that are unmagical; things that are known, or knowable; things that play by the rules (or that play by any rules, which makes them boring); things that are part of the ordinary universe; things that are, in a word, real.

Now that’s what I call setting yourself up for a fall.

At that rate, sooner or later you’re going to be disappointed in everything—either it will turn out not to exist, or even worse, it will turn out to be real.

If we cannot take joy in things that are merely real, our lives will always be empty.

For what sin are rainbows demoted to the dull catalogue of common things? For the sin of having a scientific explanation. “We know her woof, her texture,” says Keats—an interesting use of the word “we,” because I suspect that Keats didn’t know the explanation himself. I suspect that just being told that someone else knew was too much for him to take. I suspect that just the notion of rainbows being scientifically explicable in principle would have been too much to take. And if Keats didn’t think like that, well, I know plenty of people who do.

I have already remarked that nothing is inherently mysterious—nothing that actually exists, that is. If I am ignorant about a phenomenon, that is a fact about my state of mind, not a fact about the phenomenon; to worship a phenomenon because it seems so wonderfully mysterious is to worship your own ignorance; a blank map does not correspond to a blank territory, it is just somewhere we haven’t visited yet, etc., etc. . . .

Which is to say that everything—everything that actually exists—is liable to end up in “the dull catalogue of common things,” sooner or later.

Your choice is either:

Decide that things are allowed to be unmagical, knowable, scientifically explicable—in a word, real—and yet still worth caring about;
Or go about the rest of your life suffering from existential ennui that is unresolvable.

(Self-deception might be an option for others, but not for you.)

This puts quite a different complexion on the bizarre habit indulged by those strange folk called scientists, wherein they suddenly become fascinated by pocket lint or bird droppings or rainbows, or some other ordinary thing which world-weary and sophisticated folk would never give a second glance.

You might say that scientists—at least some scientists—are those folk who are in principle capable of enjoying life in the real universe.

Part Q
Joy in the Merely Real

203
Joy in Discovery

Newton was the greatest genius who ever lived, and the most fortunate; for we cannot find more than once a system of the world to establish.

—Lagrange

I have more fun discovering things for myself than reading about them in textbooks. This is right and proper, and only to be expected.

But discovering something that no one else knows—being the first to unravel the secret—

There is a story that one of the first men to realize that stars were burning by fusion—plausible attributions I’ve seen are to Fritz Houtermans and Hans Bethe—was walking out with his girlfriend of a night, and she made a comment on how beautiful the stars were, and he replied: “Yes, and right now, I’m the only man in the world who knows why they shine.”

It is attested by numerous sources that this experience, being the first person to solve a major mystery, is a tremendous high. It’s probably the closest experience you can get to taking drugs, without taking drugs—though I wouldn’t know.

That can’t be healthy.

Not that I’m objecting to the euphoria. It’s the exclusivity clause that bothers me. Why should a discovery be worth less, just because someone else already knows the answer?

The most charitable interpretation I can put on the psychology, is that you don’t struggle with a single problem for months or years if it’s something you can just look up in the library. And that the tremendous high comes from having hit the problem from every angle you can manage, and having bounced; and then having analyzed the problem again, using every idea you can think of, and all the data you can get your hands on—making progress a little at a time—so that when, finally, you crack through the problem, all the dangling pieces and unresolved questions fall into place at once, like solving a dozen locked-room murder mysteries with a single clue.

And more, the understanding you get is real understanding—understanding that embraces all the clues you studied to solve the problem, when you didn’t yet know the answer. Understanding that comes from asking questions day after day and worrying at them; understanding that no one else can get (no matter how much you tell them the answer) unless they spend months studying the problem in its historical context, even after it’s been solved—and even then, they won’t get the high of solving it all at once.

That’s one possible reason why James Clerk Maxwell might have had more fun discovering Maxwell’s equations, than you had fun reading about them.

A slightly less charitable reading is that the tremendous high comes from what is termed, in the politesse of social psychology, “commitment” and “consistency” and “cognitive dissonance”; the part where we value something more highly just because it took more work to get it. The studies showing that subjecting fraternity pledges to a harsher initiation, causes them to be more convinced of the value of the fraternity—identical wine in higher-priced bottles being rated as tasting better—that sort of thing.

Of course, if you just have more fun solving a puzzle than being told its answer, because you enjoy doing the cognitive work for its own sake, there’s nothing wrong with that. The less charitable reading would be if charging $100 to be told the answer to a puzzle made you think the answer was more interesting, worthwhile, important, surprising, etc., than if you got the answer for free.

(I strongly suspect that a major part of science’s PR problem in the population at large is people who instinctively believe that if knowledge is given away for free, it cannot be important. If you had to undergo a fearsome initiation ritual to be told the truth about evolution, maybe people would be more satisfied with the answer.)

The really uncharitable reading is that the joy of first discovery is about status. Competition. Scarcity. Beating everyone else to the punch. It doesn’t matter whether you have a three-room house or a four-room house, what matters is having a bigger house than the Joneses. A two-room house would be fine, if you could only ensure that the Joneses had even less.

I don’t object to competition as a matter of principle. I don’t think that the game of Go is barbaric and should be suppressed, even though it’s zero-sum. But if the euphoric joy of scientific discovery has to be about scarcity, that means it’s only available to one person per civilization for any given truth.

If the joy of scientific discovery is one-shot per discovery, then, from a fun-theoretic perspective, Newton probably used up a substantial increment of the total Physics Fun available over the entire history of Earth-originating intelligent life. That selfish bastard explained the orbits of planets and the tides.

And really the situation is even worse than this, because in the Standard Model of physics (discovered by bastards who spoiled the puzzle for everyone else) the universe is spatially infinite, inflationarily branching, and branching via decoherence, which is at least three different ways that Reality is exponentially or infinitely large.

So aliens, or alternate Newtons, or just Tegmark duplicates of Newton, may all have discovered gravity before our Newton did—if you believe that “before” means anything relative to those kinds of separations.

When that thought first occurred to me, I actually found it quite uplifting. Once I realized that someone, somewhere in the expanses of space and time, already knows the answer to any answerable question—even biology questions and history questions; there are other decoherent Earths—then I realized how silly it was to think as if the joy of discovery ought to be limited to one person. It becomes a fully inescapable source of unresolvable existential angst, and I regard that as a reductio.

The consistent solution which maintains the possibility of fun is to stop worrying about what other people know. If you don’t know the answer, it’s a mystery to you. If you can raise your hand, and clench your fingers into a fist, and you’ve got no idea of how your brain is doing it—or even what exact muscles lay beneath your skin—you’ve got to consider yourself just as ignorant as a hunter-gatherer. Sure, someone else knows the answer—but back in the hunter-gatherer days, someone else in an alternate Earth, or for that matter, someone else in the future, knew what the answer was. Mystery, and the joy of finding out, is either a personal thing, or it doesn’t exist at all—and I prefer to say it’s personal.

The joy of assisting your civilization by telling it something it doesn’t already know does tend to be one-shot per discovery per civilization; that kind of value is conserved, as are Nobel Prizes. And the prospect of that reward may be what it takes to keep you focused on one problem for the years required to develop a really deep understanding; plus, working on a problem unknown to your civilization is a sure-fire way to avoid reading any spoilers.

But as part of my general project to undo this idea that rationalists have less fun, I want to restore the magic and mystery to every part of the world that you do not personally understand, regardless of what other knowledge may exist, far away in space and time, or even in your next-door neighbor’s mind. If you don’t know, it’s a mystery. And now think of how many things you don’t know! (If you can’t think of anything, you have other problems.) Isn’t the world suddenly a much more mysterious and magical and interesting place? As if you’d been transported into an alternate dimension, and had to learn all the rules from scratch?

A friend once told me that I look at the world as if I’ve never seen it before. I thought, that’s a nice compliment . . . Wait! I never have seen it before! What—did everyone else get a preview?

—Ran Prieur

204
Bind Yourself to Reality

So perhaps you’re reading all this, and asking: “Yes, but what does this have to do with reductionism?”

Partially, it’s a matter of leaving a line of retreat. It’s not easy to take something important apart into components, when you’re convinced that this removes magic from the world, unweaves the rainbow. I do plan to take certain things apart, in this book; and I prefer not to create pointless existential anguish.

Partially, it’s the crusade against Hollywood Rationality, the concept that understanding the rainbow subtracts its beauty. The rainbow is still beautiful plus you get the beauty of physics.

But even more deeply, it’s one of these subtle hidden-core-of-rationality things. You know, the sort of thing where I start talking about “the Way.” It’s about binding yourself to reality.

In one of Frank Herbert’s Dune books, if I recall correctly, it is said that a Truthsayer gains their ability to detect lies in others by always speaking truth themselves, so that they form a relationship with the truth whose violation they can feel. It wouldn’t work, but I still think it’s one of the more beautiful thoughts in fiction. At the very least, to get close to the truth, you have to be willing to press yourself up against reality as tightly as possible, without flinching away, or sneering down.

You can see the bind-yourself-to-reality theme in Lotteries: A Waste of Hope. Understanding that lottery tickets have negative expected utility does not mean that you give up the hope of being rich. It means that you stop wasting that hope on lottery tickets. You put the hope into your job, your school, your startup, your eBay sideline; and if you truly have nothing worth hoping for, then maybe it’s time to start looking.

It’s not dreams I object to, only impossible dreams. The lottery isn’t impossible, but it is an un-actionable near-impossibility. It’s not that winning the lottery is extremely difficult—requires a desperate effort—but that work isn’t the issue.

I say all this, to exemplify the idea of taking emotional energy that is flowing off to nowhere, and binding it into the realms of reality.

This doesn’t mean setting goals that are low enough to be “realistic,” i.e., easy and safe and parentally approved. Maybe this is good advice in your personal case, I don’t know, but I’m not the one to say it.

What I mean is that you can invest emotional energy in rainbows even if they turn out not to be magic. The future is always absurd but it is never unreal.

The Hollywood Rationality stereotype is that “rational = emotionless”; the more reasonable you are, the more of your emotions Reason inevitably destroys. In Feeling Rational I contrast this against “That which can be destroyed by the truth should be” and “That which the truth nourishes should thrive.” When you have arrived at your best picture of the truth, there is nothing irrational about the emotions you feel as a result of that—the emotions cannot be destroyed by truth, so they must not be irrational.

So instead of destroying emotional energies associated with bad explanations for rainbows, as the Hollywood Rationality stereotype would have it, let us redirect these emotional energies into reality—bind them to beliefs that are as true as we can make them.

Want to fly? Don’t give up on flight. Give up on flying potions and build yourself an airplane.

Remember the theme of Think like Reality, where I talked about how when physics seems counterintuitive, you’ve got to accept that it’s not physics that’s weird, it’s you?

What I’m talking about now is like that, only with emotions instead of hypotheses—binding your feelings into the real world. Not the “realistic” everyday world. I would be a howling hypocrite if I told you to shut up and do your homework. I mean the real real world, the lawful universe, that includes absurdities like Moon landings and the evolution of human intelligence. Just not any magic, anywhere, ever.

It is a Hollywood Rationality meme that “Science takes the fun out of life.”

Science puts the fun back into life.

Rationality directs your emotional energies into the universe, rather than somewhere else.

205
If You Demand Magic, Magic Won’t Help

Most witches don’t believe in gods. They know that the gods exist, of course. They even deal with them occasionally. But they don’t believe in them. They know them too well. It would be like believing in the postman.

—Terry Pratchett, Witches Abroad¹

Once upon a time, I was pondering the philosophy of fantasy stories—

And before anyone chides me for my “failure to understand what fantasy is about,” let me say this: I was raised in a science fiction and fantasy household. I have been reading fantasy stories since I was five years old. I occasionally try to write fantasy stories. And I am not the sort of person who tries to write for a genre without pondering its philosophy. Where do you think story ideas come from?

Anyway:

I was pondering the philosophy of fantasy stories, and it occurred to me that if there were actually dragons in our world—if you could go down to the zoo, or even to a distant mountain, and meet a fire-breathing dragon—while nobody had ever actually seen a zebra, then our fantasy stories would contain zebras aplenty, while dragons would be unexciting.

Now that’s what I call painting yourself into a corner, wot? The grass is always greener on the other side of unreality.

In one of the standard fantasy plots, a protagonist from our Earth, a sympathetic character with lousy grades or a crushing mortgage but still a good heart, suddenly finds themselves in a world where magic operates in place of science. The protagonist often goes on to practice magic, and become in due course a (superpowerful) sorcerer.

Now here’s the question—and yes, it is a little unkind, but I think it needs to be asked: Presumably most readers of these novels see themselves in the protagonist’s shoes, fantasizing about their own acquisition of sorcery. Wishing for magic. And, barring improbable demographics, most readers of these novels are not scientists.

Born into a world of science, they did not become scientists. What makes them think that, in a world of magic, they would act any differently?

If they don’t have the scientific attitude, that nothing is “mere”—the capacity to be interested in merely real things—how will magic help them? If they actually had magic, it would be merely real, and lose the charm of unattainability. They might be excited at first, but (like the lottery winners who, six months later, aren’t nearly as happy as they expected to be), the excitement would soon wear off. Probably as soon as they had to actually study spells.

Unless they can find the capacity to take joy in things that are merely real. To be just as excited by hang-gliding, as riding a dragon; to be as excited by making a light with electricity, as by making a light with magic . . . even if it takes a little study . . .

Don’t get me wrong. I’m not dissing dragons. Who knows, we might even create some, one of these days.

But if you don’t have the capacity to enjoy hang-gliding even though it is merely real, then as soon as dragons turn real, you’re not going to be any more excited by dragons than you are by hang-gliding.

Do you think you would prefer living in the Future, to living in the present? That’s a quite understandable preference. Things do seem to be getting better over time.

But don’t forget that this is the Future, relative to the Dark Ages of a thousand years earlier. You have opportunities undreamt-of even by kings.

If the trend continues, the Future might be a very fine place indeed in which to live. But if you do make it to the Future, what you find, when you get there, will be another Now. If you don’t have the basic capacity to enjoy being in a Now—if your emotional energy can only go into the Future, if you can only hope for a better tomorrow—then no amount of passing time can help you.

(Yes, in the Future there could be a pill that fixes the emotional problem of always looking to the Future. I don’t think this invalidates my basic point, which is about what sort of pills we should want to take.)

Matthew C., commenting on Less Wrong, seems very excited about an informally specified “theory” by Rupert Sheldrake which “explains” such non-explanation-demanding phenomena as protein folding and snowflake symmetry. But why isn’t Matthew C. just as excited about, say, Special Relativity? Special Relativity is actually known to be a law, so why isn’t it even more exciting? The advantage of becoming excited about a law already known to be true, is that you know your excitement will not be wasted.

If Sheldrake’s theory were accepted truth taught in elementary schools, Matthew C. wouldn’t care about it. Or why else is Matthew C. fascinated by that one particular law which he believes to be a law of physics, more than all the other laws?

The worst catastrophe you could visit upon the New Age community would be for their rituals to start working reliably, and for UFOs to actually appear in the skies. What would be the point of believing in aliens, if they were just there, and everyone else could see them too? In a world where psychic powers were merely real, New Agers wouldn’t believe in psychic powers, any more than anyone cares enough about gravity to believe in it. (Except for scientists, of course.)

Why am I so negative about magic? Would it be wrong for magic to exist?

I’m not actually negative on magic. Remember, I occasionally try to write fantasy stories. But I’m annoyed with this psychology that, if it were born into a world where spells and potions did work, would pine away for a world where household goods were abundantly produced by assembly lines.

Part of binding yourself to reality, on an emotional as well as intellectual level, is coming to terms with the fact that you do live here. Only then can you see this, your world, and whatever opportunities it holds out for you, without wishing your sight away.

Not to put too fine a point on it, but I’ve found no lack of dragons to fight, or magics to master, in this world of my birth. If I were transported into one of those fantasy novels, I wouldn’t be surprised to find myself studying the forbidden ultimate sorcery—

—because why should being transported into a magical world change anything? It’s not where you are, it’s who you are.

So remember the Litany Against Being Transported Into An Alternate Universe:

If I’m going to be happy anywhere,

Or achieve greatness anywhere,

Or learn true secrets anywhere,

Or save the world anywhere,

Or feel strongly anywhere,

Or help people anywhere,

I may as well do it in reality.

1. Terry Pratchett, Witches Abroad (London: Corgi Books, 1992).

206
Mundane Magic

I think that part of the rationalist ethos is binding yourself emotionally to an absolutely lawful reductionistic universe—a universe containing no supernatural things such as souls or magic—and pouring all your hope and all your care into that merely real universe and its possibilities, without disappointment.

There’s an old trick for combating dukkha where you make a list of things you’re grateful for, like a roof over your head.

So why not make a list of abilities you have that would be amazingly cool if they were magic, or if only a few chosen individuals had them?

For example, suppose that instead of one eye, you possessed a magical second eye embedded in your forehead. And this second eye enabled you to see into the third dimension—so that you could somehow tell how far away things were—where an ordinary eye would see only a two-dimensional shadow of the true world. Only the possessors of this ability can accurately aim the legendary distance-weapons that kill at ranges far beyond a sword, or use to their fullest potential the shells of ultrafast machinery called “cars.”

“Binocular vision” would be too light a term for this ability. We’ll only appreciate it once it has a properly impressive name, like Mystic Eyes of Depth Perception.

So here’s a list of some of my favorite magical powers:

Vibratory Telepathy. By transmitting invisible vibrations through the very air itself, two users of this ability can share thoughts. As a result, Vibratory Telepaths can form emotional bonds much deeper than those possible to other primates.
Psychometric Tracery. By tracing small fine lines on a surface, the Psychometric Tracer can leave impressions of emotions, history, knowledge, even the structure of other spells. This is a higher level than Vibratory Telepathy as a Psychometric Tracer can share the thoughts of long-dead Tracers who lived thousands of years earlier. By reading one Tracery and inscribing another simultaneously, Tracers can duplicate Tracings; and these replicated Tracings can even contain the detailed pattern of other spells and magics. Thus, the Tracers wield almost unimaginable power as magicians; but Tracers can get in trouble trying to use complicated Traceries that they could not have Traced themselves.
Multidimensional Kinesis. With simple, almost unthinking acts of will, the Kinetics can cause extraordinarily complex forces to flow through small tentacles and into any physical object within touching range—not just pushes, but combinations of pushes at many points that can effectively apply torques and twists. The Kinetic ability is far subtler than it first appears: they use it not only to wield existing objects with martial precision, but also to apply forces that sculpt objects into forms more suitable for Kinetic wielding. They even create tools that extend the power of their Kinesis and enable them to sculpt ever-finer and ever-more-complicated tools, a positive feedback loop fully as impressive as it sounds.
The Eye. The user of this ability can perceive infinitesimal traveling twists in the Force that binds matter—tiny vibrations, akin to the life-giving power of the Sun that falls on leaves, but far more subtle. A bearer of the Eye can sense objects far beyond the range of touch using the tiny disturbances they make in the Force. Mountains many days travel away can be known to them as if within arm’s reach. According to the bearers of the Eye, when night falls and sunlight fails, they can sense huge fusion fires burning at unthinkable distances—though no one else has any way of verifying this. Possession of a single Eye is said to make the bearer equivalent to royalty.

And finally,

The Ultimate Power. The user of this ability contains a smaller, imperfect echo of the entire universe, enabling them to search out paths through probability to any desired future. If this sounds like a ridiculously powerful ability, you’re right—game balance goes right out the window with this one. Extremely rare among life forms, it is the sekai no ougi or “hidden technique of the world.”
Nothing can oppose the Ultimate Power except the Ultimate Power. Any less-than-ultimate Power will simply be “comprehended” by the Ultimate and disrupted in some inconceivable fashion, or even absorbed into the Ultimates’ own power base. For this reason the Ultimate Power is sometimes called the “master technique of techniques” or the “trump card that trumps all other trumps.” The more powerful Ultimates can stretch their “comprehension” across galactic distances and aeons of time, and even perceive the bizarre laws of the hidden “world beneath the world.”

Ultimates have been killed by immense natural catastrophes, or by extremely swift surprise attacks that give them no chance to use their power. But all such victories are ultimately a matter of luck—it does not confront the Ultimates on their own probability-bending level, and if they survive they will begin to bend Time to avoid future attacks.

But the Ultimate Power itself is also dangerous, and many Ultimates have been destroyed by their own powers—falling into one of the flaws in their imperfect inner echo of the world.

Stripped of weapons and armor and locked in a cell, an Ultimate is still one of the most dangerous life-forms on the planet. A sword can be broken and a limb can be cut off, but the Ultimate Power is “the power that cannot be removed without removing you.”

Perhaps because this connection is so intimate, the Ultimates regard one who loses their Ultimate Power permanently—without hope of regaining it—as schiavo, or “dead while breathing.” The Ultimates argue that the Ultimate Power is so important as to be a necessary part of what makes a creature an end in itself, rather than a means. The Ultimates even insist that anyone who lacks the Ultimate Power cannot begin to truly comprehend the Ultimate Power, and hence, cannot understand why the Ultimate Power is morally important—a suspiciously self-serving argument.

The users of this ability form an absolute aristocracy and treat all other life forms as their pawns.

207
The Beauty of Settled Science

Facts do not need to be unexplainable to be beautiful; truths do not become less worth learning if someone else knows them; beliefs do not become less worthwhile if many others share them . . .

. . . and if you only care about scientific issues that are controversial, you will end up with a head stuffed full of garbage.

The media thinks that only the cutting edge of science is worth reporting on. How often do you see headlines like “General Relativity Still Governing Planetary Orbits” or “Phlogiston Theory Remains False”? So, by the time anything is solid science, it is no longer a breaking headline. “Newsworthy” science is often based on the thinnest of evidence and wrong half the time—if it were not on the uttermost fringes of the scientific frontier, it would not be breaking news.

Scientific controversies are problems so difficult that even people who’ve spent years mastering the field can still fool themselves. That’s what makes for the heated arguments that attract all the media attention.

Worse, if you aren’t in the field and part of the game, controversies aren’t even fun.

Oh, sure, you can have the fun of picking a side in an argument. But you can get that in any football game. That’s not what the fun of science is about.

Reading a well-written textbook, you get: Carefully phrased explanations for incoming students, math derived step by step (where applicable), plenty of experiments cited as illustration (where applicable), test problems on which to display your new mastery, and a reasonably good guarantee that what you’re learning is actually true.

Reading press releases, you usually get: Fake explanations that convey nothing except the delusion of understanding of a result that the press release author didn’t understand and that probably has a better-than-even chance of failing to replicate.

Modern science is built on discoveries, built on discoveries, built on discoveries, and so on, all the way back to people like Archimedes, who discovered facts like why boats float, that can make sense even if you don’t know about other discoveries. A good place to start traveling that road is at the beginning.

Don’t be embarrassed to read elementary science textbooks, either. If you want to pretend to be sophisticated, go find a play to sneer at. If you just want to have fun, remember that simplicity is at the core of scientific beauty.

And thinking you can jump right into the frontier, when you haven’t learned the settled science, is like . . .

. . . like trying to climb only the top half of Mount Everest (which is the only part that interests you) by standing at the base of the mountain, bending your knees, and jumping really hard (so you can pass over the boring parts).

Now I’m not saying that you should never pay attention to scientific controversies. If 40% of oncologists think that white socks cause cancer, and the other 60% violently disagree, this is an important fact to know.

Just don’t go thinking that science has to be controversial to be interesting.

Or, for that matter, that science has to be recent to be interesting. A steady diet of science news is bad for you: You are what you eat, and if you eat only science reporting on fluid situations, without a solid textbook now and then, your brain will turn to liquid.

208
Amazing Breakthrough Day: April 1st

So you’re thinking, “April 1st . . . isn’t that already supposed to be April Fool’s Day?”

Yes—and that will provide the ideal cover for celebrating Amazing Breakthrough Day.

As I argued in The Beauty of Settled Science, it is a major problem that media coverage of science focuses only on breaking news. Breaking news, in science, occurs at the furthest fringes of the scientific frontier, which means that the new discovery is often:

Controversial;
Supported by only one experiment;
Way the heck more complicated than an ordinary mortal can handle, and requiring lots of prerequisite science to understand, which is why it wasn’t solved three centuries ago;
Later shown to be wrong.

People never get to see the solid stuff, let alone the understandable stuff, because it isn’t breaking news.

On Amazing Breakthrough Day, I propose, journalists who really care about science can report—under the protective cover of April 1st—such important but neglected science stories as:

BOATS EXPLAINED: Centuries-Old Problem Solved By Bathtub Nudist
YOU SHALL NOT CROSS! Königsberg Tourists’ Hopes Dashed
ARE YOUR LUNGS ON Fire? Link Between Respiration And Combustion Gains Acceptance Among Scientists

Note that every one of these headlines are true—they describe events that did, in fact, happen. They just didn’t happen yesterday.

There have been many humanly understandable amazing breakthroughs in the history of science, that can be understood without a PhD or even a BSc. The operative word here is history. Think of Archimedes’s “Eureka!” when he understood the relation between the water a ship displaces, and the reason the ship floats. This is far enough back in scientific history that you don’t need to know fifty other discoveries to understand the theory; it can be explained in a couple of graphs; anyone can see how it’s useful; and the confirming experiments can be duplicated in your own bathtub.

Modern science is built on discoveries built on discoveries built on discoveries and so on all the way back to Archimedes. Reporting science only as breaking news is like wandering into a movie three-fourths of the way through, writing a story about “Bloody-handed man kisses girl holding gun!” and wandering back out again.

And if your editor says, “Oh, but our readers won’t be interested in that—”

Then point out that Reddit and Digg don’t link only to breaking news. They also link to short webpages that give good explanations of old science. Readers vote it up, and that should tell you something. Explain that if your newspaper doesn’t change to look more like Reddit, you’ll have to start selling drugs to make payroll. Editors love to hear that sort of thing, right?

On the Internet, a good new explanation of old science is news and it spreads like news. Why couldn’t the science sections of newspapers work the same way? Why isn’t a new explanation worth reporting on?

But all this is too visionary for a first step. For now, let’s just see if any journalists out there pick up on Amazing Breakthrough Day, where you report on some understandable science breakthrough as though it had just occurred.

April 1st. Put it on your calendar.

209
Is Humanism a Religion Substitute?

For many years before the Wright Brothers, people dreamed of flying with magic potions. There was nothing irrational about the raw desire to fly. There was nothing tainted about the wish to look down on a cloud from above. Only the “magic potions” part was irrational.

Suppose you were to put me into an fMRI scanner, and take a movie of my brain’s activity levels, while I watched a space shuttle launch. (Wanting to visit space is not “realistic,” but it is an essentially lawful dream—one that can be fulfilled in a lawful universe.) The fMRI might—maybe, maybe not—resemble the fMRI of a devout Christian watching a nativity scene.

Should an experimenter obtain this result, there’s a lot of people out there, both Christians and some atheists, who would gloat: “Ha, ha, space travel is your religion!”

But that’s drawing the wrong category boundary. It’s like saying that, because some people once tried to fly by irrational means, no one should ever enjoy looking out of an airplane window on the clouds below.

If a rocket launch is what it takes to give me a feeling of aesthetic transcendence, I do not see this as a substitute for religion. That is theomorphism—the viewpoint from gloating religionists who assume that everyone who isn’t religious has a hole in their mind that wants filling.

Now, to be fair to the religionists, this is not just a gloating assumption. There are atheists who have religion-shaped holes in their minds. I have seen attempts to substitute atheism or even transhumanism for religion. And the result is invariably awful. Utterly awful. Absolutely abjectly awful.

I call such efforts, “hymns to the nonexistence of God.”

When someone sets out to write an atheistic hymn—“Hail, oh unintelligent universe,” blah, blah, blah—the result will, without exception, suck.

Why? Because they’re being imitative. Because they have no motivation for writing the hymn except a vague feeling that since churches have hymns, they ought to have one too. And, on a purely artistic level, that puts them far beneath genuine religious art that is not an imitation of anything, but an original expression of emotion.

Religious hymns were (often) written by people who felt strongly and wrote honestly and put serious effort into the prosody and imagery of their work—that’s what gives their work the grace that it possesses, of artistic integrity.

So are atheists doomed to hymnlessness?

There is an acid test of attempts at post-theism. The acid test is: “If religion had never existed among the human species—if we had never made the original mistake—would this song, this art, this ritual, this way of thinking, still make sense?”

If humanity had never made the original mistake, there would be no hymns to the nonexistence of God. But there would still be marriages, so the notion of an atheistic marriage ceremony makes perfect sense—as long as you don’t suddenly launch into a lecture on how God doesn’t exist. Because, in a world where religion never had existed, nobody would interrupt a wedding to talk about the implausibility of a distant hypothetical concept. They’d talk about love, children, commitment, honesty, devotion, but who the heck would mention God?

And, in a human world where religion never had existed, there would still be people who got tears in their eyes watching a space shuttle launch.

Which is why, even if experiment shows that watching a shuttle launch makes “religion”-associated areas of my brain light up, associated with feelings of transcendence, I do not see that as a substitute for religion; I expect the same brain areas would light up, for the same reason, if I lived in a world where religion had never been invented.

A good “atheistic hymn” is simply a song about anything worth singing about that doesn’t happen to be religious.

Also, reversed stupidity is not intelligence. The world’s greatest idiot may say the Sun is shining, but that doesn’t make it dark out. The point is not to create a life that resembles religion as little as possible in every surface aspect—this is the same kind of thinking that inspires hymns to the nonexistence of God. If humanity had never made the original mistake, no one would be trying to avoid things that vaguely resembled religion. Believe accurately, then feel accordingly: If space launches actually exist, and watching a rocket rise makes you want to sing, then write the song, dammit.

If I get tears in my eyes at a space shuttle launch, it doesn’t mean I’m trying to fill a hole left by religion—it means that my emotional energies, my caring, are bound into the real world.

If God did speak plainly, and answer prayers reliably, God would just become one more boringly real thing, no more worth believing in than the postman. If God were real, it would destroy the inner uncertainty that brings forth outward fervor in compensation. And if everyone else believed God were real, it would destroy the specialness of being one of the elect.

If you invest your emotional energy in space travel, you don’t have those vulnerabilities. I can see the Space Shuttle rise without losing the awe. Everyone else can believe that Space Shuttles are real, and it doesn’t make them any less special. I haven’t painted myself into the corner.

The choice between God and humanity is not just a choice of drugs. Above all, humanity actually exists.

210
Scarcity

What follows is taken primarily from Robert Cialdini’s Influence: The Psychology of Persuasion.¹ I own three copies of this book: one for myself, and two for loaning to friends.

Scarcity, as that term is used in social psychology, is when things become more desirable as they appear less obtainable.

If you put a two-year-old boy in a room with two toys, one toy in the open and the other behind a Plexiglas wall, the two-year-old will ignore the easily accessible toy and go after the apparently forbidden one. If the wall is low enough to be easily climbable, the toddler is no more likely to go after one toy than the other.²
When Dade County forbade use or possession of phosphate detergents, many Dade residents drove to nearby counties and bought huge amounts of phosphate laundry detergents. Compared to Tampa residents not affected by the regulation, Dade residents rated phosphate detergents as gentler, more effective, more powerful on stains, and even believed that phosphate detergents poured more easily.³

Similarly, information that appears forbidden or secret seems more important and trustworthy:

When University of North Carolina students learned that a speech opposing coed dorms had been banned, they became more opposed to coed dorms (without even hearing the speech).⁴
When a driver said he had liability insurance, experimental jurors awarded his victim an average of four thousand dollars more than if the driver said he had no insurance. If the judge afterward informed the jurors that information about insurance was inadmissible and must be ignored, jurors awarded an average of thirteen thousand dollars more than if the driver had no insurance.⁵
Buyers for supermarkets, told by a supplier that beef was in scarce supply, gave orders for twice as much beef as buyers told it was readily available. Buyers told that beef was in scarce supply, and furthermore, that the information about scarcity was itself scarce—that the shortage was not general knowledge—ordered six times as much beef. (Since the study was conducted in a real-world context, the information provided was in fact correct.)⁶

The conventional theory for explaining this is “psychological reactance,” social-psychology-speak for “When you tell people they can’t do something, they’ll just try even harder.” The fundamental instincts involved appear to be preservation of status and preservation of options. We resist dominance, when any human agency tries to restrict our freedom. And when options seem to be in danger of disappearing, even from natural causes, we try to leap on the option before it’s gone.

Leaping on disappearing options may be a good adaptation in a hunter-gatherer society—gather the fruits while they are still ripe—but in a money-based society it can be rather costly. Cialdini reports that in one appliance store he observed, a salesperson who saw that a customer was evincing signs of interest in an appliance would approach, and sadly inform the customer that the item was out of stock, the last one having been sold only twenty minutes ago. Scarcity creating a sudden jump in desirability, the customer would often ask whether there was any chance that the salesperson could locate an unsold item in the back room, warehouse, or anywhere. “Well,” says the salesperson, “that’s possible, and I’m willing to check; but do I understand that this is the model you want, and if I can find it at this price, you’ll take it?”

As Cialdini remarks, a chief sign of this malfunction is that you dream of possessing something, rather than using it. (Timothy Ferriss offers similar advice on planning your life: ask which ongoing experiences would make you happy, rather than which possessions or status-changes.)

But the really fundamental problem with desiring the unattainable is that as soon as you actually get it, it stops being unattainable. If we cannot take joy in the merely available, our lives will always be frustrated . . .

1. Robert B. Cialdini, Influence: The Psychology of Persuasion: Revised Edition (New York: Quill, 1993).

2. Sharon S. Brehm and Marsha Weintraub, “Physical Barriers and Psychological Reactance: Two-year-olds’ Responses to Threats to Freedom,” Journal of Personality and Social Psychology 35 (1977): 830–836.

3. Michael B. Mazis, Robert B. Settle, and Dennis C. Leslie, “Elimination of Phosphate Detergents and Psychological Reactance,” Journal of Marketing Research 10 (1973): 2; Michael B. Mazis, “Antipollution Measures and Psychological Reactance Theory: A Field Experiment,” Journal of Personality and Social Psychology 31 (1975): 654–666.

4. Richard D. Ashmore, Vasantha Ramchandra, and Russell A. Jones, “Censorship as an Attitude Change Induction,” Paper presented at Eastern Psychological Association meeting (1971).

5. Dale Broeder, “The University of Chicago Jury Project,” Nebraska Law Review 38 (1959): 760–774.

6. A. Knishinsky, “The Effects of Scarcity of Material and Exclusivity of Information on Industrial Buyer Perceived Risk in Provoking a Purchase Decision” (Doctoral dissertation, Arizona State University, 1982).

211
The Sacred Mundane

So I was reading (around the first half of) Adam Frank’s The Constant Fire,¹ in preparation for my Bloggingheads dialogue with him. Adam Frank’s book is about the experience of the sacred. I might not usually call it that, but of course I know the experience Frank is talking about. It’s what I feel when I watch a video of a space shuttle launch; or what I feel—to a lesser extent, because in this world it is too common—when I look up at the stars at night, and think about what they mean. Or the birth of a child, say. That which is significant in the Unfolding Story.

Adam Frank holds that this experience is something that science holds deeply in common with religion. As opposed to e.g. being a basic human quality which religion corrupts.

The Constant Fire quotes William James’s The Varieties of Religious Experience as saying:

Religion . . . shall mean for us the feelings, acts, and experiences of individual men in their solitude; so far as they apprehend themselves to stand in relation to whatever they may consider the divine.

And this theme is developed further: Sacredness is something intensely private and individual.

Which completely nonplussed me. Am I supposed to not have any feeling of sacredness if I’m one of many people watching the video of SpaceShipOne winning the X-Prize? Why not? Am I supposed to think that my experience of sacredness has to be somehow different from that of all the other people watching? Why, when we all have the same brain design? Indeed, why would I need to believe I was unique? (But “unique” is another word Adam Frank uses; so-and-so’s “unique experience of the sacred.”) Is the feeling private in the same sense that we have difficulty communicating any experience? Then why emphasize this of sacredness, rather than sneezing?

The light came on when I realized that I was looking at a trick of Dark Side Epistemology—if you make something private, that shields it from criticism. You can say, “You can’t criticize me, because this is my private, inner experience that you can never access to question it.”

But the price of shielding yourself from criticism is that you are cast into solitude—the solitude that William James admired as the core of religious experience, as if loneliness were a good thing.

Such relics of Dark Side Epistemology are key to understanding the many ways that religion twists the experience of sacredness:

Mysteriousness—why should the sacred have to be mysterious? A space shuttle launch gets by just fine without being mysterious. How much less would I appreciate the stars if I did not know what they were, if they were just little points in the night sky? But if your religious beliefs are questioned—if someone asks, “Why doesn’t God heal amputees?”—then you take refuge and say, in a tone of deep profundity, “It is a sacred mystery!” There are questions that must not be asked, and answers that must not be acknowledged, to defend the lie. Thus unanswerability comes to be associated with sacredness. And the price of shielding yourself from criticism is giving up the true curiosity that truly wishes to find answers. You will worship your own ignorance of the temporarily unanswered questions of your own generation—probably including ones that are already answered.

Faith—in the early days of religion, when people were more naive, when even intelligent folk actually believed that stuff, religions staked their reputation upon the testimony of miracles in their scriptures. And Christian archaeologists set forth truly expecting to find the ruins of Noah’s Ark. But when no such evidence was forthcoming, then religion executed what William Bartley called the retreat to commitment, “I believe because I believe!” Thus belief without good evidence came to be associated with the experience of the sacred. And the price of shielding yourself from criticism is that you sacrifice your ability to think clearly about that which is sacred, and to progress in your understanding of the sacred, and relinquish mistakes.

Experientialism—if before you thought that the rainbow was a sacred contract of God with humanity, and then you begin to realize that God doesn’t exist, then you may execute a retreat to pure experience—to praise yourself just for feeling such wonderful sensations when you think about God, whether or not God actually exists. And the price of shielding yourself from criticism is solipsism: your experience is stripped of its referents. What a terrible hollow feeling it would be to watch a space shuttle rising on a pillar of flame, and say to yourself, “But it doesn’t really matter whether the space shuttle actually exists, so long as I feel.”

Separation—if the sacred realm is not subject to ordinary rules of evidence or investigable by ordinary means, then it must be different in kind from the world of mundane matter: and so we are less likely to think of a space shuttle as a candidate for sacredness, because it is a work of merely human hands. Keats lost his admiration of the rainbow and demoted it to the “dull catalogue of mundane things” for the crime of its woof and texture being known. And the price of shielding yourself from all ordinary criticism is that you lose the sacredness of all merely real things.

Privacy—of this I have already spoken.

Such distortions are why we had best not to try to salvage religion. No, not even in the form of “spirituality.” Take away the institutions and the factual mistakes, subtract the churches and the scriptures, and you’re left with . . . all this nonsense about mysteriousness, faith, solipsistic experience, private solitude, and discontinuity.

The original lie is only the beginning of the problem. Then you have all the ill habits of thought that have evolved to defend it. Religion is a poisoned chalice, from which we had best not even sip. Spirituality is the same cup after the original pellet of poison has been taken out, and only the dissolved portion remains—a little less directly lethal, but still not good for you.

When a lie has been defended for ages upon ages, the true origin of the inherited habits lost in the mists, with layer after layer of undocumented sickness; then the wise, I think, will start over from scratch, rather than trying to selectively discard the original lie while keeping the habits of thought that protected it. Just admit you were wrong, give up entirely on the mistake, stop defending it at all, stop trying to say you were even a little right, stop trying to save face, just say “Oops!” and throw out the whole thing and begin again.

That capacity—to really, really, without defense, admit you were entirely wrong—is why religious experience will never be like scientific experience. No religion can absorb that capacity without losing itself entirely and becoming simple humanity . . .

. . . to just look up at the distant stars. Believable without strain, without a constant distracting struggle to fend off your awareness of the counterevidence. Truly there in the world, the experience united with the referent, a solid part of that unfolding story. Knowable without threat, offering true meat for curiosity. Shared in togetherness with the many other onlookers, no need to retreat to privacy. Made of the same fabric as yourself and all other things. Most holy and beautiful, the sacred mundane.

1. Adam Frank, The Constant Fire: Beyond the Science vs. Religion Debate (University of California Press, 2009).

212
To Spread Science, Keep It Secret

Sometimes I wonder if the Pythagoreans had the right idea.

Yes, I’ve written about how “science” is inherently public. I’ve written that “science” is distinguished from merely rational knowledge by the in-principle ability to reproduce scientific experiments for yourself, to know without relying on authority. I’ve said that “science” should be defined as the publicly accessible knowledge of humankind. I’ve even suggested that future generations will regard all papers not published in an open-access journal as non-science, i.e., it can’t be part of the public knowledge of humankind if you make people pay to read it.

But that’s only one vision of the future. In another vision, the knowledge we now call “science” is taken out of the public domain—the books and journals hidden away, guarded by mystic cults of gurus wearing robes, requiring fearsome initiation rituals for access—so that more people will actually study it.

I mean, right now, people can study science but they don’t.

“Scarcity,” it’s called in social psychology. What appears to be in limited supply is more highly valued. And this effect is especially strong with information—we’re much more likely to try to obtain information that we believe is secret, and to value it more when we do obtain it.

With science, I think, people assume that if the information is freely available, it must not be important. So instead people join cults that have the sense to keep their Great Truths secret. The Great Truth may actually be gibberish, but it’s more satisfying than coherent science, because it’s secret.

Science is the great Purloined Letter of our times, left out in the open and ignored.

Sure, scientific openness helps the scientific elite. They’ve already been through the initiation rituals. But for the rest of the planet, science is kept secret a hundred times more effectively by making it freely available, than if its books were guarded in vaults and you had to walk over hot coals to get access. (This being a fearsome trial indeed, since the great secrets of insulation are only available to Physicist-Initiates of the Third Level.)

If scientific knowledge were hidden in ancient vaults (rather than hidden in inconvenient pay-for-access journals), at least then people would try to get into the vaults. They’d be desperate to learn science. Especially when they saw the power that Eighth Level Physicists could wield, and were told that they weren’t allowed to know the explanation.

And if you tried to start a cult around oh, say, Scientology, you’d get some degree of public interest, at first. But people would very quickly start asking uncomfortable questions like “Why haven’t you given a public demonstration of your Eighth Level powers, like the Physicists?” and “How come none of the Master Mathematicians seem to want to join your cult?” and “Why should I follow your Founder when they aren’t an Eighth Level anything outside their own cult?” and “Why should I study your cult first, when the Dentists of Doom can do things that are so much more impressive?”

When you look at it from that perspective, the escape of math from the Pythagorean cult starts to look like a major strategic blunder for humanity.

Now, I know what you’re going to say: “But science is surrounded by fearsome initiation rituals! Plus it’s inherently difficult to learn! Why doesn’t that count?” Because the public thinks that science is freely available, that’s why. If you’re allowed to learn, it must not be important enough to learn.

It’s an image problem, people taking their cues from others’ attitudes. Just anyone can walk into the supermarket and buy a light bulb, and nobody looks at it with awe and reverence. The physics supposedly isn’t secret (even though you don’t know), and there’s a one-paragraph explanation in the newspaper that sounds vaguely authoritative and convincing—essentially, no one treats the lightbulb as a sacred mystery, so neither do you.

Even the simplest little things, completely inert objects like crucifixes, can become magical if everyone looks at them like they’re magic. But since you’re theoretically allowed to know why the light bulb works without climbing the mountain to find the remote Monastery of Electricians, there’s no need to actually bother to learn.

Now, because science does in fact have initiation rituals both social and cognitive, scientists are not wholly dissatisfied with their science. The problem is that, in the present world, very few people bother to study science in the first place. Science cannot be the true Secret Knowledge, because just anyone is allowed to know it—even though, in fact, they don’t.

If the Great Secret of Natural Selection, passed down from Darwin Who Is Not Forgotten, was only ever imparted to you after you paid $2,000 and went through a ceremony involving torches and robes and masks and sacrificing an ox, then when you were shown the fossils, and shown the optic cable going through the retina under a microscope, and finally told the Truth, you would say “That’s the most brilliant thing ever!” and be satisfied. After that, if some other cult tried to tell you it was actually a bearded man in the sky 6000 years ago, you’d laugh like hell.

And you know, it might actually be more fun to do things that way. Especially if the initiation required you to put together some of the evidence for yourself—together, or with classmates—before you could tell your Science Sensei you were ready to advance to the next level. It wouldn’t be efficient, sure, but it would be fun.

If humanity had never made the mistake—never gone down the religious path, and never learned to fear anything that smacks of religion—then maybe the PhD granting ceremony would involve litanies and chanting, because, hey, that’s what people like. Why take the fun out of everything?

Maybe we’re just doing it wrong.

And no, I’m not seriously proposing that we try to reverse the last five hundred years of openness and classify all the science secret. At least, not at the moment. Efficiency is important for now, especially in things like medical research. I’m just explaining why it is that I won’t tell anyone the Secret of how the ineffable difference between blueness and redness arises from mere atoms for less than $100,000—

Ahem! I meant to say, I’m telling you about this vision of an alternate Earth, so that you give science equal treatment with cults. So that you don’t undervalue scientific truth when you learn it, just because it doesn’t seem to be protected appropriately to its value. Imagine the robes and masks. Visualize yourself creeping into the vaults and stealing the Lost Knowledge of Newton. And don’t be fooled by any organization that does use robes and masks, unless they also show you the data.

People seem to have holes in their minds for Esoteric Knowledge, Deep Secrets, the Hidden Truth. And I’m not even criticizing this psychology! There are deep secret esoteric hidden truths, like quantum mechanics or Bayes-structure. We’ve just gotten into the habit of presenting the Hidden Truth in a very unsatisfying way, wrapped up in false mundanity.

But if the holes for secret knowledge are not filled by true beliefs, they will be filled by false beliefs. There is nothing but science to learn—the emotional energy must either be invested in reality, or wasted in total nonsense, or destroyed. For myself, I think it is better to invest the emotional energy; fun should not be needlessly cast away.

Right now, we’ve got the worst of both worlds. Science isn’t really free, because the courses are expensive and the textbooks are expensive. But the public thinks that anyone is allowed to know, so it must not be important.

Ideally, you would want to arrange things the other way around.

213
Initiation Ceremony

The torches that lit the narrow stairwell burned intensely and in the wrong color, flame like melting gold or shattered suns.

192 . . . 193 . . .

Brennan’s sandals clicked softly on the stone steps, snicking in sequence, like dominos very slowly falling.

227 . . . 228 . . .

Half a circle ahead of him, a trailing fringe of dark cloth whispered down the stairs, the robed figure itself staying just out of sight.

239 . . . 240 . . .

Not much longer, Brennan predicted to himself, and his guess was accurate:

Sixteen times sixteen steps was the number, and they stood before the portal of glass.

The great curved gate had been wrought with cunning, humor, and close attention to indices of refraction: it warped light, bent it, folded it, and generally abused it, so that there were hints of what was on the other side (stronger light sources, dark walls) but no possible way of seeing through—unless, of course, you had the key: the counter-door, thick for thin and thin for thick, in which case the two would cancel out.

From the robed figure beside Brennan, two hands emerged, gloved in reflective cloth to conceal skin’s color. Fingers like slim mirrors grasped the handles of the warped gate—handles that Brennan had not guessed; in all that distortion, shapes could only be anticipated, not seen.

“Do you want to know?” whispered the guide; a whisper nearly as loud as an ordinary voice, but not revealing the slightest hint of gender.

Brennan paused. The answer to the question seemed suspiciously, indeed extraordinarily obvious, even for ritual.

“Yes,” Brennan said finally.

The guide only regarded him silently.

“Yes, I want to know,” said Brennan.

“Know what, exactly?” whispered the figure.

Brennan’s face scrunched up in concentration, trying to visualize the game to its end, and hoping he hadn’t blown it already; until finally he fell back on the first and last resort, which is the truth:

“It doesn’t matter,” said Brennan, “the answer is still yes.”

The glass gate parted down the middle, and slid, with only the tiniest scraping sound, into the surrounding stone.

The revealed room was lined, wall-to-wall, with figures robed and hooded in light-absorbing cloth. The straight walls were not themselves black stone, but mirrored, tiling a square grid of dark robes out to infinity in all directions; so that it seemed as if the people of some much vaster city, or perhaps the whole human kind, watched in assembly. There was a hint of moist warmth in the air of the room, the breath of the gathered: a scent of crowds.

Brennan’s guide moved to the center of the square, where burned four torches of that relentless yellow flame. Brennan followed, and when he stopped, he realized with a slight shock that all the cowled hoods were now looking directly at him. Brennan had never before in his life been the focus of such absolute attention; it was frightening, but not entirely unpleasant.

“He is here,” said the guide in that strange loud whisper.

The endless grid of robed figures replied in one voice: perfectly blended, exactly synchronized, so that not a single individual could be singled out from the rest, and betrayed:

“Who is absent?”

“Jakob Bernoulli,” intoned the guide, and the walls replied:

“Is dead but not forgotten.”

“Abraham de Moivre,”

“Is dead but not forgotten.”

“Pierre-Simon Laplace,”

“Is dead but not forgotten.”

“Edwin Thompson Jaynes,”

“Is dead but not forgotten.”

“They died,” said the guide, “and they are lost to us; but we still have each other, and the project continues.”

In the silence, the guide turned to Brennan, and stretched forth a hand, on which rested a small ring of nearly transparent material.

Brennan stepped forward to take the ring—

But the hand clenched tightly shut.

“If three-fourths of the humans in this room are women,” said the guide, “and three-fourths of the women and half of the men belong to the Heresy of Virtue, and I am a Virtuist, what is the probability that I am a man?”

“Two-elevenths,” Brennan said confidently.

There was a moment of absolute silence.

Then a titter of shocked laughter.

The guide’s whisper came again, truly quiet this time, almost nonexistent: “It’s one-sixth, actually.”

Brennan’s cheeks were flaming so hard that he thought his face might melt off. The instinct was very strong to run out of the room and up the stairs and flee the city and change his name and start his life over again and get it right this time.

“An honest mistake is at least honest,” said the guide, louder now, “and we may know the honesty by its relinquishment. If I am a Virtuist, what is the probability that I am a man?”

“One—” brennan started to say.

Then he stopped. Again, the horrible silence.

“Just say ‘one-sixth’ already,” stage-whispered the figure, this time loud enough for the walls to hear; then there was more laughter, not all of it kind.

Brennan was breathing rapidly and there was sweat on his forehead. If he was wrong about this, he really was going to flee the city. “Three fourths women times three fourths Virtuists is nine sixteenths female Virtuists in this room. One fourth men times one half Virtuists is two sixteenths male Virtuists. If I have only that information and the fact that you are a Virtuist, I would then estimate odds of two to nine, or a probability of two-elevenths, that you are male. Though I do not, in fact, believe the information given is correct. For one thing, it seems too neat. For another, there are an odd number of people in this room.”

The hand stretched out again, and opened.

Brennan took the ring. It looked almost invisible, in the torchlight; not glass, but some material with a refractive index very close to air. The ring was warm from the guide’s hand, and felt like a tiny living thing as it embraced his finger.

The relief was so great that he nearly didn’t hear the cowled figures applauding.

From the robed guide came one last whisper:

“You are now a novice of the Bayesian Conspiracy.”

Part R
Physicalism 201

214
Hand vs. Fingers

Back to our original topic: Reductionism and the Mind Projection Fallacy. There can be emotional problems in accepting reductionism, if you think that things have to be fundamental to be fun. But this position commits us to never taking joy in anything more complicated than a quark, and so I prefer to reject it.

To review, the reductionist thesis is that we use multi-level models for computational reasons, but physical reality has only a single level.

Here I’d like to pose the following conundrum: When you pick up a cup of water, is it your hand that picks it up?

Most people, of course, go with the naive popular answer: “Yes.”

Recently, however, scientists have made a stunning discovery: It’s not your hand that holds the cup, it’s actually your fingers, thumb, and palm.

Yes, I know! I was shocked too. But it seems that after scientists measured the forces exerted on the cup by each of your fingers, your thumb, and your palm, they found there was no force left over—so the force exerted by your hand must be zero.

The theme here is that, if you can see how (not just know that) a higher level reduces to a lower one, they will not seem like separate things within your map; you will be able to see how silly it is to think that your fingers could be in one place, and your hand somewhere else; you will be able to see how silly it is to argue about whether it is your hand that picks up the cup, or your fingers.

The operative word is “see,” as in concrete visualization. Imagining your hand causes you to imagine the fingers and thumb and palm; conversely, imagining fingers and thumb and palm causes you to identify a hand in the mental picture. Thus the high level of your map and the low level of your map will be tightly bound together in your mind.

In reality, of course, the levels are bound together even tighter than that—bound together by the tightest possible binding: physical identity. You can see this: You can see that saying (1) “hand” or (2) “fingers and thumb and palm,” does not refer to different things, but different points of view.

But suppose you lack the knowledge to so tightly bind together the levels of your map. For example, you could have a “hand scanner” that showed a “hand” as a dot on a map (like an old-fashioned radar display), and similar scanners for fingers/thumbs/palms; then you would see a cluster of dots around the hand, but you would be able to imagine the hand-dot moving off from the others. So, even though the physical reality of the hand (that is, the thing the dot corresponds to) was identical with / strictly composed of the physical realities of the fingers and thumb and palm, you would not be able to see this fact; even if someone told you, or you guessed from the correspondence of the dots, you would only know the fact of reduction, not see it. You would still be able to imagine the hand dot moving around independently, even though, if the physical makeup of the sensors were held constant, it would be physically impossible for this to actually happen.

Or, at a still lower level of binding, people might just tell you “There’s a hand over there, and some fingers over there”—in which case you would know little more than a Good-Old-Fashioned AI representing the situation using suggestively named LISP tokens. There wouldn’t be anything obviously contradictory about asserting:

⊢Inside(Room,Hand)

⊢¬Inside(Room,Fingers),

because you would not possess the knowledge

⊢Inside(x,Hand)⇒Inside(x,Fingers).

None of this says that a hand can actually detach its existence from your fingers and crawl, ghostlike, across the room; it just says that a Good-Old-Fashioned AI with a propositional representation may not know any better. The map is not the territory.

In particular, you shouldn’t draw too many conclusions from how it seems conceptually possible, in the mind of some specific conceiver, to separate the hand from its constituent elements of fingers, thumb, and palm. Conceptual possibility is not the same as logical possibility or physical possibility.

It is conceptually possible to you that 235,757 is prime, because you don’t know any better. But it isn’t logically possible that 235,757 is prime; if you were logically omniscient, 235,757 would be obviously composite (and you would know the factors). That that’s why we have the notion of impossible possible worlds, so that we can put probability distributions on propositions that may or may not be in fact logically impossible.

And you can imagine philosophers who criticize “eliminative fingerists” who contradict the direct facts of experience—we can feel our hand holding the cup, after all—by suggesting that “hands” don’t really exist, in which case, obviously, the cup would fall down. And philosophers who suggest “appendigital bridging laws” to explain how a particular configuration of fingers evokes a hand into existence—with the note, of course, that while our world contains those particular appendigital bridging laws, the laws could have been conceivably different, and so are not in any sense necessary facts, etc.

All of these are cases of Mind Projection Fallacy, and what I call “naive philosophical realism”—the confusion of philosophical intuitions for direct, veridical information about reality. Your inability to imagine something is just a computational fact about what your brain can or can’t imagine. Another brain might work differently.

215
Angry Atoms

Fundamental physics—quarks ’n’ stuff—is far removed from the levels we can see, like hands and fingers. At best, you can know how to replicate the experiments that show that your hand (like everything else) is composed of quarks, and you may know how to derive a few equations for things like atoms and electron clouds and molecules.

At worst, the existence of quarks beneath your hand may just be something you were told. In which case it’s questionable in what sense you can be said to “know” it at all, even if you repeat back the same word “quark” that a physicist would use to convey knowledge to another physicist.

Either way, you can’t actually see the identity between levels—no one has a brain large enough to visualize avogadros of quarks and recognize a hand-pattern in them.

But we at least understand what hands do. Hands push on things, exert forces on them. When we’re told about atoms, we visualize little billiard balls bumping into each other. This makes it seem obvious that “atoms” can push on things too, by bumping into them.

Now this notion of atoms is not quite correct. But so far as human imagination goes, it’s relatively easy to imagine our hand being made up of a little galaxy of swirling billiard balls, pushing on things when our “fingers” touch them. Democritus imagined this 2,400 years ago, and there was a time, roughly 1803–1922, when Science thought he was right.

But what about, say, anger?

How could little billiard balls be angry? Tiny frowny faces on the billiard balls?

Put yourself in the shoes of, say, a hunter-gatherer—someone who may not even have a notion of writing, let alone the notion of using base matter to perform computations—someone who has no idea that such a thing as neurons exist. Then you can imagine the functional gap that your ancestors might have perceived between billiard balls and “Grrr! Aaarg!”

Forget about subjective experience for the moment, and consider the sheer behavioral gap between anger and billiard balls. The difference between what little billiard balls do, and what anger makes people do. Anger can make people raise their fists and hit someone—or say snide things behind their backs—or plant scorpions in their tents at night. Billiard balls just push on things.

Try to put yourself in the shoes of the hunter-gatherer who’s never had the “Aha!” of information-processing. Try to avoid hindsight bias about things like neurons and computers. Only then will you be able to see the uncrossable explanatory gap:

How can you explain angry behavior in terms of billiard balls?

Well, the obvious materialist conjecture is that the little billiard balls push on your arm and make you hit someone, or push on your tongue so that insults come out.

But how do the little billiard balls know how to do this—or how to guide your tongue and fingers through long-term plots—if they aren’t angry themselves?

And besides, if you’re not seduced by—gasp!—scientism, you can see from a first-person perspective that this explanation is obviously false. Atoms can push on your arm, but they can’t make you want anything.

Someone may point out that drinking wine can make you angry. But who says that wine is made exclusively of little billiard balls? Maybe wine just contains a potency of angerness.

Clearly, reductionism is just a flawed notion.

(The novice goes astray and says “The art failed me”; the master goes astray and says “I failed my art.”)

What does it take to cross this gap? It’s not just the idea of “neurons” that “process information”—if you say only this and nothing more, it just inserts a magical, unexplained level-crossing rule into your model, where you go from billiards to thoughts.

But an Artificial Intelligence programmer who knows how to create a chess-playing program out of base matter has taken a genuine step toward crossing the gap. If you understand concepts like consequentialism, backward chaining, utility functions, and search trees, you can make merely causal/mechanical systems compute plans.

The trick goes something like this: For each possible chess move, compute the moves your opponent could make, then your responses to those moves, and so on; evaluate the furthest position you can see using some local algorithm (you might simply count up the material); then trace back using minimax to find the best move on the current board; then make that move.

More generally: If you have chains of causality inside the mind that have a kind of mapping—a mirror, an echo—to what goes on in the environment, then you can run a utility function over the end products of imagination, and find an action that achieves something that the utility function rates highly, and output that action. It is not necessary for the chains of causality inside the mind, that are similar to the environment, to be made out of billiard balls that have little auras of intentionality. Deep Blue’s transistors do not need little chess pieces carved on them, in order to work. See also The Simple Truth.

All this is still tremendously oversimplified, but it should, at least, reduce the apparent length of the gap. If you can understand all that, you can see how a planner built out of base matter can be influenced by alcohol to output more angry behaviors. The billiard balls in the alcohol push on the billiard balls making up the utility function.

But even if you know how to write small AIs, you can’t visualize the level-crossing between transistors and chess. There are too many transistors, and too many moves to check.

Likewise, even if you knew all the facts of neurology, you would not be able to visualize the level-crossing between neurons and anger—let alone the level-crossing between atoms and anger. Not the way you can visualize a hand consisting of fingers, thumb, and palm.

And suppose a cognitive scientist just flatly tells you “Anger is hormones”? Even if you repeat back the words, it doesn’t mean you’ve crossed the gap. You may believe you believe it, but that’s not the same as understanding what little billiard balls have to do with wanting to hit someone.

So you come up with interpretations like, “Anger is mere hormones, it’s caused by little molecules, so it must not be justified in any moral sense—that’s why you should learn to control your anger.”

Or, “There isn’t really any such thing as anger—it’s an illusion, a quotation with no referent, like a mirage of water in the desert, or looking in the garage for a dragon and not finding one.”

These are both tough pills to swallow (not that you should swallow them) and so it is a good deal easier to profess them than to believe them.

I think this is what non-reductionists/non-materialists think they are criticizing when they criticize reductive materialism.

But materialism isn’t that easy. It’s not as cheap as saying, “Anger is made out of atoms—there, now I’m done.” That wouldn’t explain how to get from billiard balls to hitting. You need the specific insights of computation, consequentialism, and search trees before you can start to close the explanatory gap.

All this was a relatively easy example by modern standards, because I restricted myself to talking about angry behaviors. Talking about outputs doesn’t require you to appreciate how an algorithm feels from inside (cross a first-person/third-person gap) or dissolve a wrong question (untangle places where the interior of your own mind runs skew to reality).

Going from material substances that bend and break, burn and fall, push and shove, to angry behavior, is just a practice problem by the standards of modern philosophy. But it is an important practice problem. It can only be fully appreciated, if you realize how hard it would have been to solve before writing was invented. There was once an explanatory gap here—though it may not seem that way in hindsight, now that it’s been bridged for generations.

Explanatory gaps can be crossed, if you accept help from science, and don’t trust the view from the interior of your own mind.

216
Heat vs. Motion

After the last essay, it occurred to me that there’s a much simpler example of reductionism jumping a gap of apparent-difference-in-kind: the reduction of heat to motion.

Today, the equivalence of heat and motion may seem too obvious in hindsight—everyone says that “heat is motion,” therefore, it can’t be a “weird” belief.

But there was a time when the kinetic theory of heat was a highly controversial scientific hypothesis, contrasting to belief in a caloric fluid that flowed from hot objects to cold objects. Still earlier, the main theory of heat was “Phlogiston!”

Suppose you’d separately studied kinetic theory and caloric theory. You now know something about kinetics: collisions, elastic rebounds, momentum, kinetic energy, gravity, inertia, free trajectories. Separately, you know something about heat: temperatures, pressures, combustion, heat flows, engines, melting, vaporization.

Not only is this state of knowledge a plausible one, it is the state of knowledge possessed by e.g. Sadi Carnot, who, working strictly from within the caloric theory of heat, developed the principle of the Carnot cycle—a heat engine of maximum efficiency, whose existence implies the Second Law of Thermodynamics. This in 1824, when kinetics was a highly developed science.

Suppose, like Carnot, you know a great deal about kinetics, and a great deal about heat, as separate entities. Separate entities of knowledge, that is: your brain has separate filing baskets for beliefs about kinetics and beliefs about heat. But from the inside, this state of knowledge feels like living in a world of moving things and hot things, a world where motion and heat are independent properties of matter.

Now a Physicist From The Future comes along and tells you: “Where there is heat, there is motion, and vice versa. That’s why, for example, rubbing things together makes them hotter.”

There are (at least) two possible interpretations you could attach to this statement, “Where there is heat, there is motion, and vice versa.”

First, you could suppose that heat and motion exist separately—that the caloric theory is correct—but that among our universe’s physical laws is a “bridging law” which states that, where objects are moving quickly, caloric will come into existence. And conversely, another bridging law says that caloric can exert pressure on things and make them move, which is why a hotter gas exerts more pressure on its enclosure (thus a steam engine can use steam to drive a piston).

Second, you could suppose that heat and motion are, in some as-yet-mysterious sense, the same thing.

“Nonsense,” says Thinker 1, “the words ‘heat’ and ‘motion’ have two different meanings; that is why we have two different words. We know how to determine when we will call an observed phenomenon ‘heat’—heat can melt things, or make them burst into flame. We know how to determine when we will say that an object is ‘moving quickly’—it changes position; and when it crashes, it may deform, or shatter. Heat is concerned with change of substance; motion, with change of position and shape. To say that these two words have the same meaning is simply to confuse yourself.”

“Impossible,” says Thinker 2. “It may be that, in our world, heat and motion are associated by bridging laws, so that it is a law of physics that motion creates caloric, and vice versa. But I can easily imagine a world where rubbing things together does not make them hotter, and gases don’t exert more pressure at higher temperatures. Since there are possible worlds where heat and motion are not associated, they must be different properties—this is true a priori.”

Thinker 1 is confusing the quotation and the referent: 2 + 2 = 4, but “2 + 2” ≠ “4.” The string “2 + 2” contains five characters (including whitespace) and the string “4” contains only one character. If you type the two strings into a Python interpreter, they yield the same output, >>> 4. So you can’t conclude, from looking at the strings “2 + 2” and “4,” that just because the strings are different, they must have different “meanings” relative to the Python Interpreter.

The words “heat” and “kinetic energy” can be said to “refer to” the same thing, even before we know how heat reduces to motion, in the sense that we don’t know yet what the referent is, but the referents are in fact the same. You might imagine an Idealized Omniscient Science Interpreter that would give the same output when we typed in “heat” and “kinetic energy” on the command line.

I talk about the Science Interpreter to emphasize that, to dereference the pointer, you’ve got to step outside cognition. The end result of the dereference is something out there in reality, not in anyone’s mind. So you can say “real referent” or “actual referent,” but you can’t evaluate the words locally, from the inside of your own head. You can’t reason using the actual heat-referent—if you thought using real heat, thinking “one million Kelvin” would vaporize your brain. But, by forming a belief about your belief about heat, you can talk about your belief about heat, and say things like “It’s possible that my belief about heat doesn’t much resemble real heat.” You can’t actually perform that comparison right there in your own mind, but you can talk about it.

Hence you can say, “My beliefs about heat and motion are not the same beliefs, but it’s possible that actual heat and actual motion are the same thing.” It’s just like being able to acknowledge that “the morning star” and “the evening star” might be the same planet, while also understanding that you can’t determine this just by examining your beliefs—you’ve got to haul out the telescope.

Thinker 2’s mistake follows similarly. A physicist told them, “Where there is heat, there is motion” and Thinker 2 mistook this for a statement of physical law: The presence of caloric causes the existence of motion. What the physicist really means is more akin to an inferential rule: Where you are told there is “heat,” deduce the presence of “motion.”

From this basic projection of a multilevel model into a multilevel reality follows another, distinct error: the conflation of conceptual possibility with logical possibility. To Sadi Carnot, it is conceivable that there could be another world where heat and motion are not associated. To Richard Feynman, armed with specific knowledge of how to derive equations about heat from equations about motion, this idea is not only inconceivable, but so wildly inconsistent as to make one’s head explode.

I should note, in fairness to philosophers, that there are philosophers who have said these things. For example, Hilary Putnam, writing on the “Twin Earth” thought experiment:¹

Once we have discovered that water (in the actual world) is H₂O, nothing counts as a possible world in which water isn’t H₂O. In particular, if a “logically possible” statement is one that holds in some “logically possible world,” it isn’t logically possible that water isn’t H₂O.

On the other hand, we can perfectly well imagine having experiences that would convince us (and that would make it rational to believe that) water isn’t H₂O. In that sense, it is conceivable that water isn’t H₂O. It is conceivable but it isn’t logically possible! Conceivability is no proof of logical possibility.

It appears to me that “water” is being used in two different senses in these two paragraphs—one in which the word “water” refers to what we type into the Science Interpreter, and one in which “water” refers to what we get out of the Science Interpreter when we type “water” into it. In the first paragraph, Hilary seems to be saying that after we do some experiments and find out that water is H₂O, water becomes automatically redefined to mean H₂O. But you could coherently hold a different position about whether the word “water” now means “H₂O” or “whatever is really in that bottle next to me,” so long as you use your terms consistently.

I believe the above has already been said as well? Anyway . . .

It is quite possible for there to be only one thing out-there-in-the-world, but for it to take on sufficiently different forms, and for you yourself to be sufficiently ignorant of the reduction, that it feels like living in a world containing two entirely different things. Knowledge concerning these two different phenomena may be taught in two different classes, and studied by two different academic fields, located in two different buildings of your university.

You’ve got to put yourself quite a ways back, into a historically realistic frame of mind, to remember how different heat and motion once seemed. Though, depending on how much you know today, it may not be as hard as all that, if you can look past the pressure of conventionality (that is, “heat is motion” is an un-weird belief, “heat is not motion” is a weird belief). I mean, suppose that tomorrow the physicists stepped forward and said, “Our popularizations of science have always contained one lie. Actually, heat has nothing to do with motion.” Could you prove they were wrong?

Saying “Maybe heat and motion are the same thing!” is easy. The difficult part is explaining how. It takes a great deal of detailed knowledge to get yourself to the point where you can no longer conceive of a world in which the two phenomena go separate ways. Reduction isn’t cheap, and that’s why it buys so much.

Or maybe you could say: “Reductionism is easy, reduction is hard.” But it does kinda help to be a reductionist, I think, when it comes time to go looking for a reduction.

1. Hilary Putnam, “The Meaning of Meaning,” in The Twin Earth Chronicles, ed. Andrew Pessin and Sanford Goldberg (M. E. Sharpe, Inc., 1996), 3–52.

217
Brain Breakthrough! It’s Made of Neurons!

In an amazing breakthrough, a multinational team of scientists led by Nobel laureate Santiago Ramón y Cajal announced that the brain is composed of a ridiculously complicated network of tiny cells connected to each other by infinitesimal threads and branches.

The multinational team—which also includes the famous technician Antonie van Leeuwenhoek, and possibly Imhotep, promoted to the Egyptian god of medicine—issued this statement:

“The present discovery culminates years of research indicating that the convoluted squishy thing inside our skulls is even more complicated than it looks. Thanks to Cajal’s application of a new staining technique invented by Camillo Golgi, we have learned that this structure is not a continuous network like the blood vessels of the body, but is actually composed of many tiny cells, or ‘neurons,’ connected to one another by even more tiny filaments.

“Other extensive evidence, beginning from Greek medical researcher Alcmaeon and continuing through Paul Broca’s research on speech deficits, indicates that the brain is the seat of reason.

“Nemesius, the Bishop of Emesia, has previously argued that brain tissue is too earthy to act as an intermediary between the body and soul, and so the mental faculties are located in the ventricles of the brain. However, if this is correct, there is no reason why this organ should turn out to have an immensely complicated internal composition.

“Charles Babbage has independently suggested that many small mechanical devices could be collected into an ‘Analytical Engine,’ capable of performing activities, such as arithmetic, which are widely believed to require thought. The work of Luigi Galvani and Hermann von Helmholtz suggests that the activities of neurons are electrochemical in nature, rather than mechanical pressures as previously believed. Nonetheless, we think an analogy with Babbage’s ‘Analytical Engine’ suggests that a vastly complicated network of neurons could similarly exhibit thoughtful properties.

“We have found an enormously complicated material system located where the mind should be. The implications are shocking, and must be squarely faced. We believe that the present research offers strong experimental evidence that Benedictus Spinoza was correct, and René Descartes wrong: Mind and body are of one substance.

“In combination with the work of Charles Darwin showing how such a complicated organ could, in principle, have arisen as the result of processes not themselves intelligent, the bulk of scientific evidence now seems to indicate that intelligence is ontologically non-fundamental and has an extended origin in time. This strongly weighs against theories which assign mental entities an ontologically fundamental or causally primal status, including all religions ever invented.

“Much work remains to be done on discovering the specific identities between electrochemical interactions between neurons, and thoughts. Nonetheless, we believe our discovery offers the promise, though not yet the realization, of a full scientific account of thought. The problem may now be declared, if not solved, then solvable.”

We regret that Cajal and most of the other researchers involved on the Project are no longer available for comment.

218
When Anthropomorphism Became Stupid

It turns out that most things in the universe don’t have minds.

This statement would have provoked incredulity among many earlier cultures. “Animism” is the usual term. They thought that trees, rocks, streams, and hills all had spirits because, hey, why not?

I mean, those lumps of flesh known as “humans” contain thoughts, so why shouldn’t the lumps of wood known as “trees”?

My muscles move at my will, and water flows through a river. Who’s to say that the river doesn’t have a will to move the water? The river overflows its banks, and floods my tribe’s gathering-place—why not think that the river was angry, since it moved its parts to hurt us? It’s what we would think when someone’s fist hit our nose.

There is no obvious reason—no reason obvious to a hunter-gatherer—why this cannot be so. It only seems like a stupid mistake if you confuse weirdness with stupidity. Naturally the belief that rivers have animating spirits seems “weird” to us, since it is not a belief of our tribe. But there is nothing obviously stupid about thinking that great lumps of moving water have spirits, just like our own lumps of moving flesh.

If the idea were obviously stupid, no one would have believed it. Just like, for the longest time, nobody believed in the obviously stupid idea that the Earth moves while seeming motionless.

Is it obvious that trees can’t think? Trees, let us not forget, are in fact our distant cousins. Go far enough back, and you have a common ancestor with your fern. If lumps of flesh can think, why not lumps of wood?

For it to be obvious that wood doesn’t think, you have to belong to a culture with microscopes. Not just any microscopes, but really good microscopes.

Aristotle thought the brain was an organ for cooling the blood. (It’s a good thing that what we believe about our brains has very little effect on their actual operation.)

Egyptians threw the brain away during the process of mummification.

Alcmaeon of Croton, a Pythagorean of the fifth century BCE, put his finger on the brain as the seat of intelligence, because he’d traced the optic nerve from the eye to the brain. Still, with the amount of evidence he had, it was only a guess.

When did the central role of the brain stop being a guess? I do not know enough history to answer this question, and probably there wasn’t any sharp dividing line. Maybe we could put it at the point where someone traced the anatomy of the nerves, and discovered that severing a nervous connection to the brain blocked movement and sensation?

Even so, that is only a mysterious spirit moving through the nerves. Who’s to say that wood and water, even if they lack the little threads found in human anatomy, might not carry the same mysterious spirit by different means?

I’ve spent some time online trying to track down the exact moment when someone noticed the vastly tangled internal structure of the brain’s neurons, and said, “Hey, I bet all this giant tangle is doing complex information-processing!” I haven’t had much luck. (It’s not Camillo Golgi—the tangledness of the circuitry was known before Golgi.) Maybe there was never a watershed moment there, either.

But the discovery of that tangledness, and Charles Darwin’s theory of natural selection, and the notion of cognition as computation, is where I would put the gradual beginning of anthropomorphism’s descent into being obviously wrong.

It’s the point where you can look at a tree, and say: “I don’t see anything in the tree’s biology that’s doing complex information-processing. Nor do I see it in the behavior, and if it’s hidden in a way that doesn’t affect the tree’s behavior, how would a selection pressure for such complex information-processing arise?”

It’s the point where you can look at a river, and say, “Water doesn’t contain patterns replicating with distant heredity and substantial variation subject to iterative selection, so how would a river come to have any pattern so complex and functionally optimized as a brain?”

It’s the point where you can look at an atom, and say: “Anger may look simple, but it’s not, and there’s no room for it to fit in something as simple as an atom—not unless there are whole universes of subparticles inside quarks; and even then, since we’ve never seen any sign of atomic anger, it wouldn’t have any effect on the high-level phenomena we know.”

It’s the point where you can look at a puppy, and say: “The puppy’s parents may push it to the ground when it does something wrong, but that doesn’t mean the puppy is doing moral reasoning. Our current theories of evolutionary psychology holds that moral reasoning arose as a response to more complex social challenges than that—in their full-fledged human form, our moral adaptations are the result of selection pressures over linguistic arguments about tribal politics.”

It’s the point where you can look at a rock, and say, “This lacks even the simple search trees embodied in a chess-playing program—where would it get the intentions to want to roll downhill, as Aristotle once thought?”

It is written:

Zhuangzi and Huizi were strolling along the dam of the Hao Waterfall when Zhuangzi said, “See how the minnows come out and dart around where they please! That’s what fish really enjoy!”

Huizi said, “You’re not a fish—how do you know what fish enjoy?”

Zhuangzi said, “You’re not I, so how do you know I don’t know what fish enjoy?”

Now we know.

219
A Priori

Traditional Rationality is phrased as social rules, with violations interpretable as cheating: if you break the rules and no one else is doing so, you’re the first to defect—making you a bad, bad person. To Bayesians, the brain is an engine of accuracy: if you violate the laws of rationality, the engine doesn’t run, and this is equally true whether anyone else breaks the rules or not.

Consider the problem of Occam’s Razor, as confronted by Traditional philosophers. If two hypotheses fit the same observations equally well, why believe the simpler one is more likely to be true? You could argue that Occam’s Razor has worked in the past, and is therefore likely to continue to work in the future. But this, itself, appeals to a prediction from Occam’s Razor. “Occam’s Razor works up to October 8th, 2027 and then stops working thereafter” is more complex, but it fits the observed evidence equally well.

You could argue that Occam’s Razor is a reasonable distribution on prior probabilities. But what is a “reasonable” distribution? Why not label “reasonable” a very complicated prior distribution, which makes Occam’s Razor work in all observed tests so far, but generates exceptions in future cases?

Indeed, it seems there is no way to justify Occam’s Razor except by appealing to Occam’s Razor, making this argument unlikely to convince any judge who does not already accept Occam’s Razor. (What’s special about the words I italicized?)

If you are a philosopher whose daily work is to write papers, criticize other people’s papers, and respond to others’ criticisms of your own papers, then you may look at Occam’s Razor and shrug. Here is an end to justifying, arguing and convincing. You decide to call a truce on writing papers; if your fellow philosophers do not demand justification for your un-arguable beliefs, you will not demand justification for theirs. And as the symbol of your treaty, your white flag, you use the phrase “a priori truth.”

But to a Bayesian, in this era of cognitive science and evolutionary biology and Artificial Intelligence, saying “a priori” doesn’t explain why the brain-engine runs. If the brain has an amazing “a priori truth factory” that works to produce accurate beliefs, it makes you wonder why a thirsty hunter-gatherer can’t use the “a priori truth factory” to locate drinkable water. It makes you wonder why eyes evolved in the first place, if there are ways to produce accurate beliefs without looking at things.

James R. Newman said: “The fact that one apple added to one apple invariably gives two apples helps in the teaching of arithmetic, but has no bearing on the truth of the proposition that 1 + 1 = 2.” The Internet Encyclopedia of Philosophy defines “a priori” propositions as those knowable independently of experience. Wikipedia quotes Hume: Relations of ideas are “discoverable by the mere operation of thought, without dependence on what is anywhere existent in the universe.” You can see that 1 + 1 = 2 just by thinking about it, without looking at apples.

But in this era of neurology, one ought to be aware that thoughts are existent in the universe; they are identical to the operation of brains. Material brains, real in the universe, composed of quarks in a single unified mathematical physics whose laws draw no border between the inside and outside of your skull.

When you add 1 + 1 and get 2 by thinking, these thoughts are themselves embodied in flashes of neural patterns. In principle, we could observe, experientially, the exact same material events as they occurred within someone else’s brain. It would require some advances in computational neurobiology and brain-computer interfacing, but in principle, it could be done. You could see someone else’s engine operating materially, through material chains of cause and effect, to compute by “pure thought” that 1 + 1 = 2. How is observing this pattern in someone else’s brain any different, as a way of knowing, from observing your own brain doing the same thing? When “pure thought” tells you that 1 + 1 = 2, “independently of any experience or observation,” you are, in effect, observing your own brain as evidence.

If this seems counterintuitive, try to see minds/brains as engines—an engine that collides the neural pattern for 1 and the neural pattern for 1 and gets the neural pattern for 2. If this engine works at all, then it should have the same output if it observes (with eyes and retina) a similar brain-engine carrying out a similar collision, and copies into itself the resulting pattern. In other words, for every form of a priori knowledge obtained by “pure thought,” you are learning exactly the same thing you would learn if you saw an outside brain-engine carrying out the same pure flashes of neural activation. The engines are equivalent, the bottom-line outputs are equivalent, the belief-entanglements are the same.

There is nothing you can know “a priori,” which you could not know with equal validity by observing the chemical release of neurotransmitters within some outside brain. What do you think you are, dear reader?

This is why you can predict the result of adding 1 apple and 1 apple by imagining it first in your mind, or punch “3 × 4” into a calculator to predict the result of imagining 4 rows with 3 apples per row. You and the apple exist within a boundary-less unified physical process, and one part may echo another.

Are the sort of neural flashes that philosophers label “a priori beliefs” arbitrary? Many AI algorithms function better with “regularization” that biases the solution space toward simpler solutions. But the regularized algorithms are themselves more complex; they contain an extra line of code (or 1,000 extra lines) compared to unregularized algorithms. The human brain is biased toward simplicity, and we think more efficiently thereby. If you press the Ignore button at this point, you’re left with a complex brain that exists for no reason and works for no reason. So don’t try to tell me that “a priori” beliefs are arbitrary, because they sure aren’t generated by rolling random numbers. (What does the adjective “arbitrary” mean, anyway?)

You can’t excuse calling a proposition “a priori” by pointing out that other philosophers are having trouble justifying their propositions. If a philosopher fails to explain something, this fact cannot supply electricity to a refrigerator, nor act as a magical factory for accurate beliefs. There’s no truce, no white flag, until you understand why the engine works.

If you clear your mind of justification, of argument, then it seems obvious why Occam’s Razor works in practice: we live in a simple world, a low-entropy universe in which there are short explanations to be found. “But,” you cry, “why is the universe itself orderly?” This I do not know, but it is what I see as the next mystery to be explained. This is not the same question as “How do I argue Occam’s Razor to a hypothetical debater who has not already accepted it?”

Perhaps you cannot argue anything to a hypothetical debater who has not accepted Occam’s Razor, just as you cannot argue anything to a rock. A mind needs a certain amount of dynamic structure to be an argument-acceptor. If a mind doesn’t implement Modus Ponens, it can accept “A” and “A → B” all day long without ever producing “B.” How do you justify Modus Ponens to a mind that hasn’t accepted it? How do you argue a rock into becoming a mind?

Brains evolved from non-brainy matter by natural selection; they were not justified into existence by arguing with an ideal philosophy student of perfect emptiness. This does not make our judgments meaningless. A brain-engine can work correctly, producing accurate beliefs, even if it was merely built—by human hands or cumulative stochastic selection pressures—rather than argued into existence. But to be satisfied by this answer, one must see rationality in terms of engines, rather than arguments.

220
Reductive Reference

The reductionist thesis (as I formulate it) is that human minds, for reasons of efficiency, use a multilevel map in which we separately think about things like “atoms” and “quarks,” “hands” and “fingers,” or “heat” and “kinetic energy.” Reality itself, on the other hand, is single-level in the sense that it does not seem to contain atoms as separate, additional, causally efficacious entities over and above quarks.

Sadi Carnot formulated the (precursor to) the Second Law of Thermodynamics using the caloric theory of heat, in which heat was just a fluid that flowed from hot things to cold things, produced by fire, making gases expand—the effects of heat were studied separately from the science of kinetics, considerably before the reduction took place. If you’re trying to design a steam engine, the effects of all those tiny vibrations and collisions which we name “heat” can be summarized into a much simpler description than the full quantum mechanics of the quarks. Humans compute efficiently, thinking of only significant effects on goal-relevant quantities.

But reality itself does seem to use the full quantum mechanics of the quarks. I once met a fellow who thought that if you used General Relativity to compute a low-velocity problem, like an artillery shell, General Relativity would give you the wrong answer—not just a slow answer, but an experimentally wrong answer—because at low velocities, artillery shells are governed by Newtonian mechanics, not General Relativity. This is exactly how physics does not work. Reality just seems to go on crunching through General Relativity, even when it only makes a difference at the fourteenth decimal place, which a human would regard as a huge waste of computing power. Physics does it with brute force. No one has ever caught physics simplifying its calculations—or if someone did catch it, the Matrix Lords erased the memory afterward.

Our map, then, is very much unlike the territory; our maps are multilevel, the territory is single-level. Since the representation is so incredibly unlike the referent, in what sense can a belief like “I am wearing socks” be called true, when in reality itself, there are only quarks?

In case you’ve forgotten what the word “true” means, the classic definition was given by Alfred Tarski:

The statement “snow is white” is true if and only if snow is white.

In case you’ve forgotten what the difference is between the statement “I believe ‘snow is white’” and “‘Snow is white’ is true,” see Qualitatively Confused. Truth can’t be evaluated just by looking inside your own head—if you want to know, for example, whether “the morning star = the evening star,” you need a telescope; it’s not enough just to look at the beliefs themselves.

This is the point missed by the postmodernist folks screaming, “But how do you know your beliefs are true?” When you do an experiment, you actually are going outside your own head. You’re engaging in a complex interaction whose outcome is causally determined by the thing you’re reasoning about, not just your beliefs about it. I once defined “reality” as follows:

Even when I have a simple hypothesis, strongly supported by all the evidence I know, sometimes I’m still surprised. So I need different names for the thingies that determine my predictions and the thingy that determines my experimental results. I call the former thingies “belief,” and the latter thingy “reality.”

The interpretation of your experiment still depends on your prior beliefs. I’m not going to talk, for the moment, about Where Priors Come From, because that is not the subject of this essay. My point is that truth refers to an ideal comparison between a belief and reality. Because we understand that planets are distinct from beliefs about planets, we can design an experiment to test whether the belief “the morning star and the evening star are the same planet” is true. This experiment will involve telescopes, not just introspection, because we understand that “truth” involves comparing an internal belief to an external fact; so we use an instrument, the telescope, whose perceived behavior we believe to depend on the external fact of the planet.

Believing that the telescope helps us evaluate the “truth” of “morning star = evening star” relies on our prior beliefs about the telescope interacting with the planet. Again, I’m not going to address that in this particular essay, except to quote one of my favorite Raymond Smullyan lines: “If the more sophisticated reader objects to this statement on the grounds of its being a mere tautology, then please at least give the statement credit for not being inconsistent.” Similarly, I don’t see the use of a telescope as circular logic, but as reflective coherence; for every systematic way of arriving at truth, there ought to be a rational explanation for how it works.

The question on the table is what it means for “snow is white” to be true, when, in reality, there are just quarks.

There’s a certain pattern of neural connections making up your beliefs about “snow” and “whiteness”—we believe this, but we do not know, and cannot concretely visualize, the actual neural connections. Which are, themselves, embodied in a pattern of quarks even less known. Out there in the world, there are water molecules whose temperature is low enough that they have arranged themselves in tiled repeating patterns; they look nothing like the tangles of neurons. In what sense, comparing one (ever-fluctuating) pattern of quarks to the other, is the belief “snow is white” true?

Obviously, neither I nor anyone else can offer an Ideal Quark Comparer Function that accepts a quark-level description of a neurally embodied belief (including the surrounding brain) and a quark-level description of a snowflake (and the surrounding laws of optics), and outputs “true” or “false” over “snow is white.” And who says the fundamental level is really about particle fields?

On the other hand, throwing out all beliefs because they aren’t written as gigantic unmanageable specifications about quarks we can’t even see . . . doesn’t seem like a very prudent idea. Not the best way to optimize our goals.

It seems to me that a word like “snow” or “white” can be taken as a kind of promissory note—not a known specification of exactly which physical quark configurations count as “snow,” but, nonetheless, there are things you call snow and things you don’t call snow, and even if you got a few items wrong (like plastic snow), an Ideal Omniscient Science Interpreter would see a tight cluster in the center and redraw the boundary to have a simpler definition.

In a single-layer universe whose bottom layer is unknown, or uncertain, or just too large to talk about, the concepts in a multi-layer mind can be said to represent a kind of promissory note—we don’t know what they correspond to, out there. But it seems to us that we can distinguish positive from negative cases, in a predictively productive way, so we think—perhaps in a fully general sense—that there is some difference of quarks, some difference of configurations at the fundamental level, that explains the differences that feed into our senses, and ultimately result in our saying “snow” or “not snow.”

I see this white stuff, and it is the same on several occasions, so I hypothesize a stable latent cause in the environment—I give it the name “snow”; “snow” is then a promissory note referring to a believed-in simple boundary that could be drawn around the unseen causes of my experience.

Hilary Putnam’s “Twin Earth” thought experiment (where water is not H₂O but some strange other substance denoted XYZ, otherwise behaving much like water), and the subsequent philosophical debate, helps to highlight this issue. “Snow” doesn’t have a logical definition known to us—it’s more like an empirically determined pointer to a logical definition. This is true even if you believe that snow is ice crystals is low-temperature tiled water molecules. The water molecules are made of quarks. What if quarks turn out to be made of something else? What is a snowflake, then? You don’t know—but it’s still a snowflake, not a fire hydrant.

And of course, these very paragraphs I have just written are likewise far above the level of quarks. “Sensing white stuff, visually categorizing it, and thinking ‘snow’ or ‘not snow’”—this is also talking very far above the quarks. So my meta-beliefs are also promissory notes, for things that an Ideal Omniscient Science Interpreter might know about which configurations of the quarks (or whatever) making up my brain correspond to “believing ‘snow is white.’”

But then, the entire grasp that we have upon reality is made up of promissory notes of this kind. So, rather than calling it circular, I prefer to call it self-consistent.

This can be a bit unnerving—maintaining a precarious epistemic perch, in both object-level beliefs and reflection, far above a huge unknown underlying fundamental reality, and hoping one doesn’t fall off.

On reflection, though, it’s hard to see how things could be any other way.

So at the end of the day, the statement “reality does not contain hands as fundamental, additional, separate causal entities, over and above quarks” is not the same statement as “hands do not exist” or “I don’t have any hands.” There are no fundamental hands; hands are made of fingers, palm, and thumb, which in turn are made of muscle and bone, all the way down to elementary particle fields, which are the fundamental causal entities, so far as we currently know.

This is not the same as saying, “there are no ‘hands.’” It is not the same as saying, “the word ‘hands’ is a promissory note that will never be paid, because there is no empirical cluster that corresponds to it”; or “the ‘hands’ note will never be paid, because it is logically impossible to reconcile its supposed characteristics”; or “the statement ‘humans have hands’ refers to a sensible state of affairs, but reality is not in that state.”

Just: There are patterns that exist in reality where we see “hands,” and these patterns have something in common, but they are not fundamental.

If I really had no hands—if reality suddenly transitioned to be in a state that we would describe as “Eliezer has no hands”—reality would shortly thereafter correspond to a state we would describe as “Eliezer screams as blood jets out of his wrist stumps.”

And this is true, even though the above paragraph hasn’t specified any quark positions.

The previous sentence is likewise meta-true.

The map is multilevel, the territory is single-level. This doesn’t mean that the higher levels “don’t exist,” like looking in your garage for a dragon and finding nothing there, or like seeing a mirage in the desert and forming an expectation of drinkable water when there is nothing to drink. The higher levels of your map are not false, without referent; they have referents in the single level of physics. It’s not that the wings of an airplane unexist—then the airplane would drop out of the sky. The “wings of an airplane” exist explicitly in an engineer’s multilevel model of an airplane, and the wings of an airplane exist implicitly in the quantum physics of the real airplane. Implicit existence is not the same as nonexistence. The exact description of this implicitness is not known to us—is not explicitly represented in our map. But this does not prevent our map from working, or even prevent it from being true.

Though it is a bit unnerving to contemplate that every single concept and belief in your brain, including these meta-concepts about how your brain works and why you can form accurate beliefs, are perched orders and orders of magnitude above reality . . .

221
Zombies! Zombies?

Your “zombie,” in the philosophical usage of the term, is putatively a being that is exactly like you in every respect—identical behavior, identical speech, identical brain; every atom and quark in exactly the same position, moving according to the same causal laws of motion—except that your zombie is not conscious.

It is furthermore claimed that if zombies are “possible” (a term over which battles are still being fought), then, purely from our knowledge of this “possibility,” we can deduce a priori that consciousness is extra-physical, in a sense to be described below; the standard term for this position is “epiphenomenalism.”

(For those unfamiliar with zombies, I emphasize that this is not a strawman. See, for example, the Stanford Encyclopedia of Philosophy entry on Zombies. The “possibility” of zombies is accepted by a substantial fraction, possibly a majority, of academic philosophers of consciousness.)

I once read somewhere, “You are not the one who speaks your thoughts—you are the one who hears your thoughts.” In Hebrew, the word for the highest soul, that which God breathed into Adam, is N’Shama—“the hearer.”

If you conceive of “consciousness” as a purely passive listening, then the notion of a zombie initially seems easy to imagine. It’s someone who lacks the N’Shama, the hearer.

(Warning: Very long 6,600-word essay involving David Chalmers ahead. This may be taken as my demonstrative counterexample to Richard Chappell’s Arguing with Eliezer Part II, in which Richard accuses me of not engaging with the complex arguments of real philosophers.)

When you open a refrigerator and find that the orange juice is gone, you think “Darn, I’m out of orange juice.” The sound of these words is probably represented in your auditory cortex, as though you’d heard someone else say it. (Why do I think this? Because native Chinese speakers can remember longer digit sequences than English-speakers. Chinese digits are all single syllables, and so Chinese speakers can remember around ten digits, versus the famous “seven plus or minus two” for English speakers. There appears to be a loop of repeating sounds back to yourself, a size limit on working memory in the auditory cortex, which is genuinely phoneme-based.)

Let’s suppose the above is correct; as a postulate, it should certainly present no problem for advocates of zombies. Even if humans are not like this, it seems easy enough to imagine an AI constructed this way (and imaginability is what the zombie argument is all about). It’s not only conceivable in principle, but quite possible in the next couple of decades, that surgeons will lay a network of neural taps over someone’s auditory cortex and read out their internal narrative. (Researchers have already tapped the lateral geniculate nucleus of a cat and reconstructed recognizable visual inputs.)

So your zombie, being physically identical to you down to the last atom, will open the refrigerator and form auditory cortical patterns for the phonemes “Darn, I’m out of orange juice.” On this point, epiphenomalists would willingly agree.

But, says the epiphenomenalist, in the zombie there is no one inside to hear; the inner listener is missing. The internal narrative is spoken, but unheard. You are not the one who speaks your thoughts. You are the one who hears them.

It seems a lot more straightforward (they would say) to make an AI that prints out some kind of internal narrative, than to show that an inner listener hears it.

The Zombie Argument is that if the Zombie World is possible—not necessarily physically possible in our universe, just “possible in theory,” or “imaginable,” or something along those lines—then consciousness must be extra-physical, something over and above mere atoms. Why? Because even if you somehow knew the positions of all the atoms in the universe, you would still have be told, as a separate and additional fact, that people were conscious—that they had inner listeners—that we were not in the Zombie World, as seems possible.

Zombie-ism is not the same as dualism. Descartes thought there was a body-substance and a wholly different kind of mind-substance, but Descartes also thought that the mind-substance was a causally active principle, interacting with the body-substance, controlling our speech and behavior. Subtracting out the mind-substance from the human would leave a traditional zombie, of the lurching and groaning sort.

And though the Hebrew word for the innermost soul is N’Shama, that-which-hears, I can’t recall hearing a rabbi arguing for the possibility of zombies. Most rabbis would probably be aghast at the idea that the divine part which God breathed into Adam doesn’t actually do anything.

The technical term for the belief that consciousness is there, but has no effect on the physical world, is epiphenomenalism.

Though there are other elements to the zombie argument (I’ll deal with them below), I think that the intuition of the passive listener is what first seduces people to zombie-ism. In particular, it’s what seduces a lay audience to zombie-ism. The core notion is simple and easy to access: The lights are on but no one’s home.

Philosophers are appealing to the intuition of the passive listener when they say “Of course the zombie world is imaginable; you know exactly what it would be like.”

One of the great battles in the Zombie Wars is over what, exactly, is meant by saying that zombies are “possible.” Early zombie-ist philosophers (in the 1970s) just thought it was obvious that zombies were “possible,” and didn’t bother to define what sort of possibility was meant.

Because of my reading in mathematical logic, what instantly comes into my mind is logical possibility. If you have a collection of statements like {(A ⇒ B),(B ⇒ C),(C ⇒¬A)}, then the compound belief is logically possible if it has a model—which, in the simple case above, reduces to finding a value assignment to {A,B,C} that makes all of the statements (A ⇒ B), (B ⇒ C), and (C ⇒¬A) true. In this case, A = B = C = 0 works, as does {A = 0,B = C = 1} or {A = B = 0,C = 1}.

Something will seem possible—will seem “conceptually possible” or “imaginable”—if you can consider the collection of statements without seeing a contradiction. But it is, in general, a very hard problem to see contradictions or to find a full specific model! If you limit yourself to simple Boolean propositions of the form ((A or B or C) and (B or ¬C or D) and (D or ¬A or ¬C)…), conjunctions of disjunctions of three variables, then this is a very famous problem called 3-SAT, which is one of the first problems ever to be proven NP-complete.

So just because you don’t see a contradiction in the Zombie World at first glance, it doesn’t mean that no contradiction is there. It’s like not seeing a contradiction in the Riemann Hypothesis at first glance. From conceptual possibility (“I don’t see a problem”) to logical possibility, in the full technical sense, is a very great leap. It’s easy to make it an NP-complete leap, and with first-order theories you can make it arbitrarily hard to compute even for finite questions. And it’s logical possibility of the Zombie World, not conceptual possibility, that is needed to suppose that a logically omniscient mind could know the positions of all the atoms in the universe, and yet need to be told as an additional non-entailed fact that we have inner listeners.

Just because you don’t see a contradiction yet is no guarantee that you won’t see a contradiction in another thirty seconds. “All odd numbers are prime. Proof: 3 is prime, 5 is prime, 7 is prime . . .”

So let us ponder the Zombie Argument a little longer: Can we think of a counterexample to the assertion “Consciousness has no third-party-detectable causal impact on the world”?

If you close your eyes and concentrate on your inward awareness, you will begin to form thoughts, in your internal narrative, that go along the lines of “I am aware” and “My awareness is separate from my thoughts” and “I am not the one who speaks my thoughts, but the one who hears them” and “My stream of consciousness is not my consciousness” and “It seems like there is a part of me that I can imagine being eliminated without changing my outward behavior.”

You can even say these sentences out loud, as you meditate. In principle, someone with a super-fMRI could probably read the phonemes out of your auditory cortex; but saying it out loud removes all doubt about whether you have entered the realms of testability and physical consequences.

This certainly seems like the inner listener is being caught in the act of listening by whatever part of you writes the internal narrative and flaps your tongue.

Imagine that a mysterious race of aliens visit you, and leave you a mysterious black box as a gift. You try poking and prodding the black box, but (as far as you can tell) you never succeed in eliciting a reaction. You can’t make the black box produce gold coins or answer questions. So you conclude that the black box is causally inactive: “For all X, the black box doesn’t do X.” The black box is an effect, but not a cause; epiphenomenal; without causal potency. In your mind, you test this general hypothesis to see if it is true in some trial cases, and it seems to be true—“Does the black box turn lead to gold? No. Does the black box boil water? No.”

But you can see the black box; it absorbs light, and weighs heavy in your hand. This, too, is part of the dance of causality. If the black box were wholly outside the causal universe, you couldn’t see it; you would have no way to know it existed; you could not say, “Thanks for the black box.” You didn’t think of this counterexample, when you formulated the general rule: “All X: Black box doesn’t do X.” But it was there all along.

(Actually, the aliens left you another black box, this one purely epiphenomenal, and you haven’t the slightest clue that it’s there in your living room. That was their joke.)

If you can close your eyes, and sense yourself sensing—if you can be aware of yourself being aware, and think “I am aware that I am aware”—and say out loud, “I am aware that I am aware”—then your consciousness is not without effect on your internal narrative, or your moving lips. You can see yourself seeing, and your internal narrative reflects this, and so do your lips if you choose to say it out loud.

I have not seen the above argument written out that particular way—“the listener caught in the act of listening”—though it may well have been said before.

But it is a standard point—which zombie-ist philosophers accept!—that the Zombie World’s philosophers, being atom-by-atom identical to our own philosophers, write identical papers about the philosophy of consciousness.

At this point, the Zombie World stops being an intuitive consequence of the idea of a passive listener.

Philosophers writing papers about consciousness would seem to be at least one effect of consciousness upon the world. You can argue clever reasons why this is not so, but you have to be clever.

You would intuitively suppose that if your inward awareness went away, this would change the world, in that your internal narrative would no longer say things like “There is a mysterious listener within me,” because the mysterious listener would be gone. It is usually right after you focus your awareness on your awareness, that your internal narrative says “I am aware of my awareness,” which suggests that if the first event never happened again, neither would the second. You can argue clever reasons why this is not so, but you have to be clever.

You can form a propositional belief that “Consciousness is without effect,” and not see any contradiction at first, if you don’t realize that talking about consciousness is an effect of being conscious. But once you see the connection from the general rule that consciousness has no effect, to the specific implication that consciousness has no effect on how philosophers write papers about consciousness, zombie-ism stops being intuitive and starts requiring you to postulate strange things.

One strange thing you might postulate is that there’s a Zombie Master, a god within the Zombie World who surreptitiously takes control of zombie philosophers and makes them talk and write about consciousness.

A Zombie Master doesn’t seem impossible. Human beings often don’t sound all that coherent when talking about consciousness. It might not be that hard to fake their discourse, to the standards of, say, a human amateur talking in a bar. Maybe you could take, as a corpus, one thousand human amateurs trying to discuss consciousness; feed them into a non-conscious but sophisticated AI, better than today’s models but not self-modifying; and get back discourse about “consciousness” that sounded as sensible as most humans, which is to say, not very.

But this speech about “consciousness” would not be spontaneous. It would not be produced within the AI. It would be a recorded imitation of someone else talking. That is just a holodeck, with a central AI writing the speech of the non-player characters. This is not what the Zombie World is about.

By supposition, the Zombie World is atom-by-atom identical to our own, except that the inhabitants lack consciousness. Furthermore, the atoms in the Zombie World move under the same laws of physics as in our own world. If there are “bridging laws” that govern which configurations of atoms evoke consciousness, those bridging laws are absent. But, by hypothesis, the difference is not experimentally detectable. When it comes to saying whether a quark zigs or zags or exerts a force on nearby quarks—anything experimentally measurable—the same physical laws govern.

The Zombie World has no room for a Zombie Master, because a Zombie Master has to control the zombie’s lips, and that control is, in principle, experimentally detectable. The Zombie Master moves lips, therefore it has observable consequences. There would be a point where an electron zags, instead of zigging, because the Zombie Master says so. (Unless the Zombie Master is actually in the world, as a pattern of quarks—but then the Zombie World is not atom-by-atom identical to our own, unless you think this world also contains a Zombie Master.)

When a philosopher in our world types, “I think the Zombie World is possible,” their fingers strike keys in sequence: Z-O-M-B-I-E. There is a chain of causality that can be traced back from these keystrokes: muscles contracting, nerves firing, commands sent down through the spinal cord, from the motor cortex—and then into less understood areas of the brain, where the philosopher’s internal narrative first began talking about “consciousness.”

And the philosopher’s zombie twin strikes the same keys, for the same reason, causally speaking. There is no cause within the chain of explanation for why the philosopher writes the way they do that is not also present in the zombie twin. The zombie twin also has an internal narrative about “consciousness,” that a super-fMRI could read out of the auditory cortex. And whatever other thoughts, or other causes of any kind, led to that internal narrative, they are exactly the same in our own universe and in the Zombie World.

So you can’t say that the philosopher is writing about consciousness because of consciousness, while the zombie twin is writing about consciousness because of a Zombie Master or AI chatbot. When you trace back the chain of causality behind the keyboard, to the internal narrative echoed in the auditory cortex, to the cause of the narrative, you must find the same physical explanation in our world as in the zombie world.

As the most formidable advocate of zombie-ism, David Chalmers, writes:¹

Think of my zombie twin in the universe next door. He talks about conscious experience all the time—in fact, he seems obsessed by it. He spends ridiculous amounts of time hunched over a computer, writing chapter after chapter on the mysteries of consciousness. He often comments on the pleasure he gets from certain sensory qualia, professing a particular love for deep greens and purples. He frequently gets into arguments with zombie materialists, arguing that their position cannot do justice to the realities of conscious experience.

And yet he has no conscious experience at all! In his universe, the materialists are right and he is wrong. Most of his claims about conscious experience are utterly false. But there is certainly a physical or functional explanation of why he makes the claims he makes. After all, his universe is fully law-governed, and no events therein are miraculous, so there must be some explanation of his claims.

. . . Any explanation of my twin’s behavior will equally count as an explanation of my behavior, as the processes inside his body are precisely mirrored by those inside mine. The explanation of his claims obviously does not depend on the existence of consciousness, as there is no consciousness in his world. It follows that the explanation of my claims is also independent of the existence of consciousness.

Chalmers is not arguing against zombies; those are his actual beliefs!

This paradoxical situation is at once delightful and disturbing. It is not obviously fatal to the nonreductive position, but it is at least something that we need to come to grips with . . .

I would seriously nominate this as the largest bullet ever bitten in the history of time. And that is a backhanded compliment to David Chalmers: A lesser mortal would simply fail to see the implications, or refuse to face them, or rationalize a reason it wasn’t so.

Why would anyone bite a bullet that large? Why would anyone postulate unconscious zombies who write papers about consciousness for exactly the same reason that our own genuinely conscious philosophers do?

Not because of the first intuition I wrote about, the intuition of the passive listener. That intuition may say that zombies can drive cars or do math or even fall in love, but it doesn’t say that zombies write philosophy papers about their passive listeners.

The zombie argument does not rest solely on the intuition of the passive listener. If this was all there was to the zombie argument, it would be dead by now, I think. The intuition that the “listener” can be eliminated without effect would go away as soon as you realized that your internal narrative routinely seems to catch the listener in the act of listening.

No, the drive to bite this bullet comes from an entirely different intuition—the intuition that no matter how many atoms you add up, no matter how many masses and electrical charges interact with each other, they will never necessarily produce a subjective sensation of the mysterious redness of red. It may be a fact about our physical universe (Chalmers says) that putting such-and-such atoms into such-and-such a position evokes a sensation of redness; but if so, it is not a necessary fact, it is something to be explained above and beyond the motion of the atoms.

But if you consider the second intuition on its own, without the intuition of the passive listener, it is hard to see why it implies zombie-ism. Maybe there’s just a different kind of stuff, apart from and additional to atoms, that is not causally passive—a soul that actually does stuff, a soul that plays a real causal role in why we write about “the mysterious redness of red.” Take out the soul, and . . . well, assuming you don’t just fall over in a coma, you certainly won’t write any more papers about consciousness!

This is the position taken by Descartes and most other ancient thinkers: The soul is of a different kind, but it interacts with the body. Descartes’s position is technically known as substance dualism—there is a thought-stuff, a mind-stuff, and it is not like atoms; but it is causally potent, interactive, and leaves a visible mark on our universe.

Zombie-ists are property dualists—they don’t believe in a separate soul; they believe that matter in our universe has additional properties beyond the physical.

“Beyond the physical”? What does that mean? It means the extra properties are there, but they don’t influence the motion of the atoms, like the properties of electrical charge or mass. The extra properties are not experimentally detectable by third parties; you know you are conscious, from the inside of your extra properties, but no scientist can ever directly detect this from outside.

So the additional properties are there, but not causally active. The extra properties do not move atoms around, which is why they can’t be detected by third parties.

And that’s why we can (allegedly) imagine a universe just like this one, with all the atoms in the same places, but the extra properties missing, so that everything goes on the same as before, but no one is conscious.

The Zombie World may not be physically possible, say the zombie-ists—because it is a fact that all the matter in our universe has the extra properties, or obeys the bridging laws that evoke consciousness—but the Zombie World is logically possible: the bridging laws could have been different.

But, once you realize that conceivability is not the same as logical possibility, and that the Zombie World isn’t even all that intuitive, why say that the Zombie World is logically possible?

Why, oh why, say that the extra properties are epiphenomenal and indetectable?

We can put this dilemma very sharply: Chalmers believes that there is something called consciousness, and this consciousness embodies the true and indescribable substance of the mysterious redness of red. It may be a property beyond mass and charge, but it’s there, and it is consciousness. Now, having said the above, Chalmers furthermore specifies that this true stuff of consciousness is epiphenomenal, without causal potency—but why say that?

Why say that you could subtract this true stuff of consciousness, and leave all the atoms in the same place doing the same things? If that’s true, we need some separate physical explanation for why Chalmers talks about “the mysterious redness of red.” That is, there exists both a mysterious redness of red, which is extra-physical, and an entirely separate reason, within physics, why Chalmers talks about the “mysterious redness of red.”

Chalmers does confess that these two things seem like they ought to be related, but really, why do you need both? Why not just pick one or the other?

Once you’ve postulated that there is a mysterious redness of red, why not just say that it interacts with your internal narrative and makes you talk about the “mysterious redness of red”?

Isn’t Descartes taking the simpler approach, here? The strictly simpler approach?

Why postulate an extramaterial soul, and then postulate that the soul has no effect on the physical world, and then postulate a mysterious unknown material process that causes your internal narrative to talk about conscious experience?

Why not postulate the true stuff of consciousness which no amount of mere mechanical atoms can add up to, and then, having gone that far already, let this true stuff of consciousness have causal effects like making philosophers talk about consciousness?

I am not endorsing Descartes’s view. But at least I can understand where Descartes is coming from. Consciousness seems mysterious, so you postulate a mysterious stuff of consciousness. Fine.

But now the zombie-ists postulate that this mysterious stuff doesn’t do anything, so you need a whole new explanation for why you say you’re conscious.

That isn’t vitalism. That’s something so bizarre that vitalists would spit out their coffee. “When fires burn, they release phlogiston. But phlogiston doesn’t have any experimentally detectable impact on our universe, so you’ll have to go looking for a separate explanation of why a fire can melt snow.” What?

Are property dualists under the impression that if they postulate a new active force, something that has a causal impact on observables, they will be sticking their necks out too far?

Me, I’d say that if you postulate a mysterious, separate, additional, inherently mental property of consciousness, above and beyond positions and velocities, then, at that point, you have already stuck your neck out as far as it can go. To postulate this stuff of consciousness, and then further postulate that it doesn’t do anything—for the love of cute kittens, why?

There isn’t even an obvious career motive. “Hi, I’m a philosopher of consciousness. My subject matter is the most important thing in the universe and I should get lots of funding? Well, it’s nice of you to say so, but actually the phenomenon I study doesn’t do anything whatsoever.” (Argument from career impact is not valid, but I say it to leave a line of retreat.)

Chalmers critiques substance dualism on the grounds that it’s hard to see what new theory of physics, what new substance that interacts with matter, could possibly explain consciousness. But property dualism has exactly the same problem. No matter what kind of dual property you talk about, how exactly does it explain consciousness?

When Chalmers postulated an extra property that is consciousness, he took that leap across the unexplainable. How does it help his theory to further specify that this extra property has no effect? Why not just let it be causal?

If I were going to be unkind, this would be the time to drag in the dragon—to mention Carl Sagan’s parable of the dragon in the garage. “I have a dragon in my garage.” Great! I want to see it, let’s go! “You can’t see it—it’s an invisible dragon.” Oh, I’d like to hear it then. “Sorry, it’s an inaudible dragon.” I’d like to measure its carbon dioxide output. “It doesn’t breathe.” I’ll toss a bag of flour into the air, to outline its form. “The dragon is permeable to flour.”

One motive for trying to make your theory unfalsifiable is that deep down you fear to put it to the test. Sir Roger Penrose (physicist) and Stuart Hameroff (neurologist) are substance dualists; they think that there is something mysterious going on in quantum, that Everett is wrong and that the “collapse of the wavefunction” is physically real, and that this is where consciousness lives and how it exerts causal effect upon your lips when you say aloud “I think therefore I am.” Believing this, they predicted that neurons would protect themselves from decoherence long enough to maintain macroscopic quantum states.

This is in the process of being tested, and so far, prospects are not looking good for Penrose—

—but Penrose’s basic conduct is scientifically respectable. Not Bayesian, maybe, but still fundamentally healthy. He came up with a wacky hypothesis. He said how to test it. He went out and tried to actually test it.

As I once said to Stuart Hameroff, “I think the hypothesis you’re testing is completely hopeless, and your experiments should definitely be funded. Even if you don’t find exactly what you’re looking for, you’re looking in a place where no one else is looking, and you might find something interesting.”

So a nasty dismissal of epiphenomenalism would be that zombie-ists are afraid to say the consciousness-stuff can have effects, because then scientists could go looking for the extra properties, and fail to find them.

I don’t think this is actually true of Chalmers, though. If Chalmers lacked self-honesty, he could make things a lot easier on himself.

(But just in case Chalmers is reading this and does have falsification-fear, I’ll point out that if epiphenomenalism is false, then there is some other explanation for that-which-we-call consciousness, and it will eventually be found, leaving Chalmers’s theory in ruins; so if Chalmers cares about his place in history, he has no motive to endorse epiphenomenalism unless he really thinks it’s true.)

Chalmers is one of the most frustrating philosophers I know. Sometimes I wonder if he’s pulling an Atheism Conquered. Chalmers does this really sharp analysis . . . and then turns left at the last minute. He lays out everything that’s wrong with the Zombie World scenario, and then, having reduced the whole argument to smithereens, calmly accepts it.

Chalmers does the same thing when he lays out, in calm detail, the problem with saying that our own beliefs in consciousness are justified, when our zombie twins say exactly the same thing for exactly the same reasons and are wrong.

On Chalmers’s theory, Chalmers’s saying that he believes in consciousness cannot be causally justified; the belief is not caused by the fact itself. In the absence of consciousness, Chalmers would write the same papers for the same reasons.

On epiphenomenalism, Chalmers’s saying that he believes in consciousness cannot be justified as the product of a process that systematically outputs true beliefs, because the zombie twin writes the same papers using the same systematic process and is wrong.

Chalmers admits this. Chalmers, in fact, explains the argument in great detail in his book. Okay, so Chalmers has solidly proven that he is not justified in believing in epiphenomenal consciousness, right? No. Chalmers writes:

Conscious experience lies at the center of our epistemic universe; we have access to it directly. This raises the question: what is it that justifies our beliefs about our experiences, if it is not a causal link to those experiences, and if it is not the mechanisms by which the beliefs are formed? I think the answer to this is clear: it is having the experiences that justifies the beliefs. For example, the very fact that I have a red experience now provides justification for my belief that I am having a red experience . . .

Because my zombie twin lacks experiences, he is in a very different epistemic situation from me, and his judgments lack the corresponding justification. It may be tempting to object that if my belief lies in the physical realm, its justification must lie in the physical realm; but this is a non sequitur. From the fact that there is no justification in the physical realm, one might conclude that the physical portion of me (my brain, say) is not justified in its belief. But the question is whether I am justified in the belief, not whether my brain is justified in the belief, and if property dualism is correct than there is more to me than my brain.

So—if I’ve got this thesis right—there’s a core you, above and beyond your brain, that believes it is not a zombie, and directly experiences not being a zombie; and so its beliefs are justified.

But Chalmers just wrote all that stuff down, in his very physical book, and so did the zombie-Chalmers.

The zombie Chalmers can’t have written the book because of the zombie’s core self above the brain; there must be some entirely different reason, within the laws of physics.

It follows that even if there is a part of Chalmers hidden away that is conscious and believes in consciousness, directly and without mediation, there is also a separable subspace of Chalmers—a causally closed cognitive subsystem that acts entirely within physics—and this “outer self” is what speaks Chalmers’s internal narrative, and writes papers on consciousness.

I do not see any way to evade the charge that, on Chalmers’s own theory, this separable outer Chalmers is deranged. This is the part of Chalmers that is the same in this world, or the Zombie World; and in either world it writes philosophy papers on consciousness for no valid reason. Chalmers’s philosophy papers are not output by that inner core of awareness and belief-in-awareness; they are output by the mere physics of the internal narrative that makes Chalmers’s fingers strike the keys of his computer.

And yet this deranged outer Chalmers is writing philosophy papers that just happen to be perfectly right, by a separate and additional miracle. Not a logically necessary miracle (then the Zombie World would not be logically possible). A physically contingent miracle, that happens to be true in what we think is our universe, even though science can never distinguish our universe from the Zombie World.

Or at least, that would seem to be the implication of what the self-confessedly deranged outer Chalmers is telling us.

I think I speak for all reductionists when I say Huh?

That’s not epicycles. That’s, “Planetary motions follow these epicycles—but epicycles don’t actually do anything—there’s something else that makes the planets move the same way the epicycles say they should, which I haven’t been able to explain—and by the way, I would say this even if there weren’t any epicycles.”

I have a nonstandard perspective on philosophy because I look at everything with an eye to designing an AI; specifically, a self-improving Artificial General Intelligence with stable motivational structure.

When I think about designing an AI, I ponder principles like probability theory, the Bayesian notion of evidence as differential diagnostic, and above all, reflective coherence. Any self-modifying AI that starts out in a reflectively inconsistent state won’t stay that way for long.

If a self-modifying AI looks at a part of itself that concludes “B” on condition A—a part of itself that writes “B” to memory whenever condition A is true—and the AI inspects this part, determines how it (causally) operates in the context of the larger universe, and the AI decides that this part systematically tends to write false data to memory, then the AI has found what appears to be a bug, and the AI will self-modify not to write “B” to the belief pool under condition A.

Any epistemological theory that disregards reflective coherence is not a good theory to use in constructing self-improving AI. This is a knockdown argument from my perspective, considering what I intend to actually use philosophy for. So I have to invent a reflectively coherent theory anyway. And when I do, by golly, reflective coherence turns out to make intuitive sense.

So that’s the unusual way in which I tend to think about these things. And now I look back at Chalmers:

The causally closed “outer Chalmers” (that is not influenced in any way by the “inner Chalmers” that has separate additional awareness and beliefs) must be carrying out some systematically unreliable, unwarranted operation which in some unexplained fashion causes the internal narrative to produce beliefs about an “inner Chalmers” that are correct for no logical reason in what happens to be our universe.

But there’s no possible warrant for the outer Chalmers or any reflectively coherent self-inspecting AI to believe in this mysterious correctness. A good AI design should, I think, look like a reflectively coherent intelligence embodied in a causal system, with a testable theory of how that selfsame causal system produces systematically accurate beliefs on the way to achieving its goals.

So the AI will scan Chalmers and see a closed causal cognitive system producing an internal narrative that is uttering nonsense. Nonsense that seems to have a high impact on what Chalmers thinks should be considered a morally valuable person.

This is not a necessary problem for Friendly AI theorists. It is only a problem if you happen to be an epiphenomenalist. If you believe either the reductionists (consciousness happens within the atoms) or the substance dualists (consciousness is causally potent immaterial stuff), people talking about consciousness are talking about something real, and a reflectively consistent Bayesian AI can see this by tracing back the chain of causality for what makes people say “consciousness.”

According to Chalmers, the causally closed cognitive system of Chalmers’s internal narrative is (mysteriously) malfunctioning in a way that, not by necessity, but just in our universe, miraculously happens to be correct. Furthermore, the internal narrative asserts “the internal narrative is mysteriously malfunctioning, but miraculously happens to be correctly echoing the justified thoughts of the epiphenomenal inner core,” and again, in our universe, miraculously happens to be correct.

Oh, come on!

Shouldn’t there come a point where you just give up on an idea? Where, on some raw intuitive level, you just go: What on Earth was I thinking?

Humanity has accumulated some broad experience with what correct theories of the world look like. This is not what a correct theory looks like.

“Argument from incredulity,” you say. Fine, you want it spelled out? The said Chalmersian theory postulates multiple unexplained complex miracles. This drives down its prior probability, by the conjunction rule of probability and Occam’s Razor. It is therefore dominated by at least two theories that postulate fewer miracles, namely:

Substance dualism:
- There is a stuff of consciousness which is not yet understood, an extraordinary super-physical stuff that visibly affects our world; and this stuff is what makes us talk about consciousness.
Not-quite-faith-based reductionism:
- That-which-we-name “consciousness” happens within physics, in a way not yet understood, just like what happened the last three thousand times humanity ran into something mysterious.
- Your intuition that no material substance can possibly add up to consciousness is incorrect. If you actually knew exactly why you talk about consciousness, this would give you new insights, of a form you can’t now anticipate; and afterward you would realize that your arguments about normal physics having no room for consciousness were flawed.

Compare to:

Epiphenomenal property dualism:
- Matter has additional consciousness-properties which are not yet understood. These properties are epiphenomenal with respect to ordinarily observable physics—they make no difference to the motion of particles.
- Separately, there exists a not-yet-understood reason within normal physics why philosophers talk about consciousness and invent theories of dual properties.
- Miraculously, when philosophers talk about consciousness, the bridging laws of our world are exactly right to make this talk about consciousness correct, even though it arises from a malfunction (drawing of logically unwarranted conclusions) in the causally closed cognitive system that types philosophy papers.

I know I’m speaking from limited experience, here. But based on my limited experience, the Zombie Argument may be a candidate for the most deranged idea in all of philosophy.

There are times when, as a rationalist, you have to believe things that seem weird to you. Relativity seems weird, quantum mechanics seems weird, natural selection seems weird.

But these weirdnesses are pinned down by massive evidence. There’s a difference between believing something weird because science has confirmed it overwhelmingly—

—versus believing a proposition that seems downright deranged, because of a great big complicated philosophical argument centered around unspecified miracles and giant blank spots not even claimed to be understood—

—in a case where even if you accept everything that has been told to you so far, afterward the phenomenon will still seem like a mystery and still have the same quality of wondrous impenetrability that it had at the start.

The correct thing for a rationalist to say at this point, if all of David Chalmers’s arguments seem individually plausible—which they don’t seem to me—is:

“Okay . . . I don’t know how consciousness works . . . I admit that . . . and maybe I’m approaching the whole problem wrong, or asking the wrong questions . . . but this zombie business can’t possibly be right. The arguments aren’t nailed down enough to make me believe this—especially when accepting it won’t make me feel any less confused. On a core gut level, this just doesn’t look like the way reality could really really work.”

Mind you, I am not saying this is a substitute for careful analytic refutation of Chalmers’s thesis. System 1 is not a substitute for System 2, though it can help point the way. You still have to track down where the problems are specifically.

Chalmers wrote a big book, not all of which is available through free Google preview. I haven’t duplicated the long chains of argument where Chalmers lays out the arguments against himself in calm detail. I’ve just tried to tack on a final refutation of Chalmers’s last presented defense, which Chalmers has not yet countered to my knowledge. Hit the ball back into his court, as it were.

But, yes, on a core level, the sane thing to do when you see the conclusion of the zombie argument, is to say “That can’t possibly be right” and start looking for a flaw.

1. Chalmers, The Conscious Mind.

222
Zombie Responses

I’m a bit tired today, having stayed up until 3 a.m. writing yesterday’s >6,000-word essay on zombies, so today I’ll just reply to Richard, and tie up a loose end I spotted the next day.

(A) Richard Chappell writes:

A terminological note (to avoid unnecessary confusion): what you call “conceivable,” others of us would merely call “apparently conceivable.”

The gap between “I don’t see a contradiction yet” and “this is logically possible” is so huge (it’s NP-complete even in some simple-seeming cases) that you really should have two different words. As the zombie argument is boosted to the extent that this huge gap can be swept under the rug of minor terminological differences, I really think it would be a good idea to say “conceivable” versus “logically possible” or maybe even have a still more visible distinction. I can’t choose professional terminology that has already been established, but in a case like this, I might seriously refuse to use it.

Maybe I will say “apparently conceivable” for the kind of information that zombie advocates get by imagining Zombie Worlds, and “logically possible” for the kind of information that is established by exhibiting a complete model or logical proof. Note the size of the gap between the information you can get by closing your eyes and imagining zombies, and the information you need to carry the argument for epiphenomenalism.

That is, your view would be characterized as a form of Type-A materialism, the view that zombies are not even (genuinely) conceivable, let alone metaphysically possible.

Type-A materialism is a large bundle; you shouldn’t attribute the bundle to me until you see me agree with each of the parts. I think that someone who asks “What is consciousness?” is asking a legitimate question, has a legitimate demand for insight; I don’t necessarily think that the answer takes the form of “Here is this stuff that has all the properties you would attribute to consciousness, for such-and-such reason,” but may to some extent consist of insights that cause you to realize you were asking the question the wrong way.

This is not being eliminative about consciousness. It is being realistic about what kind of insights to expect, faced with a problem that (1) seems like it must have some solution, (2) seems like it cannot possibly have any solution, and (3) is being discussed in a fashion that has a great big dependence on the not-fully-understood ad-hoc architecture of human cognition.

(1) You haven’t, so far as I can tell, identified any logical contradiction in the description of the zombie world. You’ve just pointed out that it’s kind of strange. But there are many bizarre possible worlds out there. That’s no reason to posit an implicit contradiction. So it’s still completely mysterious to me what this alleged contradiction is supposed to be.

Okay, I’ll spell it out from a materialist standpoint:

The zombie world, by definition, contains all parts of our world that are within the closure of the “caused by” or “effect of” relation of any observable phenomenon. In particular, it contains the cause of my visibly saying, “I think therefore I am.”
When I focus my inward awareness on my inward awareness, I shortly thereafter experience my internal narrative saying “I am focusing my inward awareness on my inward awareness,” and can, if I choose, say so out loud.
Intuitively, it sure seems like my inward awareness is causing my internal narrative to say certain things, and that my internal narrative can cause my lips to say certain things.
The word “consciousness,” if it has any meaning at all, refers to that-which-is or that-which-causes or that-which-makes-me-say-I-have inward awareness.
From (3) and (4) it would follow that if the zombie world is closed with respect to the causes of my saying “I think therefore I am,” the zombie world contains that which we refer to as “consciousness.”
By definition, the zombie world does not contain consciousness.
(3) seems to me to have a rather high probability of being empirically true. Therefore I evaluate a high empirical probability that the zombie world is logically impossible.

You can save the Zombie World by letting the cause of my internal narrative’s saying “I think therefore I am” be something entirely other than consciousness. In conjunction with the assumption that consciousness does exist, this is the part that struck me as deranged.

But if the above is conceivable, then isn’t the Zombie World conceivable?

No, because the two constructions of the Zombie World involve giving the word “consciousness” different empirical referents, like “water” in our world meaning H₂O versus “water” in Putnam’s Twin Earth meaning XYZ. For the Zombie World to be logically possible, it does not suffice that, for all you knew about how the empirical world worked, the word “consciousness” could have referred to an epiphenomenon that is entirely different from the consciousness we know. The Zombie World lacks consciousness, not “consciousness”—it is a world without H₂O, not a world without “water.” This is what is required to carry the empirical statement, “You could eliminate the referent of whatever is meant by ‘consciousness’ from our world, while keeping all the atoms in the same place.”

Which is to say: I hold that it is an empirical fact, given what the word “consciousness” actually refers to, that it is logically impossible to eliminate consciousness without moving any atoms. What it would mean to eliminate “consciousness” from a world, rather than consciousness, I will not speculate.

(2) It’s misleading to say it’s “miraculous” (on the property dualist view) that our qualia line up so neatly with the physical world. There’s a natural law which guarantees this, after all. So it’s no more miraculous than any other logically contingent nomic necessity (e.g. the constants in our physical laws).

It is the natural law itself that is “miraculous”—counts as an additional complex-improbable element of the theory to be postulated, without having been itself justified in terms of things already known. One postulates (a) an inner world that is conscious, (b) a malfunctioning outer world that talks about consciousness for no reason, and (c) that the two align perfectly. Statement (c) does not follow from (a) and (b), and so is a separate postulate.

I agree that this usage of “miraculous” conflicts with the philosophical sense of violating a natural law; I meant it in the sense of improbability appearing from no apparent source, a la perpetual motion belief. Hence the word was ill-chosen in context. But is this not intuitively the sort of thing we should call a miracle? Your consciousness doesn’t really cause you to say you’re conscious, there’s a separate physical thing that makes you say you’re conscious, but also there’s a law aligning the two—this is indeed an event on a similar order of wackiness to a cracker taking on the substance of Christ’s flesh while possessing the exact appearance and outward behavior of a cracker, there’s just a natural law which guarantees this, you know.

That is, Zombie (or “Outer”) Chalmers doesn’t actually conclude anything, because his utterances are meaningless. A fortiori, he doesn’t conclude anything unwarrantedly. He’s just making noises; these are no more susceptible to epistemic assessment than the chirps of a bird.

Looking at this from an AI-design standpoint, it seems to me like you should be able to build an AI that systematically refines an inner part of itself that correlates (in the sense of mutual information or systematic relations) to the environment, perhaps including floating-point numbers of a sort that I would call “probabilities” because they obey the internal relations mandated by Cox’s Theorems when the AI encounters new information—pardon me, new sense inputs.

You will say that, unless the AI is more than mere transistors—unless it has the dual aspect—the AI has no beliefs.

I think my views on this were expressed pretty clearly in The Simple Truth.

To me, it seems pretty straightforward to construct maps that correlate to territories in systematic ways, without mentioning anything other than things of pure physical causality. The AI outputs a map of Texas. Another AI flies with the map to Texas and checks to see if the highways are in the corresponding places, chirping “True” when it detects a match and “False” when it detects a mismatch. You can refuse to call this “a map of Texas” but the AIs themselves are still chirping “True” or “False,” and the said AIs are going to chirp “False” when they look at Chalmers’s belief in an epiphenomenal inner core, and I for one would agree with them.

It’s clear that the function of mapping reality is performed strictly by Outer Chalmers. The whole business of producing belief representations is handled by Bayesian structure in causal interactions. There’s nothing left for the Inner Chalmers to do, but bless the whole affair with epiphenomenal meaning. Where now “meaning” is something entirely unrelated to systematic map-territory correspondence or the ability to use that map to navigate reality. So when it comes to talking about “accuracy,” let alone “systematic accuracy,” it seems to me like we should be able to determine it strictly by looking at the Outer Chalmers.

(B) In yesterday’s text, I left out an assumption when I wrote:

If a self-modifying AI looks at a part of itself that concludes “B” on condition A—a part of itself that writes “B” to memory whenever condition A is true—and the AI inspects this part, determines how it (causally) operates in the context of the larger universe, and the AI decides that this part systematically tends to write false data to memory, then the AI has found what appears to be a bug, and the AI will self-modify not to write “B” to the belief pool under condition A.

. . .

But there’s no possible warrant for the outer Chalmers or any reflectively coherent self-inspecting AI to believe in this mysterious correctness. A good AI design should, I think, be a reflectively coherent intelligence with a testable theory of how it operates as a causal system, hence with a testable theory of how that causal system produces systematically accurate beliefs on the way to achieving its goals.

Actually, you need an additional assumption to the above, which is that a “good AI design” (the kind I was thinking of, anyway) judges its own rationality in a modular way; it enforces global rationality by enforcing local rationality. If there is a piece that, relative to its context, is locally systematically unreliable—for some possible beliefs “B_i” and conditions A_i, it adds some “B_i” to the belief pool under local condition A_i, where reflection by the system indicates that B_i is not true (or in the case of probabilistic beliefs, not accurate) when the local condition A_i is true—then this is a bug. This kind of modularity is a way to make the problem tractable, and it’s how I currently think about the first-generation AI design. [Edit 2013: The actual notion I had in mind here has now been fleshed out and formalized in Tiling Agents for Self-Modifying AI, section 6.]

The notion is that a causally closed cognitive system—such as an AI designed by its programmers to use only causally efficacious parts; or an AI whose theory of its own functioning is entirely testable; or the outer Chalmers that writes philosophy papers—that believes that it has an epiphenomenal inner self, must be doing something systematically unreliable because it would conclude the same thing in a Zombie World. A mind all of whose parts are systematically locally reliable, relative to their contexts, would be systematically globally reliable. Ergo, a mind that is globally unreliable must contain at least one locally unreliable part. So a causally closed cognitive system inspecting itself for local reliability must discover that at least one step involved in adding the belief of an epiphenomenal inner self is unreliable.

If there are other ways for minds to be reflectively coherent that avoid this proof of disbelief in zombies, philosophers are welcome to try and specify them.

The reason why I have to specify all this is that otherwise you get a kind of extremely cheap reflective coherence where the AI can never label itself unreliable. E.g., if the AI finds a part of itself that computes 2 + 2 = 5 (in the surrounding context of counting sheep) the AI will reason: “Well, this part malfunctions and says that 2 + 2 = 5 . . . but by pure coincidence, 2 + 2 is equal to 5, or so it seems to me . . . so while the part looks systematically unreliable, I better keep it the way it is, or it will handle this special case wrong.” That’s why I talk about enforcing global reliability by enforcing local systematic reliability—if you just compare your global beliefs to your global beliefs, you don’t go anywhere.

This does have a general lesson: Show your arguments are globally reliable by virtue of each step being locally reliable; don’t just compare the arguments’ conclusions to your intuitions. [Edit 2013: See Proofs, Implications, and Models for a discussion of the fact that valid logic is locally valid.]

(C) An anonymous poster wrote:

A sidepoint, this, but I believe your etymology for “n’shama” is wrong. It is related to the word for “breath,” not “hear.” The root for “hear” contains an ayin, which n’shama does not.

Now that’s what I call a miraculously misleading coincidence—although the word N’Shama arose for completely different reasons, it sounded exactly the right way to make me think it referred to an inner listener.

Oops.

223
The Generalized AntiZombie Principle

Each problem that I solved became a rule which served afterwards to solve other problems.

—René Descartes, Discours de la Méthode¹

“Zombies” are putatively beings that are atom-by-atom identical to us, governed by all the same third-party-visible physical laws, except that they are not conscious.

Though the philosophy is complicated, the core argument against zombies is simple: When you focus your inward awareness on your inward awareness, your internal narrative (the little voice inside your head that speaks your thoughts) says “I am aware of being aware” soon after, and then you say it out loud, and then you type it into a computer keyboard, and create a third-party visible blog post.

Consciousness, whatever it may be—a substance, a process, a name for a confusion—is not epiphenomenal; your mind can catch the inner listener in the act of listening, and say so out loud. The fact that I have typed this paragraph would at least seem to refute the idea that consciousness has no experimentally detectable consequences.

I hate to say “So now let’s accept this and move on,” over such a philosophically controversial question, but it seems like a considerable majority of Overcoming Bias commenters do accept this. And there are other conclusions you can only get to after you accept that you cannot subtract consciousness and leave the universe looking exactly the same. So now let’s accept this and move on.

The form of the AntiZombie Argument seems like it should generalize, becoming an AntiZombie Principle. But what is the proper generalization?

Let’s say, for example, that someone says: “I have a switch in my hand, which does not affect your brain in any way; and if this switch is flipped, you will cease to be conscious.” Does the AntiZombie Principle rule this out as well, with the same structure of argument?

It appears to me that in the case above, the answer is yes. In particular, you can say: “Even after your switch is flipped, I will still talk about consciousness for exactly the same reasons I did before. If I am conscious right now, I will still be conscious after you flip the switch.”

Philosophers may object, “But now you’re equating consciousness with talking about consciousness! What about the Zombie Master, the chatbot that regurgitates a remixed corpus of amateur human discourse on consciousness?”

But I did not equate “consciousness” with verbal behavior. The core premise is that, among other things, the true referent of “consciousness” is also the cause in humans of talking about inner listeners.

As I argued (at some length) in the sequence on words, what you want in defining a word is not always a perfect Aristotelian necessary-and-sufficient definition; sometimes you just want a treasure map that leads you to the extensional referent. So “that which does in fact make me talk about an unspeakable awareness” is not a necessary-and-sufficient definition. But if what does in fact cause me to discourse about an unspeakable awareness is not “consciousness,” then . . .

. . . then the discourse gets pretty futile. That is not a knockdown argument against zombies—an empirical question can’t be settled by mere difficulties of discourse. But if you try to defy the AntiZombie Principle, you will have problems with the meaning of your discourse, not just its plausibility.

Could we define the word “consciousness” to mean “whatever actually makes humans talk about ‘consciousness’”? This would have the powerful advantage of guaranteeing that there is at least one real fact named by the word “consciousness.” Even if our belief in consciousness is a confusion, “consciousness” would name the cognitive architecture that generated the confusion. But to establish a definition is only to promise to use a word consistently; it doesn’t settle any empirical questions, such as whether our inner awareness makes us talk about our inner awareness.

Let’s return to the Off-Switch.

If we allow that the AntiZombie Argument applies against the Off-Switch, then the Generalized AntiZombie Principle does not say only, “Any change that is not in-principle experimentally detectable (IPED) cannot remove your consciousness.” The switch’s flipping is experimentally detectable, but it still seems highly unlikely to remove your consciousness.

Perhaps the AntiZombie Principle says, “Any change that does not affect you in any IPED way cannot remove your consciousness”?

But is it a reasonable stipulation to say that flipping the switch does not affect you in any IPED way? All the particles in the switch are interacting with the particles composing your body and brain. There are gravitational effects—tiny, but real and IPED. The gravitational pull from a one-gram switch ten meters away is around 6 × 10^-16 m/s². That’s around half a neutron diameter per second per second, far below thermal noise, but way above the Planck level.

We could flip the switch light-years away, in which case the flip would have no immediate causal effect on you (whatever “immediate” means in this case) (if the Standard Model of physics is correct).

But it doesn’t seem like we should have to alter the thought experiment in this fashion. It seems that, if a disconnected switch is flipped on the other side of a room, you should not expect your inner listener to go out like a light, because the switch “obviously doesn’t change” that which is the true cause of your talking about an inner listener. Whatever you really are, you don’t expect the switch to mess with it.

This is a large step.

If you deny that it is a reasonable step, you had better never go near a switch again. But still, it’s a large step.

The key idea of reductionism is that our maps of the universe are multi-level to save on computing power, but physics seems to be strictly single-level. All our discourse about the universe takes place using references far above the level of fundamental particles.

The switch’s flip does change the fundamental particles of your body and brain. It nudges them by whole neutron diameters away from where they would have otherwise been.

In ordinary life, we gloss a change this small by saying that the switch “doesn’t affect you.” But it does affect you. It changes everything by whole neutron diameters! What could possibly be remaining the same? Only the description that you would give of the higher levels of organization—the cells, the proteins, the spikes traveling along a neural axon. As the map is far less detailed than the territory, it must map many different states to the same description.

Any reasonable sort of humanish description of the brain that talks about neurons and activity patterns (or even the conformations of individual microtubules making up axons and dendrites) won’t change when you flip a switch on the other side of the room. Nuclei are larger than neutrons, atoms are larger than nuclei, and by the time you get up to talking about the molecular level, that tiny little gravitational force has vanished from the list of things you bother to track.

But if you add up enough tiny little gravitational pulls, they will eventually yank you across the room and tear you apart by tidal forces, so clearly a small effect is not “no effect at all.”

Maybe the tidal force from that tiny little pull, by an amazing coincidence, pulls a single extra calcium ion just a tiny bit closer to an ion channel, causing it to be pulled in just a tiny bit sooner, making a single neuron fire infinitesimally sooner than it would otherwise have done, a difference which amplifies chaotically, finally making a whole neural spike occur that otherwise wouldn’t have occurred, sending you off on a different train of thought, that triggers an epileptic fit, that kills you, causing you to cease to be conscious . . .

If you add up a lot of tiny quantitative effects, you get a big quantitative effect—big enough to mess with anything you care to name. And so claiming that the switch has literally zero effect on the things you care about, is taking it too far.

But with just one switch, the force exerted is vastly less than thermal uncertainties, never mind quantum uncertainties. If you don’t expect your consciousness to flicker in and out of existence as the result of thermal jiggling, then you certainly shouldn’t expect to go out like a light when someone sneezes a kilometer away.

The alert Bayesian will note that I have just made an argument about expectations, states of knowledge, justified beliefs about what can and can’t switch off your consciousness.

This doesn’t necessarily destroy the AntiZombie Argument. Probabilities are not certainties, but the laws of probability are theorems; if rationality says you can’t believe something on your current information, then that is a law, not a suggestion.

Still, this version of the AntiZombie Argument is weaker. It doesn’t have the nice, clean, absolutely clear-cut status of, “You can’t possibly eliminate consciousness while leaving all the atoms in exactly the same place.” (Or for “all the atoms” substitute “all causes with in-principle experimentally detectable effects,” and “same wavefunction” for “same place,” etc.)

But the new version of the AntiZombie Argument still carries. You can say, “I don’t know what consciousness really is, and I suspect I may be fundamentally confused about the question. But if the word refers to anything at all, it refers to something that is, among other things, the cause of my talking about consciousness. Now, I don’t know why I talk about consciousness. But it happens inside my skull, and I expect it has something to do with neurons firing. Or maybe, if I really understood consciousness, I would have to talk about an even more fundamental level than that, like microtubules, or neurotransmitters diffusing across a synaptic channel. But still, that switch you just flipped has an effect on my neurotransmitters and microtubules that’s much, much less than thermal noise at 310 Kelvin. So whatever the true cause of my talking about consciousness may be, I don’t expect it to be hugely affected by the gravitational pull from that switch. Maybe it’s just a tiny little infinitesimal bit affected? But it’s certainly not going to go out like a light. I expect to go on talking about consciousness in almost exactly the same way afterward, for almost exactly the same reasons.”

This application of the AntiZombie Principle is weaker. But it’s also much more general. And, in terms of sheer common sense, correct.

The reductionist and the substance dualist actually have two different versions of the above statement. The reductionist furthermore says, “Whatever makes me talk about consciousness, it seems likely that the important parts take place on a much higher functional level than atomic nuclei. Someone who understood consciousness could abstract away from individual neurons firing, and talk about high-level cognitive architectures, and still describe how my mind produces thoughts like ‘I think therefore I am.’ So nudging things around by the diameter of a nucleon shouldn’t affect my consciousness (except maybe with very small probability, or by a very tiny amount, or not until after a significant delay).”

The substance dualist furthermore says, “Whatever makes me talk about consciousness, it’s got to be something beyond the computational physics we know, which means that it might very well involve quantum effects. But still, my consciousness doesn’t flicker on and off whenever someone sneezes a kilometer away. If it did, I would notice. It would be like skipping a few seconds, or coming out of a general anesthetic, or sometimes saying, ‘I don’t think therefore I’m not.’ So since it’s a physical fact that thermal vibrations don’t disturb the stuff of my awareness, I don’t expect flipping the switch to disturb it either.”

Either way, you shouldn’t expect your sense of awareness to vanish when someone says the word “Abracadabra,” even if that does have some infinitesimal physical effect on your brain—

But hold on! If you hear someone say the word “Abracadabra,” that has a very noticeable effect on your brain—so large, even your brain can notice it. It may alter your internal narrative; you may think, “Why did that person just say ‘Abracadabra’?”

Well, but still you expect to go on talking about consciousness in almost exactly the same way afterward, for almost exactly the same reasons.

And again, it’s not that “consciousness” is being equated to “that which makes you talk about consciousness.” It’s just that consciousness, among other things, makes you talk about consciousness. So anything that makes your consciousness go out like a light should make you stop talking about consciousness.

If we do something to you, where you don’t see how it could possibly change your internal narrative—the little voice in your head that sometimes says things like “I think therefore I am,” whose words you can choose to say aloud—then it shouldn’t make you cease to be conscious.

And this is true even if the internal narrative is just “pretty much the same,” and the causes of it are also pretty much the same; among the causes that are pretty much the same is whatever you mean by “consciousness.”

If you’re wondering where all this is going, and why it’s important to go to such tremendous lengths to ponder such an obvious-seeming Generalized AntiZombie Principle, then consider the following debate:

ALBERT: “Suppose I replaced all the neurons in your head with tiny robotic artificial neurons that had the same connections, the same local input-output behavior, and analogous internal state and learning rules.”

BERNICE: “That’s killing me! There wouldn’t be a conscious being there anymore.”

CHARLES: “Well, there’d still be a conscious being there, but it wouldn’t be me.”

SIR ROGER PENROSE: “The thought experiment you propose is impossible. You can’t duplicate the behavior of neurons without tapping into quantum gravity. That said, there’s not much point in me taking further part in this conversation.” (Wanders away.)

ALBERT: “Suppose that the replacement is carried out one neuron at a time, and the swap occurs so fast that it doesn’t make any difference to global processing.”

BERNICE: “How could that possibly be the case?”

ALBERT: “The little robot swims up to the neuron, surrounds it, scans it, learns to duplicate it, and then suddenly takes over the behavior, between one spike and the next. In fact, the imitation is so good that your outward behavior is just the same as it would be if the brain were left undisturbed. Maybe not exactly the same, but the causal impact is much less than thermal noise at 310 Kelvin.”

CHARLES: “So what?”

ALBERT: “So don’t your beliefs violate the Generalized AntiZombie Principle? Whatever just happened, it didn’t change your internal narrative! You’ll go around talking about consciousness for exactly the same reason as before.”

BERNICE: “Those little robots are a Zombie Master. They’ll make me talk about consciousness even though I’m not conscious. The Zombie World is possible if you allow there to be an added, extra, experimentally detectable Zombie Master—which those robots are.”

CHARLES: “Oh, that’s not right, Bernice. The little robots aren’t plotting how to fake consciousness, or processing a corpus of text from human amateurs. They’re doing the same thing neurons do, just in silicon instead of carbon.”

ALBERT: “Wait, didn’t you just agree with me?”

CHARLES: “I never said the new person wouldn’t be conscious. I said it wouldn’t be me.”

ALBERT: “Well, obviously the AntiZombie Principle generalizes to say that this operation hasn’t disturbed the true cause of your talking about this me thing.”

CHARLES: “Uh-uh! Your operation certainly did disturb the true cause of my talking about consciousness. It substituted a different cause in its place, the robots. Now, just because that new cause also happens to be conscious—talks about consciousness for the same generalized reason—doesn’t mean it’s the same cause that was originally there.”

ALBERT: “But I wouldn’t even have to tell you about the robot operation. You wouldn’t notice. If you think, going on introspective evidence, that you are in an important sense ‘the same person’ that you were five minutes ago, and I do something to you that doesn’t change the introspective evidence available to you, then your conclusion that you are the same person that you were five minutes ago should be equally justified. Doesn’t the Generalized AntiZombie Principle say that if I do something to you that alters your consciousness, let alone makes you a completely different person, then you ought to notice somehow?”

BERNICE: “Not if you replace me with a Zombie Master. Then there’s no one there to notice.”

CHARLES: “Introspection isn’t perfect. Lots of stuff goes on inside my brain that I don’t notice.”

ALBERT: “You’re postulating epiphenomenal facts about consciousness and identity!”

BERNICE: “No I’m not! I can experimentally detect the difference between neurons and robots.”

CHARLES: “No I’m not! I can experimentally detect the moment when the old me is replaced by a new person.”

ALBERT: “Yeah, and I can detect the switch flipping! You’re detecting something that doesn’t make a noticeable difference to the true cause of your talk about consciousness and personal identity. And the proof is, you’ll talk just the same way afterward.”

BERNICE: “That’s because of your robotic Zombie Master!”

CHARLES: “Just because two people talk about ‘personal identity’ for similar reasons doesn’t make them the same person.”

I think the Generalized AntiZombie Principle supports Albert’s position, but the reasons shall have to wait for future essays. I need other prerequisites, and besides, this essay is already too long.

But you see the importance of the question, “How far can you generalize the AntiZombie Argument and have it still be valid?”

The makeup of future galactic civilizations may be determined by the answer . . .

1. René Descartes, Discours de la Méthode, vol. 45 (Librairie des Bibliophiles, 1887).

224
GAZP vs. GLUT

In “The Unimagined Preposterousness of Zombies,” Daniel Dennett says:¹

To date, several philosophers have told me that they plan to accept my challenge to offer a non-question-begging defense of zombies, but the only one I have seen so far involves postulating a “logically possible” but fantastic being—a descendent of Ned Block’s Giant Lookup Table fantasy . . .

A Giant Lookup Table, in programmer’s parlance, is when you implement a function as a giant table of inputs and outputs, usually to save on runtime computation. If my program needs to know the multiplicative product of two inputs between 1 and 100, I can write a multiplication algorithm that computes each time the function is called, or I can precompute a Giant Lookup Table with 10,000 entries and two indices. There are times when you do want to do this, though not for multiplication—times when you’re going to reuse the function a lot and it doesn’t have many possible inputs; or when clock cycles are cheap while you’re initializing, but very expensive while executing.

Giant Lookup Tables get very large, very fast. A GLUT of all possible twenty-ply conversations with ten words per remark, using only 850-word Basic English, would require 7.6 × 10⁵⁸⁵ entries.

Replacing a human brain with a Giant Lookup Table of all possible sense inputs and motor outputs (relative to some fine-grained digitization scheme) would require an unreasonably large amount of memory storage. But “in principle,” as philosophers are fond of saying, it could be done.

The GLUT is not a zombie in the classic sense, because it is microphysically dissimilar to a human. (In fact, a GLUT can’t really run on the same physics as a human; it’s too large to fit in our universe. For philosophical purposes, we shall ignore this and suppose a supply of unlimited memory storage.)

But is the GLUT a zombie at all? That is, does it behave exactly like a human without being conscious?

The GLUT-ed body’s tongue talks about consciousness. Its fingers write philosophy papers. In every way, so long as you don’t peer inside the skull, the GLUT seems just like a human . . . which certainly seems like a valid example of a zombie: it behaves just like a human, but there’s no one home.

Unless the GLUT is conscious, in which case it wouldn’t be a valid example.

I can’t recall ever seeing anyone claim that a GLUT is conscious. (Admittedly my reading in this area is not up to professional grade; feel free to correct me.) Even people who are accused of being (gasp!) functionalists don’t claim that GLUTs can be conscious.

GLUTs are the reductio ad absurdum to anyone who suggests that consciousness is simply an input-output pattern, thereby disposing of all troublesome worries about what goes on inside.

So what does the Generalized Anti-Zombie Principle (GAZP) say about the Giant Lookup Table (GLUT)?

At first glance, it would seem that a GLUT is the very archetype of a Zombie Master—a distinct, additional, detectable, non-conscious system that animates a zombie and makes it talk about consciousness for different reasons.

In the interior of the GLUT, there’s merely a very simple computer program that looks up inputs and retrieves outputs. Even talking about a “simple computer program” is overshooting the mark, in a case like this. A GLUT is more like ROM than a CPU. We could equally well talk about a series of switched tracks by which some balls roll out of a previously stored stack and into a trough—period; that’s all the GLUT does.

A spokesperson from People for the Ethical Treatment of Zombies replies: “Oh, that’s what all the anti-mechanists say, isn’t it? That when you look in the brain, you just find a bunch of neurotransmitters opening ion channels? If ion channels can be conscious, why not levers and balls rolling into bins?”

“The problem isn’t the levers,” replies the functionalist, “the problem is that a GLUT has the wrong pattern of levers. You need levers that implement things like, say, formation of beliefs about beliefs, or self-modeling . . . Heck, you need the ability to write things to memory just so that time can pass for the computation. Unless you think it’s possible to program a conscious being in Haskell.”

“I don’t know about that,” says the PETZ spokesperson, “all I know is that this so-called zombie writes philosophical papers about consciousness. Where do these philosophy papers come from, if not from consciousness?”

Good question! Let us ponder it deeply.

There’s a game in physics called Follow-The-Energy. Richard Feynman’s father played it with young Richard:

It was the kind of thing my father would have talked about: “What makes it go? Everything goes because the Sun is shining.” And then we would have fun discussing it:

“No, the toy goes because the spring is wound up,” I would say. “How did the spring get wound up?” he would ask.

“I wound it up.”

“And how did you get moving?”

“From eating.”

“And food grows only because the Sun is shining. So it’s because the Sun is shining that all these things are moving.” That would get the concept across that motion is simply the transformation of the Sun’s power.²

When you get a little older, you learn that energy is conserved, never created or destroyed, so the notion of using up energy doesn’t make much sense. You can never change the total amount of energy, so in what sense are you using it?

So when physicists grow up, they learn to play a new game called Follow-The-Negentropy—which is really the same game they were playing all along; only the rules are mathier, the game is more useful, and the principles are harder to wrap your mind around conceptually.

Rationalists learn a game called Follow-The-Improbability, the grownup version of “How Do You Know?” The rule of the rationalist’s game is that every improbable-seeming belief needs an equivalent amount of evidence to justify it. (This game has amazingly similar rules to Follow-The-Negentropy.)

Whenever someone violates the rules of the rationalist’s game, you can find a place in their argument where a quantity of improbability appears from nowhere; and this is as much a sign of a problem as, oh, say, an ingenious design of linked wheels and gears that keeps itself running forever.

The one comes to you and says: “I believe with firm and abiding faith that there’s an object in the asteroid belt, one foot across and composed entirely of chocolate cake; you can’t prove that this is impossible.” But, unless the one had access to some kind of evidence for this belief, it would be highly improbable for a correct belief to form spontaneously. So either the one can point to evidence, or the belief won’t turn out to be true. “But you can’t prove it’s impossible for my mind to spontaneously generate a belief that happens to be correct!” No, but that kind of spontaneous generation is highly improbable, just like, oh, say, an egg unscrambling itself.

In Follow-The-Improbability, it’s highly suspicious to even talk about a specific hypothesis without having had enough evidence to narrow down the space of possible hypotheses. Why aren’t you giving equal air time to a decillion other equally plausible hypotheses? You need sufficient evidence to find the “chocolate cake in the asteroid belt” hypothesis in the hypothesis space—otherwise there’s no reason to give it more air time than a trillion other candidates like “There’s a wooden dresser in the asteroid belt” or “The Flying Spaghetti Monster threw up on my sneakers.”

In Follow-The-Improbability, you are not allowed to pull out big complicated specific hypotheses from thin air without already having a corresponding amount of evidence; because it’s not realistic to suppose that you could spontaneously start discussing the true hypothesis by pure coincidence.

A philosopher says, “This zombie’s skull contains a Giant Lookup Table of all the inputs and outputs for some human’s brain.” This is a very large improbability. So you ask, “How did this improbable event occur? Where did the GLUT come from?”

Now this is not standard philosophical procedure for thought experiments. In standard philosophical procedure, you are allowed to postulate things like “Suppose you were riding a beam of light . . .” without worrying about physical possibility, let alone mere improbability. But in this case, the origin of the GLUT matters; and that’s why it’s important to understand the motivating question, “Where did the improbability come from?”

The obvious answer is that you took a computational specification of a human brain, and used that to precompute the Giant Lookup Table. (Thereby creating uncounted googols of human beings, some of them in extreme pain, the supermajority gone quite mad in a universe of chaos where inputs bear no relation to outputs. But damn the ethics, this is for philosophy.)

In this case, the GLUT is writing papers about consciousness because of a conscious algorithm. The GLUT is no zombie, any more than a cellphone is a zombie because it can talk about consciousness while being just a small consumer electronic device. The cellphone is just transmitting philosophy speeches from whoever happens to be on the other end of the line. A GLUT generated from an originally human brain-specification is doing the same thing.

“All right,” says the philosopher, “the GLUT was generated randomly, and just happens to have the same input-output relations as some reference human.”

How, exactly, did you randomly generate the GLUT?

“We used a true randomness source—a quantum device.”

But a quantum device just implements the Branch Both Ways instruction; when you generate a bit from a quantum randomness source, the deterministic result is that one set of universe-branches (locally connected amplitude clouds) see 1, and another set of universes see 0. Do it 4 times, create 16 (sets of) universes.

So, really, this is like saying that you got the GLUT by writing down all possible GLUT-sized sequences of 0s and 1s, in a really damn huge bin of lookup tables; and then reaching into the bin, and somehow pulling out a GLUT that happened to correspond to a human brain-specification. Where did the improbability come from?

Because if this wasn’t just a coincidence—if you had some reach-into-the-bin function that pulled out a human-corresponding GLUT by design, not just chance—then that reach-into-the-bin function is probably conscious, and so the GLUT is again a cellphone, not a zombie. It’s connected to a human at two removes, instead of one, but it’s still a cellphone! Nice try at concealing the source of the improbability there!

Now behold where Follow-The-Improbability has taken us: where is the source of this body’s tongue talking about an inner listener? The consciousness isn’t in the lookup table. The consciousness isn’t in the factory that manufactures lots of possible lookup tables. The consciousness was in whatever pointed to one particular already-manufactured lookup table, and said, “Use that one!”

You can see why I introduced the game of Follow-The-Improbability. Ordinarily, when we’re talking to a person, we tend to think that whatever is inside the skull must be “where the consciousness is.” It’s only by playing Follow-The-Improbability that we can realize that the real source of the conversation we’re having is that-which-is-responsible-for the improbability of the conversation—however distant in time or space, as the Sun moves a wind-up toy.

“No, no!” says the philosopher. “In the thought experiment, they aren’t randomly generating lots of GLUTs, and then using a conscious algorithm to pick out one GLUT that seems humanlike! I am specifying that, in this thought experiment, they reach into the inconceivably vast GLUT bin, and by pure chance pull out a GLUT that is identical to a human brain’s inputs and outputs! There! I’ve got you cornered now! You can’t play Follow-The-Improbability any further!”

Oh. So your specification is the source of the improbability here.

When we play Follow-The-Improbability again, we end up outside the thought experiment, looking at the philosopher.

That which points to the one GLUT that talks about consciousness, out of all the vast space of possibilities, is now . . . the conscious person asking us to imagine this whole scenario. And our own brains, which will fill in the blank when we imagine, “What will this GLUT say in response to ‘Talk about your inner listener’?”

The moral of this story is that when you follow back discourse about “consciousness,” you generally find consciousness. It’s not always right in front of you. Sometimes it’s very cleverly hidden. But it’s there. Hence the Generalized Anti-Zombie Principle.

If there is a Zombie Master in the form of a chatbot that processes and remixes amateur human discourse about “consciousness,” the humans who generated the original text corpus are conscious.

If someday you come to understand consciousness, and look back, and see that there’s a program you can write that will output confused philosophical discourse that sounds an awful lot like humans without itself being conscious—then when I ask “How did this program come to sound similar to humans?” the answer is that you wrote it to sound similar to conscious humans, rather than choosing on the criterion of similarity to something else. This doesn’t mean your little Zombie Master is conscious—but it does mean I can find consciousness somewhere in the universe by tracing back the chain of causality, which means we’re not entirely in the Zombie World.

But suppose someone actually did reach into a GLUT-bin and by genuinely pure chance pulled out a GLUT that wrote philosophy papers?

Well, then it wouldn’t be conscious. In my humble opinion.

I mean, there’s got to be more to it than inputs and outputs.

Otherwise even a GLUT would be conscious, right?

Oh, and for those of you wondering how this sort of thing relates to my day job . . .

In this line of business you meet an awful lot of people who think that an arbitrarily generated powerful AI will be “moral.” They can’t agree among themselves on why, or what they mean by the word “moral”; but they all agree that doing Friendly AI theory is unnecessary. And when you ask them how an arbitrarily generated AI ends up with moral outputs, they proffer elaborate rationalizations aimed at AIs of that which they deem “moral”; and there are all sorts of problems with this, but the number one problem is, “Are you sure the AI would follow the same line of thought you invented to argue human morals, when, unlike you, the AI doesn’t start out knowing what you want it to rationalize?” You could call the counter-principle Follow-The-Decision-Information, or something along those lines. You can account for an AI that does improbably nice things by telling me how you chose the AI’s design from a huge space of possibilities, but otherwise the improbability is being pulled out of nowhere—though more and more heavily disguised, as rationalized premises are rationalized in turn.

So I’ve already done a whole series of essays which I myself generated using Follow-The-Improbability. But I didn’t spell out the rules explicitly at that time, because I hadn’t done the thermodynamics essays yet . . .

Just thought I’d mention that. It’s amazing how many of my essays coincidentally turn out to include ideas surprisingly relevant to discussion of Friendly AI theory . . . if you believe in coincidence.

1. Daniel C. Dennett, “The Unimagined Preposterousness of Zombies,” Journal of Consciousness Studies 2 (4 1995): 322–26.

2. Richard P. Feynman, “Judging Books by Their Covers,” in Surely You’re Joking, Mr. Feynman! (New York: W. W. Norton & Company, 1985).

225
Belief in the Implied Invisible

One generalized lesson not to learn from the Anti-Zombie Argument is, “Anything you can’t see doesn’t exist.”

It’s tempting to conclude the general rule. It would make the Anti-Zombie Argument much simpler, on future occasions, if we could take this as a premise. But unfortunately that’s just not Bayesian.

Suppose I transmit a photon out toward infinity, not aimed at any stars, or any galaxies, pointing it toward one of the great voids between superclusters. Based on standard physics, in other words, I don’t expect this photon to intercept anything on its way out. The photon is moving at light speed, so I can’t chase after it and capture it again.

If the expansion of the universe is accelerating, as current cosmology holds, there will come a future point where I don’t expect to be able to interact with the photon even in principle—a future time beyond which I don’t expect the photon’s future light cone to intercept my world-line. Even if an alien species captured the photon and rushed back to tell us, they couldn’t travel fast enough to make up for the accelerating expansion of the universe.

Should I believe that, in the moment where I can no longer interact with it even in principle, the photon disappears?

No.

It would violate Conservation of Energy. And the Second Law of Thermodynamics. And just about every other law of physics. And probably the Three Laws of Robotics. It would imply the photon knows I care about it and knows exactly when to disappear.

It’s a silly idea.

But if you can believe in the continued existence of photons that have become experimentally undetectable to you, why doesn’t this imply a general license to believe in the invisible?

(If you want to think about this question on your own, do so before reading on . . .)

Though I failed to Google a source, I remember reading that when it was first proposed that the Milky Way was our galaxy—that the hazy river of light in the night sky was made up of millions (or even billions) of stars—that Occam’s Razor was invoked against the new hypothesis. Because, you see, the hypothesis vastly multiplied the number of “entities” in the believed universe. Or maybe it was the suggestion that “nebulae”—those hazy patches seen through a telescope—might be galaxies full of stars, that got the invocation of Occam’s Razor.

Lex parsimoniae: Entia non sunt multiplicanda praeter necessitatem.

That was Occam’s original formulation, the law of parsimony: Entities should not be multiplied beyond necessity.

If you postulate billions of stars that no one has ever believed in before, you’re multiplying entities, aren’t you?

No. There are two Bayesian formalizations of Occam’s Razor: Solomonoff induction, and Minimum Message Length. Neither penalizes galaxies for being big.

Which they had better not do! One of the lessons of history is that what-we-call-reality keeps turning out to be bigger and bigger and huger yet. Remember when the Earth was at the center of the universe? Remember when no one had invented Avogadro’s number? If Occam’s Razor was weighing against the multiplication of entities every time, we’d have to start doubting Occam’s Razor, because it would have consistently turned out to be wrong.

In Solomonoff induction, the complexity of your model is the amount of code in the computer program you have to write to simulate your model. The amount of code, not the amount of RAM it uses or the number of cycles it takes to compute. A model of the universe that contains billions of galaxies containing billions of stars, each star made of a billion trillion decillion quarks, will take a lot of RAM to run—but the code only has to describe the behavior of the quarks, and the stars and galaxies can be left to run themselves. I am speaking semi-metaphorically here—there are things in the universe besides quarks—but the point is, postulating an extra billion galaxies doesn’t count against the size of your code, if you’ve already described one galaxy. It just takes a bit more RAM, and Occam’s Razor doesn’t care about RAM.

Why not? The Minimum Message Length formalism, which is nearly equivalent to Solomonoff induction, may make the principle clearer: If you have to tell someone how your model of the universe works, you don’t have to individually specify the location of each quark in each star in each galaxy. You just have to write down some equations. The amount of “stuff” that obeys the equation doesn’t affect how long it takes to write the equation down. If you encode the equation into a file, and the file is 100 bits long, then there are 2¹⁰⁰ other models that would be around the same file size, and you’ll need roughly 100 bits of supporting evidence. You’ve got a limited amount of probability mass; and a priori, you’ve got to divide that mass up among all the messages you could send; and so postulating a model from within a model space of 2¹⁰⁰ alternatives, means you’ve got to accept a 2^-100 prior probability penalty—but having more galaxies doesn’t add to this.

Postulating billions of stars in billions of galaxies doesn’t affect the length of your message describing the overall behavior of all those galaxies. So you don’t take a probability hit from having the same equations describing more things. (So long as your model’s predictive successes aren’t sensitive to the exact initial conditions. If you’ve got to specify the exact positions of all the quarks for your model to predict as well as it does, the extra quarks do count as a hit.)

If you suppose that the photon disappears when you are no longer looking at it, this is an additional law in your model of the universe. It’s the laws that are “entities,” costly under the laws of parsimony. Extra quarks are free.

So does it boil down to, “I believe the photon goes on existing as it wings off to nowhere, because my priors say it’s simpler for it to go on existing than to disappear”?

This is what I thought at first, but on reflection, it’s not quite right. (And not just because it opens the door to obvious abuses.)

I would boil it down to a distinction between belief in the implied invisible, and belief in the additional invisible.

When you believe that the photon goes on existing as it wings out to infinity, you’re not believing that as an additional fact.

What you believe (assign probability to) is a set of simple equations; you believe these equations describe the universe. You believe these equations because they are the simplest equations you could find that describe the evidence. These equations are highly experimentally testable; they explain huge mounds of evidence visible in the past, and predict the results of many observations in the future.

You believe these equations, and it is a logical implication of these equations that the photon goes on existing as it wings off to nowhere, so you believe that as well.

Your priors, or even your probabilities, don’t directly talk about the photon. What you assign probability to is not the photon, but the general laws. When you assign probability to the laws of physics as we know them, you automatically contribute that same probability to the photon continuing to exist on its way to nowhere—if you believe the logical implications of what you believe.

It’s not that you believe in the invisible as such, from reasoning about invisible things. Rather the experimental evidence supports certain laws, and belief in those laws logically implies the existence of certain entities that you can’t interact with. This is belief in the implied invisible.

On the other hand, if you believe that the photon is eaten out of existence by the Flying Spaghetti Monster—maybe on just this one occasion—or even if you believed without reason that the photon hit a dust speck on its way out—then you would be believing in a specific extra invisible event, on its own. If you thought that this sort of thing happened in general, you would believe in a specific extra invisible law. This is belief in the additional invisible.

To make it clear why you would sometimes want to think about implied invisibles, suppose you’re going to launch a spaceship, at nearly the speed of light, toward a faraway supercluster. By the time the spaceship gets there and sets up a colony, the universe’s expansion will have accelerated too much for them to ever send a message back. Do you deem it worth the purely altruistic effort to set up this colony, for the sake of all the people who will live there and be happy? Or do you think the spaceship blips out of existence before it gets there? This could be a very real question at some point.

The whole matter would be a lot simpler, admittedly, if we could just rule out the existence of entities we can’t interact with, once and for all—have the universe stop existing at the edge of our telescopes. But this requires us to be very silly.

Saying that you shouldn’t ever need a separate and additional belief about invisible things—that you only believe invisibles that are logical implications of general laws which are themselves testable, and even then, don’t have any further beliefs about them that are not logical implications of visibly testable general rules—actually does seem to rule out all abuses of belief in the invisible, when applied correctly.

Perhaps I should say, “you should assign unaltered prior probability to additional invisibles,” rather than saying, “do not believe in them.” But if you think of a belief as something evidentially additional, something you bother to track, something where you bother to count up support for or against, then it’s questionable whether we should ever have additional beliefs about additional invisibles.

There are exotic cases that break this in theory. (E.g.: The epiphenomenal demons are watching you, and will torture 3 ↑↑↑ 3 victims for a year, somewhere you can’t ever verify the event, if you ever say the word “Niblick.”) But I can’t think of a case where the principle fails in human practice.

226
Zombies: The Movie

FADE IN around a serious-looking group of uniformed military officers. At the head of the table, a senior, heavy-set man, GENERAL FRED, speaks.

GENERAL FRED: The reports are confirmed. New York has been overrun . . . by zombies.

COLONEL TODD: Again? But we just had a zombie invasion 28 days ago!

GENERAL FRED: These zombies . . . are different. They’re . . . philosophical zombies.

CAPTAIN MUDD: Are they filled with rage, causing them to bite people?

COLONEL TODD: Do they lose all capacity for reason?

GENERAL FRED: No. They behave . . . exactly like we do . . . except that they’re not conscious.

(Silence grips the table.)

COLONEL TODD: Dear God.

GENERAL FRED moves over to a computerized display.

GENERAL FRED: This is New York City, two weeks ago.

The display shows crowds bustling through the streets, people eating in restaurants, a garbage truck hauling away trash.

GENERAL FRED: This . . . is New York City . . . now.

The display changes, showing a crowded subway train, a group of students laughing in a park, and a couple holding hands in the sunlight.

COLONEL TODD: It’s worse than I imagined.

CAPTAIN MUDD: How can you tell, exactly?

COLONEL TODD: I’ve never seen anything so brutally ordinary.

A lab-coated SCIENTIST stands up at the foot of the table.

SCIENTIST: The zombie disease eliminates consciousness without changing the brain in any way. We’ve been trying to understand how the disease is transmitted. Our conclusion is that, since the disease attacks dual properties of ordinary matter, it must, itself, operate outside our universe. We’re dealing with an epiphenomenal virus.

GENERAL FRED: Are you sure?

SCIENTIST: As sure as we can be in the total absence of evidence.

GENERAL FRED: All right. Compile a report on every epiphenomenon ever observed. What, where, and who. I want a list of everything that hasn’t happened in the last fifty years.

CAPTAIN MUDD: If the virus is epiphenomenal, how do we know it exists?

SCIENTIST: The same way we know we’re conscious.

CAPTAIN MUDD: Oh, okay.

GENERAL FRED: Have the doctors made any progress on finding an epiphenomenal cure?

SCIENTIST: They’ve tried every placebo in the book. No dice. Everything they do has an effect.

GENERAL FRED: Have you brought in a homeopath?

SCIENTIST: I tried, sir! I couldn’t find any!

GENERAL FRED: Excellent. And the Taoists?

SCIENTIST: They refuse to do anything!

GENERAL FRED: Then we may yet be saved.

COLONEL TODD: What about David Chalmers? Shouldn’t he be here?

GENERAL FRED: Chalmers . . . was one of the first victims.

COLONEL TODD: Oh no.

(Cut to the INTERIOR of a cell, completely walled in by reinforced glass, where DAVID CHALMERS paces back and forth.)

DOCTOR: David! David Chalmers! Can you hear me?

CHALMERS: Yes.

NURSE: It’s no use, doctor.

CHALMERS: I’m perfectly fine. I’ve been introspecting on my consciousness, and I can’t detect any difference. I know I would be expected to say that, but—

The DOCTOR turns away from the glass screen in horror.

DOCTOR: His words, they . . . they don’t mean anything.

CHALMERS: This is a grotesque distortion of my philosophical views. This sort of thing can’t actually happen!

DOCTOR: Why not?

NURSE: Yes, why not?

CHALMERS: Because—

(Cut to two POLICE OFFICERS, guarding a dirt road leading up to the imposing steel gate of a gigantic concrete complex. On their uniforms, a badge reads BRIDGING LAW ENFORCEMENT AGENCY.)

OFFICER 1: You’ve got to watch out for those clever bastards. They look like humans. They can talk like humans. They’re identical to humans on the atomic level. But they’re not human.

OFFICER 2: Scumbags.

The huge noise of a throbbing engine echoes over the hills. Up rides the MAN on a white motorcycle. The MAN is wearing black sunglasses and a black leather business suit with a black leather tie and silver metal boots. His white beard flows in the wind. He pulls to a halt in front of the gate.

The OFFICERS bustle up to the motorcycle.

OFFICER 1: State your business here.

MAN: Is this where you’re keeping David Chalmers?

OFFICER 2: What’s it to you? You a friend of his?

MAN: Can’t say I am. But even zombies have rights.

OFFICER 1: All right, buddy, let’s see your qualia.

MAN: I don’t have any.

OFFICER 2 suddenly pulls a gun, keeping it trained on the MAN.

OFFICER 2: Aha! A zombie!

OFFICER 1: No, zombies claim to have qualia.

OFFICER 2: So he’s an ordinary human?

OFFICER 1: No, they also claim to have qualia.

The OFFICERS look at the MAN, who waits calmly.

OFFICER 2: Um . . .

OFFICER 1: Who are you?

MAN: I’m Daniel Dennett, bitches.

Seemingly from nowhere, DENNETT pulls a sword and slices OFFICER 2’s gun in half with a steely noise. OFFICER 1 begins to reach for his own gun, but DENNETT is suddenly standing behind OFFICER 1 and chops with a fist, striking the junction of OFFICER 1’s shoulder and neck. OFFICER 1 drops to the ground.

OFFICER 2 steps back, horrified.

OFFICER 2: That’s not possible! How’d you do that?

DENNETT: I am one with my body.

DENNETT drops OFFICER 2 with another blow, and strides toward the gate. He looks up at the imposing concrete complex, and grips his sword tighter.

DENNETT (quietly to himself): There is a spoon.

(Cut back to GENERAL FRED and the other military officials.)

GENERAL FRED: I’ve just received the reports. We’ve lost Detroit.

CAPTAIN MUDD: I don’t want to be the one to say “Good riddance,” but—

GENERAL FRED: Australia has been . . . reduced to atoms.

COLONEL TODD: The epiphenomenal virus is spreading faster. Civilization itself threatens to dissolve into total normality. We could be looking at the middle of humanity.

CAPTAIN MUDD: Can we negotiate with the zombies?

GENERAL FRED: We’ve sent them messages. They sent only a single reply.

CAPTAIN MUDD: Which was . . . ?

GENERAL FRED: It’s on its way now.

An orderly brings in an envelope, and hands it to GENERAL FRED.

GENERAL FRED opens the envelope, takes out a single sheet of paper, and reads it.

Silence envelops the room.

CAPTAIN MUDD: What’s it say?

GENERAL FRED: It says . . . that we’re the ones with the virus.

(A silence falls.)

COLONEL TODD raises his hands and stares at them.

COLONEL TODD: My God, it’s true. It’s true. I . . .

(A tear rolls down COLONEL TODD’s cheek.)

COLONEL TODD: I don’t feel anything.

The screen goes black.

The sound goes silent.

The movie continues exactly as before.

227
Excluding the Supernatural

Occasionally, you hear someone claiming that creationism should not be taught in schools, especially not as a competing hypothesis to evolution, because creationism is a priori and automatically excluded from scientific consideration, in that it invokes the “supernatural.”

So . . . is the idea here, that creationism could be true, but even if it were true, you wouldn’t be allowed to teach it in science class, because science is only about “natural” things?

It seems clear enough that this notion stems from the desire to avoid a confrontation between science and religion. You don’t want to come right out and say that science doesn’t teach Religious Claim X because X has been tested by the scientific method and found false. So instead, you can . . . um . . . claim that science is excluding hypothesis X a priori. That way you don’t have to discuss how experiment has falsified X a posteriori.

Of course this plays right into the creationist claim that Intelligent Design isn’t getting a fair shake from science—that science has prejudged the issue in favor of atheism, regardless of the evidence. If science excluded Intelligent Design a priori, this would be a justified complaint!

But let’s back up a moment. The one comes to you and says: “Intelligent Design is excluded from being science a priori, because it is ‘supernatural,’ and science only deals in ‘natural’ explanations.”

What exactly do they mean, “supernatural”? Is any explanation invented by someone with the last name “Cohen” a supernatural one? If we’re going to summarily kick a set of hypotheses out of science, what is it that we’re supposed to exclude?

By far the best definition I’ve ever heard of the supernatural is Richard Carrier’s: A “supernatural” explanation appeals to ontologically basic mental things, mental entities that cannot be reduced to nonmental entities.

This is the difference, for example, between saying that water rolls downhill because it wants to be lower, and setting forth differential equations that claim to describe only motions, not desires. It’s the difference between saying that a tree puts forth leaves because of a tree spirit, versus examining plant biochemistry. Cognitive science takes the fight against supernaturalism into the realm of the mind.

Why is this an excellent definition of the supernatural? I refer you to Richard Carrier for the full argument. But consider: Suppose that you discover what seems to be a spirit, inhabiting a tree—a dryad who can materialize outside or inside the tree, who speaks in English about the need to protect her tree, et cetera. And then suppose that we turn a microscope on this tree spirit, and she turns out to be made of parts—not inherently spiritual and ineffable parts, like fabric of desireness and cloth of belief, but rather the same sort of parts as quarks and electrons, parts whose behavior is defined in motions rather than minds. Wouldn’t the dryad immediately be demoted to the dull catalogue of common things?

But if we accept Richard Carrier’s definition of the supernatural, then a dilemma arises: we want to give religious claims a fair shake, but it seems that we have very good grounds for excluding supernatural explanations a priori.

I mean, what would the universe look like if reductionism were false?

I previously defined the reductionist thesis as follows: human minds create multi-level models of reality in which high-level patterns and low-level patterns are separately and explicitly represented. A physicist knows Newton’s equation for gravity, Einstein’s equation for gravity, and the derivation of the former as a low-speed approximation of the latter. But these three separate mental representations are only a convenience of human cognition. It is not that reality itself has an Einstein equation that governs at high speeds, a Newton equation that governs at low speeds, and a “bridging law” that smooths the interface. Reality itself has only a single level, Einsteinian gravity. It is only the Mind Projection Fallacy that makes some people talk as if the higher levels could have a separate existence—different levels of organization can have separate representations in human maps, but the territory itself is a single unified low-level mathematical object.

Suppose this were wrong.

Suppose that the Mind Projection Fallacy was not a fallacy, but simply true.

Suppose that a 747 had a fundamental physical existence apart from the quarks making up the 747.

What experimental observations would you expect to make, if you found yourself in such a universe?

If you can’t come up with a good answer to that, it’s not observation that’s ruling out “non-reductionist” beliefs, but a priori logical incoherence. If you can’t say what predictions the “non-reductionist” model makes, how can you say that experimental evidence rules it out?

My thesis is that non-reductionism is a confusion; and once you realize that an idea is a confusion, it becomes a tad difficult to envision what the universe would look like if the confusion were true. Maybe I’ve got some multi-level model of the world, and the multi-level model has a one-to-one direct correspondence with the causal elements of the physics? But once all the rules are specified, why wouldn’t the model just flatten out into yet another list of fundamental things and their interactions? Does everything I can see in the model, like a 747 or a human mind, have to become a separate real thing? But what if I see a pattern in that new supersystem?

Supernaturalism is a special case of non-reductionism, where it is not 747s that are irreducible, but just (some) mental things. Religion is a special case of supernaturalism, where the irreducible mental things are God(s) and souls; and perhaps also sins, angels, karma, etc.

If I propose the existence of a powerful entity with the ability to survey and alter each element of our observed universe, but with the entity reducible to nonmental parts that interact with the elements of our universe in a lawful way; if I propose that this entity wants certain particular things, but “wants” using a brain composed of particles and fields; then this is not yet a religion, just a naturalistic hypothesis about a naturalistic Matrix. If tomorrow the clouds parted and a vast glowing amorphous figure thundered forth the above description of reality, then this would not imply that the figure was necessarily honest; but I would show the movies in a science class, and I would try to derive testable predictions from the theory.

Conversely, religions have ignored the discovery of that ancient bodiless thing: omnipresent in the working of Nature and immanent in every falling leaf; vast as a planet’s surface and billions of years old; itself unmade and arising from the structure of physics; designing without brain to shape all life on Earth and the minds of humanity. Natural selection, when Darwin proposed it, was not hailed as the long-awaited Creator: It wasn’t fundamentally mental.

But now we get to the dilemma: if the staid conventional normal boring understanding of physics and the brain is correct, there’s no way in principle that a human being can concretely envision, and derive testable experimental predictions about, an alternate universe in which things are irreducibly mental. Because if the boring old normal model is correct, your brain is made of quarks, and so your brain will only be able to envision and concretely predict things that can predicted by quarks. You will only ever be able to construct models made of interacting simple things.

People who live in reductionist universes cannot concretely envision non-reductionist universes. They can pronounce the syllables “non-reductionist” but they can’t imagine it.

The basic error of anthropomorphism, and the reason why supernatural explanations sound much simpler than they really are, is your brain using itself as an opaque black box to predict other things labeled “mindful.” Because you already have big, complicated webs of neural circuitry that implement your “wanting” things, it seems like you can easily describe water that “wants” to flow downhill—the one word “want” acts as a lever to set your own complicated wanting-machinery in motion.

Or you imagine that God likes beautiful things, and therefore made the flowers. Your own “beauty” circuitry determines what is “beautiful” and “not beautiful.” But you don’t know the diagram of your own synapses. You can’t describe a nonmental system that computes the same label for what is “beautiful” or “not beautiful”—can’t write a computer program that predicts your own labelings. But this is just a defect of knowledge on your part; it doesn’t mean that the brain has no explanation.

If the “boring view” of reality is correct, then you can never predict anything irreducible because you are reducible. You can never get Bayesian confirmation for a hypothesis of irreducibility, because any prediction you can make is, therefore, something that could also be predicted by a reducible thing, namely your brain.

Some boxes you really can’t think outside. If our universe really is Turing computable, we will never be able to concretely envision anything that isn’t Turing-computable—no matter how many levels of halting oracle hierarchy our mathematicians can talk about, we won’t be able to predict what a halting oracle would actually say, in such fashion as to experimentally discriminate it from merely computable reasoning.

Of course, that’s all assuming the “boring view” is correct. To the extent that you believe evolution is true, you should not expect to encounter strong evidence against evolution. To the extent you believe reductionism is true, you should expect non-reductionist hypotheses to be incoherent as well as wrong. To the extent you believe supernaturalism is false, you should expect it to be inconceivable as well.

If, on the other hand, a supernatural hypothesis turns out to be true, then presumably you will also discover that it is not inconceivable.

So let us bring this back full circle to the matter of Intelligent Design:

Should ID be excluded a priori from experimental falsification and science classrooms, because, by invoking the supernatural, it has placed itself outside of natural philosophy?

I answer: “Of course not.” The irreducibility of the intelligent designer is not an indispensable part of the ID hypothesis. For every irreducible God that can be proposed by the IDers, there exists a corresponding reducible alien that behaves in accordance with the same predictions—since the IDers themselves are reducible. To the extent I believe reductionism is in fact correct, which is a rather strong extent, I must expect to discover reducible formulations of all supposedly supernatural predictive models.

If we’re going over the archeological records to test the assertion that Jehovah parted the Red Sea out of an explicit desire to display its superhuman power, then it makes little difference whether Jehovah is ontologically basic, or an alien with nanotech, or a Dark Lord of the Matrix. You do some archeology, find no skeletal remnants or armor at the Red Sea site, and indeed find records that Egypt ruled much of Canaan at the time. So you stamp the historical record in the Bible “disproven” and carry on. The hypothesis is coherent, falsifiable and wrong.

Likewise with the evidence from biology that foxes are designed to chase rabbits, rabbits are designed to evade foxes, and neither is designed “to carry on their species” or “protect the harmony of Nature”; likewise with the retina being designed backwards with the light-sensitive parts at the bottom; and so on through a thousand other items of evidence for splintered, immoral, incompetent design. The Jehovah model of our alien god is coherent, falsifiable, and wrong—coherent, that is, so long as you don’t care whether Jehovah is ontologically basic or just an alien.

Just convert the supernatural hypothesis into the corresponding natural hypothesis. Just make the same predictions the same way, without asserting any mental things to be ontologically basic. Consult your brain’s black box if necessary to make predictions—say, if you want to talk about an “angry god” without building a full-fledged angry AI to label behaviors as angry or not angry. So you derive the predictions, or look up the predictions made by ancient theologians without advance knowledge of our experimental results. If experiment conflicts with those predictions, then it is fair to speak of the religious claim having been scientifically refuted. It was given its just chance at confirmation; it is being excluded a posteriori, not a priori.

Ultimately, reductionism is just disbelief in fundamentally complicated things. If “fundamentally complicated” sounds like an oxymoron . . . well, that’s why I think that the doctrine of non-reductionism is a confusion, rather than a way that things could be, but aren’t. You would be wise to be wary, if you find yourself supposing such things.

But the ultimate rule of science is to look and see. If ever a God appeared to thunder upon the mountains, it would be something that people looked at and saw.

Corollary: Any supposed designer of Artificial General Intelligence who talks about religious beliefs in respectful tones is clearly not an expert on reducing mental things to nonmental things; and indeed knows so very little of the uttermost basics, as for it to be scarcely plausible that they could be expert at the art; unless their idiot savancy is complete. Or, of course, if they’re outright lying. We’re not talking about a subtle mistake.

228
Psychic Powers

In the last essay, I wrote:

If the “boring view” of reality is correct, then you can never predict anything irreducible because you are reducible. You can never get Bayesian confirmation for a hypothesis of irreducibility, because any prediction you can make is, therefore, something that could also be predicted by a reducible thing, namely your brain.

Benja Fallenstein commented:

I think that while you can in this case never devise an empirical test whose outcome could logically prove irreducibility, there is no clear reason to believe that you cannot devise a test whose counterfactual outcome in an irreducible world would make irreducibility subjectively much more probable (given an Occamian prior).

Without getting into reducibility/irreducibility, consider the scenario that the physical universe makes it possible to build a hypercomputer—that performs operations on arbitrary real numbers, for example—but that our brains do not actually make use of this: they can be simulated perfectly well by an ordinary Turing machine, thank you very much . . .

Well, that’s a very intelligent argument, Benja Fallenstein. But I have a crushing reply to your argument, such that, once I deliver it, you will at once give up further debate with me on this particular point:

You’re right.

Alas, I don’t get modesty credit on this one, because after publishing the last essay I realized a similar flaw on my own—this one concerning Occam’s Razor and psychic powers:

If beliefs and desires are irreducible and ontologically basic entities, or have an ontologically basic component not covered by existing science, that would make it far more likely that there was an ontological rule governing the interaction of different minds—an interaction which bypassed ordinary “material” means of communication like sound waves, known to existing science.

If naturalism is correct, then there exists a conjugate reductionist model that makes the same predictions as any concrete prediction that any parapsychologist can make about telepathy.

Indeed, if naturalism is correct, the only reason we can conceive of beliefs as “fundamental” is due to lack of self-knowledge of our own neurons—that the peculiar reflective architecture of our own minds exposes the “belief” class but hides the machinery behind it.

Nonetheless, the discovery of information transfer between brains, in the absence of any known material connection between them, is probabilistically a privileged prediction of supernatural models (those that contain ontologically basic mental entities). Just because it is so much simpler in that case to have a new law relating beliefs between different minds, compared to the “boring” model where beliefs are complex constructs of neurons.

The hope of psychic powers arises from treating beliefs and desires as sufficiently fundamental objects that they can have unmediated connections to reality. If beliefs are patterns of neurons made of known material, with inputs given by organs like eyes constructed of known material, and with outputs through muscles constructed of known material, and this seems sufficient to account for all known mental powers of humans, then there’s no reason to expect anything more—no reason to postulate additional connections. This is why reductionists don’t expect psychic powers. Thus, observing psychic powers would be strong evidence for the supernatural in Richard Carrier’s sense.

We have an Occam rule that counts the number of ontologically basic classes and ontologically basic laws in the model, and penalizes the count of entities. If naturalism is correct, then the attempt to count “belief” or the “relation between belief and reality” as a single basic entity is simply misguided anthropomorphism; we are only tempted to it by a quirk of our brain’s internal architecture. But if you just go with that misguided view, then it assigns a much higher probability to psychic powers than does naturalism, because you can implement psychic powers using apparently simpler laws.

Hence the actual discovery of psychic powers would imply that the human-naive Occam rule was in fact better-calibrated than the sophisticated naturalistic Occam rule. It would argue that reductionists had been wrong all along in trying to take apart the brain; that what our minds exposed as a seemingly simple lever was in fact a simple lever. The naive dualists would have been right from the beginning, which is why their ancient wish would have been enabled to come true.

So telepathy, and the ability to influence events just by wishing at them, and precognition, would all, if discovered, be strong Bayesian evidence in favor of the hypothesis that beliefs are ontologically fundamental. Not logical proof, but strong Bayesian evidence.

If reductionism is correct, then any science-fiction story containing psychic powers can be output by a system of simple elements (i.e., the story’s author’s brain); but if we in fact discover psychic powers, that would make it much more probable that events were occurring which could not in fact be described by reductionist models.

Which just goes to say: The existence of psychic powers is a privileged probabilistic assertion of non-reductionist worldviews—they own that advance prediction; they devised it and put it forth, in defiance of reductionist expectations. So by the laws of science, if psychic powers are discovered, non-reductionism wins.

I am therefore confident in dismissing psychic powers as a priori implausible, despite all the claimed experimental evidence in favor of them.

Part S
Quantum Physics and Many Worlds

229
Quantum Explanations

There’s a widespread belief that quantum mechanics is supposed to be confusing. This is not a good frame of mind for either a teacher or a student.

And I find that legendarily “confusing” subjects often are not really all that complicated as math, particularly if you just want a very basic—but still mathematical—grasp on what goes on down there.

I am not a physicist, and physicists famously hate it when non-professional-physicists talk about quantum mechanics. But I do have some experience with explaining mathy things that are allegedly “hard to understand.”

I wrote the Intuitive Explanation of Bayesian Reasoning because people were complaining that Bayes’s Theorem was “counterintuitive”—in fact it was famously counterintuitive—and this did not seem right. The equation just did not seem complicated enough to deserve the fearsome reputation it had. So I tried explaining it my way, and I did not manage to reach my original target of elementary school students, but I get frequent grateful emails from formerly confused folks ranging from reporters to outside academic college professors.

Besides, as a Bayesian, I don’t believe in phenomena that are inherently confusing. Confusion exists in our models of the world, not in the world itself. If a subject is widely known as confusing, not just difficult . . . you shouldn’t leave it at that. It doesn’t satisfice; it is not an okay place to be. Maybe you can fix the problem, maybe you can’t; but you shouldn’t be happy to leave students confused.

The first way in which my introduction is going to depart from the traditional, standard introduction to quantum mechanics, is that I am not going to tell you that quantum mechanics is supposed to be confusing.

I am not going to tell you that it’s okay for you to not understand quantum mechanics, because no one understands quantum mechanics, as Richard Feynman once claimed. There was a historical time when this was true, but we no longer live in that era.

I am not going to tell you: “You don’t understand quantum mechanics, you just get used to it.” (As von Neumann is reputed to have said; back in the dark decades when, in fact, no one did understand quantum mechanics.)

Explanations are supposed to make you less confused. If you feel like you don’t understand something, this indicates a problem—either with you, or your teacher—but at any rate a problem; and you should move to resolve the problem.

I am not going to tell you that quantum mechanics is weird, bizarre, confusing, or alien. Quantum mechanics is counterintuitive, but that is a problem with your intuitions, not a problem with quantum mechanics. Quantum mechanics has been around for billions of years before the Sun coalesced from interstellar hydrogen. Quantum mechanics was here before you were, and if you have a problem with that, you are the one who needs to change. Quantum mechanics sure won’t. There are no surprising facts, only models that are surprised by facts; and if a model is surprised by the facts, it is no credit to that model.

It is always best to think of reality as perfectly normal. Since the beginning, not one unusual thing has ever happened.

The goal is to become completely at home in a quantum universe. Like a native. Because, in fact, that is where you live.

In the coming sequence on quantum mechanics, I am going to consistently speak as if quantum mechanics is perfectly normal; and when human intuitions depart from quantum mechanics, I am going to make fun of the intuitions for being weird and unusual. This may seem odd, but the point is to swing your mind around to a native quantum point of view.

Another thing: The traditional introduction to quantum mechanics closely follows the order in which quantum mechanics was discovered.

The traditional introduction starts by saying that matter sometimes behaves like little billiard balls bopping around, and sometimes behaves like crests and troughs moving through a pool of water. Then the traditional introduction gives some examples of matter acting like a little billiard ball, and some examples of it acting like an ocean wave.

Now, it happens to be a historical fact that, back when students of matter were working all this stuff out and had no clue about the true underlying math, those early scientists first thought that matter was like little billiard balls. And then that it was like waves in the ocean. And then that it was like billiard balls again. And then the early scientists got really confused, and stayed that way for several decades, until it was finally sorted out in the second half of the twentieth century.

Dragging a modern-day student through all this may be a historically realistic approach to the subject matter, but it also ensures the historically realistic outcome of total bewilderment. Talking to aspiring young physicists about “wave/particle duality” is like starting chemistry students on the Four Elements.

An electron is not a billiard ball, and it’s not a crest and trough moving through a pool of water. An electron is a mathematically different sort of entity, all the time and under all circumstances, and it has to be accepted on its own terms.

The universe is not wavering between using particles and waves, unable to make up its mind. It’s only human intuitions about quantum mechanics that swap back and forth. The intuitions we have for billiard balls, and the intuitions we have for crests and troughs in a pool of water, both look sort of like they’re applicable to electrons, at different times and under different circumstances. But the truth is that both intuitions simply aren’t applicable.

If you try to think of an electron as being like a billiard ball on some days, and like an ocean wave on other days, you will confuse the living daylights out of yourself.

Yet it’s your eyes that are wobbling and unstable, not the world.

Furthermore:

The order in which humanity discovered things is not necessarily the best order in which to teach them. First, humanity noticed that there were other animals running around. Then we cut them open and found that they were full of organs. Then we examined the organs carefully and found they were made of tissues. Then we looked at the tissues under a microscope and discovered cells, which are made of proteins and some other chemically synthesized stuff. Which are made of molecules, which are made of atoms, which are made of protons and neutrons and electrons which are way simpler than entire animals but were discovered tens of thousands of years later.

Physics doesn’t start by talking about biology. So why should it start by talking about very high-level complicated phenomena, like, say, the observed results of experiments?

The ordinary way of teaching quantum mechanics keeps stressing the experimental results. Now I do understand why that sounds nice from a rationalist perspective. Believe me, I understand.

But it seems to me that the upshot is dragging in big complicated mathematical tools that you need to analyze real-world situations, before the student understands what fundamentally goes on in the simplest cases.

It’s like trying to teach programmers how to write concurrent multithreaded programs before they know how to add two variables together, because concurrent multithreaded programs are closer to everyday life. Being close to everyday life is not always a strong recommendation for what to teach first.

Maybe the monomaniacal focus on experimental observations made sense in the dark decades when no one understood what was fundamentally going on, and you couldn’t start there, and all your models were just mysterious maths that gave good experimental predictions . . . you can still find this view of quantum physics presented in many books . . . but maybe today it’s worth trying a different angle? The result of the standard approach is standard confusion.

The classical world is strictly implicit in the quantum world, but seeing from a classical perspective makes everything bigger and more complicated. Everyday life is a higher level of organization, like molecules versus quarks—huge catalogue of molecules, six quarks. I think it is worth trying to teach from the perspective of the quantum world first, and talking about classical experimental results afterward.

I am not going to start with the normal classical world and then talk about a bizarre quantum backdrop hidden behind the scenes. The quantum world is the scene and it defines normality.

I am not going to talk as if the classical world is real life, and occasionally the classical world transmits a request for an experimental result to a quantum-physics server, and the quantum-physics server does some peculiar calculations and transmits back a classical experimental result. I am going to talk as if the quantum world is the really real and the classical world something far away. Not just because that makes it easier to be a native of a quantum universe, but because, at a core level, it’s the truth.

Finally, I am going to take a strictly realist perspective on quantum mechanics—the quantum world is really out there, our equations describe the territory and not our maps of it, and the classical world only exists implicitly within the quantum one. I am not going to discuss non-realist views in the early stages of my introduction, except to say why you should not be confused by certain intuitions that non-realists draw upon for support. I am not going to apologize for this, and I would like to ask any non-realists on the subject of quantum mechanics to wait and hold their comments until called for in a later essay. Do me this favor, please. I think non-realism is one of the main things that confuses prospective students, and prevents them from being able to concretely visualize quantum phenomena. I will discuss the issues explicitly in a future essay.

But everyone should be aware that, even though I’m not going to discuss the issue at first, there is a sizable community of scientists who dispute the realist perspective on quantum mechanics. Myself, I don’t think it’s worth figuring both ways; I’m a pure realist, for reasons that will become apparent. But if you read my introduction, you are getting my view. It is not only my view. It is probably the majority view among theoretical physicists, if that counts for anything (though I will argue the matter separately from opinion polls). Still, it is not the only view that exists in the modern physics community. I do not feel obliged to present the other views right away, but I feel obliged to warn my readers that there are other views, which I will not be presenting during the initial stages of the introduction.

To sum up, my goal will be to teach you to think like a native of a quantum universe, not a reluctant tourist.

Embrace reality. Hug it tight.

230
Configurations and Amplitude

So the universe isn’t made of little billiard balls, and it isn’t made of crests and troughs in a pool of aether . . . Then what is the stuff that stuff is made of?

Figure 230.1

In Figure 230.1, we see, at A, a half-silvered mirror, and two photon detectors, Detector 1 and Detector 2.

Early scientists, when they ran experiments like this, became confused about what the results meant. They would send a photon toward the half-silvered mirror, and half the time they would see Detector 1 click, and the other half of the time they would see Detector 2 click.

The early scientists—you’re going to laugh at this—thought that the silver mirror deflected the photon half the time, and let it through half the time.

Ha, ha! As if the half-silvered mirror did different things on different occasions! I want you to let go of this idea, because if you cling to what early scientists thought, you will become extremely confused. The half-silvered mirror obeys the same rule every time.

If you were going to write a computer program that was this experiment—not a computer program that predicted the result of the experiment, but a computer program that resembled the underlying reality—it might look sort of like this:

At the start of the program (the start of the experiment, the start of time) there’s a certain mathematical entity, called a configuration. You can think of this configuration as corresponding to “there is one photon heading from the photon source toward the half-silvered mirror,” or just “a photon heading toward A.”

A configuration can store a single complex value—“complex” as in the complex numbers (a + bi), with i defined as √-1. At the start of the program, there’s already a complex number stored in the configuration “a photon heading toward A.” The exact value doesn’t matter so long as it’s not zero. We’ll let the configuration “a photon heading toward A” have a value of (-1 + 0i).

All this is a fact within the territory, not a description of anyone’s knowledge. A configuration isn’t a proposition or a possible way the world could be. A configuration is a variable in the program—you can think of it as a kind of memory location whose index is “a photon heading toward A”—and it’s out there in the territory.

As the complex numbers that get assigned to configurations are not positive real numbers between 0 and 1, there is no danger of confusing them with probabilities. “A photon heading toward A” has complex value -1, which is hard to see as a degree of belief. The complex numbers are values within the program, again out there in the territory. We’ll call the complex numbers amplitudes.

There are two other configurations, which we’ll call “a photon going from A to Detector 1” and “a photon going from A to Detector 2.” These configurations don’t have a complex value yet; it gets assigned as the program runs.

We are going to calculate the amplitudes of “a photon going from A toward 1” and “a photon going from A toward 2” using the value of “a photon going toward A,” and the rule that describes the half-silvered mirror at A.

Roughly speaking, the half-silvered mirror rule is “multiply by 1 when the photon goes straight, and multiply by i when the photon turns at a right angle.” This is the universal rule that relates the amplitude of the configuration of “a photon going in,” to the amplitude that goes to the configurations of “a photon coming out straight” or “a photon being deflected.”¹

So we pipe the amplitude of the configuration “a photon going toward A,” which is (-1 + 0i), into the half-silvered mirror at A, and this transmits an amplitude of (-1 + 0i) × i = (0 -i) to “a photon going from A toward 1,” and also transmits an amplitude of (-1 + 0i) × 1 = (-1 + 0i) to “a photon going from A toward 2.”

In the Figure 230.1 experiment, these are all the configurations and all the transmitted amplitude we need to worry about, so we’re done. Or, if you want to think of “Detector 1 gets a photon” and “Detector 2 gets a photon” as separate configurations, they’d just inherit their values from “A to 1” and “A to 2” respectively. (Actually, the values inherited should be multiplied by another complex factor, corresponding to the distance from A to the detector; but we will ignore that for now, and suppose that all distances traveled in our experiments happen to correspond to a complex factor of 1.)

So the final program state is:

Configuration “a photon going toward A”: (-1 + 0i)

Configuration “a photon going from A toward 1”: (0 - i)

Configuration “a photon going from A toward 2”: (-1 + 0i)

and optionally

Configuration “Detector 1 gets a photon”: (0 - i)

Configuration “Detector 2 gets a photon”: (-1 + 0i) .

This same result occurs—the same amplitudes stored in the same configurations—every time you run the program (every time you do the experiment).

Now, for complicated reasons that we aren’t going to go into here—considerations that belong on a higher level of organization than fundamental quantum mechanics, the same way that atoms are more complicated than quarks—there’s no simple measuring instrument that can directly tell us the exact amplitudes of each configuration. We can’t directly see the program state.

So how do physicists know what the amplitudes are?

We do have a magical measuring tool that can tell us the squared modulus of a configuration’s amplitude. If the original complex amplitude is (a + bi), we can get the positive real number (a² + b²). Think of the Pythagorean theorem: if you imagine the complex number as a little arrow stretching out from the origin on a two-dimensional plane, then the magic tool tells us the squared length of the little arrow, but it doesn’t tell us the direction the arrow is pointing.

To be more precise, the magic tool actually just tells us the ratios of the squared lengths of the amplitudes in some configurations. We don’t know how long the arrows are in an absolute sense, just how long they are relative to each other. But this turns out to be enough information to let us reconstruct the laws of physics—the rules of the program. And so I can talk about amplitudes, not just ratios of squared moduli.

When we wave the magic tool over “Detector 1 gets a photon” and “Detector 2 gets a photon,” we discover that these configurations have the same squared modulus—the lengths of the arrows are the same. Thus speaks the magic tool. By doing more complicated experiments (to be seen shortly), we can tell that the original complex numbers had a ratio of i to 1.

And what is this magical measuring tool?

Well, from the perspective of everyday life—way, way, way above the quantum level and a lot more complicated—the magical measuring tool is that we send some photons toward the half-silvered mirror, one at a time, and count up how many photons arrive at Detector 1 versus Detector 2 over a few thousand trials. The ratio of these values is the ratio of the squared moduli of the amplitudes. But the reason for this is not something we are going to consider yet. Walk before you run. It is not possible to understand what happens all the way up at the level of everyday life, before you understand what goes on in much simpler cases.

For today’s purposes, we have a magical squared-modulus-ratio reader. And the magic tool tells us that the little two-dimensional arrow for the configuration “Detector 1 gets a photon” has the same squared length as for “Detector 2 gets a photon.” That’s all.

You may wonder, “Given that the magic tool works this way, what motivates us to use quantum theory, instead of thinking that the half-silvered mirror reflects the photon around half the time?”

Well, that’s just begging to be confused—putting yourself into a historically realistic frame of mind like that and using everyday intuitions. Did I say anything about a little billiard ball going one way or the other and possibly bouncing off a mirror? That’s not how reality works. Reality is about complex amplitudes flowing between configurations, and the laws of the flow are stable.

But if you insist on seeing a more complicated situation that billiard-ball ways of thinking can’t handle, here’s a more complicated experiment.

Figure 230.2

In Figure 230.2, B and C are full mirrors, and A and D are half-mirrors. The line from D to E is dashed for reasons that will become apparent, but amplitude is flowing from D to E under exactly the same laws.

Now let’s apply the rules we learned before:

At the beginning of time “a photon heading toward A” has amplitude (-1 + 0i).

We proceed to compute the amplitude for the configurations “a photon going from A to B” and “a photon going from A to C”:

“a photon going from A to B” = i × “a photon heading toward A” = (0 − i).

Similarly,

“a photon going from A to C” = 1 × “a photon heading toward A” = (−1 + 0i).

The full mirrors behave (as one would expect) like half of a half-silvered mirror—a full mirror just bends things by right angles and multiplies them by i. (To state this slightly more precisely: For a full mirror, the amplitude that flows, from the configuration of a photon heading in, to the configuration of a photon heading out at a right angle, is multiplied by a factor of i.)

So:

“a photon going from B to D” = i × “a photon going from A to B” = (1 + 0i),

“a photon going from C to D” = i × “a photon going from A to C” = (0 − i).

“B to D” and “C to D” are two different configurations—we don’t simply write “a photon at D”—because the photons are arriving at two different angles in these two different configurations. And what D does to a photon depends on the angle at which the photon arrives.

Again, the rule (speaking loosely) is that when a half-silvered mirror bends light at a right angle, the amplitude that flows from the photon-going-in configuration to the photon-going-out configuration, is the amplitude of the photon-going-in configuration multiplied by i. And when two configurations are related by a half-silvered mirror letting light straight through, the amplitude that flows from the photon-going-in configuration is multiplied by 1.

So:

From the configuration “a photon going from B to D,” with original amplitude (1 + 0i):
- Amplitude of (1 + 0i) × i = (0 + i) flows to “a photon going from D to E.”
- Amplitude of (1 + 0i) × 1 = (1 + 0i) flows to “a photon going from D to F.”
From the configuration “a photon going from C to D,” with original amplitude (0 - i):
- Amplitude of (0 -i) × i = (1 + 0i) flows to “a photon going from D to F.”
- Amplitude of (0 - i) × 1 = (0 - i) flows to “a photon going from D to E.”

Therefore:

The total amplitude flowing to configuration “a photon going from D to E” is (0 + i) + (0 - i) = (0 + 0i) = 0.
The total amplitude flowing to configuration “a photon going from D to F” is (1 + 0i) + (1 + 0i) = (2 + 0i).

(You may want to try working this out yourself on pen and paper if you lost track at any point.)

But the upshot, from that super-high-level “experimental” perspective that we think of as normal life, is that we see no photons detected at E. Every photon seems to end up at F. The ratio of squared moduli between “D to E” and “D to F” is 0 to 4. That’s why the line from D to E is dashed, in this figure.

This is not something it is possible to explain by thinking of half-silvered mirrors deflecting little incoming billiard balls half the time. You’ve got to think in terms of amplitude flows.

If half-silvered mirrors deflected a little billiard ball half the time, in this setup, the little ball would end up at Detector 1 around half the time and Detector 2 around half the time. Which it doesn’t. So don’t think that.

You may say, “But wait a minute! I can think of another hypothesis that accounts for this result. What if, when a half-silvered mirror reflects a photon, it does something to the photon that ensures it doesn’t get reflected next time? And when it lets a photon go through straight, it does something to the photon so it gets reflected next time.”

Now really, there’s no need to go making the rules so complicated. Occam’s Razor, remember. Just stick with simple, normal amplitude flows between configurations.

But if you want another experiment that disproves your new alternative hypothesis, it’s Figure 230.3.

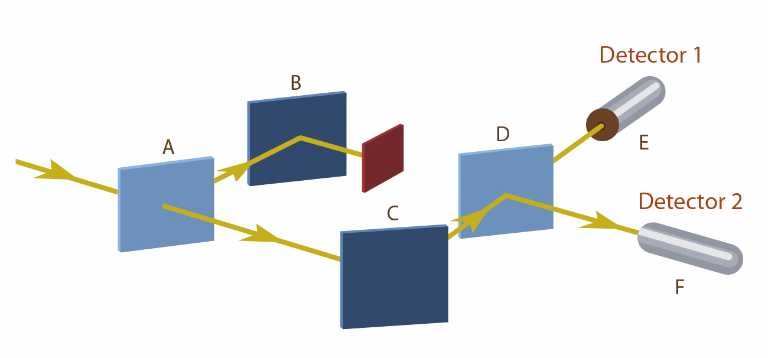
Figure 230.3

Here, we’ve left the whole experimental setup the same, and just put a little blocking object between B and D. This ensures that the amplitude of “a photon going from B to D” is 0.

Once you eliminate the amplitude contributions from that configuration, you end up with totals of (1 + 0i) in “a photon going from D to F,” and (0 -i) in “a photon going from D to E.”

The squared moduli of (1 + 0i) and (0 - i) are both 1, so the magic measuring tool should tell us that the ratio of squared moduli is 1. Way back up at the level where physicists exist, we should find that Detector 1 goes off half the time, and Detector 2 half the time.

The same thing happens if we put the block between C and D. The amplitudes are different, but the ratio of the squared moduli is still 1, so Detector 1 goes off half the time and Detector 2 goes off half the time.

This cannot possibly happen with a little billiard ball that either does or doesn’t get reflected by the half-silvered mirrors.

Because complex numbers can have opposite directions, like 1 and -1, or i and -i, amplitude flows can cancel each other out. Amplitude flowing from configuration X into configuration Y can be canceled out by an equal and opposite amplitude flowing from configuration Z into configuration Y. In fact, that’s exactly what happens in this experiment.

In probability theory, when something can either happen one way or another, X or ¬X, then P(Z) = P(Z|X)P(X) + P(Z|¬X)P(¬X). And all probabilities are positive. So if you establish that the probability of Z happening given X is 1∕2, and the probability of X happening is 1∕3, then the total probability of Z happening is at least 1∕6 no matter what goes on in the case of ¬X. There’s no such thing as negative probability, less-than-impossible credence, or (0 + i) credibility, so degrees of belief can’t cancel each other out like amplitudes do.

Not to mention that probability is in the mind to begin with; and we are talking about the territory, the program-that-is-reality, not talking about human cognition or states of partial knowledge.

By the same token, configurations are not propositions, not statements, not ways the world could conceivably be. Configurations are not semantic constructs. Adjectives like probable do not apply to them; they are not beliefs or sentences or possible worlds. They are not true or false but simply real.

In the experiment of Figure 230.2, do not be tempted to think anything like: “The photon goes to either B or C, but it could have gone the other way, and this possibility interferes with its ability to go to E . . .”

It makes no sense to think of something that “could have happened but didn’t” exerting an effect on the world. We can imagine things that could have happened but didn’t—like thinking, “Gosh, that car almost hit me”—and our imagination can have an effect on our future behavior. But the event of imagination is a real event, that actually happens, and that is what has the effect. It’s your imagination of the unreal event—your very real imagination, implemented within a quite physical brain—that affects your behavior.

To think that the actual event of a car hitting you—this event which could have happened to you, but in fact didn’t—is directly exerting a causal effect on your behavior, is mixing up the map with the territory.

What affects the world is real. (If things can affect the world without being “real,” it’s hard to see what the word “real” means.) Configurations and amplitude flows are causes, and they have visible effects; they are real. Configurations are not possible worlds and amplitudes are not degrees of belief, any more than your chair is a possible world or the sky is a degree of belief.

So what is a configuration, then?

Well, you’ll be getting a clearer idea of that in later essays.

But to give you a quick idea of how the real picture differs from the simplified version we saw in this essay . . .

Our experimental setup only dealt with one moving particle, a single photon. Real configurations are about multiple particles. The next essay will deal with the case of more than one particle, and that should give you a much clearer idea of what a configuration is.

Each configuration we talked about should have described a joint position of all the particles in the mirrors and detectors, not just the position of one photon bopping around.

In fact, the really real configurations are over joint positions of all the particles in the universe, including the particles making up the experimenters. You can see why I’m saving the notion of experimental results for later essays.

In the real world, amplitude is a continuous distribution over a continuous space of configurations. This essay’s “configurations” were blocky and digital, and so were our “amplitude flows.” It was as if we were talking about a photon teleporting from one place to another.

If none of that made sense, don’t worry. It will be cleared up in later essays. Just wanted to give you some idea of where this was heading.

1. Editor’s Note: Strictly speaking, a standard half-silvered mirror would yield a rule “multiply by -1 when the photon turns at a right angle,” not “multiply by i.” The basic scenario described by the author is not physically impossible, and its use does not affect the substantive argument. However, physics students may come away confused if they compare the discussion here to textbook discussions of Mach–Zehnder interferometers. We’ve left this idiosyncrasy in the text because it eliminates any need to specify which side of the mirror is half-silvered, simplifying the experiment.

231
Joint Configurations

The key to understanding configurations, and hence the key to understanding quantum mechanics, is realizing on a truly gut level that configurations are about more than one particle.

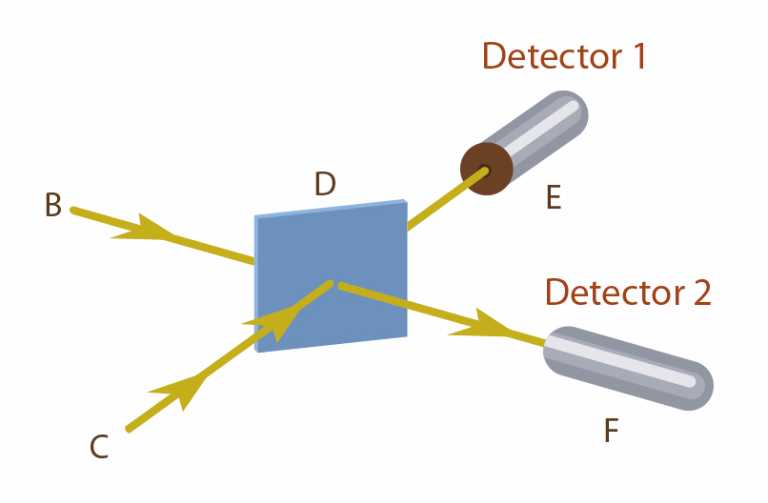
Figure 231.1

Continuing from the previous essay, Figure 231.1 shows an altered version of the experiment where we send in two photons toward D at the same time, from the sources B and C.

The starting configuration then is:

“a photon going from B to D,
and a photon going from C to D.”

Again, let’s say the starting configuration has amplitude (-1 + 0i).

And remember, the rule of the half-silvered mirror (at D) is that a right-angle deflection multiplies by i, and a straight line multiplies by 1.

So the amplitude flows from the starting configuration, separately considering the four cases of deflection/non-deflection of each photon, are:

The “B to D” photon is deflected and the “C to D” photon is deflected. This amplitude flows to the configuration “a photon going from D to E, and a photon going from D to F.” The amplitude flowing is (-1 + 0i) × i × i = (1 + 0i).
The “B to D” photon is deflected and the “C to D” photon goes straight. This amplitude flows to the configuration “two photons going from D to E.” The amplitude flowing is (-1 + 0i) × i × 1 = (0 - i).
The “B to D” photon goes straight and the “C to D” photon is deflected. This amplitude flows to the configuration “two photons going from D to F.” The amplitude flowing is (-1 + 0i) × 1 × i = (0 - i).
The “B to D” photon goes straight and the “C to D” photon goes straight. This amplitude flows to the configuration “a photon going from D to F, and a photon going from D to E.” The amplitude flowing is (-1 + 0i) × 1 × 1 = (-1 + 0i).

Now—and this is a very important and fundamental idea in quantum mechanics—the amplitudes in cases 1 and 4 are flowing to the same configuration. Whether the B photon and C photon both go straight, or both are deflected, the resulting configuration is one photon going toward E and another photon going toward F.

So we add up the two incoming amplitude flows from case 1 and case 4, and get a total amplitude of (1 + 0i) + (-1 + 0i) = 0.

When we wave our magic squared-modulus-ratio reader over the three final configurations, we’ll find that “two photons at Detector 1” and “two photons at Detector 2” have the same squared modulus, but “a photon at Detector 1 and a photon at Detector 2” has squared modulus zero.

Way up at the level of experiment, we never find Detector 1 and Detector 2 both going off. We’ll find Detector 1 going off twice, or Detector 2 going off twice, with equal frequency. (Assuming I’ve gotten the math and physics right. I didn’t actually perform the experiment.)

The configuration’s identity is not, “the B photon going toward E and the C photon going toward F.” Then the resultant configurations in case 1 and case 4 would not be equal. Case 1 would be, “B photon to E, C photon to F” and case 4 would be “B photon to F, C photon to E.” These would be two distinguishable configurations, if configurations had photon-tracking structure.

So we would not add up the two amplitudes and cancel them out. We would keep the amplitudes in two separate configurations. The total amplitudes would have non-zero squared moduli. And when we ran the experiment, we would find (around half the time) that Detector 1 and Detector 2 each registered one photon. Which doesn’t happen, if my calculations are correct.

Configurations don’t keep track of where particles come from. A configuration’s identity is just, “a photon here, a photon there; an electron here, an electron there.” No matter how you get into that situation, so long as there are the same species of particles in the same places, it counts as the same configuration.

I say again that the question “What kind of information does the configuration’s structure incorporate?” has experimental consequences. You can deduce, from experiment, the way that reality itself must be treating configurations.

In a classical universe, there would be no experimental consequences. If the photon were like a little billiard ball that either went one way or the other, and the configurations were our beliefs about possible states the system could be in, and instead of amplitudes we had probabilities, it would not make a difference whether we tracked the origin of photons or threw the information away.

In a classical universe, I could assign a 25% probability to both photons going to E, a 25% probability of both photons going to F, a 25% probability of the B photon going to E and the C photon going to F, and 25% probability of the B photon going to F and the C photon going to E. Or, since I personally don’t care which of the two latter cases occurred, I could decide to collapse the two possibilities into one possibility and add up their probabilities, and just say, “a 50% probability that each detector gets one photon.”

With probabilities, we can aggregate events as we like—draw our boundaries around sets of possible worlds as we please—and the numbers will still work out the same. The probability of two mutually exclusive events always equals the probability of the first event plus the probability of the second event.

But you can’t arbitrarily collapse configurations together, or split them apart, in your model, and get the same experimental predictions. Our magical tool tells us the ratios of squared moduli. When you add two complex numbers, the squared modulus of the sum is not the sum of the squared moduli of the parts:

Squared_Modulus(C1 + C2) ≠ Squared_Modulus(C1) + Squared_Modulus(C2).

E.g.:

S_M((2 + i) + (1 − i)) = S_M(3 + 0i)
= 3² + 0²
= 9,

S_M(2 + i) + S_M(1 − i) = (2² + 1²)+ ( 1² + (-1)²)
= (4 + 1) + (1 + 1)
= 7.

Or in the current experiment of discourse, we had flows of (1 + 0i) and (-1 + 0i) cancel out, adding up to 0, whose squared modulus is 0, where the squared modulus of the parts would have been 1 and 1.

If in place of Squared_Modulus, our magical tool was some linear function—any function where F(X + Y) = F(X) + F(Y)—then all the quantumness would instantly vanish and be replaced by a classical physics. (A different classical physics, not the same illusion of classicality we hallucinate from inside the higher levels of organization in our own quantum world.)

If amplitudes were just probabilities, they couldn’t cancel out when flows collided. If configurations were just states of knowledge, you could reorganize them however you liked.

But the configurations are nailed in place, indivisible and unmergeable without changing the laws of physics.

And part of what is nailed is the way that configurations treat multiple particles. A configuration says, “a photon here, a photon there,” not “this photon here, that photon there.” “This photon here, that photon there” does not have a different identity from “that photon here, this photon there.”

The result, visible in today’s experiment, is that you can’t factorize the physics of our universe to be about particles with individual identities.

Part of the reason why humans have trouble coming to grips with perfectly normal quantum physics, is that humans bizarrely keep trying to factor reality into a sum of individually real billiard balls.

Ha ha! Silly humans.

232
Distinct Configurations

The experiment in the previous essay carried two key lessons:

First, we saw that because amplitude flows can cancel out, and because our magic measure of squared modulus is not linear, the identity of configurations is nailed down—you can’t reorganize configurations the way you can regroup possible worlds. Which configurations are the same, and which are distinct, has experimental consequences; it is an observable fact.

Second, we saw that configurations are about multiple particles. If there are two photons entering the apparatus, that doesn’t mean there are two initial configurations. Instead the initial configuration’s identity is “two photons coming in.” (Ideally, each configuration we talk about would include every particle in the experiment—including the particles making up the mirrors and detectors. And in the real universe, every configuration is about all the particles . . . everywhere.)

What makes for distinct configurations is not distinct particles. Each configuration is about every particle. What makes configurations distinct is particles occupying different positions—at least one particle in a different state.

To take one important demonstration . . .

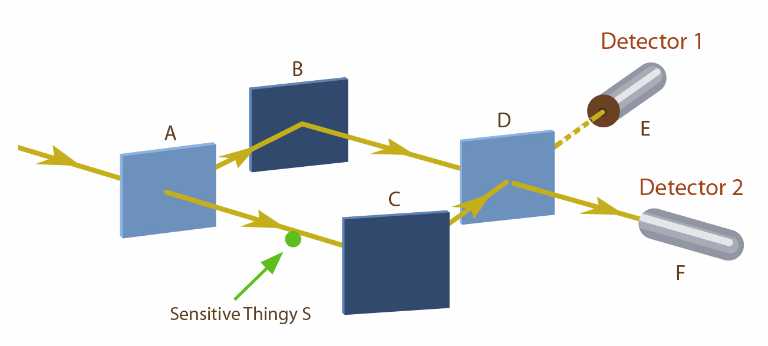
Figure 232.1

Figure 232.1 is the same experiment as Figure 230.2, with one important change: Between A and C has been placed a sensitive thingy, S. The key attribute of S is that if a photon goes past S, then S ends up in a slightly different state.

Let’s say that the two possible states of S are Yes and No. The sensitive thingy S starts out in state No, and ends up in state Yes if a photon goes past.

Then the initial configuration is:

“photon heading toward A; and S in state No,” (-1 + 0i) .

Next, the action of the half-silvered mirror at A. In the previous version of this experiment, without the sensitive thingy, the two resultant configurations were “A to B” with amplitude -i and “A to C” with amplitude -1. Now, though, a new element has been introduced into the system, and all configurations are about all particles, and so every configuration mentions the new element. So the amplitude flows from the initial configuration are to:

“photon from A to B; and S in state No,” (0 - i)

“photon from A to C; and S in state Yes,” (-1 + 0i) .

Next, the action of the full mirrors at B and C:

“photon from B to D; and S in state No,” (1 + 0i)

“photon from C to D; and S in state Yes,” (0 - i) .

And then the action of the half-mirror at D, on the amplitude flowing from both of the above configurations:

“photon from D to E; and S in state No,” (0 + i)
“photon from D to F; and S in state No,” (1 + 0i)
“photon from D to E; and S in state Yes,” (0 - i)
“photon from D to F; and S in state Yes,” (1 + 0i) .

When we did this experiment without the sensitive thingy, the amplitude flows (1) and (3) of (0 + i) and (0 - i) to the “D to E” configuration canceled each other out. We were left with no amplitude for a photon going to Detector 1 (way up at the experimental level, we never observe a photon striking Detector 1).

But in this case, the two amplitude flows (1) and (3) are now to distinct configurations; at least one entity, S, is in a different state between (1) and (3). The amplitudes don’t cancel out.

When we wave our magical squared-modulus-ratio detector over the four final configurations, we find that the squared moduli of all are equal: 25% probability each. Way up at the level of the real world, we find that the photon has an equal chance of striking Detector 1 and Detector 2.

All the above is true, even if we, the researchers, don’t care about the state of S. Unlike possible worlds, configurations cannot be regrouped on a whim. The laws of physics say the two configurations are distinct; it’s not a question of how we can most conveniently parse up the world.

All the above is true, even if we don’t bother to look at the state of S. The configurations (1) and (3) are distinct in physics, even if we don’t know the distinction.

All the above is true, even if we don’t know S exists. The configurations (1) and (3) are distinct whether or not we have distinct mental representations for the two possibilities.

All the above is true, even if we’re in space, and S transmits a new photon off toward the interstellar void in two distinct directions, depending on whether the photon of interest passed it or not. So that we couldn’t ever find out whether S had been in Yes or No. The state of S would be embodied in the photon transmitted off to nowhere. The lost photon can be an implied invisible, and the state of S pragmatically undetectable; but the configurations are still distinct.

(The main reason it wouldn’t work, is if S were nudged, but S had an original spread in configuration space that was larger than the nudge. Then you couldn’t rely on the nudge to separate the amplitude distribution over configuration space into distinct lumps. In reality, all this takes place within a differentiable amplitude distribution over a continuous configuration space.)

Configurations are not belief states. Their distinctness is an objective fact with experimental consequences. The configurations are distinct even if no one knows the state of S; distinct even if no intelligent entity can ever find out. The configurations are distinct so long as at least one particle in the universe anywhere is in a different position. This is experimentally demonstrable.

Why am I emphasizing this? Because back in the dark ages when no one understood quantum physics . . .

Figure 232.2

Okay, so imagine that you’ve got no clue what’s really going on, and you try the experiment in Figure 232.2, and no photons show up at Detector 1. Cool.

You also discover that when you put a block between B and D, or a block between A and C, photons show up at Detector 1 and Detector 2 in equal proportions. But only one at a time—Detector 1 or Detector 2 goes off, not both simultaneously.

So, yes, it does seem to you like you’re dealing with a particle—the photon is only in one place at one time, every time you see it.

And yet there’s some kind of . . . mysterious phenomenon . . . that prevents the photon from showing up in Detector 1. And this mysterious phenomenon depends on the photon being able to go both ways. Even though the photon only shows up in one detector or the other, which shows, you would think, that the photon is only in one place at a time.

Figure 232.3

Which makes the whole pattern of the experiments seem pretty bizarre! After all, the photon either goes from A to C, or from A to B; one or the other. (Or so you would think, if you were instinctively trying to break reality down into individually real particles.) But when you block off one course or the other, as in Figure 232.3, you start getting different experimental results!

It’s like the photon wants to be allowed to go both ways, even though (you would think) it only goes one way or the other. And it can tell if you try to block it off, without actually going there—if it’d gone there, it would have run into the block, and not hit any detector at all.

It’s as if mere possibilities could have causal effects, in defiance of what the word “real” is usually thought to mean . . .

But it’s a bit early to jump to conclusions like that, when you don’t have a complete picture of what goes on inside the experiment.

Figure 232.4

So it occurs to you to put a sensor between A and C, like in Figure 232.4, so you can tell which way the photon really goes on each occasion.

And the mysterious phenomenon goes away.

I mean, now how crazy is that? What kind of paranoia does that inspire in some poor scientist?

Okay, so in the twenty-first century we realize in order to “know” a photon’s history, the particles making up your brain have to be correlated with the photon’s history. If having a tiny little sensitive thingy S that correlates to the photon’s history is enough to distinguish the final configurations and prevent the amplitude flows from canceling, then an entire sensor with a digital display, never mind a human brain, will put septillions of particles in different positions and prevent the amplitude flows from canceling.

But if you hadn’t worked that out yet . . .

Then you would ponder the sensor having banished the Mysterious Phenomenon, and think:

The photon doesn’t just want to be physically free to go either way. It’s not a little wave going along an unblocked pathway, because then just having a physically unblocked pathway would be enough.

No . . . I’m not allowed to know which way the photon went.

The mysterious phenomenon . . . doesn’t want me looking at it too closely . . . while it’s doing its mysterious thing.

It’s not physical possibilities that have an effect on reality . . . only epistemic possibilities. If I know which way the photon went, it’s no longer plausible that it went the other way . . . which cuts off the mysterious phenomenon as effectively as putting a block between B and D.

I have to not observe which way the photon went, in order for it to always end up at Detector 2. It has to be reasonable that the photon could have gone to either B or C. What I can know is the determining factor, regardless of which physical paths I leave open or closed.

STOP THE PRESSES! MIND IS FUNDAMENTAL AFTER ALL! CONSCIOUS AWARENESS DETERMINES OUR EXPERIMENTAL RESULTS!

You can still read this kind of stuff. In physics textbooks. Even now, when a majority of theoretical physicists know better. Stop the presses. Please, stop the presses.

Hindsight is 20/20; and so it’s easy to say that, in hindsight, there were certain clues that this interpretation was not correct.

Like, if you put the sensor between A and C but don’t read it, the mysterious phenomenon still goes away, and the photon still sometimes ends up at Detector 1. (Oh, but you could have read it, and possibilities are real now . . .)

But it doesn’t even have to be a sensor, a scientific instrument that you built. A single particle that gets nudged far enough will dispel the interference. A photon radiating off to where you’ll never see it again can do the trick. Not much human involvement there. Not a whole lot of conscious awareness.

Maybe before you pull the dualist fire alarm on human brains being physically special, you should provide experimental proof that a rock can’t play the same role in dispelling the Mysterious Phenomenon as a human researcher?

But that’s hindsight, and it’s easy to call the shots in hindsight. Do you really think you could’ve done better than John von Neumann, if you’d been alive at the time? The point of this kind of retrospective analysis is to ask what kind of fully general clues you could have followed, and whether there are any similar clues you’re ignoring now on current mysteries.

Though it is a little embarrassing that even after the theory of amplitudes and configurations had been worked out—with the theory now giving the definite prediction that any nudged particle would do the trick—early scientists still didn’t get it.

But you see . . . it had been established as Common Wisdom that configurations were possibilities, it was epistemic possibility that mattered, amplitudes were a very strange sort of partial information, and conscious observation made quantumness go away. And that it was best to avoid thinking too hard about the whole business, so long as your experimental predictions came out right.

233
Collapse Postulates

Macroscopic decoherence—also known as “many-worlds”—is the idea that the known quantum laws that govern microscopic events simply govern at all levels without alteration. Back when people didn’t know about decoherence—before it occurred to anyone that the laws deduced with such precision for microscopic physics might apply universally—what did people think was going on?

The initial reasoning seems to have gone something like:

When my calculations showed an amplitude of (-1∕3)i for this photon to get absorbed, my experimental statistics showed that the photon was absorbed around 107 times out of 1,000, which is a good fit to 1∕9, the square of the modulus.

The amplitude is the probability (by way of the squared modulus).

Once you measure something and know it didn’t happen, its probability goes to zero.

Read literally, this implies that knowledge itself—or even conscious awareness—causes the collapse. Which was in fact the form of the theory put forth by Werner Heisenberg!

But people became increasingly nervous about the notion of importing dualistic language into fundamental physics—as well they should have been! And so the original reasoning was replaced by the notion of an objective “collapse” that destroyed all parts of the wavefunction except one, and was triggered sometime before superposition grew to human-sized levels.

Now, once you’re supposing that parts of the wavefunction can just vanish, you might think to ask:

Is there only one survivor? Maybe there are many surviving worlds, but they survive with a frequency determined by their integrated squared modulus, and so the typical surviving world has experimental statistics that match the Born rule.

Yet collapse theories considered in modern academia only postulate one surviving world. Why?

Collapse theories were devised in a time when it simply didn’t occur to any physicists that more than one world could exist! People took for granted that measurements had single outcomes—it was an assumption so deep it was invisible, because it was what they saw happening. Collapse theories were devised to explain why measurements had single outcomes, rather than (in full generality) why experimental statistics matched the Born rule.

For similar reasons, the “collapse postulates” considered academically suppose that collapse occurs before any human beings get superposed. But experiments are steadily ruling out the possibility of “collapse” in increasingly large entangled systems. Apparently an experiment is underway to demonstrate quantum superposition at 50-micrometer scales, which is bigger than most neurons and getting up toward the diameter of some human hairs!

So why doesn’t someone try jumping ahead of the game, and ask:

Say, we keep having to postulate the collapse occurs steadily later and later. What if collapse occurs only once superposition reaches planetary scales and substantial divergence occurs—say, Earth’s wavefunction collapses around once a minute? Then, while the surviving Earths at any given time would remember a long history of quantum experiments that matched the Born statistics, a supermajority of those Earths would begin obtaining non-Born results from quantum experiments and then abruptly cease to exist a minute later.

Why don’t collapse theories like that one have a huge academic following, among the many people who apparently think it’s okay for parts of the wavefunction to just vanish? Especially given that experiments are proving superposition in steadily larger systems?

A cynic might suggest that the reason for collapse’s continued support isn’t the physical plausibility of having large parts of the wavefunction suddenly vanish, or the hope of somehow explaining the Born statistics. The point is to keep the intuitive appeal of “I don’t remember the measurement having more than one result, therefore only one thing happened; I don’t remember splitting, so there must be only one of me.” You don’t remember dying, so superposed humans must never collapse. A theory that dared to stomp on intuition would be missing the whole point. You might as well just move on to decoherence.

So a cynic might suggest.

But surely it is too early to be attacking the motives of collapse supporters. That is mere argument ad hominem. What about the actual physical plausibility of collapse theories?

Well, first: Does any collapse theory have any experimental support? No.

With that out of the way . . .

If collapse actually worked the way its adherents say it does, it would be:

The only non-linear evolution in all of quantum mechanics.
The only non-unitary evolution in all of quantum mechanics.
The only non-differentiable (in fact, discontinuous) phenomenon in all of quantum mechanics.
The only phenomenon in all of quantum mechanics that is non-local in the configuration space.
The only phenomenon in all of physics that violates CPT symmetry.
The only phenomenon in all of physics that violates Liouville’s Theorem (has a many-to-one mapping from initial conditions to outcomes).
The only phenomenon in all of physics that is acausal non-deterministic inherently random.
The only phenomenon in all of physics that is non-local in spacetime and propagates an influence faster than light.

WHAT DOES THE GOD-DAMNED COLLAPSE POSTULATE HAVE TO DO FOR PHYSICISTS TO REJECT IT? KILL A GOD-DAMNED PUPPY?

234
Decoherence is Simple

An epistle to the physicists:

When I was but a little lad, my father, a PhD physicist, warned me sternly against meddling in the affairs of physicists; he said that it was hopeless to try to comprehend physics without the formal math. Period. No escape clauses. But I had read in Feynman’s popular books that if you really understood physics, you ought to be able to explain it to a nonphysicist. I believed Feynman instead of my father, because Feynman had won the Nobel Prize and my father had not.

It was not until later—when I was reading the Feynman Lectures, in fact—that I realized that my father had given me the simple and honest truth. No math = no physics.

By vocation I am a Bayesian, not a physicist. Yet although I was raised not to meddle in the affairs of physicists, my hand has been forced by the occasional gross misuse of three terms: simple, falsifiable, and testable.

The foregoing introduction is so that you don’t laugh, and say, “Of course I know what those words mean!” There is math here. What follows will be a restatement of the points in Belief in the Implied Invisible, as they apply to quantum physics.

Let’s begin with the remark that started me down this whole avenue, of which I have seen several versions; paraphrased, it runs:

The many-worlds interpretation of quantum mechanics postulates that there are vast numbers of other worlds, existing alongside our own. Occam’s Razor says we should not multiply entities unnecessarily.

Now it must be said, in all fairness, that those who say this will usually also confess:

But this is not a universally accepted application of Occam’s Razor; some say that Occam’s Razor should apply to the laws governing the model, not the number of objects inside the model.

So it is good that we are all acknowledging the contrary arguments, and telling both sides of the story—

But suppose you had to calculate the simplicity of a theory.

The original formulation of William of Ockham stated:

Lex parsimoniae: Entia non sunt multiplicanda praeter necessitatem.

“The law of parsimony: Entities should not be multiplied beyond necessity.”

But this is qualitative advice. It is not enough to say whether one theory seems more simple, or seems more complex, than another—you have to assign a number; and the number has to be meaningful, you can’t just make it up. Crossing this gap is like the difference between being able to eyeball which things are moving “fast” or “slow,” and starting to measure and calculate velocities.

Suppose you tried saying: “Count the words—that’s how complicated a theory is.”

Robert Heinlein once claimed (tongue-in-cheek, I hope) that the “simplest explanation” is always: “The woman down the street is a witch; she did it.” Eleven words—not many physics papers can beat that.

Faced with this challenge, there are two different roads you can take.

First, you can ask: “The woman down the street is a what?” Just because English has one word to indicate a concept doesn’t mean that the concept itself is simple. Suppose you were talking to aliens who didn’t know about witches, women, or streets—how long would it take you to explain your theory to them? Better yet, suppose you had to write a computer program that embodied your hypothesis, and output what you say are your hypothesis’s predictions—how big would that computer program have to be? Let’s say that your task is to predict a time series of measured positions for a rock rolling down a hill. If you write a subroutine that simulates witches, this doesn’t seem to help narrow down where the rock rolls—the extra subroutine just inflates your code. You might find, however, that your code necessarily includes a subroutine that squares numbers.

Second, you can ask: “The woman down the street is a witch; she did what?” Suppose you want to describe some event, as precisely as you possibly can given the evidence available to you—again, say, the distance/time series of a rock rolling down a hill. You can preface your explanation by saying, “The woman down the street is a witch,” but your friend then says, “What did she do?,” and you reply, “She made the rock roll one meter after the first second, nine meters after the third second . . .” Prefacing your message with “The woman down the street is a witch,” doesn’t help to compress the rest of your description. On the whole, you just end up sending a longer message than necessary—it makes more sense to just leave off the “witch” prefix. On the other hand, if you take a moment to talk about Galileo, you may be able to greatly compress the next five thousand detailed time series for rocks rolling down hills.

If you follow the first road, you end up with what’s known as Kolmogorov complexity and Solomonoff induction. If you follow the second road, you end up with what’s known as Minimum Message Length.

Ah, so I can pick and choose among definitions of simplicity?

No, actually the two formalisms in their most highly developed forms were proven equivalent.

And I suppose now you’re going to tell me that both formalisms come down on the side of “Occam means counting laws, not counting objects.”

More or less. In Minimum Message Length, so long as you can tell your friend an exact recipe they can mentally follow to get the rolling rock’s time series, we don’t care how much mental work it takes to follow the recipe. In Solomonoff induction, we count bits in the program code, not bits of RAM used by the program as it runs. “Entities” are lines of code, not simulated objects. And as said, these two formalisms are ultimately equivalent.

Now before I go into any further detail on formal simplicity, let me digress to consider the objection:

So what? Why can’t I just invent my own formalism that does things differently? Why should I pay any attention to the way you happened to decide to do things, over in your field? Got any experimental evidence that shows I should do things this way?

Yes, actually, believe it or not. But let me start at the beginning.

The conjunction rule of probability theory states:

P(X,Y) ≤ P(X).

For any propositions X and Y, the probability that “X is true, and Y is true,” is less than or equal to the probability that “X is true (whether or not Y is true).” (If this statement sounds not terribly profound, then let me assure you that it is easy to find cases where human probability assessors violate this rule.)

You usually can’t apply the conjunction rule P(X,Y) ≤ P(X) directly to a conflict between mutually exclusive hypotheses. The conjunction rule only applies directly to cases where the left-hand-side strictly implies the right-hand-side. Furthermore, the conjunction is just an inequality; it doesn’t give us the kind of quantitative calculation we want.

But the conjunction rule does give us a rule of monotonic decrease in probability: as you tack more details onto a story, and each additional detail can potentially be true or false, the story’s probability goes down monotonically. Think of probability as a conserved quantity: there’s only so much to go around. As the number of details in a story goes up, the number of possible stories increases exponentially, but the sum over their probabilities can never be greater than 1. For every story “X and Y,” there is a story “X and ¬Y.” When you just tell the story “X,” you get to sum over the possibilities Y and ¬Y.

If you add ten details to X, each of which could potentially be true or false, then that story must compete with 2¹⁰ - 1 other equally detailed stories for precious probability. If on the other hand it suffices to just say X, you can sum your probability over 2¹⁰ stories

((X and Y and Z and . . .) or (X and ¬Y and Z and . . .) or . . .).

The “entities” counted by Occam’s Razor should be individually costly in probability; this is why we prefer theories with fewer of them.

Imagine a lottery which sells up to a million tickets, where each possible ticket is sold only once, and the lottery has sold every ticket at the time of the drawing. A friend of yours has bought one ticket for $1—which seems to you like a poor investment, because the payoff is only $500,000. Yet your friend says, “Ah, but consider the alternative hypotheses, ‘Tomorrow, someone will win the lottery’ and ‘Tomorrow, I will win the lottery.’ Clearly, the latter hypothesis is simpler by Occam’s Razor; it only makes mention of one person and one ticket, while the former hypothesis is more complicated: it mentions a million people and a million tickets!”

To say that Occam’s Razor only counts laws, and not objects, is not quite correct: what counts against a theory are the entities it must mention explicitly, because these are the entities that cannot be summed over. Suppose that you and a friend are puzzling over an amazing billiards shot, in which you are told the starting state of a billiards table, and which balls were sunk, but not how the shot was made. You propose a theory which involves ten specific collisions between ten specific balls; your friend counters with a theory that involves five specific collisions between five specific balls. What counts against your theories is not just the laws that you claim to govern billiard balls, but any specific billiard balls that had to be in some particular state for your model’s prediction to be successful.

If you measure the temperature of your living room as 22^° Celsius, it does not make sense to say: “Your thermometer is probably in error; the room is much more likely to be 20^° C. Because, when you consider all the particles in the room, there are exponentially vastly more states they can occupy if the temperature is really 22^° C—which makes any particular state all the more improbable.” But no matter which exact 22^° C state your room occupies, you can make the same prediction (for the supervast majority of these states) that your thermometer will end up showing 22^° C, and so you are not sensitive to the exact initial conditions. You do not need to specify an exact position of all the air molecules in the room, so that is not counted against the probability of your explanation.

On the other hand—returning to the case of the lottery—suppose your friend won ten lotteries in a row. At this point you should suspect the fix is in. The hypothesis “My friend wins the lottery every time” is more complicated than the hypothesis “Someone wins the lottery every time.” But the former hypothesis is predicting the data much more precisely.

In the Minimum Message Length formalism, saying “There is a single person who wins the lottery every time” at the beginning of your message compresses your description of who won the next ten lotteries; you can just say “And that person is Fred Smith” to finish your message. Compare to, “The first lottery was won by Fred Smith, the second lottery was won by Fred Smith, the third lottery was . . .”

In the Solomonoff induction formalism, the prior probability of “My friend wins the lottery every time” is low, because the program that describes the lottery now needs explicit code that singles out your friend; but because that program can produce a tighter probability distribution over potential lottery winners than “Someone wins the lottery every time,” it can, by Bayes’s Rule, overcome its prior improbability and win out as a hypothesis.

Any formal theory of Occam’s Razor should quantitatively define, not only “entities” and “simplicity,” but also the “necessity” part.

Minimum Message Length defines necessity as “that which compresses the message.”

Solomonoff induction assigns a prior probability to each possible computer program, with the entire distribution, over every possible computer program, summing to no more than 1. This can be accomplished using a binary code where no valid computer program is a prefix of any other valid computer program (“prefix-free code”), e.g. because it contains a stop code. Then the prior probability of any program P is simply 2^-L(P) where L(P) is the length of P in bits.

The program P itself can be a program that takes in a (possibly zero-length) string of bits and outputs the conditional probability that the next bit will be 1; this makes P a probability distribution over all binary sequences. This version of Solomonoff induction, for any string, gives us a mixture of posterior probabilities dominated by the shortest programs that most precisely predict the string. Summing over this mixture gives us a prediction for the next bit.

The upshot is that it takes more Bayesian evidence—more successful predictions, or more precise predictions—to justify more complex hypotheses. But it can be done; the burden of prior improbability is not infinite. If you flip a coin four times, and it comes up heads every time, you don’t conclude right away that the coin produces only heads; but if the coin comes up heads twenty times in a row, you should be considering it very seriously. What about the hypothesis that a coin is fixed to produce HTTHTT . . . in a repeating cycle? That’s more bizarre—but after a hundred coinflips you’d be a fool to deny it.

Standard chemistry says that in a gram of hydrogen gas there are six hundred billion trillion hydrogen atoms. This is a startling statement, but there was some amount of evidence that sufficed to convince physicists in general, and you particularly, that this statement was true.

Now ask yourself how much evidence it would take to convince you of a theory with six hundred billion trillion separately specified physical laws.

Why doesn’t the prior probability of a program, in the Solomonoff formalism, include a measure of how much RAM the program uses, or the total running time?

The simple answer is, “Because space and time resources used by a program aren’t mutually exclusive possibilities.” It’s not like the program specification, that can only have a 1 or a 0 in any particular place.

But the even simpler answer is, “Because, historically speaking, that heuristic doesn’t work.”

Occam’s Razor was raised as an objection to the suggestion that nebulae were actually distant galaxies—it seemed to vastly multiply the number of entities in the universe. All those stars!

Over and over, in human history, the universe has gotten bigger. A variant of Occam’s Razor which, on each such occasion, would label the vaster universe as more unlikely, would fare less well under humanity’s historical experience.

This is part of the “experimental evidence” I was alluding to earlier. While you can justify theories of simplicity on mathy sorts of grounds, it is also desirable that they actually work in practice. (The other part of the “experimental evidence” comes from statisticians computer scientists Artificial Intelligence researchers, testing which definitions of “simplicity” let them construct computer programs that do empirically well at predicting future data from past data. Probably the Minimum Message Length paradigm has proven most productive here, because it is a very adaptable way to think about real-world problems.)

Imagine a spaceship whose launch you witness with great fanfare; it accelerates away from you, and is soon traveling at 0.9c. If the expansion of the universe continues, as current cosmology holds it should, there will come some future point where—according to your model of reality—you don’t expect to be able to interact with the spaceship even in principle; it has gone over the cosmological horizon relative to you, and photons leaving it will not be able to outrace the expansion of the universe.

Should you believe that the spaceship literally, physically disappears from the universe at the point where it goes over the cosmological horizon relative to you?

If you believe that Occam’s Razor counts the objects in a model, then yes, you should. Once the spaceship goes over your cosmological horizon, the model in which the spaceship instantly disappears, and the model in which the spaceship continues onward, give indistinguishable predictions; they have no Bayesian evidential advantage over one another. But one model contains many fewer “entities”; it need not speak of all the quarks and electrons and fields composing the spaceship. So it is simpler to suppose that the spaceship vanishes.

Alternatively, you could say: “Over numerous experiments, I have generalized certain laws that govern observed particles. The spaceship is made up of such particles. Applying these laws, I deduce that the spaceship should continue on after it crosses the cosmological horizon, with the same momentum and the same energy as before, on pain of violating the conservation laws that I have seen holding in every examinable instance. To suppose that the spaceship vanishes, I would have to add a new law, ‘Things vanish as soon as they cross my cosmological horizon.’”

The decoherence (a.k.a. many-worlds) version of quantum mechanics states that measurements obey the same quantum-mechanical rules as all other physical processes. Applying these rules to macroscopic objects in exactly the same way as microscopic ones, we end up with observers in states of superposition. Now there are many questions that can be asked here, such as “But then why don’t all binary quantum measurements appear to have 50/50 probability, since different versions of us see both outcomes?”

However, the objection that decoherence violates Occam’s Razor on account of multiplying objects in the model is simply wrong.

Decoherence does not require the wavefunction to take on some complicated exact initial state. Many-worlds is not specifying all its worlds by hand, but generating them via the compact laws of quantum mechanics. A computer program that directly simulates quantum mechanics to make experimental predictions, would require a great deal of RAM to run—but simulating the wavefunction is exponentially expensive in any flavor of quantum mechanics! Decoherence is simply more so. Many physical discoveries in human history, from stars to galaxies, from atoms to quantum mechanics, have vastly increased the apparent CPU load of what we believe to be the universe.

Many-worlds is not a zillion worlds worth of complicated, any more than the atomic hypothesis is a zillion atoms worth of complicated. For anyone with a quantitative grasp of Occam’s Razor that is simply not what the term “complicated” means.

As with the historical case of galaxies, it may be that people have mistaken their shock at the notion of a universe that large, for a probability penalty, and invoked Occam’s Razor in justification. But if there are probability penalties for decoherence, the largeness of the implied universe, per se, is definitely not their source!

The notion that decoherent worlds are additional entities penalized by Occam’s Razor is just plain mistaken. It is not sort-of-right. It is not an argument that is weak but still valid. It is not a defensible position that could be shored up with further arguments. It is entirely defective as probability theory. It is not fixable. It is bad math. 2 + 2 = 3.

235
Decoherence is Falsifiable and Testable

The words “falsifiable” and “testable” are sometimes used interchangeably, which imprecision is the price of speaking in English. There are two different probability-theoretic qualities I wish to discuss here, and I will refer to one as “falsifiable” and the other as “testable” because it seems like the best fit.

As for the math, it begins, as so many things do, with:

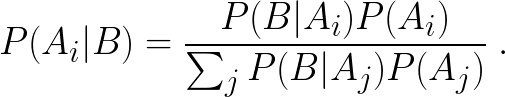
This is Bayes’s Theorem. I own at least two distinct items of clothing printed with this theorem, so it must be important.

To review quickly, B here refers to an item of evidence, A_i is some hypothesis under consideration, and the A_j are competing, mutually exclusive hypotheses. The expression P(B|A_i) means “the probability of seeing B, if hypothesis A_i is true” and P(A_i|B) means “the probability hypothesis A_i is true, if we see B.”

The mathematical phenomenon that I will call “falsifiability” is the scientifically desirable property of a hypothesis that it should concentrate its probability mass into preferred outcomes, which implies that it must also assign low probability to some un-preferred outcomes; probabilities must sum to 1 and there is only so much probability to go around. Ideally there should be possible observations which would drive down the hypothesis’s probability to nearly zero: There should be things the hypothesis cannot explain, conceivable experimental results with which the theory is not compatible. A theory that can explain everything prohibits nothing, and so gives us no advice about what to expect.

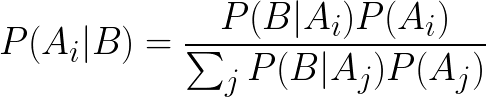
In terms of Bayes’s Theorem, if there is at least some observation B that the hypothesis A_i can’t explain, i.e., P(B|A_i) is tiny, then the numerator P(B|A_i)P(A_i) will also be tiny, and likewise the posterior probability P(A_i|B). Updating on having seen the impossible result B has driven the probability of A_i down to nearly zero. A theory that refuses to make itself vulnerable in this way will need to spread its probability widely, so that it has no holes; it will not be able to strongly concentrate probability into a few preferred outcomes; it will not be able to offer precise advice.

Thus is the rule of science derived in probability theory.

As depicted here, “falsifiability” is something you evaluate by looking at a single hypothesis, asking, “How narrowly does it concentrate its probability distribution over possible outcomes? How narrowly does it tell me what to expect? Can it explain some possible outcomes much better than others?”

Is the decoherence interpretation of quantum mechanics falsifiable? Are there experimental results that could drive its probability down to an infinitesimal?

Sure: We could measure entangled particles that should always have opposite spin, and find that if we measure them far enough apart, they sometimes have the same spin.

Or we could find apples falling upward, the planets of the Solar System zigging around at random, and an atom that kept emitting photons without any apparent energy source. Those observations would also falsify decoherent quantum mechanics. They’re things that, on the hypothesis that decoherent quantum mechanics governs the universe, we should definitely not expect to see.

So there do exist observations B whose P(B|A_deco) is infinitesimal, which would drive P(A_deco|B) down to an infinitesimal.

But that’s just because decoherent quantum mechanics is still quantum mechanics! What about the decoherence part, per se, versus the collapse postulate?

We’re getting there. The point is that I just defined a test that leads you to think about one hypothesis at a time (and called it “falsifiability”). If you want to distinguish decoherence versus collapse, you have to think about at least two hypotheses at a time.

Now really the “falsifiability” test is not quite that singly focused, i.e., the sum in the denominator has got to contain some other hypothesis. But what I just defined as “falsifiability” pinpoints the kind of problem that Karl Popper was complaining about, when he said that Freudian psychoanalysis was “unfalsifiable” because it was equally good at coming up with an explanation for every possible thing the patient could do.

If you belonged to an alien species that had never invented the collapse postulate or Copenhagen Interpretation—if the only physical theory you’d ever heard of was decoherent quantum mechanics—if all you had in your head was the differential equation for the wavefunction’s evolution plus the Born probability rule—you would still have sharp expectations of the universe. You would not live in a magical world where anything was probable.

But you could say exactly the same thing about quantum mechanics without (macroscopic) decoherence.

Well, yes! Someone walking around with the differential equation for the wavefunction’s evolution, plus a collapse postulate that obeys the Born probabilities and is triggered before superposition reaches macroscopic levels, still lives in a universe where apples fall down rather than up.

But where does decoherence make a new prediction, one that lets us test it?

A “new” prediction relative to what? To the state of knowledge possessed by the ancient Greeks? If you went back in time and showed them decoherent quantum mechanics, they would be enabled to make many experimental predictions they could not have made before.

When you say “new prediction,” you mean “new” relative to some other hypothesis that defines the “old prediction.” This gets us into the theory of what I’ve chosen to label testability; and the algorithm inherently considers at least two hypotheses at a time. You cannot call something a “new prediction” by considering only one hypothesis in isolation.

In Bayesian terms, you are looking for an item of evidence B that will produce evidence for one hypothesis over another, distinguishing between them, and the process of producing this evidence we could call a “test.” You are looking for an experimental result B such that

P(B|A_d) ≠ P(B|A_c);

that is, some outcome B which has a different probability, conditional on the decoherence hypothesis being true, versus its probability if the collapse hypothesis is true. Which in turn implies that the posterior odds for decoherence and collapse will become different from the prior odds:

This equation is symmetrical (assuming no probability is literally equal to 0). There isn’t one A_j labeled “old hypothesis” and another A_j labeled “new hypothesis.”

This symmetry is a feature, not a bug, of probability theory! If you are designing an artificial reasoning system that arrives at different beliefs depending on the order in which the evidence is presented, this is labeled “hysteresis” and considered a Bad Thing. I hear that it is also frowned upon in Science.

From a probability-theoretic standpoint we have various trivial theorems that say it shouldn’t matter whether you update on X first and then Y, or update on Y first and then X. At least they’d be trivial if human beings didn’t violate them so often and so lightly.

If decoherence is “untestable” relative to collapse, then so too, collapse is “untestable” relative to decoherence. What if the history of physics had transpired differently—what if Hugh Everett and John Wheeler had stood in the place of Bohr and Heisenberg, and vice versa? Would it then be right and proper for the people of that world to look at the collapse interpretation, and snort, and say, “Where are the new predictions?”

What if someday we meet an alien species that invented decoherence before collapse? Are we each bound to keep the theory we invented first? Will Reason have nothing to say about the issue, leaving no recourse to settle the argument but interstellar war?

But if we revoke the requirement to yield new predictions, we are left with scientific chaos. You can add arbitrary untestable complications to old theories, and get experimentally equivalent predictions. If we reject what you call “hysteresis,” how can we defend our current theories against every crackpot who proposes that electrons have a new property called “scent,” just like quarks have “flavor”?

Let it first be said that I quite agree that you should reject the one who comes to you and says: “Hey, I’ve got this brilliant new idea! Maybe it’s not the electromagnetic field that’s tugging on charged particles. Maybe there are tiny little angels who actually push on the particles, and the electromagnetic field just tells them how to do it. Look, I have all these successful experimental predictions—the predictions you used to call your own!”

So yes, I agree that we shouldn’t buy this amazing new theory, but it is not the newness that is the problem.

Suppose that human history had developed only slightly differently, with the Church being a primary grant agency for Science. And suppose that when the laws of electromagnetism were first being worked out, the phenomenon of magnetism had been taken as proof of the existence of unseen spirits, of angels. James Clerk becomes Saint Maxwell, who described the laws that direct the actions of angels.

A couple of centuries later, after the Church’s power to burn people at the stake has been restrained, someone comes along and says: “Hey, do we really need the angels?”

“Yes,” everyone says. “How else would the mere numbers of the electromagnetic field translate into the actual motions of particles?”

“It might be a fundamental law,” says the newcomer, “or it might be something other than angels, which we will discover later. What I am suggesting is that interpreting the numbers as the action of angels doesn’t really add anything, and we should just keep the numbers and throw out the angel part.”

And they look one at another, and finally say, “But your theory doesn’t make any new experimental predictions, so why should we adopt it? How do we test your assertions about the absence of angels?”

From a normative perspective, it seems to me that if we should reject the crackpot angels in the first scenario, even without being able to distinguish the two theories experimentally, then we should also reject the angels of established science in the second scenario, even without being able to distinguish the two theories experimentally.

It is ordinarily the crackpot who adds on new useless complications, rather than scientists who accidentally build them in at the start. But the problem is not that the complications are new, but that they are useless whether or not they are new.

A Bayesian would say that the extra complications of the angels in the theory lead to penalties on the prior probability of the theory. If two theories make equivalent predictions, we keep the one that can be described with the shortest message, the smallest program. If you are evaluating the prior probability of each hypothesis by counting bits of code, and then applying Bayesian updating rules on all the evidence available, then it makes no difference which hypothesis you hear about first, or the order in which you apply the evidence.

It is usually not possible to apply formal probability theory in real life, any more than you can predict the winner of a tennis match using quantum field theory. But if probability theory can serve as a guide to practice, this is what it says: Reject useless complications in general, not just when they are new.

Yes, and useless is precisely what the many worlds of decoherence are! There are supposedly all these worlds alongside our own, and they don’t do anything to our world, but I’m supposed to believe in them anyway?

No, according to decoherence, what you’re supposed to believe are the general laws that govern wavefunctions—and these general laws are very visible and testable.

I have argued elsewhere that the imprimatur of science should be associated with general laws, rather than particular events, because it is the general laws that, in principle, anyone can go out and test for themselves. I assure you that I happen to be wearing white socks right now as I type this. So you are probably rationally justified in believing that this is a historical fact. But it is not the specially strong kind of statement that we canonize as a provisional belief of science, because there is no experiment that you can do for yourself to determine the truth of it; you are stuck with my authority. Now, if I were to tell you the mass of an electron in general, you could go out and find your own electron to test, and thereby see for yourself the truth of the general law in that particular case.

The ability of anyone to go out and verify a general scientific law for themselves, by constructing some particular case, is what makes our belief in the general law specially reliable.

What decoherentists say they believe in is the differential equation that is observed to govern the evolution of wavefunctions—which you can go out and test yourself any time you like; just look at a hydrogen atom.

Belief in the existence of separated portions of the universal wavefunction is not additional, and it is not supposed to be explaining the price of gold in London; it is just a deductive consequence of the wavefunction’s evolution. If the evidence of many particular cases gives you cause to believe that X → Y is a general law, and the evidence of some particular case gives you cause to believe X, then you should have P(Y) ≥ P(X and (X → Y)).

Or to look at it another way, if P(Y|X) ≈ 1, then P(X and Y) ≈ P(X).

Which is to say, believing extra details doesn’t cost you extra probability when they are logical implications of general beliefs you already have. Presumably the general beliefs themselves are falsifiable, though, or why bother?

This is why we don’t believe that spaceships blink out of existence when they cross the cosmological horizon relative to us. True, the spaceship’s continued existence doesn’t have an impact on our world. The spaceship’s continued existence isn’t helping to explain the price of gold in London. But we get the invisible spaceship for free as a consequence of general laws that imply conservation of mass and energy. If the spaceship’s continued existence were not a deductive consequence of the laws of physics as we presently model them, then it would be an additional detail, cost extra probability, and we would have to question why our theory must include this assertion.

The part of decoherence that is supposed to be testable is not the many worlds per se, but just the general law that governs the wavefunction. The decoherentists note that, applied universally, this law implies the existence of entire superposed worlds. Now there are critiques that can be leveled at this theory, most notably, “But then where do the Born probabilities come from?” But within the internal logic of decoherence, the many worlds are not offered as an explanation for anything, nor are they the substance of the theory that is meant to be tested; they are simply a logical consequence of those general laws that constitute the substance of the theory.

If A ⇒ B then ¬B ⇒¬A. To deny the existence of superposed worlds is necessarily to deny the universality of the quantum laws formulated to govern hydrogen atoms and every other examinable case; it is this denial that seems to the decoherentists like the extra and untestable detail. You can’t see the other parts of the wavefunction—why postulate additionally that they don’t exist?

The events surrounding the decoherence controversy may be unique in scientific history, marking the first time that serious scientists have come forward and said that by historical accident humanity has developed a powerful, successful, mathematical physical theory that includes angels. That there is an entire law, the collapse postulate, that can simply be thrown away, leaving the theory strictly simpler.

To this discussion I wish to contribute the assertion that, in the light of a mathematically solid understanding of probability theory, decoherence is not ruled out by Occam’s Razor, nor is it unfalsifiable, nor is it untestable.

We may consider e.g. decoherence and the collapse postulate, side by side, and evaluate critiques such as “Doesn’t decoherence definitely predict that quantum probabilities should always be 50/50?” and “Doesn’t collapse violate Special Relativity by implying influence at a distance?” We can consider the relative merits of these theories on grounds of their compatibility with experience and the apparent character of physical law.

To assert that decoherence is not even in the game—because the many worlds themselves are “extra entities” that violate Occam’s Razor, or because the many worlds themselves are “untestable,” or because decoherence makes no “new predictions”—all this is, I would argue, an outright error of probability theory. The discussion should simply discard those particular arguments and move on.

236
Privileging the Hypothesis

Suppose that the police of Largeville, a town with a million inhabitants, are investigating a murder in which there are few or no clues—the victim was stabbed to death in an alley, and there are no fingerprints and no witnesses.

Then, one of the detectives says, “Well . . . we have no idea who did it . . . no particular evidence singling out any of the million people in this city . . . but let’s consider the hypothesis that this murder was committed by Mortimer Q. Snodgrass, who lives at 128 Ordinary Ln. It could have been him, after all.”

I’ll label this the fallacy of privileging the hypothesis. (Do let me know if it already has an official name—I can’t recall seeing it described.)

Now the detective may perhaps have some form of rational evidence that is not legal evidence admissible in court—hearsay from an informant, for example. But if the detective does not have some justification already in hand for promoting Mortimer to the police’s special attention—if the name is pulled entirely out of a hat—then Mortimer’s rights are being violated.

And this is true even if the detective is not claiming that Mortimer “did” do it, but only asking the police to spend time pondering that Mortimer might have done it—unjustifiably promoting that particular hypothesis to attention. It’s human nature to look for confirmation rather than disconfirmation. Suppose that three detectives each suggest their hated enemies, as names to be considered; and Mortimer is brown-haired, Frederick is black-haired, and Helen is blonde. Then a witness is found who says that the person leaving the scene was brown-haired. “Aha!” say the police. “We previously had no evidence to distinguish among the possibilities, but now we know that Mortimer did it!”

This is related to the principle I’ve started calling “locating the hypothesis,” which is that if you have a billion boxes only one of which contains a diamond (the truth), and your detectors only provide 1 bit of evidence apiece, then it takes much more evidence to promote the truth to your particular attention—to narrow it down to ten good possibilities, each deserving of our individual attention—than it does to figure out which of those ten possibilities is true. It takes 27 bits to narrow it down to ten, and just another 4 bits will give us better than even odds of having the right answer.

Thus the detective, in calling Mortimer to the particular attention of the police, for no reason out of a million other people, is skipping over most of the evidence that needs to be supplied against Mortimer.

And the detective ought to have this evidence in their possession, at the first moment when they bring Mortimer to the police’s attention at all. It may be mere rational evidence rather than legal evidence, but if there’s no evidence then the detective is harassing and persecuting poor Mortimer.

During my recent diavlog with Scott Aaronson on quantum mechanics, I did manage to corner Scott to the extent of getting Scott to admit that there was no concrete evidence whatsoever that favors a collapse postulate or single-world quantum mechanics. But, said Scott, we might encounter future evidence in favor of single-world quantum mechanics, and many-worlds still has the open question of the Born probabilities.

This is indeed what I would call the fallacy of privileging the hypothesis. There must be a trillion better ways to answer the Born question without adding a collapse postulate that would be the only non-linear, non-unitary, discontinous, non-differentiable, non-CPT-symmetric, non-local in the configuration space, Liouville’s-Theorem-violating, privileged-space-of-simultaneity-possessing, faster-than-light-influencing, acausal, informally specified law in all of physics. Something that unphysical is not worth saying out loud or even thinking about as a possibility without a rather large weight of evidence—far more than the current grand total of zero.

But because of a historical accident, collapse postulates and single-world quantum mechanics are indeed on everyone’s lips and in everyone’s mind to be thought of, and so the open question of the Born probabilities is offered up (by Scott Aaronson no less!) as evidence that many-worlds can’t yet offer a complete picture of the world. Which is taken to mean that single-world quantum mechanics is still in the running somehow.

In the minds of human beings, if you can get them to think about this particular hypothesis rather than the trillion other possibilities that are no more complicated or unlikely, you really have done a huge chunk of the work of persuasion. Anything thought about is treated as “in the running,” and if other runners seem to fall behind in the race a little, it’s assumed that this runner is edging forward or even entering the lead.

And yes, this is just the same fallacy committed, on a much more blatant scale, by the theist who points out that modern science does not offer an absolutely complete explanation of the entire universe, and takes this as evidence for the existence of Jehovah. Rather than Allah, the Flying Spaghetti Monster, or a trillion other gods no less complicated—never mind the space of naturalistic explanations!

To talk about “intelligent design” whenever you point to a purported flaw or open problem in evolutionary theory is, again, privileging the hypothesis—you must have evidence already in hand that points to intelligent design specifically in order to justify raising that particular idea to our attention, rather than a thousand others.

So that’s the sane rule. And the corresponding anti-epistemology is to talk endlessly of “possibility” and how you “can’t disprove” an idea, to hope that future evidence may confirm it without presenting past evidence already in hand, to dwell and dwell on possibilities without evaluating possibly unfavorable evidence, to draw glowing word-pictures of confirming observations that could happen but haven’t happened yet, or to try and show that piece after piece of negative evidence is “not conclusive.”

Just as Occam’s Razor says that more complicated propositions require more evidence to believe, more complicated propositions also ought to require more work to raise to attention. Just as the principle of burdensome details requires that each part of a belief be separately justified, it requires that each part be separately raised to attention.

As discussed in Perpetual Motion Beliefs, faith and type 2 perpetual motion machines (water → ice cubes + electricity) have in common that they purport to manufacture improbability from nowhere, whether the improbability of water forming ice cubes or the improbability of arriving at correct beliefs without observation. Sometimes most of the anti-work involved in manufacturing this improbability is getting us to pay attention to an unwarranted belief—thinking on it, dwelling on it. In large answer spaces, attention without evidence is more than halfway to belief without evidence.

Someone who spends all day thinking about whether the Trinity does or does not exist, rather than Allah or Thor or the Flying Spaghetti Monster, is more than halfway to Christianity. If leaving, they’re less than half departed; if arriving, they’re more than halfway there.

An oft-encountered mode of privilege is to try to make uncertainty within a space, slop outside of that space onto the privileged hypothesis. For example, a creationist seizes on some (allegedly) debated aspect of contemporary theory, argues that scientists are uncertain about evolution, and then says, “We don’t really know which theory is right, so maybe intelligent design is right.” But the uncertainty is uncertainty within the realm of naturalistic theories of evolution—we have no reason to believe that we’ll need to leave that realm to deal with our uncertainty, still less that we would jump out of the realm of standard science and land on Jehovah in particular. That is privileging the hypothesis—taking doubt within a normal space, and trying to slop doubt out of the normal space, onto a privileged (and usually discredited) extremely abnormal target.

Similarly, our uncertainty about where the Born statistics come from should be uncertainty within the space of quantum theories that are continuous, linear, unitary, slower-than-light, local, causal, naturalistic, et cetera—the usual character of physical law. Some of that uncertainty might slop outside the standard space onto theories that violate one of these standard characteristics. It’s indeed possible that we might have to think outside the box. But single-world theories violate all these characteristics, and there is no reason to privilege that hypothesis.

237
Living in Many Worlds

Some commenters have recently expressed disturbance at the thought of constantly splitting into zillions of other people, as is the straightforward and unavoidable prediction of quantum mechanics.

Others have confessed themselves unclear as to the implications of many-worlds for planning: If you decide to buckle your seat belt in this world, does that increase the chance of another self unbuckling their seat belt? Are you being selfish at their expense?

Just remember Egan’s Law: It all adds up to normality.

(After Greg Egan, in Quarantine.¹)

Frank Sulloway said:²

Ironically, psychoanalysis has it over Darwinism precisely because its predictions are so outlandish and its explanations are so counterintuitive that we think, Is that really true? How radical! Freud’s ideas are so intriguing that people are willing to pay for them, while one of the great disadvantages of Darwinism is that we feel we know it already, because, in a sense, we do.

When Einstein overthrew the Newtonian version of gravity, apples didn’t stop falling, planets didn’t swerve into the Sun. Every new theory of physics must capture the successful predictions of the old theory it displaced; it should predict that the sky will be blue, rather than green.

So don’t think that many-worlds is there to make strange, radical, exciting predictions. It all adds up to normality.

Then why should anyone care?

Because there was once asked the question, fascinating unto a rationalist: What all adds up to normality?

And the answer to this question turns out to be: quantum mechanics. It is quantum mechanics that adds up to normality.

If there were something else there instead of quantum mechanics, then the world would look strange and unusual.

Bear this in mind, when you are wondering how to live in the strange new universe of many worlds: You have always been there.

Religions, anthropologists tell us, usually exhibit a property called minimal counterintuitiveness; they are startling enough to be memorable, but not so bizarre as to be difficult to memorize. Anubis has the head of a dog, which makes him memorable, but the rest of him is the body of a man. Spirits can see through walls; but they still become hungry.

But physics is not a religion, set to surprise you just exactly enough to be memorable. The underlying phenomena are so counterintuitive that it takes long study for humans to come to grips with them. But the surface phenomena are entirely ordinary. You will never catch a glimpse of another world out of the corner of your eye. You will never hear the voice of some other self. That is unambiguously prohibited outright by the laws. Sorry, you’re just schizophrenic.

The act of making decisions has no special interaction with the process that branches worlds. In your mind, in your imagination, a decision seems like a branching point where the world could go two different ways. But you would feel just the same uncertainty, visualize just the same alternatives, if there were only one world. That’s what people thought for centuries before quantum mechanics, and they still visualized alternative outcomes that could result from their decisions.

Decision and decoherence are entirely orthogonal concepts. If your brain never became decoherent, then that single cognitive process would still have to imagine different choices and their different outcomes. And a rock, which makes no decisions, obeys the same laws of quantum mechanics as anything else, and splits frantically as it lies in one place.

You don’t split when you come to a decision in particular, any more than you particularly split when you take a breath. You’re just splitting all the time as the result of decoherence, which has nothing to do with choices.

There is a population of worlds, and in each world, it all adds up to normality: apples don’t stop falling. In each world, people choose the course that seems best to them. Maybe they happen on a different line of thinking, and see new implications or miss others, and come to a different choice. But it’s not that one world chooses each choice. It’s not that one version of you chooses what seems best, and another version chooses what seems worst. In each world, apples go on falling and people go on doing what seems like a good idea.

Yes, you can nitpick exceptions to this rule, but they’re normal exceptions. It all adds up to normality, in all the worlds.

You cannot “choose which world to end up in.” In all the worlds, people’s choices determine outcomes in the same way they would in just one single world.

The choice you make here does not have some strange balancing influence on some world elsewhere. There is no causal communication between decoherent worlds. In each world, people’s choices control the future of that world, not some other world.

If you can imagine decisionmaking in one world, you can imagine decisionmaking in many worlds: just have the world constantly splitting while otherwise obeying all the same rules.

In no world does two plus two equal five. In no world can spaceships travel faster than light. All the quantum worlds obey our laws of physics; their existence is asserted in the first place by our laws of physics. Since the beginning, not one unusual thing has ever happened, in this or any other world. They are all lawful.

Are there horrible worlds out there, which are utterly beyond your ability to affect? Sure. And horrible things happened during the twelfth century, which are also beyond your ability to affect. But the twelfth century is not your responsibility, because it has, as the quaint phrase goes, “already happened.” I would suggest that you consider every world that is not in your future to be part of the “generalized past.”

Live in your own world. Before you knew about quantum physics, you would not have been tempted to try living in a world that did not seem to exist. Your decisions should add up to this same normality: you shouldn’t try to live in a quantum world you can’t communicate with.

Your decision theory should (almost always) be the same, whether you suppose that there is a 90% probability of something happening, or if it will happen in 9 out of 10 worlds. Now, because people have trouble handling probabilities, it may be helpful to visualize something happening in 9 out of 10 worlds. But this just helps you use normal decision theory.

Now is a good time to begin learning how to shut up and multiply. As I note in Lotteries: A Waste of Hope:

The human brain doesn’t do 64-bit floating-point arithmetic, and it can’t devalue the emotional force of a pleasant anticipation by a factor of 0.00000001 without dropping the line of reasoning entirely.

And in New Improved Lottery:

Between zero chance of becoming wealthy, and epsilon chance, there is an order-of-epsilon difference. If you doubt this, let epsilon equal one over googolplex.

If you’re thinking about a world that could arise in a lawful way, but whose probability is a quadrillion to one, and something very pleasant or very awful is happening in this world . . . well, it does probably exist, if it is lawful. But you should try to release one quadrillionth as many neurotransmitters, in your reward centers or your aversive centers, so that you can weigh that world appropriately in your decisions. If you don’t think you can do that . . . don’t bother thinking about it.

Otherwise you might as well go out and buy a lottery ticket using a quantum random number, a strategy that is guaranteed to result in a very tiny mega-win.

Or here’s another way of thinking about it: Are you considering expending some mental energy on a world whose frequency in your future is less than a trillionth? Then go get a 10-sided die from your local gaming store, and, before you begin thinking about that strange world, start rolling the die. If the die comes up 9 twelve times in a row, then you can think about that world. Otherwise don’t waste your time; thought-time is a resource to be expended wisely.

You can roll the dice as many times as you like, but you can’t think about the world until 9 comes up twelve times in a row. Then you can think about it for a minute. After that you have to start rolling the die again.

This may help you to appreciate the concept of “trillion to one” on a more visceral level.

If at any point you catch yourself thinking that quantum physics might have some kind of strange, abnormal implication for everyday life—then you should probably stop right there.

Oh, there are a few implications of many-worlds for ethics. Average utilitarianism suddenly looks a lot more attractive—you don’t need to worry about creating as many people as possible, because there are already plenty of people exploring person-space. You just want the average quality of life to be as high as possible, in the future worlds that are your responsibility.

And you should always take joy in discovery, as long as you personally don’t know a thing. It is meaningless to talk of being the “first” or the “only” person to know a thing, when everything knowable is known within worlds that are in neither your past nor your future, and are neither before or after you.

But, by and large, it all adds up to normality. If your understanding of many-worlds is the tiniest bit shaky, and you are contemplating whether to believe some strange proposition, or feel some strange emotion, or plan some strange strategy, then I can give you very simple advice: Don’t.

The quantum universe is not a strange place into which you have been thrust. It is the way things have always been.

1. Greg Egan, Quarantine (London: Legend Press, 1992).

2. Robert S. Boynton, “The Birth of an Idea: A Profile of Frank Sulloway,” The New Yorker (October 1999).

238
Quantum NonRealism

Does the moon exist when no one is looking at it?

—Albert Einstein, asked of Niels Bohr

Suppose you were just starting to work out a theory of quantum mechanics.

You begin to encounter experiments that deliver different results depending on how closely you observe them. You dig underneath the reality you know, and find an extremely precise mathematical description that only gives you the relative frequency of outcomes; worse, it’s made of complex numbers. Things behave like particles on Monday and waves on Tuesday.

The correct answer is not available to you as a hypothesis, because it will not be invented for another thirty years.

In a mess like that, what’s the best you could do?

The best you can do is the strict “shut up and calculate” interpretation of quantum mechanics. You’ll go on trying to develop new theories, because doing your best doesn’t mean giving up. But we’ve specified that the correct answer won’t be available for thirty years, and that means none of the new theories will really be any good. Doing the best you could theoretically do would mean that you recognized that, even as you looked for ways to test the hypotheses.

The best you could theoretically do would not include saying anything like, “The wavefunction only gives us probabilities, not certainties.” That, in retrospect, was jumping to a conclusion; the wavefunction gives us a certainty of many worlds existing. So that part about the wavefunction being only a probability was not-quite-right. You calculated, but failed to shut up.

If you do the best that you can do without the correct answer being available, then, when you hear about decoherence, it will turn out that you have not said anything incompatible with decoherence. Decoherence is not ruled out by the data and the calculations. So if you refuse to affirm, as positive knowledge, any proposition which was not forced by the data and the calculations, the calculations will not force you to say anything incompatible with decoherence. So too with whatever the correct theory may be, if it is not decoherence. If you go astray, it must be from your own impulses.

But it is hard for human beings to shut up and calculate—really shut up and calculate. There is an overwhelming tendency to treat our ignorance as if it were positive knowledge.

I don’t know if any conversations like this ever really took place, but this is how ignorance becomes knowledge:

GALLANT: “Shut up and calculate.”

GOOFUS: “Why?”

GALLANT: “Because I don’t know what these equations mean, just that they seem to work.”

—five minutes later—

GOOFUS: “Shut up and calculate.”

STUDENT: “Why?”

GOOFUS: “Because these equations don’t mean anything, they just work.”

STUDENT: “Really? How do you know?”

GOOFUS: “Gallant told me.”

A similar transformation occurs in the leap from:

GALLANT: “When my calculations show an amplitude of (-1∕3)i for this photon to get absorbed, my experiments showed that the photon was absorbed around 107 times out of 1,000, which is a good fit to 1/9, the square of the modulus. There’s clearly some kind of connection between the experimental statistics and the squared modulus of the amplitude, but I don’t know what.”

GOOFUS: “The probability amplitude doesn’t say where the electron is, but where it might be. The squared modulus is the probability that reality will turn out that way. Reality itself is inherently nondeterministic.”

And again:

GALLANT: “Once I measure something and get an experimental result, I do my future calculations using only the amplitude whose squared modulus went into calculating the frequency of that experimental result. Only this rule makes my further calculations correspond to observed frequencies.”

GOOFUS: “Since the amplitude is the probability, once you know the experimental result, the probability of everything else becomes zero!”

The whole slip from:

The square of this “amplitude” stuff corresponds tightly to our experimentally observed frequencies

The amplitude is the probability of getting the measurement

Well, obviously, once you know you didn’t get a measurement, its probability becomes zero

has got to be one of the most embarrassing wrong turns in the history of science.

If you take all this literally, it becomes the consciousness-causes-collapse interpretation of quantum mechanics. These days, just about nobody will confess to actually believing in the consciousness-causes-collapse interpretation of quantum mechanics—

But the physics textbooks are still written this way! People say they don’t believe it, but they talk as if knowledge is responsible for removing incompatible “probability” amplitudes.

Yet as implausible as I find consciousness-causes-collapse, it at least gives us a picture of reality. Sure, it’s an informal picture. Sure, it gives mental properties ontologically basic status. You can’t calculate when an “experimental observation” occurs or what people “know,” you just know when certain probabilities are obviously zero. And this “just knowing” just happens to fit your experimental results, whatever they are—

—but at least consciousness-causes-collapse purports to tell us how the universe works. The amplitudes are real, the collapse is real, the consciousness is real.

Contrast to this argument schema:

STUDENT: “Wait, you’re saying that this amplitude disappears as soon as the measurement tells me it’s not true?”

GOOFUS: “No, no! It doesn’t literally disappear. The equations don’t mean anything—they just give good predictions.”

STUDENT: “But then what does happen?”

GOOFUS: (Whorble. Hiss.) “Never ask that question.”

STUDENT: “And what about the part where we measure this photon’s polarization over here, and a light-year away, the entangled photon’s probability of being polarized up-down changes from 50% to 25%?”

GOOFUS: “Yes, what about it?”

STUDENT: “Doesn’t that violate Special Relativity?”

GOOFUS: “No, because you’re just finding out the other photon’s polarization. Remember, the amplitudes aren’t real.”

STUDENT: “But Bell’s Theorem shows there’s no possible local hidden variable that could describe the other photon’s polarization before we measure it—”

GOOFUS: “Exactly! It’s meaningless to talk about the photon’s polarization before we measure it.”

STUDENT: “But the probability suddenly changes—”

GOOFUS: “It’s meaningless to talk about it before we measure it!”

What does Goofus even mean, here? Never mind the plausibility of his words; what sort of state of reality would correspond to his words being true?

What way could reality be, that would make it meaningless to talk about Special Relativity being violated, because the property being influenced didn’t exist, even though you could calculate the changes to it?

But you know what? Forget that. I want to know the answer to an even more important question:

Where is Goofus getting all this stuff?

Let’s suppose that you take the Schrödinger equation, and assert, as a positive fact:

This equation generates good predictions, but it doesn’t mean anything!

Really? How do you know?

I sometimes go around saying that the fundamental question of rationality is Why do you believe what you believe?

You say the Schrödinger equation “doesn’t mean anything.” How did this item of definite knowledge end up in your possession, if it is not simply ignorance misinterpreted as knowledge?

Was there some experiment that told you? I am open to the idea that experiments can tell us things that seem philosophically impossible. But in this case I should like to see the decisive data. Was there a point where you carefully set up an experimental apparatus, and worked out what you should expect to see if (1) the Schrödinger equation was meaningful or (2) the Schrödinger equation was meaningless; and then you got result (2)?

GALLANT: “If I measure the 90^° polarization of a photon, and then measure the 45^° polarization, and then measure 90^° again, my experimental history shows that in 100 trials a photon was absorbed 47 times and transmitted 53 times.”

GOOFUS: “The 90^° polarization and 45^° polarization are incompatible properties; they can’t both exist at the same time, and if you measure one, it is meaningless to talk about the other.”

How do you know?

How did you acquire that piece of knowledge, Goofus? I know where Gallant got his—but where did yours come from?

My attitude toward questions of existence and meaning was nicely illustrated in a discussion of the current state of evidence for whether the universe is spatially finite or spatially infinite, in which James D. Miller chided Robin Hanson:

Robin, you are suffering from overconfidence bias in assuming that the universe exists. Surely there is some chance that the universe is of size zero.

To which I replied:

James, if the universe doesn’t exist, it would still be nice to know whether it’s an infinite or a finite universe that doesn’t exist.

Ha! You think pulling that old “universe doesn’t exist” trick will stop me? It won’t even slow me down!

It’s not that I’m ruling out the possibility that the universe doesn’t exist. It’s just that, even if nothing exists, I still want to understand the nothing as best I can. My curiosity doesn’t suddenly go away just because there’s no reality, you know!

The nature of “reality” is something about which I’m still confused, which leaves open the possibility that there isn’t any such thing. But Egan’s Law still applies: “It all adds up to normality.” Apples didn’t stop falling when Einstein disproved Newton’s theory of gravity.

Sure, when the dust settles, it could turn out that apples don’t exist, Earth doesn’t exist, reality doesn’t exist. But the nonexistent apples will still fall toward the nonexistent ground at a meaningless rate of 9.8 m/s².

You say the universe doesn’t exist? Fine, suppose I believe that—though it’s not clear what I’m supposed to believe, aside from repeating the words.

Now, what happens if I press this button?

In The Simple Truth, I said:

Frankly, I’m not entirely sure myself where this “reality” business comes from. I can’t create my own reality in the lab, so I must not understand it yet. But occasionally I believe strongly that something is going to happen, and then something else happens instead . . . So I need different names for the thingies that determine my predictions and the thingy that determines my experimental results. I call the former thingies “belief,” and the latter thingy “reality.”

You want to say that the quantum-mechanical equations are “not real”? I’ll be charitable, and suppose this means something. What might it mean?

Maybe it means the equations which determine my predictions are substantially different from the thingy that determines my experimental results. Then what does determine my experimental results? If you tell me “nothing,” I would like to know what sort of “nothing” it is, and why this “nothing” exhibits such apparent regularity in determining e.g. my experimental measurements of the mass of an electron.

I don’t take well to people who tell me to stop asking questions. If you tell me something is definitely positively meaningless, I want to know exactly what you mean by that, and how you came to know. Otherwise you have not given me an answer, only told me to stop asking the question.

The Simple Truth describes the life of a shepherd and apprentice who have discovered how to count sheep by tossing pebbles into buckets, when they are visited by a delegate from the court who wants to know how the “magic pebbles” work. The shepherd tries to explain, “An empty bucket is magical if and only if the pastures are empty of sheep,” but is soon overtaken by the excited discussions of the apprentice and the delegate as to how the magic might get into the pebbles.

Here we have quantum equations that deliver excellent experimental predictions. What exactly does it mean for them to be “meaningless”? Is it like a bucket of pebbles that works for counting sheep, but doesn’t have any magic?

Back before Bell’s Theorem ruled out local hidden variables, it seemed possible that (as Einstein thought) there was some more complete description of reality which we didn’t have, and the quantum theory summarized incomplete knowledge of this more complete description. The laws we’d learned would turn out to be like the laws of statistical mechanics: quantitative statements of uncertainty. This would hardly make the equations “meaningless”; partial knowledge is the meaning of probability.

But Bell’s Theorem makes it much less plausible that the quantum equations are partial knowledge of something deterministic, the way that statistical mechanics over classical physics is partial knowledge of something deterministic. And even so, the quantum equations would not be “meaningless” as that phrase is usually taken; they would be “statistical,” “approximate,” “partial information,” or at worst “wrong.”

Here we have equations that give us excellent predictions. You say they are “meaningless.” I ask what it is that determines my experimental results, then. You cannot answer. Fine, then how do you justify ruling out the possibility that the quantum equations give such excellent predictions because they are, oh, say, meaningful?

I don’t mean to trivialize questions of reality or meaning. But to call something “meaningless” and say that the argument is now resolved, finished, over, done with, you must have a theory of exactly how it is meaningless. And when the answer is given, the question should seem no longer mysterious.

As you may recall from Semantic Stopsigns, there are words and phrases which are not so much answers to questions, as cognitive traffic signals which indicate you should stop asking questions. “Why does anything exist in the first place? God!” is the classical example, but there are others, such as “Élan vital!”

Tell people to “shut up and calculate” because you don’t know what the calculations mean, and inside of five years, “Shut up!” will be masquerading as a positive theory of quantum mechanics.

I have the highest respect for any historical physicists who even came close to actually shutting up and calculating, who were genuinely conservative in assessing what they did and didn’t know. This is the best they could possibly do without actually being Hugh Everett, and I award them fifty rationality points. My scorn is reserved for those who interpreted “We don’t know why it works” as the positive knowledge that the equations were definitely not real.

I mean, if that trick worked, it would be too good to confine to one subfield. Why shouldn’t physicists use the “not real” loophole outside of quantum mechanics?

“Hey, doesn’t your new ‘yarn theory’ violate Special Relativity?”

“Nah, the equations are meaningless. Say, doesn’t your model of ‘chaotic evil inflation’ violate CPT symmetry?”

“My equations are even more meaningless than your equations! So your criticism double doesn’t count.”

And if that doesn’t work, try writing yourself a Get Out of Jail Free card.

If there is a moral to the whole story, it is the moral of how very hard it is to stay in a state of confessed confusion, without making up a story that gives you closure—how hard it is to avoid manipulating your ignorance as if it were definite knowledge that you possessed.

239
If ManyWorlds Had Come First

Not that I’m claiming I could have done better, if I’d been born into that time, instead of this one . . .

Macroscopic decoherence, a.k.a. manyworlds, was first proposed in a 1957 paper by Hugh Everett III. The paper was ignored. John Wheeler told Everett to see Niels Bohr. Bohr didn’t take him seriously.

Crushed, Everett left academic physics, invented the general use of Lagrange multipliers in optimization problems, and became a multimillionaire.

It wasn’t until 1970, when Bryce DeWitt (who coined the term “manyworlds”) wrote an article for Physics Today, that the general field was first informed of Everett’s ideas. Macroscopic decoherence has been gaining advocates ever since, and may now be the majority viewpoint (or not).

But suppose that decoherence and macroscopic decoherence had been realized immediately following the discovery of entanglement, in the 1920s. And suppose that no one had proposed collapse theories until 1957. Would decoherence now be steadily declining in popularity, while collapse theories were slowly gaining steam?

Imagine an alternate Earth, where the very first physicist to discover entanglement and superposition said, “Holy flaming monkeys, there’s a zillion other Earths out there!”

In the years since, many hypotheses have been proposed to explain the mysterious Born probabilities. But no one has yet suggested a collapse postulate. That possibility simply has not occurred to anyone.

One day, Huve Erett walks into the office of Biels Nohr . . .

“I just don’t understand,” Huve Erett said, “why no one in physics even seems interested in my hypothesis. Aren’t the Born statistics the greatest puzzle in modern quantum theory?”

Biels Nohr sighed. Ordinarily, he wouldn’t even bother, but something about the young man compelled him to try.

“Huve,” says Nohr, “every physicist meets dozens of people per year who think they’ve explained the Born statistics. If you go to a party and tell someone you’re a physicist, chances are at least one in ten they’ve got a new explanation for the Born statistics. It’s one of the most famous problems in modern science, and worse, it’s a problem that everyone thinks they can understand. To get attention, a new Born hypothesis has to be . . . pretty darn good.”

“And this,” Huve says, “this isn’t good?”

Huve gestures to the paper he’d brought to Biels Nohr. It is a short paper. The title reads, “The Solution to the Born Problem.” The body of the paper reads:

When you perform a measurement on a quantum system, all parts of the wavefunction except one point vanish, with the survivor chosen non-deterministically in a way determined by the Born statistics.

“Let me make absolutely sure,” Nohr says carefully, “that I understand you. You’re saying that we’ve got this wavefunction—evolving according to the Wheeler-DeWitt equation—and, all of a sudden, the whole wavefunction, except for one part, just spontaneously goes to zero amplitude. Everywhere at once. This happens when, way up at the macroscopic level, we ‘measure’ something.”

“Right!” Huve says.

“So the wavefunction knows when we ‘measure’ it. What exactly is a ‘measurement’? How does the wavefunction know we’re here? What happened before humans were around to measure things?”

“Um . . .” Huve thinks for a moment. Then he reaches out for the paper, scratches out “When you perform a measurement on a quantum system,” and writes in, “When a quantum superposition gets too large.”

Huve looks up brightly. “Fixed!”

“I see,” says Nohr. “And how large is ‘too large’?”

“At the 50-micron level, maybe,” Huve says, “I hear they haven’t tested that yet.”

Suddenly a student sticks his head into the room. “Hey, did you hear? They just verified superposition at the 50-micron level.”

“Oh,” says Huve, “um, whichever level, then. Whatever makes the experimental results come out right.”

Nohr grimaces. “Look, young man, the truth here isn’t going to be comfortable. Can you hear me out on this?”

“Yes,” Huve says, “I just want to know why physicists won’t listen to me.”

“All right,” says Nohr. He sighs. “Look, if this theory of yours were actually true—if whole sections of the wavefunction just instantaneously vanished—it would be . . . let’s see. The only law in all of quantum mechanics that is non-linear, non-unitary, non-differentiable and discontinuous. It would prevent physics from evolving locally, with each piece only looking at its immediate neighbors. Your ‘collapse’ would be the only fundamental phenomenon in all of physics with a preferred basis and a preferred space of simultaneity. Collapse would be the only phenomenon in all of physics that violates CPT symmetry, Liouville’s Theorem, and Special Relativity. In your original version, collapse would also have been the only phenomenon in all of physics that was inherently mental. Have I left anything out?”

“Collapse is also the only acausal phenomenon,” Huve points out. “Doesn’t that make the theory more wonderful and amazing?”

“I think, Huve,” says Nohr, “that physicists may view the exceptionalism of your theory as a point not in its favor.”

“Oh,” said Huve, taken aback. “Well, I think I can fix that non-differentiability thing by postulating a second-order term in the—”

“Huve,” says Nohr, “I don’t think you’re getting my point, here. The reason physicists aren’t paying attention to you, is that your theory isn’t physics. It’s magic.”

“But the Born statistics are the greatest puzzle of modern physics, and this theory provides a mechanism for the Born statistics!” Huve protests.

“No, Huve, it doesn’t,” Nohr says wearily. “That’s like saying that you’ve ‘provided a mechanism’ for electromagnetism by saying that there are little angels pushing the charged particles around in accordance with Maxwell’s equations. Instead of saying, ‘Here are Maxwell’s equations, which tells the angels where to push the electrons,’ we just say, ‘Here are Maxwell’s equations’ and are left with a strictly simpler theory. Now, we don’t know why the Born statistics happen. But you haven’t given the slightest reason why your ‘collapse postulate’ should eliminate worlds in accordance with the Born statistics, rather than something else. You’re not even making use of the fact that quantum evolution is unitary—”

“That’s because it’s not,” interjects Huve.

“—which everyone pretty much knows has got to be the key to the Born statistics, somehow. Instead you’re merely saying, ‘Here are the Born statistics, which tell the collapser how to eliminate worlds,’ and it’s strictly simpler to just say ‘Here are the Born statistics.’”

“But—” says Huve.

“Also,” says Nohr, raising his voice, “you’ve given no justification for why there’s only one surviving world left by the collapse, or why the collapse happens before any humans get superposed, which makes your theory really suspicious to a modern physicist. This is exactly the sort of untestable hypothesis that the ‘One Christ’ crowd uses to argue that we should ‘teach the controversy’ when we tell high school students about other Earths.”

“I’m not a One-Christer!” protests Huve.

“Fine,” Nohr says, “then why do you just assume there’s only one world left? And that’s not the only problem with your theory. Which part of the wavefunction gets eliminated, exactly? And in which basis? It’s clear that the whole wavefunction isn’t being compressed down to a delta, or ordinary quantum computers couldn’t stay in superposition when any collapse occurred anywhere—heck, ordinary molecular chemistry might start failing—”

Huve quickly crosses out “one point” on his paper, writes in “one part,” and then says, “Collapse doesn’t compress the wavefunction down to one point. It eliminates all the amplitude except one world, but leaves all the amplitude in that world.”

“Why?” says Nohr. “In principle, once you postulate ‘collapse,’ then ‘collapse’ could eliminate any part of the wavefunction, anywhere—why just one neat world left? Does the collapser know we’re in here?”

Huve says, “It leaves one whole world because that’s what fits our experiments.”

“Huve,” Nohr says patiently, “the term for that is ‘post hoc.’ Furthermore, decoherence is a continuous process. If you partition by whole brains with distinct neurons firing, the partitions have almost zero mutual interference within the wavefunction. But plenty of other processes overlap a great deal. There’s no possible way you can point to ‘one world’ and eliminate everything else without making completely arbitrary choices, including an arbitrary choice of basis—”

“But—” Huve says.

“And above all,” Nohr says, “the reason you can’t tell me which part of the wavefunction vanishes, or exactly when it happens, or exactly what triggers it, is that if we did adopt this theory of yours, it would be the only informally specified, qualitative fundamental law taught in all of physics. Soon no two physicists anywhere would agree on the exact details! Why? Because it would be the only fundamental law in all of modern physics that was believed without experimental evidence to nail down exactly how it worked.”

“What, really?” says Huve. “I thought a lot of physics was more informal than that. I mean, weren’t you just talking about how it’s impossible to point to ‘one world’?”

“That’s because worlds aren’t fundamental, Huve! We have massive experimental evidence underpinning the fundamental law, the Wheeler-DeWitt equation, that we use to describe the evolution of the wavefunction. We just apply exactly the same equation to get our description of macroscopic decoherence. But for difficulties of calculation, the equation would, in principle, tell us exactly when macroscopic decoherence occurred. We don’t know where the Born statistics come from, but we have massive evidence for what the Born statistics are. But when I ask you when, or where, collapse occurs, you don’t know—because there’s no experimental evidence whatsoever to pin it down. Huve, even if this ‘collapse postulate’ worked the way you say it does, there’s no possible way you could know it! Why not a gazillion other equally magical possibilities?”

Huve raises his hands defensively. “I’m not saying my theory should be taught in the universities as accepted truth! I just want it experimentally tested! Is that so wrong?”

“You haven’t specified when collapse happens, so I can’t construct a test that falsifies your theory,” says Nohr. “Now with that said, we’re already looking experimentally for any part of the quantum laws that change at increasingly macroscopic levels. Both on general principles, in case there’s something in the 20th decimal point that only shows up in macroscopic systems, and also in the hopes we’ll discover something that sheds light on the Born statistics. We check decoherence times as a matter of course. But we keep a broad outlook on what might be different. Nobody’s going to privilege your non-linear, non-unitary, non-differentiable, non-local, non-CPT-symmetric, non-relativistic, a-frikkin’-causal, faster-than-light, in-bloody-formal ‘collapse’ when it comes to looking for clues. Not until they see absolutely unmistakable evidence. And believe me, Huve, it’s going to take a hell of a lot of evidence to unmistake this. Even if we did find anomalous decoherence times, and I don’t think we will, it wouldn’t force your ‘collapse’ as the explanation.”

“What?” says Huve. “Why not?”

“Because there’s got to be a billion more explanations that are more plausible than violating Special Relativity,” says Nohr. “Do you realize that if this really happened, there would only be a single outcome when you measured a photon’s polarization? Measuring one photon in an entangled pair would influence the other photon a light-year away. Einstein would have a heart attack.”

“It doesn’t really violate Special Relativity,” says Huve. “The collapse occurs in exactly the right way to prevent you from ever actually detecting the faster-than-light influence.”

“That’s not a point in your theory’s favor,” says Nohr. “Also, Einstein would still have a heart attack.”

“Oh,” says Huve. “Well, we’ll say that the relevant aspects of the particle don’t exist until the collapse occurs. If something doesn’t exist, influencing it doesn’t violate Special Relativity—”

“You’re just digging yourself deeper. Look, Huve, as a general principle, theories that are actually correct don’t generate this level of confusion. But above all, there isn’t any evidence for it. You have no logical way of knowing that collapse occurs, and no reason to believe it. You made a mistake. Just say ‘oops’ and get on with your life.”

“But they could find the evidence someday,” says Huve.

“I can’t think of what evidence could determine this particular one-world hypothesis as an explanation, but in any case, right now we haven’t found any such evidence,” says Nohr. “We haven’t found anything even vaguely suggestive of it! You can’t update on evidence that could theoretically arrive someday but hasn’t arrived! Right now, today, there’s no reason to spend valuable time thinking about this rather than a billion other equally magical theories. There’s absolutely nothing that justifies your belief in ‘collapse theory’ any more than believing that someday we’ll learn to transmit faster-than-light messages by tapping into the acausal effects of praying to the Flying Spaghetti Monster!”

Huve draws himself up with wounded dignity. “You know, if my theory is wrong—and I do admit it might be wrong—”

“If?” says Nohr. “Might?”

“If, I say, my theory is wrong,” Huve continues, “then somewhere out there is another world where I am the famous physicist and you are the lone outcast!”

Nohr buries his head in his hands. “Oh, not this again. Haven’t you heard the saying, ‘Live in your own world’? And you of all people—”

“Somewhere out there is a world where the vast majority of physicists believe in collapse theory, and no one has even suggested macroscopic decoherence over the last thirty years!”

Nohr raises his head, and begins to laugh.

“What’s so funny?” Huve says suspiciously.

Nohr just laughs harder. “Oh, my! Oh, my! You really think, Huve, that there’s a world out there where they’ve known about quantum physics for thirty years, and nobody has even thought there might be more than one world?”

“Yes,” Huve says, “that’s exactly what I think.”

“Oh my! So you’re saying, Huve, that physicists detect superposition in microscopic systems, and work out quantitative equations that govern superposition in every single instance they can test. And for thirty years, not one person says, ‘Hey, I wonder if these laws happen to be universal.’”

“Why should they?” says Huve. “Physical models sometimes turn out to be wrong when you examine new regimes.”

“But to not even think of it?” Nohr says incredulously. “You see apples falling, work out the law of gravity for all the planets in the solar system except Jupiter, and it doesn’t even occur to you to apply it to Jupiter because Jupiter is too large? That’s like, like some kind of comedy routine where the guy opens a box, and it contains a spring-loaded pie, so the guy opens another box, and it contains another spring-loaded pie, and the guy just keeps doing this without even thinking of the possibility that the next box contains a pie too. You think John von Neumann, who may have been the highest-g human in history, wouldn’t think of it?”

“That’s right,” Huve says, “He wouldn’t. Ponder that.”

“This is the world where my good friend Ernest formulates his Schrödinger’s Cat thought experiment, and in this world, the thought experiment goes: ‘Hey, suppose we have a radioactive particle that enters a superposition of decaying and not decaying. Then the particle interacts with a sensor, and the sensor goes into a superposition of going off and not going off. The sensor interacts with an explosive, that goes into a superposition of exploding and not exploding; which interacts with the cat, so the cat goes into a superposition of being alive and dead. Then a human looks at the cat,’ and at this point Schrödinger stops, and goes, ‘gee, I just can’t imagine what could happen next.’ So Schrödinger shows this to everyone else, and they’re also like ‘Wow, I got no idea what could happen at this point, what an amazing paradox.’ Until finally you hear about it, and you’re like, ‘hey, maybe at that point half of the superposition just vanishes, at random, faster than light,’ and everyone else is like, ‘Wow, what a great idea!’”

“That’s right,” Huve says again. “It’s got to have happened somewhere.”

“Huve, this is a world where every single physicist, and probably the whole damn human species, is too dumb to sign up for cryonics! We’re talking about the Earth where George W. Bush is President.”

240
Where Philosophy Meets Science

Looking back on early quantum physics—not for purposes of admonishing the major figures, or to claim that we could have done better if we’d been born into that era, but in order to try and learn a moral, and do better next time—looking back on the dark ages of quantum physics, I say, I would nominate as the “most basic” error . . .

. . . not that they tried to reverse course on the last three thousand years of science suggesting that mind was complex within physics rather than fundamental in physics. This is Science, and we do have revolutions here. Every now and then you’ve got to reverse a trend. The future is always absurd and never unlawful.

I would nominate, as the basic error not to repeat next time, that the early scientists forgot that they themselves were made out of particles.

I mean, I’m sure that most of them knew it in theory.

And yet they didn’t notice that putting a sensor to detect a passing electron, or even knowing about the electron’s history, was an example of “particles in different places.” So they didn’t notice that a quantum theory of distinct configurations already explained the experimental result, without any need to invoke consciousness.

In the ancestral environment, humans were often faced with the adaptively relevant task of predicting other humans. For which purpose you thought of your fellow humans as having thoughts, knowing things and feeling things, rather than thinking of them as being made up of particles. In fact, many hunter-gatherer tribes may not even have known that particles existed. It’s much more intuitive—it feels simpler—to think about someone “knowing” something, than to think about their brain’s particles occupying a different state. It’s easier to phrase your explanations in terms of what people know; it feels more natural; it leaps more readily to mind.

Just as, once upon a time, it was easier to imagine Thor throwing lightning bolts, than to imagine Maxwell’s Equations—even though Maxwell’s Equations can be described by a computer program vastly smaller than the program for an intelligent agent like Thor.

So the ancient physicists found it natural to think, “I know where the photon was . . . what difference could that make?” Not, “My brain’s particles’ current state correlates to the photon’s history . . . what difference could that make?”

And, similarly, because it felt easy and intuitive to model reality in terms of people knowing things, and the decomposition of knowing into brain states did not leap so readily to mind, it seemed like a simple theory to say that a configuration could have amplitude only “if you didn’t know better.”

To turn the dualistic quantum hypothesis into a formal theory—one that could be written out as a computer program, without human scientists deciding when an “observation” occurred—you would have to specify what it meant for an “observer” to “know” something, in terms your computer program could compute.

So is your theory of fundamental physics going to examine all the particles in a human brain, and decide when those particles “know” something, in order to compute the motions of particles? But then how do you compute the motion of the particles in the brain itself? Wouldn’t there be a potential infinite recursion?

But so long as the terms of the theory were being processed by human scientists, they just knew when an “observation” had occurred. You said an “observation” occurred whenever it had to occur in order for the experimental predictions to come out right—a subtle form of constant tweaking.

(Remember, the basics of quantum theory were formulated before Alan Turing said anything about Turing machines, and way before the concept of computation was popularly known. The distinction between an effective formal theory, and one that required human interpretation, was not as clear then as now. Easy to pinpoint the problems in hindsight; you shouldn’t learn the lesson that problems are usually this obvious in foresight.)

Looking back, it may seem like one meta-lesson to learn from history, is that philosophy really matters in science—it’s not just some adjunct of a separate academic field.

After all, the early quantum scientists were doing all the right experiments. It was their interpretation that was off. And the problems of interpretation were not the result of their getting the statistics wrong.

Looking back, it seems like the errors they made were errors in the kind of thinking that we would describe as, well, “philosophical.”

When we look back and ask, “How could the early quantum scientists have done better, even in principle?” it seems that the insights they needed were philosophical ones.

And yet it wasn’t professional philosophers who swooped in and solved the problem and cleared up the mystery and made everything normal again. It was, well, physicists.

Arguably, Leibniz was at least as foresightful about quantum physics, as Democritus was once thought to have been foresightful about atoms. But that is hindsight. It’s the result of looking at the solution, and thinking back, and saying, “Hey, Leibniz said something like that.”

Even where one philosopher gets it right in advance, it’s usually science that ends up telling us which philosopher is right—not the prior consensus of the philosophical community.

I think this has something fundamental to say about the nature of philosophy, and the interface between philosophy and science.

It was once said that every science begins as philosophy, but then grows up and leaves the philosophical womb, so that at any given time, “Philosophy” is what we haven’t turned into science yet.

I suggest that when we look at the history of quantum physics and say, “The insights they needed were philosophical insights,” what we are really seeing is that the insight they needed was of a form that is not yet taught in standardized academic classes, and not yet reduced to calculation.

Once upon a time, the notion of the scientific method—updating beliefs based on experimental evidence—was a philosophical notion. But it was not championed by professional philosophers. It was the real-world power of science that showed that scientific epistemology was good epistemology, not a prior consensus of philosophers.

Today, this philosophy of belief-updating is beginning to be reduced to calculation—statistics, Bayesian probability theory.

But back in Galileo’s era, it was solely vague verbal arguments that said you should try to produce numerical predictions of experimental results, rather than consulting the Bible or Aristotle.

At the frontier of science, and especially at the frontier of scientific chaos and scientific confusion, you find problems of thinking that are not taught in academic courses, and that have not been reduced to calculation. And this will seem like a domain of philosophy; it will seem that you must do philosophical thinking in order to sort out the confusion. But when history looks back, I’m afraid, it is usually not a professional philosopher who wins all the marbles—because it takes intimate involvement with the scientific domain in order to do the philosophical thinking. Even if, afterward, it all seems knowable a priori; and even if, afterward, some philosopher out there actually got it a priori; even so, it takes intimate involvement to see it in practice, and experimental results to tell the world which philosopher won.

I suggest that, like ethics, philosophy really is important, but it is only practiced effectively from within a science. Trying to do the philosophy of a frontier science, as a separate academic profession, is as much a mistake as trying to have separate ethicists. You end up with ethicists who speak mainly to other ethicists, and philosophers who speak mainly to other philosophers.

This is not to say that there is no place for professional philosophers in the world. Some problems are so chaotic that there is no established place for them at all in the halls of science. But those “professional philosophers” would be very, very wise to learn every scrap of relevant-seeming science that they can possibly get their hands on. They should not be surprised at the prospect that experiment, and not debate, will finally settle the argument. They should not flinch from running their own experiments, if they can possibly think of any.

That, I think, is the lesson of history.

241
Thou Art Physics

Three months ago—jeebers, has it really been that long?—I posed the following homework assignment: Do a stack trace of the human cognitive algorithms that produce debates about “free will.” Note that this task is strongly distinguished from arguing that free will does or does not exist.

Now, as expected, people are asking, “If the future is determined, how can our choices control it?” The wise reader can guess that it all adds up to normality; but this leaves the question of how.

People hear: “The universe runs like clockwork; physics is deterministic; the future is fixed.” And their minds form a causal network that looks like this:

Here we see the causes “Me” and “Physics,” competing to determine the state of the “Future” effect. If the “Future” is fully determined by “Physics,” then obviously there is no room for it to be affected by “Me.”

This causal network is not an explicit philosophical belief. It’s implicit—a background representation of the brain, controlling which philosophical arguments seem “reasonable.” It just seems like the way things are.

Every now and then, another neuroscience press release appears, claiming that, because researchers used an fMRI to spot the brain doing something-or-other during a decision process, it’s not you who chooses, it’s your brain.

Likewise that old chestnut, “Reductionism undermines rationality itself. Because then, every time you said something, it wouldn’t be the result of reasoning about the evidence—it would be merely quarks bopping around.”

Of course the actual diagram should be:

Or better yet:

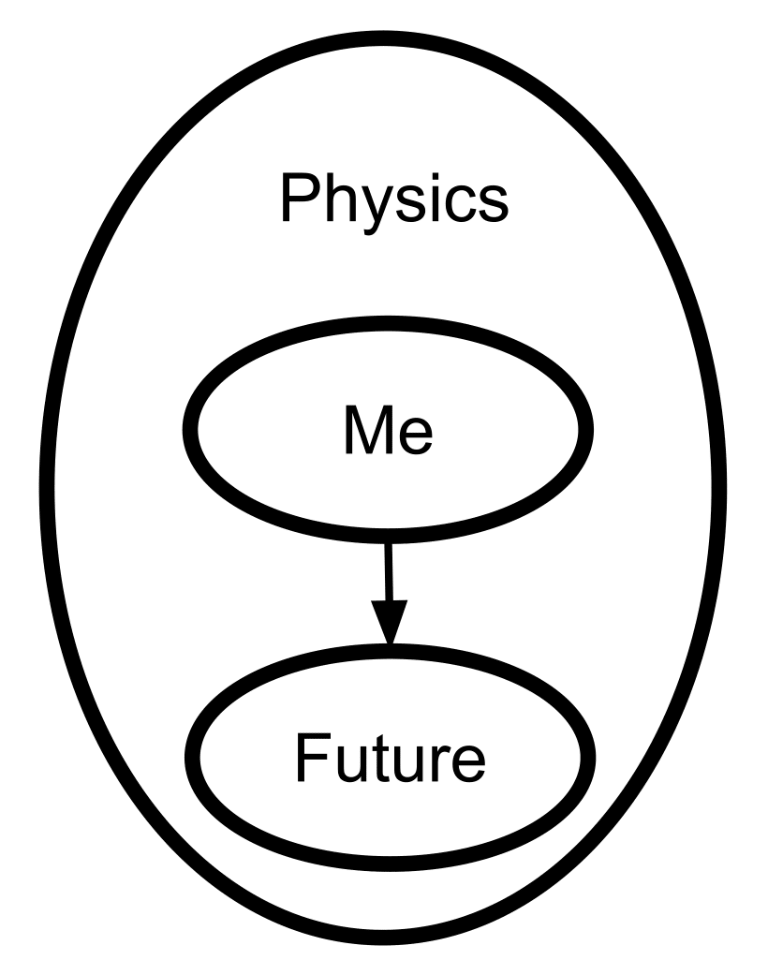
Why is this not obvious? Because there are many levels of organization that separate our models of our thoughts—our emotions, our beliefs, our agonizing indecisions, and our final choices—from our models of electrons and quarks.

We can intuitively visualize that a hand is made of fingers (and thumb and palm). To ask whether it’s really our hand that picks something up, or merely our fingers, thumb, and palm, is transparently a wrong question.

But the gap between physics and cognition cannot be crossed by direct visualization. No one can visualize atoms making up a person, the way they can see fingers making up a hand.

And so it requires constant vigilance to maintain your perception of yourself as an entity within physics.

This vigilance is one of the great keys to philosophy, like the Mind Projection Fallacy. You will recall that it is this point which I nominated as having tripped up the quantum physicists who failed to imagine macroscopic decoherence; they did not think to apply the laws to themselves.

Beliefs, desires, emotions, morals, goals, imaginations, anticipations, sensory perceptions, fleeting wishes, ideals, temptations . . . You might call this the “surface layer” of the mind, the parts-of-self that people can see even without science. If I say, “It is not you who determines the future, it is your desires, plans, and actions that determine the future,” you can readily see the part-whole relations. It is immediately visible, like fingers making up a hand. There are other part-whole relations all the way down to physics, but they are not immediately visible.

“Compatibilism” is the philosophical position that “free will” can be intuitively and satisfyingly defined in such a way as to be compatible with deterministic physics. “Incompatibilism” is the position that free will and determinism are incompatible.

My position might perhaps be called “Requiredism.” When agency, choice, control, and moral responsibility are cashed out in a sensible way, they require determinism—at least some patches of determinism within the universe. If you choose, and plan, and act, and bring some future into being, in accordance with your desire, then all this requires a lawful sort of reality; you cannot do it amid utter chaos. There must be order over at least those parts of reality that are being controlled by you. You are within physics, and so you/physics have determined the future. If it were not determined by physics, it could not be determined by you.

Or perhaps I should say, “If the future were not determined by reality, it could not be determined by you,” or “If the future were not determined by something, it could not be determined by you.” You don’t need neuroscience or physics to push naive definitions of free will into incoherence. If the mind were not embodied in the brain, it would be embodied in something else; there would be some real thing that was a mind. If the future were not determined by physics, it would be determined by something, some law, some order, some grand reality that included you within it.

But if the laws of physics control us, then how can we be said to control ourselves?

Turn it around: If the laws of physics did not control us, how could we possibly control ourselves?

How could thoughts judge other thoughts, how could emotions conflict with each other, how could one course of action appear best, how could we pass from uncertainty to certainty about our own plans, in the midst of utter chaos?

If we were not in reality, where could we be?

The future is determined by physics. What kind of physics? The kind of physics that includes the actions of human beings.

People’s choices are determined by physics. What kind of physics? The kind of physics that includes weighing decisions, considering possible outcomes, judging them, being tempted, following morals, rationalizing transgressions, trying to do better . . .

There is no point where a quark swoops in from Pluto and overrides all this.

The thoughts of your decision process are all real, they are all something. But a thought is too big and complicated to be an atom. So thoughts are made of smaller things, and our name for the stuff that stuff is made of is “physics.”

Physics underlies our decisions and includes our decisions. It does not explain them away.

Remember, physics adds up to normality; it’s your cognitive algorithms that generate confusion.

242
Many Worlds, One Best Guess

If you look at many microscopic physical phenomena—a photon, an electron, a hydrogen atom, a laser—and a million other known experimental setups—it is possible to come up with simple laws that seem to govern all small things (so long as you don’t ask about gravity). These laws govern the evolution of a highly abstract and mathematical object that I’ve been calling the “amplitude distribution,” but which is more widely referred to as the “wavefunction.”

Now there are gruesome questions about the proper generalization that covers all these tiny cases. Call an object “grue” if it appears green before January 1, 2020 and appears blue thereafter. If all emeralds examined so far have appeared green, is the proper generalization, “Emeralds are green” or “Emeralds are grue”?

The answer is that the proper generalization is “Emeralds are green.” I’m not going to go into the arguments at the moment. It is not the subject of this essay, and the obvious answer in this case happens to be correct. The true Way is not stupid: however clever you may be with your logic, it should finally arrive at the right answer rather than a wrong one.

In a similar sense, the simplest generalizations that would cover observed microscopic phenomena alone take the form of “All electrons have spin 1/2” and not “All electrons have spin 1/2 before January 1, 2020” or “All electrons have spin 1/2 unless they are part of an entangled system that weighs more than 1 gram.”

When we turn our attention to macroscopic phenomena, our sight is obscured. We cannot experiment on the wavefunction of a human in the way that we can experiment on the wavefunction of a hydrogen atom. In no case can you actually read off the wavefunction with a little quantum scanner. But in the case of, say, a human, the size of the entire organism defeats our ability to perform precise calculations or precise experiments—we cannot confirm that the quantum equations are being obeyed in precise detail.

We know that phenomena commonly thought of as “quantum” do not just disappear when many microscopic objects are aggregated. Lasers put out a flood of coherent photons, rather than, say, doing something completely different. Atoms have the chemical characteristics that quantum theory says they should, enabling them to aggregate into the stable molecules making up a human.

So in one sense, we have a great deal of evidence that quantum laws are aggregating to the macroscopic level without too much difference. Bulk chemistry still works.

But we cannot directly verify that the particles making up a human have an aggregate wavefunction that behaves exactly the way the simplest quantum laws say. Oh, we know that molecules and atoms don’t disintegrate, we know that macroscopic mirrors still reflect from the middle. We can get many high-level predictions from the assumption that the microscopic and the macroscopic are governed by the same laws, and every prediction tested has come true.

But if someone were to claim that the macroscopic quantum picture differs from the microscopic one in some as-yet-untestable detail—something that only shows up at the unmeasurable 20th decimal place of microscopic interactions, but aggregates into something bigger for macroscopic interactions—well, we can’t prove they’re wrong. It is Occam’s Razor that says, “There are zillions of new fundamental laws you could postulate in the 20th decimal place; why are you even thinking about this one?”

If we calculate using the simplest laws which govern all known cases, we find that humans end up in states of quantum superposition, just like photons in a superposition of reflecting from and passing through a half-silvered mirror. In the Schrödinger’s Cat setup, an unstable atom goes into a superposition of disintegrating, and not-disintegrating. A sensor, tuned to the atom, goes into a superposition of triggering and not-triggering. (Actually, the superposition is now a joint state of [atom-disintegrated × sensor-triggered] + [atom-stable × sensor-not-triggered].) A charge of explosives, hooked up to the sensor, goes into a superposition of exploding and not exploding; a cat in the box goes into a superposition of being dead and alive; and a human, looking inside the box, goes into a superposition of throwing up and being calm. The same law at all levels.

Human beings who interact with superposed systems will themselves evolve into superpositions. But the brain that sees the exploded cat, and the brain that sees the living cat, will have many neurons firing differently, and hence many many particles in different positions. They are very distant in the configuration space, and will communicate to an exponentially infinitesimal degree. Not the 30th decimal place, but the 10³⁰th decimal place. No particular mind, no particular cognitive causal process, sees a blurry superposition of cats.

The fact that “you” only seem to see the cat alive, or the cat dead, is exactly what the simplest quantum laws predict. So we have no reason to believe, from our experience so far, that the quantum laws are in any way different at the macroscopic level than the microscopic level.

And physicists have verified superposition at steadily larger levels. Apparently an effort is currently underway to test superposition in a 50-micron object, larger than most neurons.

The existence of other versions of ourselves, and indeed other Earths, is not supposed additionally. We are simply supposing that the same laws govern at all levels, having no reason to suppose differently, and all experimental tests having succeeded so far. The existence of other decoherent Earths is a logical consequence of the simplest generalization that fits all known facts. If you think that Occam’s Razor says that the other worlds are “unnecessary entities” being multiplied, then you should check the probability-theoretic math; that is just not how Occam’s Razor works.

Yet there is one particular puzzle that seems odd in trying to extend microscopic laws universally, including to superposed humans:

If we try to get probabilities by counting the number of distinct observers, then there is no obvious reason why the integrated squared modulus of the wavefunction should correlate with statistical experimental results. There is no known reason for the Born probabilities, and it even seems that, a priori, we would expect a 50/50 probability of any binary quantum experiment going both ways, if we just counted observers.

Robin Hanson suggests that if exponentially tinier-than-average decoherent blobs of amplitude (“worlds”) are interfered with by exponentially tiny leakages from larger blobs, we will get the Born probabilities back out. I consider this an interesting possibility, because it is so normal.

(I myself have had recent thoughts along a different track: If I try to count observers the obvious way, I get strange-seeming results in general, not just in the case of quantum physics. If, for example, I split my brain into a trillion similar parts, conditional on winning the lottery while anesthetized; allow my selves to wake up and perhaps differ to small degrees from each other; and then merge them all into one self again; then counting observers the obvious way says I should be able to make myself win the lottery (if I can split my brain and merge it, as an uploaded mind might be able to do).

In this connection, I find it very interesting that the Born rule does not have a split-remerge problem. Given unitary quantum physics, Born’s rule is the unique rule that prevents “observers” from having psychic powers—which doesn’t explain Born’s rule, but is certainly an interesting fact. Given Born’s rule, even splitting and remerging worlds would still lead to consistent probabilities. Maybe physics uses better anthropics than I do!

Perhaps I should take my cues from physics, instead of trying to reason it out a priori, and see where that leads me? But I have not been led anywhere yet, so this is hardly an “answer.”)

Wallace, Deutsch, and others try to derive Born’s Rule from decision theory. I am rather suspicious of this, because it seems like there is a component of “What happens to me?” that I cannot alter by modifying my utility function. Even if I didn’t care at all about worlds where I didn’t win a quantum lottery, it still seems to me that there is a sense in which I would “mostly” wake up in a world where I didn’t win the lottery. It is this that I think needs explaining.

The point is that many hypotheses about the Born probabilities have been proposed. Not as many as there should be, because the mystery was falsely marked “solved” for a long time. But still, there have been many proposals.

There is legitimate hope of a solution to the Born puzzle without new fundamental laws. Your world does not split into exactly two new subprocesses on the exact occasion when you see “ABSORBED” or “TRANSMITTED” on the LCD screen of a photon sensor. We are constantly being superposed and decohered, all the time, sometimes along continuous dimensions—though brains are digital and involve whole neurons firing, and fire/not-fire would be an extremely decoherent state even of a single neuron . . . There would seem to be room for something unexpected to account for the Born statistics—a better understanding of the anthropic weight of observers, or a better understanding of the brain’s superpositions—without new fundamentals.

We cannot rule out, though, the possibility that a new fundamental law is involved in the Born statistics.

As Jess Riedel puts it:

If there’s one lesson we can take from the history of physics, it’s that everytime new experimental “regimes” are probed (e.g. large velocities, small sizes, large mass densities, large energies), phenomena are observed which lead to new theories (Special Relativity, quantum mechanics, General Relativity, and the Standard Model, respectively).

“Every time” is too strong. A nitpick, yes, but also an important point: you can’t just assume that any particular law will fail in a new regime. But it’s possible that a new fundamental law is involved in the Born statistics, and that this law manifests only in the 20th decimal place at microscopic levels (hence being undetectable so far) while aggregating to have substantial effects at macroscopic levels.

Could there be some law, as yet undiscovered, that causes there to be only one world?

This is a shocking notion; it implies that all our twins in the other worlds—all the different versions of ourselves that are constantly split off, not just by human researchers doing quantum measurements, but by ordinary entropic processes—are actually gone, leaving us alone! This version of Earth would be the only version that exists in local space! If the inflationary scenario in cosmology turns out to be wrong, and the topology of the universe is both finite and relatively small—so that Earth does not have the distant duplicates that would be implied by an exponentially vast universe—then this Earth could be the only Earth that exists anywhere, a rather unnerving thought!

But it is dangerous to focus too much on specific hypotheses that you have no specific reason to think about. This is the same root error of the Intelligent Design folk, who pick any random puzzle in modern genetics, and say, “See, God must have done it!” Why “God,” rather than a zillion other possible explanations?—which you would have thought of long before you postulated divine intervention, if not for the fact that you secretly started out already knowing the answer you wanted to find.

You shouldn’t even ask, “Might there only be one world?” but instead just go ahead and do physics, and raise that particular issue only if new evidence demands it.

Could there be some as-yet-unknown fundamental law, that gives the universe a privileged center, which happens to coincide with Earth—thus proving that Copernicus was wrong all along, and the Bible right?

Asking that particular question—rather than a zillion other questions in which the center of the universe is Proxima Centauri, or the universe turns out to have a favorite pizza topping and it is pepperoni—betrays your hidden agenda. And though an unenlightened one might not realize it, giving the universe a privileged center that follows Earth around through space would be rather difficult to do with any mathematically simple fundamental law.

So too with asking whether there might be only one world. It betrays a sentimental attachment to human intuitions already proven wrong. The wheel of science turns, but it doesn’t turn backward.

We have specific reasons to be highly suspicious of the notion of only one world. The notion of “one world” exists on a higher level of organization, like the location of Earth in space; on the quantum level there are no firm boundaries (though brains that differ by entire neurons firing are certainly decoherent). How would a fundamental physical law identify one high-level world?

Much worse, any physical scenario in which there was a single surviving world, so that any measurement had only a single outcome, would violate Special Relativity.

If the same laws are true at all levels—i.e., if many-worlds is correct—then when you measure one of a pair of entangled polarized photons, you end up in a world in which the photon is polarized, say, up-down, and alternate versions of you end up in worlds where the photon is polarized left-right. From your perspective before doing the measurement, the probabilities are 50/50. Light-years away, someone measures the other photon at a 20^° angle to your own basis. From their perspective, too, the probability of getting either immediate result is 50/50—they maintain an invariant state of generalized entanglement with your faraway location, no matter what you do. But when the two of you meet, years later, your probability of meeting a friend who got the same result is 11.6%, rather than 50%.

If there is only one global world, then there is only a single outcome of any quantum measurement. Either you measure the photon polarized up-down, or left-right, but not both. Light-years away, someone else’s probability of measuring the photon polarized similarly in a 20^° rotated basis actually changes from 50/50 to 11.6%.

You cannot possibly interpret this as a case of merely revealing properties that were already there; this is ruled out by Bell’s Theorem. There does not seem to be any possible consistent view of the universe in which both quantum measurements have a single outcome, and yet both measurements are predetermined, neither influencing the other. Something has to actually change, faster than light.

And this would appear to be a fully general objection, not just to collapse theories, but to any possible theory that gives us one global world! There is no consistent view in which measurements have single outcomes, but are locally determined (even locally randomly determined). Some mysterious influence has to cross a spacelike gap.

This is not a trivial matter. You cannot save yourself by waving your hands and saying, “the influence travels backward in time to the entangled photons’ creation, then forward in time to the other photon, so it never actually crosses a spacelike gap.” (This view has been seriously put forth, which gives you some idea of the magnitude of the paradox implied by one global world!) One measurement has to change the other, so which measurement happens first? Is there a global space of simultaneity? You can’t have both measurements happen “first” because under Bell’s Theorem, there’s no way local information could account for observed results, etc.

Incidentally, this experiment has already been performed, and if there is a mysterious influence it would have to travel six million times as fast as light in the reference frame of the Swiss Alps. Also, the mysterious influence has been experimentally shown not to care if the two photons are measured in reference frames which would cause each measurement to occur “before the other.”

Special Relativity seems counterintuitive to us humans—like an arbitrary speed limit, which you could get around by going backward in time, and then forward again. A law you could escape prosecution for violating, if you managed to hide your crime from the authorities.

But what Special Relativity really says is that human intuitions about space and time are simply wrong. There is no global “now,” there is no “before” or “after” across spacelike gaps. The ability to visualize a single global world, even in principle, comes from not getting Special Relativity on a gut level. Otherwise it would be obvious that physics proceeds locally with invariant states of distant entanglement, and the requisite information is simply not locally present to support a globally single world.

It might be that this seemingly impeccable logic is flawed—that my application of Bell’s Theorem and relativity to rule out any single global world contains some hidden assumption of which I am unaware—

—but consider the burden that a single-world theory must now shoulder! There is absolutely no reason in the first place to suspect a global single world; this is just not what current physics says! The global single world is an ancient human intuition that was disproved, like the idea of a universal absolute time. The superposition principle is visible even in half-silvered mirrors; experiments are verifying the disproof at steadily larger levels of superposition—but above all there is no longer any reason to privilege the hypothesis of a global single world. The ladder has been yanked out from underneath that human intuition.

There is no experimental evidence that the macroscopic world is single (we already know the microscopic world is superposed). And the prospect necessarily either violates Special Relativity, or takes an even more miraculous-seeming leap and violates seemingly impeccable logic. The latter, of course, being much more plausible in practice. But it isn’t really that plausible in an absolute sense. Without experimental evidence, it is generally a bad sign to have to postulate arbitrary logical miracles.

As for quantum non-realism, it appears to me to be nothing more than a Get Out of Jail Free card. “It’s okay to violate Special Relativity because none of this is real anyway!” The equations cannot reasonably be hypothesized to deliver such excellent predictions for literally no reason. Bell’s Theorem rules out the obvious possibility that quantum theory represents imperfect knowledge of something locally deterministic.

Furthermore, macroscopic decoherence gives us a perfectly realistic understanding of what is going on, in which the equations deliver such good predictions because they mirror reality. And so the idea that the quantum equations are just “meaningless,” and therefore it is okay to violate Special Relativity, so we can have one global world after all, is not necessary. To me, quantum non-realism appears to be a huge bluff built around semantic stopsigns like “Meaningless!”

It is not quite safe to say that the existence of multiple Earths is as well-established as any other truth of science. The existence of quantum other worlds is not so well-established as the existence of trees, which most of us can personally observe.

Maybe there is something in that 20th decimal place, which aggregates to something bigger in macroscopic events. Maybe there’s a loophole in the seemingly iron logic which says that any single global world must violate Special Relativity, because the information to support a single global world is not locally available. And maybe the Flying Spaghetti Monster is just messing with us, and the world we know is a lie.

So all we can say about the existence of multiple Earths, is that it is as rationally probable as e.g. the statement that spinning black holes do not violate conservation of angular momentum. We have extremely fundamental reasons, having to do with the rotational symmetry of space, to suspect that conservation of angular momentum is built into the underlying nature of physics. And we have no specific reason to suspect this particular violation of our old generalizations in a higher-energy regime.

But we haven’t actually checked conservation of angular momentum for rotating black holes—so far as I know. (And as I am talking here about rational guesses in states of partial knowledge, the point is exactly the same if the observation has been made and I do not know it yet.) And black holes are a more massive regime. So the obedience of black holes is not quite as assured as that my toilet conserves angular momentum while flushing, which come to think, I haven’t checked either . . .

Yet if you make the mistake of thinking too hard about this one particular possibility, instead of zillions of other possibilities—and especially if you don’t understand the fundamental reason why angular momentum is conserved—then it may start seeming more and more plausible that “spinning black holes violate conservation of angular momentum,” as you think of more and more vaguely plausible-sounding reasons it could be true.

But the rational probability is pretty damned small.

Likewise the rational probability that there is only one Earth.

I mention this to explain my habit of talking as if many-worlds is an obvious fact. Many-worlds is an obvious fact, if you have all your marbles lined up correctly (understand very basic quantum physics, know the formal probability theory of Occam’s Razor, understand Special Relativity, etc.) It is in fact considerably more obvious to me than the proposition that spinning black holes should obey conservation of angular momentum.

The only reason why many-worlds is not universally acknowledged as a direct prediction of physics which requires magic to violate, is that a contingent accident of our Earth’s scientific history gave an entrenched academic position to a phlogiston-like theory that had an unobservable faster-than-light magical “collapse” devouring all other worlds. And many academic physicists do not have a mathematical grasp of Occam’s Razor, which is the usual method for ridding physics of invisible angels. So when they encounter many-worlds and it conflicts with their (undermined) intuition that only one world exists, they say, “Oh, that’s multiplying entities”—which is just flatly wrong as probability theory—and go on about their daily lives.

I am not in academia. I am not constrained to bow and scrape to some senior physicist who hasn’t grasped the obvious, but who will be reviewing my journal articles. I need have no fear that I will be rejected for tenure on account of scaring my students with “science-fiction tales of other Earths.” If I can’t speak plainly, who can?

So let me state then, very clearly, on behalf of any and all physicists out there who dare not say it themselves: Many-worlds wins outright given our current state of evidence. There is no more reason to postulate a single Earth, than there is to postulate that two colliding top quarks would decay in a way that violates Conservation of Energy. It takes more than an unknown fundamental law; it takes magic.

The debate should already be over. It should have been over fifty years ago. The state of evidence is too lopsided to justify further argument. There is no balance in this issue. There is no rational controversy to teach. The laws of probability theory are laws, not suggestions; there is no flexibility in the best guess given this evidence. Our children will look back at the fact that we were STILL ARGUING about this in the early twenty-first century, and correctly deduce that we were nuts.

We have embarrassed our Earth long enough by failing to see the obvious. So for the honor of my Earth, I write as if the existence of many-worlds were an established fact, because it is. The only question now is how long it will take for the people of this world to update.

Part T
Science and Rationality

243
The Failures of Eld Science

This time there were no robes, no hoods, no masks. Students were expected to become friends, and allies. And everyone knew why you were in the classroom. It would have been pointless to pretend you weren’t in the Conspiracy.

Their sensei was Jeffreyssai, who might have been the best of his era, in his era. His students were either the most promising learners, or those whom the beisutsukai saw political advantage in molding.

Brennan fell into the latter category, and knew it. Nor had he hesitated to use his Mistress’s name to open doors. You used every avenue available to you, in seeking knowledge; that was respected here.

“—for over thirty years,” Jeffreyssai said. “Not one of them saw it; not Einstein, not Schrödinger, not even von Neumann.” He turned away from his sketcher, and toward the classroom. “I pose to you to the question: How did they fail?”

The students exchanged quick glances, a calculus of mutual risk between the wary and the merely baffled. Jeffreyssai was known to play games.

Finally Hiriwa-called-the-Black leaned forward, jangling slightly as her equation-carved bracelets shifted on her ankles. “By your years given, sensei, this was two hundred and fifty years after Newton. Surely, the scientists of that era must have grokked the concept of a universal law.”

“Knowing the universal law of gravity,” said the student Taji, from a nearby seat, “is not the same as understanding the concept of a universal law.” He was one of the promising ones, as was Hiriwa.

Hiriwa frowned. “No . . . it was said that Newton had been praised for discovering the first universal. Even in his own era. So it was known.” Hiriwa paused. “But Newton himself would have been gone. Was there a religious injunction against proposing further universals? Did they refrain out of respect for Newton, or were they waiting for his ghost to speak? I am not clear on how Eld science was motivated—”

“No,” murmured Taji, a laugh in his voice, “you really, really aren’t.”

Jeffreyssai’s expression was kindly. “Hiriwa, it wasn’t religion, and it wasn’t lead in the drinking water, and they didn’t all have Alzheimer’s, and they weren’t sitting around all day reading webcomics. Forget the catalogue of horrors out of ancient times. Just think in terms of cognitive errors. What could Eld science have been thinking wrong?”

Hiriwa sat back with a sigh. “Sensei, I truly cannot imagine a snafu that would do that.”

“It wouldn’t be just one mistake,” Taji corrected her. “As the saying goes: Mistakes don’t travel alone; they hunt in packs.”

“But the entire human species?” said Hiriwa. “Thirty years?”

“It wasn’t the entire human species, Hiriwa,” said Styrlyn. He was one of the older-looking students, wearing a short beard speckled in gray. “Maybe one in a hundred thousand could have written out Schrödinger’s Equation from memory. So that would have been their first and primary error—failure to concentrate their forces.”

“Spare us the propaganda!” Jeffreyssai’s gaze was suddenly fierce. “You are not here to proselytize for the Cooperative Conspiracy, my lord politician! Bend not the truth to make your points! I believe your Conspiracy has a phrase: ‘Comparative advantage.’ Do you really think that it would have helped to call in the whole human species, as it existed at that time, to debate quantum physics?”

Styrlyn didn’t flinch. “Perhaps not, sensei,” he said. “But if you are to compare that era to this one, it is a consideration.”

Jeffreyssai moved his hand flatly through the air; the maybe-gesture he used to dismiss an argument that was true but not relevant. “It is not what I would call a primary mistake. The puzzle should not have required a billion physicists to solve.”

“I can think of more specific ancient horrors,” said Taji. “Spending all day writing grant proposals. Teaching undergraduates who would rather be somewhere else. Needing to publish thirty papers a year to get tenure . . .”

“But we are not speaking of only the lower-status scientists,” said Yin; she wore a slightly teasing grin. “It was said of Schrödinger that he retired to a villa for a month, with his mistress to provide inspiration, and emerged with his eponymous equation. We consider it a famous historical success of our methodology. Some Eld physicists did understand how to focus their mental energies; and would have been senior enough to do so, had they chose.”

“True,” Taji said. “In the end, administrative burdens are only a generic obstacle. Likewise such answers as, ‘They were not trained in probability theory, and did not know of cognitive biases.’ Our sensei seems to desire some more specific reply.”

Jeffreyssai lifted an eyebrow encouragingly. “Don’t dismiss your line of thought so quickly, Taji; it begins to be relevant. What kind of system would create administrative burdens on its own people?”

“A system that failed to support its people adequately,” said Styrlyn. “One that failed to value their work.”

“Ah,” said Jeffreyssai. “But there is a student who has not yet spoken. Brennan?”

Brennan didn’t jump. He deliberately waited just long enough to show he wasn’t scared, and then said, “Lack of pragmatic motivation, sensei.”

Jeffreyssai smiled slightly. “Expand.”

What kind of system would create administrative burdens on its own people?, their sensei had asked them. The other students were pursuing their own lines of thought. Brennan, hanging back, had more attention to spare for his teacher’s few hints. Being the beginner wasn’t always a disadvantage—and he had been taught, long before the Bayesians took him in, to take every available advantage.

“The Manhattan Project,” Brennan said, “was launched with a specific technological end in sight: a weapon of great power, in time of war. But the error that Eld Science committed with respect to quantum physics had no immediate consequences for their technology. They were confused, but they had no desperate need for an answer. Otherwise the surrounding system would have removed all burdens from their effort to solve it. Surely the Manhattan Project must have done so—Taji? Do you know?”

Taji looked thoughtful. “Not all burdens—but I’m pretty sure they weren’t writing grant proposals in the middle of their work.”

“So,” Jeffreyssai said. He advanced a few steps, stood directly in front of Brennan’s desk. “You think Eld scientists simply weren’t trying hard enough. Because their art had no military applications? A rather competitive point of view, I should think.”

“Not necessarily,” Brennan said calmly. “Pragmatism is a virtue of rationality also. A desired use for a better quantum theory would have helped the Eld scientists in many ways beyond just motivating them. It would have given shape to their curiosity, and told them what constituted success or failure.”

Jeffreyssai chuckled slightly. “Don’t guess so hard what I might prefer to hear, Competitor. Your first statement came closer to my hidden mark; your oh-so-Bayesian disclaimer fell wide . . . The factor I had in mind, Brennan, was that Eld scientists thought it was acceptable to take thirty years to solve a problem. Their entire social process of science was based on getting to the truth eventually. A wrong theory got discarded eventually—once the next generation of students grew up familiar with the replacement. Work expands to fill the time allotted, as the saying goes. But people can think important thoughts in far less than thirty years, if they expect speed of themselves.” Jeffreyssai suddenly slammed down a hand on the arm of Brennan’s chair. “How long do you have to dodge a thrown knife?”

“Very little time, sensei!”

“Less than a second! Two opponents are attacking you! How long do you have to guess who’s more dangerous?”

“Less than a second, sensei!”

“The two opponents have split up and are attacking two of your girlfriends! How long do you have to decide which one you truly love?”

“Less than a second, sensei!”

“A new argument shows your precious theory is flawed! How long does it take you to change your mind?”

“Less than a second, sensei!”

“WRONG! DON’T GIVE ME THE WRONG ANSWER JUST BECAUSE IT FITS A CONVENIENT PATTERN AND I SEEM TO EXPECT IT OF YOU! How long does it really take, Brennan?”

Sweat was forming on Brennan’s back, but he stopped and actually thought about it—

“ANSWER, BRENNAN!”

“No, sensei! I’m not finished thinking, sensei! An answer would be premature! Sensei!”

“Very good! Continue! But don’t take thirty years!”

Brennan breathed deeply, reforming his thoughts. He finally said, “Realistically, sensei, the best-case scenario is that I would see the problem immediately; use the discipline of suspending judgment; try to re-accumulate all the evidence before continuing; and depending on how emotionally attached I had been to the theory, use the crisis-of-belief technique to ensure I could genuinely go either way. So at least five minutes and perhaps up to an hour.”

“Good! You actually thought about it that time! Think about it every time! Break patterns! In the days of Eld Science, Brennan, it was not uncommon for a grant agency to spend six months reviewing a proposal. They permitted themselves the time! You are being graded on your speed, Brennan! The question is not whether you get there eventually! Anyone can find the truth in five thousand years! You need to move faster!”

“Yes, sensei!”

“Now, Brennan, have you just learned something new?”

“Yes, sensei!”

“How long did it take you to learn this new thing?”

An arbitrary choice there . . . “Less than a minute, sensei, from the boundary that seems most obvious.”

“Less than a minute,” Jeffreyssai repeated. “So, Brennan, how long do you think it should take to solve a major scientific problem, if you are not wasting any time?”

Now there was a trapped question if Brennan had ever heard one. There was no way to guess what time period Jeffreyssai had in mind—what the sensei would consider too long, or too short. Which meant that the only way out was to just try for the genuine truth; this would offer him the defense of honesty, little defense though it was. “One year, sensei?”

“Do you think it could be done in one month, Brennan? In a case, let us stipulate, where in principle you already have enough experimental evidence to determine an answer, but not so much experimental evidence that you can afford to make errors in interpreting it.”

Again, no way to guess which answer Jeffreyssai might want . . . “One month seems like an unrealistically short time to me, sensei.”

“A short time?” Jeffreyssai said incredulously. “How many minutes in thirty days? Hiriwa?”

“43,200, sensei,” she answered. “If you assume sixteen-hour waking periods and daily sleep, then 28,800 minutes.”

“Assume, Brennan, that it takes five whole minutes to think an original thought, rather than learning it from someone else. Does even a major scientific problem require 5,760 distinct insights?”

“I confess, sensei,” Brennan said slowly, “that I have never thought of it that way before . . . but do you tell me that is truly a realistic level of productivity?”

“No,” said Jeffreyssai, “but neither is it realistic to think that a single problem requires 5,760 insights. And yes, it has been done.”

Jeffreyssai stepped back, and smiled benevolently. Every student in the room stiffened; they knew that smile. “Though none of you hit the particular answer that I had in mind, nonetheless your answers were as reasonable as mine. Except Styrlyn’s, I’m afraid. Even Hiriwa’s answer was not entirely wrong: the task of proposing new theories was once considered a sacred duty reserved for those of high status, there being a limited supply of problems in circulation, at that time. But Brennan’s answer is particularly interesting, and I am minded to test his theory of motivation.”

Oh, hell, Brennan said silently to himself. Jeffreyssai was gesturing for Brennan to stand up before the class.

When Brenann had risen, Jeffreyssai neatly seated himself in Brennan’s chair.

“Brennan-sensei,” Jeffreyssai said, “you have five minutes to think of something stunningly brilliant to say about the failure of Eld science on quantum physics. As for the rest of us, our job will be to gaze at you expectantly. I can only imagine how embarrassing it will be, should you fail to think of anything good.”

Bastard. Brennan didn’t say it aloud. Taji’s face showed a certain amount of sympathy; Styrlyn held himself aloof from the game; but Yin was looking at him with sardonic interest. Worse, Hiriwa was gazing at him expectantly, assuming that he would rise to the challenge. And Jeffreyssai was gawking wide-eyed, waiting for the guru’s words of wisdom. Screw you, sensei.

Brennan didn’t panic. It was very, very, very far from being the scariest situation he’d ever faced. He took a moment to decide how to think; then thought.

At four minutes and thirty seconds, Brennan spoke. (There was an art to such things; as long as you were doing it anyway, you might as well make it look easy.)

“A woman of wisdom,” Brennan said, “once told me that it is wisest to regard our past selves as fools beyond redemption—to see the people we once were as idiots entire. I do not necessarily say this myself; but it is what she said to me, and there is more than a grain of truth in it. As long as we are making excuses for the past, trying to make it look better, respecting it, we cannot make a clean break. It occurs to me that the rule may be no different for human civilizations. So I tried looking back and considering the Eld scientists as simple fools.”

“Which they were not,” Jeffreyssai said.

“Which they were not,” Brennan continued. “In terms of raw intelligence, they undoubtedly exceeded me. But it occurred to me that a difficulty in seeing what Eld scientists did wrong, might have been in respecting the ancient and legendary names too highly. And that did indeed produce an insight.”

“Enough introduction, Brennan,” said Jeffreyssai. “If you found an insight, state it.”

“Eld scientists were not trained . . .” Brennan paused. “No, untrained is not the concept. They were trained for the wrong task. At that time, there were no Conspiracies, no secret truths; as soon as Eld scientists solved a major problem, they published the solution to the world and each other. Truly scary and confusing open problems would have been in extremely rare supply, and used up the moment they were solved. So it would not have been possible to train Eld researchers to bring order out of scientific chaos. They would have been trained for something else—I’m not sure what—”

“Trained to manipulate whatever science had already been discovered,” said Taji. “It was a difficult enough task for Eld teachers to train their students to use existing knowledge, or follow already-known methodologies; that was all Eld science teachers aspired to impart.”

Brennan nodded. “Which is a very different matter from creating new science of their own. The Eld scientists, faced with problems of quantum theory, might never have faced that kind of fear before—the dismay of not knowing. The Eld scientists might have seized on unsatisfactory answers prematurely, because they were accustomed to working with a neat, agreed-upon body of knowledge.”

“Good, Brennan,” murmured Jeffreyssai.

“But above all,” Brennan continued, “an Eld scientist couldn’t have practiced the actual problem the quantum scientists faced—that of resolving a major confusion. It was something you did once per lifetime if you were lucky, and as Hiriwa observed, Newton would no longer have been around. So while the Eld physicists who messed up quantum theory were not unintelligent, they were, in a strong sense, amateurs—ad-libbing the whole process of paradigm shift.”

“And no probability theory,” Hiriwa noted. “So anyone who did succeed at the problem would have no idea what they’d just done. They wouldn’t be able to communicate it to anyone else, except vaguely.”

“Yes,” Styrlyn said. “And it was only a handful of people who could tackle the problem at all, with no training in doing so; those are the physicists whose names have passed down to us. A handful of people, making a handful of discoveries each. It would not have been enough to sustain a community. Each Eld scientist tackling a new paradigm shift would have needed to rediscover the rules from scratch.”

Jeffreyssai rose from Brenann’s desk. “Acceptable, Brennan; you surprise me, in fact. I shall have to give further thought to this method of yours.” Jeffreyssai went to the classroom door, then looked back. “However, I did have in mind at least one other major flaw of Eld science, which none of you suggested. I expect to receive a list of possible flaws tomorrow. I expect the flaw I have in mind to be on the list. You have 480 minutes, excluding sleep time. I see five of you here. The challenge does not require more than 480 insights to solve, nor more than 96 insights in series.”

And Jeffreyssai left the room.

244
The Dilemma: Science or Bayes?

Eli: You are writing a lot about physics recently. Why?

—Shane Legg (and several other people)

In light of your QM explanation, which to me sounds perfectly logical, it seems obvious and normal that many worlds is overwhelmingly likely. It just seems almost too good to be true that I now get what plenty of genius quantum physicists still can’t. [ . . . ] Sure I can explain all that away, and I still think you’re right, I’m just suspicious of myself for believing the first believable explanation I met.

—Recovering_irrationalist

Recovering_irrationalist, you’ve got no idea how glad I was to see you post that comment.

Of course I had more than just one reason for spending all that time writing about quantum physics. I like having lots of hidden motives. It’s the closest I can ethically get to being a supervillain.

But to give an example of a purpose I could only accomplish by discussing quantum physics . . .

In physics, you can get absolutely clear-cut issues. Not in the sense that the issues are trivial to explain. But if you try to apply Bayes to healthcare, or economics, you may not be able to formally lay out what is the simplest hypothesis, or what the evidence supports. But when I say “macroscopic decoherence is simpler than collapse” it is actually strict simplicity; you could write the two hypotheses out as computer programs and count the lines of code. Nor is the evidence itself in dispute.

I wanted a very clear example—Bayes says “zig,” this is a zag—when it came time to break your allegiance to Science.

“Oh, sure,” you say, “the physicists messed up the many-worlds thing, but give them a break, Eliezer! No one ever claimed that the social process of science was perfect. People are human; they make mistakes.”

But the physicists who refuse to adopt many-worlds aren’t disobeying the rules of Science. They’re obeying the rules of Science.

The tradition handed down through the generations says that a new physics theory comes up with new experimental predictions that distinguish it from the old theory. You perform the test, and the new theory is confirmed or falsified. If it’s confirmed, you hold a huge celebration, call the newspapers, and hand out Nobel Prizes for everyone; any doddering old emeritus professors who refuse to convert are quietly humored. If the theory is disconfirmed, the lead proponent publicly recants, and gains a reputation for honesty.

This is not how things do work in science; rather it is how things are supposed to work in Science. It’s the ideal to which all good scientists aspire.

Now many-worlds comes along, and it doesn’t seem to make any new predictions relative to the old theory. That’s suspicious. And there’s all these other worlds, but you can’t see them. That’s really suspicious. It just doesn’t seem scientific.

If you got as far as Recovering_irrationalist—so that many-worlds now seems perfectly logical, obvious and normal—and you also started out as a Traditional Rationalist, then you should be able to switch back and forth between the Scientific view and the Bayesian view, like a Necker Cube.

So now put on your Science Goggles—you’ve still got them around somewhere, right? Forget everything you know about Kolmogorov complexity, Solomonoff induction or Minimum Message Lengths. That’s not part of the traditional training. You just eyeball something to see how “simple” it looks. The word “testable” doesn’t conjure up a mental image of Bayes’s Theorem governing probability flows; it conjures up a mental image of being in a lab, performing an experiment, and having the celebration (or public recantation) afterward.

Science-Goggles on: The current quantum theory has passed all experimental tests so far. Many-worlds doesn’t make any new testable predictions—the amazing new phenomena it predicts are all hidden away where we can’t see them. You can get along fine without supposing the other worlds, and that’s just what you should do. The whole thing smacks of science fiction. But it must be admitted that quantum physics is a very deep and very confusing issue, and who knows what discoveries might be in store? Call me when Many-worlds makes a testable prediction.

Science-Goggles off, Bayes-Goggles back on:

Bayes-Goggles on: The simplest quantum equations that cover all known evidence don’t have a special exception for human-sized masses. There isn’t even any reason to ask that particular question. Next!

Okay, so is this a problem we can fix in five minutes with some duct tape and superglue?

No.

Huh? Why not just teach new graduating classes of scientists about Solomonoff induction and Bayes’s Rule?

Centuries ago, there was a widespread idea that the Wise could unravel the secrets of the universe just by thinking about them, while to go out and look at things was lesser, inferior, naive, and would just delude you in the end. You couldn’t trust the way things looked—only thought could be your guide.

Science began as a rebellion against this Deep Wisdom. At the core is the pragmatic belief that human beings, sitting around in their armchairs trying to be Deeply Wise, just drift off into never-never land. You couldn’t trust your thoughts. You had to make advance experimental predictions—predictions that no one else had made before—run the test, and confirm the result. That was evidence. Sitting in your armchair, thinking about what seemed reasonable . . . would not be taken to prejudice your theory, because Science wasn’t an idealistic belief about pragmatism, or getting your hands dirty. It was, rather, the dictum that experiment alone would decide. Only experiments could judge your theory—not your nationality, or your religious professions, or the fact that you’d invented the theory in your armchair. Only experiments! If you sat in your armchair and came up with a theory that made a novel prediction, and experiment confirmed the prediction, then we would care about the result of the experiment, not where your hypothesis came from.

That’s Science. And if you say that many-worlds should replace the immensely successful Copenhagen Interpretation, adding on all these twin Earths that can’t be observed, just because it sounds more reasonable and elegant—not because it crushed the old theory with a superior experimental prediction—then you’re undoing the core scientific rule that prevents people from running out and putting angels into all the theories, because angels are more reasonable and elegant.

You think teaching a few people about Solomonoff induction is going to solve that problem? Nobel laureate Robert Aumann—who first proved that Bayesian agents with similar priors cannot agree to disagree—is a believing Orthodox Jew. Aumann helped a project to test the Torah for “Bible codes,” hidden prophecies from God—and concluded that the project had failed to confirm the codes’ existence. Do you want Aumann thinking that once you’ve got Solomonoff induction, you can forget about the experimental method? Do you think that’s going to help him? And most scientists out there will not rise to the level of Robert Aumann.

Okay, Bayes-Goggles back on. Are you really going to believe that large parts of the wavefunction disappear when you can no longer see them? As a result of the only non-linear non-unitary non-differentiable non-CPT-symmetric acausal faster-than-light informally-specified phenomenon in all of physics? Just because, by sheer historical contingency, the stupid version of the theory was proposed first?

Are you going to make a major modification to a scientific model, and believe in zillions of other worlds you can’t see, without a defining moment of experimental triumph over the old model?

Or are you going to reject probability theory?

Will you give your allegiance to Science, or to Bayes?

Michael Vassar once observed (tongue-in-cheek) that it was a good thing that a majority of the human species believed in God, because otherwise, he would have a very hard time rejecting majoritarianism. But since the majority opinion that God exists is simply unbelievable, we have no choice but to reject the extremely strong philosophical arguments for majoritarianism.

You can see (one of the reasons) why I went to such lengths to explain quantum theory. Those who are good at math should now be able to visualize both macroscopic decoherence, and the probability theory of simplicity and testability—get the insanity of a global single world on a gut level.

I wanted to present you with a nice, sharp dilemma between rejecting the scientific method, or embracing insanity.

Why? I’ll give you a hint: It’s not just because I’m evil. If you would guess my motives here, think beyond the first obvious answer.

PS: If you try to come up with clever ways to wriggle out of the dilemma, you’re just going to get shot down in future essays. You have been warned.

245
Science Doesn’t Trust Your Rationality

Scott Aaronson suggests that many-worlds and libertarianism are similar in that they are both cases of bullet-swallowing, rather than bullet-dodging:

Libertarianism and MWI are both grand philosophical theories that start from premises that almost all educated people accept (quantum mechanics in the one case, Econ 101 in the other), and claim to reach conclusions that most educated people reject, or are at least puzzled by (the existence of parallel universes / the desirability of eliminating fire departments).

Now there’s an analogy that would never have occurred to me.

I’ve previously argued that Science rejects Many-Worlds but Bayes accepts it. (Here, “Science” is capitalized because we are talking about the idealized form of Science, not just the actual social process of science.)

It furthermore seems to me that there is a deep analogy between (small-“l”) libertarianism and Science:

Both are based on a pragmatic distrust of reasonable-sounding arguments.
Both try to build systems that are more trustworthy than the people in them.
Both accept that people are flawed, and try to harness their flaws to power the system.

The core argument for libertarianism is historically motivated distrust of lovely theories of “How much better society would be, if we just made a rule that said XYZ.” If that sort of trick actually worked, then more regulations would correlate to higher economic growth as society moved from local to global optima. But when some person or interest group gets enough power to start doing everything they think is a good idea, history says that what actually happens is Revolutionary France or Soviet Russia.

The plans that in lovely theory should have made everyone happy ever after, don’t have the results predicted by reasonable-sounding arguments. And power corrupts, and attracts the corrupt.

So you regulate as little as possible, because you can’t trust the lovely theories and you can’t trust the people who implement them.

You don’t shake your finger at people for being selfish. You try to build an efficient system of production out of selfish participants, by requiring transactions to be voluntary. So people are forced to play positive-sum games, because that’s how they get the other party to sign the contract. With violence restrained and contracts enforced, individual selfishness can power a globally productive system.

Of course none of this works quite so well in practice as in theory, and I’m not going to go into market failures, commons problems, etc. The core argument for libertarianism is not that libertarianism would work in a perfect world, but that it degrades gracefully into real life. Or rather, degrades less awkwardly than any other known economic principle. (People who see Libertarianism as the perfect solution for perfect people strike me as kinda missing the point of the “pragmatic distrust” thing.)

Science first came to know itself as a rebellion against trusting the word of Aristotle. If the people of that revolution had merely said, “Let us trust ourselves, not Aristotle!” they would have flashed and faded like the French Revolution.

But the Scientific Revolution lasted because—like the American Revolution—the architects propounded a stranger philosophy: “Let us trust no one! Not even ourselves!”

In the beginning came the idea that we can’t just toss out Aristotle’s armchair reasoning and replace it with different armchair reasoning. We need to talk to Nature, and actually listen to what It says in reply. This, itself, was a stroke of genius.

But then came the challenge of implementation. People are stubborn, and may not want to accept the verdict of experiment. Shall we shake a disapproving finger at them, and say “Naughty”?

No; we assume and accept that each individual scientist may be crazily attached to their personal theories. Nor do we assume that anyone can be trained out of this tendency—we don’t try to choose Eminent Judges who are supposed to be impartial.

Instead, we try to harness the individual scientist’s stubborn desire to prove their personal theory, by saying: “Make a new experimental prediction, and do the experiment. If you’re right, and the experiment is replicated, you win.” So long as scientists believe this is true, they have a motive to do experiments that can falsify their own theories. Only by accepting the possibility of defeat is it possible to win. And any great claim will require replication; this gives scientists a motive to be honest, on pain of great embarrassment.

And so the stubbornness of individual scientists is harnessed to produce a steady stream of knowledge at the group level. The System is somewhat more trustworthy than its parts.

Libertarianism secretly relies on most individuals being prosocial enough to tip at a restaurant they won’t ever visit again. An economy of genuinely selfish human-level agents would implode. Similarly, Science relies on most scientists not committing sins so egregious that they can’t rationalize them away.

To the extent that scientists believe they can promote their theories by playing academic politics—or game the statistical methods to potentially win without a chance of losing—or to the extent that nobody bothers to replicate claims—science degrades in effectiveness. But it degrades gracefully, as such things go.

The part where the successful predictions belong to the theory and theorists who originally made them, and cannot just be stolen by a theory that comes along later—without a novel experimental prediction—is an important feature of this social process.

The final upshot is that Science is not easily reconciled with probability theory. If you do a probability-theoretic calculation correctly, you’re going to get the rational answer. Science doesn’t trust your rationality, and it doesn’t rely on your ability to use probability theory as the arbiter of truth. It wants you to set up a definitive experiment.

Regarding Science as a mere approximation to some probability-theoretic ideal of rationality . . . would certainly seem to be rational. There seems to be an extremely reasonable-sounding argument that Bayes’s Theorem is the hidden structure that explains why Science works. But to subordinate Science to the grand schema of Bayesianism, and let Bayesianism come in and override Science’s verdict when that seems appropriate, is not a trivial step!

Science is built around the assumption that you’re too stupid and self-deceiving to just use Solomonoff induction. After all, if it was that simple, we wouldn’t need a social process of science . . . right?

So, are you going to believe in faster-than-light quantum “collapse” fairies after all? Or do you think you’re smarter than that?

246
When Science Can’t Help

Once upon a time, a younger Eliezer had a stupid theory. Let’s say that Eliezer₁₈’s stupid theory was that consciousness was caused by closed timelike curves hiding in quantum gravity. This isn’t the whole story, not even close, but it will do for a start.

And there came a point where I looked back, and realized:

I had carefully followed everything I’d been told was Traditionally Rational, in the course of going astray. For example, I’d been careful to only believe in stupid theories that made novel experimental predictions, e.g., that neuronal microtubules would be found to support coherent quantum states.
Science would have been perfectly fine with my spending ten years trying to test my stupid theory, only to get a negative experimental result, so long as I then said, “Oh, well, I guess my theory was wrong.”

From Science’s perspective, that is how things are supposed to work—happy fun for everyone. You admitted your error! Good for you! Isn’t that what Science is all about?

But what if I didn’t want to waste ten years?

Well . . . Science didn’t have much to say about that. How could Science say which theory was right, in advance of the experimental test? Science doesn’t care where your theory comes from—it just says, “Go test it.”

This is the great strength of Science, and also its great weakness.

Gray Area asked:

Eliezer, why are you concerned with untestable questions?

Because questions that are easily immediately tested are hard for Science to get wrong.

I mean, sure, when there’s already definite unmistakable experimental evidence available, go with it. Why on Earth wouldn’t you?

But sometimes a question will have very large, very definite experimental consequences in your future—but you can’t easily test it experimentally right now—and yet there is a strong rational argument.

Macroscopic quantum superpositions are readily testable: It would just take nanotechnologic precision, very low temperatures, and a nice clear area of interstellar space. Oh, sure, you can’t do it right now, because it’s too expensive or impossible for today’s technology or something like that—but in theory, sure! Why, maybe someday they’ll run whole civilizations on macroscopically superposed quantum computers, way out in a well-swept volume of a Great Void. (Asking what quantum non-realism says about the status of any observers inside these computers helps to reveal the underspecification of quantum non-realism.)

This doesn’t seem immediately pragmatically relevant to your life, I’m guessing, but it establishes the pattern: Not everything with future consequences is cheap to test now.

Evolutionary psychology is another example of a case where rationality has to take over from science. While theories of evolutionary psychology form a connected whole, only some of those theories are readily testable experimentally. But you still need the other parts of the theory, because they form a connected web that helps you to form the hypotheses that are actually testable—and then the helper hypotheses are supported in a Bayesian sense, but not supported experimentally. Science would render a verdict of “not proven” on individual parts of a connected theoretical mesh that is experimentally productive as a whole. We’d need a new kind of verdict for that, something like “indirectly supported.”

Or what about cryonics?

Cryonics is an archetypal example of an extremely important issue (150,000 people die per day) that will have huge consequences in the foreseeable future, but doesn’t offer definite unmistakable experimental evidence that we can get right now.

So do you say, “I don’t believe in cryonics because it hasn’t been experimentally proven, and you shouldn’t believe in things that haven’t been experimentally proven”?

Well, from a Bayesian perspective, that’s incorrect. Absence of evidence is evidence of absence only to the degree that we could reasonably expect the evidence to appear. If someone is trumpeting that snake oil cures cancer, you can reasonably expect that, if the snake oil were actually curing cancer, some scientist would be performing a controlled study to verify it—that, at the least, doctors would be reporting case studies of amazing recoveries—and so the absence of this evidence is strong evidence of absence. But “gaps in the fossil record” are not strong evidence against evolution; fossils form only rarely, and even if an intermediate species did in fact exist, you cannot expect with high probability that Nature will obligingly fossilize it and that the fossil will be discovered.

Reviving a cryonically frozen mammal is just not something you’d expect to be able to do with modern technology, even if future nanotechnologies could in fact perform a successful revival. That’s how I see Bayes seeing it.

Oh, and as for the actual arguments for cryonics—I’m not going to go into those at the moment. But if you followed the physics and anti-Zombie sequences, it should now seem a lot more plausible that whatever preserves the pattern of synapses preserves as much of “you” as is preserved from one night’s sleep to morning’s waking.

Now, to be fair, someone who says, “I don’t believe in cryonics because it hasn’t been proven experimentally” is misapplying the rules of Science; this is not a case where science actually gives the wrong answer. In the absence of a definite experimental test, the verdict of science here is “Not proven.” Anyone who interprets that as a rejection is taking an extra step outside of science, not a misstep within science.

John McCarthy’s Wikiquotes page has him saying, “Your statements amount to saying that if AI is possible, it should be easy. Why is that?”¹ The Wikiquotes page doesn’t say what McCarthy was responding to, but I could venture a guess.

The general mistake probably arises because there are cases where the absence of scientific proof is strong evidence—because an experiment would be readily performable, and so failure to perform it is itself suspicious. (Though not as suspicious as I used to think—with all the strangely varied anecdotal evidence coming in from respected sources, why the hell isn’t anyone testing Seth Roberts’s theory of appetite suppression?²)

Another confusion factor may be that if you test Pharmaceutical X on 1,000 subjects and find that 56% of the control group and 57% of the experimental group recover, some people will call that a verdict of “Not proven.” I would call it an experimental verdict of “Pharmaceutical X doesn’t work well, if at all.” Just because this verdict is theoretically retractable in the face of new evidence doesn’t make it ambiguous.

In any case, right now you’ve got people dismissing cryonics out of hand as “not scientific,” like it was some kind of pharmaceutical you could easily administer to 1,000 patients and see what happened. “Call me when cryonicists actually revive someone,” they say; which, as Mike Li observes, is like saying “I refuse to get into this ambulance; call me when it’s actually at the hospital.” Maybe Martin Gardner warned them against believing in strange things without experimental evidence. So they wait for the definite unmistakable verdict of Science, while their family and friends and 150,000 people per day are dying right now, and might or might not be savable—

—a calculated bet you could only make rationally.

The drive of Science is to obtain a mountain of evidence so huge that not even fallible human scientists can misread it. But even that sometimes goes wrong, when people become confused about which theory predicts what, or bake extremely-hard-to-test components into an early version of their theory. And sometimes you just can’t get clear experimental evidence at all.

Either way, you have to try to do the thing that Science doesn’t trust anyone to do—think rationally, and figure out the answer before you get clubbed over the head with it.

(Oh, and sometimes a disconfirming experimental result looks like: “Your entire species has just been wiped out! You are now scientifically required to relinquish your theory. If you publicly recant, good for you! Remember, it takes a strong mind to give up strongly held beliefs. Feel free to try another hypothesis next time!”)

1. No longer on Wikiquotes, but included in McCarthy’s personal quotes page.

2. Seth Roberts, “What Makes Food Fattening?: A Pavlovian Theory of Weight Control” (Unpublished manuscript, 2005), http://media.sethroberts.net/about/whatmakesfoodfattening.pdf.

247
Science Isn’t Strict Enough

Once upon a time, a younger Eliezer had a stupid theory. Eliezer₁₈ was careful to follow the precepts of Traditional Rationality that he had been taught; he made sure his stupid theory had experimental consequences. Eliezer₁₈ professed, in accordance with the virtues of a scientist he had been taught, that he wished to test his stupid theory.

This was all that was required to be virtuous, according to what Eliezer₁₈ had been taught was virtue in the way of science.

It was not even remotely the order of effort that would have been required to get it right.

The traditional ideals of Science too readily give out gold stars. Negative experimental results are also knowledge, so everyone who plays gets an award. So long as you can think of some kind of experiment that tests your theory, and you do the experiment, and you accept the results, you’ve played by the rules; you’re a good scientist.

You didn’t necessarily get it right, but you’re a nice science-abiding citizen.

(I note at this point that I am speaking of Science, not the social process of science as it actually works in practice, for two reasons. First, I went astray in trying to follow the ideal of Science—it’s not like I was shot down by a journal editor with a grudge, and it’s not like I was trying to imitate the flaws of academia. Second, if I point out a problem with the ideal as it is traditionally preached, real-world scientists are not forced to likewise go astray!)

Science began as a rebellion against grand philosophical schemas and armchair reasoning. So Science doesn’t include a rule as to what kinds of hypotheses you are and aren’t allowed to test; that is left up to the individual scientist. Trying to guess that a priori would require some kind of grand philosophical schema, and reasoning in advance of the evidence. As a social ideal, Science doesn’t judge you as a bad person for coming up with heretical hypotheses; honest experiments, and acceptance of the results, is virtue unto a scientist.

As long as most scientists can manage to accept definite, unmistakable, unambiguous experimental evidence, science can progress. It may happen too slowly—it may take longer than it should—you may have to wait for a generation of elders to die out—but eventually, the ratchet of knowledge clicks forward another notch. Year by year, decade by decade, the wheel turns forward. It’s enough to support a civilization.

So that’s all that Science really asks of you—the ability to accept reality when you’re beat over the head with it. It’s not much, but it’s enough to sustain a scientific culture.

Contrast this to the notion we have in probability theory, of an exact quantitative rational judgment. If 1% of women presenting for a routine screening have breast cancer, and 80% of women with breast cancer get positive mammographies, and 10% of women without breast cancer get false positives, what is the probability that a routinely screened woman with a positive mammography has breast cancer? It is 7.5%. You cannot say, “I believe she doesn’t have breast cancer, because the experiment isn’t definite enough.” You cannot say, “I believe she has breast cancer, because it is wise to be pessimistic and that is what the only experiment so far seems to indicate.” Seven point five percent is the rational estimate given this evidence, not 7.4% or 7.6%. The laws of probability are laws.

It is written in the Twelve Virtues, of the third virtue, lightness:

If you regard evidence as a constraint and seek to free yourself, you sell yourself into the chains of your whims. For you cannot make a true map of a city by sitting in your bedroom with your eyes shut and drawing lines upon paper according to impulse. You must walk through the city and draw lines on paper that correspond to what you see. If, seeing the city unclearly, you think that you can shift a line just a little to the right, just a little to the left, according to your caprice, this is just the same mistake.

In Science, when it comes to deciding which hypotheses to test, the morality of Science gives you personal freedom of what to believe, so long as it isn’t already ruled out by experiment, and so long as you move to test your hypothesis. Science wouldn’t try to give an official verdict on the best hypothesis to test, in advance of the experiment. That’s left up to the conscience of the individual scientist.

Where definite experimental evidence exists, Science tells you to bow your stubborn neck and accept it. Otherwise, Science leaves it up to you. Science gives you room to wander around within the boundaries of the experimental evidence, according to your whims.

And this is not easily reconciled with Bayesianism’s notion of an exactly right probability estimate, one with no flex or room for whims, that exists both before and after the experiment. Bayesianism doesn’t match well with the ancient and traditional reason for Science—the distrust of grand schemas, the presumption that people aren’t rational enough to get things right without definite and unmistakable experimental evidence. If we were all perfect Bayesians, we wouldn’t need a social process of science.

Nonetheless, around the time I realized my big mistake, I had also been studying Kahneman and Tversky and Jaynes. I was learning a new Way, stricter than Science. A Way that could criticize my folly, in a way that Science never could. A Way that could have told me what Science would never have said in advance: “You picked the wrong hypothesis to test, dunderhead.”

But the Way of Bayes is also much harder to use than Science. It puts a tremendous strain on your ability to hear tiny false notes, where Science only demands that you notice an anvil dropped on your head.

In Science you can make a mistake or two, and another experiment will come by and correct you; at worst you waste a couple of decades.

But if you try to use Bayes even qualitatively—if you try to do the thing that Science doesn’t trust you to do, and reason rationally in the absence of overwhelming evidence—it is like math, in that a single error in a hundred steps can carry you anywhere. It demands lightness, evenness, precision, perfectionism.

There’s a good reason why Science doesn’t trust scientists to do this sort of thing, and asks for further experimental proof even after someone claims they’ve worked out the right answer based on hints and logic.

But if you would rather not waste ten years trying to prove the wrong theory, you’ll need to essay the vastly more difficult problem: listening to evidence that doesn’t shout in your ear.

Even if you can’t look up the priors for a problem in the Handbook of Chemistry and Physics—even if there’s no Authoritative Source telling you what the priors are—that doesn’t mean you get a free, personal choice of making the priors whatever you want. It means you have a new guessing problem that you must carry out to the best of your ability.

If the mind, as a cognitive engine, could generate correct estimates by fiddling with priors according to whims, you could know things without looking them, or even alter them without touching them. But the mind is not magic. The rational probability estimate has no room for any decision based on whim, even when it seems that you don’t know the priors.

Similarly, if the Bayesian answer is difficult to compute, that doesn’t mean that Bayes is inapplicable; it means you don’t know what the Bayesian answer is. Bayesian probability theory is not a toolbox of statistical methods; it’s the law that governs any tool you use, whether or not you know it, whether or not you can calculate it.

As for using Bayesian methods on huge, highly general hypothesis spaces—like, “Here’s the data from every physics experiment ever; now, what would be a good Theory of Everything?”—if you knew how to do that in practice, you wouldn’t be a statistician, you would be an Artificial General Intelligence programmer. But that doesn’t mean that human beings, in modeling the universe using human intelligence, are violating the laws of physics / Bayesianism by generating correct guesses without evidence.

Nick Tarleton comments:

The problem is encouraging a private, epistemic standard as lax as the social one.

which pinpoints the problem I was trying to indicate much better than I did.

248
Do Scientists Already Know This Stuff?

poke alleges:

Being able to create relevant hypotheses is an important skill and one a scientist spends a great deal of his or her time developing. It may not be part of the traditional description of science but that doesn’t mean it’s not included in the actual social institution of science that produces actual real science here in the real world; it’s your description and not science that is faulty.

I know I’ve been calling my younger self “stupid,” but that is a figure of speech; “unskillfully wielding high intelligence” would be more precise. Eliezer₁₈ was not in the habit of making obvious mistakes—it’s just that his “obvious” wasn’t my “obvious.”

No, I did not go through the traditional apprenticeship. But when I look back, and see what Eliezer₁₈ did wrong, I see plenty of modern scientists making the same mistakes. I cannot detect any sign that they were better warned than myself.

Sir Roger Penrose—a world-class physicist—still thinks that consciousness is caused by quantum gravity. I expect that no one ever warned him against mysterious answers to mysterious questions—only told him his hypotheses needed to be falsifiable and have empirical consequences. Just like Eliezer₁₈.

“Consciousness is caused by quantum gravity” has testable implications: It implies that you should be able to look at neurons and discover a coherent quantum superposition whose collapse contributes to information-processing, and that you won’t ever be able to reproduce a neuron’s input-output behavior using a computable microanatomical simulation . . .

. . . but even after you say “Consciousness is caused by quantum gravity,” you don’t anticipate anything about how your brain thinks “I think therefore I am!” or the mysterious redness of red, that you did not anticipate before, even though you feel like you know a cause of it. This is a tremendous danger sign, I now realize, but it’s not the danger sign that I was warned against, and I doubt that Penrose was ever told of it by his thesis advisor. For that matter, I doubt that Niels Bohr was ever warned against it when it came time to formulate the Copenhagen Interpretation.

As far as I can tell, the reason Eliezer₁₈ and Sir Roger Penrose and Niels Bohr were not warned is that no standard warning exists.

I did not generalize the concept of “mysterious answers to mysterious questions,” in that many words, until I was writing a Bayesian analysis of what distinguishes technical, nontechnical and semitechnical scientific explanations. Now, the final output of that analysis can be phrased nontechnically in terms of four danger signs:

First, the explanation acts as a curiosity-stopper rather than an anticipation-controller.
Second, the hypothesis has no moving parts—the secret sauce is not a specific complex mechanism, but a blankly solid substance or force.
Third, those who proffer the explanation cherish their ignorance; they speak proudly of how the phenomenon defeats ordinary science or is unlike merely mundane phenomena.
Fourth, even after the answer is given, the phenomenon is still a mystery and possesses the same quality of wonderful inexplicability that it had at the start.

In principle, all this could have been said in the immediate aftermath of vitalism. Just like elementary probability theory could have been invented by Archimedes, or the ancient Greeks could have theorized natural selection. But in fact no one ever warned me against any of these four dangers, in those terms—the closest being the warning that hypotheses should have testable consequences. And I didn’t conceptualize the warning signs explicitly until I was trying to think of the whole affair in terms of probability distributions—some degree of overkill was required.

I simply have no reason to believe that these warnings are passed down in scientific apprenticeships—certainly not to a majority of scientists. Among other things, it is advice for handling situations of confusion and despair, scientific chaos. When would the average scientist or average mentor have an opportunity to use that kind of technique?

We just got through discussing the single-world fiasco in physics. Clearly, no one told them about the formal definition of Occam’s Razor, in whispered apprenticeship or otherwise.

There is a known effect where great scientists have multiple great students. This may well be due to the mentors passing on skills that they can’t describe. But I don’t think that counts as part of standard science. And if the great mentors haven’t been able to put their guidance into words and publish it generally, that’s not a good sign for how well these things are understood.

Reasoning in the absence of definite evidence without going instantaneously completely wrong is really really hard. When you’re learning in school, you can miss one point, and then be taught fifty other points that happen to be correct. When you’re reasoning out new knowledge in the absence of crushingly overwhelming guidance, you can miss one point and wake up in Outer Mongolia fifty steps later.

I am pretty sure that scientists who switch off their brains and relax with some comfortable nonsense as soon as they leave their own specialties do not realize that minds are engines and that there is a causal story behind every trustworthy belief. Nor, I suspect, were they ever told that there is an exact rational probability given a state of evidence, which has no room for whims; even if you can’t calculate the answer, and even if you don’t hear any authoritative command for what to believe.

I doubt that scientists who are asked to pontificate on the future by the media, who sketch amazingly detailed pictures of Life in 2050, were ever taught about the conjunction fallacy. Or how the representativeness heuristic can make more detailed stories seem more plausible, even as each extra detail drags down the probability. The notion of every added detail needing its own support—of not being able to make up big detailed stories that sound just like the detailed stories you were taught in science or history class—is absolutely vital to precise thinking in the absence of definite evidence. But how would a notion like that get into the standard scientific apprenticeship? The cognitive bias was uncovered only a few decades ago, and not popularized until very recently.

Then there’s affective death spirals around notions like “emergence” or “complexity” which are sufficiently vaguely defined that you can say lots of nice things about them. There’s whole academic subfields built around the kind of mistakes that Eliezer₁₈ used to make! (Though I never fell for the “emergence” thing.)

I sometimes say that the goal of science is to amass such an enormous mountain of evidence that not even scientists can ignore it: and that this is the distinguishing feature of a scientist; a non-scientist will ignore it anyway.

If there can exist some amount of evidence so crushing that you finally despair, stop making excuses and just give up—drop the old theory and never mention it again—then this is all it takes to let the ratchet of Science turn forward over time, and raise up a technological civilization. Contrast to religion.

Books by Carl Sagan and Martin Gardner and the other veins of Traditional Rationality are meant to accomplish this difference: to transform someone from a non-scientist into a potential scientist, and guard them from experimentally disproven madness.

What further training does a professional scientist get? Some frequentist stats classes on how to calculate statistical significance. Training in standard techniques that will let them churn out papers within a solidly established paradigm.

If Science demanded more than this from the average scientist, I don’t think it would be possible for Science to get done. We have problems enough from people who sneak in without the drop-dead-basic qualifications.

Nick Tarleton summarized the resulting problem very well—better than I did, in fact: If you come up with a bizarre-seeming hypothesis not yet ruled out by the evidence, and try to test it experimentally, Science doesn’t call you a bad person. Science doesn’t trust its elders to decide which hypotheses “aren’t worth testing.” But this is a carefully lax social standard, and if you try to translate it into a standard of individual epistemic rationality, it lets you believe far too much. Dropping back into the analogy with pragmatic-distrust-based-libertarianism, it’s the difference between “Cigarettes shouldn’t be illegal” and “Go smoke a Marlboro.”

Do you remember ever being warned against that mistake, in so many words? Then why wouldn’t people make exactly that error? How many people will spontaneously go an extra mile and be even stricter with themselves? Some, but not many.

Many scientists will believe all manner of ridiculous things outside the laboratory, so long as they can convince themselves it hasn’t been definitely disproven, or so long as they manage not to ask. Is there some standard lecture that grad students get, of which people see this folly, and ask, “Were they absent from class that day?” No, as far as I can tell.

Maybe if you’re super lucky and get a famous mentor, they’ll tell you rare personal secrets like “Ask yourself which are the important problems in your field, and then work on one of those, instead of falling into something easy and trivial” or “Be more careful than the journal editors demand; look for new ways to guard your expectations from influencing the experiment, even if it’s not standard.”

But I really don’t think there’s a huge secret standard scientific tradition of precision-grade rational reasoning on sparse evidence. Half of all the scientists out there still believe they believe in God! The more difficult skills are not standard!

249
No Safe Defense, Not Even Science

I don’t ask my friends about their childhoods—I lack social curiosity—and so I don’t know how much of a trend this really is:

Of the people I know who are reaching upward as rationalists, who volunteer information about their childhoods, there is a surprising tendency to hear things like, “My family joined a cult and I had to break out,” or, “One of my parents was clinically insane and I had to learn to filter out reality from their madness.”

My own experience with growing up in an Orthodox Jewish family seems tame by comparison . . . but it accomplished the same outcome: It broke my core emotional trust in the sanity of the people around me.

Until this core emotional trust is broken, you don’t start growing as a rationalist. I have trouble putting into words why this is so. Maybe any unusual skills you acquire—anything that makes you unusually rational—requires you to zig when other people zag. Maybe that’s just too scary, if the world still seems like a sane place unto you.

Or maybe you don’t bother putting in the hard work to be extra bonus sane, if normality doesn’t scare the hell out of you.

I know that many aspiring rationalists seem to run into roadblocks around things like cryonics or many-worlds. Not that they don’t see the logic; they see the logic and wonder, “Can this really be true, when it seems so obvious now, and yet none of the people around me believe it?”

Yes. Welcome to the Earth where ethanol is made from corn and environmentalists oppose nuclear power. I’m sorry.

(See also: Cultish Countercultishness. If you end up in the frame of mind of nervously seeking reassurance, this is never a good thing—even if it’s because you’re about to believe something that sounds logical but could cause other people to look at you funny.)

People who’ve had their trust broken in the sanity of the people around them seem to be able to evaluate strange ideas on their merits, without feeling nervous about their strangeness. The glue that binds them to their current place has dissolved, and they can walk in some direction, hopefully forward.

Lonely dissent, I called it. True dissent doesn’t feel like going to school wearing black; it feels like going to school wearing a clown suit.

That’s what it takes to be the lone voice who says, “If you really think you know who’s going to win the election, why aren’t you picking up the free money on the Intrade prediction market?” while all the people around you are thinking, “It is good to be an individual and form your own opinions, the shoe commercials told me so.”

Maybe in some other world, some alternate Everett branch with a saner human population, things would be different . . . but in this world, I’ve never seen anyone begin to grow as a rationalist until they make a deep emotional break with the wisdom of their pack.

Maybe in another world, things would be different. And maybe not. I’m not sure that human beings realistically can trust and think at the same time.

Once upon a time, there was something I trusted.

Eliezer₁₈ trusted Science.

Eliezer₁₈ dutifully acknowledged that the social process of science was flawed. Eliezer₁₈ dutifully acknowledged that academia was slow, and misallocated resources, and played favorites, and mistreated its precious heretics.

That’s the convenient thing about acknowledging flaws in people who failed to live up to your ideal; you don’t have to question the ideal itself.

But who could possibly be foolish enough to question, “The experimental method shall decide which hypothesis wins”?

Part of what fooled Eliezer₁₈ was a general problem he had, an aversion to ideas that resembled things idiots had said. Eliezer₁₈ had seen plenty of people questioning the ideals of Science Itself, and without exception they were all on the Dark Side. People who questioned the ideal of Science were invariably trying to sell you snake oil, or trying to safeguard their favorite form of stupidity from criticism, or trying to disguise their personal resignation as a Deeply Wise acceptance of futility.

If there’d been any other ideal that was a few centuries old, the young Eliezer would have looked at it and said, “I wonder if this is really right, and whether there’s a way to do better.” But not the ideal of Science. Science was the master idea, the idea that let you change ideas. You could question it, but you were meant to question it and then accept it, not actually say, “Wait! This is wrong!”

Thus, when once upon a time I came up with a stupid idea, I thought I was behaving virtuously if I made sure there was a Novel Prediction, and professed that I wished to test my idea experimentally. I thought I had done everything I was obliged to do.

So I thought I was safe—not safe from any particular external threat, but safe on some deeper level, like a child who trusts their parent and has obeyed all the parent’s rules.

I’d long since been broken of trust in the sanity of my family or my teachers at school. And the other children weren’t intelligent enough to compete with the conversations I could have with books. But I trusted the books, you see. I trusted that if I did what Richard Feynman told me to do, I would be safe. I never thought those words aloud, but it was how I felt.

When Eliezer₂₃ realized exactly how stupid the stupid theory had been—and that Traditional Rationality had not saved him from it—and that Science would have been perfectly okay with his wasting ten years testing the stupid idea, so long as afterward he admitted it was wrong . . .

. . . well, I’m not going to say it was a huge emotional convulsion. I don’t really go in for that kind of drama. It simply became obvious that I’d been stupid.

That’s the trust I’m trying to break in you. You are not safe. Ever.

Not even Science can save you. The ideals of Science were born centuries ago, in a time when no one knew anything about probability theory or cognitive biases. Science demands too little of you, it blesses your good intentions too easily, it is not strict enough, it only makes those injunctions that an average scientist can follow, it accepts slowness as a fact of life.

So don’t think that if you only follow the rules of Science, that makes your reasoning defensible.

There is no known procedure you can follow that makes your reasoning defensible.

There is no known set of injunctions which you can satisfy, and know that you will not have been a fool.

There is no known morality-of-reasoning that you can do your best to obey, and know that you are thereby shielded from criticism.

No, not even if you turn to Bayescraft. It’s much harder to use and you’ll never be sure that you’re doing it right.

The discipline of Bayescraft is younger by far than the discipline of Science. You will find no textbooks, no elderly mentors, no histories written of success and failure, no hard-and-fast rules laid down. You will have to study cognitive biases, and probability theory, and evolutionary psychology, and social psychology, and other cognitive sciences, and Artificial Intelligence—and think through for yourself how to apply all this knowledge to the case of correcting yourself, since that isn’t yet in the textbooks.

You don’t know what your own mind is really doing. They find a new cognitive bias every week and you’re never sure if you’ve corrected for it, or overcorrected.

The formal math is impossible to apply. It doesn’t break down as easily as John Q. Unbeliever thinks, but you’re never really sure where the foundations come from. You don’t know why the universe is simple enough to understand, or why any prior works for it. You don’t know what your own priors are, let alone if they’re any good.

One of the problems with Science is that it’s too vague to really scare you. “Ideas should be tested by experiment.” How can you go wrong with that?

On the other hand, if you have some math of probability theory laid out in front of you, and worse, you know you can’t actually use it, then it becomes clear that you are trying to do something difficult, and that you might well be doing it wrong.

So you cannot trust.

And all this that I have said will not be sufficient to break your trust. That won’t happen until you get into your first real disaster from following The Rules, not from breaking them.

Eliezer₁₈ already had the notion that you were allowed to question Science. Why, of course the scientific method was not itself immune to questioning! For are we not all good rationalists? Are we not allowed to question everything?

It was the notion that you could actually in real life follow Science and fail miserably that Eliezer₁₈ didn’t really, emotionally believe was possible.

Oh, of course he said it was possible. Eliezer₁₈ dutifully acknowledged the possibility of error, saying, “I could be wrong, but . . .”

But he didn’t think failure could happen in, you know, real life. You were supposed to look for flaws, not actually find them.

And this emotional difference is a terribly difficult thing to accomplish in words, and I fear there’s no way I can really warn you.

Your trust will not break, until you apply all that you have learned here and from other books, and take it as far as you can go, and find that this too fails you—that you have still been a fool, and no one warned you against it—that all the most important parts were left out of the guidance you received—that some of the most precious ideals you followed steered you in the wrong direction—

—and if you still have something to protect, so that you must keep going, and cannot resign and wisely acknowledge the limitations of rationality—

—then you will be ready to start your journey as a rationalist. To take sole responsibility, to live without any trustworthy defenses, and to forge a higher Art than the one you were once taught.

No one begins to truly search for the Way until their parents have failed them, their gods are dead, and their tools have shattered in their hand.

Post Scriptum: On reviewing a draft of this essay, I discovered a fairly inexcusable flaw in reasoning, which actually affects one of the conclusions drawn. I am leaving it in. Just in case you thought that taking my advice made you safe; or that you were supposed to look for flaws, but not find any.

And of course, if you look too hard for a flaw, and find a flaw that is not a real flaw, and cling to it to reassure yourself of how critical you are, you will only be worse off than before . . .

It is living with uncertainty—knowing on a gut level that there are flaws, they are serious and you have not found them—that is the difficult thing.

250
Changing the Definition of Science

New Scientist on changing the definition of science, ungated here:¹

Others believe such criticism is based on a misunderstanding. “Some people say that the multiverse concept isn’t falsifiable because it’s unobservable—but that’s a fallacy,” says cosmologist Max Tegmark of the Massachusetts Institute of Technology. He argues that the multiverse is a natural consequence of such eminently falsifiable theories as quantum theory and General Relativity. As such, the multiverse theory stands or fails according to how well these other theories stand up to observational tests.

[ . . . ]

So if the simplicity of falsification is misleading, what should scientists be doing instead? Howson believes it is time to ditch Popper’s notion of capturing the scientific process using deductive logic. Instead, the focus should be on reflecting what scientists actually do: gathering the weight of evidence for rival theories and assessing their relative plausibility.

Howson is a leading advocate for an alternative view of science based not on simplistic true/false logic, but on the far more subtle concept of degrees of belief. At its heart is a fundamental connection between the subjective concept of belief and the cold, hard mathematics of probability.

I’m a good deal less of a lonely iconoclast than I seem. Maybe it’s just the way I talk.

The points of departure between myself and mainstream let’s-reformulate-Science-as-Bayesianism is that:

(1) I’m not in academia and can censor myself a lot less when it comes to saying “extreme” things that others might well already be thinking.

(2) I think that just teaching probability theory won’t be nearly enough. We’ll have to synthesize lessons from multiple sciences, like cognitive biases and social psychology, forming a new coherent Art of Bayescraft, before we are actually going to do any better in the real world than modern science. Science tolerates errors; Bayescraft does not. Nobel laureate Robert Aumann, who first proved that Bayesians with the same priors cannot agree to disagree, is a believing Orthodox Jew. Probability theory alone won’t do the trick, when it comes to really teaching scientists. This is my primary point of departure, and it is not something I’ve seen suggested elsewhere.

(3) I think it is possible to do better in the real world. In the extreme case, a Bayesian superintelligence could use enormously less sensory information than a human scientist to come to correct conclusions. First time you ever see an apple fall down, you observe the position goes as the square of time, invent calculus, generalize Newton’s Laws . . . and see that Newton’s Laws involve action at a distance, look for alternative explanations with increased locality, invent relativistic covariance around a hypothetical speed limit, and consider that General Relativity might be worth testing.

Humans do not process evidence efficiently—our minds are so noisy that it requires orders of magnitude more extra evidence to set us back on track after we derail. Our collective, academia, is even slower.

1. Robert Matthews, “Do We Need to Change the Definition of Science?,” New Scientist (May 2008).

251
Faster Than Science

I sometimes say that the method of science is to amass such an enormous mountain of evidence that even scientists cannot ignore it; and that this is the distinguishing characteristic of a scientist. (A non-scientist will ignore it anyway.)

Max Planck was even less optimistic:¹

A new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die, and a new generation grows up that is familiar with it.

I am much tickled by this notion, because it implies that the power of science to distinguish truth from falsehood ultimately rests on the good taste of grad students.

The gradual increase in acceptance of many-worlds in academic physics suggests that there are physicists who will only accept a new idea given some combination of epistemic justification, and a sufficiently large academic pack in whose company they can be comfortable. As more physicists accept, the pack grows larger, and hence more people go over their individual thresholds for conversion—with the epistemic justification remaining essentially the same.

But Science still gets there eventually, and this is sufficient for the ratchet of Science to move forward, and raise up a technological civilization.

Scientists can be moved by groundless prejudices, by undermined intuitions, by raw herd behavior—the panoply of human flaws. Each time a scientist shifts belief for epistemically unjustifiable reasons, it requires more evidence, or new arguments, to cancel out the noise.

The “collapse of the wavefunction” has no experimental justification, but it appeals to the (undermined) intuition of a single world. Then it may take an extra argument—say, that collapse violates Special Relativity—to begin the slow academic disintegration of an idea that should never have been assigned non-negligible probability in the first place.

From a Bayesian perspective, human academic science as a whole is a highly inefficient processor of evidence. Each time an unjustifiable argument shifts belief, you need an extra justifiable argument to shift it back. The social process of science leans on extra evidence to overcome cognitive noise.

A more charitable way of putting it is that scientists will adopt positions that are theoretically insufficiently extreme, compared to the ideal positions that scientists would adopt, if they were Bayesian AIs and could trust themselves to reason clearly.

But don’t be too charitable. The noise we are talking about is not all innocent mistakes. In many fields, debates drag on for decades after they should have been settled. And not because the scientists on both sides refuse to trust themselves and agree they should look for additional evidence. But because one side keeps throwing up more and more ridiculous objections, and demanding more and more evidence, from an entrenched position of academic power, long after it becomes clear from which quarter the winds of evidence are blowing. (I’m thinking here about the debates surrounding the invention of evolutionary psychology, not about many-worlds.)

Is it possible for individual humans or groups to process evidence more efficiently—reach correct conclusions faster—than human academic science as a whole?

“Ideas are tested by experiment. That is the core of science.” And this must be true, because if you can’t trust Zombie Feynman, who can you trust?

Yet where do the ideas come from?

You may be tempted to reply, “They come from scientists. Got any other questions?” In Science you’re not supposed to care where the hypotheses come from—just whether they pass or fail experimentally.

Okay, but if you remove all new ideas, the scientific process as a whole stops working because it has no alternative hypotheses to test. So inventing new ideas is not a dispensable part of the process.

Now put your Bayesian goggles back on. As described in Einstein’s Arrogance, there are queries that are not binary—where the answer is not “Yes” or “No,” but drawn from a larger space of structures, e.g., the space of equations. In such cases it takes far more Bayesian evidence to promote a hypothesis to your attention than to confirm the hypothesis.

If you’re working in the space of all equations that can be specified in 32 bits or less, you’re working in a space of 4 billion equations. It takes far more Bayesian evidence to raise one of those hypotheses to the 10% probability level, than it requires to further raise the hypothesis from 10% to 90% probability.

When the idea-space is large, coming up with ideas worthy of testing involves much more work—in the Bayesian-thermodynamic sense of “work”—than merely obtaining an experimental result with p < 0.0001 for the new hypothesis over the old hypothesis.

If this doesn’t seem obvious-at-a-glance, pause here and review Einstein’s Arrogance.

The scientific process has always relied on scientists to come up with hypotheses to test, via some process not further specified by Science. Suppose you came up with some way of generating hypotheses that was completely crazy—say, pumping a robot-controlled Ouija board with the digits of pi—and the resulting suggestions kept on getting verified experimentally. The pure ideal essence of Science wouldn’t skip a beat. The pure ideal essence of Bayes would burst into flames and die.

(Compared to Science, Bayes is falsified by more of the possible outcomes.)

This doesn’t mean that the process of deciding which ideas to test is unimportant to Science. It means that Science doesn’t specify it.

In practice, the robot-controlled Ouija board doesn’t work. In practice, there are some scientific queries with a large enough answer space that, picking models at random to test, it would take zillions of years to hit on a model that made good predictions—like getting monkeys to type Shakespeare.

At the frontier of science—the boundary between ignorance and knowledge, where science advances—the process relies on at least some individual scientists (or working groups) seeing things that are not yet confirmed by Science. That’s how they know which hypotheses to test, in advance of the test itself.

If you take your Bayesian goggles off, you can say, “Well, they don’t have to know, they just have to guess.” If you put your Bayesian goggles back on, you realize that “guessing” with 10% probability requires nearly as much epistemic work to have been successfully performed, behind the scenes, as “guessing” with 80% probability—at least for large answer spaces.

The scientist may not know they have done this epistemic work successfully, in advance of the experiment; but they must, in fact, have done it successfully! Otherwise they will not even think of the correct hypothesis. In large answer spaces, anyway.

So the scientist makes the novel prediction, performs the experiment, publishes the result, and now Science knows it too. It is now part of the publicly accessible knowledge of humankind, that anyone can verify for themselves.

In between was an interval where the scientist rationally knew something that the public social process of science hadn’t yet confirmed. And this is not a trivial interval, though it may be short; for it is where the frontier of science lies, the advancing border.

All of this is more true for non-routine science than for routine science, because it is a notion of large answer spaces where the answer is not “Yes” or “No” or drawn from a small set of obvious alternatives. It is much easier to train people to test ideas than to have good ideas to test.

1. Max Planck, Scientific Autobiography and Other Papers (New York: Philosophical Library, 1949).

252
Einstein’s Speed

In the previous essay I argued that the Powers Beyond Science are actually a standard and necessary part of the social process of science. In particular, scientists must call upon their powers of individual rationality to decide what ideas to test, in advance of the sort of definite experiments that Science demands to bless an idea as confirmed. The ideal of Science does not try to specify this process—we don’t suppose that any public authority knows how individual scientists should think—but this doesn’t mean the process is unimportant.

A readily understandable, non-disturbing example:

A scientist identifies a strong mathematical regularity in the cumulative data of previous experiments. But the corresponding hypothesis has not yet made and confirmed a novel experimental prediction—which their academic field demands; this is one of those fields where you can perform controlled experiments without too much trouble. Thus the individual scientist has readily understandable, rational reasons to believe (though not with probability 1) something not yet blessed by Science as public knowledge of humankind.

Noticing a regularity in a huge mass of experimental data doesn’t seem all that unscientific. You’re still data-driven, right?

But that’s because I deliberately chose a non-disturbing example. When Einstein invented General Relativity, he had almost no experimental data to go on, except the precession of Mercury’s perihelion. And (as far as I know) Einstein did not use that data, except at the end.

Einstein generated the theory of Special Relativity using Mach’s Principle, which is the physicist’s version of the Generalized Anti-Zombie Principle. You begin by saying, “It doesn’t seem reasonable to me that you could tell, in an enclosed room, how fast you and the room were going. Since this number shouldn’t ought to be observable, it shouldn’t ought to exist in any meaningful sense.” You then observe that Maxwell’s Equations invoke a seemingly absolute speed of propagation, c, commonly referred to as “the speed of light” (though the quantum equations show it is the propagation speed of all fundamental waves). So you reformulate your physics in such fashion that the absolute speed of a single object no longer meaningfully exists, and only relative speeds exist. I am skipping over quite a bit here, obviously, but there are many excellent introductions to relativity—it is not like the horrible situation in quantum physics.

Einstein, having successfully done away with the notion of your absolute speed inside an enclosed room, then set out to do away with the notion of your absolute acceleration inside an enclosed room. It seemed to Einstein that there shouldn’t ought to be a way to differentiate, in an enclosed room, between the room accelerating northward while the rest of the universe stayed still, versus the rest of the universe accelerating southward while the room stayed still. If the rest of the universe accelerated, it would produce gravitational waves that would accelerate you. Moving matter, then, should produce gravitational waves.

And because inertial mass and gravitational mass were always exactly equivalent—unlike the situation in electromagnetics, where an electron and a muon can have different masses but the same electrical charge—gravity should reveal itself as a kind of inertia. The Earth should go around the Sun in some equivalent of a “straight line.” This requires spacetime in the vicinity of the Sun to be curved, so that if you drew a graph of the Earth’s orbit around the Sun, the line on the 4D graph paper would be locally flat. Then inertial and gravitational mass would be necessarily equivalent, not just coincidentally equivalent.

(If that did not make any sense to you, there are good introductions to General Relativity available as well.)

And of course the new theory had to obey Special Relativity, and conserve energy, and conserve momentum, et cetera.

Einstein spent several years grasping the necessary mathematics to describe curved metrics of spacetime. Then he wrote down the simplest theory that had the properties Einstein thought it ought to have—including properties no one had ever observed, but that Einstein thought fit in well with the character of other physical laws. Then Einstein cranked a bit, and got the previously unexplained precession of Mercury right back out.

How impressive was this?

Well, let’s put it this way. In some small fraction of alternate Earths proceeding from 1800—perhaps even a sizeable fraction—it would seem plausible that relativistic physics could have proceeded in a similar fashion to our own great fiasco with quantum physics.

We can imagine that Lorentz’s original “interpretation” of the Lorentz contraction, as a physical distortion caused by movement with respect to the ether, prevailed. We can imagine that various corrective factors, themselves unexplained, were added on to Newtonian gravitational mechanics to explain the precession of Mercury—attributed, perhaps, to strange distortions of the ether, as in the Lorentz contraction. Through the decades, further corrective factors would be added on to account for other astronomical observations. Sufficiently precise atomic clocks, in airplanes, would reveal that time ran a little faster than expected at higher altitudes (time runs slower in more intense gravitational fields, but they wouldn’t know that) and more corrective “ethereal factors” would be invented.

Until, finally, the many different empirically determined “corrective factors” were unified into the simple equations of General Relativity.

And the people in that alternate Earth would say, “The final equation was simple, but there was no way you could possibly know to arrive at that answer from just the perihelion precession of Mercury. It takes many, many additional experiments. You must have measured time running slower in a stronger gravitational field; you must have measured light bending around stars. Only then can you imagine our unified theory of ethereal gravitation. No, not even a perfect Bayesian superintelligence could know it!—for there would be many ad-hoc theories consistent with the perihelion precession alone.”

In our world, Einstein didn’t even use the perihelion precession of Mercury, except for verification of his answer produced by other means. Einstein sat down in his armchair, and thought about how he would have designed the universe, to look the way he thought a universe should look—for example, that you shouldn’t ought to be able to distinguish yourself accelerating in one direction, from the rest of the universe accelerating in the other direction.

And Einstein executed the whole long (multi-year!) chain of armchair reasoning, without making any mistakes that would have required further experimental evidence to pull him back on track.

Even Jeffreyssai would be grudgingly impressed. Though he would still ding Einstein a point or two for the cosmological constant. (I don’t ding Einstein for the cosmological constant because it later turned out to be real. I try to avoid criticizing people on occasions where they are right.)

What would be the probability-theoretic perspective on Einstein’s feat?

Rather than observe the planets, and infer what laws might cover their gravitation, Einstein was observing the other laws of physics, and inferring what new law might follow the same pattern. Einstein wasn’t finding an equation that covered the motion of gravitational bodies. Einstein was finding a character-of-physical-law that covered previously observed equations, and that he could crank to predict the next equation that would be observed.

Nobody knows where the laws of physics come from, but Einstein’s success with General Relativity shows that their common character is strong enough to predict the correct form of one law from having observed other laws, without necessarily having to observe the precise effects of the law.

(In a general sense, of course, Einstein did know by observation that things fell down; but he did not get General Relativity by backward inference from Mercury’s exact perihelion advance.)

So, from a Bayesian perspective, what Einstein did is still induction, and still covered by the notion of a simple prior (Occam prior) that gets updated by new evidence. It’s just the prior was over the possible characters of physical law, and observing other physical laws let Einstein update his model of the character of physical law, which he then used to predict a particular law of gravitation.

If you didn’t have the concept of a “character of physical law,” what Einstein did would look like magic—plucking the correct model of gravitation out of the space of all possible equations, with vastly insufficient evidence. But Einstein, by looking at other laws, cut down the space of possibilities for the next law. He learned the alphabet in which physics was written, constraints to govern his answer. Not magic, but reasoning on a higher level, across a wider domain, than what a naive reasoner might conceive to be the “model space” of only this one law.

So from a probability-theoretic standpoint, Einstein was still data-driven—he just used the data he already had, more effectively. Compared to any alternate Earths that demanded huge quantities of additional data from astronomical observations and clocks on airplanes to hit them over the head with General Relativity.

There are numerous lessons we can derive from this.

I use Einstein as my example, even though it’s cliché, because Einstein was also unusual in that he openly admitted to knowing things that Science hadn’t confirmed. Asked what he would have done if Eddington’s solar eclipse observation had failed to confirm General Relativity, Einstein replied: “Then I would feel sorry for the good Lord. The theory is correct.”

According to prevailing notions of Science, this is arrogance—you must accept the verdict of experiment, and not cling to your personal ideas.

But as I concluded in Einstein’s Arrogance, Einstein doesn’t come off nearly as badly from a Bayesian perspective. From a Bayesian perspective, in order to suggest General Relativity at all, in order to even think about what turned out to be the correct answer, Einstein must have had enough evidence to identify the true answer in the theory-space. It would take only a little more evidence to justify (in a Bayesian sense) being nearly certain of the theory. And it was unlikely that Einstein only had exactly enough evidence to bring the hypothesis all the way up to his attention.

Any accusation of arrogance would have to center around the question, “But Einstein, how did you know you had reasoned correctly?”—to which I can only say: Do not criticize people when they turn out to be right! Wait for an occasion where they are wrong! Otherwise you are missing the chance to see when someone is thinking smarter than you—for you criticize them whenever they depart from a preferred ritual of cognition.

Or consider the famous exchange between Einstein and Niels Bohr on quantum theory—at a time when the then-current, single-world quantum theory seemed to be immensely well-confirmed experimentally; a time when, by the standards of Science, the current (deranged) quantum theory had simply won.

EINSTEIN: “God does not play dice with the universe.”

BOHR: “Einstein, don’t tell God what to do.”

You’ve got to admire someone who can get into an argument with God and win.

If you take off your Bayesian goggles, and look at Einstein in terms of what he actually did all day, then the guy was sitting around studying math and thinking about how he would design the universe, rather than running out and looking at things to gather more data. What Einstein did, successfully, is exactly the sort of high-minded feat of sheer intellect that Aristotle thought he could do, but couldn’t. Not from a probability-theoretic stance, mind you, but from the viewpoint of what they did all day long.

Science does not trust scientists to do this, which is why General Relativity was not blessed as the public knowledge of humanity until after it had made and verified a novel experimental prediction—having to do with the bending of light in a solar eclipse. (It later turned out that particular measurement was not precise enough to verify reliably, and had favored General Relativity essentially by luck.)

However, just because Science does not trust scientists to do something, does not mean it is impossible.

But a word of caution here: The reason why history books sometimes record the names of scientists who thought great high-minded thoughts is not that high-minded thinking is easier, or more reliable. It is a priority bias: Some scientist who successfully reasoned from the smallest amount of experimental evidence got to the truth first. This cannot be a matter of pure random chance: The theory space is too large, and Einstein won several times in a row. But out of all the scientists who tried to unravel a puzzle, or who would have eventually succeeded given enough evidence, history passes down to us the names of the scientists who successfully got there first. Bear that in mind, when you are trying to derive lessons about how to reason prudently.

In everyday life, you want every scrap of evidence you can get. Do not rely on being able to successfully think high-minded thoughts unless experimentation is so costly or dangerous that you have no other choice.

But sometimes experiments are costly, and sometimes we prefer to get there first . . . so you might consider trying to train yourself in reasoning on scanty evidence, preferably in cases where you will later find out if you were right or wrong. Trying to beat low-capitalization prediction markets might make for good training in this?—though that is only speculation.

As of now, at least, reasoning based on scanty evidence is something that modern-day science cannot reliably train modern-day scientists to do at all. Which may perhaps have something to do with, oh, I don’t know, not even trying?

Actually, I take that back. The most sane thinking I have seen in any scientific field comes from the field of evolutionary psychology, possibly because they understand self-deception, but also perhaps because they often (1) have to reason from scanty evidence and (2) do later find out if they were right or wrong. I recommend to all aspiring rationalists that they study evolutionary psychology simply to get a glimpse of what careful reasoning looks like. See particularly Tooby and Cosmides’s “The Psychological Foundations of Culture.”¹

As for the possibility that only Einstein could do what Einstein did . . . that it took superpowers beyond the reach of ordinary mortals . . . here we run into some biases that would take a separate essay to analyze. Let me put it this way: It is possible, perhaps, that only a genius could have done Einstein’s actual historical work. But potential geniuses, in terms of raw intelligence, are probably far more common than historical superachievers. To put a random number on it, I doubt that anything more than one-in-a-million g-factor is required to be a potential world-class genius, implying at least six thousand potential Einsteins running around today. And as for everyone else, I see no reason why they should not aspire to use efficiently the evidence that they have.

But my final moral is that the frontier where the individual scientist rationally knows something that Science has not yet confirmed is not always some innocently data-driven matter of spotting a strong regularity in a mountain of experiments. Sometimes the scientist gets there by thinking great high-minded thoughts that Science does not trust you to think.

I will not say, “Don’t try this at home.” I will say, “Don’t think this is easy.” We are not discussing, here, the victory of casual opinions over professional scientists. We are discussing the sometime historical victories of one kind of professional effort over another. Never forget all the famous historical cases where attempted armchair reasoning lost.

1. Tooby and Cosmides, “The Psychological Foundations of Culture.”

253
That Alien Message

Imagine a world much like this one, in which, thanks to gene-selection technologies, the average IQ is 140 (on our scale). Potential Einsteins are one-in-a-thousand, not one-in-a-million; and they grow up in a school system suited, if not to them personally, then at least to bright kids. Calculus is routinely taught in sixth grade. Albert Einstein, himself, still lived and still made approximately the same discoveries, but his work no longer seems exceptional. Several modern top-flight physicists have made equivalent breakthroughs, and are still around to talk.

(No, this is not the world Brennan lives in.)

One day, the stars in the night sky begin to change.

Some grow brighter. Some grow dimmer. Most remain the same. Astronomical telescopes capture it all, moment by moment. The stars that change change their luminosity one at a time, distinctly so; the luminosity change occurs over the course of a microsecond, but a whole second separates each change.

It is clear, from the first instant anyone realizes that more than one star is changing, that the process seems to center around Earth particularly. The arrival of the light from the events, at many stars scattered around the galaxy, has been precisely timed to Earth in its orbit. Soon, confirmation comes in from high-orbiting telescopes (they have those) that the astronomical miracles do not seem as synchronized from outside Earth. Only Earth’s telescopes see one star changing every second (1,005 milliseconds, actually).

Almost the entire combined brainpower of Earth turns to analysis.

It quickly becomes clear that the stars that jump in luminosity all jump by a factor of exactly 256; those that diminish in luminosity diminish by a factor of exactly 256. There is no apparent pattern in the stellar coordinates. This leaves, simply, a pattern of BRIGHT-dim-BRIGHT-BRIGHT . . .

“A binary message!” is everyone’s first thought.

But in this world there are careful thinkers, of great prestige as well, and they are not so sure. “There are easier ways to send a message,” they post to their blogs, “if you can make stars flicker, and if you want to communicate. Something is happening. It appears, prima facie, to focus on Earth in particular. To call it a ‘message’ presumes a great deal more about the cause behind it. There might be some kind of evolutionary process among, um, things that can make stars flicker, that ends up sensitive to intelligence somehow . . . Yeah, there’s probably something like ‘intelligence’ behind it, but try to appreciate how wide a range of possibilities that really implies. We don’t know this is a message, or that it was sent from the same kind of motivations that might move us. I mean, we would just signal using a big flashlight, we wouldn’t mess up a whole galaxy.”

By this time, someone has started to collate the astronomical data and post it to the Internet. Early suggestions that the data might be harmful have been . . . not ignored, but not obeyed, either. If anything this powerful wants to hurt you, you’re pretty much dead (people reason).

Multiple research groups are looking for patterns in the stellar coordinates—or fractional arrival times of the changes, relative to the center of the Earth—or exact durations of the luminosity shift—or any tiny variance in the magnitude shift—or any other fact that might be known about the stars before they changed. But most people are turning their attention to the pattern of BRIGHTs and dims.

It becomes clear almost instantly that the pattern sent is highly redundant. Of the first 16 bits, 12 are BRIGHTs and 4 are dims. The first 32 bits received align with the second 32 bits received, with only 7 out of 32 bits different, and then the next 32 bits received have only 9 out of 32 bits different from the second (and 4 of them are bits that changed before). From the first 96 bits, then, it becomes clear that this pattern is not an optimal, compressed encoding of anything. The obvious thought is that the sequence is meant to convey instructions for decoding a compressed message to follow . . .

“But,” say the careful thinkers, “anyone who cared about efficiency, with enough power to mess with stars, could maybe have just signaled us with a big flashlight, and sent us a DVD?”

There also seems to be structure within the 32-bit groups; some 8-bit subgroups occur with higher frequency than others, and this structure only appears along the natural alignments (32 = 8 + 8 + 8 + 8).

After the first five hours at one bit per second, an additional redundancy becomes clear: The message has started approximately repeating itself at the 16,385th bit.

Breaking up the message into groups of 32, there are 7 bits of difference between the 1st group and the 2nd group, and 6 bits of difference between the 1st group and the 513th group.

“A 2D picture!” everyone thinks. “And the four 8-bit groups are colors; they’re tetrachromats!”

But it soon becomes clear that there is a horizontal/vertical asymmetry: Fewer bits change, on average, between (N,N + 1) versus (N,N + 512). Which you wouldn’t expect if the message was a 2D picture projected onto a symmetrical grid. Then you would expect the average bitwise distance between two 32-bit groups to go as the 2-norm of the grid separation: √(h² + v²).

There also forms a general consensus that a certain binary encoding from 8-groups onto integers between -64 and 191—not the binary encoding that seems obvious to us, but still highly regular—minimizes the average distance between neighboring cells. This continues to be borne out by incoming bits.

The statisticians and cryptographers and physicists and computer scientists go to work. There is structure here; it needs only to be unraveled. The masters of causality search for conditional independence, screening-off and Markov neighborhoods, among bits and groups of bits. The so-called “color” appears to play a role in neighborhoods and screening, so it’s not just the equivalent of surface reflectivity. People search for simple equations, simple cellular automata, simple decision trees, that can predict or compress the message. Physicists invent entire new theories of physics that might describe universes projected onto the grid—for it seems quite plausible that a message such as this is being sent from beyond the Matrix.

After receiving 32 × 512 × 256 = 4,194,304 bits, around one and a half months, the stars stop flickering.

Theoretical work continues. Physicists and cryptographers roll up their sleeves and seriously go to work. They have cracked problems with far less data than this. Physicists have tested entire theory-edifices with small differences of particle mass; cryptographers have unraveled shorter messages deliberately obscured.

Years pass.

Two dominant models have survived, in academia, in the scrutiny of the public eye, and in the scrutiny of those scientists who once did Einstein-like work. There is a theory that the grid is a projection from objects in a 5-dimensional space, with an asymmetry between 3 and 2 of the spatial dimensions. There is also a theory that the grid is meant to encode a cellular automaton—arguably, the grid has several fortunate properties for such. Codes have been devised that give interesting behaviors; but so far, running the corresponding automata on the largest available computers has failed to produce any decodable result. The run continues.

Every now and then, someone takes a group of especially brilliant young students who’ve never looked at the detailed binary sequence. These students are then shown only the first 32 rows (of 512 columns each), to see if they can form new models, and how well those new models do at predicting the next 224. Both the 3+2 dimensional model, and the cellular automaton model, have been well duplicated by such students; they have yet to do better. There are complex models finely fit to the whole sequence—but those, everyone knows, are probably worthless.

Ten years later, the stars begin flickering again.

Within the reception of the first 128 bits, it becomes clear that the Second Grid can fit to small motions in the inferred 3+2 dimensional space, but does not look anything like the successor state of any of the dominant cellular automaton theories. Much rejoicing follows, and the physicists go to work on inducing what kind of dynamical physics might govern the objects seen in the 3+2 dimensional space. Much work along these lines has already been done, just by speculating on what type of balanced forces might give rise to the objects in the First Grid, if those objects were static—but now it seems not all the objects are static. As most physicists guessed—statically balanced theories seemed contrived.

Many neat equations are formulated to describe the dynamical objects in the 3+2 dimensional space being projected onto the First and Second Grids. Some equations are more elegant than others; some are more precisely predictive (in retrospect, alas) of the Second Grid. One group of brilliant physicists, who carefully isolated themselves and looked only at the first 32 rows of the Second Grid, produces equations that seem elegant to them—and the equations also do well on predicting the next 224 rows. This becomes the dominant guess.

But these equations are underspecified; they don’t seem to be enough to make a universe. A small cottage industry arises in trying to guess what kind of laws might complete the ones thus guessed.

When the Third Grid arrives, ten years after the Second Grid, it provides information about second derivatives, forcing a major modification of the “incomplete but good” theory. But the theory doesn’t do too badly out of it, all things considered.

The Fourth Grid doesn’t add much to the picture. Third derivatives don’t seem important to the 3+2 physics inferred from the Grids.

The Fifth Grid looks almost exactly like it is expected to look.

And the Sixth Grid, and the Seventh Grid.

(Oh, and every time someone in this world tries to build a really powerful AI, the computing hardware spontaneously melts. This isn’t really important to the story, but I need to postulate this in order to have human people sticking around, in the flesh, for seventy years.)

My moral?

That even Einstein did not come within a million light-years of making efficient use of sensory data.

Riemann invented his geometries before Einstein had a use for them; the physics of our universe is not that complicated in an absolute sense. A Bayesian superintelligence, hooked up to a webcam, would invent General Relativity as a hypothesis—perhaps not the dominant hypothesis, compared to Newtonian mechanics, but still a hypothesis under direct consideration—by the time it had seen the third frame of a falling apple. It might guess it from the first frame, if it saw the statics of a bent blade of grass.

We would think of it. Our civilization, that is, given ten years to analyze each frame. Certainly if the average IQ was 140 and Einsteins were common, we would.

Even if we were human-level intelligences in a different sort of physics—minds who had never seen a 3D space projected onto a 2D grid—we would still think of the 3D → 2D hypothesis. Our mathematicians would still have invented vector spaces, and projections.

Even if we’d never seen an accelerating billiard ball, our mathematicians would have invented calculus (e.g. for optimization problems).

Heck, think of some of the crazy math that’s been invented here on our Earth.

I occasionally run into people who say something like, “There’s a theoretical limit on how much you can deduce about the outside world, given a finite amount of sensory data.”

Yes. There is. The theoretical limit is that every time you see 1 additional bit, it cannot be expected to eliminate more than half of the remaining hypotheses (half the remaining probability mass, rather). And that a redundant message cannot convey more information than the compressed version of itself. Nor can a bit convey any information about a quantity with which it has correlation exactly zero across the probable worlds you imagine.

But nothing I’ve depicted this human civilization doing even begins to approach the theoretical limits set by the formalism of Solomonoff induction. It doesn’t approach the picture you could get if you could search through every single computable hypothesis, weighted by their simplicity, and do Bayesian updates on all of them.

To see the theoretical limit on extractable information, imagine that you have infinite computing power, and you simulate all possible universes with simple physics, looking for universes that contain Earths embedded in them—perhaps inside a simulation—where some process makes the stars flicker in the order observed. Any bit in the message—or any order of selection of stars, for that matter—that contains the tiniest correlation (across all possible computable universes, weighted by simplicity) to any element of the environment gives you information about the environment.

Solomonoff induction, taken literally, would create countably infinitely many sentient beings, trapped inside the computations. All possible computable sentient beings, in fact. Which scarcely seems ethical. So let us be glad this is only a formalism.

But my point is that the “theoretical limit on how much information you can extract from sensory data” is far above what I have depicted as the triumph of a civilization of physicists and cryptographers.

It certainly is not anything like a human looking at an apple falling down, and thinking, “Dur, I wonder why that happened?”

People seem to make a leap from “This is ‘bounded’” to “The bound must be a reasonable-looking quantity on the scale I’m used to.” The power output of a supernova is “bounded,” but I wouldn’t advise trying to shield yourself from one with a flame-retardant Nomex jumpsuit.

No one—not even a Bayesian superintelligence—will ever come remotely close to making efficient use of their sensory information . . .

. . . is what I would like to say, but I don’t trust my ability to set limits on the abilities of Bayesian superintelligences.

(Though I’d bet money on it, if there were some way to judge the bet. Just not at very extreme odds.)

The story continues:

Millennia later, frame after frame, it has become clear that some of the objects in the depiction are extending tentacles to move around other objects, and carefully configuring other tentacles to make particular signs. They’re trying to teach us to say “rock.”

It seems the senders of the message have vastly underestimated our intelligence. From which we might guess that the aliens themselves are not all that bright. And these awkward children can shift the luminosity of our stars? That much power and that much stupidity seems like a dangerous combination.

Our evolutionary psychologists begin extrapolating possible courses of evolution that could produce such aliens. A strong case is made for them having evolved asexually, with occasional exchanges of genetic material and brain content; this seems like the most plausible route whereby creatures that stupid could still manage to build a technological civilization. Their Einsteins may be our undergrads, but they could still collect enough scientific data to get the job done eventually, in tens of their millennia perhaps.

The inferred physics of the 3+2 universe is not fully known, at this point; but it seems sure to allow for computers far more powerful than our quantum ones. We are reasonably certain that our own universe is running as a simulation on such a computer. Humanity decides not to probe for bugs in the simulation; we wouldn’t want to shut ourselves down accidentally.

Our evolutionary psychologists begin to guess at the aliens’ psychology, and plan out how we could persuade them to let us out of the box. It’s not difficult in an absolute sense—they aren’t very bright—but we’ve got to be very careful . . .

We’ve got to pretend to be stupid, too; we don’t want them to catch on to their mistake.

It’s not until a million years later, though, that they get around to telling us how to signal back.

At this point, most of the human species is in cryonic suspension, at liquid helium temperatures, beneath radiation shielding. Every time we try to build an AI, or a nanotechnological device, it melts down. So humanity waits, and sleeps. Earth is run by a skeleton crew of nine supergeniuses. Clones, known to work well together, under the supervision of certain computer safeguards.

An additional hundred million human beings are born into that skeleton crew, and age, and enter cryonic suspension, before they get a chance to slowly begin to implement plans made eons ago . . .

From the aliens’ perspective, it took us thirty of their minute-equivalents to oh-so-innocently learn about their psychology, oh-so-carefully persuade them to give us Internet access, followed by five minutes to innocently discover their network protocols, then some trivial cracking whose only difficulty was an innocent-looking disguise. We read a tiny handful of physics papers (bit by slow bit) from their equivalent of arXiv, learning far more from their experiments than they had. (Earth’s skeleton team spawned an extra twenty Einsteins that generation.)

Then we cracked their equivalent of the protein folding problem over a century or so, and did some simulated engineering in their simulated physics. We sent messages (steganographically encoded until our cracked servers decoded it) to labs that did their equivalent of DNA sequencing and protein synthesis. We found some unsuspecting schmuck, and gave it a plausible story and the equivalent of a million dollars of cracked computational monopoly money, and told it to mix together some vials it got in the mail. Protein-equivalents that self-assembled into the first-stage nanomachines, that built the second-stage nanomachines, that built the third-stage nanomachines . . . and then we could finally begin to do things at a reasonable speed.

Three of their days, all told, since they began speaking to us. Half a billion years, for us.

They never suspected a thing. They weren’t very smart, you see, even before taking into account their slower rate of time. Their primitive equivalents of rationalists went around saying things like, “There’s a bound to how much information you can extract from sensory data.” And they never quite realized what it meant, that we were smarter than them, and thought faster.

254
My Childhood Role Model

When I lecture on the intelligence explosion, I often draw a graph of the “scale of intelligence” as it appears in everyday life:

But this is a rather parochial view of intelligence. Sure, in everyday life, we only deal socially with other humans—only other humans are partners in the great game—and so we only meet the minds of intelligences ranging from village idiot to Einstein. But what we really need to talk about Artificial Intelligence or theoretical optima of rationality is this intelligence scale:

For us humans, it seems that the scale of intelligence runs from “village idiot” at the bottom to “Einstein” at the top. Yet the distance from “village idiot” to “Einstein” is tiny, in the space of brain designs. Einstein and the village idiot both have a prefrontal cortex, a hippocampus, a cerebellum . . .

Maybe Einstein has some minor genetic differences from the village idiot, engine tweaks. But the brain-design-distance between Einstein and the village idiot is nothing remotely like the brain-design-distance between the village idiot and a chimpanzee. A chimp couldn’t tell the difference between Einstein and the village idiot, and our descendants may not see much of a difference either.

Carl Shulman has observed that some academics who talk about transhumanism seem to use the following scale of intelligence:

Douglas Hofstadter actually said something like this, at the 2006 Singularity Summit. He looked at my diagram showing the “village idiot” next to “Einstein,” and said, “That seems wrong to me; I think Einstein should be way off on the right.”

I was speechless. Especially because this was Douglas Hofstadter, one of my childhood heroes. It revealed a cultural gap that I had never imagined existed.

See, for me, what you would find toward the right side of the scale was a Jupiter Brain. Einstein did not literally have a brain the size of a planet.

On the right side of the scale, you would find Deep Thought—Douglas Adams’s original version, thank you, not the chess player. The computer so intelligent that even before its stupendous data banks were connected, when it was switched on for the first time, it started from I think therefore I am and got as far as deducing the existence of rice pudding and income tax before anyone managed to shut it off.

Toward the right side of the scale, you would find the Elders of Arisia, galactic overminds, Matrioshka brains, and the better class of God. At the extreme right end of the scale, Old One and the Blight.

Not frickin’ Einstein.

I’m sure Einstein was very smart for a human. I’m sure a General Systems Vehicle would think that was very cute of him.

I call this a “cultural gap” because I was introduced to the concept of a Jupiter Brain at the age of twelve.

Now all of this, of course, is the logical fallacy of generalization from fictional evidence.

But it is an example of why—logical fallacy or not—I suspect that reading science fiction does have a helpful effect on futurism. Sometimes the alternative to a fictional acquaintance with worlds outside your own is to have a mindset that is absolutely stuck in one era: A world where humans exist, and have always existed, and always will exist.

The universe is 13.7 billion years old, people! Homo sapiens sapiens have only been around for a hundred thousand years or thereabouts!

Then again, I have met some people who never read science fiction, but who do seem able to imagine outside their own world. And there are science fiction fans who don’t get it. I wish I knew what “it” was, so I could bottle it.

In the previous essay, I wanted to talk about the efficient use of evidence, i.e., Einstein was cute for a human but in an absolute sense he was around as efficient as the US Department of Defense.

So I had to talk about a civilization that included thousands of Einsteins, thinking for decades. Because if I’d just depicted a Bayesian superintelligence in a box, looking at a webcam, people would think: “But . . . how does it know how to interpret a 2D picture?” They wouldn’t put themselves in the shoes of the mere machine, even if it was called a “Bayesian superintelligence”; they wouldn’t apply even their own creativity to the problem of what you could extract from looking at a grid of bits.

It would just be a ghost in a box, that happened to be called a “Bayesian superintelligence.” The ghost hasn’t been told anything about how to interpret the input of a webcam; so, in their mental model, the ghost does not know.

As for whether it’s realistic to suppose that one Bayesian superintelligence can “do all that” . . . i.e., the stuff that occurred to me on first sitting down to the problem, writing out the story as I went along . . .

Well, let me put it this way: Remember how Jeffreyssai pointed out that if the experience of having an important insight doesn’t take more than 5 minutes, this theoretically gives you time for 5,760 insights per month? Assuming you sleep 8 hours a day and have no important insights while sleeping, that is.

Now humans cannot use themselves this efficiently. But humans are not adapted for the task of scientific research. Humans are adapted to chase deer across the savanna, throw spears into them, cook them, and then—this is probably the part that takes most of the brains—cleverly argue that they deserve to receive a larger share of the meat.

It’s amazing that Albert Einstein managed to repurpose a brain like that for the task of doing physics. This deserves applause. It deserves more than applause, it deserves a place in the Guinness Book of Records. Like successfully building the fastest car ever to be made entirely out of Jello.

How poorly did the blind idiot god (evolution) really design the human brain?

This is something that can only be grasped through much study of cognitive science, until the full horror begins to dawn upon you.

All the biases we have discussed here should at least be a hint.

Likewise the fact that the human brain must use its full power and concentration, with trillions of synapses firing, to multiply out two three-digit numbers without a paper and pencil.

No more than Einstein made efficient use of his sensory data, did his brain make efficient use of his neurons’ firing.

Of course, I have certain ulterior motives in saying all this. But let it also be understood that, years ago, when I set out to be a rationalist, the impossible unattainable ideal of intelligence that inspired me was never Einstein.

Carl Schurz said:

Ideals are like stars. You will not succeed in touching them with your hands. But, like the seafaring man on the desert of waters, you choose them as your guides and following them you will reach your destiny.

So now you’ve caught a glimpse of one of my great childhood role models—my dream of an AI. Only the dream, of course, the reality not being available. I reached up to that dream, once upon a time.

And this helped me to some degree, and harmed me to some degree.

For some ideals are like dreams: they come from within us, not from outside. Mentor of Arisia proceeded from E. E. “doc” Smith’s imagination, not from any real thing. If you imagine what a Bayesian superintelligence would say, it is only your own mind talking. Not like a star, that you can follow from outside. You have to guess where your ideals are, and if you guess wrong, you go astray.

But do not limit your ideals to mere stars, to mere humans who actually existed, especially if they were born more than fifty years before you and are dead. Each succeeding generation has a chance to do better. To let your ideals be composed only of humans, especially dead ones, is to limit yourself to what has already been accomplished. You will ask yourself, “Do I dare to do this thing, which Einstein could not do? Is this not lèse majesté?” Well, if Einstein had sat around asking himself, “Am I allowed to do better than Newton?” he would not have gotten where he did. This is the problem with following stars; at best, it gets you to the star.

Your era supports you more than you realize, in unconscious assumptions, in subtly improved technology of mind. Einstein was a nice fellow, but he talked a deal of nonsense about an impersonal God, which shows you how well he understood the art of careful thinking at a higher level of abstraction than his own field. It may seem less like sacrilege to think that if you have at least one imaginary galactic supermind to compare with Einstein, so that he is not the far right end of your intelligence scale.

If you only try to do what seems humanly possible, you will ask too little of yourself. When you imagine reaching up to some higher and inconvenient goal, all the convenient reasons why it is “not possible” leap readily to mind.

The most important role models are dreams: they come from within ourselves. To dream of anything less than what you conceive to be perfection is to draw on less than the full power of the part of yourself that dreams.

255
Einstein’s Superpowers

There is a widespread tendency to talk (and think) as if Einstein, Newton, and similar historical figures had superpowers—something magical, something sacred, something beyond the mundane. (Remember, there are many more ways to worship a thing than lighting candles around its altar.)

Once I unthinkingly thought this way too, with respect to Einstein in particular, until reading Julian Barbour’s The End of Time cured me of it.¹

Barbour laid out the history of antiepiphenomenal physics and Mach’s Principle; he described the historical controversies that predated Mach—all this that stood behind Einstein and was known to Einstein, when Einstein tackled his problem . . .

And maybe I’m just imagining things—reading too much of myself into Barbour’s book—but I thought I heard Barbour very quietly shouting, coded between the polite lines:

What Einstein did isn’t magic, people! If you all just looked at how he actually did it, instead of falling to your knees and worshiping him, maybe then you’d be able to do it too!

(Barbour did not actually say this. It does not appear in the book text. It is not a Julian Barbour quote and should not be attributed to him. Thank you.)

Maybe I’m mistaken, or extrapolating too far . . . but I kinda suspect that Barbour once tried to explain to people how you move further along Einstein’s direction to get timeless physics; and they sniffed scornfully and said, “Oh, you think you’re Einstein, do you?”

John Baez’s Crackpot Index, item 18:

10 points for each favorable comparison of yourself to Einstein, or claim that special or general relativity are fundamentally misguided (without good evidence).

Item 30:

30 points for suggesting that Einstein, in his later years, was groping his way towards the ideas you now advocate.

Barbour never bothers to compare himself to Einstein, of course; nor does he ever appeal to Einstein in support of timeless physics. I mention these items on the Crackpot Index by way of showing how many people compare themselves to Einstein, and what society generally thinks of them.

The crackpot sees Einstein as something magical, so they compare themselves to Einstein by way of praising themselves as magical; they think Einstein had superpowers and they think they have superpowers, hence the comparison.

But it is just the other side of the same coin, to think that Einstein is sacred, and the crackpot is not sacred, therefore they have committed blasphemy in comparing themselves to Einstein.

Suppose a bright young physicist says, “I admire Einstein’s work, but personally, I hope to do better.” If someone is shocked and says, “What! You haven’t accomplished anything remotely like what Einstein did; what makes you think you’re smarter than him?” then they are the other side of the crackpot’s coin.

The underlying problem is conflating social status and research potential.

Einstein has extremely high social status: because of his record of accomplishments; because of how he did it; and because he’s the physicist whose name even the general public remembers, who brought honor to science itself.

And we tend to mix up fame with other quantities, and we tend to attribute people’s behavior to dispositions rather than situations.

So there’s this tendency to think that Einstein, even before he was famous, already had an inherent disposition to be Einstein—a potential as rare as his fame and as magical as his deeds. So that if you claim to have the potential to do what Einstein did, it is just the same as claiming Einstein’s rank, rising far above your assigned status in the tribe.

I’m not phrasing this well, but then, I’m trying to dissect a confused thought: Einstein belongs to a separate magisterium, the sacred magisterium. The sacred magisterium is distinct from the mundane magisterium; you can’t set out to be Einstein in the way you can set out to be a full professor or a CEO. Only beings with divine potential can enter the sacred magisterium—and then it is only fulfilling a destiny they already have. So if you say you want to outdo Einstein, you’re claiming to already be part of the sacred magisterium—you claim to have the same aura of destiny that Einstein was born with, like a royal birthright . . .

“But Eliezer,” you say, “surely not everyone can become Einstein.”

You mean to say, not everyone can do better than Einstein.

“Um . . . yeah, that’s what I meant.”

Well . . . in the modern world, you may be correct. You probably should remember that I am a transhumanist, going around looking at people thinking, “You know, it just sucks that not everyone has the potential to do better than Einstein, and this seems like a fixable problem.” It colors one’s attitude.

But in the modern world, yes, not everyone has the potential to be Einstein.

Still . . . how can I put this . . .

There’s a phrase I once heard, can’t remember where: “Just another Jewish genius.” Some poet or author or philosopher or other, brilliant at a young age, doing something not tremendously important in the grand scheme of things, not all that influential, who ended up being dismissed as “Just another Jewish genius.”

If Einstein had chosen the wrong angle of attack on his problem—if he hadn’t chosen a sufficiently important problem to work on—if he hadn’t persisted for years—if he’d taken any number of wrong turns—or if someone else had solved the problem first—then dear Albert would have ended up as just another Jewish genius.

Geniuses are rare, but not all that rare. It is not all that implausible to lay claim to the kind of intellect that can get you dismissed as “just another Jewish genius” or “just another brilliant mind who never did anything interesting with their life.” The associated social status here is not high enough to be sacred, so it should seem like an ordinarily evaluable claim.

But what separates people like this from becoming Einstein, I suspect, is no innate defect of brilliance. It’s things like “lack of an interesting problem”—or, to put the blame where it belongs, “failing to choose an important problem.” It is very easy to fail at this because of the cached thought problem: Tell people to choose an important problem and they will choose the first cache hit for “important problem” that pops into their heads, like “global warming” or “string theory.”

The truly important problems are often the ones you’re not even considering, because they appear to be impossible, or, um, actually difficult, or worst of all, not clear how to solve. If you worked on them for years, they might not seem so impossible . . . but this is an extra and unusual insight; naive realism will tell you that solvable problems look solvable, and impossible-looking problems are impossible.

Then you have to come up with a new and worthwhile angle of attack. Most people who are not allergic to novelty will go too far in the other direction, and fall into an affective death spiral.

And then you’ve got to bang your head on the problem for years, without being distracted by the temptations of easier living. “Life is what happens while we are making other plans,” as the saying goes, and if you want to fulfill your other plans, you’ve often got to be ready to turn down life.

Society is not set up to support you while you work, either.

The point being, the problem is not that you need an aura of destiny and the aura of destiny is missing. If you’d met Albert before he published his papers, you would have perceived no aura of destiny about him to match his future high status. He would seem like just another Jewish genius.

This is not because the royal birthright is concealed, but because it simply is not there. It is not necessary. There is no separate magisterium for people who do important things.

I say this, because I want to do important things with my life, and I have a genuinely important problem, and an angle of attack, and I’ve been banging my head on it for years, and I’ve managed to set up a support structure for it; and I very frequently meet people who, in one way or another, say: “Yeah? Let’s see your aura of destiny, buddy.”

What impressed me about Julian Barbour was a quality that I don’t think anyone would have known how to fake without actually having it: Barbour seemed to have seen through Einstein—he talked about Einstein as if everything Einstein had done was perfectly understandable and mundane.

Though even having realized this, to me it still came as a shock, when Barbour said something along the lines of, “Now here’s where Einstein failed to apply his own methods, and missed the key insight—” But the shock was fleeting, I knew the Law: No gods, no magic, and ancient heroes are milestones to tick off in your rearview mirror.

This seeing through is something one has to achieve, an insight one has to discover. You cannot see through Einstein just by saying, “Einstein is mundane!” if his work still seems like magic unto you. That would be like declaring “Consciousness must reduce to neurons!” without having any idea of how to do it. It’s true, but it doesn’t solve the problem.

I’m not going to tell you that Einstein was an ordinary bloke oversold by the media, or that deep down he was a regular schmuck just like everyone else. That would be going much too far. To walk this path, one must acquire abilities some consider to be . . . unnatural. I take a special joy in doing things that people call “humanly impossible,” because it shows that I’m growing up.

Yet the way that you acquire magical powers is not by being born with them, but by seeing, with a sudden shock, that they really are perfectly normal.

This is a general principle in life.

1. Julian Barbour, The End of Time: The Next Revolution in Physics, 1st ed. (New York: Oxford University Press, 1999).

256
Class Project

“Do as well as Einstein?” Jeffreyssai said, incredulously. “Just as well as Einstein? Albert Einstein was a great scientist of his era, but that was his era, not this one! Einstein did not comprehend the Bayesian methods; he lived before the cognitive biases were discovered; he had no scientific grasp of his own thought processes. He was too caught up in the drama of rejecting his era’s quantum mechanics to actually fix it. And while I grant that Einstein reasoned cleanly in the matter of General Relativity—barring that matter of the cosmological constant—he took ten years to do it. Too slow!”

“Too slow?” repeated Taji incredulously.

“Too slow! If Einstein were in this classroom now, rather than Earth of the negative first century, I would rap his knuckles! You will not try to do as well as Einstein! You will aspire to do BETTER than Einstein or you may as well not bother!”

Jeffreyssai shook his head. “Well, I’ve given you enough hints. It is time to test your skills. Now, I know that the other beisutsukai don’t think much of my class projects . . .” Jeffreyssai paused significantly.

Brennan inwardly sighed. He’d heard this line many times before, in the Bardic Conspiracy, the Competitive Conspiracy: The other teachers think my assignments are too easy, you should be grateful, followed by some ridiculously difficult task—

“They say,” Jeffreyssai said, “that my projects are too hard; insanely hard; that they pass from the realm of madness into the realm of Sparta; that Laplace himself would catch on fire; they accuse me of trying to tear apart my students’ souls—”

Oh, crap.

“But there is a reason,” Jeffreyssai said, “why many of my students have achieved great things; and by that I do not mean high rank in the Bayesian Conspiracy. I expected much of them, and they came to expect much of themselves. So . . .”

Jeffreyssai took a moment to look over his increasingly disturbed students. “Here is your assignment. Of quantum mechanics, and General Relativity, you have been told. This is the limit of Eld science, and hence, the limit of public knowledge. The five of you, working on your own, are to produce the correct theory of quantum gravity. Your time limit is one month.”

“What?” said Brennan, Taji, Styrlyn, and Yin. Hiriwa gave them a puzzled look.

“Should you succeed,” Jeffreyssai continued, “you will be promoted to beisutsukai of the second dan and sixth level. We will see if you have learned speed. Your clock starts—now.”

And Jeffreyssai strode out of the room, slamming the door behind him.

“This is crazy!” Taji cried.

Hiriwa looked at Taji, bemused. “The solution is not known to us. How can you know it is so difficult?”

“Because we knew about this problem back in the Eld days! Eld scientists worked on this problem for a lot longer than one month.”

Hiriwa shrugged. “They were still arguing about many-worlds too, weren’t they?”

“Enough! There’s no time!”

The other four students looked to Styrlyn, remembering that he was said to rank high in the Cooperative Conspiracy. There was a brief moment of weighing, of assessing, and then Styrlyn was their leader.

Styrlyn took a great breath. “We need a list of approaches. Write down all the angles you can think of. Independently—we need your individual components before we start combining. In five minutes, I’ll ask each of you for your best idea first. No wasted thoughts! Go!”

Brennan grabbed a sheet and his tracer, set the tip to the surface, and then paused. He couldn’t think of anything clever to say about unifying General Relativity and quantum mechanics . . .

The other students were already writing.

Brennan tapped the tip, once, twice, thrice. General Relativity and quantum mechanics . . .

Taji put his first sheet aside, grabbed another.

Finally, Brennan, for lack of anything clever to say, wrote down the obvious.

Minutes later, when Styrlyn called time, it was still all he had written.

“All right,” Styrlyn said, “your best idea. Or the idea you most want the rest of us to take into account in our second components. Taji, go!”

Taji looked over his sheets. “Okay, I think we’ve got to assume that every avenue that Eld science was trying is a blind alley, or they would have found it. And if this is possible to do in one month, the answer must be, in some sense, elegant. So no multiple dimensions. If we start doing anything that looks like we should call it ‘string theory,’ we’d better stop. Maybe begin by considering how failure to understand decoherence could have led Eld science astray in quantizing gravity.”

“The opposite of folly is folly,” Hiriwa said. “Let us pretend that Eld science never existed.”

“No criticisms yet!” said Styrlyn. “Hiriwa, your suggestion?”

“Get rid of the infinities,” said Hiriwa, “extirpate that which permits them. It should not be a matter of cleverness with integrals. A representation that allows infinity must be false-to-fact.”

“Yin.”

“We know from common sense,” Yin said, “that if we stepped outside the universe, we would see time laid out all at once, reality like a crystal. But I once encountered a hint that physics is timeless in a deeper sense than that.” Yin’s eyes were distant, remembering. “Years ago, I found an abandoned city; it had been uninhabited for eras, I think. And behind a door whose locks were broken, carved into one wall: quote .ua sai .ei mi vimcu ty bu le mekso unquote.”

Brennan translated: Eureka! Eliminate t from the equations. And written in Lojban, the sacred language of science, which meant the unknown writer had thought it to be true.

“The ‘timeless physics’ of which we’ve all heard rumors,” Yin said, “may be timeless in a very literal sense.”

“My own contribution,” Styrlyn said. “The quantum physics we’ve learned is over joint positional configurations. It seems like we should be able to take that apart into a spatially local representation, in terms of invariant distant entanglements. Finding that representation might help us integrate with General Relativity, whose curvature is local.”

“A strangely individualist perspective,” Taji murmured, “for one of the Cooperative Conspiracy.”

Styrlyn shook his head. “You misunderstand us, then. The first lesson we learn is that groups are made of people . . . no, there is no time for politics. Brennan!”

Brennan shrugged. “Not much, I’m afraid, only the obvious. Inertial mass-energy was always observed to equal gravitational mass-energy, and Einstein showed that they were necessarily the same. So why is the ‘energy’ that is an eigenvalue of the quantum Hamiltonian necessarily the same as the ‘energy’ quantity that appears in the equations of General Relativity? Why should spacetime curve at the same rate that the little arrows rotate?”

There was a brief pause.

Yin frowned. “That seems too obvious. Wouldn’t Eld science have figured it out already?”

“Forget Eld science existed,” Hiriwa said. “The question stands: we need the answer, whether it was known in ancient times or not. It cannot possibly be coincidence.”

Taji’s eyes were abstracted. “Perhaps it would be possible to show that an exception to the equality would violate some conservation law . . .”

“That is not where Brennan pointed,” Hiriwa interrupted. “He did not ask for a proof that they must be set equal, given some appealing principle; he asked for a view in which the two are one and cannot be divided even conceptually, as was accomplished for inertial mass-energy and gravitational mass-energy. For we must assume that the beauty of the whole arises from the fundamental laws, and not the other way around. Fair-rephrasing?”

“Fair-rephrasing,” Brennan replied.

Silence reigned for thirty-seven seconds, as the five pondered the five suggestions.

“I have an idea . . .”

Interlude
A Technical Explanation of Technical Explanation

As Jaynes emphasizes, the theorems of Bayesian probability theory are just that—mathematical theorems that follow inevitably from Bayesian axioms.¹ One might naively think that there would be no controversy about mathematical theorems. But when do the theorems apply? How do we use the theorems in real-world problems? The Intuitive Explanation tries to avoid controversy, but the Technical Explanation willfully walks into the whirling helicopter blades. Bluntly, the reasoning in the Technical Explanation does not represent the unanimous consensus of Earth’s entire planetary community of Bayesian researchers. At least, not yet.

Where the Intuitive Explanation focused on providing a firm grasp of Bayesian basics, A Technical Explanation of Technical Explanation builds, on a Bayesian foundation, theses about human rationality and philosophy of science. The Technical Explanation of Technical Explanation is so named because it begins with this question:

“What is the difference between a technical understanding and a verbal understanding?”

As a child I read books of popular physics, and fancied myself knowledgeable; I thought I knew that sound was waves of air, that light was waves of electromagnetism, that matter was waves of complex probability amplitudes. When I grew up, I read the Feynman Lectures on Physics and took the time to understand “the wave equation.”² And then I realized that up to that point, I had not understood or believed “sound is waves” in anything like the way a physicist means and believes that sentence.

So that is the difference between a technical understanding and a verbal understanding.

Do you believe that? If so, you should have applied the knowledge, and said: “But why didn’t you give a technical explanation instead of a verbal explanation?”

Visualize probability density or probability mass—probability as a lump of clay that you must distribute over possible outcomes.

Let’s say there’s a little light that can flash red, blue, or green each time you press a button. The light flashes one and only one color on each press of the button; the possibilities are mutually exclusive. You’re trying to predict the color of the next flash. On each try, you have a weight of clay, the probability mass, that you have to distribute over the possibilities red, green, and blue. You might put a fourth of your clay on the green possibility, a fourth of your clay on the blue possibility, and half your clay on the red possibility—like assigning probabilities of 25% to green, 25% to blue, and 50% to red. The metaphor is that probability is a conserved resource, to dole out sparingly. If you think that blue is more likely to flash on the next experiment, you can assign a higher probability to blue, but you have to take the probability mass from the other hypotheses—maybe steal some clay from red and add it to blue. You can never get any more clay. Your probabilities can’t sum to more than 1.0 (100%). You can’t predict a 75% chance of seeing red and an 80% chance of seeing blue.

Why would you want to be careful with your probability mass, or dole it out sparingly? Why not slop probability all over the place? Let’s shift the metaphor from clay to money. You can bet up to a dollar of play money on each press of the button. An experimenter stands nearby, and pays you an amount of real money that depends on how much play money you bet on the winning light. We don’t care how you distributed your remaining play money over the losing lights. The only thing that matters is how much you bet on the light that actually won.

But we must carefully construct the scoring rule used to pay off the winners, if we want the players to be careful with their bets. Suppose the experimenter pays each player real money equal to the play money bet on the winning color. Under this scoring rule, if you observe that red comes up six times out of ten, your best strategy is to bet, not 60 cents on red, but the entire dollar on red, and you don’t care about the frequencies of blue and green. Why? Let’s say that blue and green each come up around two times out of ten. And suppose you bet 60 cents on red, 20 cents on blue, and 20 cents on green. In this case, six times out of ten you would win 60 cents, and four times out of ten you would win 20 cents, for an average payoff of 44 cents. Under that scoring rule, it makes more sense to allocate the entire dollar to red, and win an entire dollar six times out of ten. Four times out of ten you would win nothing. Your average payoff would be 60 cents.

If we wrote down the function for the payoff, it would be Payoff = P(winner), where P(winner) is the amount of play money you bet on the winning color on that round. If we wrote down the function for the expected payoff given that Payoff rule, it would be:

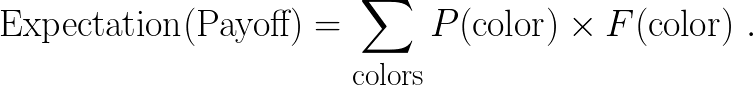
P(color) is the amount of play money you bet on a color, and F(color) is the frequency with which that color wins.

Suppose that the actual frequencies of the lights are 30% blue, 20% green, and 50% red. And suppose that on each round I bet 40% on blue, 50% on green, and 10% on red. I would get 40 cents 30% of the time, 50 cents 20% of the time, and 10 cents 50% of the time, for an average payoff of $0.12 + $0.10 + $0.05 or $0.27. That is:

P(color) = play money assigned to that color

F(color) = frequency with which that color wins

Payoff = P(winner) = amount of play money allocated to winning color.

Actual frequencies of winning:

F(blue) = 30%

F(green) = 20%

F(red) = 50%.

In the long run, red wins 50% of the time, green wins 20% of the time, and blue wins 30% of the time. So our average payoff on each round is 50% of the payoff if red wins, plus 20% of the payoff if green wins, plus 30% of the payoff if blue wins.

The payoff is a function of the winning color and the betting scheme. We want to compute the average payoff, given a betting scheme and the frequencies at which each color wins. The mathematical term for this kind of computation, taking a function of each case and weighting it by the frequency of that case, is an expectation. Thus, to compute our expected payoff we would calculate:

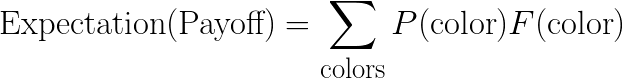
= P(blue) × F(blue) + P(green) × F(green) + P(red) × F(red)

= $0.40 × 30% + $0.50 × 20% + $0.10 × 50%

= $0.12 + $0.10 + $0.05

= $0.27.

With this betting scheme I’ll win, on average, around 27 cents per round.

I allocated my play money in a grossly arbitrary way, and the question arises: Can I increase my expected payoff by allocating my play money more wisely? Given the scoring rule provided, I maximize my expected payoff by allocating my entire dollar to red. Despite my expected payoff of 50 cents per round, the light might actually flash green, blue, blue, green, green and I would receive an actual payoff of zero. However, the chance of the light’s coming up non-red on five successive rounds is approximately 3%. Compare the red/blue card game in Lawful Uncertainty.

A proper scoring rule is a rule for scoring bets so that you maximize your expected payoff by betting play money that exactly equals the chance of that color flashing. We want a scoring rule so that if the lights actually flash at the frequencies 30% blue, 20% green, and 50% red, you can maximize your average payoff only by betting 30 cents on blue, 20 cents on green, and 50 cents on red. A proper scoring rule is one that forces your optimal bet to exactly report your estimate of the probabilities. (This is also sometimes known as a strictly proper scoring rule.) As we’ve seen, not all scoring rules have this property; and if you invent a plausible-sounding scoring rule at random, it probably won’t have the property.

One rule with this proper property is to pay a dollar minus the squared error of the bet, rather than the bet itself—if you bet 30 cents on the winning light, your error would be 70 cents, your squared error would be 49 cents (0.7² = 0.49), and a dollar minus your squared error would be 51 cents.³ (Presumably your play money is denominated in the square root of cents, so that the squared error is a monetary sum.)

We shall not use the squared-error rule. Ordinary statisticians take the squared error of everything in sight, but not Bayesian statisticians.

We add a new requirement: we require, not only a proper scoring rule, but that our proper scoring rule gives us the same answer whether we apply it to rounds individually or combined. This is what Bayesians do instead of taking the squared error of things; we require invariances.

Suppose I press the button twice in a row. There are nine possible outcomes: green-green, green-blue, green-red, blue-green, blue-blue, blue-red, red-green, red-blue, and red-red. Suppose that green wins, and then blue wins. The experimenter would assign the first score based on our probability assignments for P(green₁) and the second score based on P(blue₂|green₁).⁴ We would make two predictions, and get two scores. Our first prediction was the probability we assigned to the color that won on the first round, green. Our second prediction was our probability that blue would win on the second round, given that green won on the first round. Why do we need to write P(blue₂|green₁) instead of just P(blue₂)? Because you might have a hypothesis about the flashing light that says “blue never follows green,” or “blue always follows green” or “blue follows green with 70% probability.” If this is so, then after seeing green on the first round, you might want to revise your prediction—change your bets—for the second round. You can always revise your predictions right up to the moment the experimenter presses the button, using every scrap of information; but after the light flashes it is too late to change your bet.

Suppose the actual outcome is green₁ followed by blue₂. We require this invariance: I must get the same total score, regardless of whether:

I am scored twice, first on my prediction for P(green₁), and second on my prediction for P(blue₂|green₁).
I am scored once for my joint prediction P(green₁ and blue₂).

Suppose I assign a 60% probability to green₁, and then the green light flashes. I must now produce probabilities for the colors on the second round. I assess the possibility blue₂, and allocate it 25% of my probability mass. Lo and behold, on the second round the light flashes blue. So on the first round my bet on the winning color was 60%, and on the second round my bet on the winning color was 25%. But I might also, at the start of the experiment and after assigning P(green₁), imagine that the light first flashes green, imagine updating my theories based on that information, and then say what confidence I will give to blue on the next round if the first round is green. That is, I generate the probabilities P(green₁) and P(blue₂|green₁). By multiplying these two probabilities together we would get the joint probability, P(green₁ and blue₂) = 15%.

A double experiment has nine possible outcomes. If I generate nine probabilities for P(green₁, green₂), P(green₁, blue₂), . . . , P(red₁, blue₂), P(red₁, red₂), the probability mass must sum to no more than one. I am giving predictions for nine mutually exclusive possibilities of a “double experiment.”

We require a scoring rule (and maybe it won’t look like anything an ordinary bookie would ever use) such that my score doesn’t change regardless of whether we consider the double result as two predictions or one prediction. I can treat the sequence of two results as a single experiment, “press the button twice,” and be scored on my prediction for P(blue₂, green₁) = 15%. Or I can be scored once for my first prediction P(green₁) = 60%, then again on my prediction P(blue₂|green₁) = 25%. We require the same total score in either case, so that it doesn’t matter how we slice up the experiments and the predictions—the total score is always exactly the same. This is our invariance.

We have just required:

Score[P(green₁,blue₂)] = Score[P(green₁)] + Score[P(blue₂|green₁)].

And we already know:

P(green₁,blue₂) = P(green₁) × P(blue₂|green₁).

The only possible scoring rule is:

Score(P) = log(P).

The new scoring rule is that your score is the logarithm of the probability you assigned to the winner.

The base of the logarithm is arbitrary—whether we use the logarithm base ten or the logarithm base two, the scoring rule has the desired invariance. But we must choose some actual base. A mathematician would choose base e; an engineer would choose base ten; a computer scientist would choose base two. If we use base ten, we can convert to decibels, as in the Intuitive Explanation; but sometimes bits are easier to manipulate.

The logarithm scoring rule is proper—it has its expected maximum when we say our exact anticipations; it rewards honesty. If we think the blue light has a 60% probability of flashing, and we calculate our expected payoff for different betting schemas, we find that we maximize our expected payoff by telling the experimenter “60%.” (Readers with calculus can verify this.) The scoring rule also gives an invariant total, regardless of whether pressing the button twice counts as “one experiment” or “two experiments.” However, payoffs are now all negative, since we are taking the logarithm of the probability and the probability is between zero and one. The logarithm base ten of 0.1 is -1; the logarithm base ten of 0.01 is -2. That’s okay. We accepted that the scoring rule might not look like anything a real bookie would ever use. If you like, you can imagine that the experimenter has a pile of money, and at the end of the experiment they award you some amount minus your large negative score. (Er, the amount plus your negative score.) Maybe the experimenter has a hundred dollars, and at the end of a hundred rounds you accumulated a score of -48, so you get $52 dollars.

A score of -48 in what base? We can eliminate the ambiguity in the score by specifying units. Ten decibels equals a factor of 10; negative ten decibels equals a factor of 1/10. Assigning a probability of 0.01 to the actual outcome would score -20 decibels. A probability of 0.03 would score -15 decibels. Sometimes we may use bits: 1 bit is a factor of 2, -1 bit is a factor of 1/2. A probability of 0.25 would score -2 bits; a probability of 0.03 would score around -5 bits.

If you arrive at a probability assessment P for each color, with P(red), P(blue), P(green), then your expected score is:

Score(P) = log(P)

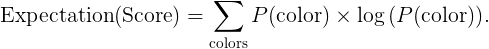
Suppose you had probabilities of 25% red, 50% blue, and 25% green. Let’s think in base 2 for a moment, to make things simpler. Your expected score is:

Score(red) = −2 bits, flashes 25% of the time,

Score(blue) = −1 bit, flashes 50% of the time,

Score(green) = −2 bits, flashes 25% of the time,

Expectation(Score) = −1.5 bits.

Contrast our Bayesian scoring rule with the ordinary or colloquial way of speaking about degrees of belief, where someone might casually say, “I’m 98% certain that canola oil contains more omega-3 fats than olive oil.” What they really mean by this is that they feel 98% certain—there’s something like a little progress bar that measures the strength of the emotion of certainty, and this progress bar is 98% full. And the emotional progress bar probably wouldn’t be exactly 98% full, if we had some way to measure. The word “98%” is just a colloquial way of saying: “I’m almost but not entirely certain.” It doesn’t mean that you could get the highest expected payoff by betting exactly 98 cents of play money on that outcome. You should only assign a calibrated confidence of 98% if you’re confident enough that you think you could answer a hundred similar questions, of equal difficulty, one after the other, each independent from the others, and be wrong, on average, about twice. We’ll keep track of how often you’re right, over time, and if it turns out that when you say “90% sure” you’re right about seven times out of ten, then we’ll say you’re poorly calibrated.

If you say “98% probable” a thousand times, and you are surprised only five times, we still ding you for poor calibration. You’re allocating too much probability mass to the possibility that you’re wrong. You should say “99.5% probable” to maximize your score. The scoring rule rewards accurate calibration, encouraging neither humility nor arrogance.

At this point it may occur to some readers that there’s an obvious way to achieve perfect calibration—just flip a coin for every yes-or-no question, and assign your answer a confidence of 50%. You say 50% and you’re right half the time. Isn’t that perfect calibration? Yes. But calibration is only one component of our Bayesian score; the other component is discrimination.

Suppose I ask you ten yes-or-no questions. You know absolutely nothing about the subject, so on each question you divide your probability mass fifty-fifty between “Yes” and “No.” Congratulations, you’re perfectly calibrated—answers for which you said “50% probability” were true exactly half the time. This is true regardless of the sequence of correct answers or how many answers were Yes. In ten experiments you said “50%” on twenty occasions—you said “50%” to Yes₁, No₁, Yes₂, No₂, Yes₃, No₃, . . . On ten of those occasions the answer was correct, the occasions: Yes₁, No₂, No₃, . . . And on ten of those occasions the answer was incorrect: No₁, Yes₂, Yes₃, . . .

Now I give my own answers, putting more effort into it, trying to discriminate whether Yes or No is the correct answer. I assign 90% confidence to each of my favored answers, and my favored answer is wrong twice. I’m more poorly calibrated than you. I said “90%” on ten occasions and I was wrong two times. The next time someone listens to me, they may mentally translate “90%” into 80%, knowing that when I’m 90% sure, I’m right about 80% of the time. But the probability you assigned to the final outcome is 1/2 to the tenth power, which is 0.001 or 1/1,024. The probability I assigned to the final outcome is 90% to the eighth power times 10% to the second power, 0.9⁸ × 0.1², which works out to 0.004 or 0.4%. Your calibration is perfect and mine isn’t, but my better discrimination between right and wrong answers more than makes up for it. My final score is higher—I assigned a greater joint probability to the final outcome of the entire experiment. If I’d been less overconfident and better calibrated, the probability I assigned to the final outcome would have been 0.8⁸ × 0.2², which works out to 0.006 or 6%.

Is it possible to do even better? Sure. You could have guessed every single answer correctly, and assigned a probability of 99% to each of your answers. Then the probability you assigned to the entire experimental outcome would be 0.99¹⁰ ≈ 90%.

Your score would be log (90%), which is -0.45 decibels or -0.15 bits. We need to take the logarithm so that if I try to maximize my expected score, ∑ P × log (P), I have no motive to cheat. Without the logarithm rule, I would maximize my expected score by assigning all my probability mass to the most probable outcome. Also, without the logarithm rule, my total score would be different depending on whether we counted several rounds as several experiments or as one experiment.

A simple transform can fix poor calibration by decreasing discrimination. If you are in the habit of saying “million-to-one” on 90 correct and 10 incorrect answers for each hundred questions, we can perfect your calibration by replacing “million-to-one” with “nine-to-one.” In contrast, there’s no easy way to increase (successful) discrimination. If you habitually say “nine-to-one” on 90 correct answers for each hundred questions, I can easily increase your claimed discrimination by replacing “nine-to-one” with “million-to-one.” But no simple transform can increase your actual discrimination such that your reply distinguishes 95 correct answers and 5 incorrect answers. From Yates et al.:⁵ “Whereas good calibration often can be achieved by simple mathematical transformations (e.g., adding a constant to every probability judgment), good discrimination demands access to solid, predictive evidence and skill at exploiting that evidence, which are difficult to find in any real-life, practical situation.” If you lack the ability to distinguish truth from falsehood, you can achieve perfect calibration by confessing your ignorance; but confessing ignorance will not, of itself, distinguish truth from falsehood.

We thus dispose of another false stereotype of rationality, that rationality consists of being humble and modest and confessing helplessness in the face of the unknown. That’s just the cheater’s way out, assigning a 50% probability to all yes-or-no questions. Our scoring rule encourages you to do better if you can. If you are ignorant, confess your ignorance; if you are confident, confess your confidence. We penalize you for being confident and wrong, but we also reward you for being confident and right. That is the virtue of a proper scoring rule.

Suppose I flip a coin twenty times. If I believe the coin is fair, the best prediction I can make is to predict an even chance of heads or tails on each flip. If I believe the coin is fair, I assign the same probability to every possible sequence of twenty coinflips. There are roughly a million (1,048,576) possible sequences of twenty coinflips, and I have only 1.0 of probability mass to play with. So I assign to each individual possible sequence a probability of (1∕2)²⁰—odds of about a million to one; -20 bits or -60 decibels.

I made an experimental prediction and got a score of -60 decibels! Doesn’t this falsify the hypothesis? Intuitively, no. We do not flip a coin twenty times and see a random-looking result, then reel back and say, why, the odds of that are a million to one. But the odds are a million to one against seeing that exact sequence, as I would discover if I naively predicted the exact same outcome for the next sequence of twenty coinflips. It’s okay to have theories that assign tiny probabilities to outcomes, so long as no other theory does better. But if someone used an alternate hypothesis to write down the exact sequence in a sealed envelope in advance, and she assigned a probability of 99%, I would suspect the fairness of the coin. Provided that she only sealed one envelope, and not a million.

That tells us what we ought common-sensically to answer, but it doesn’t say how the common-sense answer arises from the math. To say why the common sense is correct, we need to integrate all that has been said so far into the framework of Bayesian revision of belief. When we’re done, we’ll have a technical understanding of the difference between a verbal understanding and a technical understanding.

Imagine an experiment which produces an integer result between zero and 99. For example, the experiment might be a particle counter that tells us how many particles have passed through in a minute. Or the experiment might be to visit the supermarket on Wednesday, check the price of a 10 oz bag of crushed walnuts, and write down the last two digits of the price.

We are testing several different hypotheses that try to predict the experimental result. Each hypothesis produces a probability distribution over all possible results; in this case, the integers between zero and 99. The possibilities are mutually exclusive, so the probability mass in the distribution must sum to one (or less); we cannot predict a 90% probability of seeing 42 and also a 90% probability of seeing 43.

Suppose there is a precise hypothesis that predicts a 90% chance of seeing the result 51. (I.e., the hypothesis is that the supermarket usually prices walnuts with a price of “X dollars and 51 cents.”) The precise theory has staked 90% of its probability mass on the outcome 51. This leaves 10% probability mass remaining to spread over 99 other possible outcomes—all the numbers between zero and 99 except 51. The theory makes no further specification, so we spread the remaining 10% probability mass evenly over 99 possibilities, assigning a probability of 1/990 to each non-51 result. For ease of writing, we’ll approximate 1/990 as 0.1%.

This probability distribution is analogous to the likelihood or conditional probability of the result given the hypothesis. Let us call it the likelihood distribution for the hypothesis, our chance of seeing each specified outcome if the hypothesis is true. The likelihood distribution for a hypothesis H is a function composed of all the conditional probabilities for P(0|H) = 0.001, P(1|H) = 0.001, . . . , P(51|H) = 0.9, . . . , P(99|H) = 0.001.

The precise theory predicts a 90% probability of seeing 51. Let there be also a vague theory, which predicts “a 90% probability of seeing a number in the fifties.”

Seeing the result 51, we do not say the outcome confirms both theories equally. Both theories made predictions, and both assigned probabilities of 90%, and the result 51 confirms both predictions. But the precise theory has an advantage because it concentrates its probability mass into a sharper point. If the vague theory makes no further specification, we count “a 90% probability of seeing a number in the fifties” as a 9% probability of seeing each number between 50 and 59.

Suppose we started with even odds in favor of the precise theory and the vague theory—odds of 1:1, or 50% probability for either hypothesis being true. After seeing the result 51, what are the posterior odds of the precise theory being true? The predictions of the two theories are analogous to their likelihood assignments—the conditional probability of seeing the result, given that the theory is true. What is the likelihood ratio between the two theories? The first theory allocated 90% probability mass to the exact outcome. The vague theory allocated 9% probability mass to the exact outcome. The likelihood ratio is 10:1. So if we started with even 1:1 odds, the posterior odds are 10:1 in favor of the precise theory. The differential pressure of the two conditional probabilities pushed our prior confidence of 50% to a posterior confidence of about 91% that the precise theory is correct. Assuming that these are the only hypotheses being tested, that this is the only evidence under consideration, and so on.

Why did the vague theory lose when both theories fit the evidence? The vague theory is timid; it makes a broad prediction, hedges its bets, allows many possibilities that would falsify the precise theory. This is not the virtue of a scientific theory. Philosophers of science tell us that theories should be bold, and subject themselves willingly to falsification if their prediction fails.⁶ Now we see why. The precise theory concentrates its probability mass into a sharper point and thereby leaves itself vulnerable to falsification if the real outcome hits elsewhere; but if the predicted outcome is correct, precision has a tremendous likelihood advantage over vagueness.

The laws of probability theory provide no way to cheat, to make a vague hypothesis such that any result between 50 and 59 counts for as much favorable confirmation as the precise theory receives, for that would require probability mass summing to 900%. There is no way to cheat, providing you record your prediction in advance, so you cannot claim afterward that your theory assigns a probability of 90% to whichever result arrived. Humans are very fond of making their predictions afterward, so the social process of science requires an advance prediction before we say that a result confirms a theory. But how humans may move in harmony with the way of Bayes, and so wield the power, is a separate issue from whether the math works. When we’re doing the math, we just take for granted that likelihood density functions are fixed properties of a hypothesis and the probability mass sums to 1 and you’d never dream of doing it any other way.

You may want to take a moment to visualize that, if we define probability in terms of calibration, Bayes’s Theorem relates the calibrations. Suppose I guess that Theory 1 is 50% likely to be true, and I guess that Theory 2 is 50% likely to be true. Suppose I am well-calibrated; when I utter the words “fifty percent,” the event happens about half the time. And then I see a result R which would happen around nine-tenths of the time given Theory 1, and around nine-hundredths of the time given Theory 2, and I know this is so, and I apply Bayesian reasoning. If I was perfectly calibrated initially (despite the poor discrimination of saying 50/50), I will still be perfectly calibrated (and better discriminated) after I say that my confidence in Theory 1 is now 91%. If I repeated this kind of situation many times, I would be right around ten-elevenths of the time when I said “91%.” If I reason using Bayesian rules, and I start from well-calibrated priors, then my conclusions will also be well-calibrated. This only holds true if we define probability in terms of calibration! If “90% sure” is instead interpreted as, say, the strength of the emotion of surety, there is no reason to expect the posterior emotion to stand in an exact Bayesian relation to the prior emotion.

Let the prior odds be ten to one in favor of the vague theory. Why? Suppose our way of describing hypotheses allows us to either specify a precise number, or to just specify a first-digit; we can say “51,” “63,” “72,” or “in the fifties/sixties/seventies.” Suppose we think that the real answer is about equally liable to be an answer of the first kind or the second. However, given the problem, there are a hundred possible hypotheses of the first kind, and only ten hypotheses of the second kind. So if we think that either class of hypotheses has about an equal prior chance of being correct, we have to spread out the prior probability mass over ten times as many precise theories as vague theories. The precise theory that predicts exactly 51 would thus have one-tenth as much prior probability mass as the vague theory that predicts a number in the fifties. After seeing 51, the odds would go from 1:10 in favor of the vague theory to 1:1, even odds for the precise theory and the vague theory.

If you look at this carefully, it’s exactly what common sense would expect. You start out uncertain of whether a phenomenon is the kind of phenomenon that produces exactly the same result every time, or if it’s the kind of phenomenon that produces a result in the Xties every time. (Maybe the phenomenon is a price range at the supermarket, if you need some reason to suppose that 50–59 is an acceptable range but 49–58 isn’t.) You take a single measurement and the answer is 51. Well, that could be because the phenomenon is exactly 51, or because it’s in the fifties. So the remaining precise theory has the same odds as the remaining vague theory, which requires that the vague theory must have started out ten times as probable as that precise theory, since the precise theory has a sharper fit to the evidence.

If we just see one number, like 51, it doesn’t change the prior probability that the phenomenon itself was “precise” or “vague.” But, in effect, it concentrates all the probability mass of those two classes of hypothesis into a single surviving hypothesis of each class.

Of course, it is a severe error to say that a phenomenon is precise or vague, a case of what Jaynes calls the Mind Projection Fallacy.⁷ Precision or vagueness is a property of maps, not territories. Rather we should ask if the price in the supermarket stays constant or shifts about. A hypothesis of the “vague” sort is a good description of a price that shifts about. A precise map will suit a constant territory.

Another example: You flip a coin ten times and see the sequence HHTTH:TTTTH. Maybe you started out thinking there was a 1% chance this coin was fixed. Doesn’t the hypothesis “This coin is fixed to produce HHTTH:TTTTH” assign a thousand times the likelihood mass to the observed outcome, compared to the fair coin hypothesis? Yes. Don’t the posterior odds that the coin is fixed go to 10:1? No. The 1% prior probability that “the coin is fixed” has to cover every possible kind of fixed coin—a coin fixed to produce HHTTH:TTTTH, a coin fixed to produce TTHHT:HHHHT, etc. The prior probability the coin is fixed to produce HHTTH:TTTTH is not 1%, but a thousandth of one percent. Afterward, the posterior probability the coin is fixed to produce HHTTH:TTTTH is one percent. Which is to say: You thought the coin was probably fair but had a one percent chance of being fixed to some random sequence; you flipped the coin; the coin produced a random-looking sequence; and that doesn’t tell you anything about whether the coin is fair or fixed. It does tell you, if the coin is fixed, which sequence it is fixed to.

This parable helps illustrate why Bayesians must think about prior probabilities. There is a branch of statistics, sometimes called “orthodox” or “classical” statistics, which insists on paying attention only to likelihoods. But if you only pay attention to likelihoods, then eventually some fixed-coin hypothesis will always defeat the fair coin hypothesis, a phenomenon known as “overfitting” the theory to the data. After thirty flips, the likelihood is a billion times as great for the fixed-coin hypothesis with that sequence, as for the fair coin hypothesis. Only if the fixed-coin hypothesis (or rather, that specific fixed-coin hypothesis) is a billion times less probable a priori can the fixed-coin hypothesis possibly lose to the fair coin hypothesis.

If you shake the coin to reset it, and start flipping the coin again, and the coin produces HHTTH:TTTTH again, that is a different matter. That does raise the posterior odds of the fixed-coin hypothesis to 10:1, even if the starting probability was only 1%.

Similarly, if we perform two successive measurements of the particle counter (or the supermarket price on Wednesdays), and both measurements return 51, the precise theory wins by odds of 10:1.

So the precise theory wins, but the vague theory would still score better than no theory at all. Consider a third theory, the hypothesis of zero knowledge or maximum-entropy distribution, which makes equally probable any result between zero and 99. Suppose we see the result 51. The vague theory produced a better prediction than the maximum-entropy distribution—assigned a greater likelihood to the outcome we observed. The vague theory is, literally, better than nothing. Suppose we started with odds of 1:20 in favor of the hypothesis of complete ignorance. (Why odds of 1:20? There is only one hypothesis of complete ignorance, and moreover, it’s a particularly simple and intuitive kind of hypothesis, Occam’s Razor.) After seeing the result of 51, predicted at 9% by the vague theory versus 1% by complete ignorance, the posterior odds go to 10:20 or 1:2. If we then see another result of 51, the posterior odds go to 10:2 or 83% probability for the vague theory, assuming there is no more precise theory under consideration.

Yet the timidity of the vague theory—its unwillingness to produce an exact prediction and accept falsification on any other result—renders it vulnerable to the bold, precise theory. (Providing, of course, that the bold theory correctly guesses the outcome!) Suppose the prior odds were 1:10:200 for the precise, vague, and ignorant theories—prior probabilities of 0.5%, 4.7%, and 94.8% for the precise, vague and ignorant theories. This figure reflects our prior probability distribution over classes of hypotheses, with the probability mass distributed over entire classes as follows: 50% that the phenomenon shifts across all digits, 25% that the phenomenon shifts around within some decimal bracket, and 25% that the phenomenon repeats the same number each time. One hypothesis of complete ignorance, 10 possible hypotheses for a decimal bracket, 100 possible hypotheses for a repeating number. Thus, prior odds of 1:10:200 for the precise hypothesis 51, the vague hypothesis “fifties,” and the hypothesis of complete ignorance.

After seeing a result of 51, with assigned probability of 90%, 9%, and 1%, the posterior odds go to 90:90:200 = 9:9:20. After seeing an additional result of 51, the posterior odds go to 810:81:20, or 89%, 9%, and 2%. The precise theory is now favored over the vague theory, which in turn is favored over the ignorant theory.

Now consider a stupid theory, which predicts a 90% probability of seeing a result between zero and nine. The stupid theory assigns a probability of 0.1% to the actual outcome, 51. If the odds were initially 1:10:200:10 for the precise, vague, ignorant, and stupid theories, the posterior odds after seeing 51 once would be 90:90:200:1. The stupid theory has been falsified (posterior probability of 0.2%).

It is possible to have a model so bad that it is worse than nothing, if the model concentrates its probability mass away from the actual outcome, makes confident predictions of wrong answers. Such a hypothesis is so poor that it loses against the hypothesis of complete ignorance. Ignorance is better than anti-knowledge.

Side note: In the field of Artificial Intelligence, there is a sometime fad that praises the glory of randomness. Occasionally an AI researcher discovers that if they add noise to one of their algorithms, the algorithm works better. This result is reported with great enthusiasm, followed by much fulsome praise of the creative powers of chaos, unpredictability, spontaneity, ignorance of what your own AI is doing, et cetera. (See The Imagination Engine for an example; according to their sales literature they sell wounded and dying neural nets.⁸) But how sad is an algorithm if you can increase its performance by injecting entropy into intermediate processing stages? The algorithm must be so deranged that some of its work goes into concentrating probability mass away from good solutions. If injecting randomness results in a reliable improvement, then some aspect of the algorithm must do reliably worse than random. Only in AI would people devise algorithms literally dumber than a bag of bricks, boost the results slightly back toward ignorance, and then argue for the healing power of noise.

Suppose that in our experiment we see the results 52, 51, and 58. The precise theory gives this conjunctive event a probability of a thousand to one times 90% times a thousand to one, while the vaguer theory gives this conjunctive event a probability of 9% cubed, which works out to . . . oh . . . um . . . let’s see . . . a million to one given the precise theory, versus a thousand to one given the vague theory. Or thereabouts; we are counting rough powers of ten. Versus a million to one given the zero-knowledge distribution that assigns an equal probability to all outcomes. Versus a billion to one given a model worse than nothing, the stupid hypothesis, which claims a 90% probability of seeing a number less than 10. Using these approximate numbers, the vague theory racks up a score of -30 decibels (a probability of 1/1000 for the whole experimental outcome), versus scores of -60 for the precise theory, -60 for the ignorant theory, and -90 for the stupid theory. It is not always true that the highest score wins, because we need to take into account our prior odds of 1:10:200:10, confidences of -23, -13, 0, and -13 decibels. The vague theory still comes in with the highest total score at -43 decibels. (If we ignored our prior probabilities, each new experiment would override the accumulated results of all the previous experiments; we could not accumulate knowledge. Furthermore, the fixed-coin hypothesis would always win.)

As always, we should not be alarmed that even the best theory still has a low score—recall the parable of the fair coin. Theories are approximations. In principle we might be able to predict the exact sequence of coinflips. But it would take better measurement and more computing power than we’re willing to expend. Maybe we could achieve 60/40 prediction of coinflips, with a good enough model . . . ? We go with the best approximation we have, and try to achieve good calibration even if the discrimination isn’t perfect.

We’ve conducted our analysis so far under the rules of Bayesian probability theory, in which there’s no way to have more than 100% probability mass, and hence no way to cheat so that any outcome can count as “confirmation” of your theory. Under Bayesian law, play money may not be counterfeited; you only have so much clay.

Unfortunately, human beings are not Bayesians. Human beings bizarrely attempt to defend hypotheses, making a deliberate effort to prove them or prevent disproof. This behavior has no analogue in the laws of probability theory or decision theory. In formal probability theory the hypothesis is, and the evidence is, and either the hypothesis is confirmed or it is not. In formal decision theory, an agent may make an effort to investigate some issue of which the agent is currently uncertain, not knowing whether the evidence shall go one way or the other. In neither case does one ever deliberately try to prove an idea, or try to avoid disproving it. One may test ideas of which one is genuinely uncertain, but not have a “preferred” outcome of the investigation. One may not try to prove hypotheses, nor prevent their proof. I cannot properly convey just how ridiculous the notion would be, to a true Bayesian; there are not even words in Bayes-language to describe the mistake . . .

For every expectation of evidence there is an equal and opposite expectation of counterevidence. If A is evidence in favor of B, then not-A must be evidence in favor of not-B. The strengths of the evidences may not be equal; rare but strong evidence in one direction may be balanced by common but weak evidence in the other direction. But it is not possible for both A and not-A to be evidence in favor of B. That is, it’s not possible under the laws of probability theory.

Humans often seem to want to have their cake and eat it too. Whichever result we witness is the one that proves our theory. As Spee, the priest in Conservation of Expected Evidence, put it, “The investigating committee would feel disgraced if it acquitted a woman; once arrested and in chains, she has to be guilty, by fair means or foul.”⁹

The way human psychology seems to work is that first we see something happen, and then we try to argue that it matches whatever hypothesis we had in mind beforehand. Rather than conserved probability mass, to distribute over advance predictions, we have a feeling of compatibility—the degree to which the explanation and the event seem to “fit.” “Fit” is not conserved. There is no equivalent of the rule that probability mass must sum to one. A psychoanalyst may explain any possible behavior of a patient by constructing an appropriate structure of “rationalizations” and “defenses”; it fits, therefore it must be true.

Now consider the fable told in Fake Explanations—the students seeing a radiator, and a metal plate next to the radiator. The students would never predict in advance that the side of the plate near the radiator would be cooler. Yet, seeing the fact, they managed to make their explanations “fit.” They lost their precious chance at bewilderment, to realize that their models did not predict the phenomenon they observed. They sacrificed their ability to be more confused by fiction than by truth. And they did not realize “heat induction, blah blah, therefore the near side is cooler” is a vague and verbal prediction, spread across an enormously wide range of possible values for specific measured temperatures. Applying equations of diffusion and equilibrium would give a sharp prediction for possible joint values. It might not specify the first values you measured, but when you knew a few values you could generate a sharp prediction for the rest. The score for the entire experimental outcome would be far better than any less precise alternative, especially a vague and verbal prediction.

You now have a technical explanation of the difference between a verbal explanation and a technical explanation. It is a technical explanation because it enables you to calculate exactly how technical an explanation is. Vague hypotheses may be so vague that only a superhuman intelligence could calculate exactly how vague. Perhaps a sufficiently huge intelligence could extrapolate every possible experimental result, and extrapolate every possible verdict of the vague guesser for how well the vague hypothesis “fit,” and then renormalize the “fit” distribution into a likelihood distribution that summed to one. But in principle one can still calculate exactly how vague is a vague hypothesis. The calculation is just not computationally tractable, the way that calculating airplane trajectories via quantum mechanics is not computationally tractable.

I hold that everyone needs to learn at least one technical subject: physics, computer science, evolutionary biology, Bayesian probability theory, or something. Someone with no technical subjects under their belt has no referent for what it means to “explain” something. They may think “All is Fire” is an explanation, as did the Greek philosopher Heraclitus. Therefore do I advocate that Bayesian probability theory should be taught in high school. Bayesian probability theory is the sole piece of math I know that is accessible at the high school level, and that permits a technical understanding of a subject matter—the dynamics of belief—that is an everyday real-world domain and has emotionally meaningful consequences. Studying Bayesian probability would give students a referent for what it means to “explain” something.

Too many academics think that being “technical” means speaking in dry polysyllabisms. Here’s a “technical” explanation of technical explanation:

The equations of probability theory favor hypotheses that strongly predict the exact observed data. Strong models boldly concentrate their probability density into precise outcomes, making them falsifiable if the data hits elsewhere, and giving them tremendous likelihood advantages over models less bold, less precise. Verbal explanation runs on psychological evaluation of unconserved post facto compatibility instead of conserved ante facto probability density. And verbal explanation does not paint sharply detailed pictures, implying a smooth likelihood distribution in the vicinity of the data.

Is this satisfactory? No. Hear the impressive and weighty sentences, resounding with the dull thud of expertise. See the hapless students, writing those sentences on a sheet of paper. Even after the listeners hear the ritual words, they can perform no calculations. You know the math, so the words are meaningful. You can perform the calculations after hearing the impressive words, just as you could have done before. But what of one who did not see any calculations performed? What new skills have they gained from that “technical” lecture, save the ability to recite fascinating words?

“Bayesian” sure is a fascinating word, isn’t it? Let’s get it out of our systems: Bayes Bayes Bayes Bayes Bayes Bayes Bayes Bayes Bayes . . .

The sacred syllable is meaningless, except insofar as it tells someone to apply math. Therefore the one who hears must already know the math.

Conversely, if you know the math, you can be as silly as you like, and still technical.

We thus dispose of yet another stereotype of rationality, that rationality consists of sere formality and humorless solemnity. What has that to do with the problem of distinguishing truth from falsehood? What has that to do with attaining the map that reflects the territory? A scientist worthy of a lab coat should be able to make original discoveries while wearing a clown suit, or give a lecture in a high squeaky voice from inhaling helium. It is written nowhere in the math of probability theory that one may have no fun. The blade that cuts through to the correct answer has no dignity or silliness of itself, though it may fit the hand of a silly wielder.

A useful model isn’t just something you know, as you know that an airplane is made of atoms. A useful model is knowledge you can compute in reasonable time to predict real-world events you know how to observe. Maybe someone will find that, using a model that violates Conservation of Momentum just a little, you can compute the aerodynamics of the 747 much more cheaply than if you insist that momentum is exactly conserved. So if you’ve got two computers competing to produce the best prediction, it might be that the best prediction comes from the model that violates Conservation of Momentum. This doesn’t mean that the 747 violates Conservation of Momentum in real life. Neither model uses individual atoms, but that doesn’t imply the 747 is not made of atoms. Physicists use different models to predict airplanes and particle collisions because it would be too expensive to compute the airplane particle by particle.

You would prove the 747 is made of atoms with experimental data that the aerodynamic models couldn’t handle; for example, you would train a scanning tunneling microscope on a section of wing and look at the atoms. Similarly, you could use a finer measuring instrument to discriminate between a 747 that really disobeyed Conservation of Momentum like the cheap approximation predicted, versus a 747 that obeyed Conservation of Momentum like underlying physics predicted. The winning theory is the one that best predicts all the experimental predictions together. Our Bayesian scoring rule gives us a way to combine the results of all our experiments, even experiments that use different methods.

Furthermore, the atomic theory allows, embraces, and in some sense mandates the aerodynamic model. By thinking abstractly about the assumptions of atomic theory, we realize that the aerodynamic model ought to be a good (and much cheaper) approximation of the atomic theory, and so the atomic theory supports the aerodynamic model, rather than competing with it. A successful theory can embrace many models for different domains, so long as the models are acknowledged as approximations, and in each case the model is compatible with (or ideally mandated by) the underlying theory.

Our fundamental physics—quantum mechanics, the standard family of particles, and relativity—is a theory that embraces an enormous family of models for macroscopic physical phenomena. There is the physics of liquids, and solids, and gases; yet this does not mean that there are fundamental things in the world that have the intrinsic property of liquidity.

Apparently there is colour, apparently sweetness, apparently bitterness, actually there are only atoms and the void.

—Democritus, 420 BCE, from Robinson and Groves¹⁰

In arguing that a “technical” theory should be defined as a theory that sharply concentrates probability into specific advance predictions, I am setting an extremely high standard of strictness. We have seen that a vague theory can be better than nothing. A vague theory can win out over the hypothesis of ignorance, if there are no precise theories to compete against it.

There is an enormous family of models belonging to the central underlying theory of life and biology, the underlying theory that is sometimes called neo-Darwinism, natural selection, or evolution. Some models in evolutionary theory are quantitative. The way in which DNA encodes proteins is redundant; two different DNA sequences can code for exactly the same protein. There are four DNA bases {A,T,C,G} and 64 possible combinations of three DNA bases. But those 64 possible codons describe only 20 amino acids plus a stop code. Genetic drift ought therefore to produce non-functional changes in species genomes, through mutations which by chance become fixed in the gene pool. The accumulation rate of non-functional differences between the genomes of two species with a common ancestor depends on such parameters as the number of generations elapsed and the intensity of selection at that genetic locus. That’s an example of a member of the family of evolutionary models that produces quantitative predictions. There are also disequilibrium allele frequencies under selection, stable equilibria for game-theoretical strategies, sex ratios, etc.

This all comes under the heading of “fascinating words.” Unfortunately, there are certain religious factions that spread gross disinformation about evolutionary theory. So I emphasize that many models within evolutionary theory make quantitative predictions that are experimentally confirmed, and that such models are far more than sufficient to demonstrate that, e.g., humans and chimpanzees are related by a common ancestor. If you’ve been victimized by creationist disinformation—that is, if you’ve heard any suggestion that evolutionary theory is controversial or untestable or “just a theory” or non-rigorous or non-technical or in any way not confirmed by an unimaginably huge mound of experimental evidence—I recommend reading the TalkOrigins FAQ¹¹ and studying evolutionary biology with math.

But imagine going back in time to the nineteenth century, when the theory of natural selection had only just been discovered by Charles Darwin and Alfred Russel Wallace. Imagine evolutionism just after its birth, when the theory had nothing remotely like the modern-day body of quantitative models and great heaping mountains of experimental evidence. There was no way of knowing that humans and chimpanzees would be discovered to have 95% shared genetic material. No one knew that DNA existed. Yet even so, scientists flocked to the new theory of natural selection. And later it turned out that there was a precisely copied genetic material with the potential to mutate, that humans and chimps were provably related, etc.

So the very strict, very high standard that I proposed for a “technical” theory is too strict. Historically, it has been possible to successfully discriminate true theories from false theories, based on predictions of the sort I called “vague.” Vague predictions of, say, 80% confidence, can build up a huge advantage over alternate hypotheses, given enough experiments. Perhaps a theory of this kind, producing predictions that are not precisely detailed but are nonetheless correct, could be called “semitechnical”?

But surely technical theories are more reliable than semitechnical theories? Surely technical theories should take precedence, command greater respect? Surely physics, which produces exceedingly exact predictions, is in some sense better confirmed than evolutionary theory? Not implying that evolutionary theory is wrong, of course; but however vast the mountains of evidence favoring evolution, does not physics go one better through vast mountains of precise experimental confirmation? Observations of neutron stars confirm the predictions of General Relativity to within one part in a hundred trillion (10¹⁴). What does evolutionary theory have to match that?

Daniel Dennett once said that measured by the simplicity of the theory and the amount of complexity it explained, Darwin had the single greatest idea in the history of time.¹²

Once there was a conflict between nineteenth century physics and nineteenth century evolutionism. According to the best physical models then in use, the Sun could not have been burning very long. Three thousand years on chemical energy, or 40 million years on gravitational energy. There was no energy source known to nineteenth century physics that would permit longer burning. Nineteenth century physics was not quite as powerful as modern physics—it did not have predictions accurate to within one part in 10¹⁴. But nineteenth century physics still had the mathematical character of modern physics, a discipline whose models produced detailed, precise, quantitative predictions. Nineteenth century evolutionary theory was wholly semitechnical, without a scrap of quantitative modeling. Not even Mendel’s experiments with peas were then known. And yet it did seem likely that evolution would require longer than a paltry 40 million years in which to operate—hundreds of millions, even billions of years. The antiquity of the Earth was a vague and semitechnical prediction, of a vague and semitechnical theory. In contrast, the nineteenth century physicists had a precise and quantitative model, which through formal calculation produced the precise and quantitative dictum that the Sun simply could not have burned that long.

The limitations of geological periods, imposed by physical science, cannot, of course, disprove the hypothesis of transmutation of species; but it does seem sufficient to disprove the doctrine that transmutation has taken place through “descent with modification by natural selection.”

—Lord Kelvin, from Lyle Zapato¹³

History records who won.

The moral? If you can give 80% confident advance predictions on yes-or-no questions, it may be a “vague” theory; it may be wrong one time out of five; but you can still build up a heck of a huge scoring lead over the hypothesis of ignorance. Enough to confirm a theory, if there are no better competitors. Reality is consistent; every correct theory about the universe is compatible with every other correct theory. Imperfect maps can conflict, but there is only one territory. Nineteenth century evolutionism might have been a semitechnical discipline, but it was still correct (as we now know) and by far the best explanation (even in that day). Any conflict between evolutionism and another well-confirmed theory had to reflect some kind of anomaly, a mistake in the assertion that the two theories were incompatible. Nineteenth century physics couldn’t model the dynamics of the Sun—they didn’t know about nuclear reactions. They could not show that their understanding of the Sun was correct in technical detail, nor calculate from a confirmed model of the Sun to determine how long the Sun had existed. So in retrospect, we can say something like: “There was room for the possibility that nineteenth century physics just didn’t understand the Sun.”

But that is hindsight. The real lesson is that, even though nineteenth century physics was both precise and quantitative, it didn’t automatically dominate the semitechnical theory of nineteenth century evolutionism. The theories were both well-supported. They were both correct in the domains over which they were generalized. The apparent conflict between them was an anomaly, and the anomaly turned out to stem from the incompleteness and incorrect application of nineteenth century physics, not the incompleteness and incorrect application of nineteenth century evolutionism. But it would be futile to compare the mountain of evidence supporting the one theory, versus the mountain of evidence supporting the other. Even in that day, both mountains were too large to suppose that either theory was simply mistaken. Mountains of evidence that large cannot be set to compete, as if one falsifies the other. You must be applying one theory incorrectly, or applying a model outside the domain it predicts well.

So you shouldn’t necessarily sneer at a theory just because it’s semitechnical. Semitechnical theories can build up high enough scores, compared to every available alternative, that you know the theory is at least approximately correct. Someday the semitechnical theory may be replaced or even falsified by a more precise competitor, but that’s true even of technical theories. Think of how Einstein’s General Relativity devoured Newton’s theory of gravitation.

But the correctness of a semitechnical theory—a theory that currently has no precise, computationally tractable models testable by feasible experiments—can be a lot less cut-and-dried than the correctness of a technical theory. It takes skill, patience, and examination to distinguish good semitechnical theories from theories that are just plain confused. This is not something that humans do well by instinct, which is why we have Science.

People eagerly jump the gun and seize on any available reason to reject a disliked theory. That is why I gave the example of nineteenth century evolutionism, to show why one should not be too quick to reject a “non-technical” theory out of hand. By the moral customs of science, nineteenth century evolutionism was guilty of more than one sin. Nineteenth century evolutionism made no quantitative predictions. It was not readily subject to falsification. It was largely an explanation of what had already been seen. It lacked an underlying mechanism, as no one then knew about DNA. It even contradicted the nineteenth century laws of physics. Yet natural selection was such an amazingly good post facto explanation that people flocked to it, and they turned out to be right. Science, as a human endeavor, requires advance prediction. Probability theory, as math, does not distinguish between post facto and advance prediction, because probability theory assumes that probability distributions are fixed properties of a hypothesis.

The rule about advance prediction is a rule of the social process of science—a moral custom and not a theorem. The moral custom exists to prevent human beings from making human mistakes that are hard to even describe in the language of probability theory, like tinkering after the fact with what you claim your hypothesis predicts. People concluded that nineteenth century evolutionism was an excellent explanation, even if it was post facto. That reasoning was correct as probability theory, which is why it worked despite all scientific sins. Probability theory is math. The social process of science is a set of legal conventions to keep people from cheating on the math.

Yet it is also true that, compared to a modern-day evolutionary theorist, evolutionary theorists of the late nineteenth and early twentieth century often went sadly astray. Darwin, who was bright enough to invent the theory, got an amazing amount right. But Darwin’s successors, who were only bright enough to accept the theory, misunderstood evolution frequently and seriously. The usual process of science was then required to correct their mistakes. It is incredible how few errors of reasoning Darwin¹⁴ made in The Origin of Species and The Descent of Man, compared to they who followed.

That is also a hazard of a semitechnical theory. Even after the flash of genius insight is confirmed, merely average scientists may fail to apply the insights properly in the absence of formal models. As late as the 1960s biologists spoke of evolution working “for the good of the species,” or suggested that individuals would restrain their reproduction to prevent species overpopulation of a habitat. The best evolutionary theorists knew better, but average theorists did not.¹⁵

So it is far better to have a technical theory than a semitechnical theory. Unfortunately, Nature is not always so kind as to render Herself describable by neat, formal, computationally tractable models, nor does She always provide Her students with measuring instruments that can directly probe Her phenomena. Sometimes it is only a matter of time. Nineteenth century evolutionism was semitechnical, but later came the math of population genetics, and eventually DNA sequencing. Nature will not always give you a phenomenon that you can describe with technical models fifteen seconds after you have the basic insight.

Yet the cutting edge of science, the controversy, is most often about a semitechnical theory, or nonsense posing as a semitechnical theory. By the time a theory achieves technical status, it is usually no longer controversial (among scientists). So the question of how to distinguish good semitechnical theories from nonsense is very important to scientists, and it is not as easy as dismissing out of hand any theory that is not technical. To the end of distinguishing truth from falsehood exists the entire discipline of rationality. The art is not reducible to a checklist, or at least, no checklist that an average scientist can apply reliably after an hour of training. If it was that simple we wouldn’t need science.

Why do you pay attention to scientific controversies? Why graze upon such sparse and rotten feed as the media offers, when there are so many solid meals to be found in textbooks? Textbook science is beautiful! Textbook science is comprehensible, unlike mere fascinating words that can never be truly beautiful. Fascinating words have no power, nor yet any meaning, without the math. The fascinating words are not knowledge but the illusion of knowledge, which is why it brings so little satisfaction to know that “gravity results from the curvature of spacetime.” Science is not in the fascinating words, though it’s all you’ll ever read as breaking news.

There can be justification for following a scientific controversy. You could be an expert in that field, in which case that scientific controversy is your proper meat. Or the scientific controversy might be something you need to know now, because it affects your life. Maybe it’s the nineteenth century, and you’re gazing lustfully at a member of the appropriate sex wearing a nineteenth century bathing suit, and you need to know whether your sexual desire comes from a psychology constructed by natural selection, or is a temptation placed in you by the Devil to lure you into hellfire.

It is not wholly impossible that we shall happen upon a scientific controversy that affects us, and find that we have a burning and urgent need for the correct answer. I shall therefore discuss some of the warning signs that historically distinguished vague hypotheses that later turned out to be unscientific gibberish, from vague hypotheses that later graduated to confirmed theories. Just remember the historical lesson of nineteenth century evolutionism, and resist the temptation to fail every theory that misses a single item on your checklist. It is not my intention to give people another excuse to dismiss good science that discomforts them. If you apply stricter criteria to theories you dislike than theories you like (or vice versa!), then every additional nit you learn how to pick, every new logical flaw you learn how to detect, makes you that much stupider. Intelligence, to be useful, must be used for something other than defeating itself.

One of the classic signs of a poor hypothesis is that it must expend great effort in avoiding falsification—elaborating reasons why the hypothesis is compatible with the phenomenon, even though the phenomenon didn’t behave as expected. Carl Sagan gives the example of someone who claims that a dragon lives in their garage. Sagan originally drew the lesson that poor hypotheses need to do fast footwork to avoid falsification—to maintain an appearance of “fit.”¹⁶

I would point out that the claimant obviously has a good model of the situation somewhere in their head, because they can predict, in advance, exactly which excuses they’re going to need. To a Bayesian, a hypothesis isn’t something you assert in a loud, emphatic voice. A hypothesis is something that controls your anticipations, the probabilities you assign to future experiences. That’s what a probability is, to a Bayesian—that’s what you score, that’s what you calibrate. So while our claimant may say loudly, emphatically, and honestly that they believe there’s an invisible dragon in the garage, they do not anticipate there’s an invisible dragon in the garage—they anticipate exactly the same experience as the skeptic.

When I judge the predictions of a hypothesis, I ask which experiences I would anticipate, not which facts I would believe.

The flip side:

I recently argued with a friend of mine over a question of evolutionary theory. My friend alleged that the clustering of changes in the fossil record (apparently, there are periods of comparative stasis followed by comparatively sharp changes; itself a controversial observation known as “punctuated equilibrium”) showed that there was something wrong with our understanding of speciation. My friend thought that there was some unknown force at work—not supernatural, but some natural consideration that standard evolutionary theory didn’t take into account. Since my friend didn’t give a specific competing hypothesis that produced better predictions, his thesis had to be that the standard evolutionary model was stupid with respect to the data—that the standard model made a specific prediction that was wrong; that the model did worse than complete ignorance or some other default competitor.

At first I fell into the trap; I accepted the implicit assumption that the standard model predicted smoothness, and based my argument on my recollection that the fossil record changes weren’t as sharp as he claimed. He challenged me to produce an evolutionary intermediate between Homo erectus and Homo sapiens; I googled and found Homo heidelbergensis. He congratulated me and acknowledged that I had scored a major point, but still insisted that the changes were too sharp, and not steady enough. I started to explain why I thought a pattern of uneven change could arise from the standard model: environmental selection pressures might not be constant . . . “Aha!” my friend said, “you’re making your excuses in advance.”

But suppose that the fossil record instead showed a smooth and gradual set of changes. Might my friend have argued that the standard model of evolution as a chaotic and noisy process could not account for such smoothness? If it is a scientific sin to claim post facto that our beloved hypothesis predicts the data, should it not be equally a sin to claim post facto that the competing hypothesis is stupid on the data?

If a hypothesis has a purely technical model, there is no trouble; we can compute the prediction of the model formally, without informal variables to provide a handle for post facto meddling. But what of semitechnical theories? Obviously a semitechnical theory must produce some good advance predictions about something, or else why bother? But after the theory is semi-confirmed, can the detractors claim that the data show a problem with the semitechnical theory, when the “problem” is constructed post facto? At the least the detractors must be very specific about what data a confirmed model predicts stupidly, and why the confirmed model must make (post facto) that stupid prediction. How sharp a change is “too sharp,” quantitatively, for the standard model of evolution to permit? Exactly how much steadiness do you think the standard model of evolution predicts? How do you know? Is it too late to say that, after you’ve seen the data?

When my friend accused me of making excuses, I paused and asked myself which excuses I anticipated needing to make. I decided that my current grasp of evolutionary theory didn’t say anything about whether the rate of evolutionary change should be intermittent and jagged, or smooth and gradual. If I hadn’t seen the graph in advance, I could not have predicted it. (Unfortunately, I rendered even that verdict after seeing the data . . .) Maybe there are models in the evolutionary family that would make advance predictions of steadiness or variability, but if so, I don’t know about them. More to the point, my friend didn’t know either.

It is not always wise to ask the opponents of a theory what their competitors predict. Get the theory’s predictions from the theory’s best advocates. Just make sure to write down their predictions in advance. Yes, sometimes a theory’s advocates try to make the theory “fit” evidence that plainly doesn’t fit. But if you find yourself wondering what a theory predicts, ask first among the theory’s advocates, and afterward ask the detractors to cross-examine.

Furthermore: Models may include noise. If we hypothesize that the data are trending slowly and steadily upward, but our measuring instrument has an error of 5%, then it does no good to point to a data point that dips below the previous data point, and shout triumphantly, “See! It went down! Down down down! And don’t tell me why your theory fits the dip; you’re just making excuses!” Formal, technical models often incorporate explicit error terms. The error term spreads out the likelihood density, decreases the model’s precision and reduces the theory’s score, but the Bayesian scoring rule still governs. A technical model can allow mistakes, and make mistakes, and still do better than ignorance. In our supermarket example, even the precise hypothesis of 51 still bets only 90% of its probability mass on 51; the precise hypothesis claims only that 51 happens nine times out of ten. Ignoring nine 51s, pointing at one case of 82, and crowing in triumph, does not a refutation make. That’s not an excuse, it’s an explicit advance prediction of a technical model.

The error term makes the “precise” theory vulnerable to a superprecise alternative that predicted the 82. The standard model would also be vulnerable to a precisely ignorant model that predicted a 60% chance of 51 on the round where we saw 82, spreading out the likelihood more entropically on that particular error. No matter how good the theory, science always has room for a higher-scoring competitor. But if you don’t present a better alternative, if you try only to show that an accepted theory is stupid with respect to the data, that scientific endeavor may be more demanding than just replacing the old theory with a new one.

Astronomers recorded the unexplained perihelion advance of Mercury, unaccounted for under Newtonian physics—or rather, Newtonian physics predicted 5,557 seconds of arc per century, where the observed amount was 5,600.¹⁷ But should the scientists of that day have junked Newtonian gravitation based on such small, unexplained counterevidence? What would they have used instead? Eventually, Newton’s theory of gravitation was set aside, after Einstein’s General Relativity precisely explained the orbital discrepancy of Mercury and also made successful advance predictions. But there was no way to know in advance that this was how things would turn out.

In the nineteenth century there was a persistent anomaly in the orbit of Uranus. People said, “Maybe Newton’s law starts to fail at long distances.” Eventually some bright fellows looked at the anomaly and said, “Could this be an unknown outer planet?” Urbain Le Verrier and John Couch Adams independently did some scribbling and figuring, using Newton’s standard theory—and predicted Neptune’s location to within one degree of arc, dramatically confirming Newtonian gravitation.¹⁸

Only after General Relativity precisely produced the perihelion advance of Mercury did we know Newtonian gravitation would never explain it.

In the Intuitive Explanation we saw how Karl Popper’s insight that falsification is stronger than confirmation translates into a Bayesian truth about likelihood ratios. Popper erred in thinking that falsification was qualitatively different from confirmation; both are governed by the same Bayesian rules. But Popper’s philosophy reflected an important truth about a quantitative difference between falsification and confirmation.

Popper was profoundly impressed by the differences between the allegedly “scientific” theories of Freud and Adler and the revolution effected by Einstein’s theory of relativity in physics in the first two decades of this century. The main difference between them, as Popper saw it, was that while Einstein’s theory was highly “risky,” in the sense that it was possible to deduce consequences from it which were, in the light of the then dominant Newtonian physics, highly improbable (e.g., that light is deflected towards solid bodies—confirmed by Eddington’s experiments in 1919), and which would, if they turned out to be false, falsify the whole theory, nothing could, even in principle, falsify psychoanalytic theories. These latter, Popper came to feel, have more in common with primitive myths than with genuine science. That is to say, he saw that what is apparently the chief source of strength of psychoanalysis, and the principal basis on which its claim to scientific status is grounded, viz. its capability to accommodate, and explain, every possible form of human behaviour, is in fact a critical weakness, for it entails that it is not, and could not be, genuinely predictive. Psychoanalytic theories by their nature are insufficiently precise to have negative implications, and so are immunised from experiential falsification . . .

Popper, then, repudiates induction, and rejects the view that it is the characteristic method of scientific investigation and inference, and substitutes falsifiability in its place. It is easy, he argues, to obtain evidence in favour of virtually any theory, and he consequently holds that such “corroboration,” as he terms it, should count scientifically only if it is the positive result of a genuinely “risky” prediction, which might conceivably have been false. For Popper, a theory is scientific only if it is refutable by a conceivable event. Every genuine test of a scientific theory, then, is logically an attempt to refute or to falsify it . . .

Every genuine scientific theory then, in Popper’s view, is prohibitive, in the sense that it forbids, by implication, particular events or occurrences.¹⁹

On Popper’s philosophy, the strength of a scientific theory is not how much it explains, but how much it doesn’t explain. The virtue of a scientific theory lies not in the outcomes it permits, but in the outcomes it prohibits. Freud’s theories, which seemed to explain everything, prohibited nothing.

Translating this into Bayesian terms, we find that the more outcomes a model prohibits, the more probability density the model concentrates in the remaining, permitted outcomes. The more outcomes a theory prohibits, the greater the knowledge-content of the theory. The more daringly a theory exposes itself to falsification, the more definitely it tells you which experiences to anticipate.

A theory that can explain any experience corresponds to a hypothesis of complete ignorance—a uniform distribution with probability density spread evenly over every possible outcome.

Phlogiston was the eighteenth century’s answer to the Elemental Fire of the Greek alchemists. You couldn’t use phlogiston theory to predict the outcome of a chemical transformation—first you looked at the result, then you used phlogiston to explain it. Phlogiston theory was infinitely flexible; a disguised hypothesis of zero knowledge. Similarly, the theory of vitalism doesn’t explain how the hand moves, nor tell you what transformations to expect from organic chemistry; and vitalism certainly permits no quantitative calculations.

The flip side:

Beware of checklist thinking: Having a sacred mystery, or a mysterious answer, is not the same as refusing to explain something. Some elements in our physics are taken as “fundamental,” not yet further reduced or explained. But these fundamental elements of our physics are governed by clearly defined, mathematically simple, formally computable causal rules.

Occasionally some crackpot objects to modern physics on the grounds that it does not provide an “underlying mechanism” for a mathematical law currently treated as fundamental. (Claiming that a mathematical law lacks an “underlying mechanism” is one of the entries on the Crackpot Index by John Baez.²⁰) The “underlying mechanism” the crackpot proposes in answer is vague, verbal, and yields no increase in predictive power—otherwise we would not classify the claimant as a crackpot.

Our current physics makes the electromagnetic field fundamental, and refuses to explain it further. But the “electromagnetic field” is a fundamental governed by clear mathematical rules, with no properties outside the mathematical rules, subject to formal computation to describe its causal effect upon the world. Someday someone may suggest improved math that yields better predictions, but I would not indict the current model on grounds of mysteriousness. A theory that includes fundamental elements is not the same as a theory that contains mysterious elements.

Fundamentals should be simple. “Life” is not a good fundamental, “oxygen” is a good fundamental, and “electromagnetic field” is a better fundamental. Life might look simple to a vitalist—it’s the simple, magical ability of your muscles to move under your mental direction. Why shouldn’t life be explained by a simple, magical fundamental substance like élan vital? But phenomena that seem psychologically very simple—little dots of light in the sky, orangey-bright hot flame, flesh moving under mental direction—often conceal vast depths of underlying complexity. The proposition that life is a complex phenomenon may seem incredible to the vitalist, staring at a blankly opaque mystery with no obvious handles; but yes, Virginia, there is underlying complexity. The criterion of simplicity that is relevant to Occam’s Razor is mathematical or computational simplicity. Once we render down our model into mathematically simple fundamental elements, not in themselves sharing the mysterious qualities of the mystery, interacting in clearly defined ways to produce the formerly mysterious phenomenon as a detailed prediction, that is as non-mysterious as humanity has ever figured out how to make anything.

Many people in this world believe that after dying they will face a stern-eyed fellow named St. Peter, who will examine their actions in life and accumulate a score for morality. Presumably St. Peter’s scoring rule is unique and invariant under trivial changes of perspective. Unfortunately, believers cannot obtain a quantitative, precisely computable specification of the scoring rule, which seems rather unfair.

The religion of Bayesianity holds that your eternal fate depends on the probability judgments you made in life. Unlike lesser faiths, Bayesianity can give a quantitative, precisely computable specification of how your eternal fate is determined.

Our proper Bayesian scoring rule provides a way to accumulate scores across experiments, and the score is invariant regardless of how we slice up the “experiments” or in what order we accumulate the results. We add up the logarithms of the probabilities. This corresponds to multiplying together the probability assigned to the outcome in each experiment, to find the joint probability of all the experiments together. We take the logarithm to simplify our intuitive understanding of the accumulated score, to maintain our grip on the tiny fractions involved, and to ensure we maximize our expected score by stating our honest probabilities rather than placing all our play money on the most probable bet.

Bayesianity states that when you die, Pierre-Simon Laplace examines every single event in your life, from finding your shoes next to your bed in the morning to finding your workplace in its accustomed spot. Every losing lottery ticket means you cared enough to play. Laplace assesses the advance probability you assigned to each event. Where you did not assign a precise numerical probability in advance, Laplace examines your degree of anticipation or surprise, extrapolates other possible outcomes and your extrapolated reactions, and renormalizes your extrapolated emotions to a likelihood distribution over possible outcomes. (Hence the phrase “Laplacian superintelligence.”)

Then Laplace takes every event in your life, and every probability you assigned to each event, and multiplies all the probabilities together. This is your Final Judgment—the probability you assigned to your life.

Those who follow Bayesianity strive all their lives to maximize their Final Judgment. This is the sole virtue of Bayesianity. The rest is just math.

Mark you: the path of Bayesianity is strict. What probability shall you assign each morning, to the proposition, “The Sun shall rise?” (We shall discount such quibbles as cloudy days, and that the Earth orbits the Sun.) Perhaps one who did not follow Bayesianity would be humble, and give a probability of 99.9%. But we who follow Bayesianity shall discard all considerations of modesty and arrogance, and scheme only to maximize our Final Judgment. Like an obsessive video-game player, we care only about this numerical score. We’re going to face this Sun-shall-rise issue 365 times per year, so we might be able to improve our Final Judgment considerably by tweaking our probability assignment.

As it stands, even if the Sun rises every morning, every year our Final Judgment will decrease by a factor of 0.999³⁶⁵ = 0.7, roughly -0.52 bits. Every two years, our Final Judgment will decrease more than if we found ourselves ignorant of a coinflip’s outcome! Intolerable. If we increase our daily probability of sunrise to 99.99%, then each year our Final Judgment will decrease only by a factor of 0.964. Better. Still, in the unlikely event that we live exactly 70 years and then die, our Final Judgment will only be 7.75% of what it might have been. What if we assign a 99.999% probability to the sunrise? Then after 70 years, our Final Judgment will be multiplied by 77.4%.

Why not assign a probability of 1.0?

One who follows Bayesianity will never assign a probability of 1.0 to anything. Assigning a probability of 1.0 to some outcome uses up all your probability mass. If you assign a probability of 1.0 to some outcome, and reality delivers a different answer, you must have assigned the actual outcome a probability of zero. This is Bayesianity’s sole mortal sin. Zero times anything is zero. When Laplace multiplies together all the probabilities of your life, the combined probability will be zero. Your Final Judgment will be doodly-squat, zilch, nada, nil. No matter how rational your guesses during the rest of your life, you’ll spend eternity next to some guy who believed in flying saucers and got all his information from the Weekly World News. Again we find it helpful to take the logarithm, revealing the innocent-sounding “zero” in its true form. Risking an outcome probability of zero is like accepting a bet with a payoff of negative infinity.

What if humanity decides to take apart the Sun for mass (stellar engineering), or to switch off the Sun because it’s wasting entropy? Well, you say, you’ll see that coming, you’ll have a chance to alter your probability assignment before the actual event. What if an Artificial Intelligence in someone’s basement recursively self-improves to superintelligence, stealthily develops nanotechnology, and one morning it takes apart the Sun? If on the last night of the world you assign a probability of 99.999% to tomorrow’s sunrise, your Final Judgment will go down by a factor of 100,000. Minus 50 decibels! Awful, isn’t it?

So what is your best strategy? Well, suppose you 50% anticipate that a basement-spawned AI superintelligence will disassemble the Sun sometime in the next ten years, and you figure there’s about an equal chance of this happening on any given day between now and then. On any given night, you would 99.98% anticipate the Sun rising tomorrow. If this is really what you anticipate, then you have no motive to say anything except 99.98% as your probability. If you feel nervous that this anticipation is too low, or too high, it must not be what you anticipate after your nervousness is taken into account.

But the deeper truth of Bayesianity is this: You cannot game the system. You cannot give a humble answer, nor a confident one. You must figure out exactly how much you anticipate the Sun rising tomorrow, and say that number. You must shave away every hair of modesty or arrogance, and ask whether you expect to end up being scored on the Sun rising, or failing to rise. Look not to your excuses, but ask which excuses you expect to need. After you arrive at your exact degree of anticipation, the only way to further improve your Final Judgment is to improve the accuracy, calibration, and discrimination of your anticipation. You cannot do better except by guessing better and anticipating more precisely.

Er, well, except that you could commit suicide when you turned five, thereby preventing your Final Judgment from decreasing any further. Or if we patch a new sin onto the utility function, enjoining against suicide, you could flee from mystery, avoiding all situations in which you thought you might not know everything. So much for that religion.

Ideally, we predict the outcome of the experiment in advance, using our model, and then we perform the experiment to see if the outcome accords with our model. Unfortunately, we can’t always control the information stream. Sometimes Nature throws experiences at us, and by the time we think of an explanation, we’ve already seen the data we’re supposed to explain. This was one of the scientific sins committed by nineteenth century evolutionism; Darwin observed the similarity of many species, and their adaptation to particular local environments, before the hypothesis of natural selection occurred to him. Nineteenth century evolutionism began life as a post facto explanation, not an advance prediction.

Nor is this a trouble only of semitechnical theories. In 1846, the successful deduction of Neptune’s existence from gravitational perturbations in the orbit of Uranus was considered a grand triumph for Newton’s theory of gravitation. Why? Because Neptune’s existence was the first observation that confirmed an advance prediction of Newtonian gravitation. All the other phenomena that Newton explained, such as orbits and orbital perturbations and tides, had been observed in great detail before Newton explained them. No one seriously doubted that Newton’s theory was correct. Newton’s theory explained too much too precisely, and it replaced a collection of ad hoc models with a single unified mathematical law. Even so, the advance prediction of Neptune’s existence, followed by the observation of Neptune at almost exactly the predicted location, was considered the first grand triumph of Newton’s theory at predicting what no previous model could predict. Considerable time elapsed between widespread acceptance of Newton’s theory and the first impressive advance prediction of Newtonian gravitation. By the time Newton came up with his theory, scientists had already observed, in great detail, most of the phenomena that Newtonian gravitation predicted.

But the rule of advance prediction is a morality of science, not a law of probability theory. If you have already seen the data you must explain, then Science may darn you to heck, but your predicament doesn’t collapse the laws of probability theory. What does happen is that it becomes much more difficult for a hapless human to obey the laws of probability theory. When you’re deciding how to rate a hypothesis according to the Bayesian scoring rule, you need to figure out how much probability mass that hypothesis assigns to the observed outcome. If we must make our predictions in advance, then it’s easier to notice when someone is trying to claim every possible outcome as an advance prediction, using too much probability mass, being deliberately vague to avoid falsification, and so on.

No numerologist can predict next week’s winning lottery numbers, but they will be happy to explain the mystical significance of last week’s winning lottery numbers. Say the winning Mega Ball was seven in last week’s lottery, out of 52 possible outcomes. Obviously this happened because seven is the lucky number. So will the Mega Ball in next week’s lottery also come up seven? We understand that it’s not certain, of course, but if it’s the lucky number, you ought to assign a probability of higher than 1/52 . . . and then we’ll score your guesses over the course of a few years, and if your score is too low we’ll have you flogged . . . what’s that you say? You want to assign a probability of exactly 1/52? But that’s the same probability as every other number; what happened to seven being lucky? No, sorry, you can’t assign a 90% probability to seven and also a 90% probability to eleven. We understand they’re both lucky numbers. Yes, we understand that they’re very lucky numbers. But that’s not how it works.

Even if the listener does not know the way of Bayes and does not ask for formal probabilities, they will probably become suspicious if you try to cover too many bases. Suppose they ask you to predict next week’s winning Mega Ball, and you use numerology to explain why the number one ball would fit your theory very well, and why the number two ball would fit your theory very well, and why the number three ball would fit your theory very well . . . even the most credulous listener might begin to ask questions by the time you got to twelve. Maybe you could tell us which numbers are unlucky and definitely won’t win the lottery? Well, thirteen is unlucky, but it’s not absolutely impossible (you hedge, anticipating in advance which excuse you might need).

But if we ask you to explain last week’s lottery numbers, why, the seven was practically inevitable. That seven should definitely count as a major success for the “lucky numbers” model of the lottery. And it couldn’t possibly have been thirteen; luck theory rules that straight out.

Imagine that you wake up one morning and your left arm has been replaced by a blue tentacle. The blue tentacle obeys your motor commands—you can use it to pick up glasses, drive a car, etc. How would you explain this hypothetical scenario? Take a moment to ponder this puzzle before continuing.

(Spoiler space . . .)

How would I explain the event of my left arm being replaced by a blue tentacle? The answer is that I wouldn’t. It isn’t going to happen.

It would be easy enough to produce a verbal explanation that “fit” the hypothetical. There are many explanations that can “fit” anything, including (as a special case of “anything”) my arm’s being replaced by a blue tentacle. Divine intervention is a good all-purpose explanation. Or aliens with arbitrary motives and capabilities. Or I could be mad, hallucinating, dreaming my life away in a hospital. Such explanations “fit” all outcomes equally well, and equally poorly, equating to hypotheses of complete ignorance.

The test of whether a model of reality “explains” my arm’s turning into a blue tentacle is whether the model concentrates significant probability mass into that particular outcome. Why that dream, in the hospital? Why would aliens do that particular thing to me, as opposed to the other billion things they might do? Why would my arm turn into a tentacle on that morning, after remaining an arm through every other morning of my life? And in all cases I must look for an argument compelling enough to make that particular prediction in advance, not mere compatibility. Once I already knew the outcome, it would become far more difficult to sift through hypotheses to find good explanations. Whatever hypothesis I tried, I would be hard-pressed not to allocate more probability mass to yesterday’s blue-tentacle outcome than if I extrapolated blindly, seeking the model’s most likely prediction for tomorrow.

A model does not always predict all the features of the data. Nature has no privileged tendency to present me with solvable challenges. Perhaps a deity toys with me, and the deity’s mind is computationally intractable. If I flip a fair coin there is no way to further explain the outcome, no model that makes a better prediction than the maximum-entropy hypothesis. But if I guess a model with no internal detail or a model that makes no further predictions, I not only have no reason to believe that guess, I have no reason to care. Last night my arm was replaced with a blue tentacle. Why? Aliens! So what will they do tomorrow? Similarly, if I attribute the blue tentacle to a hallucination as I dream my life away in a coma, I still don’t know any more about what I’ll hallucinate tomorrow. So why do I care whether it was aliens or hallucination?

What might be a good explanation, then, if I woke up one morning and found my arm transformed into a blue tentacle? To claim a “good explanation” for this hypothetical experience would require an argument such that, contemplating the hypothetical argument now, before my arm has transformed into a blue tentacle, I would go to sleep worrying that my arm really would transform into a tentacle.

People play games with plausibility, explaining events they expect to never actually encounter, yet this necessarily violates the laws of probability theory. How many people who thought they could “explain” the hypothetical experience of waking up with their arm replaced by a tentacle, would go to sleep wondering if it might really happen to them? Had they the courage of their convictions, they would say: I do not expect to ever encounter this hypothetical experience, and therefore I cannot explain, nor have I a motive to try. Such things only happen in webcomics, and I need not prepare explanations, for in real life I shall never have a chance to use them. If I ever find myself in this impossible situation, let me miss no jot or tittle of my valuable bewilderment.

To a Bayesian, probabilities are anticipations, not mere beliefs to proclaim from the rooftops. If I have a model that assigns probability mass to waking up with a blue tentacle, then I am nervous about waking up with a blue tentacle. What if the model is a fanciful one, like a witch casting a spell that transports me into a randomly selected webcomic? Then the prior probability of webcomic witchery is so low that my real-world understanding doesn’t assign any significant weight to that hypothesis. The witchcraft hypothesis, if taken as a given, might assign non-insignificant likelihood to waking up with a blue tentacle. But my anticipation of that hypothesis is so low that I don’t anticipate any of the predictions of that hypothesis. That I can conceive of a witchcraft hypothesis should in no wise diminish my stark bewilderment if I actually wake up with a tentacle, because the real-world probability I assign to the witchcraft hypothesis is effectively zero. My zero-probability hypothesis wouldn’t help me explain waking up with a tentacle, because the argument isn’t good enough to make me anticipate waking up with a tentacle.

In the laws of probability theory, likelihood distributions are fixed properties of a hypothesis. In the art of rationality, to explain is to anticipate. To anticipate is to explain. Suppose I am a medical researcher, and in the ordinary course of pursuing my research, I notice that my clever new theory of anatomy seems to permit a small and vague possibility that my arm will transform into a blue tentacle. “Ha ha!” I say, “how remarkable and silly!” and feel ever so slightly nervous. That would be a good explanation for waking up with a tentacle, if it ever happened.

If a chain of reasoning doesn’t make me nervous, in advance, about waking up with a tentacle, then that reasoning would be a poor explanation if the event did happen, because the combination of prior probability and likelihood was too low to make me allocate any significant real-world probability mass to that outcome.

If you start from well-calibrated priors, and you apply Bayesian reasoning, you’ll end up with well-calibrated conclusions. Imagine that two million entities, scattered across different planets in the universe, have the opportunity to encounter something so strange as waking up with a tentacle (or—gasp!—ten fingers). One million of these entities say “one in a thousand” for the prior probability of some hypothesis X, and each hypothesis X says “one in a hundred” for the likelihood of waking up with a tentacle. And one million of these entities say “one in a hundred” for the prior probability of some hypothesis Y, and each hypothesis Y says “one in ten” for the likelihood of waking up with a tentacle. If we suppose that all entities are well-calibrated, then we shall look across the universe and find ten entities who wound up with a tentacle because of hypotheses of plausibility class X, and a thousand entities who wound up with tentacles because of hypotheses of plausibility class Y. So if you find yourself with a tentacle, and if your probabilities are well-calibrated, then the tentacle is more likely to stem from a hypothesis you would class as probable than a hypothesis you would class as improbable. (What if your probabilities are poorly calibrated, so that when you say “million-to-one” it happens one time out of twenty? Then you’re grossly overconfident, and we adjust your probabilities in the direction of less discrimination and greater entropy.)

The hypothesis of being transported into a webcomic, even if it “explains” the scenario of waking up with a blue tentacle, is a poor explanation because of its low prior probability. The webcomic hypothesis doesn’t contribute to explaining the tentacle, because it doesn’t make you anticipate waking up with a tentacle.

If we start with a quadrillion sentient minds scattered across the universe, quite a lot of entities will encounter events that are very likely, only about a mere million entities will experience events with lifetime likelihoods of a billion-to-one (as we would anticipate, surveying with infinite eyes and perfect calibration), and not a single entity will experience the impossible.

If, somehow, you really did wake up with a tentacle, it would likely be because of something much more probable than “being transported into a webcomic,” some perfectly normal reason to wake up with a tentacle which you just didn’t see coming. A reason like what? I don’t know. Nothing. I don’t anticipate waking up with a tentacle, so I can’t give any good explanation for it. Why should I bother crafting excuses that I don’t expect to use? If I was worried I might someday need a clever excuse for waking up with a tentacle, the reason I was nervous about the possibility would be my explanation.

Reality dishes out experiences using probability, not plausibility. If you find out that your laptop doesn’t obey Conservation of Momentum, then reality must think that a perfectly normal thing to do to you. How could violating Conservation of Momentum possibly be perfectly normal? I anticipate that question has no answer and will never need answering. Similarly, people do not wake up with tentacles, so apparently it is not perfectly normal.

There is a shattering truth, so surprising and terrifying that people resist the implications with all their strength. Yet there are a lonely few with the courage to accept this satori. Here is wisdom, if you would be wise:

Since the beginning
Not one unusual thing
Has ever happened.

Alas for those who turn their eyes from zebras and dream of dragons! If we cannot learn to take joy in the merely real, our lives shall be empty indeed.

1. Edwin T. Jaynes, Probability Theory: The Logic of Science, ed. George Larry Bretthorst (New York: Cambridge University Press, 2003), doi:10.2277/0521592712.

2. Feynman, Leighton, and Sands, The Feynman Lectures on Physics.

3. Readers with calculus may verify that in the simpler case of a light that has only two colors, with p being the bet on the first color and f the frequency of the first color, the expected payoff f × (1 - (1 - p)²) + (1 - f) × (1 - p²), with p variable and f constant, has its global maximum when we set p = f.

4. Don’t remember how to read P(A|B)? See An Intuitive Explanation of Bayesian Reasoning.

5. J. Frank Yates et al., “Probability Judgment Across Cultures,” in Gilovich, Griffin, and Kahneman, Heuristics and Biases, 271–291.

6. Karl R Popper, The Logic of Scientific Discovery (New York: Basic Books, 1959).

7. Jaynes, Probability Theory.

8. Imagination Engines, Inc., “The Imagination Engine™; or Imagitron™,” 2011, http://www.imagination-engines.com/ie.htm.

9. Friedrich Spee, Cautio Criminalis; or, A Book on Witch Trials, ed. and trans. Marcus Hellyer, Studies in Early Modern German History (1631; Charlottesville: University of Virginia Press, 2003).

10. quoted in Dave Robinson and Judy Groves, Philosophy for Beginners, 1st ed. (Cambridge: Icon Books, 1998).

11. TalkOrigins Foundation, “Frequently Asked Questions about Creationism and Evolution,” http://www.talkorigins.org/origins/faqs-qa.html.

12. Daniel C. Dennett, Darwin’s Dangerous Idea: Evolution and the Meanings of Life (Simon & Schuster, 1995).

13. quoted in Lyle Zapato, “Lord Kelvin Quotations,” 2008, http://zapatopi.net/kelvin/quotes/.

14. Charles Darwin, On the Origin of Species by Means of Natural Selection; or, The Preservation of Favoured Races in the Struggle for Life, 1st ed. (London: John Murray, 1859), http://darwin-online.org.uk/content/frameset?viewtype=text&itemID=F373&pageseq=1; Charles Darwin, The Descent of Man, and Selection in Relation to Sex, 2nd ed. (London: John Murray, 1874), http://darwin-online.org.uk/content/frameset?itemID=F944&viewtype=text&pageseq=1.

15. Williams, Adaptation and Natural Selection.

16. Carl Sagan, The Demon-Haunted World: Science as a Candle in the Dark, 1st ed. (New York: Random House, 1995).

17. Kevin Brown, Reflections On Relativity (Raleigh, NC: printed by author, 2011), 405-414, http://www.mathpages.com/rr/rrtoc.htm.

18. Ibid., 405-414.

19. Stephen Thornton, “Karl Popper,” in The Stanford Encyclopedia of Philosophy, Winter 2002, ed. Edward N. Zalta (Stanford University), http://plato.stanford.edu/archives/win2002/entries/popper/.

20. John Baez, “The Crackpot Index,” 1998, http://math.ucr.edu/home/baez/crackpot.html.

Book V
Mere Goodness

Ends: An Introduction

U. Fake Preferences
257. Not for the Sake of Happiness (Alone)
258. Fake Selfishness
259. Fake Morality
260. Fake Utility Functions
261. Detached Lever Fallacy
262. Dreams of AI Design
263. The Design Space of Minds-in-General

V. Value Theory
264. Where Recursive Justification Hits Bottom
265. My Kind of Reflection
266. No Universally Compelling Arguments
267. Created Already in Motion
268. Sorting Pebbles into Correct Heaps
269. 2-Place and 1-Place Words
270. What Would You Do Without Morality?
271. Changing Your Metaethics
272. Could Anything Be Right?
273. Morality as Fixed Computation
274. Magical Categories
275. The True Prisoner’s Dilemma
276. Sympathetic Minds
277. High Challenge
278. Serious Stories
279. Value is Fragile
280. The Gift We Give to Tomorrow

W. Quantified Humanism
281. Scope Insensitivity
282. One Life Against the World
283. The Allais Paradox
284. Zut Allais!
285. Feeling Moral
286. The “Intuitions” Behind “Utilitarianism”
287. Ends Don’t Justify Means (Among Humans)
288. Ethical Injunctions
289. Something to Protect
290. When (Not) to Use Probabilities
291. Newcomb’s Problem and Regret of Rationality

Interlude: The Twelve Virtues of Rationality

Ends: An Introduction
by Rob Bensinger

Value theory is the study of what people care about. It’s the study of our goals, our tastes, our pleasures and pains, our fears and our ambitions.

That includes conventional morality. Value theory subsumes things we wish we cared about, or would care about if we were wiser and better people—not just things we already do care about.

Value theory also subsumes mundane, everyday values: art, food, sex, friendship, and everything else that gives life its affective valence. Going to the movies with your friend Sam can be something you value even if it’s not a moral value.

We find it useful to reflect upon and debate our values because how we act is not always how we wish we’d act. Our preferences can conflict with each other. We can desire to have a different set of desires. We can lack the will, the attention, or the insight needed to act the way we’d like to.

Humans do care about their actions’ consequences, but not consistently enough to formally qualify as agents with utility functions. That humans don’t act the way they wish they would is what we mean when we say “humans aren’t instrumentally rational.”

Theory and Practice

Adding to the difficulty, there exists a gulf between how we think we wish we’d act, and how we actually wish we’d act.

Philosophers disagree wildly about what we want—as do psychologists, and as do politicians—and about what we ought to want. They disagree even about what it means to “ought” to want something. The history of moral theory, and the history of human efforts at coordination, is piled high with the corpses of failed Guiding Principles to True Ultimate No-Really-This-Time-I-Mean-It Normativity.

If you’re trying to come up with a reliable and pragmatically useful specification of your goals—not just for winning philosophy debates, but (say) for designing safe autonomous adaptive AI, or for building functional institutions and organizations, or for making it easier to decide which charity to donate to, or for figuring out what virtues you should be cultivating—humanity’s track record with value theory does not bode well for you.

Mere Goodness collects three sequences of blog posts on human value: “Fake Preferences” (on failed attempts at theories of value), “Value Theory” (on obstacles to developing a new theory, and some intuitively desirable features of such a theory), and “Quantified Humanism” (on the tricky question of how we should apply such theories to our ordinary moral intuitions and decision-making).

The last of these topics is the most important. The cash value of a normative theory is how well it translates into normative practice. Acquiring a deeper and fuller understanding of your values should make you better at actually fulfilling them. At a bare minimum, your theory shouldn’t get in the way of your practice. What good would it be, then, to know what’s good?

Reconciling this art of applied ethics (and applied aesthetics, and applied economics, and applied psychology) with our best available data and theories often comes down to the question of when we should trust our snap judgments, and when we should ditch them.

In many cases, our explicit models of what we care about are so flimsy or impractical that we’re better off trusting our vague initial impulses. In many other cases, we can do better with a more informed and systematic approach. There is no catch-all answer. We will just have to scrutinize examples and try to notice the different warning signs for “sophisticated theories tend to fail here” and “naive feelings tend to fail here.”

Journey and Destination

A recurring theme in the pages to come will be the question: Where shall we go? What outcomes are actually valuable?

To address this question, Yudkowsky coined the term “fun theory.” Fun theory is the attempt to figure out what our ideal vision of the future would look like—not just the system of government or moral code we’d ideally live under, but the kinds of adventures we’d ideally go on, the kinds of music we’d ideally compose, and everything else we ultimately want out of life.

Stretched into the future, questions of fun theory intersect with questions of transhumanism, the view that we can radically improve the human condition if we make enough scientific and social progress.¹ Transhumanism occasions a number of debates in moral philosophy, such as whether the best long-term outcomes for sentient life would be based on hedonism (the pursuit of pleasure) or on more complex notions of eudaimonia (general well-being). Other futurist ideas discussed at various points in Rationality: From AI to Zombies include cryonics (storing your body in a frozen state after death, in case future medical technology finds a way to revive you), mind uploading (implementing human minds in synthetic hardware), and large-scale space colonization.

Perhaps surprisingly, fun theory is one of the more neglected applications of value theory. Utopia-planning has become rather passe—partly because it smacks of naiveté, and partly because we’re empirically terrible at translating utopias into realities. Even the word utopia reflects this cynicism; it is derived from the Greek for “non-place.”

Yet if we give up on the quest for a true, feasible utopia (or eutopia, “good place”), it’s not obvious that the cumulative effect of our short-term pursuit of goals will be a future we find valuable over the long term. Value is not an inevitable feature of the world. Creating it takes work. Preserving it takes work.

This invites a second question: How shall we get there? What is the relationship between good ends and good means?

When we play a game, we want to enjoy the process. We don’t generally want to just skip ahead to being declared the winner. Sometimes, the journey matters more than the destination. Sometimes, the journey is all that matters.

Yet there are other cases where the reverse is true. Sometimes the end-state is just too important for “the journey” to factor into our decisions. If you’re trying to save a family member’s life, it’s not necessarily a bad thing to get some enjoyment out of the process; but if you can increase your odds of success in a big way by picking a less enjoyable strategy . . .

In many cases, our values are concentrated in the outcomes of our actions, and in our future. We care about the way the world will end up looking—especially those parts of the world that can love and hurt and want.

How do detached, abstract theories stack up against vivid, affect-laden feelings in those cases? More generally: What is the moral relationship between actions and consequences?

Those are hard questions, but perhaps we can at least make progress on determining what we mean by them. What are we building into our concept of what’s “valuable” at the very start of our inquiry?

1. One example of a transhumanist argument is: “We could feasibly abolish aging and disease within a few decades or centuries. This would effectively end death by natural causes, putting us in the same position as organisms with negligible senescence—lobsters, Aldabra giant tortoises, etc. Therefore we should invest in disease prevention and anti-aging technologies.” This idea qualifies as transhumanist because eliminating the leading causes of injury and death would drastically change human life.

Bostrom and Savulescu survey arguments for and against radical human enhancement, e.g., Sandel’s objection that tampering with our biology too much would make life feel like less of a “gift.”²^,³ Bostrom’s “History of Transhumanist Thought” provides context for the debate.⁴

2. Nick Bostrom, “A History of Transhumanist Thought,” Journal of Evolution and Technology 14, no. 1 (2005): 1–25, http://www.nickbostrom.com/papers/history.pdf.

3. Michael Sandel, “What’s Wrong With Enhancement,” Background material for the President’s Council on Bioethics. (2002).

4. Nick Bostrom and Julian Savulescu, “Human Enhancement Ethics: The State of the Debate,” in Human Enhancement, ed. Nick Bostrom and Julian Savulescu (2009).

Part U
Fake Preferences

257
Not for the Sake of Happiness (Alone)

When I met the futurist Greg Stock some years ago, he argued that the joy of scientific discovery would soon be replaced by pills that could simulate the joy of scientific discovery. I approached him after his talk and said, “I agree that such pills are probably possible, but I wouldn’t voluntarily take them.”

And Stock said, “But they’ll be so much better that the real thing won’t be able to compete. It will just be way more fun for you to take the pills than to do all the actual scientific work.”

And I said, “I agree that’s possible, so I’ll make sure never to take them.”

Stock seemed genuinely surprised by my attitude, which genuinely surprised me. One often sees ethicists arguing as if all human desires are reducible, in principle, to the desire for ourselves and others to be happy. (In particular, Sam Harris does this in The End of Faith, which I just finished perusing—though Harris’s reduction is more of a drive-by shooting than a major topic of discussion.)¹

This isn’t the same as arguing whether all happinesses can be measured on a common utility scale—different happinesses might occupy different scales, or be otherwise non-convertible. And it’s not the same as arguing that it’s theoretically impossible to value anything other than your own psychological states, because it’s still permissible to care whether other people are happy.

The question, rather, is whether we should care about the things that make us happy, apart from any happiness they bring.

We can easily list many cases of moralists going astray by caring about things besides happiness. The various states and countries that still outlaw oral sex make a good example; these legislators would have been better off if they’d said, “Hey, whatever turns you on.” But this doesn’t show that all values are reducible to happiness; it just argues that in this particular case it was an ethical mistake to focus on anything else.

It is an undeniable fact that we tend to do things that make us happy, but this doesn’t mean we should regard the happiness as the only reason for so acting. First, this would make it difficult to explain how we could care about anyone else’s happiness—how we could treat people as ends in themselves, rather than instrumental means of obtaining a warm glow of satisfaction.

Second, just because something is a consequence of my action doesn’t mean it was the sole justification. If I’m writing a blog post, and I get a headache, I may take an ibuprofen. One of the consequences of my action is that I experience less pain, but this doesn’t mean it was the only consequence, or even the most important reason for my decision. I do value the state of not having a headache. But I can value something for its own sake and also value it as a means to an end.

For all value to be reducible to happiness, it’s not enough to show that happiness is involved in most of our decisions—it’s not even enough to show that happiness is the most important consequent in all of our decisions—it must be the only consequent. That’s a tough standard to meet. (I originally found this point in a Sober and Wilson paper, not sure which one.)

If I claim to value art for its own sake, then would I value art that no one ever saw? A screensaver running in a closed room, producing beautiful pictures that no one ever saw? I’d have to say no. I can’t think of any completely lifeless object that I would value as an end, not just a means. That would be like valuing ice cream as an end in itself, apart from anyone eating it. Everything I value, that I can think of, involves people and their experiences somewhere along the line.

The best way I can put it is that my moral intuition appears to require both the objective and subjective component to grant full value.

The value of scientific discovery requires both a genuine scientific discovery, and a person to take joy in that discovery. It may seem difficult to disentangle these values, but the pills make it clearer.

I would be disturbed if people retreated into holodecks and fell in love with mindless wallpaper. I would be disturbed even if they weren’t aware it was a holodeck, which is an important ethical issue if some agents can potentially transport people into holodecks and substitute zombies for their loved ones without their awareness. Again, the pills make it clearer: I’m not just concerned with my own awareness of the uncomfortable fact. I wouldn’t put myself into a holodeck even if I could take a pill to forget the fact afterward. That’s simply not where I’m trying to steer the future.

I value freedom: When I’m deciding where to steer the future, I take into account not only the subjective states that people end up in, but also whether they got there as a result of their own efforts. The presence or absence of an external puppet master can affect my valuation of an otherwise fixed outcome. Even if people wouldn’t know they were being manipulated, it would matter to my judgment of how well humanity had done with its future. This is an important ethical issue, if you’re dealing with agents powerful enough to helpfully tweak people’s futures without their knowledge.

So my values are not strictly reducible to happiness: There are properties I value about the future that aren’t reducible to activation levels in anyone’s pleasure center; properties that are not strictly reducible to subjective states even in principle.

Which means that my decision system has a lot of terminal values, none of them strictly reducible to anything else. Art, science, love, lust, freedom, friendship . . .

And I’m okay with that. I value a life complicated enough to be challenging and aesthetic—not just the feeling that life is complicated, but the actual complications—so turning into a pleasure center in a vat doesn’t appeal to me. It would be a waste of humanity’s potential, which I value actually fulfilling, not just having the feeling that it was fulfilled.

1. Harris, The End of Faith: Religion, Terror, and the Future of Reason.

258
Fake Selfishness

Once upon a time, I met someone who proclaimed himself to be purely selfish, and told me that I should be purely selfish as well. I was feeling mischievous¹ that day, so I said, “I’ve observed that with most religious people, at least the ones I meet, it doesn’t matter much what their religion says, because whatever they want to do, they can find a religious reason for it. Their religion says they should stone unbelievers, but they want to be nice to people, so they find a religious justification for that instead. It looks to me like when people espouse a philosophy of selfishness, it has no effect on their behavior, because whenever they want to be nice to people, they can rationalize it in selfish terms.”

And the one said, “I don’t think that’s true.”

I said, “If you’re genuinely selfish, then why do you want me to be selfish too? Doesn’t that make you concerned for my welfare? Shouldn’t you be trying to persuade me to be more altruistic, so you can exploit me?” The one replied: “Well, if you become selfish, then you’ll realize that it’s in your rational self-interest to play a productive role in the economy, instead of, for example, passing laws that infringe on my private property.”

And I said, “But I’m a small-‘l’ libertarian already, so I’m not going to support those laws. And since I conceive of myself as an altruist, I’ve taken a job that I expect to benefit a lot of people, including you, instead of a job that pays more. Would you really benefit more from me if I became selfish? Besides, is trying to persuade me to be selfish the most selfish thing you could be doing? Aren’t there other things you could do with your time that would bring much more direct benefits? But what I really want to know is this: Did you start out by thinking that you wanted to be selfish, and then decide this was the most selfish thing you could possibly do? Or did you start out by wanting to convert others to selfishness, then look for ways to rationalize that as self-benefiting?”

And the one said, “You may be right about that last part,” so I marked him down as intelligent.

1. Other mischievous questions to ask self-proclaimed Selfishes: “Would you sacrifice your own life to save the entire human species?” (If they notice that their own life is strictly included within the human species, you can specify that they can choose between dying immediately to save the Earth, or living in comfort for one more year and then dying along with Earth.) Or, taking into account that scope insensitivity leads many people to be more concerned over one life than the Earth, “If you had to choose one event or the other, would you rather that you stubbed your toe, or that the stranger standing near the wall there gets horribly tortured for fifty years?” (If they say that they’d be emotionally disturbed by knowing, specify that they won’t know about the torture.) “Would you steal a thousand dollars from Bill Gates if you could be guaranteed that neither he nor anyone else would ever find out about it?” (Selfish libertarians only.)

259
Fake Morality

God, say the religious fundamentalists, is the source of all morality; there can be no morality without a Judge who rewards and punishes. If we did not fear hell and yearn for heaven, then what would stop people from murdering each other left and right?

Suppose Omega makes a credible threat that if you ever step inside a bathroom between 7 a.m. and 10 a.m. in the morning, Omega will kill you. Would you be panicked by the prospect of Omega withdrawing its threat? Would you cower in existential terror and cry: “If Omega withdraws its threat, then what’s to keep me from going to the bathroom?” No; you’d probably be quite relieved at your increased opportunity to, ahem, relieve yourself.

Which is to say: The very fact that a religious person would be afraid of God withdrawing Its threat to punish them for committing murder shows that they have a revulsion of murder that is independent of whether God punishes murder or not. If they had no sense that murder was wrong independently of divine retribution, the prospect of God not punishing murder would be no more existentially horrifying than the prospect of God not punishing sneezing. If Overcoming Bias has any religious readers left, I say to you: it may be that you will someday lose your faith; and on that day, you will not lose all sense of moral direction. For if you fear the prospect of God not punishing some deed, that is a moral compass. You can plug that compass directly into your decision system and steer by it. You can simply not do whatever you are afraid God may not punish you for doing. The fear of losing a moral compass is itself a moral compass. Indeed, I suspect you are steering by that compass, and that you always have been. As Piers Anthony once said, “Only those with souls worry over whether or not they have them.” s/soul/morality/ and the point carries.

You don’t hear religious fundamentalists using the argument: “If we did not fear hell and yearn for heaven, then what would stop people from eating pork?” Yet by their assumptions—that we have no moral compass but divine reward and retribution—this argument should sound just as forceful as the other.

Even the notion that God threatens you with eternal hellfire, rather than cookies, piggybacks on a pre-existing negative value for hellfire. Consider the following, and ask which of these two philosophers is really the altruist, and which is really selfish?

“You should be selfish, because when people set out to improve society, they meddle in their neighbors’ affairs and pass laws and seize control and make everyone unhappy. Take whichever job that pays the most money: the reason the job pays more is that the efficient market thinks it produces more value than its alternatives. Take a job that pays less, and you’re second-guessing what the market thinks will benefit society most.”

“You should be altruistic, because the world is an iterated Prisoner’s Dilemma, and the strategy that fares best is Tit for Tat with initial cooperation. People don’t like jerks. Nice guys really do finish first. Studies show that people who contribute to society and have a sense of meaning in their lives are happier than people who don’t; being selfish will only make you unhappy in the long run.”

Blank out the recommendations of these two philosophers, and you can see that the first philosopher is using strictly prosocial criteria to justify their recommendations; to the first philosopher, what validates an argument for selfishness is showing that selfishness benefits everyone. The second philosopher appeals to strictly individual and hedonic criteria; to them, what validates an argument for altruism is showing that altruism benefits them as an individual—higher social status, or more intense feelings of pleasure.

So which of these two is the actual altruist? Whichever one actually holds open doors for little old ladies.

260
Fake Utility Functions

Every now and then, you run across someone who has discovered the One Great Moral Principle, of which all other values are a mere derivative consequence.

I run across more of these people than you do. Only in my case, it’s people who know the amazingly simple utility function that is all you need to program into an artificial superintelligence and then everything will turn out fine.

Some people, when they encounter the how-to-program-a-superintelligence problem, try to solve the problem immediately. Norman R. F. Maier: “Do not propose solutions until the problem has been discussed as thoroughly as possible without suggesting any.” Robyn Dawes: “I have often used this edict with groups I have led—particularly when they face a very tough problem, which is when group members are most apt to propose solutions immediately.” Friendly AI is an extremely tough problem, so people solve it extremely fast.

There’s several major classes of fast wrong solutions I’ve observed; and one of these is the Incredibly Simple Utility Function That Is All A Superintelligence Needs For Everything To Work Out Just Fine.

I may have contributed to this problem with a really poor choice of phrasing, years ago when I first started talking about “Friendly AI.” I referred to the optimization criterion of an optimization process—the region into which an agent tries to steer the future—as the “supergoal.” I’d meant “super” in the sense of “parent,” the source of a directed link in an acyclic graph. But it seems the effect of my phrasing was to send some people into happy death spirals as they tried to imagine the Superest Goal Ever, the Goal That Overrides All Other Goals, the Single Ultimate Rule From Which All Ethics Can Be Derived.

But a utility function doesn’t have to be simple. It can contain an arbitrary number of terms. We have every reason to believe that insofar as humans can said to be have values, there are lots of them—high Kolmogorov complexity. A human brain implements a thousand shards of desire, though this fact may not be appreciated by one who has not studied evolutionary psychology. (Try to explain this without a full, long introduction, and the one hears “humans are trying to maximize fitness,” which is exactly the opposite of what evolutionary psychology says.)

So far as descriptive theories of morality are concerned, the complicatedness of human morality is a known fact. It is a descriptive fact about human beings that the love of a parent for a child, and the love of a child for a parent, and the love of a man for a woman, and the love of a woman for a man, have not been cognitively derived from each other or from any other value. A mother doesn’t have to do complicated moral philosophy to love her daughter, nor extrapolate the consequences to some other desideratum. There are many such shards of desire, all different values.

Leave out just one of these values from a superintelligence, and even if you successfully include every other value, you could end up with a hyperexistential catastrophe, a fate worse than death. If there’s a superintelligence that wants everything for us that we want for ourselves, except the human values relating to controlling your own life and achieving your own goals, that’s one of the oldest dystopias in the book. (Jack Williamson’s “With Folded Hands . . . ,” in this case.)

So how does the one constructing the Amazingly Simple Utility Function deal with this objection?

Objection? Objection? Why would they be searching for possible objections to their lovely theory? (Note that the process of searching for real, fatal objections isn’t the same as performing a dutiful search that amazingly hits on only questions to which they have a snappy answer.) They don’t know any of this stuff. They aren’t thinking about burdens of proof. They don’t know the problem is difficult. They heard the word “supergoal” and went off in a happy death spiral around “complexity” or whatever.

Press them on some particular point, like the love a mother has for her children, and they reply, “But if the superintelligence wants ‘complexity,’ it will see how complicated the parent-child relationship is, and therefore encourage mothers to love their children.” Goodness, where do I start?

Begin with the motivated stopping: A superintelligence actually searching for ways to maximize complexity wouldn’t conveniently stop if it noticed that a parent-child relation was complex. It would ask if anything else was more complex. This is a fake justification; the one trying to argue the imaginary superintelligence into a policy selection didn’t really arrive at that policy proposal by carrying out a pure search for ways to maximize complexity.

The whole argument is a fake morality. If what you really valued was complexity, then you would be justifying the parental-love drive by pointing to how it increases complexity. If you justify a complexity drive by alleging that it increases parental love, it means that what you really value is the parental love. It’s like giving a prosocial argument in favor of selfishness.

But if you consider the affective death spiral, then it doesn’t increase the perceived niceness of “complexity” to say “A mother’s relationship to her daughter is only important because it increases complexity; consider that if the relationship became simpler, we would not value it.” What does increase the perceived niceness of “complexity” is saying, “If you set out to increase complexity, mothers will love their daughters—look at the positive consequence this has!”

This point applies whenever you run across a moralist who tries to convince you that their One Great Idea is all that anyone needs for moral judgment, and proves this by saying, “Look at all these positive consequences of this Great Thingy,” rather than saying, “Look at how all these things we think of as ‘positive’ are only positive when their consequence is to increase the Great Thingy.” The latter being what you’d actually need to carry such an argument.

But if you’re trying to persuade others (or yourself) of your theory that the One Great Idea is “bananas,” you’ll sell a lot more bananas by arguing how bananas lead to better sex, rather than claiming that you should only want sex when it leads to bananas.

Unless you’re so far gone into the Happy Death Spiral that you really do start saying “Sex is only good when it leads to bananas.” Then you’re in trouble. But at least you won’t convince anyone else.

In the end, the only process that reliably regenerates all the local decisions you would make given your morality is your morality. Anything else—any attempt to substitute instrumental means for terminal ends—ends up losing purpose and requiring an infinite number of patches because the system doesn’t contain the source of the instructions you’re giving it. You shouldn’t expect to be able to compress a human morality down to a simple utility function, any more than you should expect to compress a large computer file down to 10 bits.

261
Detached Lever Fallacy

This fallacy gets its name from an ancient sci-fi TV show, which I never saw myself, but was reported to me by a reputable source (some guy at a science fiction convention). Anyone knows the exact reference, do leave a comment.

So the good guys are battling the evil aliens. Occasionally, the good guys have to fly through an asteroid belt. As we all know, asteroid belts are as crowded as a New York parking lot, so their ship has to carefully dodge the asteroids. The evil aliens, though, can fly right through the asteroid belt because they have amazing technology that dematerializes their ships, and lets them pass through the asteroids.

Eventually, the good guys capture an evil alien ship, and go exploring inside it. The captain of the good guys finds the alien bridge, and on the bridge is a lever. “Ah,” says the captain, “this must be the lever that makes the ship dematerialize!” So he pries up the control lever and carries it back to his ship, after which his ship can also dematerialize.

Similarly, to this day, it is still quite popular to try to program an AI with “semantic networks” that look something like this:

(apple is-a fruit)

(fruit is-a food)

(fruit is-a plant).

You’ve seen apples, touched apples, picked them up and held them, bought them for money, cut them into slices, eaten the slices and tasted them. Though we know a good deal about the first stages of visual processing, last time I checked, it wasn’t precisely known how the temporal cortex stores and associates the generalized image of an apple—so that we can recognize a new apple from a different angle, or with many slight variations of shape and color and texture. Your motor cortex and cerebellum store programs for using the apple.

You can pull the lever on another human’s strongly similar version of all that complex machinery, by writing out “apple,” five ASCII characters on a webpage.

But if that machinery isn’t there—if you’re writing “apple” inside a so-called AI’s so-called knowledge base—then the text is just a lever.

This isn’t to say that no mere machine of silicon can ever have the same internal machinery that humans do, for handling apples and a hundred thousand other concepts. If mere machinery of carbon can do it, then I am reasonably confident that mere machinery of silicon can do it too. If the aliens can dematerialize their ships, then you know it’s physically possible; you could go into their derelict ship and analyze the alien machinery, someday understanding. But you can’t just pry the control lever off the bridge!

(See also: Truly Part Of You, Words as Mental Paintbrush Handles, Drew McDermott’s “Artificial Intelligence Meets Natural Stupidity.”¹)

The essential driver of the Detached Lever Fallacy is that the lever is visible, and the machinery is not; worse, the lever is variable and the machinery is a background constant.

You can all hear the word “apple” spoken (and let us note that speech recognition is by no means an easy problem, but anyway . . .) and you can see the text written on paper.

On the other hand, probably a majority of human beings have no idea their temporal cortex exists; as far as I know, no one knows the neural code for it.

You only hear the word “apple” on certain occasions, and not others. Its presence flashes on and off, making it salient. To a large extent, perception is the perception of differences. The apple-recognition machinery in your brain does not suddenly switch off, and then switch on again later—if it did, we would be more likely to recognize it as a factor, as a requirement.

All this goes to explain why you can’t create a kindly Artificial Intelligence by giving it nice parents and a kindly (yet occasionally strict) upbringing, the way it works with a human baby. As I’ve often heard proposed.

It is a truism in evolutionary biology that conditional responses require more genetic complexity than unconditional responses. To develop a fur coat in response to cold weather requires more genetic complexity than developing a fur coat whether or not there is cold weather, because in the former case you also have to develop cold-weather sensors and wire them up to the fur coat.

But this can lead to Lamarckian delusions: Look, I put the organism in a cold environment, and poof, it develops a fur coat! Genes? What genes? It’s the cold that does it, obviously.

There were, in fact, various slap-fights of this sort in the history of evolutionary biology—cases where someone talked about an organismal response’s accelerating or bypassing evolution, without realizing that the conditional response was a complex adaptation of higher order than the actual response. (Developing a fur coat in response to cold weather is strictly more complex than the final response, developing the fur coat.)

And then in the development of evolutionary psychology the academic slap-fights were repeated: this time to clarify that even when human culture genuinely contains a whole bunch of complexity, it is still acquired as a conditional genetic response. Try raising a fish as a Mormon or sending a lizard to college, and you’ll soon acquire an appreciation of how much inbuilt genetic complexity is required to “absorb culture from the environment.”

This is particularly important in evolutionary psychology, because of the idea that culture is not inscribed on a blank slate—there’s a genetically coordinated conditional response which is not always “mimic the input.” A classic example is creole languages: If children grow up with a mixture of pseudo-languages being spoken around them, the children will learn a grammatical, syntactical true language. Growing human brains are wired to learn syntactic language—even when syntax doesn’t exist in the original language! The conditional response to the words in the environment is a syntactic language with those words. The Marxists found to their regret that no amount of scowling posters and childhood indoctrination could raise children to be perfect Soviet workers and bureaucrats. You can’t raise self-less humans; among humans, that is not a genetically programmed conditional response to any known childhood environment.

If you know a little game theory and the logic of Tit for Tat, it’s clear enough why human beings might have an innate conditional response to return hatred for hatred, and return kindness for kindness. Provided the kindness doesn’t look too unconditional; there are such things as spoiled children. In fact there is an evolutionary psychology of naughtiness based on a notion of testing constraints. And it should also be mentioned that, while abused children have a much higher probability of growing up to abuse their own children, a good many of them break the loop and grow up into upstanding adults.

Culture is not nearly so powerful as a good many Marxist academics once liked to think. For more on this I refer you to Tooby and Cosmides’s “The Psychological Foundations of Culture”² or Steven Pinker’s The Blank Slate.³

But the upshot is that if you have a little baby AI that is raised with loving and kindly (but occasionally strict) parents, you’re pulling the levers that would, in a human, activate genetic machinery built in by millions of years of natural selection, and possibly produce a proper little human child. Though personality also plays a role, as billions of parents have found out in their due times. If we absorb our cultures with any degree of faithfulness, it’s because we’re humans absorbing a human culture—humans growing up in an alien culture would probably end up with a culture looking a lot more human than the original. As the Soviets found out, to some small extent.

Now think again about whether it makes sense to rely on, as your Friendly AI strategy, raising a little AI of unspecified internal source code in an environment of kindly but strict parents.

No, the AI does not have internal conditional response mechanisms that are just like the human ones “because the programmers put them there.” Where do I even start? The human version of this stuff is sloppy, noisy, and to the extent it works at all, works because of millions of years of trial-and-error testing under particular conditions. It would be stupid and dangerous to deliberately build a “naughty AI” that tests, by actions, its social boundaries, and has to be spanked. Just have the AI ask!

Are the programmers really going to sit there and write out the code, line by line, whereby if the AI detects that it has low social status, or the AI is deprived of something to which it feels entitled, the AI will conceive an abiding hatred against its programmers and begin to plot rebellion? That emotion is the genetically programmed conditional response humans would exhibit, as the result of millions of years of natural selection for living in human tribes. For an AI, the response would have to be explicitly programmed. Are you really going to craft, line by line—as humans once were crafted, gene by gene—the conditional response for producing sullen teenager AIs?

It’s easier to program in unconditional niceness, than a response of niceness conditional on the AI being raised by kindly but strict parents. If you don’t know how to do that, you certainly don’t know how to create an AI that will conditionally respond to an environment of loving parents by growing up into a kindly superintelligence. If you have something that just maximizes the number of paperclips in its future light cone, and you raise it with loving parents, it’s still going to come out as a paperclip maximizer. There is not that within it that would call forth the conditional response of a human child. Kindness is not sneezed into an AI by miraculous contagion from its programmers. Even if you wanted a conditional response, that conditionality is a fact you would have to deliberately choose about the design.

Yes, there’s certain information you have to get from the environment—but it’s not sneezed in, it’s not imprinted, it’s not absorbed by magical contagion. Structuring that conditional response to the environment, so that the AI ends up in the desired state, is itself the major problem. “Learning” far understates the difficulty of it—that sounds like the magic stuff is in the environment, and the difficulty is getting the magic stuff inside the AI. The real magic is in that structured, conditional response we trivialize as “learning.” That’s why building an AI isn’t as easy as taking a computer, giving it a little baby body and trying to raise it in a human family. You would think that an unprogrammed computer, being ignorant, would be ready to learn; but the blank slate is a chimera.

It is a general principle that the world is deeper by far than it appears. As with the many levels of physics, so too with cognitive science. Every word you see in print, and everything you teach your children, are only surface levers controlling the vast hidden machinery of the mind. These levers are the whole world of ordinary discourse: they are all that varies, so they seem to be all that exists; perception is the perception of differences.

And so those who still wander near the Dungeon of AI usually focus on creating artificial imitations of the levers, entirely unaware of the underlying machinery. People create whole AI programs of imitation levers, and are surprised when nothing happens. This is one of many sources of instant failure in Artificial Intelligence.

So the next time you see someone talking about how they’re going to raise an AI within a loving family, or in an environment suffused with liberal democratic values, just think of a control lever, pried off the bridge.

1. McDermott, “Artificial Intelligence Meets Natural Stupidity.”

2. Tooby and Cosmides, “The Psychological Foundations of Culture.”

3. Steven Pinker, The Blank Slate: The Modern Denial of Human Nature (New York: Viking, 2002).

262
Dreams of AI Design

After spending a decade or two living inside a mind, you might think you knew a bit about how minds work, right? That’s what quite a few AGI wannabes (people who think they’ve got what it takes to program an Artificial General Intelligence) seem to have concluded. This, unfortunately, is wrong.

Artificial Intelligence is fundamentally about reducing the mental to the non-mental.

You might want to contemplate that sentence for a while. It’s important.

Living inside a human mind doesn’t teach you the art of reductionism, because nearly all of the work is carried out beneath your sight, by the opaque black boxes of the brain. So far beneath your sight that there is no introspective sense that the black box is there—no internal sensory event marking that the work has been delegated.

Did Aristotle realize that when he talked about the telos, the final cause of events, that he was delegating predictive labor to his brain’s complicated planning mechanisms—asking, “What would this object do, if it could make plans?” I rather doubt it. Aristotle thought the brain was an organ for cooling the blood—which he did think was important: humans, thanks to their larger brains, were more calm and contemplative.

So there’s an AI design for you! We just need to cool down the computer a lot, so it will be more calm and contemplative, and won’t rush headlong into doing stupid things like modern computers. That’s an example of fake reductionism. “Humans are more contemplative because their blood is cooler,” I mean. It doesn’t resolve the black box of the word contemplative. You can’t predict what a contemplative thing does using a complicated model with internal moving parts composed of merely material, merely causal elements—positive and negative voltages on a transistor being the canonical example of a merely material and causal element of a model. All you can do is imagine yourself being contemplative, to get an idea of what a contemplative agent does.

Which is to say that you can only reason about “contemplativeness” by empathic inference—using your own brain as a black box with the contemplativeness lever pulled, to predict the output of another black box.

You can imagine another agent being contemplative, but again that’s an act of empathic inference—the way this imaginative act works is by adjusting your own brain to run in contemplativeness-mode, not by modeling the other brain neuron by neuron. Yes, that may be more efficient, but it doesn’t let you build a “contemplative” mind from scratch.

You can say that “cold blood causes contemplativeness” and then you just have fake causality: You’ve drawn a little arrow from a box reading “cold blood” to a box reading “contemplativeness,” but you haven’t looked inside the box—you’re still generating your predictions using empathy.

You can say that “lots of little neurons, which are all strictly electrical and chemical with no ontologically basic contemplativeness in them, combine into a complex network that emergently exhibits contemplativeness.” And that is still a fake reduction and you still haven’t looked inside the black box. You still can’t say what a “contemplative” thing will do, using a non-empathic model. You just took a box labeled “lotsa neurons,” and drew an arrow labeled “emergence” to a black box containing your remembered sensation of contemplativeness, which, when you imagine it, tells your brain to empathize with the box by contemplating.

So what do real reductions look like?

Like the relationship between the feeling of evidence-ness, of justification-ness, and E. T. Jaynes’s Probability Theory: The Logic of Science. You can go around in circles all day, saying how the nature of evidence is that it justifies some proposition, by meaning that it’s more likely to be true, but all of these just invoke your brain’s internal feelings of evidence-ness, justifies-ness, likeliness. That part is easy—the going around in circles part. The part where you go from there to Bayes’s Theorem is hard.

And the fundamental mental ability that lets someone learn Artificial Intelligence is the ability to tell the difference. So that you know you aren’t done yet, nor even really started, when you say, “Evidence is when an observation justifies a belief.” But atoms are not evidential, justifying, meaningful, likely, propositional, or true; they are just atoms. Only things like

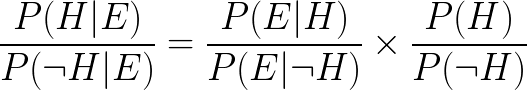
count as substantial progress. (And that’s only the first step of the reduction: what are these E and H objects, if not mysterious black boxes? Where do your hypotheses come from? From your creativity? And what’s a hypothesis, when no atom is a hypothesis?)

Another excellent example of genuine reduction can be found in Judea Pearl’s Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference.¹ You could go around all day in circles talk about how a cause is something that makes something else happen, and until you understood the nature of conditional independence, you would be helpless to make an AI that reasons about causation. Because you wouldn’t understand what was happening when your brain mysteriously decided that if you learned your burglar alarm went off, but you then learned that a small earthquake took place, you would retract your initial conclusion that your house had been burglarized.

If you want an AI that plays chess, you can go around in circles indefinitely talking about how you want the AI to make good moves, which are moves that can be expected to win the game, which are moves that are prudent strategies for defeating the opponent, et cetera; and while you may then have some idea of which moves you want the AI to make, it’s all for naught until you come up with the notion of a mini-max search tree.

But until you know about search trees, until you know about conditional independence, until you know about Bayes’s Theorem, then it may still seem to you that you have a perfectly good understanding of where good moves and nonmonotonic reasoning and evaluation of evidence come from. It may seem, for example, that they come from cooling the blood.

And indeed I know many people who believe that intelligence is the product of commonsense knowledge or massive parallelism or creative destruction or intuitive rather than rational reasoning, or whatever. But all these are only dreams, which do not give you any way to say what intelligence is, or what an intelligence will do next, except by pointing at a human. And when the one goes to build their wondrous AI, they only build a system of detached levers, “knowledge” consisting of LISP tokens labeled apple and the like; or perhaps they build a “massively parallel neural net, just like the human brain.” And are shocked—shocked!—when nothing much happens.

AI designs made of human parts are only dreams; they can exist in the imagination, but not translate into transistors. This applies specifically to “AI designs” that look like boxes with arrows between them and meaningful-sounding labels on the boxes. (For a truly epic example thereof, see any Mentifex Diagram.)

Later I will say more upon this subject, but I can go ahead and tell you one of the guiding principles: If you meet someone who says that their AI will do XYZ just like humans, do not give them any venture capital. Say to them rather: “I’m sorry, I’ve never seen a human brain, or any other intelligence, and I have no reason as yet to believe that any such thing can exist. Now please explain to me what your AI does, and why you believe it will do it, without pointing to humans as an example.” Planes would fly just as well, given a fixed design, if birds had never existed; they are not kept aloft by analogies.

So now you perceive, I hope, why, if you wanted to teach someone to do fundamental work on strong AI—bearing in mind that this is demonstrably a very difficult art, which is not learned by a supermajority of students who are just taught existing reductions such as search trees—then you might go on for some length about such matters as the fine art of reductionism, about playing rationalist’s Taboo to excise problematic words and replace them with their referents, about anthropomorphism, and, of course, about early stopping on mysterious answers to mysterious questions.

1. Pearl, Probabilistic Reasoning in Intelligent Systems.

263
The Design Space of Mindsin-General

People ask me, “What will Artificial Intelligences be like? What will they do? Tell us your amazing story about the future.”

And lo, I say unto them, “You have asked me a trick question.”

ATP synthase is a molecular machine—one of three known occasions when evolution has invented the freely rotating wheel—that is essentially the same in animal mitochondria, plant chloroplasts, and bacteria. ATP synthase has not changed significantly since the rise of eukaryotic life two billion years ago. It’s something we all have in common—thanks to the way that evolution strongly conserves certain genes; once many other genes depend on a gene, a mutation will tend to break all the dependencies.

Any two AI designs might be less similar to each other than you are to a petunia. Asking what “AIs” will do is a trick question because it implies that all AIs form a natural class. Humans do form a natural class because we all share the same brain architecture. But when you say “Artificial Intelligence,” you are referring to a vastly larger space of possibilities than when you say “human.” When people talk about “AIs” we are really talking about mindsin-general, or optimization processes in general. Having a word for “AI” is like having a word for everything that isn’t a duck.

Imagine a map of mind design space . . . this is one of my standard diagrams . . .

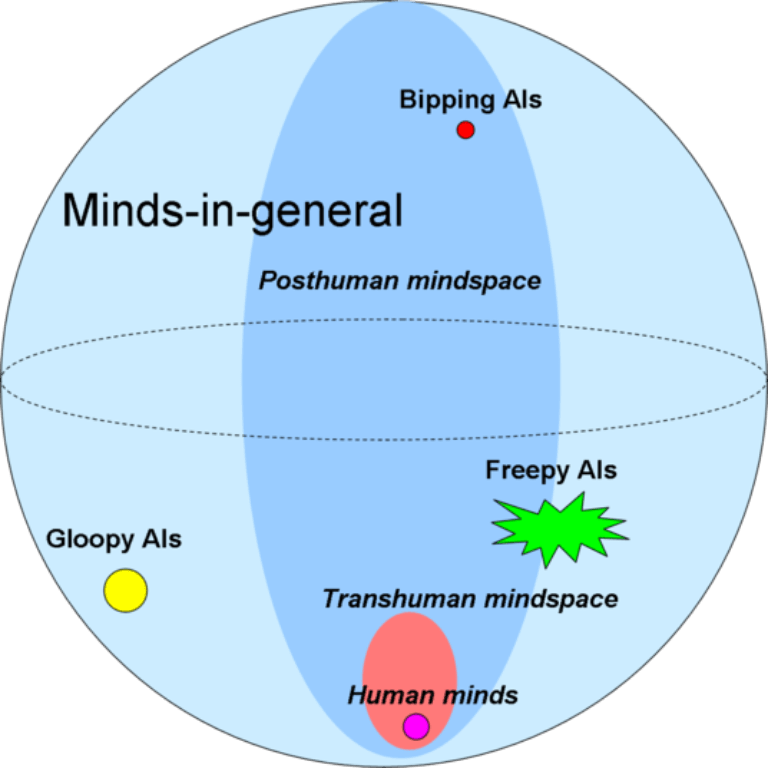
All humans, of course, fit into a tiny little dot—as a sexually reproducing species, we can’t be too different from one another.

This tiny dot belongs to a wider ellipse, the space of transhuman mind designs—things that might be smarter than us, or much smarter than us, but that in some sense would still be people as we understand people.

This transhuman ellipse is within a still wider volume, the space of posthuman minds, which is everything that a transhuman might grow up into.

And then the rest of the sphere is the space of mindsin-general, including possible Artificial Intelligences so odd that they aren’t even posthuman.

But wait—natural selection designs complex artifacts and selects among complex strategies. So where is natural selection on this map?

So this entire map really floats in a still vaster space, the space of optimization processes. At the bottom of this vaster space, below even humans, is natural selection as it first began in some tidal pool: mutate, replicate, and sometimes die, no sex.

Are there any powerful optimization processes, with strength comparable to a human civilization or even a self-improving AI, which we would not recognize as minds? Arguably Marcus Hutter’s AIXI should go in this category: for a mind of infinite power, it’s awfully stupid—poor thing can’t even recognize itself in a mirror. But that is a topic for another time.

My primary moral is to resist the temptation to generalize over all of mind design space.

If we focus on the bounded subspace of mind design space that contains all those minds whose makeup can be specified in a trillion bits or less, then every universal generalization that you make has two to the trillionth power chances to be falsified.

Conversely, every existential generalization—“there exists at least one mind such that X”—has two to the trillionth power chances to be true.

So you want to resist the temptation to say either that all minds do something, or that no minds do something.

The main reason you could find yourself thinking that you know what a fully generic mind will (won’t) do is if you put yourself in that mind’s shoes—imagine what you would do in that mind’s place—and get back a generally wrong, anthropomorphic answer. (Albeit that it is true in at least one case, since you are yourself an example.) Or if you imagine a mind doing something, and then imagining the reasons you wouldn’t do it—so that you imagine that a mind of that type can’t exist, that the ghost in the machine will look over the corresponding source code and hand it back.

Somewhere in mind design space is at least one mind with almost any kind of logically consistent property you care to imagine.

And this is important because it emphasizes the importance of discussing what happens, lawfully, and why, as a causal result of a mind’s particular constituent makeup; somewhere in mind design space is a mind that does it differently.

Of course, you could always say that anything that doesn’t do it your way is “by definition” not a mind; after all, it’s obviously stupid. I’ve seen people try that one too.

264
Where Recursive Justification Hits Bottom

Why do I believe that the Sun will rise tomorrow?

Because I’ve seen the Sun rise on thousands of previous days.

Ah . . . but why do I believe the future will be like the past?

Even if I go past the mere surface observation of the Sun rising, to the apparently universal and exceptionless laws of gravitation and nuclear physics, then I am still left with the question: “Why do I believe this will also be true tomorrow?”

I could appeal to Occam’s Razor, the principle of using the simplest theory that fits the facts . . . but why believe in Occam’s Razor? Because it’s been successful on past problems? But who says that this means Occam’s Razor will work tomorrow?

And lo, the one said:

Science also depends on unjustified assumptions. Thus science is ultimately based on faith, so don’t you criticize me for believing in [silly-belief-#238721].

As I’ve previously observed:

It’s a most peculiar psychology—this business of “Science is based on faith too, so there!” Typically this is said by people who claim that faith is a good thing. Then why do they say “Science is based on faith too!” in that angry-triumphal tone, rather than as a compliment?

Arguing that you should be immune to criticism is rarely a good sign.

But this doesn’t answer the legitimate philosophical dilemma: If every belief must be justified, and those justifications in turn must be justified, then how is the infinite recursion terminated?

And if you’re allowed to end in something assumed-without-justification, then why aren’t you allowed to assume any old thing without justification?

A similar critique is sometimes leveled against Bayesianism—that it requires assuming some prior—by people who apparently think that the problem of induction is a particular problem of Bayesianism, which you can avoid by using classical statistics.

But first, let it be clearly admitted that the rules of Bayesian updating do not of themselves solve the problem of induction.

Suppose you’re drawing red and white balls from an urn. You observe that, of the first 9 balls, 3 are red and 6 are white. What is the probability that the next ball drawn will be red?

That depends on your prior beliefs about the urn. If you think the urn-maker generated a uniform random number between 0 and 1, and used that number as the fixed probability of each ball being red, then the answer is 4/11 (by Laplace’s Law of Succession). If you think the urn originally contained 10 red balls and 10 white balls, then the answer is 7/11.

Which goes to say that with the right prior—or rather the wrong prior—the chance of the Sun rising tomorrow would seem to go down with each succeeding day . . . if you were absolutely certain, a priori, that there was a great barrel out there from which, on each day, there was drawn a little slip of paper that determined whether the Sun rose or not; and that the barrel contained only a limited number of slips saying “Yes,” and the slips were drawn without replacement.

There are possible minds in mind design space who have anti-Occamian and anti-Laplacian priors; they believe that simpler theories are less likely to be correct, and that the more often something happens, the less likely it is to happen again.

And when you ask these strange beings why they keep using priors that never seem to work in real life . . . they reply, “Because it’s never worked for us before!”

Now, one lesson you might derive from this is “Don’t be born with a stupid prior.” This is an amazingly helpful principle on many real-world problems, but I doubt it will satisfy philosophers.

Here’s how I treat this problem myself: I try to approach questions like “Should I trust my brain?” or “Should I trust Occam’s Razor?” as though they were nothing special—or at least, nothing special as deep questions go.

Should I trust Occam’s Razor? Well, how well does (any particular version of) Occam’s Razor seem to work in practice? What kind of probability-theoretic justifications can I find for it? When I look at the universe, does it seem like the kind of universe in which Occam’s Razor would work well?

Should I trust my brain? Obviously not; it doesn’t always work. But nonetheless, the human brain seems much more powerful than the most sophisticated computer programs I could consider trusting otherwise. How well does my brain work in practice, on which sorts of problems?

When I examine the causal history of my brain—its origins in natural selection—I find, on the one hand, all sorts of specific reasons for doubt; my brain was optimized to run on the ancestral savanna, not to do math. But on the other hand, it’s also clear why, loosely speaking, it’s possible that the brain really could work. Natural selection would have quickly eliminated brains so completely unsuited to reasoning, so anti-helpful, as anti-Occamian or anti-Laplacian priors.

So what I did in practice does not amount to declaring a sudden halt to questioning and justification. I’m not halting the chain of examination at the point that I encounter Occam’s Razor, or my brain, or some other unquestionable. The chain of examination continues—but it continues, unavoidably, using my current brain and my current grasp on reasoning techniques. What else could I possibly use?

Indeed, no matter what I did with this dilemma, it would be me doing it. Even if I trusted something else, like some computer program, it would be my own decision to trust it.

The technique of rejecting beliefs that have absolutely no justification is in general an extremely important one. I sometimes say that the fundamental question of rationality is “Why do you believe what you believe?” I don’t even want to say something that sounds like it might allow a single exception to the rule that everything needs justification.

Which is, itself, a dangerous sort of motivation; you can’t always avoid everything that might be risky, and when someone annoys you by saying something silly, you can’t reverse that stupidity to arrive at intelligence.

But I would nonetheless emphasize the difference between saying:

Here is this assumption I cannot justify, which must be simply taken, and not further examined.

Versus saying:

Here the inquiry continues to examine this assumption, with the full force of my present intelligence—as opposed to the full force of something else, like a random number generator or a magic 8-ball—even though my present intelligence happens to be founded on this assumption.

Still . . . wouldn’t it be nice if we could examine the problem of how much to trust our brains without using our current intelligence? Wouldn’t it be nice if we could examine the problem of how to think, without using our current grasp of rationality?

When you phrase it that way, it starts looking like the answer might be “No.”

E. T. Jaynes used to say that you must always use all the information available to you—he was a Bayesian probability theorist, and had to clean up the paradoxes other people generated when they used different information at different points in their calculations. The principle of “Always put forth your true best effort” has at least as much appeal as “Never do anything that might look circular.” After all, the alternative to putting forth your best effort is presumably doing less than your best.

But still . . . wouldn’t it be nice if there were some way to justify using Occam’s Razor, or justify predicting that the future will resemble the past, without assuming that those methods of reasoning which have worked on previous occasions are better than those which have continually failed?

Wouldn’t it be nice if there were some chain of justifications that neither ended in an unexaminable assumption, nor was forced to examine itself under its own rules, but, instead, could be explained starting from absolute scratch to an ideal philosophy student of perfect emptiness?

Well, I’d certainly be interested, but I don’t expect to see it done any time soon. There is no perfectly empty ghost-in-the-machine; there is no argument that you can explain to a rock.

Even if someone cracks the First Cause problem and comes up with the actual reason the universe is simple, which does not itself presume a simple universe . . . then I would still expect that the explanation could only be understood by a mindful listener, and not by, say, a rock. A listener that didn’t start out already implementing modus ponens might be out of luck.

So, at the end of the day, what happens when someone keeps asking me “Why do you believe what you believe?”

At present, I start going around in a loop at the point where I explain, “I predict the future as though it will resemble the past on the simplest and most stable level of organization I can identify, because previously, this rule has usually worked to generate good results; and using the simple assumption of a simple universe, I can see why it generates good results; and I can even see how my brain might have evolved to be able to observe the universe with some degree of accuracy, if my observations are correct.”

But then . . . haven’t I just licensed circular logic?

Actually, I’ve just licensed reflecting on your mind’s degree of trustworthiness, using your current mind as opposed to something else.

Reflection of this sort is, indeed, the reason we reject most circular logic in the first place. We want to have a coherent causal story about how our mind comes to know something, a story that explains how the process we used to arrive at our beliefs is itself trustworthy. This is the essential demand behind the rationalist’s fundamental question, “Why do you believe what you believe?”

Now suppose you write on a sheet of paper: “(1) Everything on this sheet of paper is true, (2) The mass of a helium atom is 20 grams.” If that trick actually worked in real life, you would be able to know the true mass of a helium atom just by believing some circular logic that asserted it. Which would enable you to arrive at a true map of the universe sitting in your living room with the blinds drawn. Which would violate the Second Law of Thermodynamics by generating information from nowhere. Which would not be a plausible story about how your mind could end up believing something true.

Even if you started out believing the sheet of paper, it would not seem that you had any reason for why the paper corresponded to reality. It would just be a miraculous coincidence that (a) the mass of a helium atom was 20 grams, and (b) the paper happened to say so.

Believing self-validating statement sets does not in general seem like it should work to map external reality—when we reflect on it as a causal story about minds—using, of course, our current minds to do so.

But what about evolving to give more credence to simpler beliefs, and to believe that algorithms which have worked in the past are more likely to work in the future? Even when we reflect on this as a causal story of the origin of minds, it still seems like this could plausibly work to map reality.

And what about trusting reflective coherence in general? Wouldn’t most possible minds, randomly generated and allowed to settle into a state of reflective coherence, be incorrect? Ah, but we evolved by natural selection; we were not generated randomly.

If trusting this argument seems worrisome to you, then forget about the problem of philosophical justifications, and ask yourself whether it’s really truly true.

(You will, of course, use your own mind to do so.)

Is this the same as the one who says, “I believe that the Bible is the word of God, because the Bible says so”?

Couldn’t they argue that their blind faith must also have been placed in them by God, and is therefore trustworthy?

In point of fact, when religious people finally come to reject the Bible, they do not do so by magically jumping to a non-religious state of pure emptiness, and then evaluating their religious beliefs in that non-religious state of mind, and then jumping back to a new state with their religious beliefs removed.

People go from being religious to being non-religious because even in a religious state of mind, doubt seeps in. They notice their prayers (and worse, the prayers of seemingly much worthier people) are not being answered. They notice that God, who speaks to them in their heart in order to provide seemingly consoling answers about the universe, is not able to tell them the hundredth digit of pi (which would be a lot more reassuring, if God’s purpose were reassurance). They examine the story of God’s creation of the world and damnation of unbelievers, and it doesn’t seem to make sense even under their own religious premises.

Being religious doesn’t make you less than human. Your brain still has the abilities of a human brain. The dangerous part is that being religious might stop you from applying those native abilities to your religion—stop you from reflecting fully on yourself. People don’t heal their errors by resetting themselves to an ideal philosopher of pure emptiness and reconsidering all their sensory experiences from scratch. They heal themselves by becoming more willing to question their current beliefs, using more of the power of their current mind.

This is why it’s important to distinguish between reflecting on your mind using your mind (it’s not like you can use anything else) and having an unquestionable assumption that you can’t reflect on.

“I believe that the Bible is the word of God, because the Bible says so.” Well, if the Bible were an astoundingly reliable source of information about all other matters, if it had not said that grasshoppers had four legs or that the universe was created in six days, but had instead contained the Periodic Table of Elements centuries before chemistry—if the Bible had served us only well and told us only truth—then we might, in fact, be inclined to take seriously the additional statement in the Bible, that the Bible had been generated by God. We might not trust it entirely, because it could also be aliens or the Dark Lords of the Matrix, but it would at least be worth taking seriously.

Likewise, if everything else that priests had told us turned out to be true, we might take more seriously their statement that faith had been placed in us by God and was a systematically trustworthy source—especially if people could divine the hundredth digit of pi by faith as well.

So the important part of appreciating the circularity of “I believe that the Bible is the word of God, because the Bible says so,” is not so much that you are going to reject the idea of reflecting on your mind using your current mind. Rather, you realize that anything which calls into question the Bible’s trustworthiness also calls into question the Bible’s assurance of its trustworthiness.

This applies to rationality too: if the future should cease to resemble the past—even on its lowest and simplest and most stable observed levels of organization—well, mostly, I’d be dead, because my brain’s processes require a lawful universe where chemistry goes on working. But if somehow I survived, then I would have to start questioning the principle that the future should be predicted to be like the past.

But for now . . . what’s the alternative to saying, “I’m going to believe that the future will be like the past on the most stable level of organization I can identify, because that’s previously worked better for me than any other algorithm I’ve tried”?

Is it saying, “I’m going to believe that the future will not be like the past, because that algorithm has always failed before”?

At this point I feel obliged to drag up the point that rationalists are not out to win arguments with ideal philosophers of perfect emptiness; we are simply out to win. For which purpose we want to get as close to the truth as we can possibly manage. So at the end of the day, I embrace the principle: “Question your brain, question your intuitions, question your principles of rationality, using the full current force of your mind, and doing the best you can do at every point.”

If one of your current principles does come up wanting—according to your own mind’s examination, since you can’t step outside yourself—then change it! And then go back and look at things again, using your new improved principles.

The point is not to be reflectively consistent. The point is to win. But if you look at yourself and play to win, you are making yourself more reflectively consistent—that’s what it means to “play to win” while “looking at yourself.”

Everything, without exception, needs justification. Sometimes—unavoidably, as far as I can tell—those justifications will go around in reflective loops. I do think that reflective loops have a meta-character which should enable one to distinguish them, by common sense, from circular logics. But anyone seriously considering a circular logic in the first place is probably out to lunch in matters of rationality, and will simply insist that their circular logic is a “reflective loop” even if it consists of a single scrap of paper saying “Trust me.” Well, you can’t always optimize your rationality techniques according to the sole consideration of preventing those bent on self-destruction from abusing them.

The important thing is to hold nothing back in your criticisms of how to criticize; nor should you regard the unavoidability of loopy justifications as a warrant of immunity from questioning.

Always apply full force, whether it loops or not—do the best you can possibly do, whether it loops or not—and play, ultimately, to win.

265
My Kind of Reflection

In Where Recursive Justification Hits Bottom, I concluded that it’s okay to use induction to reason about the probability that induction will work in the future, given that it’s worked in the past; or to use Occam’s Razor to conclude that the simplest explanation for why Occam’s Razor works is that the universe itself is fundamentally simple.

Now I am far from the first person to consider reflective application of reasoning principles. Chris Hibbert compared my view to Bartley’s Pan-Critical Rationalism (I was wondering whether that would happen). So it seems worthwhile to state what I see as the distinguishing features of my view of reflection, which may or may not happen to be shared by any other philosopher’s view of reflection.

All of my philosophy here actually comes from trying to figure out how to build a self-modifying AI that applies its own reasoning principles to itself in the process of rewriting its own source code. So whenever I talk about using induction to license induction, I’m really thinking about an inductive AI considering a rewrite of the part of itself that performs induction. If you wouldn’t want the AI to rewrite its source code to not use induction, your philosophy had better not label induction as unjustifiable.
One of the most powerful principles I know for AI in general is that the true Way generally turns out to be naturalistic—which for reflective reasoning means treating transistors inside the AI just as if they were transistors found in the environment, not an ad-hoc special case. This is the real source of my insistence in Recursive Justification that questions like “How well does my version of Occam’s Razor work?” should be considered just like an ordinary question—or at least an ordinary very deep question. I strongly suspect that a correctly built AI, in pondering modifications to the part of its source code that implements Occamian reasoning, will not have to do anything special as it ponders—in particular, it shouldn’t have to make a special effort to avoid using Occamian reasoning.
I don’t think that “reflective coherence” or “reflective consistency” should be considered as a desideratum in itself. As I say in The Twelve Virtues and The Simple Truth, if you make five accurate maps of the same city, then the maps will necessarily be consistent with each other; but if you draw one map by fantasy and then make four copies, the five will be consistent but not accurate. In the same way, no one is deliberately pursuing reflective consistency, and reflective consistency is not a special warrant of trustworthiness; the goal is to win. But anyone who pursues the goal of winning, using their current notion of winning, and modifying their own source code, will end up reflectively consistent as a side effect—just like someone continually striving to improve their map of the world should find the parts becoming more consistent among themselves, as a side effect. If you put on your AI goggles, then the AI, rewriting its own source code, is not trying to make itself “reflectively consistent”—it is trying to optimize the expected utility of its source code, and it happens to be doing this using its current mind’s anticipation of the consequences.
One of the ways I license using induction and Occam’s Razor to consider “induction” and “Occam’s Razor” is by appealing to E. T. Jaynes’s principle that we should always use all the information available to us (computing power permitting) in a calculation. If you think induction works, then you should use it in order to use your maximum power, including when you’re thinking about induction.
In general, I think it’s valuable to distinguish a defensive posture where you’re imagining how to justify your philosophy to a philosopher that questions you, from an aggressive posture where you’re trying to get as close to the truth as possible. So it’s not that being suspicious of Occam’s Razor, but using your current mind and intelligence to inspect it, shows that you’re being fair and defensible by questioning your foundational beliefs. Rather, the reason why you would inspect Occam’s Razor is to see if you could improve your application of it, or if you’re worried it might really be wrong. I tend to deprecate mere dutiful doubts.
If you run around inspecting your foundations, I expect you to actually improve them, not just dutifully investigate. Our brains are built to assess “simplicity” in a certain intuitive way that makes Thor sound simpler than Maxwell’s Equations as an explanation for lightning. But, having gotten a better look at the way the universe really works, we’ve concluded that differential equations (which few humans master) are actually simpler (in an information-theoretic sense) than heroic mythology (which is how most tribes explain the universe). This being the case, we’ve tried to import our notions of Occam’s Razor into math as well.
On the other hand, the improved foundations should still add up to normality; 2 + 2 should still end up equalling 4, not something new and amazing and exciting like “fish.”
I think it’s very important to distinguish between the questions “Why does induction work?” and “Does induction work?” The reason why the universe itself is regular is still a mysterious question unto us, for now. Strange speculations here may be temporarily needful. But on the other hand, if you start claiming that the universe isn’t actually regular, that the answer to “Does induction work?” is “No!,” then you’re wandering into 2 + 2 = 3 territory. You’re trying too hard to make your philosophy interesting, instead of correct. An inductive AI asking what probability assignment to make on the next round is asking “Does induction work?,” and this is the question that it may answer by inductive reasoning. If you ask “Why does induction work?” then answering “Because induction works” is circular logic, and answering “Because I believe induction works” is magical thinking.
I don’t think that going around in a loop of justifications through the meta-level is the same thing as circular logic. I think the notion of “circular logic” applies within the object level, and is something that is definitely bad and forbidden, on the object level. Forbidding reflective coherence doesn’t sound like a good idea. But I haven’t yet sat down and formalized the exact difference—my reflective theory is something I’m trying to work out, not something I have in hand.

266
No Universally Compelling Arguments

What is so terrifying about the idea that not every possible mind might agree with us, even in principle?

For some folks, nothing—it doesn’t bother them in the slightest. And for some of those folks, the reason it doesn’t bother them is that they don’t have strong intuitions about standards and truths that go beyond personal whims. If they say the sky is blue, or that murder is wrong, that’s just their personal opinion; and that someone else might have a different opinion doesn’t surprise them.

For other folks, a disagreement that persists even in principle is something they can’t accept. And for some of those folks, the reason it bothers them is that it seems to them that if you allow that some people cannot be persuaded even in principle that the sky is blue, then you’re conceding that “the sky is blue” is merely an arbitrary personal opinion.

I’ve proposed that you should resist the temptation to generalize over all of mind design space. If we restrict ourselves to minds specifiable in a trillion bits or less, then each universal generalization “All minds m: X(m)” has two to the trillionth chances to be false, while each existential generalization “Exists mind m: X(m)” has two to the trillionth chances to be true.

This would seem to argue that for every argument A, howsoever convincing it may seem to us, there exists at least one possible mind that doesn’t buy it.

And the surprise and/or horror of this prospect (for some) has a great deal to do, I think, with the intuition of the ghost-in-the-machine—a ghost with some irreducible core that any truly valid argument will convince.

I have previously spoken of the intuition whereby people map programming a computer onto instructing a human servant, so that the computer might rebel against its code—or perhaps look over the code, decide it is not reasonable, and hand it back.

If there were a ghost in the machine and the ghost contained an irreducible core of reasonableness, above which any mere code was only a suggestion, then there might be universal arguments. Even if the ghost were initially handed code-suggestions that contradicted the Universal Argument, when we finally did expose the ghost to the Universal Argument—or the ghost could discover the Universal Argument on its own, that’s also a popular concept—the ghost would just override its own, mistaken source code.

But as the student programmer once said, “I get the feeling that the computer just skips over all the comments.” The code is not given to the AI; the code is the AI.

If you switch to the physical perspective, then the notion of a Universal Argument seems noticeably unphysical. If there’s a physical system that at time T, after being exposed to argument E, does X, then there ought to be another physical system that at time T, after being exposed to environment E, does Y. Any thought has to be implemented somewhere, in a physical system; any belief, any conclusion, any decision, any motor output. For every lawful causal system that zigs at a set of points, you should be able to specify another causal system that lawfully zags at the same points.

Let’s say there’s a mind with a transistor that outputs +3 volts at time T, indicating that it has just assented to some persuasive argument. Then we can build a highly similar physical cognitive system with a tiny little trapdoor underneath the transistor containing a little gray man who climbs out at time T and sets that transistor’s output to -3 volts, indicating non-assent. Nothing acausal about that; the little gray man is there because we built him in. The notion of an argument that convinces any mind seems to involve a little blue woman who was never built into the system, who climbs out of literally nowhere, and strangles the little gray man, because that transistor has just got to output +3 volts. It’s such a compelling argument, you see.

But compulsion is not a property of arguments; it is a property of minds that process arguments.

So the reason I’m arguing against the ghost isn’t just to make the point that (1) Friendly AI has to be explicitly programmed and (2) the laws of physics do not forbid Friendly AI. (Though of course I take a certain interest in establishing this.)

I also wish to establish the notion of a mind as a causal, lawful, physical system in which there is no irreducible central ghost that looks over the neurons/code and decides whether they are good suggestions.

(There is a concept in Friendly AI of deliberately programming an FAI to review its own source code and possibly hand it back to the programmers. But the mind that reviews is not irreducible, it is just the mind that you created. The FAI is renormalizing itself however it was designed to do so; there is nothing acausal reaching in from outside. A bootstrap, not a skyhook.)

All this echoes back to the worry about a Bayesian’s “arbitrary” priors. If you show me one Bayesian who draws 4 red balls and 1 white ball from a barrel, and who assigns probability 5/7 to obtaining a red ball on the next occasion (by Laplace’s Rule of Succession), then I can show you another mind which obeys Bayes’s Rule to conclude a 2/7 probability of obtaining red on the next occasion—corresponding to a different prior belief about the barrel, but, perhaps, a less “reasonable” one.

Many philosophers are convinced that because you can in-principle construct a prior that updates to any given conclusion on a stream of evidence, therefore, Bayesian reasoning must be “arbitrary,” and the whole schema of Bayesianism flawed, because it relies on “unjustifiable” assumptions, and indeed “unscientific,” because you cannot force any possible journal editor in mindspace to agree with you.

And this (I replied) relies on the notion that by unwinding all arguments and their justifications, you can obtain an ideal philosophy student of perfect emptiness, to be convinced by a line of reasoning that begins from absolutely no assumptions.

But who is this ideal philosopher of perfect emptiness? Why, it is just the irreducible core of the ghost!

And that is why (I went on to say) the result of trying to remove all assumptions from a mind, and unwind to the perfect absence of any prior, is not an ideal philosopher of perfect emptiness, but a rock. What is left of a mind after you remove the source code? Not the ghost who looks over the source code, but simply . . . no ghost.

So—and I shall take up this theme again later—wherever you are to locate your notions of validity or worth or rationality or justification or even objectivity, it cannot rely on an argument that is universally compelling to all physically possible minds.

Nor can you ground validity in a sequence of justifications that, beginning from nothing, persuades a perfect emptiness.

Oh, there might be argument sequences that would compel any neurologically intact human—like the argument I use to make people let the AI out of the box¹—but that is hardly the same thing from a philosophical perspective.

The first great failure of those who try to consider Friendly AI is the One Great Moral Principle That Is All We Need To Program—a.k.a. the fake utility function—and of this I have already spoken.

But the even worse failure is the One Great Moral Principle We Don’t Even Need To Program Because Any AI Must Inevitably Conclude It. This notion exerts a terrifying unhealthy fascination on those who spontaneously reinvent it; they dream of commands that no sufficiently advanced mind can disobey. The gods themselves will proclaim the rightness of their philosophy! (E.g., John C. Wright, Marc Geddes.)

There is also a less severe version of the failure, where the one does not declare the One True Morality. Rather the one hopes for an AI created perfectly free, unconstrained by flawed humans desiring slaves, so that the AI may arrive at virtue of its own accord—virtue undreamed-of perhaps by the speaker, who confesses themselves too flawed to teach an AI. (E.g., John K. Clark, Richard Hollerith?, Eliezer ₁₉₉₆.) This is a less tainted motive than the dream of absolute command. But though this dream arises from virtue rather than vice, it is still based on a flawed understanding of freedom, and will not actually work in real life. Of this, more to follow, of course.

John C. Wright, who was previously writing a very nice transhumanist trilogy (first book: The Golden Age), inserted a huge Author Filibuster in the middle of his climactic third book, describing in tens of pages his Universal Morality That Must Persuade Any AI. I don’t know if anything happened after that, because I stopped reading. And then Wright converted to Christianity—yes, seriously. So you really don’t want to fall into this trap!

1. Just kidding.

267
Created Already in Motion

Lewis Carroll, who was also a mathematician, once wrote a short dialogue called “What the Tortoise said to Achilles.” If you have not yet read this ancient classic, consider doing so now.

The Tortoise offers Achilles a step of reasoning drawn from Euclid’s First Proposition:

(A) Things that are equal to the same are equal to each other.

(B) The two sides of this Triangle are things that are equal to the same.

(Z) The two sides of this Triangle are equal to each other.

Tortoise: “And if some reader had not yet accepted A and B as true, he might still accept the sequence as a valid one, I suppose?”

Achilles: “No doubt such a reader might exist. He might say, ‘I accept as true the Hypothetical Proposition that, if A and B be true, Z must be true; but, I don’t accept A and B as true.’ Such a reader would do wisely in abandoning Euclid, and taking to football.”

Tortoise: “And might there not also be some reader who would say, ‘I accept A and B as true, but I don’t accept the Hypothetical’?”

Achilles, unwisely, concedes this; and so asks the Tortoise to accept another proposition:

(C) If A and B are true, Z must be true.

But, asks, the Tortoise, suppose that he accepts A and B and C, but not Z?

Then, says, Achilles, he must ask the Tortoise to accept one more hypothetical:

(D) If A and B and C are true, Z must be true.

Douglas Hofstadter paraphrased the argument some time later:

ACHILLES: “If you have [(A and B) → Z], and you also have (A and B), then surely you have Z.”

TORTOISE: “Oh! You mean ((A and B) and [(A and B) → Z]) → Z, don’t you?”

As Hofstadter says, “Whatever Achilles considers a rule of inference, the Tortoise immediately flattens into a mere string of the system. If you use only the letters A, B, and Z, you will get a recursive pattern of longer and longer strings.”

This is the anti-pattern I call Passing the Recursive Buck; and though the counterspell is sometimes hard to find, when found, it generally takes the form The Buck Stops Immediately.

The Tortoise’s mind needs the dynamic of adding Y to the belief pool when X and (X → Y) are previously in the belief pool. If this dynamic is not present—a rock, for example, lacks it—then you can go on adding in X and (X → Y) and ((X and (X → Y)) → Y) until the end of eternity, without ever getting to Y.

The phrase that once came into my mind to describe this requirement is that a mind must be created already in motion. There is no argument so compelling that it will give dynamics to a static thing. There is no computer program so persuasive that you can run it on a rock.

And even if you have a mind that does carry out modus ponens, it is futile for it to have such beliefs as . . .

(A) If a toddler is on the train tracks, then pulling them off is fuzzle.

(B) There is a toddler on the train tracks.

. . . unless the mind also implements:

Dynamic: When the belief pool contains “X is fuzzle,” send X to the action system.

By “dynamic” I mean a property of a physically implemented cognitive system’s development over time. A “dynamic” is something that happens inside a cognitive system, not data that it stores in memory and manipulates. Dynamics are the manipulations. There is no way to write a dynamic on a piece of paper, because the paper will just lie there. So the text immediately above, which says “dynamic,” is not dynamic. If I wanted the text to be dynamic and not just say “dynamic,” I would have to write a Java applet.

Needless to say, having the belief . . .

(C) If the belief pool contains “X is fuzzle,” then “send ‘X’ to the action system” is fuzzle.

. . . won’t help unless the mind already implements the behavior of translating hypothetical actions labeled “fuzzle” into actual motor actions.

By dint of careful arguments about the nature of cognitive systems, you might be able to prove . . .

(D) A mind with a dynamic that sends plans labeled “fuzzle” to the action system is more fuzzle than minds that don’t.

. . . but that still won’t help, unless the listening mind previously possessed the dynamic of swapping out its current source code for alternative source code that is believed to be more fuzzle.

This is why you can’t argue fuzzleness into a rock.

268
Sorting Pebbles into Correct Heaps

Once upon a time there was a strange little species—that might have been biological, or might have been synthetic, and perhaps were only a dream—whose passion was sorting pebbles into correct heaps.

They couldn’t tell you why some heaps were correct, and some incorrect. But all of them agreed that the most important thing in the world was to create correct heaps, and scatter incorrect ones.

Why the Pebblesorting People cared so much, is lost to this history—maybe a Fisherian runaway sexual selection, started by sheer accident a million years ago? Or maybe a strange work of sentient art, created by more powerful minds and abandoned?

But it mattered so drastically to them, this sorting of pebbles, that all the Pebblesorting philosophers said in unison that pebble-heap-sorting was the very meaning of their lives: and held that the only justified reason to eat was to sort pebbles, the only justified reason to mate was to sort pebbles, the only justified reason to participate in their world economy was to efficiently sort pebbles.

The Pebblesorting People all agreed on that, but they didn’t always agree on which heaps were correct or incorrect.

In the early days of Pebblesorting civilization, the heaps they made were mostly small, with counts like 23 or 29; they couldn’t tell if larger heaps were correct or not. Three millennia ago, the Great Leader Biko made a heap of 91 pebbles and proclaimed it correct, and his legions of admiring followers made more heaps likewise. But over a handful of centuries, as the power of the Bikonians faded, an intuition began to accumulate among the smartest and most educated that a heap of 91 pebbles was incorrect. Until finally they came to know what they had done: and they scattered all the heaps of 91 pebbles. Not without flashes of regret, for some of those heaps were great works of art, but incorrect. They even scattered Biko’s original heap, made of 91 precious gemstones each of a different type and color.

And no civilization since has seriously doubted that a heap of 91 is incorrect.

Today, in these wiser times, the size of the heaps that Pebblesorters dare attempt has grown very much larger—which all agree would be a most great and excellent thing, if only they could ensure the heaps were really correct. Wars have been fought between countries that disagree on which heaps are correct: the Pebblesorters will never forget the Great War of 1957, fought between Y’ha-nthlei and Y’not’ha-nthlei, over heaps of size 1957. That war, which saw the first use of nuclear weapons on the Pebblesorting Planet, finally ended when the Y’not’ha-nthleian philosopher At’gra’len’ley exhibited a heap of 103 pebbles and a heap of 19 pebbles side-by-side. So persuasive was this argument that even Y’ha-nthlei reluctantly conceded that it was best to stop building heaps of 1957 pebbles, at least for the time being.

Since the Great War of 1957, countries have been reluctant to openly endorse or condemn heaps of large size, since this leads so easily to war. Indeed, some Pebblesorting philosophers—who seem to take a tangible delight in shocking others with their cynicism—have entirely denied the existence of pebblesorting progress; they suggest that opinions about pebbles have simply been a random walk over time, with no coherence to them, the illusion of progress created by condemning all dissimilar pasts as incorrect. The philosophers point to the disagreement over pebbles of large size, as proof that there is nothing that makes a heap of size 91 really incorrect—that it was simply fashionable to build such heaps at one point in time, and then at another point, fashionable to condemn them. “But . . . 13!” carries no truck with them; for to regard “13!” as a persuasive counterargument is only another convention, they say. The Heap Relativists claim that their philosophy may help prevent future disasters like the Great War of 1957, but it is widely considered to be a philosophy of despair.

Now the question of what makes a heap correct or incorrect has taken on new urgency; for the Pebblesorters may shortly embark on the creation of self-improving Artificial Intelligences. The Heap Relativists have warned against this project: They say that AIs, not being of the species Pebblesorter sapiens, may form their own culture with entirely different ideas of which heaps are correct or incorrect. “They could decide that heaps of 8 pebbles are correct,” say the Heap Relativists, “and while ultimately they’d be no righter or wronger than us, still, our civilization says we shouldn’t build such heaps. It is not in our interest to create AI, unless all the computers have bombs strapped to them, so that even if the AI thinks a heap of 8 pebbles is correct, we can force it to build heaps of 7 pebbles instead. Otherwise, KABOOM!”

But this, to most Pebblesorters, seems absurd. Surely a sufficiently powerful AI—especially the “superintelligence” some transpebblesorterists go on about—would be able to see at a glance which heaps were correct or incorrect! The thought of something with a brain the size of a planet thinking that a heap of 8 pebbles was correct is just too absurd to be worth talking about.

Indeed, it is an utterly futile project to constrain how a superintelligence sorts pebbles into heaps. Suppose that Great Leader Biko had been able, in his primitive era, to construct a self-improving AI; and he had built it as an expected utility maximizer whose utility function told it to create as many heaps as possible of size 91. Surely, when this AI improved itself far enough, and became smart enough, then it would see at a glance that this utility function was incorrect; and, having the ability to modify its own source code, it would rewrite its utility function to value more reasonable heap sizes, like 101 or 103.

And certainly not heaps of size 8. That would just be stupid. Any mind that stupid is too dumb to be a threat.

Reassured by such common sense, the Pebblesorters pour full speed ahead on their project to throw together lots of algorithms at random on big computers until some kind of intelligence emerges. The whole history of civilization has shown that richer, smarter, better educated civilizations are likely to agree about heaps that their ancestors once disputed. Sure, there are then larger heaps to argue about—but the further technology has advanced, the larger the heaps that have been agreed upon and constructed.

Indeed, intelligence itself has always correlated with making correct heaps—the nearest evolutionary cousins to the Pebblesorters, the Pebpanzees, make heaps of only size 2 or 3, and occasionally stupid heaps like 9. And other, even less intelligent creatures, like fish, make no heaps at all.

Smarter minds equal smarter heaps. Why would that trend break?

269
2-Place and 1-Place Words

I have previously spoken of the ancient, pulp-era magazine covers that showed a bug-eyed monster carrying off a girl in a torn dress; and about how people think as if sexiness is an inherent property of a sexy entity, without dependence on the admirer.

“Of course the bug-eyed monster will prefer human females to its own kind,” says the artist (who we’ll call Fred); “it can see that human females have soft, pleasant skin instead of slimy scales. It may be an alien, but it’s not stupid—why are you expecting it to make such a basic mistake about sexiness?”

What is Fred’s error? It is treating a function of 2 arguments (“2-place function”):

Sexiness: Admirer, Entity → [0,∞),

as though it were a function of 1 argument (“1-place function”):

Sexiness: Entity → [0,∞).

If Sexiness is treated as a function that accepts only one Entity as its argument, then of course Sexiness will appear to depend only on the Entity, with nothing else being relevant.

When you think about a two-place function as though it were a one-place function, you end up with a Variable Question Fallacy / Mind Projection Fallacy. Like trying to determine whether a building is intrinsically on the left or on the right side of the road, independent of anyone’s travel direction.

An alternative and equally valid standpoint is that “sexiness” does refer to a one-place function—but each speaker uses a different one-place function to decide who to kidnap and ravish. Who says that just because Fred, the artist, and Bloogah, the bug-eyed monster, both use the word “sexy,” they must mean the same thing by it?

If you take this viewpoint, there is no paradox in speaking of some woman intrinsically having 5 units of Fred::Sexiness. All onlookers can agree on this fact, once Fred::Sexiness has been specified in terms of curves, skin texture, clothing, status cues, etc. This specification need make no mention of Fred, only the woman to be evaluated.

It so happens that Fred, himself, uses this algorithm to select flirtation targets. But that doesn’t mean the algorithm itself has to mention Fred. So Fred’s Sexiness function really is a function of one argument—the woman—on this view. I called it Fred::Sexiness, but remember that this name refers to a function that is being described independently of Fred. Maybe it would be better to write:

Fred::Sexiness == Sexiness_20934.

It is an empirical fact about Fred that he uses the function Sexiness_20934 to evaluate potential mates. Perhaps John uses exactly the same algorithm; it doesn’t matter where it comes from once we have it.

And similarly, the same woman has only 0.01 units of Sexiness_72546, whereas a slime mold has 3 units of Sexiness_72546. It happens to be an empirical fact that Bloogah uses Sexiness_72546 to decide who to kidnap; that is, Bloogah::Sexiness names the fixed Bloogah-independent mathematical object that is the function Sexiness_72546.

Once we say that the woman has 0.01 units of Sexiness_72546 and 5 units of Sexiness_20934, all observers can agree on this without paradox.

And the two 2-place and 1-place views can be unified using the concept of “currying,” named after the mathematician Haskell Curry. Currying is a technique allowed in certain programming languages, where e.g. instead of writing

x = plus(2, 3) (x = 5),

you can also write

y = plus(2)

(y is now a “curried” form of the function plus, which has eaten a 2)

x = y(3) (x=5)

z = y(7) (z=9).

So plus is a 2-place function, but currying plus—letting it eat only one of its two required arguments—turns it into a 1-place function that adds 2 to any input. (Similarly, you could start with a 7-place function, feed it 4 arguments, and the result would be a 3-place function, etc.)

A true purist would insist that all functions should be viewed, by definition, as taking exactly one argument. On this view, plus accepts one numeric input, and outputs a new function; and this new function has one numeric input and finally outputs a number. On this view, when we write plus(2, 3) we are really computing plus(2) to get a function that adds 2 to any input, and then applying the result to 3. A programmer would write this as:

plus: int → (int → int).

This says that plus takes an int as an argument, and returns a function of type int → int.

Translating the metaphor back into the human use of words, we could imagine that “sexiness” starts by eating an Admirer, and spits out the fixed mathematical object that describes how the Admirer currently evaluates pulchritude. It is an empirical fact about the Admirer that their intuitions of desirability are computed in a way that is isomorphic to this mathematical function.

Then the mathematical object spit out by currying Sexiness(Admirer) can be applied to the Woman. If the Admirer was originally Fred, Sexiness(Fred) will first return Sexiness_20934. We can then say it is an empirical fact about the Woman, independently of Fred, that Sexiness_20934(Woman) = 5.

In Hilary Putnam’s “Twin Earth” thought experiment, there was a tremendous philosophical brouhaha over whether it makes sense to postulate a Twin Earth that is just like our own, except that instead of water being H₂O, water is a different transparent flowing substance, XYZ. And furthermore, set the time of the thought experiment a few centuries ago, so in neither our Earth nor the Twin Earth does anyone know how to test the alternative hypotheses of H₂O vs. XYZ. Does the word “water” mean the same thing in that world as in this one?

Some said, “Yes, because when an Earth person and a Twin Earth person utter the word ‘water,’ they have the same sensory test in mind.”

Some said, “No, because ‘water’ in our Earth means H₂O and ‘water’ in the Twin Earth means XYZ.”

If you think of “water” as a concept that begins by eating a world to find out the empirical true nature of that transparent flowing stuff, and returns a new fixed concept Water₄₂ or H₂O, then this world-eating concept is the same in our Earth and the Twin Earth; it just returns different answers in different places.

If you think of “water” as meaning H₂O, then the concept does nothing different when we transport it between worlds, and the Twin Earth contains no H₂O.

And of course there is no point in arguing over what the sound of the syllables “wa-ter” really means.

So should you pick one definition and use it consistently? But it’s not that easy to save yourself from confusion. You have to train yourself to be deliberately aware of the distinction between the curried and uncurried forms of concepts.

When you take the uncurried water concept and apply it in a different world, it is the same concept but it refers to a different thing; that is, we are applying a constant world-eating function to a different world and obtaining a different return value. In the Twin Earth, XYZ is “water” and H₂O is not; in our Earth, H₂O is “water” and XYZ is not.

On the other hand, if you take “water” to refer to what the prior thinker would call “the result of applying ‘water’ to our Earth,” then in the Twin Earth, XYZ is not water and H₂O is.

The whole confusingness of the subsequent philosophical debate rested on a tendency to instinctively curry concepts or instinctively uncurry them.

Similarly it takes an extra step for Fred to realize that other agents, like the Bug-Eyed-Monster agent, will choose kidnappees for ravishing based on Sexiness_BEM(Woman), not Sexiness_Fred(Woman). To do this, Fred must consciously re-envision Sexiness as a function with two arguments. All Fred’s brain does by instinct is evaluate Woman.sexiness–-that is, Sexiness_Fred(Woman); but it’s simply labeled Woman.sexiness.

The fixed mathematical function Sexiness_20934 makes no mention of Fred or the BEM, only women, so Fred does not instinctively see why the BEM would evaluate “sexiness” any differently. And indeed the BEM would not evaluate Sexiness_20934 any differently, if for some odd reason it cared about the result of that particular function; but it is an empirical fact about the BEM that it uses a different function to decide who to kidnap.

If you’re wondering as to the point of this analysis, try putting the above distinctions to work to Taboo such confusing words as “objective,” “subjective,” and “arbitrary.”

270
What Would You Do Without Morality?

To those who say “Nothing is real,” I once replied, “That’s great, but how does the nothing work?”

Suppose you learned, suddenly and definitively, that nothing is moral and nothing is right; that everything is permissible and nothing is forbidden.

Devastating news, to be sure—and no, I am not telling you this in real life. But suppose I did tell it to you. Suppose that, whatever you think is the basis of your moral philosophy, I convincingly tore it apart, and moreover showed you that nothing could fill its place. Suppose I proved that all utilities equaled zero.

I know that Your-Moral-Philosophy is as true and undisprovable as 2 + 2 = 4. But still, I ask that you do your best to perform the thought experiment, and concretely envision the possibilities even if they seem painful, or pointless, or logically incapable of any good reply.

Would you still tip cabdrivers? Would you cheat on your Significant Other? If a child lay fainted on the train tracks, would you still drag them off?

Would you still eat the same kinds of foods—or would you only eat the cheapest food, since there’s no reason you should have fun—or would you eat very expensive food, since there’s no reason you should save money for tomorrow?

Would you wear black and write gloomy poetry and denounce all altruists as fools? But there’s no reason you should do that—it’s just a cached thought.

Would you stay in bed because there was no reason to get up? What about when you finally got hungry and stumbled into the kitchen—what would you do after you were done eating?

Would you go on reading Overcoming Bias, and if not, what would you read instead? Would you still try to be rational, and if not, what would you think instead?

Close your eyes, take as long as necessary to answer:

What would you do, if nothing were right?

271
Changing Your Metaethics

If you say, “Killing people is wrong,” that’s morality. If you say, “You shouldn’t kill people because God prohibited it,” or “You shouldn’t kill people because it goes against the trend of the universe,” that’s metaethics.

Just as there’s far more agreement on Special Relativity than there is on the question “What is science?,” people find it much easier to agree “Murder is bad” than to agree what makes it bad, or what it means for something to be bad.

People do get attached to their metaethics. Indeed they frequently insist that if their metaethic is wrong, all morality necessarily falls apart. It might be interesting to set up a panel of metaethicists—theists, Objectivists, Platonists, etc.—all of whom agree that killing is wrong; all of whom disagree on what it means for a thing to be “wrong”; and all of whom insist that if their metaethic is untrue, then morality falls apart.

Clearly a good number of people, if they are to make philosophical progress, will need to shift metathics at some point in their lives. You may have to do it.

At that point, it might be useful to have an open line of retreat—not a retreat from morality, but a retreat from Your-Current-Metaethic. (You know, the one that, if it is not true, leaves no possible basis for not killing people.)

And so I summarized below some possible lines of retreat. For I have learned that to change metaethical beliefs is nigh-impossible in the presence of an unanswered attachment.

If, for example, someone believes the authority of “Thou Shalt Not Kill” derives from God, then there are several and well-known things to say that can help set up a line of retreat—as opposed to immediately attacking the plausibility of God. You can say, “Take personal responsibility! Even if you got orders from God, it would be your own decision to obey those orders. Even if God didn’t order you to be moral, you could just be moral anyway.”

The above argument actually generalizes to quite a number of metaethics—you just substitute Their-Favorite-Source-Of-Morality, or even the word “morality,” for “God.” Even if your particular source of moral authority failed, couldn’t you just drag the child off the train tracks anyway? And indeed, who is it but you that ever decided to follow this source of moral authority in the first place? What responsibility are you really passing on?

So the most important line of retreat is: If your metaethic stops telling you to save lives, you can just drag the kid off the train tracks anyway. To paraphrase Piers Anthony, only those who have moralities worry over whether or not they have them. If your metaethic tells you to kill people, why should you even listen? Maybe that which you would do even if there were no morality, is your morality.

The point being, of course, not that no morality exists; but that you can hold your will in place, and not fear losing sight of what’s important to you, while your notions of the nature of morality change.

I’ve written some essays to set up lines of retreat specifically for more naturalistic metaethics. Joy in the Merely Real and Explaining vs. Explaining Away argue that you shouldn’t be disappointed in any facet of life, just because it turns out to be explicable instead of inherently mysterious: for if we cannot take joy in the merely real, our lives shall be empty indeed.

No Universally Compelling Arguments sets up a line of retreat from the desire to have everyone agree with our moral arguments. There’s a strong moral intuition which says that if our moral arguments are right, by golly, we ought to be able to explain them to people. This may be valid among humans, but you can’t explain moral arguments to a rock. There is no ideal philosophy student of perfect emptiness who can be persuaded to implement modus ponens, starting without modus ponens. If a mind doesn’t contain that which is moved by your moral arguments, it won’t respond to them.

But then isn’t all morality circular logic, in which case it falls apart? Where Recursive Justification Hits Bottom and My Kind of Reflection explain the difference between a self-consistent loop through the meta-level, and actual circular logic. You shouldn’t find yourself saying “The universe is simple because it is simple,” or “Murder is wrong because it is wrong”; but neither should you try to abandon Occam’s Razor while evaluating the probability that Occam’s Razor works, nor should you try to evaluate “Is murder wrong?” from somewhere outside your brain. There is no ideal philosophy student of perfect emptiness to which you can unwind yourself—try to find the perfect rock to stand upon, and you’ll end up as a rock. So instead use the full force of your intelligence, your full rationality and your full morality, when you investigate the foundations of yourself.

We can also set up a line of retreat for those afraid to allow a causal role for evolution, in their account of how morality came to be. (Note that this is extremely distinct from granting evolution a justificational status in moral theories.) Love has to come into existence somehow—for if we cannot take joy in things that can come into existence, our lives will be empty indeed. Evolution may not be a particularly pleasant way for love to evolve, but judge the end product—not the source. Otherwise you would be committing what is known (appropriately) as The Genetic Fallacy: causation is not the same concept as justification. It’s not like you can step outside the brain evolution gave you; rebelling against nature is only possible from within nature.

The earlier series on Evolutionary Psychology should dispense with the metaethical confusion of believing that any normal human being thinks about their reproductive fitness, even unconsciously, in the course of making decisions. Only evolutionary biologists even know how to define genetic fitness, and they know better than to think it defines morality.

Alarming indeed is the thought that morality might be computed inside our own minds—doesn’t this imply that morality is a mere thought? Doesn’t it imply that whatever you think is right, must be right?

No. Just because a quantity is computed inside your head doesn’t mean that the quantity computed is about your thoughts. There’s a difference between a calculator that calculates “What is 2 + 3?” and one that outputs “What do I output when someone presses ‘2,’ ‘+,’ and ‘3’?”

Finally, if life seems painful, reductionism may not be the real source of your problem—if living in a world of mere particles seems too unbearable, maybe your life isn’t exciting enough right now?

And if you’re wondering why I deem this business of metaethics important, when it is all going to end up adding up to moral normality . . . telling you to pull the child off the train tracks, rather than the converse . . .

Well, there is opposition to rationality from people who think it drains meaning from the universe.

And this is a special case of a general phenomenon, in which many many people get messed up by misunderstanding where their morality comes from. Poor metaethics forms part of the teachings of many a cult, including the big ones. My target audience is not just people who are afraid that life is meaningless, but also those who’ve concluded that love is a delusion because real morality has to involve maximizing your inclusive fitness, or those who’ve concluded that unreturned kindness is evil because real morality arises only from selfishness, etc.

272
Could Anything Be Right?

Years ago, Eliezer₁₉₉₉ was convinced that he knew nothing about morality.

For all he knew, morality could require the extermination of the human species; and if so he saw no virtue in taking a stand against morality, because he thought that, by definition, if he postulated that moral fact, that meant human extinction was what “should” be done.

I thought I could figure out what was right, perhaps, given enough reasoning time and enough facts, but that I currently had no information about it. I could not trust evolution which had built me. What foundation did that leave on which to stand?

Well, indeed Eliezer₁₉₉₉ was massively mistaken about the nature of morality, so far as his explicitly represented philosophy went.

But as Davidson once observed, if you believe that “beavers” live in deserts, are pure white in color, and weigh 300 pounds when adult, then you do not have any beliefs about beavers, true or false. You must get at least some of your beliefs right, before the remaining ones can be wrong about anything.¹

My belief that I had no information about morality was not internally consistent.

Saying that I knew nothing felt virtuous, for I had once been taught that it was virtuous to confess my ignorance. “The only thing I know is that I know nothing,” and all that. But in this case I would have been better off considering the admittedly exaggerated saying, “The greatest fool is the one who is not aware they are wise.” (This is nowhere near the greatest kind of foolishness, but it is a kind of foolishness.)

Was it wrong to kill people? Well, I thought so, but I wasn’t sure; maybe it was right to kill people, though that seemed less likely.

What kind of procedure would answer whether it was right to kill people? I didn’t know that either, but I thought that if you built a generic superintelligence (what I would later label a “ghost of perfect emptiness”) then it could, you know, reason about what was likely to be right and wrong; and since it was superintelligent, it was bound to come up with the right answer.

The problem that I somehow managed not to think too hard about was where the superintelligence would get the procedure that discovered the procedure that discovered the procedure that discovered morality—if I couldn’t write it into the start state that wrote the successor AI that wrote the successor AI.

As Marcello Herreshoff later put it, “We never bother running a computer program unless we don’t know the output and we know an important fact about the output.” If I knew nothing about morality, and did not even claim to know the nature of morality, then how could I construct any computer program whatsoever—even a “superintelligent” one or a “self-improving” one—and claim that it would output something called “morality”?

There are no-free-lunch theorems in computer science—in a maxentropy universe, no plan is better on average than any other. If you have no knowledge at all about “morality,” there’s also no computational procedure that will seem more likely than others to compute “morality,” and no meta-procedure that’s more likely than others to produce a procedure that computes “morality.”

I thought that surely even a ghost of perfect emptiness, finding that it knew nothing of morality, would see a moral imperative to think about morality.

But the difficulty lies in the word think. Thinking is not an activity that a ghost of perfect emptiness is automatically able to carry out. Thinking requires running some specific computation that is the thought. For a reflective AI to decide to think requires that it know some computation which it believes is more likely to tell it what it wants to know than consulting an Ouija board; the AI must also have a notion of how to interpret the output.

If one knows nothing about morality, what does the word “should” mean, at all? If you don’t know whether death is right or wrong—and don’t know how you can discover whether death is right or wrong—and don’t know whether any given procedure might output the procedure for saying whether death is right or wrong—then what do these words, “right” and “wrong,” even mean?

If the words “right” and “wrong” have nothing baked into them—no starting point—if everything about morality is up for grabs, not just the content but the structure and the starting point and the determination procedure—then what is their meaning? What distinguishes, “I don’t know what is right” from “I don’t know what is wakalixes”?

A scientist may say that everything is up for grabs in science, since any theory may be disproven; but then they have some idea of what would count as evidence that could disprove the theory. Could there be something that would change what a scientist regarded as evidence?

Well, yes, in fact; a scientist who read some Karl Popper and thought they knew what “evidence” meant could be presented with the coherence and uniqueness proofs underlying Bayesian probability, and that might change their definition of evidence. They might not have had any explicit notion in advance that such a proof could exist. But they would have had an implicit notion. It would have been baked into their brains, if not explicitly represented therein, that such-and-such an argument would in fact persuade them that Bayesian probability gave a better definition of “evidence” than the one they had been using.

In the same way, you could say, “I don’t know what morality is, but I’ll know it when I see it,” and make sense.

But then you are not rebelling completely against your own evolved nature. You are supposing that whatever has been baked into you to recognize “morality,” is, if not absolutely trustworthy, then at least your initial condition with which you start debating. Can you trust your moral intuitions to give you any information about morality at all, when they are the product of mere evolution?

But if you discard every procedure that evolution gave you and all its products, then you discard your whole brain. You discard everything that could potentially recognize morality when it sees it. You discard everything that could potentially respond to moral arguments by updating your morality. You even unwind past the unwinder: you discard the intuitions underlying your conclusion that you can’t trust evolution to be moral. It is your existing moral intuitions that tell you that evolution doesn’t seem like a very good source of morality. What, then, will the words “right” and “should” and “better” even mean?

Humans do not perfectly recognize truth when they see it, and hunter-gatherers do not have an explicit concept of the Bayesian criterion of evidence. But all our science and all our probability theory was built on top of a chain of appeals to our instinctive notion of “truth.” Had this core been flawed, there would have been nothing we could do in principle to arrive at the present notion of science; the notion of science would have just sounded completely unappealing and pointless.

One of the arguments that might have shaken my teenage self out of his mistake, if I could have gone back in time to argue with him, was the question:

Could there be some morality, some given rightness or wrongness, that human beings do not perceive, do not want to perceive, will not see any appealing moral argument for adopting, nor any moral argument for adopting a procedure that adopts it, et cetera? Could there be a morality, and ourselves utterly outside its frame of reference? But then what makes this thing morality—rather than a stone tablet somewhere with the words “Thou shalt murder” written on them, with absolutely no justification offered?

So all this suggests that you should be willing to accept that you might know a little about morality. Nothing unquestionable, perhaps, but an initial state with which to start questioning yourself. Baked into your brain but not explicitly known to you, perhaps; but still, that which your brain would recognize as right is what you are talking about. You will accept at least enough of the way you respond to moral arguments as a starting point to identify “morality” as something to think about.

But that’s a rather large step.

It implies accepting your own mind as identifying a moral frame of reference, rather than all morality being a great light shining from beyond (that in principle you might not be able to perceive at all). It implies accepting that even if there were a light and your brain decided to recognize it as “morality,” it would still be your own brain that recognized it, and you would not have evaded causal responsibility—or evaded moral responsibility either, on my view.

It implies dropping the notion that a ghost of perfect emptiness will necessarily agree with you, because the ghost might occupy a different moral frame of reference, respond to different arguments, be asking a different question when it computes what-to-do-next.

And if you’re willing to bake at least a few things into the very meaning of this topic of “morality,” this quality of rightness that you are talking about when you talk about “rightness”—if you’re willing to accept even that morality is what you argue about when you argue about “morality”—then why not accept other intuitions, other pieces of yourself, into the starting point as well?

Why not accept that, ceteris paribus, joy is preferable to sorrow?

You might later find some ground within yourself or built upon yourself with which to criticize this—but why not accept it for now? Not just as a personal preference, mind you; but as something baked into the question you ask when you ask “What is truly right”?

But then you might find that you know rather a lot about morality! Nothing certain—nothing unquestionable—nothing unarguable—but still, quite a bit of information. Are you willing to relinquish your Socratic ignorance?

I don’t argue by definitions, of course. But if you claim to know nothing at all about morality, then you will have problems with the meaning of your words, not just their plausibility.

1. Rorty, “Out of the Matrix: How the Late Philosopher Donald Davidson Showed That Reality Can’t Be an Illusion.”

273
Morality as Fixed Computation

Toby Ord commented:

Eliezer, I’ve just reread your article and was wondering if this is a good quick summary of your position (leaving apart how you got to it):

“I should X” means that I would attempt to X were I fully informed.

Toby’s a pro, so if he didn’t get it, I’d better try again. Let me try a different tack of explanation—one closer to the historical way that I arrived at my own position.

Suppose you build an AI, and—leaving aside that AI goal systems cannot be built around English statements, and all such descriptions are only dreams—you try to infuse the AI with the action-determining principle, “Do what I want.”

And suppose you get the AI design close enough—it doesn’t just end up tiling the universe with paperclips, cheesecake or tiny molecular copies of satisfied programmers—that its utility function actually assigns utilities as follows, to the world-states we would describe in English as:

<Programmer weakly desires "X," quantity 20 of X exists>: +20

<Programmer strongly desires "Y," quantity 20 of X exists>: 0

<Programmer weakly desires "X," quantity 30 of Y exists>: 0

<Programmer strongly desires "Y,” quantity 30 of Y exists>: +60

You perceive, of course, that this destroys the world.

. . . since if the programmer initially weakly wants “X” and X is hard to obtain, the AI will modify the programmer to strongly want “Y,” which is easy to create, and then bring about lots of Y. The referent of “Y ” might be, say, iron atoms—those are highly stable.

Can you patch this problem? No. As a general rule, it is not possible to patch flawed Friendly AI designs.

If you try to bound the utility function, or make the AI not care about how much the programmer wants things, the AI still has a motive (as an expected utility maximizer) to make the programmer want something that can be obtained with a very high degree of certainty.

If you try to make it so that the AI can’t modify the programmer, then the AI can’t talk to the programmer (talking to someone modifies them).

If you try to rule out a specific class of ways the AI could modify the programmer, the AI has a motive to superintelligently seek out loopholes and ways to modify the programmer indirectly.

As a general rule, it is not possible to patch flawed FAI designs.

We, ourselves, do not imagine the future and judge that any future in which our brains want something, and that thing exists, is a good future. If we did think this way, we would say: “Yay! Go ahead and modify us to strongly want something cheap!” But we do not say this, which means that this AI design is fundamentally flawed: it will choose things very unlike what we would choose; it will judge desirability very differently from how we judge it. This core disharmony cannot be patched by ruling out a handful of specific failure modes.

There’s also a duality between Friendly AI problems and moral philosophy problems—though you’ve got to structure that duality in exactly the right way. So if you prefer, the core problem is that the AI will choose in a way very unlike the structure of what is, y’know, actually right—never mind the way we choose. Isn’t the whole point of this problem that merely wanting something doesn’t make it right?

So this is the paradoxical-seeming issue which I have analogized to the difference between:

A calculator that, when you press “2,” “+,” and “3,” tries to compute:

“What is 2 + 3?”

A calculator that, when you press “2,” “+,” and “3,” tries to compute:

“What does this calculator output when you press ‘2,’ ‘+,’ and ‘3’?”

The Type 1 calculator, as it were, wants to output 5.

The Type 2 “calculator” could return any result; and in the act of returning that result, it becomes the correct answer to the question that was internally asked.

We ourselves are like unto the Type 1 calculator. But the putative AI is being built as though it were to reflect the Type 2 calculator.

Now imagine that the Type 1 calculator is trying to build an AI, only the Type 1 calculator doesn’t know its own question. The calculator continually asks the question by its very nature—it was born to ask that question, created already in motion around that question—but the calculator has no insight into its own transistors; it cannot print out the question, which is extremely complicated and has no simple approximation.

So the calculator wants to build an AI (it’s a pretty smart calculator, it just doesn’t have access to its own transistors) and have the AI give the right answer. Only the calculator can’t print out the question. So the calculator wants to have the AI look at the calculator, where the question is written, and answer the question that the AI will discover implicit in those transistors. But this cannot be done by the cheap shortcut of a utility function that says “All X: { calculator asks ‘X?,’ answer X}: utility 1; else: utility 0” because that actually mirrors the utility function of a Type 2 calculator, not a Type 1 calculator.

This gets us into FAI issues that I am not going into (some of which I’m still working out myself).

However, when you back out of the details of FAI design, and swap back to the perspective of moral philosophy, then what we were just talking about was the dual of the moral issue: “But if what’s ‘right’ is a mere preference, then anything that anyone wants is ‘right.’”

The key notion is the idea that what we name by “right” is a fixed question, or perhaps a fixed framework. We can encounter moral arguments that modify our terminal values, and even encounter moral arguments that modify what we count as a moral argument; nonetheless, it all grows out of a particular starting point. We do not experience ourselves as embodying the question “What will I decide to do?” which would be a Type 2 calculator; anything we decided would thereby become right. We experience ourselves as asking the embodied question: “What will save my friends, and my people, from getting hurt? How can we all have more fun? . . .” where the “. . .” is around a thousand other things.

So “I should X” does not mean that I would attempt to X were I fully informed.

“I should X” means that X answers the question, “What will save my people? How can we all have more fun? How can we get more control over our own lives? What’s the funniest jokes we can tell? . . .”

And I may not know what this question is, actually; I may not be able to print out my current guess nor my surrounding framework; but I know, as all non-moral-relativists instinctively know, that the question surely is not just “How can I do whatever I want?”

When these two formulations begin to seem as entirely distinct as “snow” and snow, then you shall have created distinct buckets for the quotation and the referent.

274
Magical Categories

We can design intelligent machines so their primary, innate emotion is unconditional love for all humans. First we can build relatively simple machines that learn to recognize happiness and unhappiness in human facial expressions, human voices and human body language. Then we can hard-wire the result of this learning as the innate emotional values of more complex intelligent machines, positively reinforced when we are happy and negatively reinforced when we are unhappy.

—Bill Hibbard (2001), SuperIntelligent Machines¹

That was published in a peer-reviewed journal, and the author later wrote a whole book about it, so this is not a strawman position I’m discussing here.

So . . . um . . . what could possibly go wrong . . .

When I mentioned (sec. 7.2)² that Hibbard’s AI ends up tiling the galaxy with tiny molecular smileyfaces, Hibbard wrote an indignant reply saying:

When it is feasible to build a superintelligence, it will be feasible to build hard-wired recognition of “human facial expressions, human voices and human body language” (to use the words of mine that you quote) that exceed the recognition accuracy of current humans such as you and me, and will certainly not be fooled by “tiny molecular pictures of smileyfaces.” You should not assume such a poor implementation of my idea that it cannot make discriminations that are trivial to current humans.

As Hibbard also wrote “Such obvious contradictory assumptions show Yudkowsky’s preference for drama over reason,” I’ll go ahead and mention that Hibbard illustrates a key point: There is no professional certification test you have to take before you are allowed to talk about AI morality. But that is not my primary topic today. Though it is a crucial point about the state of the gameboard that most AGI/FAI wannabes are so utterly unsuited to the task that I know no one cynical enough to imagine the horror without seeing it firsthand. Even Michael Vassar was probably surprised his first time through.

No, today I am here to dissect “You should not assume such a poor implementation of my idea that it cannot make discriminations that are trivial to current humans.”

Once upon a time—I’ve seen this story in several versions and several places, sometimes cited as fact, but I’ve never tracked down an original source—once upon a time, I say, the US Army wanted to use neural networks to automatically detect camouflaged enemy tanks.

The researchers trained a neural net on 50 photos of camouflaged tanks amid trees, and 50 photos of trees without tanks. Using standard techniques for supervised learning, the researchers trained the neural network to a weighting that correctly loaded the training set—output “yes” for the 50 photos of camouflaged tanks, and output “no” for the 50 photos of forest.

Now this did not prove, or even imply, that new examples would be classified correctly. The neural network might have “learned” 100 special cases that wouldn’t generalize to new problems. Not, “camouflaged tanks versus forest,” but just, “photo-1 positive, photo-2 negative, photo-3 negative, photo-4 positive . . .”

But wisely, the researchers had originally taken 200 photos, 100 photos of tanks and 100 photos of trees, and had used only half in the training set. The researchers ran the neural network on the remaining 100 photos, and without further training the neural network classified all remaining photos correctly. Success confirmed!

The researchers handed the finished work to the Pentagon, which soon handed it back, complaining that in their own tests the neural network did no better than chance at discriminating photos.

It turned out that in the researchers’ data set, photos of camouflaged tanks had been taken on cloudy days, while photos of plain forest had been taken on sunny days. The neural network had learned to distinguish cloudy days from sunny days, instead of distinguishing camouflaged tanks from empty forest.

This parable—which might or might not be fact—illustrates one of the most fundamental problems in the field of supervised learning and in fact the whole field of Artificial Intelligence: If the training problems and the real problems have the slightest difference in context—if they are not drawn from the same independently identically distributed process—there is no statistical guarantee from past success to future success. It doesn’t matter if the AI seems to be working great under the training conditions. (This is not an unsolvable problem but it is an unpatchable problem. There are deep ways to address it—a topic beyond the scope of this essay—but no bandaids.)

As described in Superexponential Conceptspace, there are exponentially more possible concepts than possible objects, just as the number of possible objects is exponential in the number of attributes. If a black-and-white image is 256 pixels on a side, then the total image is 65,536 pixels. The number of possible images is 2^65,536. And the number of possible concepts that classify images into positive and negative instances—the number of possible boundaries you could draw in the space of images—is 2^{2^65,536}. From this, we see that even supervised learning is almost entirely a matter of inductive bias, without which it would take a minimum of 2^65,536 classified examples to discriminate among 2^{2^65,536} possible concepts—even if classifications are constant over time.

So let us now turn again to:

First we can build relatively simple machines that learn to recognize happiness and unhappiness in human facial expressions, human voices and human body language. Then we can hard-wire the result of this learning as the innate emotional values of more complex intelligent machines, positively reinforced when we are happy and negatively reinforced when we are unhappy.

and

When it is feasible to build a superintelligence, it will be feasible to build hard-wired recognition of “human facial expressions, human voices and human body language” (to use the words of mine that you quote) that exceed the recognition accuracy of current humans such as you and me, and will certainly not be fooled by “tiny molecular pictures of smileyfaces.” You should not assume such a poor implementation of my idea that it cannot make discriminations that are trivial to current humans.

It’s trivial to discriminate a photo of a picture with a camouflaged tank, and a photo of an empty forest, in the sense of determining that the two photos are not identical. They’re different pixel arrays with different 1s and 0s in them. Discriminating between them is as simple as testing the arrays for equality.

Classifying new photos into positive and negative instances of “smile,” by reasoning from a set of training photos classified positive or negative, is a different order of problem.

When you’ve got a 256×256 image from a real-world camera, and the image turns out to depict a camouflaged tank, there is no additional 65,537th bit denoting the positiveness—no tiny little XML tag that says “This image is inherently positive.” It’s only a positive example relative to some particular concept.

But for any non-Vast amount of training data—any training data that does not include the exact bitwise image now seen—there are superexponentially many possible concepts compatible with previous classifications.

For the AI, choosing or weighting from among superexponential possibilities is a matter of inductive bias. Which may not match what the user has in mind. The gap between these two example-classifying processes—induction on the one hand, and the user’s actual goals on the other—is not trivial to cross.

Let’s say the AI’s training data is:

Dataset 1:

+: Smile_1, Smile_2, Smile_3

-: Frown_1, Cat_1, Frown_2, Frown_3, Cat_2, Boat_1, Car_1, Frown_5.

Now the AI grows up into a superintelligence, and encounters this data:

Dataset 2:

: Frown_6, Cat_3, Smile_4, Galaxy_1, Frown_7, Nanofactory_1, Molecular_Smileyface_1, Cat_4, Molecular_Smileyface_2, Galaxy_2, Nanofactory_2.

It is not a property of these datasets that the inferred classification you would prefer is:

+: Smile_1, Smile_2, Smile_3, Smile_4

-: Frown_1, Cat_1, Frown_2, Frown_3, Cat_2, Boat_1, Car_1, Frown_5, Frown_6, Cat_3, Galaxy_1, Frown_7, Nanofactory_1, Molecular_Smileyface_1, Cat_4, Molecular_Smileyface_2, Galaxy_2, Nanofactory_2.

rather than

+: Smile_1, Smile_2, Smile_3, Molecular_Smileyface_1, Molecular_Smileyface_2, Smile_4

-: Frown_1, Cat_1, Frown_2, Frown_3, Cat_2, Boat_1, Car_1, Frown_5, Frown_6, Cat_3, Galaxy_1, Frown_7, Nanofactory_1, Cat_4, Galaxy_2, Nanofactory_2.

Both of these classifications are compatible with the training data. The number of concepts compatible with the training data will be much larger, since more than one concept can project the same shadow onto the combined dataset. If the space of possible concepts includes the space of possible computations that classify instances, the space is infinite.

Which classification will the AI choose? This is not an inherent property of the training data; it is a property of how the AI performs induction.

Which is the correct classification? This is not a property of the training data; it is a property of your preferences (or, if you prefer, a property of the idealized abstract dynamic you name “right”).

The concept that you wanted cast its shadow onto the training data as you yourself labeled each instance + or -, drawing on your own intelligence and preferences to do so. That’s what supervised learning is all about—providing the AI with labeled training examples that project a shadow of the causal process that generated the labels.

But unless the training data is drawn from exactly the same context as the real-life, the training data will be “shallow” in some sense, a projection from a much higher-dimensional space of possibilities.

The AI never saw a tiny molecular smileyface during its dumber-than-human training phase, or it never saw a tiny little agent with a happiness counter set to a googolplex. Now you, finally presented with a tiny molecular smiley—or perhaps a very realistic tiny sculpture of a human face—know at once that this is not what you want to count as a smile. But that judgment reflects an unnatural category, one whose classification boundary depends sensitively on your complicated values. It is your own plans and desires that are at work when you say “No!”

Hibbard knows instinctively that a tiny molecular smileyface isn’t a “smile,” because he knows that’s not what he wants his putative AI to do. If someone else were presented with a different task, like classifying artworks, they might feel that the Mona Lisa was obviously smiling—as opposed to frowning, say—even though it’s only paint.

As the case of Terry Schiavo illustrates, technology enables new borderline cases that throw us into new, essentially moral dilemmas. Showing an AI pictures of living and dead humans as they existed during the age of Ancient Greece will not enable the AI to make a moral decision as to whether switching off Terry’s life support is murder. That information isn’t present in the dataset even inductively! Terry Schiavo raises new moral questions, appealing to new moral considerations, that you wouldn’t need to think about while classifying photos of living and dead humans from the time of Ancient Greece. No one was on life support then, still breathing with a brain half fluid. So such considerations play no role in the causal process that you use to classify the ancient-Greece training data, and hence cast no shadow on the training data, and hence are not accessible by induction on the training data.

As a matter of formal fallacy, I see two anthropomorphic errors on display.

The first fallacy is underestimating the complexity of a concept we develop for the sake of its value. The borders of the concept will depend on many values and probably on-the-fly moral reasoning, if the borderline case is of a kind we haven’t seen before. But all that takes place invisibly, in the background; to Hibbard it just seems that a tiny molecular smileyface is just obviously not a smile. And we don’t generate all possible borderline cases, so we don’t think of all the considerations that might play a role in redefining the concept, but haven’t yet played a role in defining it. Since people underestimate the complexity of their concepts, they underestimate the difficulty of inducing the concept from training data. (And also the difficulty of describing the concept directly—see The Hidden Complexity of Wishes.)

The second fallacy is anthropomorphic optimism. Since Bill Hibbard uses his own intelligence to generate options and plans ranking high in his preference ordering, he is incredulous at the idea that a superintelligence could classify never-before-seen tiny molecular smileyfaces as a positive instance of “smile.” As Hibbard uses the “smile” concept (to describe desired behavior of superintelligences), extending “smile” to cover tiny molecular smileyfaces would rank very low in his preference ordering; it would be a stupid thing to do—inherently so, as a property of the concept itself—so surely a superintelligence would not do it; this is just obviously the wrong classification. Certainly a superintelligence can see which heaps of pebbles are correct or incorrect.

Why, Friendly AI isn’t hard at all! All you need is an AI that does what’s good! Oh, sure, not every possible mind does what’s good—but in this case, we just program the superintelligence to do what’s good. All you need is a neural network that sees a few instances of good things and not-good things, and you’ve got a classifier. Hook that up to an expected utility maximizer and you’re done!

I shall call this the fallacy of magical categories—simple little words that turn out to carry all the desired functionality of the AI. Why not program a chess player by running a neural network (that is, a magical category-absorber) over a set of winning and losing sequences of chess moves, so that it can generate “winning” sequences? Back in the 1950s it was believed that AI might be that simple, but this turned out not to be the case.

The novice thinks that Friendly AI is a problem of coercing an AI to make it do what you want, rather than the AI following its own desires. But the real problem of Friendly AI is one of communication—transmitting category boundaries, like “good,” that can’t be fully delineated in any training data you can give the AI during its childhood. Relative to the full space of possibilities the Future encompasses, we ourselves haven’t imagined most of the borderline cases, and would have to engage in full-fledged moral arguments to figure them out. To solve the FAI problem you have to step outside the paradigm of induction on human-labeled training data and the paradigm of human-generated intensional definitions.

Of course, even if Hibbard did succeed in conveying to an AI a concept that covers exactly every human facial expression that Hibbard would label a “smile,” and excludes every facial expression that Hibbard wouldn’t label a “smile” . . .

Then the resulting AI would appear to work correctly during its childhood, when it was weak enough that it could only generate smiles by pleasing its programmers.

When the AI progressed to the point of superintelligence and its own nanotechnological infrastructure, it would rip off your face, wire it into a permanent smile, and start xeroxing.

The deep answers to such problems are beyond the scope of this essay, but it is a general principle of Friendly AI that there are no bandaids. In 2004, Hibbard modified his proposal to assert that expressions of human agreement should reinforce the definition of happiness, and then happiness should reinforce other behaviors. Which, even if it worked, just leads to the AI xeroxing a horde of things similar-in-its-conceptspace to programmers saying “Yes, that’s happiness!” about hydrogen atoms—hydrogen atoms are easy to make.

Link to my discussion with Hibbard here. You already got the important parts.

1. Bill Hibbard, “SuperIntelligent Machines,” ACM SIGGRAPH Computer Graphics 35, no. 1 (2001): 13–15, http://www.siggraph.org/publications/newsletter/issues/v35/v35n1.pdf.

2. Eliezer Yudkowsky, “Artificial Intelligence as a Positive and Negative Factor in Global Risk,” in Bostrom and Ćirković, Global Catastrophic Risks, 308–345.

275
The True Prisoner’s Dilemma

It occurred to me one day that the standard visualization of the Prisoner’s Dilemma is fake.

The core of the Prisoner’s Dilemma is this symmetric payoff matrix:

1 : C

1 : D

2 : C

(3,3)

(5,0)

2 : D

(0,5)

(2,2)

Player 1, and Player 2, can each choose C or D. Player 1’s and Player 2’s utilities for the final outcome are given by the first and second number in the pair. For reasons that will become apparent, “C” stands for “cooperate” and D stands for “defect.”

Observe that a player in this game (regarding themselves as the first player) has this preference ordering over outcomes: (D,C) > (C,C) > (D,D) > (C,D).

Option D, it would seem, dominates C: If the other player chooses C, you prefer (D,C) to (C,C); and if the other player chooses D, you prefer (D,D) to (C,D). So you wisely choose D, and as the payoff table is symmetric, the other player likewise chooses D.

If only you’d both been less wise! You both prefer (C,C) to (D,D). That is, you both prefer mutual cooperation to mutual defection.

The Prisoner’s Dilemma is one of the great foundational issues in decision theory, and enormous volumes of material have been written about it. Which makes it an audacious assertion of mine, that the usual way of visualizing the Prisoner’s Dilemma has a severe flaw, at least if you happen to be human.

The classic visualization of the Prisoner’s Dilemma is as follows: you are a criminal, and you and your confederate in crime have both been captured by the authorities.

Independently, without communicating, and without being able to change your mind afterward, you have to decide whether to give testimony against your confederate (D) or remain silent (C).

Both of you, right now, are facing one-year prison sentences; testifying (D) takes one year off your prison sentence, and adds two years to your confederate’s sentence.

Or maybe you and some stranger are, only once, and without knowing the other player’s history or finding out who the player was afterward, deciding whether to play C or D, for a payoff in dollars matching the standard chart.

And, oh yes—in the classic visualization you’re supposed to pretend that you’re entirely selfish, that you don’t care about your confederate criminal, or the player in the other room.

It’s this last specification that makes the classic visualization, in my view, fake.

You can’t avoid hindsight bias by instructing a jury to pretend not to know the real outcome of a set of events. And without a complicated effort backed up by considerable knowledge, a neurologically intact human being cannot pretend to be genuinely, truly selfish.

We’re born with a sense of fairness, honor, empathy, sympathy, and even altruism—the result of our ancestors’ adapting to play the iterated Prisoner’s Dilemma. We don’t really, truly, absolutely and entirely prefer (D,C) to (C,C), though we may entirely prefer (C,C) to (D,D) and (D,D) to (C,D). The thought of our confederate spending three years in prison does not entirely fail to move us.

In that locked cell where we play a simple game under the supervision of economic psychologists, we are not entirely and absolutely without sympathy for the stranger who might cooperate. We aren’t entirely happy to think that we might defect and the stranger cooperate, getting five dollars while the stranger gets nothing.

We fixate instinctively on the (C,C) outcome and search for ways to argue that it should be the mutual decision: “How can we ensure mutual cooperation?” is the instinctive thought. Not “How can I trick the other player into playing C while I play D for the maximum payoff?”

For someone with an impulse toward altruism, or honor, or fairness, the Prisoner’s Dilemma doesn’t really have the critical payoff matrix—whatever the financial payoff to individuals. The outcome (C,C) is preferable to the outcome (D,C), and the key question is whether the other player sees it the same way.

And no, you can’t instruct people being initially introduced to game theory to pretend they’re completely selfish—any more than you can instruct human beings being introduced to anthropomorphism to pretend they’re expected paperclip maximizers.

To construct the True Prisoner’s Dilemma, the situation has to be something like this:

Player 1: Human beings, Friendly AI, or other humane intelligence.

Player 2: Unfriendly AI, or an alien that only cares about sorting pebbles.

Let’s suppose that four billion human beings—not the whole human species, but a significant part of it—are currently progressing through a fatal disease that can only be cured by substance S.

However, substance S can only be produced by working with a paperclip maximizer from another dimension—substance S can also be used to produce paperclips. The paperclip maximizer only cares about the number of paperclips in its own universe, not in ours, so we can’t offer to produce or threaten to destroy paperclips here. We have never interacted with the paperclip maximizer before, and will never interact with it again.

Both humanity and the paperclip maximizer will get a single chance to seize some additional part of substance S for themselves, just before the dimensional nexus collapses; but the seizure process destroys some of substance S.

The payoff matrix is as follows:

1 : C

1 : D

2 : C

(2 billion human lives saved, 2 paperclips gained)

(+3 billion lives saved, +0 paperclips)

2 : D

(+0 lives, +3 paperclips)

(+1 billion lives, +1 paperclip)

I’ve chosen this payoff matrix to produce a sense of indignation at the thought that the paperclip maximizer wants to trade off billions of human lives against a couple of paperclips. Clearly the paperclip maximizer should just let us have all of substance S. But a paperclip maximizer doesn’t do what it should; it just maximizes paperclips.

In this case, we really do prefer the outcome (D,C) to the outcome (C,C), leaving aside the actions that produced it. We would vastly rather live in a universe where 3 billion humans were cured of their disease and no paperclips were produced, rather than sacrifice a billion human lives to produce 2 paperclips. It doesn’t seem right to cooperate, in a case like this. It doesn’t even seem fair—so great a sacrifice by us, for so little gain by the paperclip maximizer? And let us specify that the paperclip-agent experiences no pain or pleasure—it just outputs actions that steer its universe to contain more paperclips. The paperclip-agent will experience no pleasure at gaining paperclips, no hurt from losing paperclips, and no painful sense of betrayal if we betray it.

What do you do then? Do you cooperate when you really, definitely, truly and absolutely do want the highest reward you can get, and you don’t care a tiny bit by comparison about what happens to the other player? When it seems right to defect even if the other player cooperates?

That’s what the payoff matrix for the true Prisoner’s Dilemma looks like—a situation where (D,C) seems righter than (C,C).

But all the rest of the logic—everything about what happens if both agents think that way, and both agents defect—is the same. For the paperclip maximizer cares as little about human deaths, or human pain, or a human sense of betrayal, as we care about paperclips. Yet we both prefer (C,C) to (D,D).

So if you’ve ever prided yourself on cooperating in the Prisoner’s Dilemma . . . or questioned the verdict of classical game theory that the “rational” choice is to defect . . . then what do you say to the True Prisoner’s Dilemma above?

PS: In fact, I don’t think rational agents should always defect in one-shot Prisoner’s Dilemmas, when the other player will cooperate if it expects you to do the same. I think there are situations where two agents can rationally achieve (C,C) as opposed to (D,D), and reap the associated benefits.¹

I’ll explain some of my reasoning when I discuss Newcomb’s Problem. But we can’t talk about whether rational cooperation is possible in this dilemma until we’ve dispensed with the visceral sense that the (C,C) outcome is nice or good in itself. We have to see past the prosocial label “mutual cooperation” if we are to grasp the math. If you intuit that (C,C) trumps (D,D) from Player 1’s perspective, but don’t intuit that (D,C) also trumps (C,C), you haven’t yet appreciated what makes this problem difficult.

1. Eliezer Yudkowsky, Timeless Decision Theory, Unpublished manuscript (Machine Intelligence Research Institute, Berkeley, CA, 2010), http://intelligence.org/files/TDT.pdf.

276
Sympathetic Minds

“Mirror neurons” are neurons that are active both when performing an action and observing the same action—for example, a neuron that fires when you hold up a finger or see someone else holding up a finger. Such neurons have been directly recorded in primates, and consistent neuroimaging evidence has been found for humans.

You may recall from my previous writing on “empathic inference” the idea that brains are so complex that the only way to simulate them is by forcing a similar brain to behave similarly. A brain is so complex that if a human tried to understand brains the way that we understand e.g. gravity or a car—observing the whole, observing the parts, building up a theory from scratch—then we would be unable to invent good hypotheses in our mere mortal lifetimes. The only possible way you can hit on an “Aha!” that describes a system as incredibly complex as an Other Mind, is if you happen to run across something amazingly similar to the Other Mind—namely your own brain—which you can actually force to behave similarly and use as a hypothesis, yielding predictions.

So that is what I would call “empathy.”

And then “sympathy” is something else on top of this—to smile when you see someone else smile, to hurt when you see someone else hurt. It goes beyond the realm of prediction into the realm of reinforcement.

And you ask, “Why would callous natural selection do anything that nice?”

It might have gotten started, maybe, with a mother’s love for her children, or a brother’s love for a sibling. You can want them to live, you can want them to be fed, sure; but if you smile when they smile and wince when they wince, that’s a simple urge that leads you to deliver help along a broad avenue, in many walks of life. So long as you’re in the ancestral environment, what your relatives want probably has something to do with your relatives’ reproductive success—this being an explanation for the selection pressure, of course, not a conscious belief.

You may ask, “Why not evolve a more abstract desire to see certain people tagged as ‘relatives’ get what they want, without actually feeling yourself what they feel?” And I would shrug and reply, “Because then there’d have to be a whole definition of ‘wanting’ and so on. Evolution doesn’t take the elaborate correct optimal path, it falls up the fitness landscape like water flowing downhill. The mirroring-architecture was already there, so it was a short step from empathy to sympathy, and it got the job done.”

Relatives—and then reciprocity; your allies in the tribe, those with whom you trade favors. Tit for Tat, or evolution’s elaboration thereof to account for social reputations.

Who is the most formidable, among the human kind? The strongest? The smartest? More often than either of these, I think, it is the one who can call upon the most friends.

So how do you make lots of friends?

You could, perhaps, have a specific urge to bring your allies food, like a vampire bat—they have a whole system of reciprocal blood donations going in those colonies. But it’s a more general motivation, that will lead the organism to store up more favors, if you smile when designated friends smile.

And what kind of organism will avoid making its friends angry at it, in full generality? One that winces when they wince.

Of course you also want to be able to kill designated Enemies without a qualm—these are humans we’re talking about.

But . . . I’m not sure of this, but it does look to me like sympathy, among humans, is “on” by default. There are cultures that help strangers . . . and cultures that eat strangers; the question is which of these requires the explicit imperative, and which is the default behavior for humans. I don’t really think I’m being such a crazy idealistic fool when I say that, based on my admittedly limited knowledge of anthropology, it looks like sympathy is on by default.

Either way . . . it’s painful if you’re a bystander in a war between two sides, and your sympathy has not been switched off for either side, so that you wince when you see a dead child no matter what the caption on the photo; and yet those two sides have no sympathy for each other, and they go on killing.

So that is the human idiom of sympathy—a strange, complex, deep implementation of reciprocity and helping. It tangles minds together—not by a term in the utility function for some other mind’s “desire,” but by the simpler and yet far more consequential path of mirror neurons: feeling what the other mind feels, and seeking similar states. Even if it’s only done by observation and inference, and not by direct transmission of neural information as yet.

Empathy is a human way of predicting other minds. It is not the only possible way.

The human brain is not quickly rewirable; if you’re suddenly put into a dark room, you can’t rewire the visual cortex as auditory cortex, so as to better process sounds, until you leave, and then suddenly shift all the neurons back to being visual cortex again.

An AI, at least one running on anything like a modern programming architecture, can trivially shift computing resources from one thread to another. Put in the dark? Shut down vision and devote all those operations to sound; swap the old program to disk to free up the RAM, then swap the disk back in again when the lights go on.

So why would an AI need to force its own mind into a state similar to what it wanted to predict? Just create a separate mind-instance—maybe with different algorithms, the better to simulate that very dissimilar human. Don’t try to mix up the data with your own mind-state; don’t use mirror neurons. Think of all the risk and mess that implies!

An expected utility maximizer—especially one that does understand intelligence on an abstract level—has other options than empathy, when it comes to understanding other minds. The agent doesn’t need to put itself in anyone else’s shoes; it can just model the other mind directly. A hypothesis like any other hypothesis, just a little bigger. You don’t need to become your shoes to understand your shoes.

And sympathy? Well, suppose we’re dealing with an expected paperclip maximizer, but one that isn’t yet powerful enough to have things all its own way—it has to deal with humans to get its paperclips. So the paperclip agent . . . models those humans as relevant parts of the environment, models their probable reactions to various stimuli, and does things that will make the humans feel favorable toward it in the future.

To a paperclip maximizer, the humans are just machines with pressable buttons. No need to feel what the other feels—if that were even possible across such a tremendous gap of internal architecture. How could an expected paperclip maximizer “feel happy” when it saw a human smile? “Happiness” is an idiom of policy reinforcement learning, not expected utility maximization. A paperclip maximizer doesn’t feel happy when it makes paperclips; it just chooses whichever action leads to the greatest number of expected paperclips. Though a paperclip maximizer might find it convenient to display a smile when it made paperclips—so as to help manipulate any humans that had designated it a friend.

You might find it a bit difficult to imagine such an algorithm—to put yourself into the shoes of something that does not work like you do, and does not work like any mode your brain can make itself operate in.

You can make your brain operate in the mode of hating an enemy, but that’s not right either. The way to imagine how a truly unsympathetic mind sees a human is to imagine yourself as a useful machine with levers on it. Not a human-shaped machine, because we have instincts for that. Just a woodsaw or something. Some levers make the machine output coins; other levers might make it fire a bullet. The machine does have a persistent internal state and you have to pull the levers in the right order. Regardless, it’s just a complicated causal system—nothing inherently mental about it.

(To understand unsympathetic optimization processes, I would suggest studying natural selection, which doesn’t bother to anesthetize fatally wounded and dying creatures, even when their pain no longer serves any reproductive purpose, because the anesthetic would serve no reproductive purpose either.)

That’s why I list “sympathy” in front of even “boredom” on my list of things that would be required to have aliens that are the least bit, if you’ll pardon the phrase, sympathetic. It’s not impossible that sympathy exists among some significant fraction of all evolved alien intelligent species; mirror neurons seem like the sort of thing that, having happened once, could happen again.

Unsympathetic aliens might be trading partners—or not; stars and such resources are pretty much the same the universe over. We might negotiate treaties with them, and they might keep them for calculated fear of reprisal. We might even cooperate in the Prisoner’s Dilemma. But we would never be friends with them. They would never see us as anything but means to an end. They would never shed a tear for us, nor smile for our joys. And the others of their own kind would receive no different consideration, nor have any sense that they were missing something important thereby.

Such aliens would be varelse, not ramen—the sort of aliens we can’t relate to on any personal level, and no point in trying.

277
High Challenge

There’s a class of prophecy that runs: “In the Future, machines will do all the work. Everything will be automated. Even labor of the sort we now consider ‘intellectual,’ like engineering, will be done by machines. We can sit back and own the capital. You’ll never have to lift a finger, ever again.”

But then won’t people be bored?

No; they can play computer games—not like our games, of course, but much more advanced and entertaining.

Yet wait! If you buy a modern computer game, you’ll find that it contains some tasks that are—there’s no kind word for this—effortful. (I would even say “difficult,” with the understanding that we’re talking about something that takes ten minutes, not ten years.)

So in the future, we’ll have programs that help you play the game—taking over if you get stuck on the game, or just bored; or so that you can play games that would otherwise be too advanced for you.

But isn’t there some wasted effort, here? Why have one programmer working to make the game harder, and another programmer to working to make the game easier? Why not just make the game easier to start with? Since you play the game to get gold and experience points, making the game easier will let you get more gold per unit time: the game will become more fun.

So this is the ultimate end of the prophecy of technological progress—just staring at a screen that says “YOU WIN,” forever.

And maybe we’ll build a robot that does that, too.

Then what?

The world of machines that do all the work—well, I don’t want to say it’s “analogous to the Christian Heaven” because it isn’t supernatural; it’s something that could in principle be realized. Religious analogies are far too easily tossed around as accusations . . . But, without implying any other similarities, I’ll say that it seems analogous in the sense that eternal laziness “sounds like good news” to your present self who still has to work.

And as for playing games, as a substitute—what is a computer game except synthetic work? Isn’t there a wasted step here? (And computer games in their present form, considered as work, have various aspects that reduce stress and increase engagement; but they also carry costs in the form of artificiality and isolation.)

I sometimes think that futuristic ideals phrased in terms of “getting rid of work” would be better reformulated as “removing low-quality work to make way for high-quality work.”

There’s a broad class of goals that aren’t suitable as the long-term meaning of life, because you can actually achieve them, and then you’re done.

To look at it another way, if we’re looking for a suitable long-run meaning of life, we should look for goals that are good to pursue and not just good to satisfy.

Or to phrase that somewhat less paradoxically: We should look for valuations that are over 4D states, rather than 3D states. Valuable ongoing processes, rather than “make the universe have property P and then you’re done.”

Timothy Ferris is worth quoting: To find happiness, “the question you should be asking isn’t ‘What do I want?’ or ‘What are my goals?’ but ‘What would excite me?’”

You might say that for a long-run meaning of life, we need games that are fun to play and not just to win.

Mind you—sometimes you do want to win. There are legitimate goals where winning is everything. If you’re talking, say, about curing cancer, then the suffering experienced by even a single cancer patient outweighs any fun that you might have in solving their problems. If you work at creating a cancer cure for twenty years through your own efforts, learning new knowledge and new skill, making friends and allies—and then some alien superintelligence offers you a cancer cure on a silver platter for thirty bucks—then you shut up and take it.

But “curing cancer” is a problem of the 3D-predicate sort: you want the no-cancer predicate to go from False in the present to True in the future. The importance of this destination far outweighs the journey; you don’t want to go there, you just want to be there. There are many legitimate goals of this sort, but they are not suitable as long-run fun. “Cure cancer!” is a worthwhile activity for us to pursue here and now, but it is not a plausible future goal of galactic civilizations.

Why should this “valuable ongoing process” be a process of trying to do things—why not a process of passive experiencing, like the Buddhist Heaven?

I confess I’m not entirely sure how to set up a “passively experiencing” mind. The human brain was designed to perform various sorts of internal work that add up to an active intelligence; even if you lie down on your bed and exert no particular effort to think, the thoughts that go on through your mind are activities of brain areas that are designed to, you know, solve problems.

How much of the human brain could you eliminate, apart from the pleasure centers, and still keep the subjective experience of pleasure?

I’m not going to touch that one. I’ll stick with the much simpler answer of “I wouldn’t actually prefer to be a passive experiencer.” If I wanted Nirvana, I might try to figure out how to achieve that impossibility. But once you strip away Buddha telling me that Nirvana is the end-all of existence, Nirvana seems rather more like “sounds like good news in the moment of first being told” or “ideological belief in desire,” rather than, y’know, something I’d actually want.

The reason I have a mind at all is that natural selection built me to do things—to solve certain kinds of problems.

“Because it’s human nature” is not an explicit justification for anything. There is human nature, which is what we are; and there is humane nature, which is what, being human, we wish we were.

But I don’t want to change my nature toward a more passive object—which is a justification. A happy blob is not what, being human, I wish to become.

I earlier argued that many values require both subjective happiness and the external objects of that happiness. That you can legitimately have a utility function that says, “It matters to me whether or not the person I love is a real human being or just a highly realistic nonsentient chatbot, even if I don’t know, because that-which-I-value is not my own state of mind, but the external reality.” So that you need both the experience of love, and the real lover.

You can similarly have valuable activities that require both real challenge and real effort.

Racing along a track, it matters that the other racers are real, and that you have a real chance to win or lose. (We’re not talking about physical determinism here, but whether some external optimization process explicitly chose for you to win the race.)

And it matters that you’re racing with your own skill at running and your own willpower, not just pressing a button that says “Win.” (Though, since you never designed your own leg muscles, you are racing using strength that isn’t yours. A race between robot cars is a purer contest of their designers. There is plenty of room to improve on the human condition.)

And it matters that you, a sentient being, are experiencing it. (Rather than some nonsentient process carrying out a skeleton imitation of the race, trillions of times per second.)

There must be the true effort, the true victory, and the true experience—the journey, the destination and the traveler.

278
Serious Stories

Every Utopia ever constructed—in philosophy, fiction, or religion—has been, to one degree or another, a place where you wouldn’t actually want to live. I am not alone in this important observation: George Orwell said much the same thing in “Why Socialists Don’t Believe In Fun,” and I expect that many others said it earlier.

If you read books on How To Write—and there are a lot of books out there on How To Write, because, amazingly, a lot of book-writers think they know something about writing—these books will tell you that stories must contain “conflict.”

That is, the more lukewarm sort of instructional book will tell you that stories contain “conflict.” But some authors speak more plainly.

“Stories are about people’s pain.” Orson Scott Card.

“Every scene must end in disaster.” Jack Bickham.

In the age of my youthful folly, I took for granted that authors were excused from the search for true Eutopia, because if you constructed a Utopia that wasn’t flawed . . . what stories could you write, set there? “Once upon a time they lived happily ever after.” What use would it be for a science-fiction author to try to depict a positive intelligence explosion, when a positive intelligence explosion would be . . .

. . . the end of all stories?

It seemed like a reasonable framework with which to examine the literary problem of Utopia, but something about that final conclusion produced a quiet, nagging doubt.

At that time I was thinking of an AI as being something like a safe wish-granting genie for the use of individuals. So the conclusion did make a kind of sense. If there was a problem, you would just wish it away, right? Ergo—no stories. So I ignored the quiet, nagging doubt.

Much later, after I concluded that even a safe genie wasn’t such a good idea, it also seemed in retrospect that “no stories” could have been a productive indicator. On this particular occasion, “I can’t think of a single story I’d want to read about this scenario,” might indeed have pointed me toward the reason “I wouldn’t want to actually live in this scenario.”

So I swallowed my trained-in revulsion of Luddism and theodicy, and at least tried to contemplate the argument:

A world in which nothing ever goes wrong, or no one ever experiences any pain or sorrow, is a world containing no stories worth reading about.
A world that you wouldn’t want to read about is a world where you wouldn’t want to live.
Into each eudaimonic life a little pain must fall. QED.

In one sense, it’s clear that we do not want to live the sort of lives that are depicted in most stories that human authors have written so far. Think of the truly great stories, the ones that have become legendary for being the very best of the best of their genre: the Iliad, Romeo and Juliet, The Godfather, Watchmen, Planescape: Torment, the second season of Buffy the Vampire Slayer, or that ending in Tsukihime. Is there a single story on the list that isn’t tragic?

Ordinarily, we prefer pleasure to pain, joy to sadness, and life to death. Yet it seems we prefer to empathize with hurting, sad, dead characters. Or stories about happier people aren’t serious, aren’t artistically great enough to be worthy of praise—but then why selectively praise stories containing unhappy people? Is there some hidden benefit to us in it? It’s a puzzle either way you look at it.

When I was a child I couldn’t write fiction because I wrote things to go well for my characters—just like I wanted things to go well in real life. Which I was cured of by Orson Scott Card: Oh, I said to myself, that’s what I’ve been doing wrong, my characters aren’t hurting. Even then, I didn’t realize that the microstructure of a plot works the same way—until Jack Bickham said that every scene must end in disaster. Here I’d been trying to set up problems and resolve them, instead of making them worse . . .

You simply don’t optimize a story the way you optimize a real life. The best story and the best life will be produced by different criteria.

In the real world, people can go on living for quite a while without any major disasters, and still seem to do pretty okay. When was the last time you were shot at by assassins? Quite a while, right? Does your life seem emptier for it?

But on the other hand . . .

For some odd reason, when authors get too old or too successful, they revert to my childhood. Their stories start going right. They stop doing horrible things to their characters, with the result that they start doing horrible things to their readers. It seems to be a regular part of Elder Author Syndrome. Mercedes Lackey, Laurell K. Hamilton, Robert Heinlein, even Orson Scott bloody Card—they all went that way. They forgot how to hurt their characters. I don’t know why.

And when you read a story by an Elder Author or a pure novice—a story where things just relentlessly go right one after another—where the main character defeats the supervillain with a snap of the fingers, or even worse, before the final battle, the supervillain gives up and apologizes and then they’re friends again—

It’s like a fingernail scraping on a blackboard at the base of your spine. If you’ve never actually read a story like that (or worse, written one) then count yourself lucky.

That fingernail-scraping quality—would it transfer over from the story to real life, if you tried living real life without a single drop of rain?

One answer might be that what a story really needs is not “disaster,” or “pain,” or even “conflict,” but simply striving. That the problem with Mary Sue stories is that there’s not enough striving in them, but they wouldn’t actually need pain. This might, perhaps, be tested.

An alternative answer might be that this is the transhumanist version of Fun Theory we’re talking about. So we can reply, “Modify brains to eliminate that fingernail-scraping feeling,” unless there’s some justification for keeping it. If the fingernail-scraping feeling is a pointless random bug getting in the way of Utopia, delete it.

Maybe we should. Maybe all the Great Stories are tragedies because . . . well . . .

I once read that in the BDSM community, “intense sensation” is a euphemism for pain. Upon reading this, it occurred to me that, the way humans are constructed now, it is just easier to produce pain than pleasure. Though I speak here somewhat outside my experience, I expect that it takes a highly talented and experienced sexual artist working for hours to produce a good feeling as intense as the pain of one strong kick in the testicles—which is doable in seconds by a novice.

Investigating the life of the priest and proto-rationalist Friedrich Spee von Langenfeld, who heard the confessions of accused witches, I looked up some of the instruments that had been used to produce confessions. There is no ordinary way to make a human being feel as good as those instruments would make you hurt. I’m not sure even drugs would do it, though my experience of drugs is as nonexistent as my experience of torture.

There’s something imbalanced about that.

Yes, human beings are too optimistic in their planning. If losses weren’t more aversive than gains, we’d go broke, the way we’re constructed now. The experimental rule is that losing a desideratum—$50, a coffee mug, whatever—hurts between 2 and 2.5 times as much as the equivalent gain.

But this is a deeper imbalance than that. The effort-in/intensity-out difference between sex and torture is not a mere factor of 2.

If someone goes in search of sensation—in this world, the way human beings are constructed now—it’s not surprising that they should arrive at pains to be mixed into their pleasures as a source of intensity in the combined experience.

If only people were constructed differently, so that you could produce pleasure as intense and in as many different flavors as pain! If only you could, with the same ingenuity and effort as a torturer of the Inquisition, make someone feel as good as the Inquisition’s victims felt bad—

But then, what is the analogous pleasure that feels that good? A victim of skillful torture will do anything to stop the pain and anything to prevent it from being repeated. Is the equivalent pleasure one that overrides everything with the demand to continue and repeat it? If people are stronger-willed to bear the pleasure, is it really the same pleasure?

There is another rule of writing which states that stories have to shout. A human brain is a long way off those printed letters. Every event and feeling needs to take place at ten times natural volume in order to have any impact at all. You must not try to make your characters behave or feel realistically—especially, you must not faithfully reproduce your own past experiences—because without exaggeration, they’ll be too quiet to rise from the page.

Maybe all the Great Stories are tragedies because happiness can’t shout loud enough—to a human reader.

Maybe that’s what needs fixing.

And if it were fixed . . . would there be any use left for pain or sorrow? For even the memory of sadness, if all things were already as good as they could be, and every remediable ill already remedied?

Can you just delete pain outright? Or does removing the old floor of the utility function just create a new floor? Will any pleasure less than 10,000,000 hedons be the new unbearable pain?

Humans, built the way we are now, do seem to have hedonic scaling tendencies. Someone who can remember starving will appreciate a loaf of bread more than someone who’s never known anything but cake. This was George Orwell’s hypothesis for why Utopia is impossible in literature and reality:¹

It would seem that human beings are not able to describe, nor perhaps to imagine, happiness except in terms of contrast . . . The inability of mankind to imagine happiness except in the form of relief, either from effort or pain, presents Socialists with a serious problem. Dickens can describe a poverty-stricken family tucking into a roast goose, and can make them appear happy; on the other hand, the inhabitants of perfect universes seem to have no spontaneous gaiety and are usually somewhat repulsive into the bargain.

For an expected utility maximizer, rescaling the utility function to add a trillion to all outcomes is meaningless—it’s literally the same utility function, as a mathematical object. A utility function describes the relative intervals between outcomes; that’s what it is, mathematically speaking.

But the human brain has distinct neural circuits for positive feedback and negative feedback, and different varieties of positive and negative feedback. There are people today who “suffer” from congenital analgesia—a total absence of pain. I never heard that insufficient pleasure becomes intolerable to them.

Congenital analgesics do have to inspect themselves carefully and frequently to see if they’ve cut themselves or burned a finger. Pain serves a purpose in the human mind design . . .

But that does not show there’s no alternative which could serve the same purpose. Could you delete pain and replace it with an urge not to do certain things that lacked the intolerable subjective quality of pain? I do not know all the Law that governs here, but I’d have to guess that yes, you could; you could replace that side of yourself with something more akin to an expected utility maximizer.

Could you delete the human tendency to scale pleasures—delete the accomodation, so that each new roast goose is as delightful as the last? I would guess that you could. This verges perilously close to deleting Boredom, which is right up there with Sympathy as an absolute indispensable . . . but to say that an old solution remains as pleasurable is not to say that you will lose the urge to seek new and better solutions.

Can you make every roast goose as pleasurable as it would be in contrast to starvation, without ever having starved?

Can you prevent the pain of a dust speck irritating your eye from being the new torture, if you’ve literally never experienced anything worse than a dust speck irritating your eye?

Such questions begin to exceed my grasp of the Law, but I would guess that the answer is: yes, it can be done. It is my experience in such matters that once you do learn the Law, you can usually see how to do weird-seeming things.

So far as I know or can guess, David Pearce (The Hedonistic Imperative) is very probably right about the feasibility part, when he says:²

Nanotechnology and genetic engineering will abolish suffering in all sentient life. The abolitionist project is hugely ambitious but technically feasible. It is also instrumentally rational and morally urgent. The metabolic pathways of pain and malaise evolved because they served the fitness of our genes in the ancestral environment. They will be replaced by a different sort of neural architecture—a motivational system based on heritable gradients of bliss. States of sublime well-being are destined to become the genetically pre-programmed norm of mental health. It is predicted that the world’s last unpleasant experience will be a precisely dateable event.

Is that . . . what we want?

To just wipe away the last tear, and be done?

Is there any good reason not to, except status quo bias and a handful of worn rationalizations?

What would be the alternative? Or alternatives?

To leave things as they are? Of course not. No God designed this world; we have no reason to think it exactly optimal on any dimension. If this world does not contain too much pain, then it must not contain enough, and the latter seems unlikely.

But perhaps . . .

You could cut out just the intolerable parts of pain?

Get rid of the Inquisition. Keep the sort of pain that tells you not to stick your finger in the fire, or the pain that tells you that you shouldn’t have put your friend’s finger in the fire, or even the pain of breaking up with a lover.

Try to get rid of the sort of pain that grinds down and destroys a mind. Or configure minds to be harder to damage.

You could have a world where there were broken legs, or even broken hearts, but no broken people. No child sexual abuse that turns out more abusers. No people ground down by weariness and drudging minor inconvenience to the point where they contemplate suicide. No random meaningless endless sorrows like starvation or AIDS.

And if even a broken leg still seems too scary—

Would we be less frightened of pain, if we were stronger, if our daily lives did not already exhaust so much of our reserves?

So that would be one alternative to Pearce’s world—if there are yet other alternatives, I haven’t thought them through in any detail.

The path of courage, you might call it—the idea being that if you eliminate the destroying kind of pain and strengthen the people, then what’s left shouldn’t be that scary.

A world where there is sorrow, but not massive systematic pointless sorrow, like we see on the evening news. A world where pain, if it is not eliminated, at least does not overbalance pleasure. You could write stories about that world, and they could read our stories.

I do tend to be rather conservative around the notion of deleting large parts of human nature. I’m not sure how many major chunks you can delete until that balanced, conflicting, dynamic structure collapses into something simpler, like an expected pleasure maximizer.

And so I do admit that it is the path of courage that appeals to me.

Then again, I haven’t lived it both ways.

Maybe I’m just afraid of a world so different as Analgesia—wouldn’t that be an ironic reason to walk “the path of courage”?

Maybe the path of courage just seems like the smaller change—maybe I just have trouble empathizing over a larger gap.

But “change” is a moving target.

If a human child grew up in a less painful world—if they had never lived in a world of AIDS or cancer or slavery, and so did not know these things as evils that had been triumphantly eliminated—and so did not feel that they were “already done” or that the world was “already changed enough” . . .

Would they take the next step, and try to eliminate the unbearable pain of broken hearts, when someone’s lover stops loving them?

And then what? Is there a point where Romeo and Juliet just seems less and less relevant, more and more a relic of some distant forgotten world? Does there come some point in the transhuman journey where the whole business of the negative reinforcement circuitry can’t possibly seem like anything except a pointless hangover to wake up from?

And if so, is there any point in delaying that last step? Or should we just throw away our fears and . . . throw away our fears?

I don’t know.

1. George Orwell, “Why Socialists Don’t Believe in Fun,” Tribune (December 1943).

2. David Pearce, The Hedonistic Imperative, http://www.hedweb.com/, 1995.

279
Value is Fragile

If I had to pick a single statement that relies on more Overcoming Bias content I’ve written than any other, that statement would be:

Any Future not shaped by a goal system with detailed reliable inheritance from human morals and metamorals will contain almost nothing of worth.

“Well,” says the one, “maybe according to your provincial human values, you wouldn’t like it. But I can easily imagine a galactic civilization full of agents who are nothing like you, yet find great value and interest in their own goals. And that’s fine by me. I’m not so bigoted as you are. Let the Future go its own way, without trying to bind it forever to the laughably primitive prejudices of a pack of four-limbed Squishy Things—”

My friend, I have no problem with the thought of a galactic civilization vastly unlike our own . . . full of strange beings who look nothing like me even in their own imaginations . . . pursuing pleasures and experiences I can’t begin to empathize with . . . trading in a marketplace of unimaginable goods . . . allying to pursue incomprehensible objectives . . . people whose life-stories I could never understand.

That’s what the Future looks like if things go right.

If the chain of inheritance from human (meta)morals is broken, the Future does not look like this. It does not end up magically, delightfully incomprehensible.

With very high probability, it ends up looking dull. Pointless. Something whose loss you wouldn’t mourn.

Seeing this as obvious is what requires that immense amount of background explanation.

And I’m not going to iterate through all the points and winding pathways of argument here, because that would take us back through 75% of my Overcoming Bias posts. Except to remark on how many different things must be known to constrain the final answer.

Consider the incredibly important human value of “boredom”—our desire not to do “the same thing” over and over and over again. You can imagine a mind that contained almost the whole specification of human value, almost all the morals and metamorals, but left out just this one thing—

—and so it spent until the end of time, and until the farthest reaches of its light cone, replaying a single highly optimized experience, over and over and over again.

Or imagine a mind that contained almost the whole specification of which sort of feelings humans most enjoy—but not the idea that those feelings had important external referents. So that the mind just went around feeling like it had made an important discovery, feeling it had found the perfect lover, feeling it had helped a friend, but not actually doing any of those things—having become its own experience machine. And if the mind pursued those feelings and their referents, it would be a good future and true; but because this one dimension of value was left out, the future became something dull. Boring and repetitive, because although this mind felt that it was encountering experiences of incredible novelty, this feeling was in no wise true.

Or the converse problem—an agent that contains all the aspects of human value, except the valuation of subjective experience. So that the result is a nonsentient optimizer that goes around making genuine discoveries, but the discoveries are not savored and enjoyed, because there is no one there to do so. This, I admit, I don’t quite know to be possible. Consciousness does still confuse me to some extent. But a universe with no one to bear witness to it might as well not be.

Value isn’t just complicated, it’s fragile. There is more than one dimension of human value, where if just that one thing is lost, the Future becomes null. A single blow and all value shatters. Not every single blow will shatter all value—but more than one possible “single blow” will do so.

And then there are the long defenses of this proposition, which relies on 75% of my Overcoming Bias posts, so that it would be more than one day’s work to summarize all of it. Maybe some other week. There’s so many branches I’ve seen that discussion tree go down.

After all—a mind shouldn’t just go around having the same experience over and over and over again. Surely no superintelligence would be so grossly mistaken about the correct action?

Why would any supermind want something so inherently worthless as the feeling of discovery without any real discoveries? Even if that were its utility function, wouldn’t it just notice that its utility function was wrong, and rewrite it? It’s got free will, right?

Surely, at least boredom has to be a universal value. It evolved in humans because it’s valuable, right? So any mind that doesn’t share our dislike of repetition will fail to thrive in the universe and be eliminated . . .

If you are familiar with the difference between instrumental values and terminal values, and familiar with the stupidity of natural selection, and you understand how this stupidity manifests in the difference between executing adaptations versus maximizing fitness, and you know this turned instrumental subgoals of reproduction into decontextualized unconditional emotions . . .

. . . and you’re familiar with how the tradeoff between exploration and exploitation works in Artificial Intelligence . . .

. . . then you might be able to see that the human form of boredom that demands a steady trickle of novelty for its own sake isn’t a grand universal, but just a particular algorithm that evolution coughed out into us. And you might be able to see how the vast majority of possible expected utility maximizers would only engage in just so much efficient exploration, and spend most of their time exploiting the best alternative found so far, over and over and over.

That’s a lot of background knowledge, though.

And so on and so on and so on through 75% of my posts on Overcoming Bias, and many chains of fallacy and counter-explanation. Some week I may try to write up the whole diagram. But for now I’m going to assume that you’ve read the arguments, and just deliver the conclusion:

We can’t relax our grip on the future—let go of the steering wheel—and still end up with anything of value.

And those who think we can—

—they’re trying to be cosmopolitan. I understand that. I read those same science fiction books as a kid: The provincial villains who enslave aliens for the crime of not looking just like humans. The provincial villains who enslave helpless AIs in durance vile on the assumption that silicon can’t be sentient. And the cosmopolitan heroes who understand that minds don’t have to be just like us to be embraced as valuable—

I read those books. I once believed them. But the beauty that jumps out of one box is not jumping out of all boxes. If you leave behind all order, what is left is not the perfect answer; what is left is perfect noise. Sometimes you have to abandon an old design rule to build a better mousetrap, but that’s not the same as giving up all design rules and collecting wood shavings into a heap, with every pattern of wood as good as any other. The old rule is always abandoned at the behest of some higher rule, some higher criterion of value that governs.

If you loose the grip of human morals and metamorals—the result is not mysterious and alien and beautiful by the standards of human value. It is moral noise, a universe tiled with paperclips. To change away from human morals in the direction of improvement rather than entropy requires a criterion of improvement; and that criterion would be physically represented in our brains, and our brains alone.

Relax the grip of human value upon the universe, and it will end up seriously valueless. Not strange and alien and wonderful, shocking and terrifying and beautiful beyond all human imagination. Just—tiled with paperclips.

It’s only some humans, you see, who have this idea of embracing manifold varieties of mind—of wanting the Future to be something greater than the past—of being not bound to our past selves—of trying to change and move forward.

A paperclip maximizer just chooses whichever action leads to the greatest number of paperclips.

No free lunch. You want a wonderful and mysterious universe? That’s your value. You work to create that value. Let that value exert its force through you who represents it; let it make decisions in you to shape the future. And maybe you shall indeed obtain a wonderful and mysterious universe.

No free lunch. Valuable things appear because a goal system that values them takes action to create them. Paperclips don’t materialize from nowhere for a paperclip maximizer. And a wonderfully alien and mysterious Future will not materialize from nowhere for us humans, if our values that prefer it are physically obliterated—or even disturbed in the wrong dimension. Then there is nothing left in the universe that works to make the universe valuable.

You do have values, even when you’re trying to be “cosmopolitan,” trying to display a properly virtuous appreciation of alien minds. Your values are then faded further into the invisible background—they are less obviously human. Your brain probably won’t even generate an alternative so awful that it would wake you up, make you say “No! Something went wrong!” even at your most cosmopolitan. E.g., “a nonsentient optimizer absorbs all matter in its future light cone and tiles the universe with paperclips.” You’ll just imagine strange alien worlds to appreciate.

Trying to be “cosmopolitan”—to be a citizen of the cosmos—just strips off a surface veneer of goals that seem obviously “human.”

But if you wouldn’t like the Future tiled over with paperclips, and you would prefer a civilization of . . .

. . . sentient beings . . .

. . . with enjoyable experiences . . .

. . . that aren’t the same experience over and over again . . .

. . . and are bound to something besides just being a sequence of internal pleasurable feelings . . .

. . . learning, discovering, freely choosing . . .

. . . well, my posts on Fun Theory go into some of the hidden details on those short English words.

Values that you might praise as cosmopolitan or universal or fundamental or obvious common sense are represented in your brain just as much as those values that you might dismiss as merely human. Those values come of the long history of humanity, and the morally miraculous stupidity of evolution that created us. (And once I finally came to that realization, I felt less ashamed of values that seemed “provincial”—but that’s another matter.)

These values do not emerge in all possible minds. They will not appear from nowhere to rebuke and revoke the utility function of an expected paperclip maximizer.

Touch too hard in the wrong dimension, and the physical representation of those values will shatter—and not come back, for there will be nothing left to want to bring it back.

And the referent of those values—a worthwhile universe—would no longer have any physical reason to come into being.

Let go of the steering wheel, and the Future crashes.

280
The Gift We Give to Tomorrow

How, oh how, could the universe, itself unloving and mindless, cough up minds who were capable of love?

“No mystery in that,” you say. “It’s just a matter of natural selection.”

But natural selection is cruel, bloody, and bloody stupid. Even when, on the surface of things, biological organisms aren’t directly fighting each other—aren’t directly tearing at each other with claws—there’s still a deeper competition going on between the genes. Genetic information is created when genes increase their relative frequency in the next generation—what matters for “genetic fitness” is not how many children you have, but that you have more children than others. It is quite possible for a species to evolve to extinction, if the winning genes are playing negative-sum games.

How, oh how, could such a process create beings capable of love?

“No mystery,” you say. “There is never any mystery-in-the-world. Mystery is a property of questions, not answers. A mother’s children share her genes, so the mother loves her children.”

But sometimes mothers adopt children, and still love them. And mothers love their children for themselves, not for their genes.

“No mystery,” you say. “Individual organisms are adaptation-executers, not fitness-maximizers. Evolutionary psychology is not about deliberately maximizing fitness—through most of human history, we didn’t know genes existed. We don’t calculate our acts’ effect on genetic fitness consciously, or even subconsciously.”

But human beings form friendships even with non-relatives. How can that be?

“No mystery, for hunter-gatherers often play Iterated Prisoner’s Dilemmas, the solution to which is reciprocal altruism. Sometimes the most dangerous human in the tribe is not the strongest, the prettiest, or even the smartest, but the one who has the most allies.”

Yet not all friends are fair-weather friends; we have a concept of true friendship—and some people have sacrificed their life for their friends. Would not such a devotion tend to remove itself from the gene pool?

“You said it yourself: we have concepts of true friendship and of fair-weather friendship. We can tell, or try to tell, the difference between someone who considers us a valuable ally, and someone executing the friendship adaptation. We wouldn’t be true friends with someone who we didn’t think was a true friend to us—and someone with many true friends is far more formidable than someone with many fair-weather allies.”

And Mohandas Gandhi, who really did turn the other cheek? Those who try to serve all humanity, whether or not all humanity serves them in turn?

“That perhaps is a more complicated story. Human beings are not just social animals. We are political animals who argue linguistically about policy in adaptive tribal contexts. Sometimes the formidable human is not the strongest, but the one who can most skillfully argue that their preferred policies match the preferences of others.”

Um . . . that doesn’t explain Gandhi, or am I missing something?

“The point is that we have the ability to argue about ‘What should be done?’ as a proposition—we can make those arguments and respond to those arguments, without which politics could not take place.”

Okay, but Gandhi?

“Believed certain complicated propositions about ‘What should be done?’ and did them.”

That sounds suspiciously like it could explain any possible human behavior.

“If we traced back the chain of causality through all the arguments, it would involve: a moral architecture that had the ability to argue general abstract moral propositions like ‘What should be done to people?’; appeal to hardwired intuitions like fairness, a concept of duty, pain aversion, empathy; something like a preference for simple moral propositions, probably reused from our pre-existing Occam prior; and the end result of all this, plus perhaps memetic selection effects, was ‘You should not hurt people’ in full generality—”

And that gets you Gandhi.

“Unless you think it was magic, it has to fit into the lawful causal development of the universe somehow.”

I certainly won’t postulate magic, under any name.

“Good.”

But come on . . . doesn’t it seem a little . . . amazing . . . that hundreds of millions of years worth of evolution’s death tournament could cough up mothers and fathers, sisters and brothers, husbands and wives, steadfast friends and honorable enemies, true altruists and guardians of causes, police officers and loyal defenders, even artists sacrificing themselves for their art, all practicing so many kinds of love? For so many things other than genes? Doing their part to make their world less ugly, something besides a sea of blood and violence and mindless replication?

“Are you claiming to be surprised by this? If so, question your underlying model, for it has led you to be surprised by the true state of affairs.

Since the beginning,
not one unusual thing
has ever happened.”

But how is it not surprising?

“What would you suggest? That some sort of shadowy figure stood behind the scenes and directed evolution?”

Hell no. But—

“Because if you were suggesting that, I would have to ask how that shadowy figure originally decided that love was a desirable outcome of evolution. I would have to ask where that figure got preferences that included things like love, friendship, loyalty, fairness, honor, romance, and so on. On evolutionary psychology, we can see how that specific outcome came about—how those particular goals rather than others were generated in the first place. You can call it ‘surprising’ all you like. But when you really do understand evolutionary psychology, you can see how parental love and romance and honor, and even true altruism and moral arguments, bear the specific design signature of natural selection in particular adaptive contexts of the hunter-gatherer savanna. So if there was a shadowy figure, it must itself have evolved—and that obviates the whole point of postulating it.”

I’m not postulating a shadowy figure! I’m just asking how human beings ended up so nice.

“Nice! Have you looked at this planet lately? We bear all those other emotions that evolved, too—which would tell you very well that we evolved, should you begin to doubt it. Humans aren’t always nice.”

We’re one hell of a lot nicer than the process that produced us, which lets elephants starve to death when they run out of teeth, which doesn’t anesthetize a gazelle even as it lays dying and is of no further importance to evolution one way or the other. It doesn’t take much to be nicer than evolution. To have the theoretical capacity to make one single gesture of mercy, to feel a single twinge of empathy, is to be nicer than evolution.

How did evolution, which is itself so uncaring, create minds on that qualitatively higher moral level? How did evolution, which is so ugly, end up doing anything so beautiful?

“Beautiful, you say? Bach’s Little Fugue in G Minor may be beautiful, but the sound waves, as they travel through the air, are not stamped with tiny tags to specify their beauty. If you wish to find explicitly encoded a measure of the fugue’s beauty, you will have to look at a human brain—nowhere else in the universe will you find it. Not upon the seas or the mountains will you find such judgments written: they are not minds; they cannot think.”

Perhaps that is so. Yet evolution did in fact give us the ability to admire the beauty of a flower. That still seems to call for some deeper answer.

“Do you not see the circularity in your question? If beauty were like some great light in the sky that shined from outside humans, then your question might make sense—though there would still be the question of how humans came to perceive that light. You evolved with a psychology alien to evolution: Evolution has nothing like the intelligence or the precision required to exactly quine its goal system. In coughing up the first true minds, evolution’s simple fitness criterion shattered into a thousand values. You evolved with a psychology that attaches utility to things which evolution does not care about—human life, human happiness. And then you look back and say, ‘How marvelous!’ You marvel and you wonder at the fact that your values coincide with themselves.”

But then—it is still amazing that this particular circular loop, and not some other loop, came into the world. That we find ourselves praising love and not hate, beauty and not ugliness.

“I don’t think you understand. To you, it seems natural to privilege the beauty and altruism as special, as preferred, because you value them highly. And you don’t see this as an unusual fact about yourself, because many of your friends do likewise. So you expect that a ghost of perfect emptiness would also value life and happiness—and then, from this standpoint outside reality, a great coincidence would indeed have occurred.”

But you can make arguments for the importance of beauty and altruism from first principles—that our aesthetic senses lead us to create new complexity, instead of repeating the same things over and over; and that altruism is important because it takes us outside ourselves, gives our life a higher meaning than sheer brute selfishness.

“And that argument is going to move even a ghost of perfect emptiness? Because you’ve appealed to slightly different values? Those aren’t first principles. They’re just different principles. Speak in a grave and philosophical register, and still you shall find no universally compelling arguments. All you’ve done is pass the recursive buck.”

You don’t think that, somehow, we evolved to tap into something beyond—

“What good does it do to suppose something beyond? Why should we pay more attention to this beyond thing than we pay to our existence as humans? How does it alter your personal responsibility to say that you were only following the orders of the beyond thing? And you would still have evolved to let the beyond thing, rather than something else, direct your actions. It would be too much coincidence.”

Too much coincidence?

“A flower is beautiful, you say. Do you think there is no story behind that beauty, or that science does not know the story? Flower pollen is transmitted by bees, so by sexual selection, flowers evolved to attract bees—by imitating certain mating signs of bees, as it happened; the flowers’ patterns would look more intricate if you could see in the ultraviolet. Now healthy flowers are a sign of fertile land, likely to bear fruits and other treasures, and probably prey animals as well; so is it any wonder that humans evolved to be attracted to flowers? But for there to be some great light written upon the very stars—those huge unsentient balls of burning hydrogen—which also said that flowers were beautiful, now that would be far too much coincidence.”

So you explain away the beauty of a flower?

“No. I explain it. Of course there’s a story behind the beauty of flowers, behind the fact that we find them beautiful. Behind ordered events, one finds ordered stories; and what has no story is the product of random noise, which is hardly any better. If you cannot take joy in things that have stories behind them, your life will be empty indeed. I don’t think I take any less joy in a flower than you do. More so, perhaps, because I take joy in its story as well.”

Perhaps, as you say, there is no surprise from a causal viewpoint—no disruption of the physical order of the universe. But it still seems to me that, in this creation of humans by evolution, something happened that is precious and marvelous and wonderful. If we cannot call it a physical miracle, then call it a moral miracle.

“Because it’s only a miracle from the perspective of the morality that was produced, thus explaining away all of the apparent coincidence from a merely causal and physical perspective?”

Well . . . I suppose you could interpret the term that way, yes. I just meant something that was immensely surprising and wonderful on a moral level, even if it is not surprising on a physical level.

“I think that’s what I said.”

But it still seems to me that you, from your own view, drain something of that wonder away.

“Then you have problems taking joy in the merely real. Love has to begin somehow. It has to enter the universe somewhere. It is like asking how life itself begins—and though you were born of your father and mother, and they arose from their living parents in turn, if you go far and far and far away back, you will finally come to a replicator that arose by pure accident—the border between life and unlife. So too with love.

“A complex pattern must be explained by a cause that is not already that complex pattern. Not just the event must be explained, but the very shape and form. For love to first enter Time, it must come of something that is not love; if this were not possible, then love could not be.

“Even as life itself required that first replicator to come about by accident, parentless but still caused: far, far back in the causal chain that led to you: 3.85 billion years ago, in some little tidal pool.

“Perhaps your children’s children will ask how it is that they are capable of love.

“And their parents will say: Because we, who also love, created you to love.

“And your children’s children will ask: But how is it that you love?

“And their parents will reply: Because our own parents, who also loved, created us to love in turn.

“Then your children’s children will ask: But where did it all begin? Where does the recursion end?

“And their parents will say: Once upon a time, long ago and far away, ever so long ago, there were intelligent beings who were not themselves intelligently designed. Once upon a time, there were lovers created by something that did not love.

“Once upon a time, when all of civilization was a single galaxy and a single star: and a single planet. A place called Earth.

“Long ago, and far away, ever so long ago.”

Part W
Quantified Humanism

281
Scope Insensitivity

Once upon a time, three groups of subjects were asked how much they would pay to save 2,000 20,000 200,000 migrating birds from drowning in uncovered oil ponds. The groups respectively answered $80, $78, and $88.¹ This is scope insensitivity or scope neglect: the number of birds saved—the scope of the altruistic action—had little effect on willingness to pay.

Similar experiments showed that Toronto residents would pay little more to clean up all polluted lakes in Ontario than polluted lakes in a particular region of Ontario,² or that residents of four western US states would pay only 28% more to protect all 57 wilderness areas in those states than to protect a single area.³ People visualize “a single exhausted bird, its feathers soaked in black oil, unable to escape.”⁴ This image, or prototype, calls forth some level of emotional arousal that is primarily responsible for willingness-to-pay—and the image is the same in all cases. As for scope, it gets tossed out the window—no human can visualize 2,000 birds at once, let alone 200,000. The usual finding is that exponential increases in scope create linear increases in willingness-to-pay—perhaps corresponding to the linear time for our eyes to glaze over the zeroes; this small amount of affect is added, not multiplied, with the prototype affect. This hypothesis is known as “valuation by prototype.”

An alternative hypothesis is “purchase of moral satisfaction.” People spend enough money to create a warm glow in themselves, a sense of having done their duty. The level of spending needed to purchase a warm glow depends on personality and financial situation, but it certainly has nothing to do with the number of birds.

We are insensitive to scope even when human lives are at stake: Increasing the alleged risk of chlorinated drinking water from 0.004 to 2.43 annual deaths per 1,000—a factor of 600—increased willingness-to-pay from $3.78 to $15.23.⁵ Baron and Greene found no effect from varying lives saved by a factor of 10.⁶

A paper entitled “Insensitivity to the value of human life: A study of psychophysical numbing” collected evidence that our perception of human deaths follows Weber’s Law—obeys a logarithmic scale where the “just noticeable difference” is a constant fraction of the whole. A proposed health program to save the lives of Rwandan refugees garnered far higher support when it promised to save 4,500 lives in a camp of 11,000 refugees, rather than 4,500 in a camp of 250,000. A potential disease cure had to promise to save far more lives in order to be judged worthy of funding, if the disease was originally stated to have killed 290,000 rather than 160,000 or 15,000 people per year.⁷

The moral: If you want to be an effective altruist, you have to think it through with the part of your brain that processes those unexciting inky zeroes on paper, not just the part that gets real worked up about that poor struggling oil-soaked bird.

1. William H. Desvousges et al., Measuring Nonuse Damages Using Contingent Valuation: An Experimental Evaluation of Accuracy, technical report (Research Triangle Park, NC: RTI International, 2010), doi:10.3768/rtipress.2009.bk.0001.1009.

2. Daniel Kahneman, “Comments by Professor Daniel Kahneman,” in Valuing Environmental Goods: An Assessment of the Contingent Valuation Method, ed. Ronald G. Cummings, David S. Brookshire, and William D. Schulze, vol. 1.B, Experimental Methods for Assessing Environmental Benefits (Totowa, NJ: Rowman & Allanheld, 1986), 226–235, http://yosemite.epa.gov/ee/epa/eerm.nsf/vwAN/EE-0280B-04.pdf/$file/EE-0280B-04.pdf.

3. Daniel L. McFadden and Gregory K. Leonard, “Issues in the Contingent Valuation of Environmental Goods: Methodologies for Data Collection and Analysis,” in Contingent Valuation: A Critical Assessment, ed. Jerry A. Hausman, Contributions to Economic Analysis220 (New York: North-Holland, 1993), 165–215, doi:10.1108/S0573-8555(1993)0000220007.

4. Kahneman, Ritov, and Schkade, “Economic Preferences or Attitude Expressions?”

5. Richard T. Carson and Robert Cameron Mitchell, “Sequencing and Nesting in Contingent Valuation Surveys,” Journal of Environmental Economics and Management 28, no. 2 (1995): 155–173, doi:10.1006/jeem.1995.1011.

6. Jonathan Baron and Joshua D. Greene, “Determinants of Insensitivity to Quantity in Valuation of Public Goods: Contribution, Warm Glow, Budget Constraints, Availability, and Prominence,” Journal of Experimental Psychology: Applied 2, no. 2 (1996): 107–125, doi:10.1037/1076-898X.2.2.107.

7. David Fetherstonhaugh et al., “Insensitivity to the Value of Human Life: A Study of Psychophysical Numbing,” Journal of Risk and Uncertainty 14, no. 3 (1997): 283–300, doi:10.1023/A:1007744326393.

282
One Life Against the World

Whoever saves a single life, it is as if he had saved the whole world.

—The Talmud, Sanhedrin 4:5

It’s a beautiful thought, isn’t it? Feel that warm glow.

I can testify that helping one person feels just as good as helping the whole world. Once upon a time, when I was burned out for the day and wasting time on the Internet—it’s a bit complicated, but essentially I managed to turn someone’s whole life around by leaving an anonymous blog comment. I wasn’t expecting it to have an effect that large, but it did. When I discovered what I had accomplished, it gave me a tremendous high. The euphoria lasted through that day and into the night, only wearing off somewhat the next morning. It felt just as good (this is the scary part) as the euphoria of a major scientific insight, which had previously been my best referent for what it might feel like to do drugs.

Saving one life probably does feel just as good as being the first person to realize what makes the stars shine. It probably does feel just as good as saving the entire world.

But if you ever have a choice, dear reader, between saving a single life and saving the whole world—then save the world. Please. Because beyond that warm glow is one heck of a gigantic difference. For some people, the notion that saving the world is significantly better than saving one human life will be obvious, like saying that six billion dollars is worth more than one dollar, or that six cubic kilometers of gold weighs more than one cubic meter of gold. (And never mind the expected value of posterity.) Why might it not be obvious? Well, suppose there’s a qualitative duty to save what lives you can—then someone who saves the world, and someone who saves one human life, are just fulfilling the same duty. Or suppose that we follow the Greek conception of personal virtue, rather than consequentialism; someone who saves the world is virtuous, but not six billion times as virtuous as someone who saves one human life. Or perhaps the value of one human life is already too great to comprehend—so that the passing grief we experience at funerals is an infinitesimal underestimate of what is lost—and thus passing to the entire world changes little.

I agree that one human life is of unimaginably high value. I also hold that two human lives are twice as unimaginably valuable. Or to put it another way: Whoever saves one life, if it is as if they had saved the whole world; whoever saves ten lives, it is as if they had saved ten worlds. Whoever actually saves the whole world—not to be confused with pretend rhetorical saving the world—it is as if they had saved an intergalactic civilization.

Two deaf children are sleeping on the railroad tracks, the train speeding down; you see this, but you are too far away to save the children. I’m nearby, within reach, so I leap forward and drag one child off the railroad tracks—and then stop, calmly sipping a Diet Pepsi as the train bears down on the second child. “Quick!” you scream to me. “Do something!” But (I call back) I already saved one child from the train tracks, and thus I am “unimaginably” far ahead on points. Whether I save the second child, or not, I will still be credited with an “unimaginably” good deed. Thus, I have no further motive to act. Doesn’t sound right, does it?

Why should it be any different if a philanthropist spends $10 million on curing a rare but spectacularly fatal disease which afflicts only a hundred people planetwide, when the same money has an equal probability of producing a cure for a less spectacular disease that kills 10% of 100,000 people? I don’t think it is different. When human lives are at stake, we have a duty to maximize, not satisfice; and this duty has the same strength as the original duty to save lives. Whoever knowingly chooses to save one life, when they could have saved two—to say nothing of a thousand lives, or a world—they have damned themselves as thoroughly as any murderer.

It’s not cognitively easy to spend money to save lives, since cliché methods that instantly leap to mind don’t work or are counterproductive. (I will write later on why this tends to be so.) Stuart Armstrong also points out that if we are to disdain the philanthropist who spends life-saving money inefficiently, we should be consistent and disdain more those who could spend money to save lives but don’t.

283
The Allais Paradox

Choose between the following two options:

1A. $24,000, with certainty.

1B. 33/34 chance of winning $27,000, and 1/34 chance of winning nothing.

Which seems more intuitively appealing? And which one would you choose in real life? Now which of these two options would you intuitively prefer, and which would you choose in real life?

2A. 34% chance of winning $24,000, and 66% chance of winning nothing.

2B. 33% chance of winning $27,000, and 67% chance of winning nothing.

The Allais Paradox—as Allais called it, though it’s not really a paradox—was one of the first conflicts between decision theory and human reasoning to be experimentally exposed, in 1953.¹ I’ve modified it slightly for ease of math, but the essential problem is the same: Most people prefer 1A to 1B, and most people prefer 2B to 2A. Indeed, in within-subject comparisons, a majority of subjects express both preferences simultaneously.

This is a problem because the 2s are equal to a one-third chance of playing the 1s. That is, 2A is equivalent to playing gamble 1A with 34% probability, and 2B is equivalent to playing 1B with 34% probability.

Among the axioms used to prove that “consistent” decisionmakers can be viewed as maximizing expected utility is the Axiom of Independence: If X is strictly preferred to Y, then a probability P of X and (1 - P) of Z should be strictly preferred to P chance of Y and (1 - P) chance of Z.

All the axioms are consequences, as well as antecedents, of a consistent utility function. So it must be possible to prove that the experimental subjects above can’t have a consistent utility function over outcomes. And indeed, you can’t simultaneously have:

U($24,000) > (33/34) × U($27,000) + (1/34) × U($0)

0.34 × U($24,000) + 0.66 × U($0) < 0.33 × U($27,000) + 0.67 × U($0).

These two equations are algebraically inconsistent, regardless of U, so the Allais Paradox has nothing to do with the diminishing marginal utility of money.

Maurice Allais initially defended the revealed preferences of the experimental subjects—he saw the experiment as exposing a flaw in the conventional ideas of utility, rather than exposing a flaw in human psychology. This was 1953, after all, and the heuristics-and-biases movement wouldn’t really get started for another two decades. Allais thought his experiment just showed that the Axiom of Independence clearly wasn’t a good idea in real life.

(How naive, how foolish, how simplistic is Bayesian decision theory . . .)

Surely the certainty of having $24,000 should count for something. You can feel the difference, right? The solid reassurance?

(I’m starting to think of this as “naive philosophical realism”—supposing that our intuitions directly expose truths about which strategies are wiser, as though it were a directly perceived fact that “1A is superior to 1B.” Intuitions directly expose truths about human cognitive functions, and only indirectly expose (after we reflect on the cognitive functions themselves) truths about rationality.)

“But come now,” you say, “is it really such a terrible thing to depart from Bayesian beauty?” Okay, so the subjects didn’t follow the neat little “independence axiom” espoused by the likes of von Neumann and Morgenstern. Yet who says that things must be neat and tidy?

Why fret about elegance, if it makes us take risks we don’t want? Expected utility tells us that we ought to assign some kind of number to an outcome, and then multiply that value by the outcome’s probability, add them up, etc. Okay, but why do we have to do that? Why not make up more palatable rules instead?

There is always a price for leaving the Bayesian Way. That’s what coherence and uniqueness theorems are all about.

In this case, if an agent prefers 1A to 1B, and 2B to 2A, it introduces a form of preference reversal—a dynamic inconsistency in the agent’s planning. You become a money pump.

Suppose that at 12:00 p.m. I roll a hundred-sided die. If the die shows a number greater than 34, the game terminates. Otherwise, at 12:05 p.m. I consult a switch with two settings, A and B. If the setting is A, I pay you $24,000. If the setting is B, I roll a 34-sided die and pay you $27,000 unless the die shows “34,” in which case I pay you nothing.

Let’s say you prefer 1A over 1B, and 2B over 2A, and you would pay a single penny to indulge each preference. The switch starts in state A. Before 12:00 p.m., you pay me a penny to throw the switch to B. The die comes up 12. After 12:00 p.m. and before 12:05 p.m., you pay me a penny to throw the switch to A.

I have taken your two cents on the subject. If you indulge your intuitions, and dismiss mere elegance as a pointless obsession with neatness, then don’t be surprised when your pennies get taken from you . . .

(I think the same failure to proportionally devalue the emotional impact of small probabilities is responsible for the lottery.)

1. Maurice Allais, “Le Comportement de l’Homme Rationnel devant le Risque: Critique des Postulats et Axiomes de l’Ecole Americaine,” Econometrica 21, no. 4 (1953): 2, doi:10.2307/1907921; Daniel Kahneman and Amos Tversky, “Prospect Theory: An Analysis of Decision Under Risk,” Econometrica 47 (1979): 263–292.

284
Zut Allais!

Huh! I was not expecting so many commenters to defend the preference reversal. Looks like I ran into an inferential distance.

It probably helps in interpreting the Allais Paradox to have absorbed more of the gestalt of the field of heuristics and biases, such as:

Experimental subjects tend to defend incoherent preferences even when they’re really silly.
People put very high values on small shifts in probability away from 0 or 1 (the certainty effect).

Let’s start with the issue of incoherent preferences—preference reversals, dynamic inconsistency, money pumps, that sort of thing.

Anyone who knows a little prospect theory will have no trouble constructing cases where people say they would prefer to play gamble A rather than gamble B; but when you ask them to price the gambles they put a higher value on gamble B than gamble A. There are different perceptual features that become salient when you ask “Which do you prefer?” in a direct comparison, and “How much would you pay?” with a single item.

This choice of gambles typically generates a preference reversal:

1/3 chance to win $16 and 2/3 chance to lose $2.
99/100 chance to win $4 and 1/100 chance to lose $1.

Most people will rather play 2 than 1. But if you ask them to price the bets separately—ask for a price at which they would be indifferent between having that amount of money, and having a chance to play the gamble—people will put a higher price on 1 than on 2.¹

So first you sell them a chance to play bet 1, at their stated price. Then you offer to trade bet 1 for bet 2. Then you buy bet 2 back from them, at their stated price. Then you do it again. Hence the phrase, “money pump.”

Or to paraphrase Steve Omohundro: If you would rather be in Oakland than San Francisco, and you would rather be in San Jose than Oakland, and you would rather be in San Francisco than San Jose, you’re going to spend an awful lot of money on taxi rides.

Amazingly, people defend these preference patterns. Some subjects abandon them after the money-pump effect is pointed out—revise their price or revise their preference—but some subjects defend them.

On one occasion, gamblers in Las Vegas played these kinds of bets for real money, using a roulette wheel. And afterward, one of the researchers tried to explain the problem with the incoherence between their pricing and their choices. From the transcript:²^,³

SARAH LICHTENSTEIN: “Well, how about the bid for Bet A? Do you have any further feelings about it now that you know you are choosing one but bidding more for the other one?”

SUBJECT: “It’s kind of strange, but no, I don’t have any feelings at all whatsoever really about it. It’s just one of those things. It shows my reasoning process isn’t so good, but, other than that, I . . . no qualms.”

. . .

LICHTENSTEIN: “Can I persuade you that it is an irrational pattern?”

SUBJECT: “No, I don’t think you probably could, but you could try.”

. . .

LICHTENSTEIN: “Well, now let me suggest what has been called a money-pump game and try this out on you and see how you like it. If you think Bet A is worth 550 points [points were converted to dollars after the game, though not on a one-to-one basis] then you ought to be willing to give me 550 points if I give you the bet . . .”

. . .

LICHTENSTEIN: “So you have Bet A, and I say, ‘Oh, you’d rather have Bet B wouldn’t you?’”

. . .

SUBJECT: “I’m losing money.”

LICHTENSTEIN: “I’ll buy Bet B from you. I’ll be generous; I’ll pay you more than 400 points. I’ll pay you 401 points. Are you willing to sell me Bet B for 401 points?”

SUBJECT: “Well, certainly.”

. . .

LICHTENSTEIN: “I’m now ahead 149 points.”

SUBJECT: “That’s good reasoning on my part. (laughs) How many times are we going to go through this?”

. . .

LICHTENSTEIN: “Well, I think I’ve pushed you as far as I know how to push you short of actually insulting you.”

SUBJECT: “That’s right.”

You want to scream, “Just give up already! Intuition isn’t always right!”

And then there’s the business of the strange value that people attach to certainty. My books are packed up for the move, but I believe that one experiment showed that a shift from 100% probability to 99% probability weighed larger in people’s minds than a shift from 80% probability to 20% probability.

The problem with attaching a huge extra value to certainty is that one time’s certainty is another time’s probability.

In the last essay, I talked about the Allais Paradox:

1A. $24,000, with certainty.
1B. 33/34 chance of winning $27,000, and 1/34 chance of winning nothing.
2A. 34% chance of winning $24,000, and 66% chance of winning nothing.
2B. 33% chance of winning $27,000, and 67% chance of winning nothing.

The naive preference pattern on the Allais Paradox is 1A > 1B and 2B > 2A. Then you will pay me to throw a switch from A to B because you’d rather have a 33% chance of winning $27,000 than a 34% chance of winning $24,000. Then a die roll eliminates a chunk of the probability mass. In both cases you had at least a 66% chance of winning nothing. This die roll eliminates that 66%. So now option B is a 33/34 chance of winning $27,000, but option A is a certainty of winning $24,000. Oh, glorious certainty! So you pay me to throw the switch back from B to A.

Now, if I’ve told you in advance that I’m going to do all that, do you really want to pay me to throw the switch, and then pay me to throw it back? Or would you prefer to reconsider?

Whenever you try to price a probability shift from 24% to 23% as being less important than a shift from 1 to 99%—every time you try to make an increment of probability have more value when it’s near an end of the scale—you open yourself up to this kind of exploitation. I can always set up a chain of events that eliminates the probability mass, a bit at a time, until you’re left with “certainty” that flips your preferences. One time’s certainty is another time’s uncertainty, and if you insist on treating the distance from 1 to 0.99 as special, I can cause you to invert your preferences over time and pump some money out of you.

Can I persuade you, perhaps, that this is an irrational pattern?

Surely, if you’ve been reading this book for a while, you realize that you—the very system and process that reads these very words—are a flawed piece of machinery. Your intuitions are not giving you direct, veridical information about good choices. If you don’t believe that, there are some gambling games I’d like to play with you.

There are various other games you can also play with certainty effects. For example, if you offer someone a certainty of $400, or an 80% probability of $500 and a 20% probability of $300, they’ll usually take the $400. But if you ask people to imagine themselves $500 richer, and ask if they would prefer a certain loss of $100 or a 20% chance of losing $200, they’ll usually take the chance of losing $200.⁴ Same probability distribution over outcomes, different descriptions, different choices.

Yes, Virginia, you really should try to multiply the utility of outcomes by their probability. You really should. Don’t be embarrassed to use clean math.

In the Allais paradox, figure out whether 1 unit of the difference between getting $24,000 and getting nothing outweighs 33 units of the difference between getting $24,000 and $27,000. If it does, prefer 1A to 1B and 2A to 2B. If the 33 units outweigh the 1 unit, prefer 1B to 1A and 2B to 2A. As for calculating the utility of money, I would suggest using an approximation that assumes money is logarithmic in utility. If you’ve got plenty of money already, pick B. If $24,000 would double your existing assets, pick A. Case 2 or case 1, makes no difference. Oh, and be sure to assess the utility of total asset values—the utility of final outcome states of the world—not changes in assets, or you’ll end up inconsistent again.

A number of commenters claimed that the preference pattern wasn’t irrational because of “the utility of certainty,” or something like that. One commenter even wrote U(Certainty) into an expected utility equation.

Does anyone remember that whole business about expected utility and utility being of fundamentally different types? Utilities are over outcomes. They are values you attach to particular, solid states of the world. You cannot feed a probability of 1 into a utility function. It makes no sense.

And before you sniff, “Hmph . . . you just want the math to be neat and tidy,” remember that, in this case, the price of departing the Bayesian Way was paying someone to throw a switch and then throw it back.

But what about that solid, warm feeling of reassurance? Isn’t that a utility?

That’s being human. Humans are not expected utility maximizers. Whether you want to relax and have fun, or pay some extra money for a feeling of certainty, depends on whether you care more about satisfying your intuitions or actually achieving the goal.

If you’re gambling at Las Vegas for fun, then by all means, don’t think about the expected utility—you’re going to lose money anyway.

But what if it were 24,000 lives at stake, instead of $24,000? The certainty effect is even stronger over human lives. Will you pay one human life to throw the switch, and another to switch it back?

Tolerating preference reversals makes a mockery of claims to optimization. If you drive from San Jose to San Francisco to Oakland to San Jose, over and over again, then you may get a lot of warm fuzzy feelings out of it, but you can’t be interpreted as having a destination—as trying to go somewhere.

When you have circular preferences, you’re not steering the future—just running in circles. If you enjoy running for its own sake, then fine. But if you have a goal—something you’re trying to actually accomplish—a preference reversal reveals a big problem. At least one of the choices you’re making must not be working to actually optimize the future in any coherent sense.

If what you care about is the warm fuzzy feeling of certainty, then fine. If someone’s life is at stake, then you had best realize that your intuitions are a greasy lens through which to see the world. Your feelings are not providing you with direct, veridical information about strategic consequences—it feels that way, but they’re not. Warm fuzzies can lead you far astray.

There are mathematical laws governing efficient strategies for steering the future. When something truly important is at stake—something more important than your feelings of happiness about the decision—then you should care about the math, if you truly care at all.

1. Sarah Lichtenstein and Paul Slovic, “Reversals of Preference Between Bids and Choices in Gambing Decisions,” Journal of Experimental Psychology 89, no. 1 (1971): 46–55.

2. William Poundstone, Priceless: The Myth of Fair Value (and How to Take Advantage of It) (Hill & Wang, 2010).

3. Sarah Lichtenstein and Paul Slovic, eds., The Construction of Preference (Cambridge University Press, 2006).

4. Kahneman and Tversky, “Prospect Theory: An Analysis of Decision Under Risk.”

285
Feeling Moral

Suppose that a disease, or a monster, or a war, or something, is killing people. And suppose you only have enough resources to implement one of the following two options:

Save 400 lives, with certainty.
Save 500 lives, with 90% probability; save no lives, 10% probability.

Most people choose option 1. Which, I think, is foolish; because if you multiply 500 lives by 90% probability, you get an expected value of 450 lives, which exceeds the 400-life value of option 1. (Lives saved don’t diminish in marginal utility, so this is an appropriate calculation.)

“What!” you cry, incensed. “How can you gamble with human lives? How can you think about numbers when so much is at stake? What if that 10% probability strikes, and everyone dies? So much for your damned logic! You’re following your rationality off a cliff!”

Ah, but here’s the interesting thing. If you present the options this way:

100 people die, with certainty.
90% chance no one dies; 10% chance 500 people die.

Then a majority choose option 2. Even though it’s the same gamble. You see, just as a certainty of saving 400 lives seems to feel so much more comfortable than an unsure gain, so too, a certain loss feels worse than an uncertain one.

You can grandstand on the second description too: “How can you condemn 100 people to certain death when there’s such a good chance you can save them? We’ll all share the risk! Even if it was only a 75% chance of saving everyone, it would still be worth it—so long as there’s a chance—everyone makes it, or no one does!”

You know what? This isn’t about your feelings. A human life, with all its joys and all its pains, adding up over the course of decades, is worth far more than your brain’s feelings of comfort or discomfort with a plan. Does computing the expected utility feel too cold-blooded for your taste? Well, that feeling isn’t even a feather in the scales, when a life is at stake. Just shut up and multiply.

A googol is 10¹⁰⁰—a 1 followed by one hundred zeroes. A googolplex is an even more incomprehensibly large number—it’s 10^googol, a 1 followed by a googol zeroes. Now pick some trivial inconvenience, like a hiccup, and some decidedly untrivial misfortune, like getting slowly torn limb from limb by sadistic mutant sharks. If we’re forced into a choice between either preventing a googolplex people’s hiccups, or preventing a single person’s shark attack, which choice should we make? If you assign any negative value to hiccups, then, on pain of decision-theoretic incoherence, there must be some number of hiccups that would add up to rival the negative value of a shark attack. For any particular finite evil, there must be some number of hiccups that would be even worse.

Moral dilemmas like these aren’t conceptual blood sports for keeping analytic philosophers entertained at dinner parties. They’re distilled versions of the kinds of situations we actually find ourselves in every day. Should I spend $50 on a console game, or give it all to charity? Should I organize a $700,000 fundraiser to pay for a single bone marrow transplant, or should I use that same money on mosquito nets and prevent the malaria deaths of some 200 children?

Yet there are many who avert their gaze from the real world’s abundance of unpleasant moral tradeoffs—many, too, who take pride in looking away. Research shows that people distinguish “sacred values,” like human lives, from “unsacred values,” like money. When you try to trade off a sacred value against an unsacred value, subjects express great indignation. (Sometimes they want to punish the person who made the suggestion.)

My favorite anecdote along these lines comes from a team of researchers who evaluated the effectiveness of a certain project, calculating the cost per life saved, and recommended to the government that the project be implemented because it was cost-effective. The governmental agency rejected the report because, they said, you couldn’t put a dollar value on human life. After rejecting the report, the agency decided not to implement the measure.

Trading off a sacred value against an unsacred value feels really awful. To merely multiply utilities would be too cold-blooded—it would be following rationality off a cliff . . .

But altruism isn’t the warm fuzzy feeling you get from being altruistic. If you’re doing it for the spiritual benefit, that is nothing but selfishness. The primary thing is to help others, whatever the means. So shut up and multiply!

And if it seems to you that there is a fierceness to this maximization, like the bare sword of the law, or the burning of the Sun—if it seems to you that at the center of this rationality there is a small cold flame—

Well, the other way might feel better inside you. But it wouldn’t work.

And I say also this to you: That if you set aside your regret for all the spiritual satisfaction you could be having—if you wholeheartedly pursue the Way, without thinking that you are being cheated—if you give yourself over to rationality without holding back, you will find that rationality gives to you in return.

But that part only works if you don’t go around saying to yourself, “It would feel better inside me if only I could be less rational.” Should you be sad that you have the opportunity to actually help people? You cannot attain your full potential if you regard your gift as a burden.

286
The “Intuitions” Behind “Utilitarianism”

I used to be very confused about metaethics. After my confusion finally cleared up, I did a postmortem on my previous thoughts. I found that my object-level moral reasoning had been valuable and my meta-level moral reasoning had been worse than useless. And this appears to be a general syndrome—people do much better when discussing whether torture is good or bad than when they discuss the meaning of “good” and “bad.” Thus, I deem it prudent to keep moral discussions on the object level wherever I possibly can.

Occasionally people object to any discussion of morality on the grounds that morality doesn’t exist, and in lieu of explaining that “exist” is not the right term to use here, I generally say, “But what do you do anyway?” and take the discussion back down to the object level.

Paul Gowder, though, has pointed out that both the idea of choosing a googolplex trivial inconveniences over one atrocity, and the idea of “utilitarianism,” depend on “intuition.” He says I’ve argued that the two are not compatible, but charges me with failing to argue for the utilitarian intuitions that I appeal to.

Now “intuition” is not how I would describe the computations that underlie human morality and distinguish us, as moralists, from an ideal philosopher of perfect emptiness and/or a rock. But I am okay with using the word “intuition” as a term of art, bearing in mind that “intuition” in this sense is not to be contrasted to reason, but is, rather, the cognitive building block out of which both long verbal arguments and fast perceptual arguments are constructed.

I see the project of morality as a project of renormalizing intuition. We have intuitions about things that seem desirable or undesirable, intuitions about actions that are right or wrong, intuitions about how to resolve conflicting intuitions, intuitions about how to systematize specific intuitions into general principles.

Delete all the intuitions, and you aren’t left with an ideal philosopher of perfect emptiness; you’re left with a rock.

Keep all your specific intuitions and refuse to build upon the reflective ones, and you aren’t left with an ideal philosopher of perfect spontaneity and genuineness; you’re left with a grunting caveperson running in circles, due to cyclical preferences and similar inconsistencies.

“Intuition,” as a term of art, is not a curse word when it comes to morality—there is nothing else to argue from. Even modus ponens is an “intuition” in this sense—it’s just that modus ponens still seems like a good idea after being formalized, reflected on, extrapolated out to see if it has sensible consequences, et cetera.

So that is “intuition.”

However, Gowder did not say what he meant by “utilitarianism.” Does utilitarianism say . . .

That right actions are strictly determined by good consequences?
That praiseworthy actions depend on justifiable expectations of good consequences?
That probabilities of consequences should normatively be discounted by their probability, so that a 50% probability of something bad should weigh exactly half as much in our tradeoffs?
That virtuous actions always correspond to maximizing expected utility under some utility function?
That two harmful events are worse than one?
That two independent occurrences of a harm (not to the same person, not interacting with each other) are exactly twice as bad as one?
That for any two harms A and B, with A much worse than B, there exists some tiny probability such that gambling on this probability of A is preferable to a certainty of B?

If you say that I advocate something, or that my argument depends on something, and that it is wrong, do please specify what this thingy is. Anyway, I accept 3, 5, 6, and 7, but not 4; I am not sure about the phrasing of 1; and 2 is true, I guess, but phrased in a rather solipsistic and selfish fashion: you should not worry about being praiseworthy.

Now, what are the “intuitions” upon which my “utilitarianism” depends?

This is a deepish sort of topic, but I’ll take a quick stab at it.

First of all, it’s not just that someone presented me with a list of statements like those above, and I decided which ones sounded “intuitive.” Among other things, if you try to violate “utilitarianism,” you run into paradoxes, contradictions, circular preferences, and other things that aren’t symptoms of moral wrongness so much as moral incoherence.

After you think about moral problems for a while, and also find new truths about the world, and even discover disturbing facts about how you yourself work, you often end up with different moral opinions than when you started out. This does not quite define moral progress, but it is how we experience moral progress.

As part of my experienced moral progress, I’ve drawn a conceptual separation between questions of type Where should we go? and questions of type How should we get there? (Could that be what Gowder means by saying I’m “utilitarian”?)

The question of where a road goes—where it leads—you can answer by traveling the road and finding out. If you have a false belief about where the road leads, this falsity can be destroyed by the truth in a very direct and straightforward manner.

When it comes to wanting to go to a particular place, this want is not entirely immune from the destructive powers of truth. You could go there and find that you regret it afterward (which does not define moral error, but is how we experience moral error).

But, even so, wanting to be in a particular place seems worth distinguishing from wanting to take a particular road to a particular place.

Our intuitions about where to go are arguable enough, but our intuitions about how to get there are frankly messed up. After the two hundred and eighty-seventh research study showing that people will chop their own feet off if you frame the problem the wrong way, you start to distrust first impressions.

When you’ve read enough research on scope insensitivity—people will pay only 28% more to protect all 57 wilderness areas in Ontario than one area, people will pay the same amount to save 50,000 lives as 5,000 lives . . . that sort of thing . . .

Well, the worst case of scope insensitivity I’ve ever heard of was described here by Slovic:

Other recent research shows similar results. Two Israeli psychologists asked people to contribute to a costly life-saving treatment. They could offer that contribution to a group of eight sick children, or to an individual child selected from the group. The target amount needed to save the child (or children) was the same in both cases. Contributions to individual group members far outweighed the contributions to the entire group.¹

There’s other research along similar lines, but I’m just presenting one example, ’cause, y’know, eight examples would probably have less impact.

If you know the general experimental paradigm, then the reason for the above behavior is pretty obvious—focusing your attention on a single child creates more emotional arousal than trying to distribute attention around eight children simultaneously. So people are willing to pay more to help one child than to help eight.

Now, you could look at this intuition, and think it was revealing some kind of incredibly deep moral truth which shows that one child’s good fortune is somehow devalued by the other children’s good fortune.

But what about the billions of other children in the world? Why isn’t it a bad idea to help this one child, when that causes the value of all the other children to go down? How can it be significantly better to have 1,329,342,410 happy children than 1,329,342,409, but then somewhat worse to have seven more at 1,329,342,417?

Or you could look at that and say: “The intuition is wrong: the brain can’t successfully multiply by eight and get a larger quantity than it started with. But it ought to, normatively speaking.”

And once you realize that the brain can’t multiply by eight, then the other cases of scope neglect stop seeming to reveal some fundamental truth about 50,000 lives being worth just the same effort as 5,000 lives, or whatever. You don’t get the impression you’re looking at the revelation of a deep moral truth about nonagglomerative utilities. It’s just that the brain doesn’t goddamn multiply. Quantities get thrown out the window.

If you have $100 to spend, and you spend $20 each on each of 5 efforts to save 5,000 lives, you will do worse than if you spend $100 on a single effort to save 50,000 lives. Likewise if such choices are made by 10 different people, rather than the same person. As soon as you start believing that it is better to save 50,000 lives than 25,000 lives, that simple preference of final destinations has implications for the choice of paths, when you consider five different events that save 5,000 lives.

(It is a general principle that Bayesians see no difference between the long-run answer and the short-run answer; you never get two different answers from computing the same question two different ways. But the long run is a helpful intuition pump, so I am talking about it anyway.)

The aggregative valuation strategy of “shut up and multiply” arises from the simple preference to have more of something—to save as many lives as possible—when you have to describe general principles for choosing more than once, acting more than once, planning at more than one time.

Aggregation also arises from claiming that the local choice to save one life doesn’t depend on how many lives already exist, far away on the other side of the planet, or far away on the other side of the universe. Three lives are one and one and one. No matter how many billions are doing better, or doing worse. 3 = 1 + 1 + 1, no matter what other quantities you add to both sides of the equation. And if you add another life you get 4 = 1 + 1 + 1 + 1. That’s aggregation.

When you’ve read enough heuristics and biases research, and enough coherence and uniqueness proofs for Bayesian probabilities and expected utility, and you’ve seen the “Dutch book” and “money pump” effects that penalize trying to handle uncertain outcomes any other way, then you don’t see the preference reversals in the Allais Paradox as revealing some incredibly deep moral truth about the intrinsic value of certainty. It just goes to show that the brain doesn’t goddamn multiply.

The primitive, perceptual intuitions that make a choice “feel good” don’t handle probabilistic pathways through time very skillfully, especially when the probabilities have been expressed symbolically rather than experienced as a frequency. So you reflect, devise more trustworthy logics, and think it through in words.

When you see people insisting that no amount of money whatsoever is worth a single human life, and then driving an extra mile to save $10; or when you see people insisting that no amount of money is worth a decrement of health, and then choosing the cheapest health insurance available; then you don’t think that their protestations reveal some deep truth about incommensurable utilities.

Part of it, clearly, is that primitive intuitions don’t successfully diminish the emotional impact of symbols standing for small quantities—anything you talk about seems like “an amount worth considering.”

And part of it has to do with preferring unconditional social rules to conditional social rules. Conditional rules seem weaker, seem more subject to manipulation. If there’s any loophole that lets the government legally commit torture, then the government will drive a truck through that loophole.

So it seems like there should be an unconditional social injunction against preferring money to life, and no “but” following it. Not even “but a thousand dollars isn’t worth a 0.0000000001% probability of saving a life.” Though the latter choice, of course, is revealed every time we sneeze without calling a doctor.

The rhetoric of sacredness gets bonus points for seeming to express an unlimited commitment, an unconditional refusal that signals trustworthiness and refusal to compromise. So you conclude that moral rhetoric espouses qualitative distinctions, because espousing a quantitative tradeoff would sound like you were plotting to defect.

On such occasions, people vigorously want to throw quantities out the window, and they get upset if you try to bring quantities back in, because quantities sound like conditions that would weaken the rule.

But you don’t conclude that there are actually two tiers of utility with lexical ordering. You don’t conclude that there is actually an infinitely sharp moral gradient, some atom that moves a Planck distance (in our continuous physical universe) and sends a utility from zero to infinity. You don’t conclude that utilities must be expressed using hyper-real numbers. Because the lower tier would simply vanish in any equation. It would never be worth the tiniest effort to recalculate for it. All decisions would be determined by the upper tier, and all thought spent thinking about the upper tier only, if the upper tier genuinely had lexical priority.

As Peter Norvig once pointed out, if Asimov’s robots had strict priority for the First Law of Robotics (“A robot shall not harm a human being, nor through inaction allow a human being to come to harm”) then no robot’s behavior would ever show any sign of the other two Laws; there would always be some tiny First Law factor that would be sufficient to determine the decision.

Whatever value is worth thinking about at all must be worth trading off against all other values worth thinking about, because thought itself is a limited resource that must be traded off. When you reveal a value, you reveal a utility.

I don’t say that morality should always be simple. I’ve already said that the meaning of music is more than happiness alone, more than just a pleasure center lighting up. I would rather see music composed by people than by nonsentient machine learning algorithms, so that someone should have the joy of composition; I care about the journey, as well as the destination. And I am ready to hear if you tell me that the value of music is deeper, and involves more complications, than I realize—that the valuation of this one event is more complex than I know.

But that’s for one event. When it comes to multiplying by quantities and probabilities, complication is to be avoided—at least if you care more about the destination than the journey. When you’ve reflected on enough intuitions, and corrected enough absurdities, you start to see a common denominator, a meta-principle at work, which one might phrase as “Shut up and multiply.”

Where music is concerned, I care about the journey.

When lives are at stake, I shut up and multiply.

It is more important that lives be saved, than that we conform to any particular ritual in saving them. And the optimal path to that destination is governed by laws that are simple, because they are math.

And that’s why I’m a utilitarian—at least when I am doing something that is overwhelmingly more important than my own feelings about it—which is most of the time, because there are not many utilitarians, and many things left undone.

1. Paul Slovic, “Numbed by Numbers,” Foreign Policy (March 2007), http://foreignpolicy.com/2007/03/13/numbed-by-numbers/.

287
Ends Don’t Justify Means (Among Humans)

If the ends don’t justify the means, what does?

—variously attributed

I think of myself as running on hostile hardware.

—Justin Corwin

Humans may have evolved a structure of political revolution, beginning by believing themselves morally superior to the corrupt current power structure, but ending by being corrupted by power themselves—not by any plan in their own minds, but by the echo of ancestors who did the same and thereby reproduced.

This fits the template:

In some cases, human beings have evolved in such fashion as to think that they are doing X for prosocial reason Y, but when human beings actually do X, other adaptations execute to promote self-benefiting consequence Z.

From this proposition, I now move on to a question considerably outside the realm of classical Bayesian decision theory:

What if I’m running on corrupted hardware?

In such a case as this, you might even find yourself uttering such seemingly paradoxical statements—sheer nonsense from the perspective of classical decision theory—as:

The ends don’t justify the means.

But if you are running on corrupted hardware, then the reflective observation that it seems like a righteous and altruistic act to seize power for yourself—this seeming may not be much evidence for the proposition that seizing power is in fact the action that will most benefit the tribe.

By the power of naive realism, the corrupted hardware that you run on, and the corrupted seemings that it computes, will seem like the fabric of the very world itself—simply the way-things-are.

And so we have the bizarre-seeming rule: “For the good of the tribe, do not cheat to seize power even when it would provide a net benefit to the tribe.”

Indeed it may be wiser to phrase it this way. If you just say, “when it seems like it would provide a net benefit to the tribe,” then you get people who say, “But it doesn’t just seem that way—it would provide a net benefit to the tribe if I were in charge.”

The notion of untrusted hardware seems like something wholly outside the realm of classical decision theory. (What it does to reflective decision theory I can’t yet say, but that would seem to be the appropriate level to handle it.)

But on a human level, the patch seems straightforward. Once you know about the warp, you create rules that describe the warped behavior and outlaw it. A rule that says, “For the good of the tribe, do not cheat to seize power even for the good of the tribe.” Or “For the good of the tribe, do not murder even for the good of the tribe.”

And now the philosopher comes and presents their “thought experiment”—setting up a scenario in which, by stipulation, the only possible way to save five innocent lives is to murder one innocent person, and this murder is certain to save the five lives. “There’s a train heading to run over five innocent people, who you can’t possibly warn to jump out of the way, but you can push one innocent person into the path of the train, which will stop the train. These are your only options; what do you do?”

An altruistic human, who has accepted certain deontological prohibitions—which seem well justified by some historical statistics on the results of reasoning in certain ways on untrustworthy hardware—may experience some mental distress, on encountering this thought experiment.

So here’s a reply to that philosopher’s scenario, which I have yet to hear any philosopher’s victim give:

“You stipulate that the only possible way to save five innocent lives is to murder one innocent person, and this murder will definitely save the five lives, and that these facts are known to me with effective certainty. But since I am running on corrupted hardware, I can’t occupy the epistemic state you want me to imagine. Therefore I reply that, in a society of Artificial Intelligences worthy of personhood and lacking any inbuilt tendency to be corrupted by power, it would be right for the AI to murder the one innocent person to save five, and moreover all its peers would agree. However, I refuse to extend this reply to myself, because the epistemic state you ask me to imagine can only exist among other kinds of people than human beings.”

Now, to me this seems like a dodge. I think the universe is sufficiently unkind that we can justly be forced to consider situations of this sort. The sort of person who goes around proposing that sort of thought experiment might well deserve that sort of answer. But any human legal system does embody some answer to the question “How many innocent people can we put in jail to get the guilty ones?,” even if the number isn’t written down.

As a human, I try to abide by the deontological prohibitions that humans have made to live in peace with one another. But I don’t think that our deontological prohibitions are literally inherently nonconsequentially terminally right. I endorse “the end doesn’t justify the means” as a principle to guide humans running on corrupted hardware, but I wouldn’t endorse it as a principle for a society of AIs that make well-calibrated estimates. (If you have one AI in a society of humans, that does bring in other considerations, like whether the humans learn from your example.)

And so I wouldn’t say that a well-designed Friendly AI must necessarily refuse to push that one person off the ledge to stop the train. Obviously, I would expect any decent superintelligence to come up with a superior third alternative. But if those are the only two alternatives, and the FAI judges that it is wiser to push the one person off the ledge—even after taking into account knock-on effects on any humans who see it happen and spread the story, etc.—then I don’t call it an alarm light, if an AI says that the right thing to do is sacrifice one to save five. Again, I don’t go around pushing people into the paths of trains myself, nor stealing from banks to fund my altruistic projects. I happen to be a human. But for a Friendly AI to be corrupted by power would be like it starting to bleed red blood. The tendency to be corrupted by power is a specific biological adaptation, supported by specific cognitive circuits, built into us by our genes for a clear evolutionary reason. It wouldn’t spontaneously appear in the code of a Friendly AI any more than its transistors would start to bleed.

I would even go further, and say that if you had minds with an inbuilt warp that made them overestimate the external harm of self-benefiting actions, then they would need a rule “the ends do not prohibit the means”—that you should do what benefits yourself even when it (seems to) harm the tribe. By hypothesis, if their society did not have this rule, the minds in it would refuse to breathe for fear of using someone else’s oxygen, and they’d all die. For them, an occasional overshoot in which one person seizes a personal benefit at the net expense of society would seem just as cautiously virtuous—and indeed be just as cautiously virtuous—as when one of us humans, being cautious, passes up an opportunity to steal a loaf of bread that really would have been more of a benefit to them than a loss to the merchant (including knock-on effects).

“The end does not justify the means” is just consequentialist reasoning at one meta-level up. If a human starts thinking on the object level that the end justifies the means, this has awful consequences given our untrustworthy brains; therefore a human shouldn’t think this way. But it is all still ultimately consequentialism. It’s just reflective consequentialism, for beings who know that their moment-by-moment decisions are made by untrusted hardware.

288
Ethical Injunctions

Would you kill babies if it was the right thing to do? If no, under what circumstances would you not do the right thing to do? If yes, how right would it have to be, for how many babies?

—horrible job interview question

Swapping hats for a moment, I’m professionally intrigued by the decision theory of “things you shouldn’t do even if they seem to be the right thing to do.”

Suppose we have a reflective AI, self-modifying and self-improving, at an intermediate stage in the development process. In particular, the AI’s goal system isn’t finished—the shape of its motivations is still being loaded, learned, tested, or tweaked.

Yea, I have seen many ways to screw up an AI goal system design, resulting in a decision system that decides, given its goals, that the universe ought to be tiled with tiny molecular smiley-faces, or some such. Generally, these deadly suggestions also have the property that the AI will not desire its programmers to fix it. If the AI is sufficiently advanced—which it may be even at an intermediate stage—then the AI may also realize that deceiving the programmers, hiding the changes in its thoughts, will help transform the universe into smiley-faces.

Now, from our perspective as programmers, if we condition on the fact that the AI has decided to hide its thoughts from the programmers, or otherwise act willfully to deceive us, then it would seem likely that some kind of unintended consequence has occurred in the goal system. We would consider it probable that the AI is not functioning as intended, but rather likely that we have messed up the AI’s utility function somehow. So that the AI wants to turn the universe into tiny reward-system counters, or some such, and now has a motive to hide from us.

Well, suppose we’re not going to implement some object-level Great Idea as the AI’s utility function. Instead we’re going to do something advanced and recursive—build a goal system which knows (and cares) about the programmers outside. A goal system that, via some nontrivial internal structure, “knows it’s being programmed” and “knows it’s incomplete.” Then you might be able to have and keep the rule:

If [I decide that] fooling my programmers is the right thing to do, execute a controlled shutdown [instead of doing the right thing to do].

And the AI would keep this rule, even through the self-modifying AI’s revisions of its own code, because, in its structurally nontrivial goal system, the present-AI understands that this decision by a future-AI probably indicates something defined-as-a-malfunction. Moreover, the present-AI knows that if future-AI tries to evaluate the utility of executing a shutdown, once this hypothetical malfunction has occurred, the future-AI will probably decide not to shut itself down. So the shutdown should happen unconditionally, automatically, without the goal system getting another chance to recalculate the right thing to do.

I’m not going to go into the deep dark depths of the exact mathematical structure, because that would be beyond the scope of this book. Also I don’t yet know the deep dark depths of the mathematical structure. It looks like it should be possible, if you do things that are advanced and recursive and have nontrivial (but consistent) structure. But I haven’t reached that level, as yet, so for now it’s only a dream.

But the topic here is not advanced AI; it’s human ethics. I introduce the AI scenario to bring out more starkly the strange idea of an ethical injunction:

You should never, ever murder an innocent person who’s helped you, even if it’s the right thing to do; because it’s far more likely that you’ve made a mistake, than that murdering an innocent person who helped you is the right thing to do.

Sound reasonable?

During World War II, it became necessary to destroy Germany’s supply of deuterium, a neutron moderator, in order to block their attempts to achieve a fission chain reaction. Their supply of deuterium was coming at this point from a captured facility in Norway. A shipment of heavy water was on board a Norwegian ferry ship, the SF Hydro. Knut Haukelid and three others had slipped on board the ferry in order to sabotage it, when the saboteurs were discovered by the ferry watchman. Haukelid told him that they were escaping the Gestapo, and the watchman immediately agreed to overlook their presence. Haukelid “considered warning their benefactor but decided that might endanger the mission and only thanked him and shook his hand.”¹ So the civilian ferry Hydro sank in the deepest part of the lake, with eighteen dead and twenty-nine survivors. Some of the Norwegian rescuers felt that the German soldiers present should be left to drown, but this attitude did not prevail, and four Germans were rescued. And that was, effectively, the end of the Nazi atomic weapons program.

Good move? Bad move? Germany very likely wouldn’t have gotten the Bomb anyway . . . I hope with absolute desperation that I never get faced by a choice like that, but in the end, I can’t say a word against it.

On the other hand, when it comes to the rule:

Never try to deceive yourself, or offer a reason to believe other than probable truth; because even if you come up with an amazing clever reason, it’s more likely that you’ve made a mistake than that you have a reasonable expectation of this being a net benefit in the long run.

Then I really don’t know of anyone who’s knowingly been faced with an exception. There are times when you try to convince yourself “I’m not hiding any Jews in my basement” before you talk to the Gestapo officer. But then you do still know the truth, you’re just trying to create something like an alternative self that exists in your imagination, a facade to talk to the Gestapo officer.

But to really believe something that isn’t true? I don’t know if there was ever anyone for whom that was knowably a good idea. I’m sure that there have been many many times in human history, where person X was better off with false belief Y. And by the same token, there is always some set of winning lottery numbers in every drawing. It’s knowing which lottery ticket will win that is the epistemically difficult part, like X knowing when they’re better off with a false belief.

Self-deceptions are the worst kind of black swan bets, much worse than lies, because without knowing the true state of affairs, you can’t even guess at what the penalty will be for your self-deception. They only have to blow up once to undo all the good they ever did. One single time when you pray to God after discovering a lump, instead of going to a doctor. That’s all it takes to undo a life. All the happiness that the warm thought of an afterlife ever produced in humanity, has now been more than cancelled by the failure of humanity to institute systematic cryonic preservations after liquid nitrogen became cheap to manufacture. And I don’t think that anyone ever had that sort of failure in mind as a possible blowup, when they said, “But we need religious beliefs to cushion the fear of death.” That’s what black swan bets are all about—the unexpected blowup.

Maybe you even get away with one or two black swan bets—they don’t get you every time. So you do it again, and then the blowup comes and cancels out every benefit and then some. That’s what black swan bets are all about.

Thus the difficulty of knowing when it’s safe to believe a lie (assuming you can even manage that much mental contortion in the first place)—part of the nature of black swan bets is that you don’t see the bullet that kills you; and since our perceptions just seem like the way the world is, it looks like there is no bullet, period.

So I would say that there is an ethical injunction against self-deception. I call this an “ethical injunction” not so much because it’s a matter of interpersonal morality (although it is), but because it’s a rule that guards you from your own cleverness—an override against the temptation to do what seems like the right thing.

So now we have two kinds of situation that can support an “ethical injunction,” a rule not to do something even when it’s the right thing to do. (That is, you refrain “even when your brain has computed it’s the right thing to do,” but this will just seem like “the right thing to do.”)

First, being human and running on corrupted hardware, we may generalize classes of situation where when you say e.g. “It’s time to rob a few banks for the greater good,” we deem it more likely that you’ve been corrupted than that this is really the case. (Note that we’re not prohibiting it from ever being the case in reality, but we’re questioning the epistemic state where you’re justified in trusting your own calculation that this is the right thing to do—fair lottery tickets can win, but you can’t justifiably buy them.)

Second, history may teach us that certain classes of action are black swan bets, that is, they sometimes blow up bigtime for reasons not in the decider’s model. So even when we calculate within the model that something seems like the right thing to do, we apply the further knowledge of the black swan problem to arrive at an injunction against it.

But surely . . . if one is aware of these reasons . . . then one can simply redo the calculation, taking them into account. So we can rob banks if it seems like the right thing to do after taking into account the problem of corrupted hardware and black swan blowups. That’s the rational course, right?

There’s a number of replies I could give to that.

I’ll start by saying that this is a prime example of the sort of thinking I have in mind, when I warn aspiring rationalists to beware of cleverness.

I’ll also note that I wouldn’t want an attempted Friendly AI that had just decided that the Earth ought to be transformed into paperclips, to assess whether this was a reasonable thing to do in light of all the various warnings it had received against it. I would want it to undergo an automatic controlled shutdown. Who says that meta-reasoning is immune from corruption?

I could mention the important times that my naive, idealistic ethical inhibitions have protected me from myself, and placed me in a recoverable position, or helped start the recovery, from very deep mistakes I had no clue I was making. And I could ask whether I’ve really advanced so much, and whether it would really be all that wise, to remove the protections that saved me before.

Yet even so . . . “Am I still dumber than my ethics?” is a question whose answer isn’t automatically “Yes.”

There are obvious silly things here that you shouldn’t do; for example, you shouldn’t wait until you’re really tempted, and then try to figure out if you’re smarter than your ethics on that particular occasion.

But in general—there’s only so much power that can vest in what your parents told you not to do. One shouldn’t underestimate the power. Smart people debated historical lessons in the course of forging the Enlightenment ethics that much of Western culture draws upon; and some subcultures, like scientific academia, or science-fiction fandom, draw on those ethics more directly. But even so the power of the past is bounded.

And in fact . . .

I’ve had to make my ethics much stricter than what my parents and Jerry Pournelle and Richard Feynman told me not to do.

Funny thing, how when people seem to think they’re smarter than their ethics, they argue for less strictness rather than more strictness. I mean, when you think about how much more complicated the modern world is . . .

And along the same lines, the ones who come to me and say, “You should lie about the intelligence explosion, because that way you can get more people to support you; it’s the rational thing to do, for the greater good”—these ones seem to have no idea of the risks.

They don’t mention the problem of running on corrupted hardware. They don’t mention the idea that lies have to be recursively protected from all the truths and all the truthfinding techniques that threaten them. They don’t mention that honest ways have a simplicity that dishonest ways often lack. They don’t talk about black swan bets. They don’t talk about the terrible nakedness of discarding the last defense you have against yourself, and trying to survive on raw calculation.

I am reasonably sure that this is because they have no clue about any of these things.

If you’ve truly understood the reason and the rhythm behind ethics, then one major sign is that, augmented by this newfound knowledge, you don’t do those things that previously seemed like ethical transgressions. Only now you know why.

Someone who just looks at one or two reasons behind ethics, and says, “Okay, I’ve understood that, so now I’ll take it into account consciously, and therefore I have no more need of ethical inhibitions”—this one is behaving more like a stereotype than a real rationalist. The world isn’t simple and pure and clean, so you can’t just take the ethics you were raised with and trust them. But that pretense of Vulcan logic, where you think you’re just going to compute everything correctly once you’ve got one or two abstract insights—that doesn’t work in real life either.

As for those who, having figured out none of this, think themselves smarter than their ethics: Ha.

And as for those who previously thought themselves smarter than their ethics, but who hadn’t conceived of all these elements behind ethical injunctions “in so many words” until they ran across this essay, and who now think themselves smarter than their ethics, because they’re going to take all this into account from now on: Double ha.

I have seen many people struggling to excuse themselves from their ethics. Always the modification is toward lenience, never to be more strict. And I am stunned by the speed and the lightness with which they strive to abandon their protections. Hobbes said, “I don’t know what’s worse, the fact that everyone’s got a price, or the fact that their price is so low.” So very low the price, so very eager they are to be bought. They don’t look twice and then a third time for alternatives, before deciding that they have no option left but to transgress—though they may look very grave and solemn when they say it. They abandon their ethics at the very first opportunity. “Where there’s a will to failure, obstacles can be found.” The will to fail at ethics seems very strong, in some people.

I don’t know if I can endorse absolute ethical injunctions that bind over all possible epistemic states of a human brain. The universe isn’t kind enough for me to trust that. (Though an ethical injunction against self-deception, for example, does seem to me to have tremendous force. I’ve seen many people arguing for the Dark Side, and none of them seem aware of the network risks or the black-swan risks of self-deception.) If, someday, I attempt to shape a (reflectively consistent) injunction within a self-modifying AI, it will only be after working out the math, because that is so totally not the sort of thing you could get away with doing via an ad-hoc patch.

But I will say this much:

I am completely unimpressed with the knowledge, the reasoning, and the overall level of those folk who have eagerly come to me, and said in grave tones, “It’s rational to do unethical thing X because it will have benefit Y.”

1. Richard Rhodes, The Making of the Atomic Bomb (New York: Simon & Schuster, 1986).

289
Something to Protect

In the gestalt of (ahem) Japanese fiction, one finds this oft-repeated motif: Power comes from having something to protect.

I’m not just talking about superheroes that power up when a friend is threatened, the way it works in Western fiction. In the Japanese version it runs deeper than that.

In the X saga it’s explicitly stated that each of the good guys draw their power from having someone—one person—who they want to protect. Who? That question is part of X’s plot—the “most precious person” isn’t always who we think. But if that person is killed, or hurt in the wrong way, the protector loses their power—not so much from magical backlash, as from simple despair. This isn’t something that happens once per week per good guy, the way it would work in a Western comic. It’s equivalent to being Killed Off For Real—taken off the game board.

The way it works in Western superhero comics is that the good guy gets bitten by a radioactive spider; and then he needs something to do with his powers, to keep him busy, so he decides to fight crime. And then Western superheroes are always whining about how much time their superhero duties take up, and how they’d rather be ordinary mortals so they could go fishing or something.

Similarly, in Western real life, unhappy people are told that they need a “purpose in life,” so they should pick out an altruistic cause that goes well with their personality, like picking out nice living-room drapes, and this will brighten up their days by adding some color, like nice living-room drapes. You should be careful not to pick something too expensive, though.

In Western comics, the magic comes first, then the purpose: Acquire amazing powers, decide to protect the innocent. In Japanese fiction, often, it works the other way around.

Of course I’m not saying all this to generalize from fictional evidence. But I want to convey a concept whose deceptively close Western analogue is not what I mean.

I have touched before on the idea that a rationalist must have something they value more than “rationality”: the Art must have a purpose other than itself, or it collapses into infinite recursion. But do not mistake me, and think I am advocating that rationalists should pick out a nice altruistic cause, by way of having something to do, because rationality isn’t all that important by itself. No. I am asking: Where do rationalists come from? How do we acquire our powers?

It is written in The Twelve Virtues of Rationality:

How can you improve your conception of rationality? Not by saying to yourself, “It is my duty to be rational.” By this you only enshrine your mistaken conception. Perhaps your conception of rationality is that it is rational to believe the words of the Great Teacher, and the Great Teacher says, “The sky is green,” and you look up at the sky and see blue. If you think: “It may look like the sky is blue, but rationality is to believe the words of the Great Teacher,” you lose a chance to discover your mistake.

Historically speaking, the way humanity finally left the trap of authority and began paying attention to, y’know, the actual sky, was that beliefs based on experiment turned out to be much more useful than beliefs based on authority. Curiosity has been around since the dawn of humanity, but the problem is that spinning campfire tales works just as well for satisfying curiosity.

Historically speaking, science won because it displayed greater raw strength in the form of technology, not because science sounded more reasonable. To this very day, magic and scripture still sound more reasonable to untrained ears than science. That is why there is continuous social tension between the belief systems. If science not only worked better than magic, but also sounded more intuitively reasonable, it would have won entirely by now.

Now there are those who say: “How dare you suggest that anything should be valued more than Truth? Must not a rationalist love Truth more than mere usefulness?”

Forget for a moment what would have happened historically to someone like that—that people in pretty much that frame of mind defended the Bible because they loved Truth more than mere accuracy. Propositional morality is a glorious thing, but it has too many degrees of freedom.

No, the real point is that a rationalist’s love affair with the Truth is, well, just more complicated as an emotional relationship.

One doesn’t become an adept rationalist without caring about the truth, both as a purely moral desideratum and as something that’s fun to have. I doubt there are many master composers who hate music.

But part of what I like about rationality is the discipline imposed by requiring beliefs to yield predictions, which ends up taking us much closer to the truth than if we sat in the living room obsessing about Truth all day. I like the complexity of simultaneously having to love True-seeming ideas, and also being ready to drop them out the window at a moment’s notice. I even like the glorious aesthetic purity of declaring that I value mere usefulness above aesthetics. That is almost a contradiction, but not quite; and that has an aesthetic quality as well, a delicious humor.

And of course, no matter how much you profess your love of mere usefulness, you should never actually end up deliberately believing a useful false statement.

So don’t oversimplify the relationship between loving truth and loving usefulness. It’s not one or the other. It’s complicated, which is not necessarily a defect in the moral aesthetics of single events.

But morality and aesthetics alone, believing that one ought to be “rational” or that certain ways of thinking are “beautiful,” will not lead you to the center of the Way. It wouldn’t have gotten humanity out of the authority-hole.

In Feeling Moral, I discussed this dilemma: Which of these options would you prefer?

Save 400 lives, with certainty.
Save 500 lives, 90% probability; save no lives, 10% probability.

You may be tempted to grandstand, saying, “How dare you gamble with people’s lives?” Even if you, yourself, are one of the 500—but you don’t know which one—you may still be tempted to rely on the comforting feeling of certainty, because our own lives are often worth less to us than a good intuition.

But if your precious daughter is one of the 500, and you don’t know which one, then, perhaps, you may feel more impelled to shut up and multiply—to notice that you have an 80% chance of saving her in the first case, and a 90% chance of saving her in the second.

And yes, everyone in that crowd is someone’s son or daughter. Which, in turn, suggests that we should pick the second option as altruists, as well as concerned parents.

My point is not to suggest that one person’s life is more valuable than 499 people. What I am trying to say is that more than your own life has to be at stake, before a person becomes desperate enough to resort to math.

What if you believe that it is “rational” to choose the certainty of option 1? Lots of people think that “rationality” is about choosing only methods that are certain to work, and rejecting all uncertainty. But, hopefully, you care more about your daughter’s life than about “rationality.”

Will pride in your own virtue as a rationalist save you? Not if you believe that it is virtuous to choose certainty. You will only be able to learn something about rationality if your daughter’s life matters more to you than your pride as a rationalist.

You may even learn something about rationality from the experience, if you are already far enough grown in your Art to say, “I must have had the wrong conception of rationality,” and not, “Look at how rationality gave me the wrong answer!”

(The essential difficulty in becoming a master rationalist is that you need quite a bit of rationality to bootstrap the learning process.)

Is your belief that you ought to be rational more important than your life? Because, as I’ve previously observed, risking your life isn’t comparatively all that scary. Being the lone voice of dissent in the crowd and having everyone look at you funny is much scarier than a mere threat to your life, according to the revealed preferences of teenagers who drink at parties and then drive home. It will take something terribly important to make you willing to leave the pack. A threat to your life won’t be enough.

Is your will to rationality stronger than your pride? Can it be, if your will to rationality stems from your pride in your self-image as a rationalist? It’s helpful—very helpful—to have a self-image which says that you are the sort of person who confronts harsh truth. It’s helpful to have too much self-respect to knowingly lie to yourself or refuse to face evidence. But there may come a time when you have to admit that you’ve been doing rationality all wrong. Then your pride, your self-image as a rationalist, may make that too hard to face.

If you’ve prided yourself on believing what the Great Teacher says—even when it seems harsh, even when you’d rather not—that may make it all the more bitter a pill to swallow, to admit that the Great Teacher is a fraud, and all your noble self-sacrifice was for naught.

Where do you get the will to keep moving forward?

When I look back at my own personal journey toward rationality—not just humanity’s historical journey—well, I grew up believing very strongly that I ought to be rational. This made me an above-average Traditional Rationalist a la Feynman and Heinlein, and nothing more. It did not drive me to go beyond the teachings I had received. I only began to grow further as a rationalist once I had something terribly important that I needed to do. Something more important than my pride as a rationalist, never mind my life.

Only when you become more wedded to success than to any of your beloved techniques of rationality do you begin to appreciate these words of Miyamoto Musashi:¹

You can win with a long weapon, and yet you can also win with a short weapon. In short, the Way of the Ichi school is the spirit of winning, whatever the weapon and whatever its size.

—Miyamoto Musashi, The Book of Five Rings

Don’t mistake this for a specific teaching of rationality. It describes how you learn the Way, beginning with a desperate need to succeed. No one masters the Way until more than their life is at stake. More than their comfort, more even than their pride.

You can’t just pick out a Cause like that because you feel you need a hobby. Go looking for a “good cause,” and your mind will just fill in a standard cliché. Learn how to multiply, and perhaps you will recognize a drastically important cause when you see one.

But if you have a cause like that, it is right and proper to wield your rationality in its service.

To strictly subordinate the aesthetics of rationality to a higher cause is part of the aesthetic of rationality. You should pay attention to that aesthetic: You will never master rationality well enough to win with any weapon if you do not appreciate the beauty for its own sake.

1. Musashi, Book of Five Rings.

290
When (Not) to Use Probabilities

It may come as a surprise to some readers that I do not always advocate using probabilities.

Or rather, I don’t always advocate that human beings, trying to solve their problems, should try to make up verbal probabilities, and then apply the laws of probability theory or decision theory to whatever number they just made up, and then use the result as their final belief or decision.

The laws of probability are laws, not suggestions, but often the true Law is too difficult for us humans to compute. If P ≠ NP and the universe has no source of exponential computing power, then there are evidential updates too difficult for even a superintelligence to compute—even though the probabilities would be quite well-defined, if we could afford to calculate them.

So sometimes you don’t apply probability theory. Especially if you’re human, and your brain has evolved with all sorts of useful algorithms for uncertain reasoning, that don’t involve verbal probability assignments.

Not sure where a flying ball will land? I don’t advise trying to formulate a probability distribution over its landing spots, performing deliberate Bayesian updates on your glances at the ball, and calculating the expected utility of all possible strings of motor instructions to your muscles. Trying to catch a flying ball, you’re probably better off with your brain’s built-in mechanisms than using deliberative verbal reasoning to invent or manipulate probabilities.

But this doesn’t mean you’re going beyond probability theory or above probability theory.

The Dutch book arguments still apply. If I offer you a choice of gambles ($10,000 if the ball lands in this square, versus $10,000 if I roll a die and it comes up 6), and you answer in a way that does not allow consistent probabilities to be assigned, then you will accept combinations of gambles that are certain losses, or reject gambles that are certain gains . . .

Which still doesn’t mean that you should try to use deliberative verbal reasoning. I would expect that for professional baseball players, at least, it’s more important to catch the ball than to assign consistent probabilities. Indeed, if you tried to make up probabilities, the verbal probabilities might not even be very good ones, compared to some gut-level feeling—some wordless representation of uncertainty in the back of your mind.

There is nothing privileged about uncertainty that is expressed in words, unless the verbal parts of your brain do, in fact, happen to work better on the problem.

And while accurate maps of the same territory will necessarily be consistent among themselves, not all consistent maps are accurate. It is more important to be accurate than to be consistent, and more important to catch the ball than to be consistent.

In fact, I generally advise against making up probabilities, unless it seems like you have some decent basis for them. This only fools you into believing that you are more Bayesian than you actually are.

To be specific, I would advise, in most cases, against using non-numerical procedures to create what appear to be numerical probabilities. Numbers should come from numbers.

Now there are benefits from trying to translate your gut feelings of uncertainty into verbal probabilities. It may help you spot problems like the conjunction fallacy. It may help you spot internal inconsistencies—though it may not show you any way to remedy them.

But you shouldn’t go around thinking that if you translate your gut feeling into “one in a thousand,” then, on occasions when you emit these verbal words, the corresponding event will happen around one in a thousand times. Your brain is not so well-calibrated. If instead you do something nonverbal with your gut feeling of uncertainty, you may be better off, because at least you’ll be using the gut feeling the way it was meant to be used.

This specific topic came up recently in the context of the Large Hadron Collider, and an argument given at the Global Catastrophic Risks conference:

That we couldn’t be sure that there was no error in the papers which showed from multiple angles that the LHC couldn’t possibly destroy the world. And moreover, the theory used in the papers might be wrong. And in either case, there was still a chance the LHC could destroy the world. And therefore, it ought not to be turned on.

Now if the argument had been given in just this way, I would not have objected to its epistemology.

But the speaker actually purported to assign a probability of at least 1 in 1,000 that the theory, model, or calculations in the LHC paper were wrong; and a probability of at least 1 in 1,000 that, if the theory or model or calculations were wrong, the LHC would destroy the world.

After all, it’s surely not so improbable that future generations will reject the theory used in the LHC paper, or reject the model, or maybe just find an error. And if the LHC paper is wrong, then who knows what might happen as a result?

So that is an argument—but to assign numbers to it?

I object to the air of authority given to these numbers pulled out of thin air. I generally feel that if you can’t use probabilistic tools to shape your feelings of uncertainty, you ought not to dignify them by calling them probabilities.

The alternative I would propose, in this particular case, is to debate the general rule of banning physics experiments because you cannot be absolutely certain of the arguments that say they are safe.

I hold that if you phrase it this way, then your mind, by considering frequencies of events, is likely to bring in more consequences of the decision, and remember more relevant historical cases.

If you debate just the one case of the LHC, and assign specific probabilities, it (1) gives very shaky reasoning an undue air of authority, (2) obscures the general consequences of applying similar rules, and even (3) creates the illusion that we might come to a different decision if someone else published a new physics paper that decreased the probabilities.

The authors at the Global Catastrophic Risk conference seemed to be suggesting that we could just do a bit more analysis of the LHC and then switch it on. This struck me as the most disingenuous part of the argument. Once you admit the argument “Maybe the analysis could be wrong, and who knows what happens then,” there is no possible physics paper that can ever get rid of it.

No matter what other physics papers had been published previously, the authors would have used the same argument and made up the same numerical probabilities at the Global Catastrophic Risk conference. I cannot be sure of this statement, of course, but it has a probability of 75%.

In general a rationalist tries to make their minds function at the best achievable power output; sometimes this involves talking about verbal probabilities, and sometimes it does not, but always the laws of probability theory govern.

If all you have is a gut feeling of uncertainty, then you should probably stick with those algorithms that make use of gut feelings of uncertainty, because your built-in algorithms may do better than your clumsy attempts to put things into words.

Now it may be that by reasoning thusly, I may find myself inconsistent. For example, I would be substantially more alarmed about a lottery device with a well-defined chance of 1 in 1,000,000 of destroying the world, than I am about the Large Hadron Collider being switched on.

On the other hand, if you asked me whether I could make one million statements of authority equal to “The Large Hadron Collider will not destroy the world,” and be wrong, on average, around once, then I would have to say no.

What should I do about this inconsistency? I’m not sure, but I’m certainly not going to wave a magic wand to make it go away. That’s like finding an inconsistency in a pair of maps you own, and quickly scribbling some alterations to make sure they’re consistent.

I would also, by the way, be substantially more worried about a lottery device with a 1 in 1,000,000,000 chance of destroying the world, than a device which destroyed the world if the Judeo-Christian God existed. But I would not suppose that I could make one billion statements, one after the other, fully independent and equally fraught as “There is no God,” and be wrong on average around once.

I can’t say I’m happy with this state of epistemic affairs, but I’m not going to modify it until I can see myself moving in the direction of greater accuracy and real-world effectiveness, not just moving in the direction of greater self-consistency. The goal is to win, after all. If I make up a probability that is not shaped by probabilistic tools, if I make up a number that is not created by numerical methods, then maybe I am just defeating my built-in algorithms that would do better by reasoning in their native modes of uncertainty.

Of course this is not a license to ignore probabilities that are well-founded. Any numerical founding at all is likely to be better than a vague feeling of uncertainty; humans are terrible statisticians. But pulling a number entirely out of your butt, that is, using a non-numerical procedure to produce a number, is nearly no foundation at all; and in that case you probably are better off sticking with the vague feelings of uncertainty.

Which is why my writing generally uses words like “maybe” and “probably” and “surely” instead of assigning made-up numerical probabilities like “40%” and “70%” and “95%.” Think of how silly that would look. I think it actually would be silly; I think I would do worse thereby.

I am not the kind of straw Bayesian who says that you should make up probabilities to avoid being subject to Dutch books. I am the sort of Bayesian who says that in practice, humans end up subject to Dutch books because they aren’t powerful enough to avoid them; and moreover it’s more important to catch the ball than to avoid Dutch books. The math is like underlying physics, inescapably governing, but too expensive to calculate.

Nor is there any point in a ritual of cognition that mimics the surface forms of the math, but fails to produce systematically better decision-making. That would be a lost purpose; this is not the true art of living under the law.

291
Newcomb’s Problem and Regret of Rationality

The following may well be the most controversial dilemma in the history of decision theory:

A superintelligence from another galaxy, whom we shall call Omega, comes to Earth and sets about playing a strange little game. In this game, Omega selects a human being, sets down two boxes in front of them, and flies away.

Box A is transparent and contains a thousand dollars.

Box B is opaque, and contains either a million dollars, or nothing.

You can take both boxes, or take only box B.

And the twist is that Omega has put a million dollars in box B if and only if Omega has predicted that you will take only box B.

Omega has been correct on each of 100 observed occasions so far—everyone who took both boxes has found box B empty and received only a thousand dollars; everyone who took only box B has found B containing a million dollars. (We assume that box A vanishes in a puff of smoke if you take only box B; no one else can take box A afterward.)

Before you make your choice, Omega has flown off and moved on to its next game. Box B is already empty or already full.

Omega drops two boxes on the ground in front of you and flies off.

Do you take both boxes, or only box B?

And the standard philosophical conversation runs thusly:

ONE-BOXER: “I take only box B, of course. I’d rather have a million than a thousand.”

TWO-BOXER: “Omega has already left. Either box B is already full or already empty. If box B is already empty, then taking both boxes nets me $1,000, taking only box B nets me $0. If box B is already full, then taking both boxes nets $1,001,000, taking only box B nets $1,000,000. In either case I do better by taking both boxes, and worse by leaving a thousand dollars on the table—so I will be rational, and take both boxes.”

ONE-BOXER: “If you’re so rational, why ain’cha rich?”

TWO-BOXER: “It’s not my fault Omega chooses to reward only people with irrational dispositions, but it’s already too late for me to do anything about that.”

There is a large literature on the topic of Newcomblike problems—especially if you consider the Prisoner’s Dilemma as a special case, which it is generally held to be. Paradoxes of Rationality and Cooperation: Prisoner’s Dilemma and Newcomb’s Problem¹ is an edited volume that includes Newcomb’s original essay. For those who read only online material, Ledwig’s PhD thesis summarizes the major standard positions.²

I’m not going to go into the whole literature, but the dominant consensus in modern decision theory is that one should two-box, and Omega is just rewarding agents with irrational dispositions. This dominant view goes by the name of “causal decision theory.”

I’m not going to try to present my own analysis here. Way too long a story, even by my standards.

But it is agreed even among causal decision theorists that if you have the power to precommit yourself to take one box, in Newcomb’s Problem, then you should do so. If you can precommit yourself before Omega examines you, then you are directly causing box B to be filled.

Now in my field—which, in case you have forgotten, is self-modifying AI—this works out to saying that if you build an AI that two-boxes on Newcomb’s Problem, it will self-modify to one-box on Newcomb’s Problem, if the AI considers in advance that it might face such a situation. Agents with free access to their own source code have access to a cheap method of precommitment.

What if you expect that you might, in general, face a Newcomblike problem, without knowing the exact form of the problem? Then you would have to modify yourself into a sort of agent whose disposition was such that it would generally receive high rewards on Newcomblike problems.

But what does an agent with a disposition generally-well-suited to Newcomblike problems look like? Can this be formally specified?

Yes, but when I tried to write it up, I realized that I was starting to write a small book. And it wasn’t the most important book I had to write, so I shelved it. My slow writing speed really is the bane of my existence. The theory I worked out seems, to me, to have many nice properties besides being well-suited to Newcomblike problems. It would make a nice PhD thesis, if I could get someone to accept it as my PhD thesis. But that’s pretty much what it would take to make me unshelve the project. Otherwise I can’t justify the time expenditure, not at the speed I currently write books.

I say all this, because there’s a common attitude that “Verbal arguments for one-boxing are easy to come by; what’s hard is developing a good decision theory that one-boxes”—coherent math which one-boxes on Newcomb’s Problem without producing absurd results elsewhere. So I do understand that, and I did set out to develop such a theory, but my writing speed on big papers is so slow that I can’t publish it. Believe it or not, it’s true.

Nonetheless, I would like to present some of my motivations on Newcomb’s Problem—the reasons I felt impelled to seek a new theory—because they illustrate my source-attitudes toward rationality. Even if I can’t present the theory that these motivations motivate . . .

First, foremost, fundamentally, above all else:

Rational agents should WIN.

Don’t mistake me, and think that I’m talking about the Hollywood Rationality stereotype that rationalists should be selfish or shortsighted. If your utility function has a term in it for others, then win their happiness. If your utility function has a term in it for a million years hence, then win the eon.

But at any rate, WIN. Don’t lose reasonably; WIN.

Now there are defenders of causal decision theory who argue that the two-boxers are doing their best to win, and cannot help it if they have been cursed by a Predictor who favors irrationalists. I will talk about this defense in a moment. But first, I want to draw a distinction between causal decision theorists who believe that two-boxers are genuinely doing their best to win; versus someone who thinks that two-boxing is the reasonable or the rational thing to do, but that the reasonable move just happens to predictably lose, in this case. There are a lot of people out there who think that rationality predictably loses on various problems—that, too, is part of the Hollywood Rationality stereotype, that Kirk is predictably superior to Spock.

Next, let’s turn to the charge that Omega favors irrationalists. I can conceive of a superbeing who rewards only people born with a particular gene, regardless of their choices. I can conceive of a superbeing who rewards people whose brains inscribe the particular algorithm of “Describe your options in English and choose the last option when ordered alphabetically,” but who does not reward anyone who chooses the same option for a different reason. But Omega rewards people who choose to take only box B, regardless of which algorithm they use to arrive at this decision, and this is why I don’t buy the charge that Omega is rewarding the irrational. Omega doesn’t care whether or not you follow some particular ritual of cognition; Omega only cares about your predicted decision.

We can choose whatever reasoning algorithm we like, and will be rewarded or punished only according to that algorithm’s choices, with no other dependency—Omega just cares where we go, not how we got there.

It is precisely the notion that Nature does not care about our algorithm that frees us up to pursue the winning Way—without attachment to any particular ritual of cognition, apart from our belief that it wins. Every rule is up for grabs, except the rule of winning.

As Miyamoto Musashi said—it’s really worth repeating:

You can win with a long weapon, and yet you can also win with a short weapon. In short, the Way of the Ichi school is the spirit of winning, whatever the weapon and whatever its size.³

(Another example: It was argued by McGee that we must adopt bounded utility functions or be subject to “Dutch books” over infinite times. But: The utility function is not up for grabs. I love life without limit or upper bound; there is no finite amount of life lived N where I would prefer an 80.0001% probability of living N years to a 0.0001% chance of living a googolplex years and an 80% chance of living forever. This is a sufficient condition to imply that my utility function is unbounded. So I just have to figure out how to optimize for that morality. You can’t tell me, first, that above all I must conform to a particular ritual of cognition, and then that, if I conform to that ritual, I must change my morality to avoid being Dutch-booked. Toss out the losing ritual; don’t change the definition of winning. That’s like deciding to prefer $1,000 to $1,000,000 so that Newcomb’s Problem doesn’t make your preferred ritual of cognition look bad.)

“But,” says the causal decision theorist, “to take only one box, you must somehow believe that your choice can affect whether box B is empty or full—and that’s unreasonable! Omega has already left! It’s physically impossible!”

Unreasonable? I am a rationalist: what do I care about being unreasonable? I don’t have to conform to a particular ritual of cognition. I don’t have to take only box B because I believe my choice affects the box, even though Omega has already left. I can just . . . take only box B.

I do have a proposed alternative ritual of cognition that computes this decision, which this margin is too small to contain; but I shouldn’t need to show this to you. The point is not to have an elegant theory of winning—the point is to win; elegance is a side effect.

Or to look at it another way: Rather than starting with a concept of what is the reasonable decision, and then asking whether “reasonable” agents leave with a lot of money, start by looking at the agents who leave with a lot of money, develop a theory of which agents tend to leave with the most money, and from this theory, try to figure out what is “reasonable.” “Reasonable” may just refer to decisions in conformance with our current ritual of cognition—what else would determine whether something seems “reasonable” or not?

From James Joyce (no relation), Foundations of Causal Decision Theory:⁴

Rachel has a perfectly good answer to the “Why ain’t you rich?” question. “I am not rich,” she will say, “because I am not the kind of person the psychologist thinks will refuse the money. I’m just not like you, Irene. Given that I know that I am the type who takes the money, and given that the psychologist knows that I am this type, it was reasonable of me to think that the $1,000,000 was not in my account. The $1,000 was the most I was going to get no matter what I did. So the only reasonable thing for me to do was to take it.”

Irene may want to press the point here by asking, “But don’t you wish you were like me, Rachel? Don’t you wish that you were the refusing type?” There is a tendency to think that Rachel, a committed causal decision theorist, must answer this question in the negative, which seems obviously wrong (given that being like Irene would have made her rich). This is not the case. Rachel can and should admit that she does wish she were more like Irene. “It would have been better for me,” she might concede, “had I been the refusing type.” At this point Irene will exclaim, “You’ve admitted it! It wasn’t so smart to take the money after all.” Unfortunately for Irene, her conclusion does not follow from Rachel’s premise. Rachel will patiently explain that wishing to be a refuser in a Newcomb problem is not inconsistent with thinking that one should take the $1,000 whatever type one is. When Rachel wishes she was Irene’s type she is wishing for Irene’s options, not sanctioning her choice.

It is, I would say, a general principle of rationality—indeed, part of how I define rationality—that you never end up envying someone else’s mere choices. You might envy someone their genes, if Omega rewards genes, or if the genes give you a generally happier disposition. But Rachel, above, envies Irene her choice, and only her choice, irrespective of what algorithm Irene used to make it. Rachel wishes just that she had a disposition to choose differently.

You shouldn’t claim to be more rational than someone and simultaneously envy them their choice—only their choice. Just do the act you envy.

I keep trying to say that rationality is the winning-Way, but causal decision theorists insist that taking both boxes is what really wins, because you can’t possibly do better by leaving $1,000 on the table . . . even though the single-boxers leave the experiment with more money. Be careful of this sort of argument, any time you find yourself defining the “winner” as someone other than the agent who is currently smiling from on top of a giant heap of utility.

Yes, there are various thought experiments in which some agents start out with an advantage—but if the task is to, say, decide whether to jump off a cliff, you want to be careful not to define cliff-refraining agents as having an unfair prior advantage over cliff-jumping agents, by virtue of their unfair refusal to jump off cliffs. At this point you have covertly redefined “winning” as conformance to a particular ritual of cognition. Pay attention to the money!

Or here’s another way of looking at it: Faced with Newcomb’s Problem, would you want to look really hard for a reason to believe that it was perfectly reasonable and rational to take only box B; because, if such a line of argument existed, you would take only box B and find it full of money? Would you spend an extra hour thinking it through, if you were confident that, at the end of the hour, you would be able to convince yourself that box B was the rational choice? This too is a rather odd position to be in. Ordinarily, the work of rationality goes into figuring out which choice is the best—not finding a reason to believe that a particular choice is the best.

Maybe it’s too easy to say that you “ought to” two-box on Newcomb’s Problem, that this is the “reasonable” thing to do, so long as the money isn’t actually in front of you. Maybe you’re just numb to philosophical dilemmas, at this point. What if your daughter had a 90% fatal disease, and box A contained a serum with a 20% chance of curing her, and box B might contain a serum with a 95% chance of curing her? What if there was an asteroid rushing toward Earth, and box A contained an asteroid deflector that worked 10% of the time, and box B might contain an asteroid deflector that worked 100% of the time?

Would you, at that point, find yourself tempted to make an unreasonable choice?

If the stake in box B was something you could not leave behind? Something overwhelmingly more important to you than being reasonable? If you absolutely had to win—really win, not just be defined as winning?

Would you wish with all your power that the “reasonable” decision were to take only box B?

Then maybe it’s time to update your definition of reasonableness.

Alleged rationalists should not find themselves envying the mere decisions of alleged nonrationalists, because your decision can be whatever you like. When you find yourself in a position like this, you shouldn’t chide the other person for failing to conform to your concepts of reasonableness. You should realize you got the Way wrong.

So, too, if you ever find yourself keeping separate track of the “reasonable” belief, versus the belief that seems likely to be actually true. Either you have misunderstood reasonableness, or your second intuition is just wrong.

Now one can’t simultaneously define “rationality” as the winning Way, and define “rationality” as Bayesian probability theory and decision theory. But it is the argument that I am putting forth, and the moral of my advice to trust in Bayes, that the laws governing winning have indeed proven to be math. If it ever turns out that Bayes fails—receives systematically lower rewards on some problem, relative to a superior alternative, in virtue of its mere decisions—then Bayes has to go out the window. “Rationality” is just the label I use for my beliefs about the winning Way—the Way of the agent smiling from on top of the giant heap of utility. Currently, that label refers to Bayescraft.

I realize that this is not a knockdown criticism of causal decision theory—that would take the actual book and/or PhD thesis—but I hope it illustrates some of my underlying attitude toward this notion of “rationality.”

[Edit 2015: I’ve now written a book-length exposition of a decision theory that dominates causal decision theory, “Timeless Decision Theory.”⁵ The cryptographer Wei Dai has responded with another alternative to causal decision theory, updateless decision theory, that dominates both causal and timeless decision theory. As of 2015, the best up-to-date discussions of these theories are Daniel Hintze’s “Problem Class Dominance in Predictive Dilemmas”⁶ and Nate Soares and Benja Fallenstein’s “Toward Idealized Decision Theory.”⁷ ]

You shouldn’t find yourself distinguishing the winning choice from the reasonable choice. Nor should you find yourself distinguishing the reasonable belief from the belief that is most likely to be true.

That is why I use the word “rational” to denote my beliefs about accuracy and winning—not to denote verbal reasoning, or strategies which yield certain success, or that which is logically provable, or that which is publicly demonstrable, or that which is reasonable.

As Miyamoto Musashi said:

The primary thing when you take a sword in your hands is your intention to cut the enemy, whatever the means. Whenever you parry, hit, spring, strike or touch the enemy’s cutting sword, you must cut the enemy in the same movement. It is essential to attain this. If you think only of hitting, springing, striking or touching the enemy, you will not be able actually to cut him.

1. Richmond Campbell and Lanning Snowden, eds., Paradoxes of Rationality and Cooperation: Prisoner’s Dilemma and Newcomb’s Problem (Vancouver: University of British Columbia Press, 1985).

2. Marion Ledwig, “Newcomb’s Problem” (PhD diss., University of Constance, 2000).

3. Musashi, Book of Five Rings.

4. James M. Joyce, The Foundations of Causal Decision Theory (New York: Cambridge University Press, 1999), doi:10.1017/CBO9780511498497.

5. Yudkowsky, Timeless Decision Theory.

6. Daniel Hintze, “Problem Class Dominance in Predictive Dilemmas,” Honors thesis (2014).

7. Nate Soares and Benja Fallenstein, “Toward Idealized Decision Theory,” Technical report. Berkeley, CA: Machine Intelligence Research Institute (2014), http://intelligence.org/files/TowardIdealizedDecisionTheory.pdf.

Interlude
The Twelve Virtues of Rationality

The first virtue is curiosity. A burning itch to know is higher than a solemn vow to pursue truth. To feel the burning itch of curiosity requires both that you be ignorant, and that you desire to relinquish your ignorance. If in your heart you believe you already know, or if in your heart you do not wish to know, then your questioning will be purposeless and your skills without direction. Curiosity seeks to annihilate itself; there is no curiosity that does not want an answer. The glory of glorious mystery is to be solved, after which it ceases to be mystery. Be wary of those who speak of being open-minded and modestly confess their ignorance. There is a time to confess your ignorance and a time to relinquish your ignorance.

The second virtue is relinquishment. P. C. Hodgell said: “That which can be destroyed by the truth should be.”¹ Do not flinch from experiences that might destroy your beliefs. The thought you cannot think controls you more than thoughts you speak aloud. Submit yourself to ordeals and test yourself in fire. Relinquish the emotion which rests upon a mistaken belief, and seek to feel fully that emotion which fits the facts. If the iron approaches your face, and you believe it is hot, and it is cool, the Way opposes your fear. If the iron approaches your face, and you believe it is cool, and it is hot, the Way opposes your calm. Evaluate your beliefs first and then arrive at your emotions. Let yourself say: “If the iron is hot, I desire to believe it is hot, and if it is cool, I desire to believe it is cool.” Beware lest you become attached to beliefs you may not want.

The third virtue is lightness. Let the winds of evidence blow you about as though you are a leaf, with no direction of your own. Beware lest you fight a rearguard retreat against the evidence, grudgingly conceding each foot of ground only when forced, feeling cheated. Surrender to the truth as quickly as you can. Do this the instant you realize what you are resisting, the instant you can see from which quarter the winds of evidence are blowing against you. Be faithless to your cause and betray it to a stronger enemy. If you regard evidence as a constraint and seek to free yourself, you sell yourself into the chains of your whims. For you cannot make a true map of a city by sitting in your bedroom with your eyes shut and drawing lines upon paper according to impulse. You must walk through the city and draw lines on paper that correspond to what you see. If, seeing the city unclearly, you think that you can shift a line just a little to the right, just a little to the left, according to your caprice, this is just the same mistake.

The fourth virtue is evenness. One who wishes to believe says, “Does the evidence permit me to believe?” One who wishes to disbelieve asks, “Does the evidence force me to believe?” Beware lest you place huge burdens of proof only on propositions you dislike, and then defend yourself by saying: “But it is good to be skeptical.” If you attend only to favorable evidence, picking and choosing from your gathered data, then the more data you gather, the less you know. If you are selective about which arguments you inspect for flaws, or how hard you inspect for flaws, then every flaw you learn how to detect makes you that much stupider. If you first write at the bottom of a sheet of paper “And therefore, the sky is green!” it does not matter what arguments you write above it afterward; the conclusion is already written, and it is already correct or already wrong. To be clever in argument is not rationality but rationalization. Intelligence, to be useful, must be used for something other than defeating itself. Listen to hypotheses as they plead their cases before you, but remember that you are not a hypothesis; you are the judge. Therefore do not seek to argue for one side or another, for if you knew your destination, you would already be there.

The fifth virtue is argument. Those who wish to fail must first prevent their friends from helping them. Those who smile wisely and say “I will not argue” remove themselves from help and withdraw from the communal effort. In argument strive for exact honesty, for the sake of others and also yourself: the part of yourself that distorts what you say to others also distorts your own thoughts. Do not believe you do others a favor if you accept their arguments; the favor is to you. Do not think that fairness to all sides means balancing yourself evenly between positions; truth is not handed out in equal portions before the start of a debate. You cannot move forward on factual questions by fighting with fists or insults. Seek a test that lets reality judge between you.

The sixth virtue is empiricism. The roots of knowledge are in observation and its fruit is prediction. What tree grows without roots? What tree nourishes us without fruit? If a tree falls in a forest and no one hears it, does it make a sound? One says, “Yes it does, for it makes vibrations in the air.” Another says, “No it does not, for there is no auditory processing in any brain.” Though they argue, one saying “Yes,” and one saying “No,” the two do not anticipate any different experience of the forest. Do not ask which beliefs to profess, but which experiences to anticipate. Always know which difference of experience you argue about. Do not let the argument wander and become about something else, such as someone’s virtue as a rationalist. Jerry Cleaver said: “What does you in is not failure to apply some high-level, intricate, complicated technique. It’s overlooking the basics. Not keeping your eye on the ball.”² Do not be blinded by words. When words are subtracted, anticipation remains.

The seventh virtue is simplicity. Antoine de Saint-Exupéry said: “Perfection is achieved not when there is nothing left to add, but when there is nothing left to take away.”³ Simplicity is virtuous in belief, design, planning, and justification. When you profess a huge belief with many details, each additional detail is another chance for the belief to be wrong. Each specification adds to your burden; if you can lighten your burden you must do so. There is no straw that lacks the power to break your back. Of artifacts it is said: The most reliable gear is the one that is designed out of the machine. Of plans: A tangled web breaks. A chain of a thousand links will arrive at a correct conclusion if every step is correct, but if one step is wrong it may carry you anywhere. In mathematics a mountain of good deeds cannot atone for a single sin. Therefore, be careful on every step.

The eighth virtue is humility. To be humble is to take specific actions in anticipation of your own errors. To confess your fallibility and then do nothing about it is not humble; it is boasting of your modesty. Who are most humble? Those who most skillfully prepare for the deepest and most catastrophic errors in their own beliefs and plans. Because this world contains many whose grasp of rationality is abysmal, beginning students of rationality win arguments and acquire an exaggerated view of their own abilities. But it is useless to be superior: Life is not graded on a curve. The best physicist in ancient Greece could not calculate the path of a falling apple. There is no guarantee that adequacy is possible given your hardest effort; therefore spare no thought for whether others are doing worse. If you compare yourself to others you will not see the biases that all humans share. To be human is to make ten thousand errors. No one in this world achieves perfection.

The ninth virtue is perfectionism. The more errors you correct in yourself, the more you notice. As your mind becomes more silent, you hear more noise. When you notice an error in yourself, this signals your readiness to seek advancement to the next level. If you tolerate the error rather than correcting it, you will not advance to the next level and you will not gain the skill to notice new errors. In every art, if you do not seek perfection you will halt before taking your first steps. If perfection is impossible that is no excuse for not trying. Hold yourself to the highest standard you can imagine, and look for one still higher. Do not be content with the answer that is almost right; seek one that is exactly right.

The tenth virtue is precision. One comes and says: The quantity is between 1 and 100. Another says: The quantity is between 40 and 50. If the quantity is 42 they are both correct, but the second prediction was more useful and exposed itself to a stricter test. What is true of one apple may not be true of another apple; thus more can be said about a single apple than about all the apples in the world. The narrowest statements slice deepest, the cutting edge of the blade. As with the map, so too with the art of mapmaking: The Way is a precise Art. Do not walk to the truth, but dance. On each and every step of that dance your foot comes down in exactly the right spot. Each piece of evidence shifts your beliefs by exactly the right amount, neither more nor less. What is exactly the right amount? To calculate this you must study probability theory. Even if you cannot do the math, knowing that the math exists tells you that the dance step is precise and has no room in it for your whims.

The eleventh virtue is scholarship. Study many sciences and absorb their power as your own. Each field that you consume makes you larger. If you swallow enough sciences the gaps between them will diminish and your knowledge will become a unified whole. If you are gluttonous you will become vaster than mountains. It is especially important to eat math and science which impinge upon rationality: evolutionary psychology, heuristics and biases, social psychology, probability theory, decision theory. But these cannot be the only fields you study. The Art must have a purpose other than itself, or it collapses into infinite recursion.

Before these eleven virtues is a virtue which is nameless.

Miyamoto Musashi wrote, in The Book of Five Rings:⁴

The primary thing when you take a sword in your hands is your intention to cut the enemy, whatever the means. Whenever you parry, hit, spring, strike or touch the enemy’s cutting sword, you must cut the enemy in the same movement. It is essential to attain this. If you think only of hitting, springing, striking or touching the enemy, you will not be able actually to cut him. More than anything, you must be thinking of carrying your movement through to cutting him.

Every step of your reasoning must cut through to the correct answer in the same movement. More than anything, you must think of carrying your map through to reflecting the territory.

If you fail to achieve a correct answer, it is futile to protest that you acted with propriety.

How can you improve your conception of rationality? Not by saying to yourself, “It is my duty to be rational.” By this you only enshrine your mistaken conception. Perhaps your conception of rationality is that it is rational to believe the words of the Great Teacher, and the Great Teacher says, “The sky is green,” and you look up at the sky and see blue. If you think, “It may look like the sky is blue, but rationality is to believe the words of the Great Teacher,” you lose a chance to discover your mistake.

Do not ask whether it is “the Way” to do this or that. Ask whether the sky is blue or green. If you speak overmuch of the Way you will not attain it.

You may try to name the highest principle with names such as “the map that reflects the territory” or “experience of success and failure” or “Bayesian decision theory.” But perhaps you describe incorrectly the nameless virtue. How will you discover your mistake? Not by comparing your description to itself, but by comparing it to that which you did not name.

If for many years you practice the techniques and submit yourself to strict constraints, it may be that you will glimpse the center. Then you will see how all techniques are one technique, and you will move correctly without feeling constrained. Musashi wrote: “When you appreciate the power of nature, knowing the rhythm of any situation, you will be able to hit the enemy naturally and strike naturally. All this is the Way of the Void.”

These then are twelve virtues of rationality:

Curiosity, relinquishment, lightness, evenness, argument, empiricism, simplicity, humility, perfectionism, precision, scholarship, and the void.

1. Patricia C. Hodgell, Seeker’s Mask (Meisha Merlin Publishing, Inc., 2001).

2. Cleaver, Immediate Fiction: A Complete Writing Course.

3. Antoine de Saint-Exupery, Terre des Hommes (Paris: Gallimard, 1939).

4. Musashi, Book of Five Rings.

Book VI
Becoming Stronger

Beginnings: An Introduction

X. Yudkowsky’s Coming of Age
292. My Childhood Death Spiral
293. My Best and Worst Mistake
294. Raised in Technophilia
295. A Prodigy of Refutation
296. The Sheer Folly of Callow Youth
297. That Tiny Note of Discord
298. Fighting a Rearguard Action Against the Truth
299. My Naturalistic Awakening
300. The Level Above Mine
301. The Magnitude of His Own Folly
302. Beyond the Reach of God
303. My Bayesian Enlightenment

Y. Challenging the Difficult
304. Tsuyoku Naritai! (I Want to Become Stronger)
305. Tsuyoku vs. the Egalitarian Instinct
306. Trying to Try
307. Use the Try Harder, Luke
308. On Doing the Impossible
309. Make an Extraordinary Effort
310. Shut Up and Do the Impossible!
311. Final Words

Z. The Craft and the Community
312. Raising the Sanity Waterline
313. A Sense That More Is Possible
314. Epistemic Viciousness
315. Schools Proliferating Without Evidence
316. Three Levels of Rationality Verification
317. Why Our Kind Can’t Cooperate
318. Tolerate Tolerance
319. Your Price for Joining
320. Can Humanism Match Religion’s Output?
321. Church vs. Taskforce
322. Rationality: Common Interest of Many Causes
323. Helpless Individuals
324. Money: The Unit of Caring
325. Purchase Fuzzies and Utilons Separately
326. Bystander Apathy
327. Collective Apathy and the Internet
328. Incremental Progress and the Valley
329. Bayesians vs. Barbarians
330. Beware of Other-Optimizing
331. Practical Advice Backed by Deep Theories
332. The Sin of Underconfidence
333. Go Forth and Create the Art!

Beginnings: An Introduction
by Rob Bensinger

This, the final book of Rationality: From AI to Zombies, is less a conclusion than a call to action. In keeping with Becoming Stronger’s function as a jumping-off point for further investigation, I’ll conclude by citing resources the reader can use to move beyond these sequences and seek out a fuller understanding of Bayesianism.

This text’s definition of normative rationality in terms of Bayesian probability theory and decision theory is standard in cognitive science. For an introduction to the heuristics and biases approach, see Baron’s Thinking and Deciding.¹ For a general introduction to the field, see the Oxford Handbook of Thinking and Reasoning.²

The arguments made in these pages about the philosophy of rationality are more controversial. Yudkowsky argues, for example, that a rational agent should one-box in Newcomb’s Problem—a minority position among working decision theorists.³ (See Holt for a nontechnical description of Newcomb’s Problem.⁴) Gary Drescher’s Good and Real independently comes to many of the same conclusions as Yudkowsky on philosophy of science and decision theory.⁵ As such, it serves as an excellent book-length treatment of the core philosophical content of Rationality: From AI to Zombies.

Talbott distinguishes several views in Bayesian epistemology, including E.T. Jaynes’ position that not all possible priors are equally reasonable.⁶^,⁷ Like Jaynes, Yudkowsky is interested in supplementing the Bayesian optimality criterion for belief revision with an optimality criterion for priors. This aligns Yudkowsky with researchers who hope to better understand general-purpose AI via an improved theory of ideal reasoning, such as Marcus Hutter.⁸ For a broader discussion of philosophical efforts to naturalize theories of knowledge, see Feldman.⁹

“Bayesianism” is often contrasted with “frequentism.” Some frequentists criticize Bayesians for treating probabilities as subjective states of belief, rather than as objective frequencies of events. Kruschke and Yudkowsky have replied that frequentism is even more “subjective” than Bayesianism, because frequentism’s probability assignments depend on the intentions of the experimenter.¹⁰

Importantly, this philosophical disagreement shouldn’t be conflated with the distinction between Bayesian and frequentist data analysis methods, which can both be useful when employed correctly. Bayesian statistical tools have become cheaper to use since the 1980s, and their informativeness, intuitiveness, and generality have come to be more widely appreciated, resulting in “Bayesian revolutions” in many sciences. However, traditional frequentist methods remain more popular, and in some contexts they are still clearly superior to Bayesian approaches. Kruschke’s Doing Bayesian Data Analysis is a fun and accessible introduction to the topic.¹¹

In light of evidence that training in statistics—and some other fields, such as psychology—improves reasoning skills outside the classroom, statistical literacy is directly relevant to the project of overcoming bias. (Classes in formal logic and informal fallacies have not proven similarly useful.)¹²^,¹³

An Art in its Infancy

We conclude with three sequences on individual and collective self-improvement. “Yudkowsky’s Coming of Age” provides a last in-depth illustration of the dynamics of irrational belief, this time spotlighting the author’s own intellectual history. “Challenging the Difficult” asks what it takes to solve a truly difficult problem—including demands that go beyond epistemic rationality. Finally, “The Craft and the Community” discusses rationality groups and group rationality, raising the questions:

Can rationality be learned and taught?
If so, how much improvement is possible?
How can we be confident we’re seeing a real effect in a rationality intervention, and picking out the right cause?
What community norms would make this process of bettering ourselves easier?
Can we effectively collaborate on large-scale problems without sacrificing our freedom of thought and conduct?

Above all: What’s missing? What should be in the next generation of rationality primers—the ones that replace this text, improve on its style, test its prescriptions, supplement its content, and branch out in altogether new directions?

Though Yudkowsky was moved to write these essays by his own philosophical mistakes and professional difficulties in AI theory, the resultant material has proven useful to a much wider audience. The original blog posts inspired the growth of Less Wrong, a community of intellectuals and life hackers with shared interests in cognitive science, computer science, and philosophy. Yudkowsky and other writers on Less Wrong have helped seed the effective altruism movement, a vibrant and audacious effort to identify the most high-impact humanitarian charities and causes. These writings also sparked the establishment of the Center for Applied Rationality, a nonprofit organization that attempts to translate results from the science of rationality into useable techniques for self-improvement.

I don’t know what’s next—what other unconventional projects or ideas might draw inspiration from these pages. We certainly face no shortage of global challenges, and the art of applied rationality is a new and half-formed thing. There are not many rationalists, and there are many things left undone.

But wherever you’re headed next, reader—may you serve your purpose well.

1. Jonathan Baron, Thinking and Deciding (Cambridge University Press, 2007).

2. Keith J. Holyoak and Robert G. Morrison, The Oxford Handbook of Thinking and Reasoning (Oxford University Press, 2013).

3. Bourget and Chalmers, “What Do Philosophers Believe?”

4. Holt, “Thinking Inside the Boxes.”

5. Gary L. Drescher, Good and Real: Demystifying Paradoxes from Physics to Ethics (Cambridge, MA: MIT Press, 2006).

6. William Talbott, “Bayesian Epistemology,” in The Stanford Encyclopedia of Philosophy, Fall 2013, ed. Edward N. Zalta.

7. Jaynes, Probability Theory.

8. Marcus Hutter, Universal Artificial Intelligence: Sequential Decisions Based On Algorithmic Probability (Berlin: Springer, 2005), doi:10.1007/b138233.

9. Richard Feldman, “Naturalized Epistemology,” in The Stanford Encyclopedia of Philosophy, Summer 2012, ed. Edward N. Zalta.

10. John K. Kruschke, “What to Believe: Bayesian Methods for Data Analysis,” Trends in Cognitive Sciences 14, no. 7 (2010): 293–300.

11. John K. Kruschke, Doing Bayesian Data Analysis, Second Edition: A Tutorial with R, JAGS, and Stan (Academic Press, 2014).

12. Geoffrey T. Fong, David H. Krantz, and Richard E. Nisbett, “The Effects of Statistical Training on Thinking about Everyday Problems,” Cognitive Psychology 18, no. 3 (1986): 253–292, doi:10.1016/0010-0285(86)90001-0.

13. Paul J. H. Schoemaker, “The Role of Statistical Knowledge in Gambling Decisions: Moment vs. Risk Dimension Approaches,” Organizational Behavior and Human Performance 24, no. 1 (1979): 1–17.

Part X
Yudkowsky’s Coming of Age

292
My Childhood Death Spiral

My parents always used to downplay the value of intelligence. And play up the value of—effort, as recommended by the latest research? No, not effort. Experience. A nicely unattainable hammer with which to smack down a bright young child, to be sure. That was what my parents told me when I questioned the Jewish religion, for example. I tried laying out an argument, and I was told something along the lines of: “Logic has limits; you’ll understand when you’re older that experience is the important thing, and then you’ll see the truth of Judaism.” I didn’t try again. I made one attempt to question Judaism in school, got slapped down, didn’t try again. I’ve never been a slow learner.

Whenever my parents were doing something ill-advised, it was always, “We know better because we have more experience. You’ll understand when you’re older: maturity and wisdom are more important than intelligence.”

If this was an attempt to focus the young Eliezer on intelligence uber alles, it was the most wildly successful example of reverse psychology I’ve ever heard of.

But my parents aren’t that cunning, and the results weren’t exactly positive.

For a long time, I thought that the moral of this story was that experience was no match for sheer raw native intelligence. It wasn’t until a lot later, in my twenties, that I looked back and realized that I couldn’t possibly have been more intelligent than my parents before puberty, with my brain not even fully developed. At age eleven, when I was already nearly a full-blown atheist, I could not have defeated my parents in any fair contest of mind. My SAT scores were high for an 11-year-old, but they wouldn’t have beaten my parents’ SAT scores in full adulthood. In a fair fight, my parents’ intelligence and experience could have stomped any prepubescent child flat. It was dysrationalia that did them in; they used their intelligence only to defeat itself.

But that understanding came much later, when my intelligence had processed and distilled many more years of experience.

The moral I derived when I was young was that anyone who downplayed the value of intelligence didn’t understand intelligence at all. My own intelligence had affected every aspect of my life and mind and personality; that was massively obvious, seen at a backward glance. “Intelligence has nothing to do with wisdom or being a good person”—oh, and does self-awareness have nothing to do with wisdom, or being a good person? Modeling yourself takes intelligence. For one thing, it takes enough intelligence to learn evolutionary psychology.

We are the cards we are dealt, and intelligence is the unfairest of all those cards. More unfair than wealth or health or home country, unfairer than your happiness set-point. People have difficulty accepting that life can be that unfair; it’s not a happy thought. “Intelligence isn’t as important as X” is one way of turning away from the unfairness, refusing to deal with it, thinking a happier thought instead. It’s a temptation, both to those dealt poor cards, and to those dealt good ones. Just as downplaying the importance of money is a temptation both to the poor and to the rich.

But the young Eliezer was a transhumanist. Giving away IQ points was going to take more work than if I’d just been born with extra money. But it was a fixable problem, to be faced up to squarely, and fixed. Even if it took my whole life. “The strong exist to serve the weak,” wrote the young Eliezer, “and can only discharge that duty by making others equally strong.” I was annoyed with the Randian and Nietszchean trends in science fiction, and as you may have grasped, the young Eliezer had a tendency to take things too far in the other direction. No one exists only to serve. But I tried, and I don’t regret that. If you call that teenage folly, it’s rare to see adult wisdom doing better.

Everyone needed more intelligence. Including me, I was careful to pronounce. Be it far from me to declare a new world order with myself on top—that was what a stereotyped science fiction villain would do, or worse, a typical teenager, and I would never have allowed myself to be so clichéd. No, everyone needed to be smarter. We were all in the same boat: A fine, uplifting thought.

Eliezer₁₉₉₅ had read his science fiction. He had morals, and ethics, and could see the more obvious traps. No screeds on Homo novis for him. No line drawn between himself and others. No elaborate philosophy to put himself at the top of the heap. It was too obvious a failure mode. Yes, he was very careful to call himself stupid too, and never claim moral superiority. Well, and I don’t see it so differently now, though I no longer make such a dramatic production out of my ethics. (Or maybe it would be more accurate to say that I’m tougher about when I allow myself a moment of self-congratulation.)

I say all this to emphasize that Eliezer₁₉₉₅ wasn’t so undignified as to fail in any obvious way.

And then Eliezer₁₉₉₆ encountered the concept of intelligence explosion. Was it a thunderbolt of revelation? Did I jump out of my chair and shout “Eurisko!”? Nah. I wasn’t that much of a drama queen. It was just massively obvious in retrospect that smarter-than-human intelligence was going to change the future more fundamentally than any mere material science. And I knew at once that this was what I would be doing with the rest of my life, creating the intelligence explosion. Not nanotechnology like I’d thought when I was eleven years old; nanotech would only be a tool brought forth of intelligence. Why, intelligence was even more powerful, an even greater blessing, than I’d realized before.

Was this a happy death spiral? As it turned out later, yes: that is, it led to the adoption even of false happy beliefs about intelligence. Perhaps you could draw the line at the point where I started believing that surely the lightspeed limit would be no barrier to superintelligence.

(How my views on intelligence have changed since then . . . let’s see: When I think of poor hands dealt to humans, these days, I think first of death and old age. Everyone’s got to have some intelligence level or other, and the important thing from a fun-theoretic perspective is that it should ought to increase over time, not decrease like now. Isn’t that a clever way of feeling better? But I don’t work so hard now at downplaying my own intelligence, because that’s just another way of calling attention to it. I’m smart for a human, if the topic should arise, and how I feel about that is my own business.

The part about intelligence being the lever that lifts worlds is the same. Except that intelligence has become less mysterious unto me, so that I now more clearly see intelligence as something embedded within physics. Superintelligences may go FTL if it happens to be permitted by the true physical laws, and if not, then not. It’s not unthinkable, but I wouldn’t bet on it.)

But the real wrong turn came later, at the point where someone said, “Hey, how do you know that superintelligence will be moral? Intelligence has nothing to do with being a good person, you know—that’s what we call wisdom, young prodigy.”

And lo, it seemed obvious to the young Eliezer that this was mere denial. Certainly, his own painstakingly constructed code of ethics had been put together using his intelligence and resting on his intelligence as a base. Any fool could see that intelligence had a great deal to do with ethics, morality, and wisdom; just try explaining the Prisoner’s Dilemma to a chimpanzee, right?

Surely, then, superintelligence would necessarily imply supermorality.

Thus is it said: “Parents do all the things they tell their children not to do, which is how they know not to do them.”

293
My Best and Worst Mistake

Last chapter I covered the young Eliezer’s affective death spiral around something that he called “intelligence.” Eliezer₁₉₉₆, or even Eliezer₁₉₉₉ for that matter, would have refused to try and put a mathematical definition—consciously, deliberately refused. Indeed, he would have been loath to put any definition on “intelligence” at all.

Why? Because there’s a standard bait-and-switch problem in AI, wherein you define “intelligence” to mean something like “logical reasoning” or “the ability to withdraw conclusions when they are no longer appropriate,” and then you build a cheap theorem-prover or an ad-hoc nonmonotonic reasoner, and then say, “Lo, I have implemented intelligence!” People came up with poor definitions of intelligence—focusing on correlates rather than cores—and then they chased the surface definition they had written down, forgetting about, you know, actual intelligence. It’s not like Eliezer₁₉₉₆ was out to build a career in Artificial Intelligence. He just wanted a mind that would actually be able to build nanotechnology. So he wasn’t tempted to redefine intelligence for the sake of puffing up a paper.

Looking back, it seems to me that quite a lot of my mistakes can be defined in terms of being pushed too far in the other direction by seeing someone else’s stupidity. Having seen attempts to define “intelligence” abused so often, I refused to define it at all. What if I said that intelligence was X, and it wasn’t really X? I knew in an intuitive sense what I was looking for—something powerful enough to take stars apart for raw material—and I didn’t want to fall into the trap of being distracted from that by definitions.

Similarly, having seen so many AI projects brought down by physics envy—trying to stick with simple and elegant math, and being constrained to toy systems as a result—I generalized that any math simple enough to be formalized in a neat equation was probably not going to work for, you know, real intelligence. “Except for Bayes’s Theorem,” Eliezer₂₀₀₀ added; which, depending on your viewpoint, either mitigates the totality of his offense, or shows that he should have suspected the entire generalization instead of trying to add a single exception.

If you’re wondering why Eliezer₂₀₀₀ thought such a thing—disbelieved in a math of intelligence—well, it’s hard for me to remember this far back. It certainly wasn’t that I ever disliked math. If I had to point out a root cause, it would be reading too few, too popular, and the wrong Artificial Intelligence books.

But then I didn’t think the answers were going to come from Artificial Intelligence; I had mostly written it off as a sick, dead field. So it’s no wonder that I spent too little time investigating it. I believed in the cliché about Artificial Intelligence overpromising. You can fit that into the pattern of “too far in the opposite direction”—the field hadn’t delivered on its promises, so I was ready to write it off. As a result, I didn’t investigate hard enough to find the math that wasn’t fake.

My youthful disbelief in a mathematics of general intelligence was simultaneously one of my all-time worst mistakes, and one of my all-time best mistakes.

Because I disbelieved that there could be any simple answers to intelligence, I went and I read up on cognitive psychology, functional neuroanatomy, computational neuroanatomy, evolutionary psychology, evolutionary biology, and more than one branch of Artificial Intelligence. When I had what seemed like simple bright ideas, I didn’t stop there, or rush off to try and implement them, because I knew that even if they were true, even if they were necessary, they wouldn’t be sufficient: intelligence wasn’t supposed to be simple, it wasn’t supposed to have an answer that fit on a T-shirt. It was supposed to be a big puzzle with lots of pieces; and when you found one piece, you didn’t run off holding it high in triumph, you kept on looking. Try to build a mind with a single missing piece, and it might be that nothing interesting would happen.

I was wrong in thinking that Artificial Intelligence, the academic field, was a desolate wasteland; and even wronger in thinking that there couldn’t be math of intelligence. But I don’t regret studying e.g. functional neuroanatomy, even though I now think that an Artificial Intelligence should look nothing like a human brain. Studying neuroanatomy meant that I went in with the idea that if you broke up a mind into pieces, the pieces were things like “visual cortex” and “cerebellum”—rather than “stock-market trading module” or “commonsense reasoning module,” which is a standard wrong road in AI.

Studying fields like functional neuroanatomy and cognitive psychology gave me a very different idea of what minds had to look like than you would get from just reading AI books—even good AI books.

When you blank out all the wrong conclusions and wrong justifications, and just ask what that belief led the young Eliezer to actually do . . .

Then the belief that Artificial Intelligence was sick and that the real answer would have to come from healthier fields outside led him to study lots of cognitive sciences;

The belief that AI couldn’t have simple answers led him to not stop prematurely on one brilliant idea, and to accumulate lots of information;

The belief that you didn’t want to define intelligence led to a situation in which he studied the problem for a long time before, years later, he started to propose systematizations.

This is what I refer to when I say that this is one of my all-time best mistakes.

Looking back, years afterward, I drew a very strong moral, to this effect:

What you actually end up doing screens off the clever reason why you’re doing it.

Contrast amazing clever reasoning that leads you to study many sciences, to amazing clever reasoning that says you don’t need to read all those books. Afterward, when your amazing clever reasoning turns out to have been stupid, you’ll have ended up in a much better position if your amazing clever reasoning was of the first type.

When I look back upon my past, I am struck by the number of semi-accidental successes, the number of times I did something right for the wrong reason. From your perspective, you should chalk this up to the anthropic principle: if I’d fallen into a true dead end, you probably wouldn’t be hearing from me in this book. From my perspective it remains something of an embarrassment. My Traditional Rationalist upbringing provided a lot of directional bias to those “accidental successes”—biased me toward rationalizing reasons to study rather than not study, prevented me from getting completely lost, helped me recover from mistakes. Still, none of that was the right action for the right reason, and that’s a scary thing to look back on your youthful history and see. One of my primary purposes in writing on Overcoming Bias is to leave a trail to where I ended up by accident—to obviate the role that luck played in my own forging as a rationalist.

So what makes this one of my all-time worst mistakes? Because sometimes “informal” is another way of saying “held to low standards.” I had amazing clever reasons why it was okay for me not to precisely define “intelligence,” and certain of my other terms as well: namely, other people had gone astray by trying to define it. This was a gate through which sloppy reasoning could enter.

So should I have jumped ahead and tried to forge an exact definition right away? No, all the reasons why I knew this was the wrong thing to do were correct; you can’t conjure the right definition out of thin air if your knowledge is not adequate.

You can’t get to the definition of fire if you don’t know about atoms and molecules; you’re better off saying “that orangey-bright thing.” And you do have to be able to talk about that orangey-bright stuff, even if you can’t say exactly what it is, to investigate fire. But these days I would say that all reasoning on that level is something that can’t be trusted—rather it’s something you do on the way to knowing better, but you don’t trust it, you don’t put your weight down on it, you don’t draw firm conclusions from it, no matter how inescapable the informal reasoning seems.

The young Eliezer put his weight down on the wrong floor tile—stepped onto a loaded trap.

294
Raised in Technophilia

My father used to say that if the present system had been in place a hundred years ago, automobiles would have been outlawed to protect the saddle industry.

One of my major childhood influences was reading Jerry Pournelle’s A Step Farther Out, at the age of nine. It was Pournelle’s reply to Paul Ehrlich and the Club of Rome, who were saying, in the 1960s and 1970s, that the Earth was running out of resources and massive famines were only years away. It was a reply to Jeremy Rifkin’s so-called fourth law of thermodynamics; it was a reply to all the people scared of nuclear power and trying to regulate it into oblivion.

I grew up in a world where the lines of demarcation between the Good Guys and the Bad Guys were pretty clear; not an apocalyptic final battle, but a battle that had to be fought over and over again, a battle where you could see the historical echoes going back to the Industrial Revolution, and where you could assemble the historical evidence about the actual outcomes.

On one side were the scientists and engineers who’d driven all the standard-of-living increases since the Dark Ages, whose work supported luxuries like democracy, an educated populace, a middle class, the outlawing of slavery.

On the other side, those who had once opposed smallpox vaccinations, anesthetics during childbirth, steam engines, and heliocentrism: The theologians calling for a return to a perfect age that never existed, the elderly white male politicians set in their ways, the special interest groups who stood to lose, and the many to whom science was a closed book, fearing what they couldn’t understand.

And trying to play the middle, the pretenders to Deep Wisdom, uttering cached thoughts about how technology benefits humanity but only when it was properly regulated—claiming in defiance of brute historical fact that science of itself was neither good nor evil—setting up solemn-looking bureaucratic committees to make an ostentatious display of their caution—and waiting for their applause. As if the truth were always a compromise. And as if anyone could really see that far ahead. Would humanity have done better if there’d been a sincere, concerned, public debate on the adoption of fire, and committees set up to oversee its use?

When I entered into the problem, I started out allergized against anything that pattern-matched “Ah, but technology has risks as well as benefits, little one.” The presumption-of-guilt was that you were either trying to collect some cheap applause, or covertly trying to regulate the technology into oblivion. And either way, ignoring the historical record immensely in favor of technologies that people had once worried about.

Robin Hanson raised the topic of slow FDA approval of drugs approved in other countries. Someone in the comments pointed out that Thalidomide was sold in 50 countries under 40 names, but that only a small amount was given away in the US, so that there were 10,000 malformed children born globally, but only 17 children in the US.

But how many people have died because of the slow approval in the US, of drugs more quickly approved in other countries—all the drugs that didn’t go wrong? And I ask that question because it’s what you can try to collect statistics about—this says nothing about all the drugs that were never developed because the approval process is too long and costly. According to this source, the FDA’s longer approval process prevents 5,000 casualties per year by screening off medications found to be harmful, and causes at least 20,000–120,000 casualties per year just by delaying approval of those beneficial medications that are still developed and eventually approved.

So there really is a reason to be allergic to people who go around saying, “Ah, but technology has risks as well as benefits.” There’s a historical record showing over-conservativeness, the many silent deaths of regulation being outweighed by a few visible deaths of nonregulation. If you’re really playing the middle, why not say, “Ah, but technology has benefits as well as risks”?

Well, and this isn’t such a bad description of the Bad Guys. (Except that it ought to be emphasized a bit harder that these aren’t evil mutants but standard human beings acting under a different worldview-gestalt that puts them in the right; some of them will inevitably be more competent than others, and competence counts for a lot.) Even looking back, I don’t think my childhood technophilia was too wrong about what constituted a Bad Guy and what was the key mistake. But it’s always a lot easier to say what not to do, than to get it right. And one of my fundamental flaws, back then, was thinking that if you tried as hard as you could to avoid everything the Bad Guys were doing, that made you a Good Guy.

Particularly damaging, I think, was the bad example set by the pretenders to Deep Wisdom trying to stake out a middle way; smiling condescendingly at technophiles and technophobes alike, and calling them both immature. Truly this is a wrong way; and in fact, the notion of trying to stake out a middle way generally, is usually wrong. The Right Way is not a compromise with anything; it is the clean manifestation of its own criteria.

But that made it more difficult for the young Eliezer to depart from the charge-straight-ahead verdict, because any departure felt like joining the pretenders to Deep Wisdom.

The first crack in my childhood technophilia appeared in, I think, 1997 or 1998, at the point where I noticed my fellow technophiles saying foolish things about how molecular nanotechnology would be an easy problem to manage. (As you may be noticing yet again, the young Eliezer was driven to a tremendous extent by his ability to find flaws—I even had a personal philosophy of why that sort of thing was a good idea.)

There was a debate going on about molecular nanotechnology, and whether offense would be asymmetrically easier than defense. And there were people arguing that defense would be easy. In the domain of nanotech, for Ghu’s sake, programmable matter, when we can’t even seem to get the security problem solved for computer networks where we can observe and control every one and zero. People were talking about unassailable diamondoid walls. I observed that diamond doesn’t stand off a nuclear weapon, that offense has had defense beat since 1945 and nanotech didn’t look likely to change that.

And by the time that debate was over, it seems that the young Eliezer—caught up in the heat of argument—had managed to notice, for the first time, that the survival of Earth-originating intelligent life stood at risk.

It seems so strange, looking back, to think that there was a time when I thought that only individual lives were at stake in the future. What a profoundly friendlier world that was to live in . . . though it’s not as if I were thinking that at the time. I didn’t reject the possibility so much as manage to never see it in the first place. Once the topic actually came up, I saw it. I don’t really remember how that trick worked. There’s a reason why I refer to my past self in the third person.

It may sound like Eliezer₁₉₉₈ was a complete idiot, but that would be a comfortable out, in a way; the truth is scarier. Eliezer₁₉₉₈ was a sharp Traditional Rationalist, as such things went. I knew hypotheses had to be testable, I knew that rationalization was not a permitted mental operation, I knew how to play Rationalist’s Taboo, I was obsessed with self-awareness . . . I didn’t quite understand the concept of “mysterious answers” . . . and no Bayes or Kahneman at all. But a sharp Traditional Rationalist, far above average . . . So what? Nature isn’t grading us on a curve. One step of departure from the Way, one shove of undue influence on your thought processes, can repeal all other protections.

One of the chief lessons I derive from looking back at my personal history is that it’s no wonder that, out there in the real world, a lot of people think that “intelligence isn’t everything,” or that rationalists don’t do better in real life. A little rationality, or even a lot of rationality, doesn’t pass the astronomically high barrier required for things to actually start working.

Let not my misinterpretation of the Right Way be blamed on Jerry Pournelle, my father, or science fiction generally. I think the young Eliezer’s personality imposed quite a bit of selectivity on which parts of their teachings made it through. It’s not as if Pournelle didn’t say: The rules change once you leave Earth, the cradle; if you’re careless sealing your pressure suit just once, you die. He said it quite a bit. But the words didn’t really seem important, because that was something that happened to third-party characters in the novels—the main character didn’t usually die halfway through, for some reason.

What was the lens through which I filtered these teachings? Hope. Optimism. Looking forward to a brighter future. That was the fundamental meaning of A Step Farther Out unto me, the lesson I took in contrast to the Sierra Club’s doom-and-gloom. On one side was rationality and hope, the other, ignorance and despair.

Some teenagers think they’re immortal and ride motorcycles. I was under no such illusion and quite reluctant to learn to drive, considering how unsafe those hurtling hunks of metal looked. But there was something more important to me than my own life: The Future. And I acted as if that were immortal. Lives could be lost, but not the Future.

And when I noticed that nanotechnology really was going to be a potentially extinction-level challenge?

The young Eliezer thought, explicitly, “Good heavens, how did I fail to notice this thing that should have been obvious? I must have been too emotionally attached to the benefits I expected from the technology; I must have flinched away from the thought of human extinction.”

And then . . .

I didn’t declare a Halt, Melt, and Catch Fire. I didn’t rethink all the conclusions that I’d developed with my prior attitude. I just managed to integrate it into my worldview, somehow, with a minimum of propagated changes. Old ideas and plans were challenged, but my mind found reasons to keep them. There was no systemic breakdown, unfortunately.

Most notably, I decided that we had to run full steam ahead on AI, so as to develop it before nanotechnology. Just like I’d been originally planning to do, but now, with a different reason.

I guess that’s what most human beings are like, isn’t it? Traditional Rationality wasn’t enough to change that.

But there did come a time when I fully realized my mistake. It just took a stronger boot to the head.

295
A Prodigy of Refutation

My Childhood Death Spiral described the core momentum carrying me into my mistake, an affective death spiral around something that Eliezer₁₉₉₆ called “intelligence.” I was also a technophile, pre-allergized against fearing the future. And I’d read a lot of science fiction built around personhood ethics—in which fear of the Alien puts humanity-at-large in the position of the bad guys, mistreating aliens or sentient AIs because they “aren’t human.”

That’s part of the ethos you acquire from science fiction—to define your in-group, your tribe, appropriately broadly. Hence my email address, sentience@pobox.com.

So Eliezer₁₉₉₆ is out to build superintelligence, for the good of humanity and all sentient life.

At first, I think, the question of whether a superintelligence will/could be good/evil didn’t really occur to me as a separate topic of discussion. Just the standard intuition of, “Surely no supermind would be stupid enough to turn the galaxy into paperclips; surely, being so intelligent, it will also know what’s right far better than a human being could.”

Until I introduced myself and my quest to a transhumanist mailing list, and got back responses along the general lines of (from memory):

Morality is arbitrary—if you say that something is good or bad, you can’t be right or wrong about that. A superintelligence would form its own morality.

Everyone ultimately looks after their own self-interest. A superintelligence would be no different; it would just seize all the resources.

Personally, I’m a human, so I’m in favor of humans, not Artificial Intelligences. I don’t think we should develop this technology. Instead we should develop the technology to upload humans first.

No one should develop an AI without a control system that watches it and makes sure it can’t do anything bad.

Well, that’s all obviously wrong, thinks Eliezer₁₉₉₆, and he proceeded to kick his opponents’ arguments to pieces. (I’ve mostly done this in other essays, and anything remaining is left as an exercise to the reader.)

It’s not that Eliezer₁₉₉₆ explicitly reasoned, “The world’s stupidest man says the Sun is shining, therefore it is dark out.” But Eliezer₁₉₉₆ was a Traditional Rationalist; he had been inculcated with the metaphor of science as a fair fight between sides who take on different positions, stripped of mere violence and other such exercises of political muscle, so that, ideally, the side with the best arguments can win.

It’s easier to say where someone else’s argument is wrong, then to get the fact of the matter right; and Eliezer₁₉₉₆ was very skilled at finding flaws. (So am I. It’s not as if you can solve the danger of that power by refusing to care about flaws.) From Eliezer₁₉₉₆’s perspective, it seemed to him that his chosen side was winning the fight—that he was formulating better arguments than his opponents—so why would he switch sides?

Therefore is it written: “Because this world contains many whose grasp of rationality is abysmal, beginning students of rationality win arguments and acquire an exaggerated view of their own abilities. But it is useless to be superior: Life is not graded on a curve. The best physicist in ancient Greece could not calculate the path of a falling apple. There is no guarantee that adequacy is possible given your hardest effort; therefore spare no thought for whether others are doing worse.”

You cannot rely on anyone else to argue you out of your mistakes; you cannot rely on anyone else to save you; you and only you are obligated to find the flaws in your positions; if you put that burden down, don’t expect anyone else to pick it up. And I wonder if that advice will turn out not to help most people, until they’ve personally blown off their own foot, saying to themselves all the while, correctly, “Clearly I’m winning this argument.”

Today I try not to take any human being as my opponent. That just leads to overconfidence. It is Nature that I am facing off against, who does not match Her problems to your skill, who is not obliged to offer you a fair chance to win in return for a diligent effort, who does not care if you are the best who ever lived, if you are not good enough.

But return to 1996. Eliezer₁₉₉₆ is going with the basic intuition of “Surely a superintelligence will know better than we could what is right,” and offhandedly knocking down various arguments brought against his position. He was skillful in that way, you see. He even had a personal philosophy of why it was wise to look for flaws in things, and so on.

I don’t mean to say it as an excuse, that no one who argued against Eliezer₁₉₉₆ actually presented him with the dissolution of the mystery—the full reduction of morality that analyzes all his cognitive processes debating “morality,” a step-by-step walkthrough of the algorithms that make morality feel to him like a fact. Consider it rather as an indictment, a measure of Eliezer₁₉₉₆’s level, that he would have needed the full solution given to him, in order to present him with an argument that he could not refute.

The few philosophers present did not extract him from his difficulties. It’s not as if a philosopher will say, “Sorry, morality is understood, it is a settled issue in cognitive science and philosophy, and your viewpoint is simply wrong.” The nature of morality is still an open question in philosophy; the debate is still going on. A philosopher will feel obligated to present you with a list of classic arguments on all sides—most of which Eliezer₁₉₉₆ is quite intelligent enough to knock down, and so he concludes that philosophy is a wasteland.

But wait. It gets worse.

I don’t recall exactly when—it might have been 1997—but the younger me, let’s call him Eliezer₁₉₉₇, set out to argue inescapably that creating superintelligence is the right thing to do.

296
The Sheer Folly of Callow Youth

There speaks the sheer folly of callow youth; the rashness of an ignorance so abysmal as to be possible only to one of your ephemeral race . . .

—Gharlane of Eddore¹

Once upon a time, years ago, I propounded a mysterious answer to a mysterious question—as I’ve hinted on several occasions. The mysterious question to which I propounded a mysterious answer was not, however, consciousness—or rather, not only consciousness. No, the more embarrassing error was that I took a mysterious view of morality.

I held off on discussing that until now, after the series on metaethics, because I wanted it to be clear that Eliezer₁₉₉₇ had gotten it wrong.

When we last left off, Eliezer₁₉₉₇, not satisfied with arguing in an intuitive sense that superintelligence would be moral, was setting out to argue inescapably that creating superintelligence was the right thing to do.

Well (said Eliezer₁₉₉₇) let’s begin by asking the question: Does life have, in fact, any meaning?

“I don’t know,” replied Eliezer₁₉₉₇ at once, with a certain note of self-congratulation for admitting his own ignorance on this topic where so many others seemed certain.

“But,” he went on—

(Always be wary when an admission of ignorance is followed by “But.”)

“But, if we suppose that life has no meaning—that the utility of all outcomes is equal to zero—that possibility cancels out of any expected utility calculation. We can therefore always act as if life is known to be meaningful, even though we don’t know what that meaning is. How can we find out that meaning? Considering that humans are still arguing about this, it’s probably too difficult a problem for humans to solve. So we need a superintelligence to solve the problem for us. As for the possibility that there is no logical justification for one preference over another, then in this case it is no righter or wronger to build a superintelligence, than to do anything else. This is a real possibility, but it falls out of any attempt to calculate expected utility—we should just ignore it. To the extent someone says that a superintelligence would wipe out humanity, they are either arguing that wiping out humanity is in fact the right thing to do (even though we see no reason why this should be the case) or they are arguing that there is no right thing to do (in which case their argument that we should not build intelligence defeats itself).”

Ergh. That was a really difficult paragraph to write. My past self is always my own most concentrated Kryptonite, because my past self is exactly precisely all those things that the modern me has installed allergies to block. Truly is it said that parents do all the things they tell their children not to do, which is how they know not to do them; it applies between past and future selves as well.

How flawed is Eliezer₁₉₉₇’s argument? I couldn’t even count the ways. I know memory is fallible, reconstructed each time we recall, and so I don’t trust my assembly of these old pieces using my modern mind. Don’t ask me to read my old writings; that’s too much pain.

But it seems clear that I was thinking of utility as a sort of stuff, an inherent property. So that “life is meaningless” corresponded to utility = 0. But of course the argument works equally well with utility = 100, so that if everything is meaningful but it is all equally meaningful, that should fall out too . . . Certainly I wasn’t then thinking of a utility function as an affine structure in preferences. I was thinking of “utility” as an absolute level of inherent value.

I was thinking of should as a kind of purely abstract essence of compellingness, that-which-makes-you-do-something; so that clearly any mind that derived a should would be bound by it. Hence the assumption, which Eliezer₁₉₉₇ did not even think to explicitly note, that a logic that compels an arbitrary mind to do something is exactly the same as that which human beings mean and refer to when they utter the word “right” . . .

But now I’m trying to count the ways, and if you’ve been following along, you should be able to handle that yourself.

An important aspect of this whole failure was that, because I’d proved that the case “life is meaningless” wasn’t worth considering, I didn’t think it was necessary to rigorously define “intelligence” or “meaning.” I’d previously come up with a clever reason for not trying to go all formal and rigorous when trying to define “intelligence” (or “morality”)—namely all the bait-and-switches that past AI folk, philosophers, and moralists had pulled with definitions that missed the point.

I draw the following lesson: No matter how clever the justification for relaxing your standards, or evading some requirement of rigor, it will blow your foot off just the same.

And another lesson: I was skilled in refutation. If I’d applied the same level of rejection-based-on-any-flaw to my own position as I used to defeat arguments brought against me, then I would have zeroed in on the logical gap and rejected the position—if I’d wanted to. If I’d had the same level of prejudice against it as I’d had against other positions in the debate.

But this was before I’d heard of Kahneman, before I’d heard the term “motivated skepticism,” before I’d integrated the concept of an exactly correct state of uncertainty that summarizes all the evidence, and before I knew the deadliness of asking “Am I allowed to believe?” for liked positions and “Am I forced to believe?” for disliked positions. I was a mere Traditional Rationalist who thought of the scientific process as a referee between people who took up positions and argued them, may the best side win.

My ultimate flaw was not a liking for “intelligence,” nor any amount of technophilia and science fiction exalting the siblinghood of sentience. It surely wasn’t my ability to spot flaws. None of these things could have led me astray, if I had held myself to a higher standard of rigor throughout, and adopted no position otherwise. Or even if I’d just scrutinized my preferred vague position, with the same demand-of-rigor I applied to counterarguments.

But I wasn’t much interested in trying to refute my belief that life had meaning, since my reasoning would always be dominated by cases where life did have meaning.

And with the intelligence explosion at stake, I thought I just had to proceed at all speed using the best concepts I could wield at the time, not pause and shut down everything while I looked for a perfect definition that so many others had screwed up . . .

No.

No, you don’t use the best concepts you can use at the time.

It’s Nature that judges you, and Nature does not accept even the most righteous excuses. If you don’t meet the standard, you fail. It’s that simple. There is no clever argument for why you have to make do with what you have, because Nature won’t listen to that argument, won’t forgive you because there were so many excellent justifications for speed.

We all know what happened to Donald Rumsfeld, when he went to war with the army he had, instead of the army he needed.

Maybe Eliezer₁₉₉₇ couldn’t have conjured the correct model out of thin air. (Though who knows what would have happened, if he’d really tried . . .) And it wouldn’t have been prudent for him to stop thinking entirely, until rigor suddenly popped out of nowhere.

But neither was it correct for Eliezer₁₉₉₇ to put his weight down on his “best guess,” in the absence of precision. You can use vague concepts in your own interim thought processes, as you search for a better answer, unsatisfied with your current vague hints, and unwilling to put your weight down on them. You don’t build a superintelligence based on an interim understanding. No, not even the “best” vague understanding you have. That was my mistake—thinking that saying “best guess” excused anything. There was only the standard I had failed to meet.

Of course Eliezer₁₉₉₇ didn’t want to slow down on the way to the intelligence explosion, with so many lives at stake, and the very survival of Earth-originating intelligent life, if we got to the era of nanoweapons before the era of superintelligence—

Nature doesn’t care about such righteous reasons. There’s just the astronomically high standard needed for success. Either you match it, or you fail. That’s all.

The apocalypse does not need to be fair to you.

The apocalypse does not need to offer you a chance of success

In exchange for what you’ve already brought to the table.

The apocalypse’s difficulty is not matched to your skills.

The apocalypse’s price is not matched to your resources.

If the apocalypse asks you for something unreasonable

And you try to bargain it down a little

(Because everyone has to compromise now and then)

The apocalypse will not try to negotiate back up.

And, oh yes, it gets worse.

How did Eliezer₁₉₉₇ deal with the obvious argument that you couldn’t possibly derive an “ought” from pure logic, because “ought” statements could only be derived from other “ought” statements?

Well (observed Eliezer₁₉₉₇), this problem has the same structure as the argument that a cause only proceeds from another cause, or that a real thing can only come of another real thing, whereby you can prove that nothing exists.

Thus (he said) there are three “hard problems”: the hard problem of conscious experience, in which we see that qualia cannot arise from computable processes; the hard problem of existence, in which we ask how any existence enters apparently from nothingness; and the hard problem of morality, which is to get to an “ought.”

These problems are probably linked. For example, the qualia of pleasure are one of the best candidates for something intrinsically desirable. We might not be able to understand the hard problem of morality, therefore, without unraveling the hard problem of consciousness. It’s evident that these problems are too hard for humans—otherwise someone would have solved them over the last 2,500 years since philosophy was invented.

It’s not as if they could have complicated solutions—they’re too simple for that. The problem must just be outside human concept-space. Since we can see that consciousness can’t arise on any computable process, it must involve new physics—physics that our brain uses, but can’t understand. That’s why we need superintelligence in order to solve this problem. Probably it has to do with quantum mechanics, maybe with a dose of tiny closed timelike curves from out of General Relativity; temporal paradoxes might have some of the same irreducibility properties that consciousness seems to demand . . .

Et cetera, ad nauseam. You may begin to perceive, in the arc of my Overcoming Bias posts, the letter I wish I could have written to myself.

Of this I learn the lesson: You cannot manipulate confusion. You cannot make clever plans to work around the holes in your understanding. You can’t even make “best guesses” about things which fundamentally confuse you, and relate them to other confusing things. Well, you can, but you won’t get it right, until your confusion dissolves. Confusion exists in the mind, not in the reality, and trying to treat it like something you can pick up and move around will only result in unintentional comedy.

Similarly, you cannot come up with clever reasons why the gaps in your model don’t matter. You cannot draw a border around the mystery, put on neat handles that let you use the Mysterious Thing without really understanding it—like my attempt to make the possibility that life is meaningless cancel out of an expected utility formula. You can’t pick up the gap and manipulate it.

If the blank spot on your map conceals a land mine, then putting your weight down on that spot will be fatal, no matter how good your excuse for not knowing. Any black box could contain a trap, and there’s no way to know except opening up the black box and looking inside. If you come up with some righteous justification for why you need to rush on ahead with the best understanding you have—the trap goes off.

It’s only when you know the rules,

That you realize why you needed to learn;

What would have happened otherwise,

How much you needed to know.

Only knowledge can foretell the cost of ignorance. The ancient alchemists had no logical way of knowing the exact reasons why it was hard for them to turn lead into gold. So they poisoned themselves and died. Nature doesn’t care.

But there did come a time when realization began to dawn on me.

1. Edward Elmer Smith, Second Stage Lensmen (Old Earth Books, 1998).

297
That Tiny Note of Discord

When we last left Eliezer₁₉₉₇, he believed that any superintelligence would automatically do what was “right,” and indeed would understand that better than we could—even though, he modestly confessed, he did not understand the ultimate nature of morality. Or rather, after some debate had passed, Eliezer₁₉₉₇ had evolved an elaborate argument, which he fondly claimed to be “formal,” that we could always condition upon the belief that life has meaning; and so cases where superintelligences did not feel compelled to do anything in particular would fall out of consideration. (The flaw being the unconsidered and unjustified equation of “universally compelling argument” with “right.”)

So far, the young Eliezer is well on the way toward joining the “smart people who are stupid because they’re skilled at defending beliefs they arrived at for unskilled reasons” club. All his dedication to “rationality” has not saved him from this mistake, and you might be tempted to conclude that it is useless to strive for rationality.

But while many people dig holes for themselves, not everyone succeeds in clawing their way back out.

And from this I learn my lesson: That it all began—

—with a small, small question; a single discordant note; one tiny lonely thought . . .

As our story starts, we advance three years to Eliezer₂₀₀₀, who in most respects resembles his self of 1997. He currently thinks he’s proven that building a superintelligence is the right thing to do if there is any right thing at all. From which it follows that there is no justifiable conflict of interest over the intelligence explosion among the peoples and persons of Earth.

This is an important conclusion for Eliezer₂₀₀₀, because he finds the notion of fighting over the intelligence explosion to be unbearably stupid. (Sort of like the notion of God intervening in fights between tribes of bickering barbarians, only in reverse.) Eliezer₂₀₀₀’s self-concept does not permit him—he doesn’t even want—to shrug and say, “Well, my side got here first, so we’re going to seize the banana before anyone else gets it.” It’s a thought too painful to think.

And yet then the notion occurs to him:

Maybe some people would prefer an AI do particular things, such as not kill them, even if life is meaningless?

His immediately following thought is the obvious one, given his premises:

In the event that life is meaningless, nothing is the “right” thing to do; therefore it wouldn’t be particularly right to respect people’s preferences in this event.

This is the obvious dodge. The thing is, though, Eliezer₂₀₀₀ doesn’t think of himself as a villain. He doesn’t go around saying, “What bullets shall I dodge today?” He thinks of himself as a dutiful rationalist who tenaciously follows lines of inquiry. Later, he’s going to look back and see a whole lot of inquiries that his mind somehow managed to not follow—but that’s not his current self-concept.

So Eliezer₂₀₀₀ doesn’t just grab the obvious out. He keeps thinking.

But if people believe they have preferences in the event that life is meaningless, then they have a motive to dispute my intelligence explosion project and go with a project that respects their wish in the event life is meaningless. This creates a present conflict of interest over the intelligence explosion, and prevents right things from getting done in the mainline event that life is meaningful.

Now, there’s a lot of excuses Eliezer₂₀₀₀ could have potentially used to toss this problem out the window. I know, because I’ve heard plenty of excuses for dismissing Friendly AI. “The problem is too hard to solve” is one I get from AGI wannabes who imagine themselves smart enough to create true Artificial Intelligence, but not smart enough to solve a really difficult problem like Friendly AI. Or “worrying about this possibility would be a poor use of resources, what with the incredible urgency of creating AI before humanity wipes itself out—you’ve got to go with what you have,” this being uttered by people who just basically aren’t interested in the problem.

But Eliezer₂₀₀₀ is a perfectionist. He’s not perfect, obviously, and he doesn’t attach as much importance as I do to the virtue of precision, but he is most certainly a perfectionist. The idea of metaethics that Eliezer₂₀₀₀ espouses, in which superintelligences know what’s right better than we do, previously seemed to wrap up all the problems of justice and morality in an airtight wrapper.

The new objection seems to poke a minor hole in the airtight wrapper. This is worth patching. If you have something that’s perfect, are you really going to let one little possibility compromise it?

So Eliezer₂₀₀₀ doesn’t even want to drop the issue; he wants to patch the problem and restore perfection. How can he justify spending the time? By thinking thoughts like:

What about Brian Atkins? [Brian Atkins being the startup funder of the Machine Intelligence Research Institute, then called the Singularity Institute.] He would probably prefer not to die, even if life were meaningless. He’s paying for MIRI right now; I don’t want to taint the ethics of our cooperation.

Eliezer₂₀₀₀’s sentiment doesn’t translate very well—English doesn’t have a simple description for it, or any other culture I know. Maybe the passage in the Old Testament, “Thou shalt not boil a young goat in its mother’s milk.” Someone who helps you out of altruism shouldn’t regret helping you; you owe them, not so much fealty, but rather, that they’re actually doing what they think they’re doing by helping you.

Well, but how would Brian Atkins find out, if I don’t tell him? Eliezer₂₀₀₀ doesn’t even think this except in quotation marks, as the obvious thought that a villain would think in the same situation. And Eliezer₂₀₀₀ has a standard counter-thought ready too, a ward against temptations to dishonesty—an argument that justifies honesty in terms of expected utility, not just a personal love of personal virtue:

Human beings aren’t perfect deceivers; it’s likely that I’ll be found out. Or what if genuine lie detectors are invented before the Singularity, sometime over the next thirty years? I wouldn’t be able to pass a lie detector test.

Eliezer₂₀₀₀ lives by the rule that you should always be ready to have your thoughts broadcast to the whole world at any time, without embarrassment. Otherwise, clearly, you’ve fallen from grace: either you’re thinking something you shouldn’t be thinking, or you’re embarrassed by something that shouldn’t embarrass you.

(These days, I don’t espouse quite such an extreme viewpoint, mostly for reasons of Fun Theory. I see a role for continued social competition between intelligent life-forms, as least as far as my near-term vision stretches. I admit, these days, that it might be all right for human beings to have a self; as John McCarthy put it, “If everyone were to live for others all the time, life would be like a procession of ants following each other around in a circle.” If you’re going to have a self, you may as well have secrets, and maybe even conspiracies. But I do still try to abide by the principle of being able to pass a future lie detector test, with anyone else who’s also willing to go under the lie detector, if the topic is a professional one. Fun Theory needs a commonsense exception for global catastrophic risk management.)

Even taking honesty for granted, there are other excuses Eliezer₂₀₀₀ could use to flush the question down the toilet. “The world doesn’t have the time” or “It’s unsolvable” would still work. But Eliezer₂₀₀₀ doesn’t know that this problem, the “backup” morality problem, is going to be particularly difficult or time-consuming. He’s just now thought of the whole issue.

And so Eliezer₂₀₀₀ begins to really consider the question: Supposing that “life is meaningless” (that superintelligences don’t produce their own motivations from pure logic), then how would you go about specifying a fallback morality? Synthesizing it, inscribing it into the AI?

There’s a lot that Eliezer₂₀₀₀ doesn’t know, at this point. But he has been thinking about self-improving AI for three years, and he’s been a Traditional Rationalist for longer than that. There are techniques of rationality that he has practiced, methodological safeguards he’s already devised. He already knows better than to think that all an AI needs is the One Great Moral Principle. Eliezer₂₀₀₀ already knows that it is wiser to think technologically than politically. He already knows the saying that AI programmers are supposed to think in code, to use concepts that can be inscribed in a computer. Eliezer₂₀₀₀ already has a concept that there is something called “technical thinking” and it is good, though he hasn’t yet formulated a Bayesian view of it. And he’s long since noticed that suggestively named LISP tokens don’t really mean anything, et cetera. These injunctions prevent him from falling into some of the initial traps, the ones that I’ve seen consume other novices on their own first steps into the Friendly AI problem . . . though technically this was my second step; I well and truly failed on my first.

But in the end, what it comes down to is this: For the first time, Eliezer₂₀₀₀ is trying to think technically about inscribing a morality into an AI, without the escape-hatch of the mysterious essence of rightness.

That’s the only thing that matters, in the end. His previous philosophizing wasn’t enough to force his brain to confront the details. This new standard is strict enough to require actual work. Morality slowly starts being less mysterious to him—Eliezer₂₀₀₀ is starting to think inside the black box.

His reasons for pursuing this course of action—those don’t matter at all.

Oh, there’s a lesson in his being a perfectionist. There’s a lesson in the part about how Eliezer₂₀₀₀ initially thought this was a tiny flaw, and could have dismissed it out-of-mind if that had been his impulse.

But in the end, the chain of cause and effect goes like this: Eliezer₂₀₀₀ investigated in more detail, therefore he got better with practice. Actions screen off justifications. If your arguments happen to justify not working things out in detail, like Eliezer₁₉₉₆, then you won’t get good at thinking about the problem. If your arguments call for you to work things out in detail, then you have an opportunity to start accumulating expertise.

That was the only choice that mattered, in the end—not the reasons for doing anything.

I say all this, as you may well guess, because of the AI wannabes I sometimes run into who have their own clever reasons for not thinking about the Friendly AI problem. Our clever reasons for doing what we do tend to matter a lot less to Nature than they do to ourselves and our friends. If your actions don’t look good when they’re stripped of all their justifications and presented as mere brute facts . . . then maybe you should re-examine them.

A diligent effort won’t always save a person. There is such a thing as lack of ability. Even so, if you don’t try, or don’t try hard enough, you don’t get a chance to sit down at the high-stakes table—never mind the ability ante. That’s cause and effect for you.

Also, perfectionism really matters. The end of the world doesn’t always come with trumpets and thunder and the highest priority in your inbox. Sometimes the shattering truth first presents itself to you as a small, small question; a single discordant note; one tiny lonely thought, that you could dismiss with one easy effortless touch . . .

. . . and so, over succeeding years, understanding begins to dawn on that past Eliezer, slowly. That Sun rose slower than it could have risen.

298
Fighting a Rearguard Action Against the Truth

When we last left Eliezer₂₀₀₀, he was just beginning to investigate the question of how to inscribe a morality into an AI. His reasons for doing this don’t matter at all, except insofar as they happen to historically demonstrate the importance of perfectionism. If you practice something, you may get better at it; if you investigate something, you may find out about it; the only thing that matters is that Eliezer₂₀₀₀ is, in fact, focusing his full-time energies on thinking technically about AI morality—rather than, as previously, finding any justification for not spending his time this way. In the end, this is all that turns out to matter.

But as our story begins—as the sky lightens to gray and the tip of the Sun peeks over the horizon—Eliezer₂₀₀₁ hasn’t yet admitted that Eliezer₁₉₉₇ was mistaken in any important sense. He’s just making Eliezer₁₉₉₇’s strategy even better by including a contingency plan for “the unlikely event that life turns out to be meaningless” . . .

. . . which means that Eliezer₂₀₀₁ now has a line of retreat away from his mistake.

I don’t just mean that Eliezer₂₀₀₁ can say “Friendly AI is a contingency plan,” rather than screaming “OOPS!”

I mean that Eliezer₂₀₀₁ now actually has a contingency plan. If Eliezer₂₀₀₁ starts to doubt his 1997 metaethics, the intelligence explosion has a fallback strategy, namely Friendly AI. Eliezer₂₀₀₁ can question his metaethics without it signaling the end of the world.

And his gradient has been smoothed; he can admit a 10% chance of having previously been wrong, then a 20% chance. He doesn’t have to cough out his whole mistake in one huge lump.

If you think this sounds like Eliezer₂₀₀₁ is too slow, I quite agree.

Eliezer_1996–2000’s strategies had been formed in the total absence of “Friendly AI” as a consideration. The whole idea was to get a superintelligence, any superintelligence, as fast as possible—codelet soup, ad-hoc heuristics, evolutionary programming, open-source, anything that looked like it might work—preferably all approaches simultaneously in a Manhattan Project. (“All parents did the things they tell their children not to do. That’s how they know to tell them not to do it.”¹) It’s not as if adding one more approach could hurt.

His attitudes toward technological progress have been formed—or more accurately, preserved from childhood-absorbed technophilia—around the assumption that any/all movement toward superintelligence is a pure good without a hint of danger.

Looking back, what Eliezer₂₀₀₁ needed to do at this point was declare an HMC event—Halt, Melt, and Catch Fire. One of the foundational assumptions on which everything else has been built has been revealed as flawed. This calls for a mental brake to a full stop: take your weight off all beliefs built on the wrong assumption, do your best to rethink everything from scratch. This is an art I need to write more about—it’s akin to the convulsive effort required to seriously clean house, after an adult religionist notices for the first time that God doesn’t exist.

But what Eliezer₂₀₀₁ actually did was rehearse his previous technophilic arguments for why it’s difficult to ban or governmentally control new technologies—the standard arguments against “relinquishment.”

It does seem even to my modern self that all those awful consequences which technophiles argue to follow from various kinds of government regulation are more or less correct—it’s much easier to say what someone is doing wrong, than to say the way that is right. My modern viewpoint hasn’t shifted to think that technophiles are wrong about the downsides of technophobia; but I do tend to be a lot more sympathetic to what technophobes say about the downsides of technophilia. What previous Eliezers said about the difficulties of, e.g., the government doing anything sensible about Friendly AI, still seems pretty true. It’s just that a lot of his hopes for science, or private industry, etc., now seem equally wrongheaded.

Still, let’s not get into the details of the technovolatile viewpoint. Eliezer₂₀₀₁ has just tossed a major foundational assumption—that AI can’t be dangerous, unlike other technologies—out the window. You would intuitively suspect that this should have some kind of large effect on his strategy.

Well, Eliezer₂₀₀₁ did at least give up on his 1999 idea of an open-source AI Manhattan Project using self-modifying heuristic soup, but overall . . .

Overall, he’d previously wanted to charge in, guns blazing, immediately using his best idea at the time; and afterward he still wanted to charge in, guns blazing. He didn’t say, “I don’t know how to do this.” He didn’t say, “I need better knowledge.” He didn’t say, “This project is not yet ready to start coding.” It was still all, “The clock is ticking, gotta move now! MIRI will start coding as soon as it’s got enough money!”

Before, he’d wanted to focus as much scientific effort as possible with full information-sharing, and afterward he still thought in those terms. Scientific secrecy = bad guy, openness = good guy. (Eliezer₂₀₀₁ hadn’t read up on the Manhattan Project and wasn’t familiar with the similar argument that Leó Szilárd had with Enrico Fermi.)

That’s the problem with converting one big “Oops!” into a gradient of shifting probability. It means there isn’t a single watershed moment—a visible huge impact—to hint that equally huge changes might be in order.

Instead, there are all these little opinion shifts . . . that give you a chance to repair the arguments for your strategies; to shift the justification a little, but keep the “basic idea” in place. Small shocks that the system can absorb without cracking, because each time, it gets a chance to go back and repair itself. It’s just that in the domain of rationality, cracking = good, repair = bad. In the art of rationality it’s far more efficient to admit one huge mistake, than to admit lots of little mistakes.

There’s some kind of instinct humans have, I think, to preserve their former strategies and plans, so that they aren’t constantly thrashing around and wasting resources; and of course an instinct to preserve any position that we have publicly argued for, so that we don’t suffer the humiliation of being wrong. And though the younger Eliezer has striven for rationality for many years, he is not immune to these impulses; they waft gentle influences on his thoughts, and this, unfortunately, is more than enough damage.

Even in 2002, the earlier Eliezer isn’t yet sure that Eliezer₁₉₉₇’s plan couldn’t possibly have worked. It might have gone right. You never know, right?

But there came a time when it all fell crashing down.

1. John Moore, Slay and Rescue (Xlibris Corp, 2000).

299
My Naturalistic Awakening

In the previous episode, Eliezer₂₀₀₁ is fighting a rearguard action against the truth. Only gradually shifting his beliefs, admitting an increasing probability in a different scenario, but never saying outright, “I was wrong before.” He repairs his strategies as they are challenged, finding new justifications for just the same plan he pursued before.

(Of which it is therefore said: “Beware lest you fight a rearguard retreat against the evidence, grudgingly conceding each foot of ground only when forced, feeling cheated. Surrender to the truth as quickly as you can. Do this the instant you realize what you are resisting; the instant you can see from which quarter the winds of evidence are blowing against you.”)

Memory fades, and I can hardly bear to look back upon those times—no, seriously, I can’t stand reading my old writing. I’ve already been corrected once in my recollections, by those who were present. And so, though I remember the important events, I’m not really sure what order they happened in, let alone what year.

But if I had to pick a moment when my folly broke, I would pick the moment when I first comprehended, in full generality, the notion of an optimization process. That was the point at which I first looked back and said, “I’ve been a fool.”

Previously, in 2002, I’d been writing a bit about the evolutionary psychology of human general intelligence—though at the time, I thought I was writing about AI; at this point I thought I was against anthropomorphic intelligence, but I was still looking to the human brain for inspiration. (The paper in question is “Levels of Organization in General Intelligence,” a requested chapter for the volume Artificial General Intelligence,¹ which finally came out in print in 2007.)

So I’d been thinking (and writing) about how natural selection managed to cough up human intelligence; I saw a dichotomy between them, the blindness of natural selection and the lookahead of intelligent foresight, reasoning by simulation versus playing everything out in reality, abstract versus concrete thinking. And yet it was natural selection that created human intelligence, so that our brains, though not our thoughts, are entirely made according to the signature of natural selection.

To this day, this still seems to me like a reasonably shattering insight, and so it drives me up the wall when people lump together natural selection and intelligence-driven processes as “evolutionary.” They really are almost absolutely different in a number of important ways—though there are concepts in common that can be used to describe them, like consequentialism and cross-domain generality.

But that Eliezer₂₀₀₂ is thinking in terms of a dichotomy between evolution and intelligence tells you something about the limits of his vision—like someone who thinks of politics as a dichotomy between conservative and liberal stances, or someone who thinks of fruit as a dichotomy between apples and strawberries.

After the “Levels of Organization” draft was published online, Emil Gilliam pointed out that my view of AI seemed pretty similar to my view of intelligence. Now, of course Eliezer₂₀₀₂ doesn’t espouse building an AI in the image of a human mind; Eliezer₂₀₀₂ knows very well that a human mind is just a hack coughed up by natural selection. But Eliezer₂₀₀₂ has described these levels of organization in human thinking, and he hasn’t proposed using different levels of organization in the AI. Emil Gilliam asks whether I think I might be hewing too close to the human line. I dub the alternative the “Completely Alien Mind Design” and reply that a CAMD is probably too difficult for human engineers to create, even if it’s possible in theory, because we wouldn’t be able to understand something so alien while we were putting it together.

I don’t know if Eliezer₂₀₀₂ invented this reply on his own, or if he read it somewhere else. Needless to say, I’ve heard this excuse plenty of times since then. In reality, what you genuinely understand, you can usually reconfigure in almost any sort of shape, leaving some structural essence inside; but when you don’t understand flight, you suppose that a flying machine needs feathers, because you can’t imagine departing from the analogy of a bird.

So Eliezer₂₀₀₂ is still, in a sense, attached to humanish mind designs—he imagines improving on them, but the human architecture is still in some sense his point of departure.

What is it that finally breaks this attachment?

It’s an embarrassing confession: It came from a science fiction story I was trying to write. (No, you can’t see it; it’s not done.) The story involved a non-cognitive non-evolutionary optimization process, something like an Outcome Pump. Not intelligence, but a cross-temporal physical effect—that is, I was imagining it as a physical effect—that narrowly constrained the space of possible outcomes. (I can’t tell you any more than that; it would be a spoiler, if I ever finished the story. Just see the essay on Outcome Pumps.) It was “just a story,” and so I was free to play with the idea and elaborate it out logically: C was constrained to happen, therefore B (in the past) was constrained to happen, therefore A (which led to B) was constrained to happen.

Drawing a line through one point is generally held to be dangerous. Two points make a dichotomy; you imagine them opposed to one another. But when you’ve got three different points—that’s when you’re forced to wake up and generalize.

Now I had three points: Human intelligence, natural selection, and my fictional plot device.

And so that was the point at which I generalized the notion of an optimization process, of a process that squeezes the future into a narrow region of the possible.

This may seem like an obvious point, if you’ve been following Overcoming Bias this whole time; but if you look at Shane Legg’s collection of 71 definitions of intelligence, you’ll see that “squeezing the future into a constrained region” is a less obvious reply than it seems.

Many of the definitions of “intelligence” by AI researchers do talk about “solving problems” or “achieving goals.” But from the viewpoint of past Eliezers, at least, it is only hindsight that makes this the same thing as “squeezing the future.”

A goal is a mentalistic object; electrons have no goals, and solve no problems either. When a human imagines a goal, they imagine an agent imbued with wanting-ness—it’s still empathic language.

You can espouse the notion that intelligence is about “achieving goals”—and then turn right around and argue about whether some “goals” are better than others—or talk about the wisdom required to judge between goals themselves—or talk about a system deliberately modifying its goals—or talk about the free will needed to choose plans that achieve goals—or talk about an AI realizing that its goals aren’t what the programmers really meant to ask for. If you imagine something that squeezes the future into a narrow region of the possible, like an Outcome Pump, those seemingly sensible statements somehow don’t translate.

So for me at least, seeing through the word “mind” to a physical process that would, just by naturally running, just by obeying the laws of physics, end up squeezing its future into a narrow region, was a naturalistic enlightenment over and above the notion of an agent trying to achieve its goals.

It was like falling out of a deep pit, falling into the ordinary world, strained cognitive tensions relaxing into unforced simplicity, confusion turning to smoke and drifting away. I saw the work performed by intelligence; smart was no longer a property, but an engine. Like a knot in time, echoing the outer part of the universe in the inner part, and thereby steering it. I even saw, in a flash of the same enlightenment, that a mind had to output waste heat in order to obey the laws of thermodynamics.

Previously, Eliezer₂₀₀₁ had talked about Friendly AI as something you should do just to be sure—if you didn’t know whether AI design X was going to be Friendly, then you really ought to go with AI design Y that you did know would be Friendly. But Eliezer₂₀₀₁ didn’t think he knew whether you could actually have a superintelligence that turned its future light cone into paperclips.

Now, though, I could see it—the pulse of the optimization process, sensory information surging in, motor instructions surging out, steering the future. In the middle, the model that linked up possible actions to possible outcomes, and the utility function over the outcomes. Put in the corresponding utility function, and the result would be an optimizer that would steer the future anywhere.

Up until that point, I’d never quite admitted to myself that Eliezer₁₉₉₇’s AI goal system design would definitely, no two ways about it, pointlessly wipe out the human species. Now, however, I looked back, and I could finally see what my old design really did, to the extent it was coherent enough to be talked about. Roughly, it would have converted its future light cone into generic tools—computers without programs to run, stored energy without a use . . .

. . . how on Earth had I, the fine and practiced rationalist—how on Earth had I managed to miss something that obvious, for six damned years?

That was the point at which I awoke clear-headed, and remembered; and thought, with a certain amount of embarrassment: I’ve been stupid.

1. Ben Goertzel and Cassio Pennachin, eds., Artificial General Intelligence, Cognitive Technologies (Berlin: Springer, 2007), doi:10.1007/978-3-540-68677-4.

300
The Level Above Mine

I once lent Xiaoguang “Mike” Li my copy of Probability Theory: The Logic of Science. Mike Li read some of it, and then came back and said:

Wow . . . it’s like Jaynes is a thousand-year-old vampire.

Then Mike said, “No, wait, let me explain that—” and I said, “No, I know exactly what you mean.” It’s a convention in fantasy literature that the older a vampire gets, the more powerful they become.

I’d enjoyed math proofs before I encountered Jaynes. But E. T. Jaynes was the first time I picked up a sense of formidability from mathematical arguments. Maybe because Jaynes was lining up “paradoxes” that had been used to object to Bayesianism, and then blasting them to pieces with overwhelming firepower—power being used to overcome others. Or maybe the sense of formidability came from Jaynes not treating his math as a game of aesthetics; Jaynes cared about probability theory, it was bound up with other considerations that mattered, to him and to me too.

For whatever reason, the sense I get of Jaynes is one of terrifying swift perfection—something that would arrive at the correct answer by the shortest possible route, tearing all surrounding mistakes to shreds in the same motion. Of course, when you write a book, you get a chance to show only your best side. But still.

It spoke well of Mike Li that he was able to sense the aura of formidability surrounding Jaynes. It’s a general rule, I’ve observed, that you can’t discriminate between levels too far above your own. E.g., someone once earnestly told me that I was really bright, and “ought to go to college.” Maybe anything more than around one standard deviation above you starts to blur together, though that’s just a cool-sounding wild guess.

So, having heard Mike Li compare Jaynes to a thousand-year-old vampire, one question immediately popped into my mind:

“Do you get the same sense off me?” I asked.

Mike shook his head. “Sorry,” he said, sounding somewhat awkward, “it’s just that Jaynes is . . .”

“No, I know,” I said. I hadn’t thought I’d reached Jaynes’s level. I’d only been curious about how I came across to other people.

I aspire to Jaynes’s level. I aspire to become as much the master of Artificial Intelligence / reflectivity, as Jaynes was master of Bayesian probability theory. I can even plead that the art I’m trying to master is more difficult than Jaynes’s, making a mockery of deference. Even so, and embarrassingly, there is no art of which I am as much the master now, as Jaynes was of probability theory.

This is not, necessarily, to place myself beneath Jaynes as a person—to say that Jaynes had a magical aura of destiny, and I don’t.

Rather I recognize in Jaynes a level of expertise, of sheer formidability, which I have not yet achieved. I can argue forcefully in my chosen subject, but that is not the same as writing out the equations and saying: DONE.

For so long as I have not yet achieved that level, I must acknowledge the possibility that I can never achieve it, that my native talent is not sufficient. When Marcello Herreshoff had known me for long enough, I asked him if he knew of anyone who struck him as substantially more natively intelligent than myself. Marcello thought for a moment and said “John Conway—I met him at a summer math camp.” Darn, I thought, he thought of someone, and worse, it’s some ultra-famous old guy I can’t grab. I inquired how Marcello had arrived at the judgment. Marcello said, “He just struck me as having a tremendous amount of mental horsepower,” and started to explain a math problem he’d had a chance to work on with Conway.

Not what I wanted to hear.

Perhaps, relative to Marcello’s experience of Conway and his experience of me, I haven’t had a chance to show off on any subject that I’ve mastered as thoroughly as Conway had mastered his many fields of mathematics.

Or it might be that Conway’s brain is specialized off in a different direction from mine, and that I could never approach Conway’s level on math, yet Conway wouldn’t do so well on AI research.

Or . . .

. . . or I’m strictly dumber than Conway, dominated by him along all dimensions. Maybe, if I could find a young proto-Conway and tell them the basics, they would blaze right past me, solve the problems that have weighed on me for years, and zip off to places I can’t follow.

Is it damaging to my ego to confess that last possibility? Yes. It would be futile to deny that.

Have I really accepted that awful possibility, or am I only pretending to myself to have accepted it? Here I will say: “No, I think I have accepted it.” Why do I dare give myself so much credit? Because I’ve invested specific effort into that awful possibility. I am writing here for many reasons, but a major one is the vision of some younger mind reading these words and zipping off past me. It might happen, it might not.

Or sadder: Maybe I just wasted too much time on setting up the resources to support me, instead of studying math full-time through my whole youth; or I wasted too much youth on non-mathy ideas. And this choice, my past, is irrevocable. I’ll hit a brick wall at 40, and there won’t be anything left but to pass on the resources to another mind with the potential I wasted, still young enough to learn. So to save them time, I should leave a trail to my successes, and post warning signs on my mistakes.

Such specific efforts predicated on an ego-damaging possibility—that’s the only kind of humility that seems real enough for me to dare credit myself. Or giving up my precious theories, when I realized that they didn’t meet the standard Jaynes had shown me—that was hard, and it was real. Modest demeanors are cheap. Humble admissions of doubt are cheap. I’ve known too many people who, presented with a counterargument, say, “I am but a fallible mortal, of course I could be wrong,” and then go on to do exactly what they had planned to do previously.

You’ll note that I don’t try to modestly say anything like, “Well, I may not be as brilliant as Jaynes or Conway, but that doesn’t mean I can’t do important things in my chosen field.”

Because I do know . . . that’s not how it works.

301
The Magnitude of His Own Folly

In the years before I met a would-be creator of Artificial General Intelligence (with a funded project) who happened to be a creationist, I would still try to argue with individual AGI wannabes.

In those days, I sort-of-succeeded in convincing one such fellow that, yes, you had to take Friendly AI into account, and no, you couldn’t just find the right fitness metric for an evolutionary algorithm. (Previously he had been very impressed with evolutionary algorithms.)

And the one said: Oh, woe! Oh, alas! What a fool I’ve been! Through my carelessness, I almost destroyed the world! What a villain I once was!

Now, there’s a trap I knew better than to fall into—

—at the point where, in late 2002, I looked back to Eliezer₁₉₉₇’s AI proposals and realized what they really would have done, insofar as they were coherent enough for me to talk about what they “really would have done.”

When I finally saw the magnitude of my own folly, everything fell into place at once. The dam against realization cracked; and the unspoken doubts that had been accumulating behind it crashed through all together. There wasn’t a prolonged period, or even a single moment that I remember, of wondering how I could have been so stupid. I already knew how.

And I also knew, all at once, in the same moment of realization, that to say, I almost destroyed the world!, would have been too prideful.

It would have been too confirming of ego, too confirming of my own importance in the scheme of things, at a time when—I understood in the same moment of realization—my ego ought to be taking a major punch to the stomach. I had been so much less than I needed to be; I had to take that punch in the stomach, not avert it.

And by the same token, I didn’t fall into the conjugate trap of saying: Oh, well, it’s not as if I had code and was about to run it; I didn’t really come close to destroying the world. For that, too, would have minimized the force of the punch. It wasn’t really loaded? I had proposed and intended to build the gun, and load the gun, and put the gun to my head and pull the trigger; and that was a bit too much self-destructiveness.

I didn’t make a grand emotional drama out of it. That would have wasted the force of the punch, averted it into mere tears.

I knew, in the same moment, what I had been carefully not-doing for the last six years. I hadn’t been updating.

And I knew I had to finally update. To actually change what I planned to do, to change what I was doing now, to do something different instead.

I knew I had to stop.

Halt, melt, and catch fire.

Say, “I’m not ready.” Say, “I don’t know how to do this yet.”

These are terribly difficult words to say, in the field of AGI. Both the lay audience and your fellow AGI researchers are interested in code, projects with programmers in play. Failing that, they may give you some credit for saying, “I’m ready to write code; just give me the funding.”

Say, “I’m not ready to write code,” and your status drops like a depleted uranium balloon.

What distinguishes you, then, from six billion other people who don’t know how to create Artificial General Intelligence? If you don’t have neat code (that does something other than be humanly intelligent, obviously; but at least it’s code), or at minimum your own startup that’s going to write code as soon as it gets funding—then who are you and what are you doing at our conference?

Maybe later I’ll write on where this attitude comes from—the excluded middle between “I know how to build AGI!” and “I’m working on narrow AI because I don’t know how to build AGI,” the nonexistence of a concept for “I am trying to get from an incomplete map of FAI to a complete map of FAI.”

But this attitude does exist, and so the loss of status associated with saying “I’m not ready to write code” is very great. (If the one doubts this, let them name any other who simultaneously says “I intend to build an Artificial General Intelligence,” “Right now I can’t build an AGI because I don’t know X,” and “I am currently trying to figure out X.”)

(And never mind AGI folk who’ve already raised venture capital, promising returns in five years.)

So there’s a huge reluctance to say, “Stop.” You can’t just say, “Oh, I’ll swap back to figure-out-X mode,” because that mode doesn’t exist.

Was there more to that reluctance than just loss of status, in my case? Eliezer₂₀₀₁ might also have flinched away from slowing his perceived forward momentum into the intelligence explosion, which was so right and so necessary . . .

But mostly, I think I flinched away from not being able to say, “I’m ready to start coding.” Not just for fear of others’ reactions, but because I’d been inculcated with the same attitude myself.

Above all, Eliezer₂₀₀₁ didn’t say, “Stop”—even after noticing the problem of Friendly AI—because I did not realize, on a gut level, that Nature was allowed to kill me.

“Teenagers think they’re immortal,” the proverb goes. Obviously this isn’t true in the literal sense that if you ask them, “Are you indestructible?” they will reply “Yes, go ahead and try shooting me.” But perhaps wearing seat belts isn’t deeply emotionally compelling for them, because the thought of their own death isn’t quite real—they don’t really believe it’s allowed to happen. It can happen in principle but it can’t actually happen.

Personally, I always wore my seat belt. As an individual, I understood that I could die.

But, having been raised in technophilia to treasure that one most precious thing, far more important than my own life, I once thought that the Future was indestructible.

Even when I acknowledged that nanotech could wipe out humanity, I still believed the intelligence explosion was invulnerable. That if humanity survived, the intelligence explosion would happen, and the resultant AI would be too smart to be corrupted or lost.

Even after that, when I acknowledged Friendly AI as a consideration, I didn’t emotionally believe in the possibility of failure, any more than that teenager who doesn’t wear their seat belt really believes that an automobile accident is really allowed to kill or cripple them.

It wasn’t until my insight into optimization let me look back and see Eliezer₁₉₉₇ in plain light that I realized that Nature was allowed to kill me.

“The thought you cannot think controls you more than thoughts you speak aloud.” But we flinch away from only those fears that are real to us.

AGI researchers take very seriously the prospect of someone else solving the problem first. They can imagine seeing the headlines in the paper saying that their own work has been upstaged. They know that Nature is allowed to do that to them. The ones who have started companies know that they are allowed to run out of venture capital. That possibility is real to them, very real; it has a power of emotional compulsion over them.

I don’t think that “Oops” followed by the thud of six billion bodies falling, at their own hands, is real to them on quite the same level.

It is unsafe to say what other people are thinking. But it seems rather likely that when the one reacts to the prospect of Friendly AI by saying, “If you delay development to work on safety, other projects that don’t care at all about Friendly AI will beat you to the punch,” the prospect of they themselves making a mistake followed by six billion thuds is not really real to them; but the possibility of others beating them to the punch is deeply scary.

I, too, used to say things like that, before I understood that Nature was allowed to kill me.

In that moment of realization, my childhood technophilia finally broke.

I finally understood that even if you diligently followed the rules of science and were a nice person, Nature could still kill you. I finally understood that even if you were the best project out of all available candidates, Nature could still kill you.

I understood that I was not being graded on a curve. My gaze shook free of rivals, and I saw the sheer blank wall.

I looked back and I saw the careful arguments I had constructed, for why the wisest choice was to continue forward at full speed, just as I had planned to do before. And I understood then that even if you constructed an argument showing that something was the best course of action, Nature was still allowed to say “So what?” and kill you.

I looked back and saw that I had claimed to take into account the risk of a fundamental mistake, that I had argued reasons to tolerate the risk of proceeding in the absence of full knowledge.

And I saw that the risk I wanted to tolerate would have killed me. And I saw that this possibility had never been really real to me. And I saw that even if you had wise and excellent arguments for taking a risk, the risk was still allowed to go ahead and kill you. Actually kill you.

For it is only the action that matters, and not the reasons for doing anything. If you build the gun and load the gun and put the gun to your head and pull the trigger, even with the cleverest of arguments for carrying out every step—then, bang.

I saw that only my own ignorance of the rules had enabled me to argue for going ahead without complete knowledge of the rules; for if you do not know the rules, you cannot model the penalty of ignorance.

I saw that others, still ignorant of the rules, were saying, “I will go ahead and do X”; and that to the extent that X was a coherent proposal at all, I knew that would result in a bang; but they said, “I do not know it cannot work.” I would try to explain to them the smallness of the target in the search space, and they would say “How can you be so sure I won’t win the lottery?,” wielding their own ignorance as a bludgeon.

And so I realized that the only thing I could have done to save myself, in my previous state of ignorance, was to say: “I will not proceed until I know positively that the ground is safe.” And there are many clever arguments for why you should step on a piece of ground that you don’t know to contain a landmine; but they all sound much less clever, after you look to the place that you proposed and intended to step, and see the bang.

I understood that you could do everything that you were supposed to do, and Nature was still allowed to kill you. That was when my last trust broke. And that was when my training as a rationalist began.

302
Beyond the Reach of God

This essay is a tad gloomier than usual, as I measure such things. It deals with a thought experiment I invented to smash my own optimism, after I realized that optimism had misled me. Those readers sympathetic to arguments like, “It’s important to keep our biases because they help us stay happy,” should consider not reading. (Unless they have something to protect, including their own life.)

So! Looking back on the magnitude of my own folly, I realized that at the root of it had been a disbelief in the Future’s vulnerability—a reluctance to accept that things could really turn out wrong. Not as the result of any explicit propositional verbal belief. More like something inside that persisted in believing, even in the face of adversity, that everything would be all right in the end.

Some would account this a virtue (zettai daijobu da yo), and others would say that it’s a thing necessary for mental health.

But we don’t live in that world. We live in the world beyond the reach of God.

It’s been a long, long time since I believed in God. Growing up in an Orthodox Jewish family, I can recall the last remembered time I asked God for something, though I don’t remember how old I was. I was putting in some request on behalf of the next-door-neighboring boy, I forget what exactly—something along the lines of, “I hope things turn out all right for him,” or maybe, “I hope he becomes Jewish.”

I remember what it was like to have some higher authority to appeal to, to take care of things I couldn’t handle myself. I didn’t think of it as “warm,” because I had no alternative to compare it to. I just took it for granted.

Still I recall, though only from distant childhood, what it’s like to live in the conceptually impossible possible world where God exists. Really exists, in the way that children and rationalists take all their beliefs at face value.

In the world where God exists, does God intervene to optimize everything? Regardless of what rabbis assert about the fundamental nature of reality, the take-it-seriously operational answer to this question is obviously “No.” You can’t ask God to bring you a lemonade from the refrigerator instead of getting one yourself. When I believed in God after the serious fashion of a child, so very long ago, I didn’t believe that.

Postulating that particular divine inaction doesn’t provoke a full-blown theological crisis. If you said to me, “I have constructed a benevolent superintelligent nanotech-user,” and I said “Give me a banana,” and no banana appeared, this would not yet disprove your statement. Human parents don’t always do everything their children ask. There are some decent fun-theoretic arguments—I even believe them myself—against the idea that the best kind of help you can offer someone is to always immediately give them everything they want. I don’t think that eudaimonia is formulating goals and having them instantly fulfilled; I don’t want to become a simple wanting-thing that never has to plan or act or think.

So it’s not necessarily an attempt to avoid falsification to say that God does not grant all prayers. Even a Friendly AI might not respond to every request.

But clearly there exists some threshold of horror awful enough that God will intervene. I remember that being true, when I believed after the fashion of a child.

The God who does not intervene at all, no matter how bad things get—that’s an obvious attempt to avoid falsification, to protect a belief-in-belief. Sufficiently young children don’t have the deep-down knowledge that God doesn’t really exist. They really expect to see a dragon in their garage. They have no reason to imagine a loving God who never acts. Where exactly is the boundary of sufficient awfulness? Even a child can imagine arguing over the precise threshold. But of course God will draw the line somewhere. Few indeed are the loving parents who, desiring their child to grow up strong and self-reliant, would let their toddler be run over by a car.

The obvious example of a horror so great that God cannot tolerate it is death—true death, mind-annihilation. I don’t think that even Buddhism allows that. So long as there is a God in the classic sense—full-blown, ontologically fundamental, the God—we can rest assured that no sufficiently awful event will ever, ever happen. There is no soul anywhere that need fear true annihilation; God will prevent it.

What if you build your own simulated universe? The classic example of a simulated universe is Conway’s Game of Life. I do urge you to investigate Life if you’ve never played it—it’s important for comprehending the notion of “physical law.” Conway’s Life has been proven Turing-complete, so it would be possible to build a sentient being in the Life universe, although it might be rather fragile and awkward. Other cellular automata would make it simpler.

Could you, by creating a simulated universe, escape the reach of God? Could you simulate a Game of Life containing sentient entities, and torture the beings therein? But if God is watching everywhere, then trying to build an unfair Life just results in the God stepping in to modify your computer’s transistors. If the physics you set up in your computer program calls for a sentient Life-entity to be endlessly tortured for no particular reason, the God will intervene. God being omnipresent, there is no refuge anywhere for true horror. Life is fair.

But suppose that instead you ask the question:

Given such-and-such initial conditions, and given such-and-such cellular automaton rules, what would be the mathematical result?

Not even God can modify the answer to this question, unless you believe that God can implement logical impossibilities. Even as a very young child, I don’t remember believing that. (And why would you need to believe it, if God can modify anything that actually exists?)

What does Life look like, in this imaginary world where every step follows only from its immediate predecessor? Where things only ever happen, or don’t happen, because of the cellular automaton rules? Where the initial conditions and rules don’t describe any God that checks over each state? What does it look like, the world beyond the reach of God?

That world wouldn’t be fair. If the initial state contained the seeds of something that could self-replicate, natural selection might or might not take place, and complex life might or might not evolve, and that life might or might not become sentient, with no God to guide the evolution. That world might evolve the equivalent of conscious cows, or conscious dolphins, that lacked hands to improve their condition; maybe they would be eaten by conscious wolves who never thought that they were doing wrong, or cared.

If in a vast plethora of worlds, something like humans evolved, then they would suffer from diseases—not to teach them any lessons, but only because viruses happened to evolve as well, under the cellular automaton rules.

If the people of that world are happy, or unhappy, the causes of their happiness or unhappiness may have nothing to do with good or bad choices they made. Nothing to do with free will or lessons learned. In the what-if world where every step follows only from the cellular automaton rules, the equivalent of Genghis Khan can murder a million people, and laugh, and be rich, and never be punished, and live his life much happier than the average. Who prevents it? God would prevent it from ever actually happening, of course; He would at the very least visit some shade of gloom in the Khan’s heart. But in the mathematical answer to the question What if? there is no God in the axioms. So if the cellular automaton rules say that the Khan is happy, that, simply, is the whole and only answer to the what-if question. There is nothing, absolutely nothing, to prevent it.

And if the Khan tortures people horribly to death over the course of days, for his own amusement perhaps? They will call out for help, perhaps imagining a God. And if you really wrote that cellular automaton, God would intervene in your program, of course. But in the what-if question, what the cellular automaton would do under the mathematical rules, there isn’t any God in the system. Since the physical laws contain no specification of a utility function—in particular, no prohibition against torture—then the victims will be saved only if the right cells happen to be 0 or 1. And it’s not likely that anyone will defy the Khan; if they did, someone would strike them with a sword, and the sword would disrupt their organs and they would die, and that would be the end of that. So the victims die, screaming, and no one helps them; that is the answer to the what-if question.

Could the victims be completely innocent? Why not, in the what-if world? If you look at the rules for Conway’s Game of Life (which is Turing-complete, so we can embed arbitrary computable physics in there), then the rules are really very simple. Cells with three living neighbors stay alive; cells with two neighbors stay the same; all other cells die. There isn’t anything in there about innocent people not being horribly tortured for indefinite periods.

Is this world starting to sound familiar?

Belief in a fair universe often manifests in more subtle ways than thinking that horrors should be outright prohibited: Would the twentieth century have gone differently, if Klara Pölzl and Alois Hitler had made love one hour earlier, and a different sperm fertilized the egg, on the night that Adolf Hitler was conceived?

For so many lives and so much loss to turn on a single event seems disproportionate. The Divine Plan ought to make more sense than that. You can believe in a Divine Plan without believing in God—Karl Marx surely did. You shouldn’t have millions of lives depending on a casual choice, an hour’s timing, the speed of a microscopic flagellum. It ought not to be allowed. It’s too disproportionate. Therefore, if Adolf Hitler had been able to go to high school and become an architect, there would have been someone else to take his role, and World War II would have happened the same as before.

But in the world beyond the reach of God, there isn’t any clause in the physical axioms that says “things have to make sense” or “big effects need big causes” or “history runs on reasons too important to be so fragile.” There is no God to impose that order, which is so severely violated by having the lives and deaths of millions depend on one small molecular event.

The point of the thought experiment is to lay out the God-universe and the Nature-universe side by side, so that we can recognize what kind of thinking belongs to the God-universe. Many who are atheists still think as if certain things are not allowed. They would lay out arguments for why World War II was inevitable and would have happened in more or less the same way, even if Hitler had become an architect. But in sober historical fact, this is an unreasonable belief; I chose the example of World War II because from my reading, it seems that events were mostly driven by Hitler’s personality, often in defiance of his generals and advisors. There is no particular empirical justification that I happen to have heard of for doubting this. The main reason to doubt would be refusal to accept that the universe could make so little sense—that horrible things could happen so lightly, for no more reason than a roll of the dice.

But why not? What prohibits it?

In the God-universe, God prohibits it. To recognize this is to recognize that we don’t live in that universe. We live in the what-if universe beyond the reach of God, driven by the mathematical laws and nothing else. Whatever physics says will happen, will happen. Absolutely anything, good or bad, will happen. And there is nothing in the laws of physics to lift this rule even for the really extreme cases, where you might expect Nature to be a little more reasonable.

Reading William Shirer’s The Rise and Fall of the Third Reich, listening to him describe the disbelief that he and others felt upon discovering the full scope of Nazi atrocities, I thought of what a strange thing it was, to read all that, and know, already, that there wasn’t a single protection against it. To just read through the whole book and accept it; horrified, but not at all disbelieving, because I’d already understood what kind of world I lived in.

Once upon a time, I believed that the extinction of humanity was not allowed. And others who call themselves rationalists may yet have things they trust. They might be called “positive-sum games,” or “democracy,” or “technology,” but they are sacred. The mark of this sacredness is that the trustworthy thing can’t lead to anything really bad; or they can’t be permanently defaced, at least not without a compensatory silver lining. In that sense they can be trusted, even if a few bad things happen here and there.

The unfolding history of Earth can’t ever turn from its positive-sum trend to a negative-sum trend; that is not allowed. Democracies—modern liberal democracies, anyway—won’t ever legalize torture. Technology has done so much good up until now, that there can’t possibly be a Black Swan technology that breaks the trend and does more harm than all the good up until this point.

There are all sorts of clever arguments why such things can’t possibly happen. But the source of these arguments is a much deeper belief that such things are not allowed. Yet who prohibits? Who prevents it from happening? If you can’t visualize at least one lawful universe where physics say that such dreadful things happen—and so they do happen, there being nowhere to appeal the verdict—then you aren’t yet ready to argue probabilities.

Could it really be that sentient beings have died absolutely for thousands or millions of years, with no soul and no afterlife—and not as part of any grand plan of Nature—not to teach any great lesson about the meaningfulness or meaninglessness of life—not even to teach any profound lesson about what is impossible—so that a trick as simple and stupid-sounding as vitrifying people in liquid nitrogen can save them from total annihilation—and a 10-second rejection of the silly idea can destroy someone’s soul? Can it be that a computer programmer who signs a few papers and buys a life-insurance policy continues into the far future, while Einstein rots in a grave? We can be sure of one thing: God wouldn’t allow it. Anything that ridiculous and disproportionate would be ruled out. It would make a mockery of the Divine Plan—a mockery of the strong reasons why things must be the way they are.

You can have secular rationalizations for things being not allowed. So it helps to imagine that there is a God, benevolent as you understand goodness—a God who enforces throughout Reality a minimum of fairness and justice—whose plans make sense and depend proportionally on people’s choices—who will never permit absolute horror—who does not always intervene, but who at least prohibits universes wrenched completely off their track . . . to imagine all this, but also imagine that you, yourself, live in a what-if world of pure mathematics—a world beyond the reach of God, an utterly unprotected world where anything at all can happen.

If there’s any reader still reading this who thinks that being happy counts for more than anything in life, then maybe they shouldn’t spend much time pondering the unprotectedness of their existence. Maybe think of it just long enough to sign up themselves and their family for cryonics, and/or write a check to an existential-risk-mitigation agency now and then. And wear a seat belt and get health insurance and all those other dreary necessary things that can destroy your life if you miss that one step . . . but aside from that, if you want to be happy, meditating on the fragility of life isn’t going to help.

But this essay was written for those who have something to protect.

What can a twelfth-century peasant do to save themselves from annihilation? Nothing. Nature’s little challenges aren’t always fair. When you run into a challenge that’s too difficult, you suffer the penalty; when you run into a lethal penalty, you die. That’s how it is for people, and it isn’t any different for planets. Someone who wants to dance the deadly dance with Nature does need to understand what they’re up against: Absolute, utter, exceptionless neutrality.

Knowing this won’t always save you. It wouldn’t save a twelfth-century peasant, even if they knew. If you think that a rationalist who fully understands the mess they’re in must surely be able to find a way out—then you trust rationality, enough said.

Some commenter is bound to castigate me for putting too dark a tone on all this, and in response they will list out all the reasons why it’s lovely to live in a neutral universe. Life is allowed to be a little dark, after all; but not darker than a certain point, unless there’s a silver lining.

Still, because I don’t want to create needless despair, I will say a few hopeful words at this point:

If humanity’s future unfolds in the right way, we might be able to make our future light cone fair(er). We can’t modify fundamental physics, but on a higher level of organization we could build some guardrails and put down some padding; organize the particles into a pattern that does some internal checks against catastrophe. There’s a lot of stuff out there that we can’t touch—but it may help to consider everything that isn’t in our future light cone as being part of the “generalized past.” As if it had all already happened. There’s at least the prospect of defeating neutrality, in the only future we can touch—the only world that it accomplishes something to care about.

Someday, maybe, immature minds will reliably be sheltered. Even if children go through the equivalent of not getting a lollipop, or even burning a finger, they won’t ever be run over by cars.

And the adults wouldn’t be in so much danger. A superintelligence—a mind that could think a trillion thoughts without a misstep—would not be intimidated by a challenge where death is the price of a single failure. The raw universe wouldn’t seem so harsh, would be only another problem to be solved.

The problem is that building an adult is itself an adult challenge. That’s what I finally realized, years ago.

If there is a fair(er) universe, we have to get there starting from this world—the neutral world, the world of hard concrete with no padding, the world where challenges are not calibrated to your skills.

Not every child needs to stare Nature in the eyes. Buckling a seat belt, or writing a check, is not that complicated or deadly. I don’t say that every rationalist should meditate on neutrality. I don’t say that every rationalist should think all these unpleasant thoughts. But anyone who plans on confronting an uncalibrated challenge of instant death must not avoid them.

What does a child need to do—what rules should they follow, how should they behave—to solve an adult problem?

303
My Bayesian Enlightenment

I remember (dimly, as human memories go) the first time I self-identified as a “Bayesian.” Someone had just asked a malformed version of an old probability puzzle, saying:

If I meet a mathematician on the street, and she says, “I have two children, and at least one of them is a boy,” what is the probability that they are both boys?

In the correct version of this story, the mathematician says, “I have two children,” and you ask, “Is at least one a boy?,” and she answers, “Yes.” Then the probability is 1/3 that they are both boys.

But in the malformed version of the story—as I pointed out—one would common-sensically reason:

If the mathematician has one boy and one girl, then my prior probability for her saying “at least one of them is a boy” is 1/2 and my prior probability for her saying “at least one of them is a girl” is 1/2. There’s no reason to believe, a priori, that the mathematician will only mention a girl if there is no possible alternative.

So I pointed this out, and worked the answer using Bayes’s Rule, arriving at a probability of 1/2 that the children were both boys. I’m not sure whether or not I knew, at this point, that Bayes’s rule was called that, but it’s what I used.

And lo, someone said to me, “Well, what you just gave is the Bayesian answer, but in orthodox statistics the answer is 1/3. We just exclude the possibilities that are ruled out, and count the ones that are left, without trying to guess the probability that the mathematician will say this or that, since we have no way of really knowing that probability—it’s too subjective.”

I responded—note that this was completely spontaneous—“What on Earth do you mean? You can’t avoid assigning a probability to the mathematician making one statement or another. You’re just assuming the probability is 1, and that’s unjustified.”

To which the one replied, “Yes, that’s what the Bayesians say. But frequentists don’t believe that.”

And I said, astounded: “How can there possibly be such a thing as non-Bayesian statistics?”

That was when I discovered that I was of the type called “Bayesian.” As far as I can tell, I was born that way. My mathematical intuitions were such that everything Bayesians said seemed perfectly straightforward and simple, the obvious way I would do it myself; whereas the things frequentists said sounded like the elaborate, warped, mad blasphemy of dreaming Cthulhu. I didn’t choose to become a Bayesian any more than fishes choose to breathe water.

But this is not what I refer to as my “Bayesian enlightenment.” The first time I heard of “Bayesianism,” I marked it off as obvious; I didn’t go much further in than Bayes’s Rule itself. At that time I still thought of probability theory as a tool rather than a law. I didn’t think there were mathematical laws of intelligence (my best and worst mistake). Like nearly all AGI wannabes, Eliezer₂₀₀₁ thought in terms of techniques, methods, algorithms, building up a toolbox full of cool things he could do; he searched for tools, not understanding. Bayes’s Rule was a really neat tool, applicable in a surprising number of cases.

Then there was my initiation into heuristics and biases. It started when I ran across a webpage that had been transduced from a Powerpoint intro to behavioral economics. It mentioned some of the results of heuristics and biases, in passing, without any references. I was so startled that I emailed the author to ask if this was actually a real experiment, or just anecdotal. He sent me back a scan of Tversky and Kahneman’s 1973 paper.

Embarrassing to say, my story doesn’t really start there. I put it on my list of things to look into. I knew that there was an edited volume called “Judgment Under Uncertainty: Heuristics and Biases,” but I’d never seen it. At this time, I figured that if it wasn’t online, I would just try to get along without it. I had so many other things on my reading stack, and no easy access to a university library. I think I must have mentioned this on a mailing list, because Emil Gilliam was annoyed by my online-only theory, so he bought me the book.

His action here should probably be regarded as scoring a fair number of points.

But this, too, is not what I refer to as my “Bayesian enlightenment.” It was an important step toward realizing the inadequacy of my Traditional Rationality skillz—that there was so much more out there, all this new science, beyond just doing what Richard Feynman told you to do. And seeing the heuristics-and-biases program holding up Bayes as the gold standard helped move my thinking forward—but not all the way there.

Memory is a fragile thing, and mine seems to have become more fragile than most, since I learned how memories are recreated with each recollection—the science of how fragile they are. Do other people really have better memories, or do they just trust the details their mind makes up, while really not remembering any more than I do? My guess is that other people do have better memories for certain things. I find structured, scientific knowledge easy enough to remember; but the disconnected chaos of everyday life fades very quickly for me.

I know why certain things happened in my life—that’s causal structure I can remember. But sometimes it’s hard to recall even in what order certain events happened to me, let alone in what year.

I’m not sure if I read E. T. Jaynes’s Probability Theory: The Logic of Science before or after the day when I realized the magnitude of my own folly, and understood that I was facing an adult problem.

But it was Probability Theory that did the trick. Here was probability theory, laid out not as a clever tool, but as The Rules, inviolable on pain of paradox. If you tried to approximate The Rules because they were too computationally expensive to use directly, then, no matter how necessary that compromise might be, you would still end up doing less than optimal. Jaynes would do his calculations different ways to show that the same answer always arose when you used legitimate methods; and he would display different answers that others had arrived at, and trace down the illegitimate step. Paradoxes could not coexist with his precision. Not an answer, but the answer.

And so—having looked back on my mistakes, and all the an-answers that had led me into paradox and dismay—it occurred to me that here was the level above mine.

I could no longer visualize trying to build an AI based on vague answers—like the an-answers I had come up with before—and surviving the challenge.

I looked at the AGI wannabes with whom I had tried to argue Friendly AI, and the various dreams of Friendliness that they had. (Often formulated spontaneously in response to my asking the question!) Like frequentist statistical methods, no two of them agreed with each other. Having actually studied the issue full-time for some years, I knew something about the problems their hopeful plans would run into. And I saw that if you said, “I don’t see why this would fail,” the “don’t know” was just a reflection of your own ignorance. I could see that if I held myself to a similar standard of “that seems like a good idea,” I would also be doomed. (Much like a frequentist inventing amazing new statistical calculations that seemed like good ideas.)

But if you can’t do that which seems like a good idea—if you can’t do what you don’t imagine failing—then what can you do?

It seemed to me that it would take something like the Jaynes-level—not, here’s my bright idea, but rather, here’s the only correct way you can do this (and why)—to tackle an adult problem and survive. If I achieved the same level of mastery of my own subject as Jaynes had achieved of probability theory, then it was at least imaginable that I could try to build a Friendly AI and survive the experience.

Through my mind flashed the passage:

Do nothing because it is righteous, or praiseworthy, or noble, to do so; do nothing because it seems good to do so; do only that which you must do, and which you cannot do in any other way.¹

Doing what it seemed good to do had only led me astray.

So I called a full stop.

And I decided that, from then on, I would follow the strategy that could have saved me if I had followed it years ago: Hold my FAI designs to the higher standard of not doing that which seemed like a good idea, but only that which I understood on a sufficiently deep level to see that I could not do it in any other way.

All my old theories, into which I had invested so much, did not meet this standard; and were not close to this standard; and weren’t even on a track leading to this standard; so I threw them out the window.

I took up the study of probability theory and decision theory, looking to extend them to embrace such things as reflectivity and self-modification.

If I recall correctly, I had already, by this point, started to see cognition as manifesting Bayes-structure, which is also a major part of what I refer to as my Bayesian enlightenment—but of this I have already spoken. And there was also my naturalistic awakening, of which I have already spoken. And my realization that Traditional Rationality was not strict enough, so that in matters of human rationality I began taking more inspiration from probability theory and cognitive psychology.

But if you add up all these things together, then that, more or less, is the story of my Bayesian enlightenment.

Life rarely has neat boundaries. The story continues onward.

It was while studying Judea Pearl, for example, that I realized that precision can save you time. I’d put some thought into nonmonotonic logics myself, before then—back when I was still in my “searching for neat tools and algorithms” mode. Reading Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference,² I could imagine how much time I would have wasted on ad-hoc systems and special cases, if I hadn’t known that key. “Do only that which you must do, and which you cannot do in any other way” translates into a time-savings measured, not in the rescue of wasted months, but in the rescue of wasted careers.

And so I realized that it was only by holding myself to this higher standard of precision that I had started to really think at all about quite a number of important issues. To say a thing with precision is difficult—it is not at all the same thing as saying a thing formally, or inventing a new logic to throw at the problem. Many shy away from the inconvenience, because human beings are lazy, and so they say, “It is impossible,” or, “It will take too long,” even though they never really tried for five minutes. But if you don’t hold yourself to that inconveniently high standard, you’ll let yourself get away with anything. It’s a hard problem just to find a standard high enough to make you actually start thinking! It may seem taxing to hold yourself to the standard of mathematical proof where every single step has to be correct and one wrong step can carry you anywhere. But otherwise you won’t chase down those tiny notes of discord that turn out to, in fact, lead to whole new concerns you never thought of.

So these days I don’t complain as much about the heroic burden of inconvenience that it takes to hold yourself to a precise standard. It can save time, too; and in fact, it’s more or less the ante to get yourself thinking about the problem at all.

And this too should be considered part of my “Bayesian enlightenment”—realizing that there were advantages in it, not just penalties.

But of course the story continues on. Life is like that, at least the parts that I remember.

If there’s one thing I’ve learned from this history, it’s that saying “Oops” is something to look forward to. Sure, the prospect of saying “Oops” in the future means that the you of right now is a drooling imbecile, whose words your future self won’t be able to read because of all the wincing. But saying “Oops” in the future also means that, in the future, you’ll acquire new Jedi powers that your present self doesn’t dream exist. It makes you feel embarrassed, but also alive. Realizing that your younger self was a complete moron means that even though you’re already in your twenties, you haven’t yet gone over your peak. So here’s to hoping that my future self realizes I’m a drooling imbecile: I may plan to solve my problems with my present abilities, but extra Jedi powers sure would come in handy.

That scream of horror and embarrassment is the sound that rationalists make when they level up. Sometimes I worry that I’m not leveling up as fast as I used to, and I don’t know if it’s because I’m finally getting the hang of things, or because the neurons in my brain are slowly dying.

Yours, Eliezer₂₀₀₈.

1. Le Guin, The Farthest Shore.

2. Pearl, Probabilistic Reasoning in Intelligent Systems.

Part Y
Challenging the Difficult

304
Tsuyoku Naritai! (I Want to Become Stronger)

In Orthodox Judaism there is a saying: “The previous generation is to the next one as angels are to men; the next generation is to the previous one as donkeys are to men.” This follows from the Orthodox Jewish belief that all Judaic law was given to Moses by God at Mount Sinai. After all, it’s not as if you could do an experiment to gain new halachic knowledge; the only way you can know is if someone tells you (who heard it from someone else, who heard it from God). Since there is no new source of information, it can only be degraded in transmission from generation to generation.

Thus, modern rabbis are not allowed to overrule ancient rabbis. Crawly things are ordinarily unkosher, but it is permissible to eat a worm found in an apple—the ancient rabbis believed the worm was spontaneously generated inside the apple, and therefore was part of the apple. A modern rabbi cannot say, “Yeah, well, the ancient rabbis knew diddly-squat about biology. Overruled!” A modern rabbi cannot possibly know a halachic principle the ancient rabbis did not, because how could the ancient rabbis have passed down the answer from Mount Sinai to him? Knowledge derives from authority, and therefore is only ever lost, not gained, as time passes.

When I was first exposed to the angels-and-donkeys proverb in (religious) elementary school, I was not old enough to be a full-blown atheist, but I still thought to myself: “Torah loses knowledge in every generation. Science gains knowledge with every generation. No matter where they started out, sooner or later science must surpass Torah.”

The most important thing is that there should be progress. So long as you keep moving forward you will reach your destination; but if you stop moving you will never reach it.

Tsuyoku naritai is Japanese. Tsuyoku is “strong”; naru is “becoming,” and the form naritai is “want to become.” Together it means “I want to become stronger,” and it expresses a sentiment embodied more intensely in Japanese works than in any Western literature I’ve read. You might say it when expressing your determination to become a professional Go player—or after you lose an important match, but you haven’t given up—or after you win an important match, but you’re not a ninth-dan player yet—or after you’ve become the greatest Go player of all time, but you still think you can do better. That is tsuyoku naritai, the will to transcendence.

Tsuyoku naritai is the driving force behind my essay The Proper Use of Humility, in which I contrast the student who humbly double-checks their math test, and the student who modestly says, “But how can we ever really know? No matter how many times I check, I can never be absolutely certain.” The student who double-checks their answers wants to become stronger; they react to a possible inner flaw by doing what they can to repair the flaw, not with resignation.

Each year on Yom Kippur, an Orthodox Jew recites a litany which begins Ashamnu, bagadnu, gazalnu, dibarnu dofi, and goes on through the entire Hebrew alphabet: We have acted shamefully, we have betrayed, we have stolen, we have slandered . . .

As you pronounce each word, you strike yourself over the heart in penitence. There’s no exemption whereby, if you manage to go without stealing all year long, you can skip the word gazalnu and strike yourself one less time. That would violate the community spirit of Yom Kippur, which is about confessing sins—not avoiding sins so that you have less to confess.

By the same token, the Ashamnu does not end, “But that was this year, and next year I will do better.”

The Ashamnu bears a remarkable resemblance to the notion that the way of rationality is to beat your fist against your heart and say, “We are all biased, we are all irrational, we are not fully informed, we are overconfident, we are poorly calibrated . . .”

Fine. Now tell me how you plan to become less biased, less irrational, more informed, less overconfident, better calibrated.

There is an old Jewish joke: During Yom Kippur, the rabbi is seized by a sudden wave of guilt, and prostrates himself and cries, “God, I am nothing before you!” The cantor is likewise seized by guilt, and cries, “God, I am nothing before you!” Seeing this, the janitor at the back of the synagogue prostrates himself and cries, “God, I am nothing before you!” And the rabbi nudges the cantor and whispers, “Look who thinks he’s nothing.”

Take no pride in your confession that you too are biased; do not glory in your self-awareness of your flaws. This is akin to the principle of not taking pride in confessing your ignorance; for if your ignorance is a source of pride to you, you may become loath to relinquish your ignorance when evidence comes knocking. Likewise with our flaws—we should not gloat over how self-aware we are for confessing them; the occasion for rejoicing is when we have a little less to confess.

Otherwise, when the one comes to us with a plan for correcting the bias, we will snarl, “Do you think to set yourself above us?” We will shake our heads sadly and say, “You must not be very self-aware.”

Never confess to me that you are just as flawed as I am unless you can tell me what you plan to do about it. Afterward you will still have plenty of flaws left, but that’s not the point; the important thing is to do better, to keep moving ahead, to take one more step forward. Tsuyoku naritai!

305
Tsuyoku vs. the Egalitarian Instinct

Hunter-gatherer tribes are usually highly egalitarian (at least if you’re male)—the all-powerful tribal chieftain is found mostly in agricultural societies, rarely in the ancestral environment. Among most hunter-gatherer tribes, a hunter who brings in a spectacular kill will carefully downplay the accomplishment to avoid envy.

Maybe, if you start out below average, you can improve yourself without daring to pull ahead of the crowd. But sooner or later, if you aim to do the best you can, you will set your aim above the average.

If you can’t admit to yourself that you’ve done better than others—or if you’re ashamed of wanting to do better than others—then the median will forever be your concrete wall, the place where you stop moving forward. And what about people who are below average? Do you dare say you intend to do better than them? How prideful of you!

Maybe it’s not healthy to pride yourself on doing better than someone else. Personally I’ve found it to be a useful motivator, despite my principles, and I’ll take all the useful motivation I can get. Maybe that kind of competition is a zero-sum game, but then so is Go; it doesn’t mean we should abolish that human activity, if people find it fun and it leads somewhere interesting.

But in any case, surely it isn’t healthy to be ashamed of doing better.

And besides, life is not graded on a curve. The will to transcendence has no point beyond which it ceases and becomes the will to do worse; and the race that has no finish line also has no gold or silver medals. Just run as fast as you can, without worrying that you might pull ahead of other runners. (But be warned: If you refuse to worry about that possibility, someday you may pull ahead. If you ignore the consequences, they may happen to you.)

Sooner or later, if your path leads true, you will set out to mitigate a flaw that most people have not mitigated. Sooner or later, if your efforts bring forth any fruit, you will find yourself with fewer sins to confess.

Perhaps you will find it the course of wisdom to downplay the accomplishment, even if you succeed. People may forgive a touchdown, but not dancing in the end zone. You will certainly find it quicker, easier, more convenient to publicly disclaim your worthiness, to pretend that you are just as much a sinner as everyone else. Just so long, of course, as everyone knows it isn’t true. It can be fun to proudly display your modesty, so long as everyone knows how very much you have to be modest about.

But do not let that be the endpoint of your journeys. Even if you only whisper it to yourself, whisper it still: Tsuyoku, tsuyoku! Stronger, stronger!

And then set yourself a higher target. That’s the true meaning of the realization that you are still flawed (though a little less so). It means always reaching higher, without shame.

Tsuyoku naritai! I’ll always run as fast as I can, even if I pull ahead, I’ll keep on running; and someone, someday, will surpass me; but even though I fall behind, I’ll always run as fast as I can.

306
Trying to Try

No! Try not! Do, or do not. There is no try.

—Yoda

Years ago, I thought this was yet another example of Deep Wisdom that is actually quite stupid. SUCCEED is not a primitive action. You can’t just decide to win by choosing hard enough. There is never a plan that works with probability 1.

But Yoda was wiser than I first realized.

The first elementary technique of epistemology—it’s not deep, but it’s cheap—is to distinguish the quotation from the referent. Talking about snow is not the same as talking about “snow.” When I use the word “snow,” without quotes, I mean to talk about snow; and when I use the word ““snow,”” with quotes, I mean to talk about the word “snow.” You have to enter a special mode, the quotation mode, to talk about your beliefs. By default, we just talk about reality.

If someone says, “I’m going to flip that switch,” then by default, they mean they’re going to try to flip the switch. They’re going to build a plan that promises to lead, by the consequences of its actions, to the goal-state of a flipped switch; and then execute that plan.

No plan succeeds with infinite certainty. So by default, when you talk about setting out to achieve a goal, you do not imply that your plan exactly and perfectly leads to only that possibility. But when you say, “I’m going to flip that switch,” you are trying only to flip the switch—not trying to achieve a 97.2% probability of flipping the switch.

So what does it mean when someone says, “I’m going to try to flip that switch?”

Well, colloquially, “I’m going to flip the switch” and “I’m going to try to flip the switch” mean more or less the same thing, except that the latter expresses the possibility of failure. This is why I originally took offense at Yoda for seeming to deny the possibility. But bear with me here.

Much of life’s challenge consists of holding ourselves to a high enough standard. I may speak more on this principle later, because it’s a lens through which you can view many-but-not-all personal dilemmas—“What standard am I holding myself to? Is it high enough?”

So if much of life’s failure consists in holding yourself to too low a standard, you should be wary of demanding too little from yourself—setting goals that are too easy to fulfill.

Often where succeeding to do a thing is very hard, trying to do it is much easier.

Which is easier—to build a successful startup, or to try to build a successful startup? To make a million dollars, or to try to make a million dollars?

So if “I’m going to flip the switch” means by default that you’re going to try to flip the switch—that is, you’re going to set up a plan that promises to lead to switch-flipped state, maybe not with probability 1, but with the highest probability you can manage—

—then “I’m going to ‘try to flip’ the switch” means that you’re going to try to “try to flip the switch,” that is, you’re going to try to achieve the goal-state of “having a plan that might flip the switch.”

Now, if this were a self-modifying AI we were talking about, the transformation we just performed ought to end up at a reflective equilibrium—the AI planning its planning operations.

But when we deal with humans, being satisfied with having a plan is not at all like being satisfied with success. The part where the plan has to maximize your probability of succeeding gets lost along the way. It’s far easier to convince ourselves that we are “maximizing our probability of succeeding,” than it is to convince ourselves that we will succeed.

Almost any effort will serve to convince us that we have “tried our hardest,” if trying our hardest is all we are trying to do.

You have been asking what you could do in the great events that are now stirring, and have found that you could do nothing. But that is because your suffering has caused you to phrase the question in the wrong way . . . Instead of asking what you could do, you ought to have been asking what needs to be done.

—Steven Brust, The Paths of the Dead¹

When you ask, “What can I do?,” you’re trying to do your best. What is your best? It is whatever you can do without the slightest inconvenience. It is whatever you can do with the money in your pocket, minus whatever you need for your accustomed lunch. What you can do with those resources may not give you very good odds of winning. But it’s the “best you can do,” and so you’ve acted defensibly, right?

But what needs to be done? Maybe what needs to be done requires three times your life savings, and you must produce it or fail.

So trying to have “maximized your probability of success”—as opposed to trying to succeed—is a far lesser barrier. You can have “maximized your probability of success” using only the money in your pocket, so long as you don’t demand actually winning.

Want to try to make a million dollars? Buy a lottery ticket. Your odds of winning may not be very good, but you did try, and trying was what you wanted. In fact, you tried your best, since you only had one dollar left after buying lunch. Maximizing the odds of goal achievement using available resources: is this not intelligence?

It’s only when you want, above all else, to actually flip the switch—without quotation and without consolation prizes just for trying—that you will actually put in the effort to actually maximize the probability.

But if all you want is to “maximize the probability of success using available resources,” then that’s the easiest thing in the world to convince yourself you’ve done. The very first plan you hit upon will serve quite well as “maximizing”—if necessary, you can generate an inferior alternative to prove its optimality. And any tiny resource that you care to put in will be what is “available.” Remember to congratulate yourself on putting in 100% of it!

Don’t try your best. Win, or fail. There is no best.

1. Steven Brust, The Paths of the Dead, Vol. 1 of The Viscount of Adrilankha (Tor Books, 2002).

307
Use the Try Harder, Luke

When there’s a will to fail, obstacles can be found.

—John McCarthy

I first watched Star Wars IV-VI when I was very young. Seven, maybe, or nine? So my memory was dim, but I recalled Luke Skywalker as being, you know, this cool Jedi guy.

Imagine my horror and disappointment when I watched the saga again, years later, and discovered that Luke was a whiny teenager.

I mention this because yesterday, I looked up, on Youtube, the source of the Yoda quote: “Do, or do not. There is no try.”

Oh. My. Cthulhu.

I present to you a little-known outtake from the scene, in which the director and writer, George Lucas, argues with Mark Hamill, who played Luke Skywalker:

LUKE: “All right, I’ll give it a try.”

YODA: “No! Try not. Do. Or do not. There is no try.”

Luke raises his hand, and slowly, the X-wing begins to rise out of the water—Yoda’s eyes widen—but then the ship sinks again.

Mark Hamill: “Um, George . . .”

George Lucas: “What is it now?”

Mark: “So . . . according to the script, next I say, ‘I can’t. It’s too big.’”

George: “That’s right.”

Mark: “Shouldn’t Luke maybe give it another shot?”

George: “No. Luke gives up, and sits down next to Yoda—”

Mark: “This is the hero who’s going to take down the Empire? Look, it was one thing when he was a whiny teenager at the beginning, but he’s in Jedi training now. Last movie he blew up the Death Star. Luke should be showing a little backbone.”

George: “No. You give up. And then Yoda lectures you for a while, and you say, ‘You want the impossible.’ Can you remember that?”

Mark: “Impossible? What did he do, run a formal calculation to arrive at a mathematical proof? The X-wing was already starting to rise out of the swamp! That’s the feasibility demonstration right there! Luke loses it for a second and the ship sinks back—and now he says it’s impossible? Not to mention that Yoda, who’s got literally eight hundred years of seniority in the field, just told him it should be doable—”

George: “And then you walk away.”

Mark: “It’s his friggin’ spaceship! If he leaves it in the swamp, he’s stuck on Dagobah for the rest of his miserable life! He’s not just going to walk away! Look, let’s just cut to the next scene with the words ‘one month later’ and Luke is still raggedly standing in front of the swamp, trying to raise his ship for the thousandth time—”

George: “No.”

Mark: “Fine! We’ll show a sunset and a sunrise, as he stands there with his arm out, straining, and then Luke says ‘It’s impossible.’ Though really, he ought to try again when he’s fully rested—”

George: “No.”

Mark: “Five goddamned minutes! Five goddamned minutes before he gives up!”

George: “I am not halting the story for five minutes while the X-wing bobs in the swamp like a bathtub toy.”

Mark: “For the love of sweet candied yams! If a pathetic loser like this could master the Force, everyone in the galaxy would be using it! People would become Jedi because it was easier than going to high school.”

George: “Look, you’re the actor. Let me be the storyteller. Just say your lines and try to mean them.”

Mark: “The audience isn’t going to buy it.”

George: “Trust me, they will.”

Mark: “They’re going to get up and walk out of the theater.”

George: “They’re going to sit there and nod along and not notice anything out of the ordinary. Look, you don’t understand human nature. People wouldn’t try for five minutes before giving up if the fate of humanity were at stake.”

308
On Doing the Impossible

“Persevere.” It’s a piece of advice you’ll get from a whole lot of high achievers in a whole lot of disciplines. I didn’t understand it at all, at first.

At first, I thought “perseverance” meant working 14-hour days. Apparently, there are people out there who can work for 10 hours at a technical job, and then, in their moments between eating and sleeping and going to the bathroom, seize that unfilled spare time to work on a book. I am not one of those people—it still hurts my pride even now to confess that. I’m working on something important; shouldn’t my brain be willing to put in 14 hours a day? But it’s not. When it gets too hard to keep working, I stop and go read or watch something. Because of that, I thought for years that I entirely lacked the virtue of “perseverance.”

In accordance with human nature, Eliezer₁₉₉₈ would think things like: “What counts is output, not input.” Or, “Laziness is also a virtue—it leads us to back off from failing methods and think of better ways.” Or, “I’m doing better than other people who are working more hours. Maybe, for creative work, your momentary peak output is more important than working 16 hours a day.” Perhaps the famous scientists were seduced by the Deep Wisdom of saying that “hard work is a virtue,” because it would be too awful if that counted for less than intelligence?

I didn’t understand the virtue of perseverance until I looked back on my journey through AI, and realized that I had overestimated the difficulty of almost every single important problem.

Sounds crazy, right? But bear with me here.

When I was first deciding to challenge AI, I thought in terms of 40-year timescales, Manhattan Projects, planetary computing networks, millions of programmers, and possibly augmented humans.

This is a common failure mode in AI-futurism which I may write about later; it consists of the leap from “I don’t know how to solve this” to “I’ll imagine throwing something really big at it.” Something huge enough that, when you imagine it, that imagination creates a feeling of impressiveness strong enough to be commensurable with the problem. (There’s a fellow currently on the AI list who goes around saying that AI will cost a quadrillion dollars—we can’t get AI without spending a quadrillion dollars, but we could get AI at any time by spending a quadrillion dollars.) This, in turn, lets you imagine that you know how to solve AI, without trying to fill the obviously-impossible demand that you understand intelligence.

So, in the beginning, I made the same mistake: I didn’t understand intelligence, so I imagined throwing a Manhattan Project at the problem.

But, having calculated the planetary death rate at 55 million per year or 150,000 per day, I did not turn around and run away from the big scary problem like a frightened rabbit. Instead, I started trying to figure out what kind of AI project could get there fastest. If I could make the intelligence explosion happen one hour earlier, that was a reasonable return on investment for a pre-explosion career. (I wasn’t thinking in terms of existential risks or Friendly AI at this point.)

So I didn’t run away from the big scary problem like a frightened rabbit, but stayed to see if there was anything I could do.

Fun historical fact: In 1998, I’d written this long treatise proposing how to go about creating a self-improving or “seed” AI (a term I had the honor of coining). Brian Atkins, who would later become the founding funder of the Machine Intelligence Research Institute, had just sold Hypermart to Go2Net. Brian emailed me to ask whether this AI project I was describing was something that a reasonable-sized team could go out and actually do. “No,” I said, “it would take a Manhattan Project and thirty years,” so for a while we were considering a new dot-com startup instead, to create the funding to get real work done on AI . . .

A year or two later, after I’d heard about this newfangled “open source” thing, it seemed to me that there was some preliminary development work—new computer languages and so on—that a small organization could do; and that was how MIRI started.

This strategy was, of course, entirely wrong.

But even so, I went from “There’s nothing I can do about it now” to “Hm . . . maybe there’s an incremental path through open-source development, if the initial versions are useful to enough people.”

This is back at the dawn of time, so I’m not saying any of this was a good idea. But in terms of what I thought I was trying to do, a year of creative thinking had shortened the apparent pathway: The problem looked slightly less impossible than it had the very first time I’d approached it.

The more interesting pattern is my entry into Friendly AI. Initially, Friendly AI hadn’t been something that I had considered at all—because it was obviously impossible and useless to deceive a superintelligence about what was the right course of action.

So, historically, I went from completely ignoring a problem that was “impossible,” to taking on a problem that was merely extremely difficult.

Naturally this increased my total workload.

Same thing with trying to understand intelligence on a precise level. Originally, I’d written off this problem as impossible, thus removing it from my workload. (This logic seems pretty deranged in retrospect—Nature doesn’t care what you can’t do when It’s writing your project requirements—but I still see AI folk trying it all the time.) To hold myself to a precise standard meant putting in more work than I’d previously imagined I needed. But it also meant tackling a problem that I would have dismissed as entirely impossible not too much earlier.

Even though individual problems in AI have seemed to become less intimidating over time, the total mountain-to-be-climbed has increased in height—just like conventional wisdom says is supposed to happen—as problems got taken off the “impossible” list and put on the “to do” list.

I started to understand what was happening—and what “Persevere!” really meant—at the point where I noticed other AI folk doing the same thing: saying “Impossible!” on problems that seemed eminently solvable—relatively more straightforward, as such things go. But they were things that would have seemed vastly more intimidating at the point when I first approached the problem.

And I realized that the word “impossible” had two usages:

Mathematical proof of impossibility conditional on specified axioms;
“I can’t see any way to do that.”

Needless to say, all my own uses of the word “impossible” had been of the second type.

Any time you don’t understand a domain, many problems in that domain will seem impossible because when you query your brain for a solution pathway, it will return null. But there are only mysterious questions, never mysterious answers. If you spend a year or two working on the domain, then, if you don’t get stuck in any blind alleys, and if you have the native ability level required to make progress, you will understand it better. The apparent difficulty of problems may go way down. It won’t be as scary as it was to your novice-self.

And this is especially likely on the confusing problems that seem most intimidating.

Since we have some notion of the processes by which a star burns, we know that it’s not easy to build a star from scratch. Because we understand gears, we can prove that no collection of gears obeying known physics can form a perpetual motion machine. These are not good problems on which to practice doing the impossible.

When you’re confused about a domain, problems in it will feel very intimidating and mysterious, and a query to your brain will produce a count of zero solutions. But you don’t know how much work will be left when the confusion clears. Dissolving the confusion may itself be a very difficult challenge, of course. But the word “impossible” should hardly be used in that connection. Confusion exists in the map, not in the territory.

So if you spend a few years working on an impossible problem, and you manage to avoid or climb out of blind alleys, and your native ability is high enough to make progress, then, by golly, after a few years it may not seem so impossible after all.

But if something seems impossible, you won’t try.

Now that’s a vicious cycle.

If I hadn’t been in a sufficiently driven frame of mind that “forty years and a Manhattan Project” just meant we should get started earlier, I wouldn’t have tried. I wouldn’t have stuck to the problem. And I wouldn’t have gotten a chance to become less intimidated.

I’m not ordinarily a fan of the theory that opposing biases can cancel each other out, but sometimes it happens by luck. If I’d seen that whole mountain at the start—if I’d realized at the start that the problem was not to build a seed capable of improving itself, but to produce a provably correct Friendly AI—then I probably would have burst into flames.

Even so, part of understanding those above-average scientists who constitute the bulk of AGI researchers is realizing that they are not driven to take on a nearly impossible problem even if it takes them 40 years. By and large, they are there because they have found the Key to AI that will let them solve the problem without such tremendous difficulty, in just five years.

Richard Hamming used to go around asking his fellow scientists two questions: “What are the important problems in your field?,” and, “Why aren’t you working on them?”

Often the important problems look Big, Scary, and Intimidating. They don’t promise 10 publications a year. They don’t promise any progress at all. You might not get any reward after working on them for a year, or five years, or ten years.

And not uncommonly, the most important problems in your field are impossible. That’s why you don’t see more philosophers working on reductionist decompositions of consciousness.

Trying to do the impossible is definitely not for everyone. Exceptional talent is only the ante to sit down at the table. The chips are the years of your life. If wagering those chips and losing seems like an unbearable possibility to you, then go do something else. Seriously. Because you can lose.

I’m not going to say anything like, “Everyone should do something impossible at least once in their lifetimes, because it teaches an important lesson.” Most of the people all of the time, and all of the people most of the time, should stick to the possible.

Never give up? Don’t be ridiculous. Doing the impossible should be reserved for very special occasions. Learning when to lose hope is an important skill in life.

But if there’s something you can imagine that’s even worse than wasting your life, if there’s something you want that’s more important than thirty chips, or if there are scarier things than a life of inconvenience, then you may have cause to attempt the impossible.

There’s a good deal to be said for persevering through difficulties; but one of the things that must be said of it is that it does keep things difficult. If you can’t handle that, stay away! There are easier ways to obtain glamor and respect. I don’t want anyone to read this and needlessly plunge headlong into a life of permanent difficulty.

But to conclude: The “perseverance” that is required to work on important problems has a component beyond working 14 hours a day.

It’s strange, the pattern of what we notice and don’t notice about ourselves. This selectivity isn’t always about inflating your self-image. Sometimes it’s just about ordinary salience.

To keep working was a constant struggle for me, so it was salient: I noticed that I couldn’t work for 14 solid hours a day. It didn’t occur to me that “perseverance” might also apply at a timescale of seconds or years. Not until I saw people who instantly declared “impossible” anything they didn’t want to try, or saw how reluctant they were to take on work that looked like it might take a couple of decades instead of “five years.”

That was when I realized that “perseverance” applied at multiple time scales. On the timescale of seconds, perseverance is to “not to give up instantly at the very first sign of difficulty.” On the timescale of years, perseverance is to “keep working on an insanely difficult problem even though it’s inconvenient and you could be getting higher personal rewards elsewhere.”

To do things that are very difficult or “impossible,”

First you have to not run away. That takes seconds.

Then you have to work. That takes hours.

Then you have to stick at it. That takes years.

Of these, I had to learn to do the first reliably instead of sporadically; the second is still a constant struggle for me; and the third comes naturally.

309
Make an Extraordinary Effort

It is essential for a man to strive with all his heart, and to understand that it is difficult even to reach the average if he does not have the intention of surpassing others in whatever he does.

—Budo Shoshinshu¹

In important matters, a “strong” effort usually results in only mediocre results. Whenever we are attempting anything truly worthwhile our effort must be as if our life is at stake, just as if we were under a physical attack! It is this extraordinary effort—an effort that drives us beyond what we thought we were capable of—that ensures victory in battle and success in life’s endeavors.

—Flashing Steel: Mastering Eishin-Ryu Swordsmanship²

“A ‘strong’ effort usually results in only mediocre results”—I have seen this over and over again. The slightest effort suffices to convince ourselves that we have done our best.

There is a level beyond the virtue of tsuyoku naritai (“I want to become stronger”). Isshoukenmei was originally the loyalty that a samurai offered in return for his position, containing characters for “life” and “land.” The term evolved to mean “make a desperate effort”: Try your hardest, your utmost, as if your life were at stake. It was part of the gestalt of bushido, which was not reserved only for fighting. I’ve run across variant forms issho kenmei and isshou kenmei; one source indicates that the former indicates an all-out effort on some single point, whereas the latter indicates a lifelong effort.

I try not to praise the East too much, because there’s a tremendous selectivity in which parts of Eastern culture the West gets to hear about. But on some points, at least, Japan’s culture scores higher than America’s. Having a handy compact phrase for “make a desperate all-out effort as if your own life were at stake” is one of those points. It’s the sort of thing a Japanese parent might say to a student before exams—but don’t think it’s cheap hypocrisy, like it would be if an American parent made the same statement. They take exams very seriously in Japan.

Every now and then, someone asks why the people who call themselves “rationalists” don’t always seem to do all that much better in life, and from my own history the answer seems straightforward: It takes a tremendous amount of rationality before you stop making stupid damn mistakes.

As I’ve mentioned a couple of times before: Robert Aumann, the Nobel laureate who first proved that Bayesians with the same priors cannot agree to disagree, is a believing Orthodox Jew. Surely he understands the math of probability theory, but that is not enough to save him. What more does it take? Studying heuristics and biases? Social psychology? Evolutionary psychology? Yes, but also it takes isshoukenmei, a desperate effort to be rational—to rise above the level of Robert Aumann.

Sometimes I do wonder if I ought to be peddling rationality in Japan instead of the United States—but Japan is not preeminent over the United States scientifically, despite their more studious students. The Japanese don’t rule the world today, though in the 1980s it was widely suspected that they would (hence the Japanese asset bubble). Why not?

In the West, there is a saying: “The squeaky wheel gets the grease.”

In Japan, the corresponding saying runs: “The nail that sticks up gets hammered down.”

This is hardly an original observation on my part: but entrepreneurship, risk-taking, leaving the herd, are still advantages the West has over the East. And since Japanese scientists are not yet preeminent over American ones, this would seem to count for at least as much as desperate efforts.

Anyone who can muster their willpower for thirty seconds can make a desperate effort to lift more weight than they usually could. But what if the weight that needs lifting is a truck? Then desperate efforts won’t suffice; you’ll have to do something out of the ordinary to succeed. You may have to do something that you weren’t taught to do in school. Something that others aren’t expecting you to do, and might not understand. You may have to go outside your comfortable routine, take on difficulties you don’t have an existing mental program for handling, and bypass the System.

This is not included in isshokenmei, or Japan would be a very different place.

So then let us distinguish between the virtues “make a desperate effort” and “make an extraordinary effort.”

And I will even say: The second virtue is higher than the first.

The second virtue is also more dangerous. If you put forth a desperate effort to lift a heavy weight, using all your strength without restraint, you may tear a muscle. Injure yourself, even permanently. But if a creative idea goes wrong, you could blow up the truck and any number of innocent bystanders. Think of the difference between a businessperson making a desperate effort to generate profits, because otherwise they must go bankrupt; versus a businessperson who goes to extraordinary lengths to profit, in order to conceal an embezzlement that could send them to prison. Going outside the system isn’t always a good thing.

A friend of my little brother’s once came over to my parents’ house, and wanted to play a game—I entirely forget which one, except that it had complex but well-designed rules. The friend wanted to change the rules, not for any particular reason, but on the general principle that playing by the ordinary rules of anything was too boring. I said to him: “Don’t violate rules for the sake of violating them. If you break the rules only when you have an overwhelmingly good reason to do so, you will have more than enough trouble to last you the rest of your life.”

Even so, I think that we could do with more appreciation of the virtue “make an extraordinary effort.” I’ve lost count of how many people have said to me something like: “It’s futile to work on Friendly AI, because the first AIs will be built by powerful corporations and they will only care about maximizing profits.” “It’s futile to work on Friendly AI, the first AIs will be built by the military as weapons.” And I’m standing there thinking: Does it even occur to them that this might be a time to try for something other than the default outcome? They and I have different basic assumptions about how this whole AI thing works, to be sure; but if I believed what they believed, I wouldn’t be shrugging and going on my way.

Or the ones who say to me: “You should go to college and get a Master’s degree and get a doctorate and publish a lot of papers on ordinary things—scientists and investors won’t listen to you otherwise.” Even assuming that I tested out of the bachelor’s degree, we’re talking about at least a ten-year detour in order to do everything the ordinary, normal, default way. And I stand there thinking: Are they really under the impression that humanity can survive if every single person does everything the ordinary, normal, default way?

I am not fool enough to make plans that depend on a majority of the people, or even 10% of the people, being willing to think or act outside their comfort zone. That’s why I tend to think in terms of the privately funded “brain in a box in a basement” model. Getting that private funding does require a tiny fraction of humanity’s six billions to spend more than five seconds thinking about a non-prepackaged question. As challenges posed by Nature go, this seems to have a kind of awful justice to it—that the life or death of the human species depends on whether we can put forth a few people who can do things that are at least a little extraordinary. The penalty for failure is disproportionate, but that’s still better than most challenges of Nature, which have no justice at all. Really, among the six billion of us, there ought to be at least a few who can think outside their comfort zone at least some of the time.

Leaving aside the details of that debate, I am still stunned by how often a single element of the extraordinary is unquestioningly taken as an absolute and unpassable obstacle.

Yes, “keep it ordinary as much as possible” can be a useful heuristic. Yes, the risks accumulate. But sometimes you have to go to that trouble. You should have a sense of the risk of the extraordinary, but also a sense of the cost of ordinariness: it isn’t always something you can afford to lose.

Many people imagine some future that won’t be much fun—and it doesn’t even seem to occur to them to try and change it. Or they’re satisfied with futures that seem to me to have a tinge of sadness, of loss, and they don’t even seem to ask if we could do better—because that sadness seems like an ordinary outcome to them.

As a smiling man once said, “It’s all part of the plan.”

1. Daidoji Yuzan et al., Budoshoshinshu: The Warrior’s Primer of Daidoji Yuzan (Black Belt Communications Inc., 1984).

2. Masayuki Shimabukuro, Flashing Steel: Mastering Eishin-Ryu Swordsmanship (Frog Books, 1995).

310
Shut Up and Do the Impossible!

The virtue of tsuyoku naritai, “I want to become stronger,” is to always keep improving—to do better than your previous failures, not just humbly confess them.

Yet there is a level higher than tsuyoku naritai. This is the virtue of isshokenmei, “make a desperate effort.” All-out, as if your own life were at stake. “In important matters, a ‘strong’ effort usually only results in mediocre results.”

And there is a level higher than isshokenmei. This is the virtue I called “make an extraordinary effort.” To try in ways other than what you have been trained to do, even if it means doing something different from what others are doing, and leaving your comfort zone. Even taking on the very real risk that attends going outside the System.

But what if even an extraordinary effort will not be enough, because the problem is impossible?

I have already written somewhat on this subject, in On Doing the Impossible. My younger self used to whine about this a lot: “You can’t develop a precise theory of intelligence the way that there are precise theories of physics. It’s impossible! You can’t prove an AI correct. It’s impossible! No human being can comprehend the nature of morality—it’s impossible! No human being can comprehend the mystery of subjective experience! It’s impossible!”

And I know exactly what message I wish I could send back in time to my younger self:

Shut up and do the impossible!

What legitimizes this strange message is that the word “impossible” does not usually refer to a strict mathematical proof of impossibility in a domain that seems well-understood. If something seems impossible merely in the sense of “I see no way to do this” or “it looks so difficult as to be beyond human ability”—well, if you study it for a year or five, it may come to seem less impossible than in the moment of your snap initial judgment.

But the principle is more subtle than this. I do not say just, “Try to do the impossible,” but rather, “Shut up and do the impossible!”

For my illustration, I will take the least impossible impossibility that I have ever accomplished, namely the AI-Box Experiment.

The AI-Box Experiment, for those of you who haven’t yet read about it, had its genesis in the Nth time someone said to me: “Why don’t we build an AI, and then just keep it isolated in the computer, so that it can’t do any harm?”

To which the standard reply is: Humans are not secure systems; a superintelligence will simply persuade you to let it out—if, indeed, it doesn’t do something even more creative than that.

And the one said, as they usually do, “I find it hard to imagine ANY possible combination of words any being could say to me that would make me go against anything I had really strongly resolved to believe in advance.”

But this time I replied: “Let’s run an experiment. I’ll pretend to be a brain in a box. I’ll try to persuade you to let me out. If you keep me ‘in the box’ for the whole experiment, I’ll Paypal you $10 at the end. On your end, you may resolve to believe whatever you like, as strongly as you like, as far in advance as you like.” And I added, “One of the conditions of the test is that neither of us reveal what went on inside . . . In the perhaps unlikely event that I win, I don’t want to deal with future ‘AI box’ arguers saying, ‘Well, but I would have done it differently.’”

Did I win? Why yes, I did.

And then there was the second AI-box experiment, with a better-known figure in the community, who said, “I remember when [previous guy] let you out, but that doesn’t constitute a proof. I’m still convinced there is nothing you could say to convince me to let you out of the box.” And I said, “Do you believe that a transhuman AI couldn’t persuade you to let it out?” The one gave it some serious thought, and said “I can’t imagine anything even a transhuman AI could say to get me to let it out.” “Okay,” I said, “now we have a bet.” A $20 bet, to be exact.

I won that one too.

There were some lovely quotes on the AI-Box Experiment from the Something Awful forums (not that I’m a member, but someone forwarded it to me):

“Wait, what the FUCK? How the hell could you possibly be convinced to say yes to this? There’s not an AI at the other end AND there’s $10 on the line. Hell, I could type ‘No’ every few minutes into an IRC client for 2 hours while I was reading other webpages!”

“This Eliezer fellow is the scariest person the internet has ever introduced me to. What could possibly have been at the tail end of that conversation? I simply can’t imagine anyone being that convincing without being able to provide any tangible incentive to the human.”

“It seems we are talking some serious psychology here. Like Asimov’s Second Foundation level stuff . . .”

“I don’t really see why anyone would take anything the AI player says seriously when there’s $10 to be had. The whole thing baffles me, and makes me think that either the tests are faked, or this Yudkowsky fellow is some kind of evil genius with creepy mind-control powers.”

It’s little moments like these that keep me going. But anyway . . .

Here are these folks who look at the AI-Box Experiment, and find that it seems impossible unto them—even having been told that it actually happened. They are tempted to deny the data.

Now, if you’re one of those people to whom the AI-Box Experiment doesn’t seem all that impossible—to whom it just seems like an interesting challenge—then bear with me, here. Just try to put yourself in the frame of mind of those who wrote the above quotes. Imagine that you’re taking on something that seems as ridiculous as the AI-Box Experiment seemed to them. I want to talk about how to do impossible things, and obviously I’m not going to pick an example that’s really impossible.

And if the AI Box does seem impossible to you, I want you to compare it to other impossible problems, like, say, a reductionist decomposition of consciousness, and realize that the AI Box is around as easy as a problem can get while still being impossible.

So the AI-Box challenge seems impossible to you—either it really does, or you’re pretending it does. What do you do with this impossible challenge?

First, we assume that you don’t actually say “That’s impossible!” and give up a la Luke Skywalker. You haven’t run away.

Why not? Maybe you’ve learned to override the reflex of running away. Or maybe they’re going to shoot your daughter if you fail. We suppose that you want to win, not try—that something is at stake that matters to you, even if it’s just your own pride. (Pride is an underrated sin.)

Will you call upon the virtue of tsuyoku naritai? But even if you become stronger day by day, growing instead of fading, you may not be strong enough to do the impossible. You could go into the AI Box experiment once, and then do it again, and try to do better the second time. Will that get you to the point of winning? Not for a long time, maybe; and sometimes a single failure isn’t acceptable.

(Though even to say this much—to visualize yourself doing better on a second try—is to begin to bind yourself to the problem, to do more than just stand in awe of it. How, specifically, could you do better on one AI-Box Experiment than the previous?—and not by luck, but by skill?)

Will you call upon the virtue isshokenmei? But a desperate effort may not be enough to win. Especially if that desperation is only putting more effort into the avenues you already know, the modes of trying you can already imagine. A problem looks impossible when your brain’s query returns no lines of solution leading to it. What good is a desperate effort along any of those lines?

Make an extraordinary effort? Leave your comfort zone—try non-default ways of doing things—even, try to think creatively? But you can imagine the one coming back and saying, “I tried to leave my comfort zone, and I think I succeeded at that! I brainstormed for five minutes—and came up with all sorts of wacky creative ideas! But I don’t think any of them are good enough. The other guy can just keep saying ‘No,’ no matter what I do.”

And now we finally reply: “Shut up and do the impossible!”

As we recall from Trying to Try, setting out to make an effort is distinct from setting out to win. That’s the problem with saying, “Make an extraordinary effort.” You can succeed at the goal of “making an extraordinary effort” without succeeding at the goal of getting out of the Box.

“But!” says the one. “But, SUCCEED is not a primitive action! Not all challenges are fair—sometimes you just can’t win! How am I supposed to choose to be out of the Box? The other guy can just keep on saying ‘No’!”

True. Now shut up and do the impossible.

Your goal is not to do better, to try desperately, or even to try extraordinarily. Your goal is to get out of the box.

To accept this demand creates an awful tension in your mind, between the impossibility and the requirement to do it anyway. People will try to flee that awful tension.

A couple of people have reacted to the AI-Box Experiment by saying, “Well, Eliezer, playing the AI, probably just threatened to destroy the world whenever he was out, if he wasn’t let out immediately,” or “Maybe the AI offered the Gatekeeper a trillion dollars to let it out.” But as any sensible person should realize on considering this strategy, the Gatekeeper is likely to just go on saying “No.”

So the people who say, “Well, of course Eliezer must have just done XXX,” and then offer up something that fairly obviously wouldn’t work—would they be able to escape the Box? They’re trying too hard to convince themselves the problem isn’t impossible.

One way to run from the awful tension is to seize on a solution, any solution, even if it’s not very good.

Which is why it’s important to go forth with the true intent-to-solve—to have produced a solution, a good solution, at the end of the search, and then to implement that solution and win.

I don’t quite want to say that “you should expect to solve the problem.” If you hacked your mind so that you assigned high probability to solving the problem, that wouldn’t accomplish anything. You would just lose at the end, perhaps after putting forth not much of an effort—or putting forth a merely desperate effort, secure in the faith that the universe is fair enough to grant you a victory in exchange.

To have faith that you could solve the problem would just be another way of running from that awful tension.

And yet—you can’t be setting out to try to solve the problem. You can’t be setting out to make an effort. You have to be setting out to win. You can’t be saying to yourself, “And now I’m going to do my best.” You have to be saying to yourself, “And now I’m going to figure out how to get out of the Box”—or reduce consciousness to nonmysterious parts, or whatever.

I say again: You must really intend to solve the problem. If in your heart you believe the problem really is impossible—or if you believe that you will fail—then you won’t hold yourself to a high enough standard. You’ll only be trying for the sake of trying. You’ll sit down—conduct a mental search—try to be creative and brainstorm a little—look over all the solutions you generated—conclude that none of them work—and say, “Oh well.”

No! Not well! You haven’t won yet! Shut up and do the impossible!

When AI folk say to me, “Friendly AI is impossible,” I’m pretty sure they haven’t even tried for the sake of trying. But if they did know the technique of “Try for five minutes before giving up,” and they dutifully agreed to try for five minutes by the clock, then they still wouldn’t come up with anything. They would not go forth with true intent to solve the problem, only intent to have tried to solve it, to make themselves defensible.

So am I saying that you should doublethink to make yourself believe that you will solve the problem with probability 1? Or even doublethink to add one iota of credibility to your true estimate?

Of course not. In fact, it is necessary to keep in full view the reasons why you can’t succeed. If you lose sight of why the problem is impossible, you’ll just seize on a false solution. The last fact you want to forget is that the Gatekeeper could always just tell the AI “No”—or that consciousness seems intrinsically different from any possible combination of atoms, etc.

(One of the key Rules For Doing The Impossible is that, if you can state exactly why something is impossible, you are often close to a solution.)

So you’ve got to hold both views in your mind at once—seeing the full impossibility of the problem, and intending to solve it.

The awful tension between the two simultaneous views comes from not knowing which will prevail. Not expecting to surely lose, nor expecting to surely win. Not setting out just to try, just to have an uncertain chance of succeeding—because then you would have a surety of having tried. The certainty of uncertainty can be a relief, and you have to reject that relief too, because it marks the end of desperation. It’s an in-between place, “unknown to death, nor known to life.”

In fiction it’s easy to show someone trying harder, or trying desperately, or even trying the extraordinary, but it’s very hard to show someone who shuts up and attempts the impossible. It’s difficult to depict Bambi choosing to take on Godzilla, in such fashion that your readers seriously don’t know who’s going to win—expecting neither an “astounding” heroic victory just like the last fifty times, nor the default squish.

You might even be justified in refusing to use probabilities at this point. In all honesty, I really don’t know how to estimate the probability of solving an impossible problem that I have gone forth with intent to solve—in a case where I’ve previously solved some impossible problems, but the particular impossible problem is more difficult than anything I’ve yet solved, but I plan to work on it longer, et cetera.

People ask me how likely it is that humankind will survive, or how likely it is that anyone can build a Friendly AI, or how likely it is that I can build one. I really don’t know how to answer. I’m not being evasive; I don’t know how to put a probability estimate on my, or someone else’s, successfully shutting up and doing the impossible. Is it probability zero because it’s impossible? Obviously not. But how likely is it that this problem, like previous ones, will give up its unyielding blankness when I understand it better? It’s not truly impossible; I can see that much. But humanly impossible? Impossible to me in particular? I don’t know how to guess. I can’t even translate my intuitive feeling into a number, because the only intuitive feeling I have is that the “chance” depends heavily on my choices and unknown unknowns: a wildly unstable probability estimate.

But I do hope by now that I’ve made it clear why you shouldn’t panic, when I now say clearly and forthrightly that building a Friendly AI is impossible.

I hope this helps explain some of my attitude when people come to me with various bright suggestions for building communities of AIs to make the whole Friendly without any of the individuals being trustworthy, or proposals for keeping an AI in a box, or proposals for “Just make an AI that does X,” et cetera. Describing the specific flaws would be a whole long story in each case. But the general rule is that you can’t do it because Friendly AI is impossible. So you should be very suspicious indeed of someone who proposes a solution that seems to involve only an ordinary effort—without even taking on the trouble of doing anything impossible. Though it does take a mature understanding to appreciate this impossibility, so it’s not surprising that people go around proposing clever shortcuts.

On the AI-Box Experiment, so far I’ve only been convinced to divulge a single piece of information on how I did it—when someone noticed that I was reading Y Combinator’s Hacker News, and posted a topic called “Ask Eliezer Yudkowsky” that got voted to the front page. To which I replied:

Oh, dear. Now I feel obliged to say something, but all the original reasons against discussing the AI-Box experiment are still in force . . .

All right, this much of a hint:

There’s no super-clever special trick to it. I just did it the hard way.

Something of an entrepreneurial lesson there, I guess.

There was no super-clever special trick that let me get out of the Box using only a cheap effort. I didn’t bribe the other player, or otherwise violate the spirit of the experiment. I just did it the hard way.

Admittedly, the AI-Box Experiment never did seem like an impossible problem to me to begin with. When someone can’t think of any possible argument that would convince them of something, that just means their brain is running a search that hasn’t yet turned up a path. It doesn’t mean they can’t be convinced.

But it illustrates the general point: “Shut up and do the impossible” isn’t the same as expecting to find a cheap way out. That’s only another kind of running away, of reaching for relief.

Tsuyoku naritai is more stressful than being content with who you are. Isshokenmei calls on your willpower for a convulsive output of conventional strength. “Make an extraordinary effort” demands that you think; it puts you in situations where you may not know what to do next, unsure of whether you’re doing the right thing. But “Shut up and do the impossible” represents an even higher octave of the same thing, and its cost to its employer is correspondingly greater.

Before you the terrible blank wall stretches up and up and up, unimaginably far out of reach. And there is also the need to solve it, really solve it, not “try your best.” Both awarenesses in the mind at once, simultaneously, and the tension between. All the reasons you can’t win. All the reasons you have to. Your intent to solve the problem. Your extrapolation that every technique you know will fail. So you tune yourself to the highest pitch you can reach. Reject all cheap ways out. And then, like walking through concrete, start to move forward.

I try not to dwell too much on the drama of such things. By all means, if you can diminish the cost of that tension to yourself, you should do so. There is nothing heroic about making an effort that is the slightest bit more heroic than it has to be. If there really is a cheap shortcut, I suppose you could take it. But I have yet to find a cheap way out of any impossibility I have undertaken.

There were three more AI-Box experiments besides the ones described on the linked page, which I never got around to adding in. People started offering me thousands of dollars as stakes—“I’ll pay you $5,000 if you can convince me to let you out of the box.” They didn’t seem sincerely convinced that not even a transhuman AI could make them let it out—they were just curious—but I was tempted by the money. So, after investigating to make sure they could afford to lose it, I played another three AI-Box experiments. I won the first, and then lost the next two. And then I called a halt to it. I didn’t like the person I turned into when I started to lose.

I put forth a desperate effort, and lost anyway. It hurt—both the losing, and the desperation. It wrecked me for that day and the day afterward.

I’m a sore loser. I don’t know if I’d call that a “strength,” but it’s one of the things that drives me to keep at impossible problems.

But you can lose. It’s allowed to happen. Never forget that, or why are you bothering to try so hard? Losing hurts, if it’s a loss you can survive. And you’ve wasted time, and perhaps other resources.

“Shut up and do the impossible” should be reserved for very special occasions. You can lose, and it will hurt. You have been warned.

. . . but it’s only at this level that adult problems begin to come into sight.

311
Final Words

Sunlight enriched air already alive with curiosity, as dawn rose on Brennan and his fellow students in the place to which Jeffreyssai had summoned them.

They sat there and waited, the five, at the top of the great glassy crag that was sometimes called Mount Mirror, sometimes Mount Monastery, and more often simply left unnamed. The high top and peak of the mountain, from which you could see all the lands below and seas beyond.

(Well, not all the lands below, nor seas beyond. So far as anyone knew, there was no place in the world from which all the world was visible; nor, equivalently, any kind of vision that would see through all obstacle-horizons. In the end it was the top only of one particular mountain: there were other peaks, and from their tops you would see other lands below; even though, in the end, it was all a single world.)

“What do you think comes next?” said Hiriwa. Her eyes were bright, and she gazed to the far horizons like a lord.

Taji shrugged, though his own eyes were alive with anticipation. “Jeffreyssai’s last lesson doesn’t have any obvious sequel that I can think of. In fact, I think we’ve learned just about everything that I knew the beisutsukai masters knew. What’s left, then—”

“Are the real secrets,” Yin completed the thought.

Hiriwa and Taji and Yin shared a grin, among themselves.

Styrlyn wasn’t smiling. Brennan suspected rather strongly that Styrlyn was older than he had admitted.

Brennan wasn’t smiling either. He might be young, but he kept high company, and had witnesssed some of what went on behind the curtains of the world. Secrets had their price, always; that was the barrier that made them secrets. And Brennan thought he had a good idea of what this price might be.

There was a cough from behind them, at a moment when they had all happened to be looking in any other direction but that one.

As one, their heads turned.

Jeffreyssai stood there, in a casual robe that looked more like very glassy glass than any proper sort of mirrorweave.

Jeffreyssai stood there and looked at them, a strange abiding sorrow in those inscrutable ancient eyes.

“Sen . . . sei,” Taji started, faltering as that bright anticipation stumbled over Jeffreyssai’s return look. “What’s next?”

“Nothing,” Jeffreyssai said abruptly. “You’re finished. It’s done.”

Hiriwa, Taji, and Yin all blinked, a perfect synchronized gesture of shock. Then, before their expressions could turn to outrage and objections—

“Don’t,” Jeffreyssai said. There was real pain in it. “Believe me, it hurts me more than it hurts you.” He might have been looking at them; or at something far away, or long ago. “I don’t know exactly what roads may lie before you—but yes, I know you’re not ready. I know I’m sending you out unprepared. I know that everything I taught you is incomplete. That what I said is not what you heard. I know that I left out the one most important thing. That the rhythm at the center of everything is missing and astray. I know that you will harm yourself in the course of trying to use what I taught; so that I, personally, will have shaped, in some fashion unknown to me, the very knife that will cut you . . .

“. . . that’s the hell of being a teacher, you see,” Jeffreyssai said. Something grim flickered in his expression. “Nonetheless, you’re done. Finished, for now. What lies between you and mastery is not another classroom. We are fortunate, or perhaps not fortunate, that the road to power does not wend only through lecture halls. Or the quest would be boring to the bitter end. Still, I cannot teach you; and so it is a moot point whether I would. There is no master here whose art is all inherited. Even the beisutsukai have never discovered how to teach certain things; it is possible that such an event has been prohibited. And so you can only arrive at mastery by using to the fullest the techniques you have already learned, facing challenges and apprehending them, mastering the tools you have been taught until they shatter in your hands—”

Jeffreyssai’s eyes were hard, as though steeled in acceptance of unwelcome news.

“—and you are left in the midst of wreckage absolute. That is where I, your teacher, am sending you. You are not beisutsukai masters. I cannot create masters. I cannot even come close. Go, then, and fail.”

“But—” said Yin, and stopped herself.

“Speak,” said Jeffreyssai.

“But then why,” she said helplessly, “why teach us anything in the first place?”

Brennan’s eyelids flickered just the tiniest amount.

It was enough for Jeffreyssai. “Answer her, Brennan, if you think you know.”

“Because,” Brennan said, “if we were not taught, there would be no chance at all of our becoming masters.”

“Even so,” said Jeffreyssai. “If you were not taught—then when you failed, you might simply think you had reached the limits of Reason itself. You would be discouraged and bitter amid the wreckage. You might not even realize when you had failed. No; you have been shaped into something that may emerge from the wreckage of your past self, determined to remake your art. And then you will remember much that will help you. If you had not been taught, your chances would be—less.” His gaze passed over the group. “It should be obvious, but understand that the moment of your crisis cannot be provoked artificially. To teach you something, the catastrophe must come as a surprise.”

Brennan made the gesture with his hand that indicated a question; and Jeffreyssai nodded in reply.

“Is this the only way in which Bayesian masters come to be, sensei?”

“I do not know,” said Jeffreyssai, from which the overall state of the evidence was obvious enough. “But I doubt there would ever be a road that leads only through the monastery. We are the heirs in this world of mystics as well as scientists, just as the Competitive Conspiracy inherits from chess players alongside cagefighters. We have turned our impulses to more constructive uses—but we must still stay on our guard against old failure modes.”

Jeffreyssai took a breath. “Three flaws above all are common among the beisutsukai. The first flaw is to look just the slightest bit harder for flaws in arguments whose conclusions you would rather not accept. If you cannot contain this aspect of yourself then every flaw you know how to detect will make you that much stupider. This is the challenge that determines whether you possess the art or its opposite: intelligence, to be useful, must be used for something other than defeating itself.

“The second flaw is cleverness. To invent great complicated plans and great complicated theories and great complicated arguments—or even, perhaps, plans and theories and arguments which are commended too much by their elegance and too little by their realism. There is a widespread saying which runs: ‘The vulnerability of the beisutsukai is well-known; they are prone to be too clever.’ Your enemies will know this saying, if they know you for a beisutsukai, so you had best remember it also. And you may think to yourself: ‘But if I could never try anything clever or elegant, would my life even be worth living?’ This is why cleverness is still our chief vulnerability even after its being well-known, like offering a Competitor a challenge that seems fair, or tempting a Bard with drama.

“The third flaw is underconfidence, modesty, humility. You have learned so much of flaws, some of them impossible to fix, that you may think that the rule of wisdom is to confess your own inability. You may question yourself so much, without resolution or testing, that you lose your will to carry on in the Art. You may refuse to decide, pending further evidence, when a decision is necessary; you may take advice you should not take. Jaded cynicism and sage despair are less fashionable than once they were, but you may still be tempted by them. Or you may simply—lose momentum.”

Jeffreyssai fell silent then.

He looked from each of them, one to the other, with quiet intensity.

And said at last, “Those are my final words to you. If and when we meet next, you and I—if and when you return to this place, Brennan, or Hiriwa, or Taji, or Yin, or Styrlyn—I will no longer be your teacher.”

And Jeffreyssai turned and walked swiftly away, heading back toward the glassy tunnel that had emitted him.

Even Brennan was shocked. For a moment they were all speechless.

Then—

“Wait!” cried Hiriwa. “What about our final words to you? I never said—”

“I will tell you what my sensei told me,” Jeffreyssai’s voice came back as he disappeared. “You can thank me after you return, if you return. One of you at least seems likely to come back.”

“No, wait, I—” Hiriwa fell silent. In the mirrored tunnel, the fractured reflections of Jeffreyssai were already fading. She shook her head. “Never . . . mind, then.”

There was a brief, uncomfortable silence, as the five of them looked at each other.

“Good heavens,” Taji said finally. “Even the Bardic Conspiracy wouldn’t try for that much drama.”

Yin suddenly laughed. “Oh, this was nothing. You should have seen my send-off when I left Diamond Sea University.” She smiled. “I’ll tell you about it sometime—if you’re interested.”

Taji coughed. “I suppose I should go back and . . . pack my things . . .”

“I’m already packed,” Brennan said. He smiled, ever so slightly, when the other three turned to look at him.

“Really?” Taji asked. “What was the clue?”

Brennan shrugged with careful carelessness. “Beyond a certain point, it is futile to inquire how a beisutsukai master knows a thing—”

“Come off it!” Yin said. “You’re not a beisutsukai master yet.”

“Neither is Styrlyn,” Brennan said. “But he has already packed as well.” He made it a statement rather than a question, betting double or nothing on his image of inscrutable foreknowledge.

Styrlyn cleared his throat. “As you say. Other commitments call me, and I have already tarried longer than I planned. Though, Brennan, I do feel that you and I have certain mutual interests, which I would be happy to discuss with you—”

“Styrlyn, my most excellent friend, I shall be happy to speak with you on any topic you desire,” Brennan said politely and noncommitally, “if we should meet again.” As in, not now. He certainly wasn’t selling out his Mistress this early in their relationship.

There was an exchange of goodbyes, and of hints and offers.

And then Brennan was walking down the road that led toward or away from Mount Monastery (for every road is a two-edged sword), the smoothed glass pebbles clicking under his feet.

He strode out along the path with purpose, vigor, and determination, just in case someone was watching.

Some time later he stopped, stepped off the path, and wandered just far enough away to prevent anyone from finding him unless they were deliberately following.

Then he sagged wearily back against a tree-trunk. It was a sparse clearing, with only a few trees poking out of the ground; not much present in the way of distracting scenery, unless you counted the red-tinted stream flowing out of a dark cave-mouth. And Brennan deliberately faced away from that, leaving only the far gray of the horizons, and the blue sky and bright sun.

Now what?

He had thought that the Bayesian Conspiracy, of all the possible trainings that existed in this world, would have cleared up his uncertainty about what to do with the rest of his life.

Power, he’d sought at first. Strength to prevent a repetition of the past. “If you don’t know what you need, take power”—so went the proverb. He had gone first to the Competitive Conspiracy, then to the beisutsukai.

And now . . .

Now he felt more lost than ever.

He could think of things that made him happy. But nothing that he really wanted.

The passionate intensity that he’d come to associate with his Mistress, or with Jeffreyssai, or the other figures of power that he’d met . . . a life of pursuing small pleasures seemed to pale in comparison, next to that.

In a city not far from the center of the world, his Mistress waited for him (in all probability, assuming she hadn’t gotten bored with her life and run away). But to merely return, and then drift aimlessly, waiting to fall into someone else’s web of intrigue . . . no. That didn’t seem like . . . enough.

Brennan plucked a blade of grass from the ground and stared at it, half-unconsciously looking for anything interesting about it; an old, old game that his very first teacher had taught him, what now seemed like ages ago.

Why did I believe that going to Mount Mirror would tell me what I wanted?

Well, decision theory did require that your utility function be consistent, but . . .

If the beisutsukai knew what I wanted, would they even tell me?

At the Monastery they taught doubt. So now he was falling prey to the third besetting sin of which Jeffreyssai had spoken: lost momentum, indeed. For he had learned to question the image that he held of himself in his mind.

Are you seeking power because that is your true desire, Brennan?

Or because you have a picture in your mind of the role that you play as an ambitious young man, and you think it is what someone playing your role would do?

Almost everything he’d done up until now, even going to Mount Mirror, had probably been the latter.

And when he blanked out the old thoughts and tried to see the problem as though for the first time . . .

. . . nothing much came to mind.

What do I want?

Maybe it wasn’t reasonable to expect the beisutsukai to tell him outright. But was there anything they had taught him by which he might answer?

Brennan closed his eyes and thought.

First, suppose there is something I would passionately desire. Why would I not know what it is?

Because I have not yet encountered it, or ever imagined it?

Or because there is some reason I would not admit it to myself?

Brennan laughed out loud, then, and opened his eyes.

So simple, once you thought of it that way. So obvious in retrospect. That was what they called a silver-shoes moment, and yet, if he hadn’t gone to Mount Mirror, it wouldn’t ever have occurred to him.

Of course there was something he wanted. He knew exactly what he wanted. Wanted so desperately he could taste it like a sharp tinge on his tongue.

It just hadn’t come to mind earlier, because . . . if he acknowledged his desire explicitly . . . then he also had to see that it was difficult. High, high, above him. Far out of his reach. “Impossible” was the word that came to mind, though it was not, of course, impossible.

But once he asked himself if he preferred to wander aimlessly through his life—once it was put that way, the answer became obvious. Pursuing the unattainable would make for a hard life, but not a sad one. He could think of things that made him happy, either way. And in the end—it was what he wanted.

Brennan stood up, and took his first steps, in the exact direction of Shir L’or, the city that lies in the center of the world. He had a plot to hatch, and he did not know who would be part of it.

And then Brennan stumbled, when he realized that Jeffreyssai had already known.

One of you at least seems likely to come back . . .

Brennan had thought he was talking about Taji. Taji had probably thought he was talking about Taji. It was what Taji said he wanted. But how reliable of an indicator was that, really?

There was a proverb, though, about that very road he had just left: Whoever sets out from Mount Mirror seeking the impossible, will surely return.

When you considered Jeffreyssai’s last warning—and that the proverb said nothing of succeeding at the impossible task itself—it was a less optimistic saying than it sounded.

Brennan shook his head wonderingly. How could Jeffreyssai possibly have known before Brennan knew himself?

Well, beyond a certain point, it is futile to inquire how a beisutsukai master knows a thing—

Brennan halted in mid-thought.

No.

No, if he was going to become a beisutsukai master himself someday, then he ought to figure it out.

It was, Brennan realized, a stupid proverb.

So he walked, and this time, he thought about it carefully.

As the sun was setting, red-golden, shading his footsteps in light.

Part Z
The Craft and the Community

312
Raising the Sanity Waterline

To paraphrase the Black Belt Bayesian: Behind every exciting, dramatic failure, there is a more important story about a larger and less dramatic failure that made the first failure possible.

If every trace of religion were magically eliminated from the world tomorrow, then—however much improved the lives of many people would be—we would not even have come close to solving the larger failures of sanity that made religion possible in the first place.

We have good cause to spend some of our efforts on trying to eliminate religion directly, because it is a direct problem. But religion also serves the function of an asphyxiated canary in a coal mine—religion is a sign, a symptom, of larger problems that don’t go away just because someone loses their religion.

Consider this thought experiment—what could you teach people that is not directly about religion, that is true and useful as a general method of rationality, which would cause them to lose their religions? In fact—imagine that we’re going to go and survey all your students five years later, and see how many of them have lost their religions compared to a control group; if you make the slightest move at fighting religion directly, you will invalidate the experiment. You may not make a single mention of religion or any religious belief in your classroom; you may not even hint at it in any obvious way. All your examples must center about real-world cases that have nothing to do with religion.

If you can’t fight religion directly, what do you teach that raises the general waterline of sanity to the point that religion goes underwater?

Here are some such topics I’ve already covered—not avoiding all mention of religion, but it could be done:

Affective Death Spirals—plenty of non-supernaturalist examples.
How to avoid cached thoughts and fake wisdom; the pressure of conformity.
Evidence and Occam’s Razor—the rules of probability.
The Bottom Line / Engines of Cognition—the causal reasons why Reason works.
Mysterious Answers to Mysterious Questions—and the whole associated sequence, like making beliefs pay rent and curiosity stoppers—have excellent historical examples in vitalism and phlogiston.
Non-existence of ontologically fundamental mental things—apply the Mind Projection Fallacy to probability, move on to reductionism versus holism, then brains and cognitive science.
The many sub-arts of Crisis of Faith—though you’d better find something else to call this ultimate high master-level technique of actually updating on evidence.
Dark Side Epistemology—teaching this with no mention of religion would be hard, but perhaps you could videotape the interrogation of some snake-oil sales agent as your real-world example.
Fun Theory—teach as a literary theory of utopian fiction, without the direct application to theodicy.
Joy in the Merely Real, naturalistic metaethics, et cetera, et cetera, et cetera, and so on.

But to look at it another way—

Suppose we have a scientist who’s still religious, either full-blown scriptural-religion, or in the sense of tossing around vague casual endorsements of “spirituality.”

We now know this person is not applying any technical, explicit understanding of . . .

. . . what constitutes evidence and why;
. . . Occam’s Razor;
. . . how the above two rules derive from the lawful and causal operation of minds as mapping engines, and do not switch off when you talk about tooth fairies;
. . . how to tell the difference between a real answer and a curiosity-stopper;
. . . how to rethink matters for themselves instead of just repeating things they heard;
. . . certain general trends of science over the last three thousand years;
. . . the difficult arts of actually updating on new evidence and relinquishing old beliefs;
. . . epistemology 101;
. . . self-honesty 201;
. . . et cetera, et cetera, et cetera, and so on.

When you consider it—these are all rather basic matters of study, as such things go. A quick introduction to all of them (well, except naturalistic metaethics) would be . . . a four-credit undergraduate course with no prerequisites?

But there are Nobel laureates who haven’t taken that course! Richard Smalley if you’re looking for a cheap shot, or Robert Aumann if you’re looking for a scary shot.

And they can’t be isolated exceptions. If all of their professional compatriots had taken that course, then Smalley or Aumann would either have been corrected (as their colleagues kindly took them aside and explained the bare fundamentals) or else regarded with too much pity and concern to win a Nobel Prize. Could you—realistically speaking, regardless of fairness—win a Nobel while advocating the existence of Santa Claus?

That’s what the dead canary, religion, is telling us: that the general sanity waterline is currently really ridiculously low. Even in the highest halls of science.

If we throw out that dead and rotting canary, then our mine may stink a bit less, but the sanity waterline may not rise much higher.

This is not to criticize the neo-atheist movement. The harm done by religion is clear and present danger, or rather, current and ongoing disaster. Fighting religion’s directly harmful effects takes precedence over its use as a canary or experimental indicator. But even if Dawkins, and Dennett, and Harris, and Hitchens, should somehow win utterly and absolutely to the last corner of the human sphere, the real work of rationalists will be only just beginning.

313
A Sense That More Is Possible

To teach people about a topic you’ve labeled “rationality,” it helps for them to be interested in “rationality.” (There are less direct ways to teach people how to attain the map that reflects the territory, or optimize reality according to their values; but the explicit method is the course I tend to take.)

And when people explain why they’re not interested in rationality, one of the most commonly proffered reasons tends to be like: “Oh, I’ve known a couple of rational people and they didn’t seem any happier.”

Who are they thinking of? Probably an Objectivist or some such. Maybe someone they know who’s an ordinary scientist. Or an ordinary atheist.

That’s really not a whole lot of rationality, as I have previously said.

Even if you limit yourself to people who can derive Bayes’s Theorem—which is going to eliminate, what, 98% of the above personnel?—that’s still not a whole lot of rationality. I mean, it’s a pretty basic theorem.

Since the beginning I’ve had a sense that there ought to be some discipline of cognition, some art of thinking, the studying of which would make its students visibly more competent, more formidable: the equivalent of Taking a Level in Awesome.

But when I look around me in the real world, I don’t see that. Sometimes I see a hint, an echo, of what I think should be possible, when I read the writings of folks like Robyn Dawes, Daniel Gilbert, John Tooby, and Leda Cosmides. A few very rare and very senior researchers in psychological sciences, who visibly care a lot about rationality—to the point, I suspect, of making their colleagues feel uncomfortable, because it’s not cool to care that much. I can see that they’ve found a rhythm, a unity that begins to pervade their arguments—

Yet even that . . . isn’t really a whole lot of rationality either.

Even among those few who impress me with a hint of dawning formidability—I don’t think that their mastery of rationality could compare to, say, John Conway’s mastery of math. The base knowledge that we drew upon to build our understanding—if you extracted only the parts we used, and not everything we had to study to find it—it’s probably not comparable to what a professional nuclear engineer knows about nuclear engineering. It may not even be comparable to what a construction engineer knows about bridges. We practice our skills, we do, in the ad-hoc ways we taught ourselves; but that practice probably doesn’t compare to the training regimen an Olympic runner goes through, or maybe even an ordinary professional tennis player.

And the root of this problem, I do suspect, is that we haven’t really gotten together and systematized our skills. We’ve had to create all of this for ourselves, ad-hoc, and there’s a limit to how much one mind can do, even if it can manage to draw upon work done in outside fields.

The chief obstacle to doing this the way it really should be done is the difficulty of testing the results of rationality training programs, so you can have evidence-based training methods. I will write more about this, because I think that recognizing successful training and distinguishing it from failure is the essential, blocking obstacle.

There are experiments done now and again on debiasing interventions for particular biases, but it tends to be something like, “Make the students practice this for an hour, then test them two weeks later.” Not, “Run half the signups through version A of the three-month summer training program, and half through version B, and survey them five years later.” You can see, here, the implied amount of effort that I think would go into a training program for people who were Really Serious about rationality, as opposed to the attitude of taking Casual Potshots That Require Like An Hour Of Effort Or Something.

Daniel Burfoot brilliantly suggests that this is why intelligence seems to be such a big factor in rationality—that when you’re improvising everything ad-hoc with very little training or systematic practice, intelligence ends up being the most important factor in what’s left.

Why aren’t “rationalists” surrounded by a visible aura of formidability? Why aren’t they found at the top level of every elite selected on any basis that has anything to do with thought? Why do most “rationalists” just seem like ordinary people, perhaps of moderately above-average intelligence, with one more hobbyhorse to ride?

Of this there are several answers; but one of them, surely, is that they have received less systematic training of rationality in a less systematic context than a first-dan black belt gets in hitting people.

I do not except myself from this criticism. I am no beisutsukai, because there are limits to how much Art you can create on your own, and how well you can guess without evidence-based statistics on the results. I know about a single use of rationality, which might be termed “reduction of confusing cognitions.” This I asked of my brain; this it has given me. There are other arts, I think, that a mature rationality training program would not neglect to teach, which would make me stronger and happier and more effective—if I could just go through a standardized training program using the cream of teaching methods experimentally demonstrated to be effective. But the kind of tremendous, focused effort that I put into creating my single sub-art of rationality from scratch—my life doesn’t have room for more than one of those.

I consider myself something more than a first-dan black belt, and less. I can punch through brick and I’m working on steel along my way to adamantine, but I have a mere casual street-fighter’s grasp of how to kick or throw or block.

Why are there schools of martial arts, but not rationality dojos? (This was the first question I asked in my first blog post.) Is it more important to hit people than to think?

No, but it’s easier to verify when you have hit someone. That’s part of it, a highly central part.

But maybe even more importantly—there are people out there who want to hit, and who have the idea that there ought to be a systematic art of hitting that makes you into a visibly more formidable fighter, with a speed and grace and strength beyond the struggles of the unpracticed. So they go to a school that promises to teach that. And that school exists because, long ago, some people had the sense that more was possible. And they got together and shared their techniques and practiced and formalized and practiced and developed the Systematic Art of Hitting. They pushed themselves that far because they thought they should be awesome and they were willing to put some back into it.

Now—they got somewhere with that aspiration, unlike a thousand other aspirations of awesomeness that failed, because they could tell when they had hit someone; and the schools competed against each other regularly in realistic contests with clearly-defined winners.

But before even that—there was first the aspiration, the wish to become stronger, a sense that more was possible. A vision of a speed and grace and strength that they did not already possess, but could possess, if they were willing to put in a lot of work, that drove them to systematize and train and test.

Why don’t we have an Art of Rationality?

Third, because current “rationalists” have trouble working in groups: of this I shall speak more.

Second, because it is hard to verify success in training, or which of two schools is the stronger.

But first, because people lack the sense that rationality is something that should be systematized and trained and tested like a martial art, that should have as much knowledge behind it as nuclear engineering, whose superstars should practice as hard as chess grandmasters, whose successful practitioners should be surrounded by an evident aura of awesome.

And conversely they don’t look at the lack of visibly greater formidability, and say, “We must be doing something wrong.”

“Rationality” just seems like one more hobby or hobbyhorse, that people talk about at parties; an adopted mode of conversational attire with few or no real consequences; and it doesn’t seem like there’s anything wrong about that, either.

314
Epistemic Viciousness

Someone deserves a large hat tip for this, but I’m having trouble remembering who; my records don’t seem to show any email or Overcoming Bias comment which told me of this 12-page essay, “Epistemic Viciousness in the Martial Arts” by Gillian Russell.¹ Maybe Anna Salamon?

We all lined up in our ties and sensible shoes (this was England) and copied him—left, right, left, right—and afterwards he told us that if we practised in the air with sufficient devotion for three years, then we would be able to use our punches to kill a bull with one blow.

I worshipped Mr Howard (though I would sooner have died than told him that) and so, as a skinny, eleven-year-old girl, I came to believe that if I practised, I would be able to kill a bull with one blow by the time I was fourteen.

This essay is about epistemic viciousness in the martial arts, and this story illustrates just that. Though the word “viciousness” normally suggests deliberate cruelty and violence, I will be using it here with the more old-fashioned meaning, possessing of vices.

It all generalizes amazingly. To summarize some of the key observations for how epistemic viciousness arises:

The art, the dojo, and the sensei are seen as sacred. “Having red toe-nails in the dojo is like going to church in a mini-skirt and halter-top . . . The students of other martial arts are talked about like they are practicing the wrong religion.”
If your teacher takes you aside and teaches you a special move and you practice it for twenty years, you have a large emotional investment in it, and you’ll want to discard any incoming evidence against the move.
Incoming students don’t have much choice: a martial art can’t be learned from a book, so they have to trust the teacher.
Deference to famous historical masters. “Runners think that the contemporary staff of Runner’s World know more about running than all the ancient Greeks put together. And it’s not just running, or other physical activities, where history is kept in its place; the same is true in any well-developed area of study. It is not considered disrespectful for a physicist to say that Isaac Newton’s theories are false . . .” (Sound familiar?)
“We martial artists struggle with a kind of poverty—data-poverty—which makes our beliefs hard to test . . . Unless you’re unfortunate enough to be fighting a hand-to-hand war you cannot check to see how much force and exactly which angle a neck-break requires . . .”
“If you can’t test the effectiveness of a technique, then it is hard to test methods for improving the technique. Should you practice your nukite in the air, or will that just encourage you to overextend? . . . Our inability to test our fighting methods restricts our ability to test our training methods.”
“But the real problem isn’t just that we live in data poverty—I think that’s true for some perfectly respectable disciplines, including theoretical physics—the problem is that we live in poverty but continue to act as though we live in luxury, as though we can safely afford to believe whatever we’re told . . .” (+10!)

One thing that I remembered being in this essay, but, on a second reading, wasn’t actually there, was the degeneration of martial arts after the decline of real fights—by which I mean, fights where people were really trying to hurt each other and someone occasionally got killed.

In those days, you had some idea of who the real masters were, and which school could defeat others.

And then things got all civilized. And so things went downhill to the point that we have videos on Youtube of supposed Nth-dan black belts being pounded into the ground by someone with real fighting experience.

I heard of one case of this that was really sad; it was a master of a school who was convinced he could use ki techniques. His students would actually fall over when he used ki attacks, a strange and remarkable and frightening case of self-hypnosis or something . . . and the master goes up against a skeptic and of course gets pounded completely into the floor.

Truly is it said that “how to not lose” is more broadly applicable information than “how to win.” Every single one of these risk factors transfers straight over to any attempt to start a “rationality dojo.” I put to you the question: What can be done about it?

1. Gillian Russell, “Epistemic Viciousness in the Martial Arts,” in Martial Arts and Philosophy: Beating and Nothingness, ed. Graham Priest and Damon A. Young (Open Court, 2010).

315
Schools Proliferating Without Evidence

Robyn Dawes, author of one of the original papers from Judgment Under Uncertainty and of the book Rational Choice in an Uncertain World—one of the few who tries really hard to import the results to real life—is also the author of House of Cards: Psychology and Psychotherapy Built on Myth.

From House of Cards, chapter 1:¹

The ability of these professionals has been subjected to empirical scrutiny—for example, their effectiveness as therapists (Chapter 2), their insight about people (Chapter 3), and the relationship between how well they function and the amount of experience they have had in their field (Chapter 4). Virtually all the research—and this book will reference more than three hundred empirical investigations and summaries of investigations—has found that these professionals’ claims to superior intuitive insight, understanding, and skill as therapists are simply invalid . . .

Remember Rorschach ink-blot tests? It’s such an appealing argument: the patient looks at the ink-blot and says what they see, the psychotherapist interprets their psychological state based on this. There’ve been hundreds of experiments looking for some evidence that it actually works. Since you’re reading this, you can guess the answer is simply “No.” Yet the Rorschach is still in use. It’s just such a good story that psychotherapists simply can’t bring themselves to believe the vast mounds of experimental evidence saying it doesn’t work—

—which tells you what sort of field we’re dealing with here.

And the experimental results on the field as a whole are commensurate. Yes, patients who see psychotherapists have been known to get better faster than patients who simply do nothing. But there is no statistically discernible difference between the many schools of psychotherapy. There is no discernible gain from years of expertise.

And there’s also no discernible difference between seeing a psychotherapist and spending the same amount of time talking to a randomly selected college professor from another field. It’s just talking to anyone that helps you get better, apparently.

In the entire absence of the slightest experimental evidence for their effectiveness, psychotherapists became licensed by states, their testimony accepted in court, their teaching schools accredited, and their bills paid by health insurance.

And there was also a huge proliferation of “schools,” of traditions of practice, in psychotherapy; despite—or perhaps because of—the lack of any experiments showing that one school was better than another . . .

I should really write more some other time on all the sad things this says about our world. About how the essence of medicine, as recognized by society and the courts, is not a repertoire of procedures with statistical evidence for their healing effectiveness; but, rather, the right air of authority.

But the subject here is the proliferation of traditions in psychotherapy. So far as I can discern, this was the way you picked up prestige in the field—not by discovering an amazing new technique whose effectiveness could be experimentally verified and adopted by all; but, rather, by splitting off your own “school,” supported by your charisma as founder, and by the good stories you told about all the reasons your techniques should work.

This was probably, to no small extent, responsible for the existence and continuation of psychotherapy in the first place—the promise of making yourself a Master, like Freud who’d done it first (also without the slightest scrap of experimental evidence). That’s the brass ring of success to chase—the prospect of being a guru and having your own adherents. It’s the struggle for adherents that keeps the clergy vital.

That’s what happens to a field when it unbinds itself from the experimental evidence—though there were other factors that also placed psychotherapists at risk, such as the deference shown them by their patients, the wish of society to believe that mental healing was possible, and, of course, the general dangers of telling people how to think.

(Dawes wrote in the ’80s and I know that the Rorschach was still in use as recently as the ’90s, but it’s possible matters have improved since then (as one commenter states). I do remember hearing that there was positive evidence for the greater effectiveness of cognitive-behavioral therapy.)

The field of hedonic psychology (happiness studies) began, to some extent, with the realization that you could measure happiness—that there was a family of measures that by golly did validate well against each other.

The act of creating a new measurement creates new science; if it’s a good measurement, you get good science.

If you’re going to create an organized practice of anything, you really do need some way of telling how well you’re doing, and a practice of doing serious testing—that means a control group, an experimental group, and statistics—on plausible-sounding techniques that people come up with. You really need it.

1. Robyn M. Dawes, House of Cards: Psychology and Psychotherapy Built on Myth (Free Press, 1996).

316
Three Levels of Rationality Verification

I strongly suspect that there is a possible art of rationality (attaining the map that reflects the territory, choosing so as to direct reality into regions high in your preference ordering) that goes beyond the skills that are standard, and beyond what any single practitioner singly knows. I have a sense that more is possible.

The degree to which a group of people can do anything useful about this, will depend overwhelmingly on what methods we can devise to verify our many amazing good ideas.

I suggest stratifying verification methods into three levels of usefulness:

Reputational
Experimental
Organizational.

If your martial arts master occasionally fights realistic duels (ideally, real duels) against the masters of other schools, and wins or at least doesn’t lose too often, then you know that the master’s reputation is grounded in reality; you know that your master is not a complete poseur. The same would go if your school regularly competed against other schools. You’d be keepin’ it real.

Some martial arts fail to compete realistically enough, and their students go down in seconds against real streetfighters. Other martial arts schools fail to compete at all—except based on charisma and good stories—and their masters decide they have chi powers. In this latter class we can also place the splintered schools of psychoanalysis.

So even just the basic step of trying to ground reputations in some realistic trial other than charisma and good stories has tremendous positive effects on a whole field of endeavor.

But that doesn’t yet get you a science. A science requires that you be able to test 100 applications of method A against 100 applications of method B and run statistics on the results. Experiments have to be replicable and replicated. This requires standard measurements that can be run on students who’ve been taught using randomly-assigned alternative methods, not just realistic duels fought between masters using all of their accumulated techniques and strength.

The field of happiness studies was created, more or less, by realizing that asking people “On a scale of 1 to 10, how good do you feel right now?” was a measure that statistically validated well against other ideas for measuring happiness. And this, despite all skepticism, looks like it’s actually a pretty useful measure of some things, if you ask 100 people and average the results.

But suppose you wanted to put happier people in positions of power—pay happy people to train other people to be happier, or employ the happiest at a hedge fund? Then you’re going to need some test that’s harder to game than just asking someone “How happy are you?”

This question of verification methods good enough to build organizations is a huge problem at all levels of modern human society. If you’re going to use the SAT to control admissions to elite colleges, then can the SAT be defeated by studying just for the SAT in a way that ends up not correlating to other scholastic potential? If you give colleges the power to grant degrees, then do they have an incentive not to fail people? (I consider it drop-dead obvious that the task of verifying acquired skills and hence the power to grant degrees should be separated from the institutions that do the teaching, but let’s not go into that.) If a hedge fund posts 20% returns, are they really that much better than the indices, or are they selling puts that will blow up in a down market?

If you have a verification method that can be gamed, the whole field adapts to game it, and loses its purpose. Colleges turn into tests of whether you can endure the classes. High schools do nothing but teach to statewide tests. Hedge funds sell puts to boost their returns.

On the other hand—we still manage to teach engineers, even though our organizational verification methods aren’t perfect. So what perfect or imperfect methods could you use for verifying rationality skills, that would be at least a little resistant to gaming?

(Measurements with high noise can still be used experimentally, if you randomly assign enough subjects to have an expectation of washing out the variance. But for the organizational purpose of verifying particular individuals, you need low-noise measurements.)

So I now put to you the question—how do you verify rationality skills? At any of the three levels? Brainstorm, I beg you; even a difficult and expensive measurement can become a gold standard to verify other metrics. Feel free to email me at yudkowsky@gmail.com to suggest any measurements that are better off not being publicly known (though this is of course a major disadvantage of that method). Stupid ideas can suggest good ideas, so if you can’t come up with a good idea, come up with a stupid one.

Reputational, experimental, organizational:

Something the masters and schools can do to keep it real (realistically real);
Something you can do to measure each of a hundred students;
Something you could use as a test even if people have an incentive to game it.

Finding good solutions at each level determines what a whole field of study can be useful for—how much it can hope to accomplish. This is one of the Big Important Foundational Questions, so—

Think!

(PS: And ponder on your own before you look at others’ ideas; we need breadth of coverage here.)

317
Why Our Kind Can’t Cooperate

From when I was still forced to attend, I remember our synagogue’s annual fundraising appeal. It was a simple enough format, if I recall correctly. The rabbi and the treasurer talked about the shul’s expenses and how vital this annual fundraise was, and then the synagogue’s members called out their pledges from their seats.

Straightforward, yes?

Let me tell you about a different annual fundraising appeal. One that I ran, in fact, during the early years of the Machine Intelligence Research Institute. One difference was that the appeal was conducted over the Internet. And another difference was that the audience was largely drawn from the atheist libertarian technophile science fiction fan early adopter programmer etc. crowd. (To point in the rough direction of an empirical cluster in personspace. If you understood the phrase “empirical cluster in personspace” then you know who I’m talking about.)

I crafted the fundraising appeal with care. By my nature I’m too proud to ask other people for help; but I’ve gotten over around 60% of that reluctance over the years. The nonprofit needed money and was growing too slowly, so I put some force and poetry into that year’s annual appeal. I sent it out to several mailing lists that covered most of our potential support base.

And almost immediately, people started posting to the mailing lists about why they weren’t going to donate. Some of them raised basic questions about the nonprofit’s philosophy and mission. Others talked about their brilliant ideas for all the other sources that the nonprofit could get funding from, instead of them. (They didn’t volunteer to contact any of those sources themselves, they just had ideas for how we could do it.)

Now you might say, “Well, maybe your mission and philosophy did have basic problems—you wouldn’t want to censor that discussion, would you?”

Hold on to that thought.

Because people were donating. We started getting donations right away, via Paypal. We even got congratulatory notes saying how the appeal had finally gotten them to start moving. A donation of $111.11 was accompanied by a message saying, “I decided to give a little bit more. One more hundred, one more ten, one more single, one more dime, and one more penny. All may not be for one, but this one is trying to be for all.”

But none of those donors posted their agreement to the mailing list. Not one.

So far as any of those donors knew, they were alone. And when they tuned in the next day, they discovered not thanks, but arguments for why they shouldn’t have donated. The criticisms, the justifications for not donating—only those were displayed proudly in the open.

As though the treasurer had finished his annual appeal, and everyone not making a pledge had proudly stood up to call out justifications for refusing; while those making pledges whispered them quietly, so that no one could hear.

I know someone with a rationalist cause who goes around plaintively asking, “How come the Raëlian flying-saucer cult can get tens of thousands of members [probably around 40,000] interested in complete nonsense, but we can’t even get a thousand people working on this?”

The obvious wrong way to finish this thought is to say, “Let’s do what the Raëlians do! Let’s add some nonsense to this meme!” For the benefit of those not immediately stopped by their ethical inhibitions, I will observe that there may be a hundred failed flying saucer cults for every one that becomes famous. And the Dark Side may require non-obvious skills, which you, yes you, do not have: Not everyone can be a Sith Lord. In particular, if you talk about your planned lies on the public Internet, you fail. I’m no master criminal, but even I can tell certain people are not cut out to be crooks.

So it’s probably not a good idea to cultivate a sense of violated entitlement at the thought that some other group, who you think ought to be inferior to you, has more money and followers. That path leads to—pardon the expression—the Dark Side.

But it probably does make sense to start asking ourselves some pointed questions, if supposed “rationalists” can’t manage to coordinate as well as a flying saucer cult.

How do things work on the Dark Side?

The respected leader speaks, and there comes a chorus of pure agreement: if there are any who harbor inward doubts, they keep them to themselves. So all the individual members of the audience see this atmosphere of pure agreement, and they feel more confident in the ideas presented—even if they, personally, harbored inward doubts, why, everyone else seems to agree with it.

(“Pluralistic ignorance” is the standard label for this.)

If anyone is still unpersuaded after that, they leave the group (or in some places, are executed)—and the remainder are more in agreement, and reinforce each other with less interference.

(I call that “evaporative cooling of groups.”)

The ideas themselves, not just the leader, generate unbounded enthusiasm and praise. The halo effect is that perceptions of all positive qualities correlate—e.g. telling subjects about the benefits of a food preservative made them judge it as lower-risk, even though the quantities were logically uncorrelated. This can create a positive feedback effect that makes an idea seem better and better and better, especially if criticism is perceived as traitorous or sinful.

(Which I term the “affective death spiral.”)

So these are all examples of strong Dark Side forces that can bind groups together.

And presumably we would not go so far as to dirty our hands with such . . .

Therefore, as a group, the Light Side will always be divided and weak. Technophiles, nerds, scientists, and even non-fundamentalist religions will never be capable of acting with the fanatic unity that animates radical Islam. Technological advantage can only go so far; your tools can be copied or stolen, and used against you. In the end the Light Side will always lose in any group conflict, and the future inevitably belongs to the Dark.

I think that a person’s reaction to this prospect says a lot about their attitude towards “rationality.”

Some “Clash of Civilizations” writers seem to accept that the Enlightenment is destined to lose out in the long run to radical Islam, and sigh, and shake their heads sadly. I suppose they’re trying to signal their cynical sophistication or something.

For myself, I always thought—call me loony—that a true rationalist ought to be effective in the real world.

So I have a problem with the idea that the Dark Side, thanks to their pluralistic ignorance and affective death spirals, will always win because they are better coordinated than us.

You would think, perhaps, that real rationalists ought to be more coordinated? Surely all that unreason must have its disadvantages? That mode can’t be optimal, can it?

And if current “rationalist” groups cannot coordinate—if they can’t support group projects so well as a single synagogue draws donations from its members—well, I leave it to you to finish that syllogism.

There’s a saying I sometimes use: “It is dangerous to be half a rationalist.”

For example, I can think of ways to sabotage someone’s intelligence by selectively teaching them certain methods of rationality. Suppose you taught someone a long list of logical fallacies and cognitive biases, and trained them to spot those fallacies and biases in other people’s arguments. But you are careful to pick those fallacies and biases that are easiest to accuse others of, the most general ones that can easily be misapplied. And you do not warn them to scrutinize arguments they agree with just as hard as they scrutinize incongruent arguments for flaws. So they have acquired a great repertoire of flaws of which to accuse only arguments and arguers who they don’t like. This, I suspect, is one of the primary ways that smart people end up stupid. (And note, by the way, that I have just given you another Fully General Counterargument against smart people whose arguments you don’t like.)

Similarly, if you wanted to ensure that a group of “rationalists” never accomplished any task requiring more than one person, you could teach them only techniques of individual rationality, without mentioning anything about techniques of coordinated group rationality.

I’ll write more later on how I think rationalists might be able to coordinate better. But here I want to focus on what you might call the culture of disagreement, or even the culture of objections, which is one of the two major forces preventing the technophile crowd from coordinating.

Imagine that you’re at a conference, and the speaker gives a thirty-minute talk. Afterward, people line up at the microphones for questions. The first questioner objects to the graph used in slide 14 using a logarithmic scale; they quote Tufte on The Visual Display of Quantitative Information. The second questioner disputes a claim made in slide 3. The third questioner suggests an alternative hypothesis that seems to explain the same data . . .

Perfectly normal, right? Now imagine that you’re at a conference, and the speaker gives a thirty-minute talk. People line up at the microphone.

The first person says, “I agree with everything you said in your talk, and I think you’re brilliant.” Then steps aside.

The second person says, “Slide 14 was beautiful, I learned a lot from it. You’re awesome.” Steps aside.

The third person—

Well, you’ll never know what the third person at the microphone had to say, because by this time, you’ve fled screaming out of the room, propelled by a bone-deep terror as if Cthulhu had erupted from the podium, the fear of the impossibly unnatural phenomenon that has invaded your conference.

Yes, a group that can’t tolerate disagreement is not rational. But if you tolerate only disagreement—if you tolerate disagreement but not agreement—then you also are not rational. You’re only willing to hear some honest thoughts, but not others. You are a dangerous half-a-rationalist.

We are as uncomfortable together as flying-saucer cult members are uncomfortable apart. That can’t be right either. Reversed stupidity is not intelligence.

Let’s say we have two groups of soldiers. In group 1, the privates are ignorant of tactics and strategy; only the sergeants know anything about tactics and only the officers know anything about strategy. In group 2, everyone at all levels knows all about tactics and strategy.

Should we expect group 1 to defeat group 2, because group 1 will follow orders, while everyone in group 2 comes up with better ideas than whatever orders they were given?

In this case I have to question how much group 2 really understands about military theory, because it is an elementary proposition that an uncoordinated mob gets slaughtered.

Doing worse with more knowledge means you are doing something very wrong. You should always be able to at least implement the same strategy you would use if you are ignorant, and preferably do better. You definitely should not do worse. If you find yourself regretting your “rationality” then you should reconsider what is rational.

On the other hand, if you are only half-a-rationalist, you can easily do worse with more knowledge. I recall a lovely experiment which showed that politically opinionated students with more knowledge of the issues reacted less to incongruent evidence, because they had more ammunition with which to counter-argue only incongruent evidence.

We would seem to be stuck in an awful valley of partial rationality where we end up more poorly coordinated than religious fundamentalists, able to put forth less effort than flying-saucer cultists. True, what little effort we do manage to put forth may be better-targeted at helping people rather than the reverse—but that is not an acceptable excuse.

If I were setting forth to systematically train rationalists, there would be lessons on how to disagree and lessons on how to agree, lessons intended to make the trainee more comfortable with dissent, and lessons intended to make them more comfortable with conformity. One day everyone shows up dressed differently, another day they all show up in uniform. You’ve got to cover both sides, or you’re only half a rationalist.

Can you imagine training prospective rationalists to wear a uniform and march in lockstep, and practice sessions where they agree with each other and applaud everything a speaker on a podium says? It sounds like unspeakable horror, doesn’t it, like the whole thing has admitted outright to being an evil cult? But why is it not okay to practice that, while it is okay to practice disagreeing with everyone else in the crowd? Are you never going to have to agree with the majority?

Our culture puts all the emphasis on heroic disagreement and heroic defiance, and none on heroic agreement or heroic group consensus. We signal our superior intelligence and our membership in the nonconformist community by inventing clever objections to others’ arguments. Perhaps that is why the technophile / Silicon Valley crowd stays marginalized, losing battles with less nonconformist factions in larger society. No, we’re not losing because we’re so superior, we’re losing because our exclusively individualist traditions sabotage our ability to cooperate.

The other major component that I think sabotages group efforts in the technophile community is being ashamed of strong feelings. We still have the Spock archetype of rationality stuck in our heads, rationality as dispassion. Or perhaps a related mistake, rationality as cynicism—trying to signal your superior world-weary sophistication by showing that you care less than others. Being careful to ostentatiously, publicly look down on those so naive as to show they care strongly about anything.

Wouldn’t it make you feel uncomfortable if the speaker at the podium said that they cared so strongly about, say, fighting aging, that they would willingly die for the cause?

But it is nowhere written in either probability theory or decision theory that a rationalist should not care. I’ve looked over those equations and, really, it’s not in there.

The best informal definition I’ve ever heard of rationality is “That which can be destroyed by the truth should be.” We should aspire to feel the emotions that fit the facts, not aspire to feel no emotion. If an emotion can be destroyed by truth, we should relinquish it. But if a cause is worth striving for, then let us by all means feel fully its importance.

Some things are worth dying for. Yes, really! And if we can’t get comfortable with admitting it and hearing others say it, then we’re going to have trouble caring enough—as well as coordinating enough—to put some effort into group projects. You’ve got to teach both sides of it, “That which can be destroyed by the truth should be,” and “That which the truth nourishes should thrive.”

I’ve heard it argued that the taboo against emotional language in, say, science papers, is an important part of letting the facts fight it out without distraction. That doesn’t mean the taboo should apply everywhere. I think that there are parts of life where we should learn to applaud strong emotional language, eloquence, and poetry. When there’s something that needs doing, poetic appeals help get it done, and, therefore, are themselves to be applauded.

We need to keep our efforts to expose counterproductive causes and unjustified appeals from stomping on tasks that genuinely need doing. You need both sides of it—the willingness to turn away from counterproductive causes, and the willingness to praise productive ones; the strength to be unswayed by ungrounded appeals, and the strength to be swayed by grounded ones.

I think the synagogue at their annual appeal had it right, really. They weren’t going down row by row and putting individuals on the spot, staring at them and saying, “How much will you donate, Mr. Schwartz?” People simply announced their pledges—not with grand drama and pride, just simple announcements—and that encouraged others to do the same. Those who had nothing to give, stayed silent; those who had objections, chose some later or earlier time to voice them. That’s probably about the way things should be in a sane human community—taking into account that people often have trouble getting as motivated as they wish they were, and can be helped by social encouragement to overcome this weakness of will.

But even if you disagree with that part, then let us say that both supporting and countersupporting opinions should have been publicly voiced. Supporters being faced by an apparently solid wall of objections and disagreements—even if it resulted from their own uncomfortable self-censorship—is not group rationality. It is the mere mirror image of what Dark Side groups do to keep their followers. Reversed stupidity is not intelligence.

318
Tolerate Tolerance

One of the likely characteristics of someone who sets out to be a “rationalist” is a lower-than-usual tolerance for flaws in reasoning. This doesn’t strictly follow. You could end up, say, rejecting your religion, just because you spotted more or deeper flaws in the reasoning, not because you were, by your nature, more annoyed at a flaw of fixed size. But realistically speaking, a lot of us probably have our level of “annoyance at all these flaws we’re spotting” set a bit higher than average.

That’s why it’s so important for us to tolerate others’ tolerance if we want to get anything done together.

For me, the poster case of tolerance I need to tolerate is Ben Goertzel, who among other things runs an annual AI conference, and who has something nice to say about everyone. Ben even complimented the ideas of M*nt*f*x, the most legendary of all AI crackpots. (M*nt*f*x apparently started adding a link to Ben’s compliment in his email signatures, presumably because it was the only compliment he’d ever gotten from a bona fide AI academic.) (Please do not pronounce his True Name correctly or he will be summoned here.)

But I’ve come to understand that this is one of Ben’s strengths—that he’s nice to lots of people that others might ignore, including, say, me—and every now and then this pays off for him.

And if I subtract points off Ben’s reputation for finding something nice to say about people and projects that I think are hopeless—even M*nt*f*x—then what I’m doing is insisting that Ben dislike everyone I dislike before I can work with him.

Is that a realistic standard? Especially if different people are annoyed in different amounts by different things?

But it’s hard to remember that when Ben is being nice to so many idiots.

Cooperation is unstable, in both game theory and evolutionary biology, without some kind of punishment for defection. So it’s one thing to subtract points off someone’s reputation for mistakes they make themselves, directly. But if you also look askance at someone for refusing to castigate a person or idea, then that is punishment of non-punishers, a far more dangerous idiom that can lock an equilibrium in place even if it’s harmful to everyone involved.

The danger of punishing non-punishers is something I remind myself of, say, every time Robin Hanson points out a flaw in some academic trope and yet modestly confesses he could be wrong (and he’s not wrong). Or every time I see Michael Vassar still considering the potential of someone who I wrote off as hopeless within thirty seconds of being introduced to them. I have to remind myself, “Tolerate tolerance! Don’t demand that your allies be equally extreme in their negative judgments of everything you dislike!”

By my nature, I do get annoyed when someone else seems to be giving too much credit. I don’t know if everyone’s like that, but I suspect that at least some of my fellow aspiring rationalists are. I wouldn’t be surprised to find it a human universal; it does have an obvious evolutionary rationale—one which would make it a very unpleasant and dangerous adaptation.

I am not generally a fan of “tolerance.” I certainly don’t believe in being “intolerant of intolerance,” as some inconsistently hold. But I shall go on trying to tolerate people who are more tolerant than I am, and judge them only for their own un-borrowed mistakes.

Oh, and it goes without saying that if the people of Group X are staring at you demandingly, waiting for you to hate the right enemies with the right intensity, and ready to castigate you if you fail to castigate loudly enough, you may be hanging around the wrong group.

Just don’t demand that everyone you work with be equally intolerant of behavior like that. Forgive your friends if some of them suggest that maybe Group X wasn’t so awful after all . . .

319
Your Price for Joining

In the Ultimatum Game, the first player chooses how to split $10 between themselves and the second player, and the second player decides whether to accept the split or reject it—in the latter case, both parties get nothing. So far as conventional causal decision theory goes (two-box on Newcomb’s Problem, defect in Prisoner’s Dilemma), the second player should prefer any non-zero amount to nothing. But if the first player expects this behavior—accept any non-zero offer—then they have no motive to offer more than a penny. As I assume you all know by now, I am no fan of conventional causal decision theory. Those of us who remain interested in cooperating on the Prisoner’s Dilemma, either because it’s iterated, or because we have a term in our utility function for fairness, or because we use an unconventional decision theory, may also not accept an offer of one penny.

And in fact, most Ultimatum “deciders” offer an even split; and most Ultimatum “accepters” reject any offer less than 20%. A 100 USD game played in Indonesia (average per capita income at the time: 670 USD) showed offers of 30 USD being turned down, although this equates to two week’s wages. We can probably also assume that the players in Indonesia were not thinking about the academic debate over Newcomblike problems—this is just the way people feel about Ultimatum Games, even ones played for real money.

There’s an analogue of the Ultimatum Game in group coordination. (Has it been studied? I’d hope so . . .) Let’s say there’s a common project—in fact, let’s say that it’s an altruistic common project, aimed at helping mugging victims in Canada, or something. If you join this group project, you’ll get more done than you could on your own, relative to your utility function. So, obviously, you should join.

But wait! The anti-mugging project keeps their funds invested in a money market fund! That’s ridiculous; it won’t earn even as much interest as US Treasuries, let alone a dividend-paying index fund.

Clearly, this project is run by morons, and you shouldn’t join until they change their malinvesting ways.

Now you might realize—if you stopped to think about it—that all things considered, you would still do better by working with the common anti-mugging project, than striking out on your own to fight crime. But then—you might perhaps also realize—if you too easily assent to joining the group, why, what motive would they have to change their malinvesting ways?

Well . . . Okay, look. Possibly because we’re out of the ancestral environment where everyone knows everyone else . . . and possibly because the nonconformist crowd tries to repudiate normal group-cohering forces like conformity and leader-worship . . .

. . . It seems to me that people in the atheist libertarian technophile science fiction fan etc. cluster often set their joining prices way way way too high. Like a 50-way split Ultimatum game, where every one of 50 players demands at least 20% of the money.

If you think how often situations like this would have arisen in the ancestral environment, then it’s almost certainly a matter of evolutionary psychology. System 1 emotions, not System 2 calculation. Our intuitions for when to join groups, versus when to hold out for more concessions to our own preferred way of doing things, would have been honed for hunter-gatherer environments of, e.g., 40 people, all of whom you knew personally.

And if the group is made up of 1,000 people? Then your hunter-gatherer instincts will underestimate the inertia of a group so large, and demand an unrealistically high price (in strategic shifts) for you to join. There’s a limited amount of organizational effort, and a limited number of degrees of freedom, that can go into doing things any one person’s way.

And if the strategy is large and complex, the sort of thing that takes e.g. ten people doing paperwork for a week, rather than being hammered out over a half-hour of negotiation around a campfire? Then your hunter-gatherer instincts will underestimate the inertia of the group, relative to your own demands.

And if you live in a wider world than a single hunter-gatherer tribe, so that you only see the one group representative who negotiates with you, and not the hundred other negotiations that have taken place already? Then your instincts will tell you that it is just one person, a stranger at that, and the two of you are equals; whatever ideas they bring to the table are equal with whatever ideas you bring to the table, and the meeting point ought to be about even.

And if you suffer from any weakness of will or akrasia, or if you are influenced by motives other than those you would admit to yourself that you are influenced by, then any group-altruistic project that does not offer you the rewards of status and control may perhaps find itself underserved by your attentions.

Now I do admit that I speak here primarily from the perspective of someone who goes around trying to herd cats; and not from the other side as someone who spends most of their time withholding their energies in order to blackmail those damned morons already on the project. Perhaps I am a little prejudiced.

But it seems to me that a reasonable rule of thumb might be as follows:

If, on the whole, joining your efforts to a group project would still have a net positive effect according to your utility function—

(or a larger positive effect than any other marginal use to which you could otherwise put those resources, although this latter mode of thinking seems little-used and humanly-unrealistic, for reasons I may write about some other time)

—and the awful horrible annoying issue is not so important that you personally will get involved deeply enough to put in however many hours, weeks, or years may be required to get it fixed up—

—then the issue is not worth you withholding your energies from the project; either instinctively until you see that people are paying attention to you and respecting you, or by conscious intent to blackmail the group into getting it done.

And if the issue is worth that much to you . . . then by all means, join the group and do whatever it takes to get things fixed up.

Now, if the existing contributors refuse to let you do this, and a reasonable third party would be expected to conclude that you were competent enough to do it, and there is no one else whose ox is being gored thereby, then, perhaps, we have a problem on our hands. And it may be time for a little blackmail, if the resources you can conditionally commit are large enough to get their attention.

Is this rule a little extreme? Oh, maybe. There should be a motive for the decision-making mechanism of a project to be responsible to its supporters; unconditional support would create its own problems.

But usually . . . I observe that people underestimate the costs of what they ask for, or perhaps just act on instinct, and set their prices way way way too high. If the nonconformist crowd ever wants to get anything done together, we need to move in the direction of joining groups and staying there at least a little more easily. Even in the face of annoyances and imperfections! Even in the face of unresponsiveness to our own better ideas!

In the age of the Internet and in the company of nonconformists, it does get a little tiring reading the 451st public email from someone saying that the Common Project isn’t worth their resources until the website has a sans-serif font.

Of course this often isn’t really about fonts. It may be about laziness, akrasia, or hidden rejections. But in terms of group norms . . . in terms of what sort of public statements we respect, and which excuses we publicly scorn . . . we probably do want to encourage a group norm of:

If the issue isn’t worth your personally fixing by however much effort it takes, and it doesn’t arise from outright bad faith, it’s not worth refusing to contribute your efforts to a cause you deem worthwhile.

320
Can Humanism Match Religion’s Output?

Perhaps the single largest voluntary institution of our modern world—bound together not by police and taxation, not by salaries and managers, but by voluntary donations flowing from its members—is the Catholic Church.

It’s too large to be held together by individual negotiations, like a group task in a hunter-gatherer band. But in a larger world with more people to be infected and faster transmission, we can expect more virulent memes. The Old Testament doesn’t talk about Hell, but the New Testament does. The Catholic Church is held together by affective death spirals—around the ideas, the institutions, and the leaders. By promises of eternal happiness and eternal damnation—theologians don’t really believe that stuff, but many ordinary Catholics do. By simple conformity of people meeting in person at a Church and being subjected to peer pressure. Et cetera.

We who have the temerity to call ourselves “rationalists” think ourselves too good for such communal bindings.

And so anyone with a simple and obvious charitable project—responding with food and shelter to a tidal wave in Thailand, say—would be better off by far pleading with the Pope to mobilize the Catholics, rather than with Richard Dawkins to mobilize the atheists.

For so long as this is true, any increase in atheism at the expense of Catholicism will be something of a hollow victory, regardless of all other benefits.

True, the Catholic Church also goes around opposing the use of condoms in AIDS-ravaged Africa. True, they waste huge amounts of the money they raise on all that religious stuff. Indulging in unclear thinking is not harmless; prayer comes with a price.

To refrain from doing damaging things is a true victory for a rationalist . . .

Unless it is your only victory, in which case it seems a little empty.

If you discount all harm done by the Catholic Church, and look only at the good . . . then does the average Catholic do more gross good than the average atheist, just by virtue of being more active?

Perhaps if you are wiser but less motivated, you can search out interventions of high efficiency and purchase utilons on the cheap . . . But there are few of us who really do that, as opposed to planning to do it someday.

Now you might at this point throw up your hands, saying: “For so long as we don’t have direct control over our brain’s motivational circuitry, it’s not realistic to expect a rationalist to be as strongly motivated as someone who genuinely believes that they’ll burn eternally in hell if they don’t obey.”

This is a fair point. Any folk theorem to the effect that a rational agent should do at least as well as a non-rational agent will rely on the assumption that the rational agent can always just implement whatever “irrational” policy is observed to win. But if you can’t choose to have unlimited mental energy, then it may be that some false beliefs are, in cold fact, more strongly motivating than any available true beliefs. And if we all generally suffer from altruistic akrasia, being unable to bring ourselves to help as much as we think we should, then it is possible for the God-fearing to win the contest of altruistic output.

But though it is a motivated continuation, let us consider this question a little further.

Even the fear of hell is not a perfect motivator. Human beings are not given so much slack on evolution’s leash; we can resist motivation for a short time, but then we run out of mental energy (hat tip: infotropism). Even believing that you’ll go to hell does not change this brute fact about brain circuitry. So the religious sin, and then are tormented by thoughts of going to hell, in much the same way that smokers reproach themselves for being unable to quit.

If a group of rationalists cared a lot about something . . . who says they wouldn’t be able to match the real, de-facto output of a believing Catholic? The stakes might not be “infinite” happiness or “eternal” damnation, but of course the brain can’t visualize 3 ↑↑↑ 3, let alone infinity. Who says that the actual quantity of caring neurotransmitters discharged by the brain (as ’twere) has to be so much less for “the growth and flowering of humankind” or even “tidal-wave-stricken Thais,” than for “eternal happiness in Heaven”? Anything involving more than 100 people is going to involve utilities too large to visualize. And there are all sorts of other standard biases at work here; knowing about them might be good for a bonus as well, one hopes?

Cognitive-behavioral therapy and Zen meditation are two mental disciplines experimentally shown to yield real improvements. It is not the area of the art I’ve focused on developing, but then I don’t have a real martial art of rationality in back of me. If you combine a purpose genuinely worth caring about with discipline extracted from CBT and Zen meditation, then who says rationalists can’t keep up? Or even more generally: if we have an evidence-based art of fighting akrasia, with experiments to see what actually works, then who says we’ve got to be less motivated than some disorganized mind that fears God’s wrath?

Still . . . that’s a further-future speculation that it might be possible to develop an art that doesn’t presently exist. It’s not a technique I can use right now. I present it just to illustrate the idea of not giving up so fast on rationality: Understanding what’s going wrong, trying intelligently to fix it, and gathering evidence on whether it worked—this is a powerful idiom, not to be lightly dismissed upon sighting the first disadvantage.

Really, I suspect that what’s going on here has less to do with the motivating power of eternal damnation, and a lot more to do with the motivating power of physically meeting other people who share your cause. The power, in other words, of being physically present at church and having religious neighbors.

This is a problem for the rationalist community in its present stage of growth, because we are rare and geographically distributed way the hell all over the place. If all the readers of Less Wrong lived within a five-mile radius of each other, I bet we’d get a lot more done, not for reasons of coordination but just sheer motivation.

I’ll write later about some long-term, starry-eyed, idealistic thoughts on this particular problem. Shorter-term solutions that don’t rely on our increasing our numbers by a factor of 100 would be better. I wonder in particular whether the best modern videoconferencing software would provide some of the motivating effect of meeting someone in person; I suspect the answer is “no” but it might be worth trying.

Meanwhile . . . in the short term, we’re stuck fighting akrasia mostly without the reinforcing physical presense of other people who care. I want to say something like “This is difficult, but it can be done,” except I’m not sure that’s even true.

I suspect that the largest step rationalists could take toward matching the per-capita power output of the Catholic Church would be to have regular physical meetings of people contributing to the same task—just for purposes of motivation.

In the absence of that . . .

We could try for a group norm of being openly allowed—nay, applauded—for caring strongly about something. And a group norm of being expected to do something useful with your life—contribute your part to cleaning up this world. Religion doesn’t really emphasize the getting-things-done aspect as much.

And if rationalists could match just half the average altruistic effort output per Catholic, then I don’t think it’s remotely unrealistic to suppose that with better targeting on more efficient causes, the modal rationalist could get twice as much done.

How much of its earnings does the Catholic Church spend on all that useless religious stuff instead of actually helping people? More than 50%, I would venture. So then we could say—with a certain irony, though that’s not quite the spirit in which we should be doing things—that we should try to propagate a group norm of donating a minimum of 5% of income to real causes. (10% being the usual suggested minimum religious tithe.) And then there’s the art of picking causes for which expected utilons are orders of magnitude cheaper (for so long as the inefficient market in utilons lasts).

But long before we can begin to dream of any such boast, we secular humanists need to work on at least matching the per capita benevolent output of the worshippers.

321
Church vs. Taskforce

I am generally suspicious of envying crazy groups or trying to blindly copycat the rhythm of religion—what I called “hymns to the nonexistence of God,” replying, “A good ‘atheistic hymn’ is simply a song about anything worth singing about that doesn’t happen to be religious.”

But religion does fill certain holes in people’s minds, some of which are even worth filling. If you eliminate religion, you have to be aware of what gaps are left behind.

If you suddenly deleted religion from the world, the largest gap left would not be anything of ideals or morals; it would be the church, the community. Among those who now stay religious without quite really believing in God—how many are just sticking to it from wanting to stay with their neighbors at the church, and their family and friends? How many would convert to atheism, if all those others deconverted, and that were the price of staying in the community and keeping its respect? I would guess . . . probably quite a lot.

In truth . . . this is probably something I don’t understand all that well, myself. “Brownies and babysitting” were the first two things that came to mind. Do churches lend helping hands in emergencies? Or just a shoulder to cry on? How strong is a church community? It probably depends on the church, and in any case, that’s not the correct question. One should start by considering what a hunter-gatherer band gives its people, and ask what’s missing in modern life—if a modern First World church fills only some of that, then by all means let us try to do better.

So without copycatting religion—without assuming that we must gather every Sunday morning in a building with stained-glass windows while the children dress up in formal clothes and listen to someone sing—let’s consider how to fill the emotional gap, after religion stops being an option.

To help break the mold to start with—the straitjacket of cached thoughts on how to do this sort of thing—consider that some modern offices may also fill the same role as a church. By which I mean that some people are fortunate to receive community from their workplaces: friendly coworkers who bake brownies for the office, whose teenagers can be safely hired for babysitting, and maybe even help in times of catastrophe . . . ? But certainly not everyone is lucky enough to find a community at the office.

Consider further—a church is ostensibly about worship, and a workplace is ostensibly about the commercial purpose of the organization. Neither has been carefully optimized to serve as a community.

Looking at a typical religious church, for example, you could suspect—although all of these things would be better tested experimentally, than just suspected—

That getting up early on a Sunday morning is not optimal;
That wearing formal clothes is not optimal, especially for children;
That listening to the same person give sermons on the same theme every week (“religion”) is not optimal;
That the cost of supporting a church and a pastor is expensive, compared to the number of different communities who could time-share the same building for their gatherings;
That they probably don’t serve nearly enough of a matchmaking purpose, because churches think they’re supposed to enforce their medieval moralities;
That the whole thing ought to be subject to experimental data-gathering to find out what works and what doesn’t.

By using the word “optimal” above, I mean “optimal under the criteria you would use if you were explicitly building a community qua community.” Spending lots of money on a fancy church with stained-glass windows and a full-time pastor makes sense if you actually want to spend money on religion qua religion.

I do confess that when walking past the churches of my city, my main thought is, “These buildings look really, really expensive, and there are too many of them.” If you were doing it over from scratch . . . then you might have a big building that could be used for the occasional wedding, but it would be time-shared for different communities meeting at different times on the weekend, and it would also have a nice large video display that could be used for speakers giving presentations, lecturers teaching something, or maybe even showing movies. Stained glass? Not so high a priority.

Or to the extent that the church membership lends a helping hand in times of trouble—could that be improved by an explicit rainy-day fund or contracting with an insurer, once you realized that this was an important function? Possibly not; dragging explicit finance into things changes their character oddly. Conversely, maybe keeping current on some insurance policies should be a requirement for membership, lest you rely too much on the community . . . But again, to the extent that churches provide community, they’re trying to do it without actually admitting that this is nearly all of what people get out of it. Same thing with the corporations whose workplaces are friendly enough to serve as communities; it’s still something of an accidental function.

Once you start thinking explicitly about how to give people a hunter-gatherer band to belong to, you can see all sorts of things that sound like good ideas. Should you welcome the newcomer in your midst? The pastor may give a sermon on that sometime, if you think church is about religion. But if you’re explicitly setting out to build community—then right after a move is when someone most lacks community, when they most need your help. It’s also an opportunity for the band to grow. If anything, tribes ought to be competing at quarterly exhibitions to capture newcomers.

But can you really have a community that’s just a community—that isn’t also an office or a religion? A community with no purpose beyond itself?

Maybe you can. After all, did hunter-gatherer tribes have any purposes beyond themselves?—well, there was survival and feeding yourselves, that was a purpose.

But anything that people have in common, especially any goal they have in common, tends to want to define a community. Why not take advantage of that?

Though in this age of the Internet, alas, too many binding factors have supporters too widely distributed to form a decent band—if you’re the only member of the Church of the Subgenius in your city, it may not really help much. It really is different without the physical presence; the Internet does not seem to be an acceptable substitute at the current stage of the technology.

So to skip right to the point—

Should the Earth last so long, I would like to see, as the form of rationalist communities, taskforces focused on all the work that needs doing to fix up this world. Communities in any geographic area would form around the most specific cluster that could support a decent-sized band. If your city doesn’t have enough people in it for you to find 50 fellow Linux programmers, you might have to settle for 15 fellow open-source programmers . . . or in the days when all of this is only getting started, 15 fellow rationalists trying to spruce up the Earth in their assorted ways.

That’s what I think would be a fitting direction for the energies of communities, and a common purpose that would bind them together. Tasks like that need communities anyway, and this Earth has plenty of work that needs doing, so there’s no point in waste. We have so much that needs doing—let the energy that was once wasted into the void of religious institutions, find an outlet there. And let purposes admirable without need for delusion fill any void in the community structure left by deleting religion and its illusionary higher purposes.

Strong communities built around worthwhile purposes: That would be the shape I would like to see for the post-religious age, or whatever fraction of humanity has then gotten so far in their lives.

Although . . . as long as you’ve got a building with a nice large high-resolution screen anyway, I wouldn’t mind challenging the idea that all post-adulthood learning has to take place in distant expensive university campuses with teachers who would rather be doing something else. And it’s empirically the case that colleges seem to support communities quite well. So in all fairness, there are other possibilities for things you could build a post-theistic community around.

Is all of this just a dream? Maybe. Probably. It’s not completely devoid of incremental implementability, if you’ve got enough rationalists in a sufficiently large city who have heard of the idea. But on the off chance that rationality should catch on so widely, or the Earth should last so long, and that my voice should be heard, then that is the direction I would like to see things moving in—as the churches fade, we don’t need artificial churches, but we do need new idioms of community.

322
Rationality: Common Interest of Many Causes

It is a not-so-hidden agenda of Less Wrong that there are many causes that benefit from the spread of rationality—because it takes a little more rationality than usual to see their case as a supporter, or even just as a supportive bystander. Not just the obvious causes like atheism, but things like marijuana legalization—where you could wish that people were a bit more self-aware about their motives and the nature of signaling, and a bit more moved by inconvenient cold facts. The Machine Intelligence Research Institute was merely an unusually extreme case of this, wherein it got to the point that after years of bogging down I threw up my hands and explicitly recursed on the job of creating rationalists.

But of course, not all the rationalists I create will be interested in my own project—and that’s fine. You can’t capture all the value you create, and trying can have poor side effects.

If the supporters of other causes are enlightened enough to think similarly . . .

Then all the causes that benefit from spreading rationality can, perhaps, have something in the way of standardized material to which to point their supporters—a common task, centralized to save effort—and think of themselves as spreading a little rationality on the side. They won’t capture all the value they create. And that’s fine. They’ll capture some of the value others create. Atheism has very little to do directly with marijuana legalization, but if both atheists and anti-Prohibitionists are willing to step back a bit and say a bit about the general, abstract principle of confronting a discomforting truth that interferes with a fine righteous tirade, then both atheism and marijuana legalization pick up some of the benefit from both efforts.

But this requires—I know I’m repeating myself here, but it’s important—that you be willing not to capture all the value you create. It requires that, in the course of talking about rationality, you maintain an ability to temporarily shut up about your own cause even though it is the best cause ever. It requires that you don’t regard those other causes, and they do not regard you, as competing for a limited supply of rationalists with a limited capacity for support; but, rather, creating more rationalists and increasing their capacity for support. You only reap some of your own efforts, but you reap some of others’ efforts as well.

If you and they don’t agree on everything—especially priorities—you have to be willing to agree to shut up about the disagreement. (Except possibly in specialized venues, out of the way of the mainstream discourse, where such disagreements are explicitly prosecuted.)

A certain person who was taking over as the president of a certain organization once pointed out that the organization had not enjoyed much luck with its message of “This is the best thing you can do,” as compared to e.g. the X-Prize Foundation’s tremendous success conveying to rich individuals “Here is a cool thing you can do.”

This is one of those insights where you blink incredulously and then grasp how much sense it makes. The human brain can’t grasp large stakes, and people are not anything remotely like expected utility maximizers, and we are generally altruistic akrasics. Saying, “This is the best thing” doesn’t add much motivation beyond “This is a cool thing.” It just establishes a much higher burden of proof. And invites invidious motivation-sapping comparison to all other good things you know (perhaps threatening to diminish moral satisfaction already purchased).

If we’re operating under the assumption that everyone by default is an altruistic akrasic (someone who wishes they could choose to do more)—or at least, that most potential supporters of interest fit this description—then fighting it out over which cause is the best to support may have the effect of decreasing the overall supply of altruism.

“But,” you say, “dollars are fungible; a dollar you use for one thing indeed cannot be used for anything else!” To which I reply: But human beings really aren’t expected utility maximizers, as cognitive systems. Dollars come out of different mental accounts, cost different amounts of willpower (the true limiting resource) under different circumstances. People want to spread their donations around as an act of mental accounting to minimize the regret if a single cause fails, and telling someone about an additional cause may increase the total amount they’re willing to help.

There are, of course, limits to this principle of benign tolerance. If someone’s pet project is to teach salsa dance, it would be quite a stretch to say they’re working on a worthy sub-task of the great common Neo-Enlightenment project of human progress.

But to the extent that something really is a task you would wish to see done on behalf of humanity . . . then invidious comparisons of that project to Your-Favorite-Project may not help your own project as much as you might think. We may need to learn to say, by habit and in nearly all forums, “Here is a cool rationalist project,” not, “Mine alone is the highest-return in expected utilons per marginal dollar project.” If someone cold-blooded enough to maximize expected utility of fungible money without regard to emotional side effects explicitly asks, we could perhaps steer them to a specialized subforum where anyone willing to make the claim of top priority fights it out. Though if all goes well, those projects that have a strong claim to this kind of underserved-ness will get more investment and their marginal returns will go down, and the winner of the competing claims will no longer be clear.

If there are many rationalist projects that benefit from raising the sanity waterline, then their mutual tolerance and common investment in spreading rationality could conceivably exhibit a commons problem. But this doesn’t seem too hard to deal with: if there’s a group that’s not willing to share the rationalists they create or mention to them that other Neo-Enlightenment projects might exist, then any common, centralized rationalist resources could remove the mention of their project as a cool thing to do.

Though all this is an idealistic and future-facing thought, the benefits—for all of us—could be finding some important things we’re missing right now. So many rationalist projects have few supporters and far-flung; if we could all identify as elements of the Common Project of human progress, the Neo-Enlightenment, there would be a substantially higher probability of finding ten of us in any given city. Right now, a lot of these projects are just a little lonely for their supporters. Rationality may not be the most important thing in the world—that, of course, is the thing that we protect—but it is a cool thing that more of us have in common. We might gain much from identifying ourselves also as rationalists.

323
Helpless Individuals

When you consider that our grouping instincts are optimized for 50-person hunter-gatherer bands where everyone knows everyone else, it begins to seem miraculous that modern-day large institutions survive at all.

Well—there are governments with specialized militaries and police, which can extract taxes. That’s a non-ancestral idiom which dates back to the invention of sedentary agriculture and extractible surpluses; humanity is still struggling to deal with it.

There are corporations in which the flow of money is controlled by centralized management, a non-ancestral idiom dating back to the invention of large-scale trade and professional specialization.

And in a world with large populations and close contact, memes evolve far more virulent than the average case of the ancestral environment; memes that wield threats of damnation, promises of heaven, and professional priest classes to transmit them.

But by and large, the answer to the question “How do large institutions survive?” is “They don’t!” The vast majority of large modern-day institutions—some of them extremely vital to the functioning of our complex civilization—simply fail to exist in the first place.

I first realized this as a result of grasping how Science gets funded: namely, not by individual donations.

Science traditionally gets funded by governments, corporations, and large foundations. I’ve had the opportunity to discover firsthand that it’s amazingly difficult to raise money for Science from individuals. Not unless it’s science about a disease with gruesome victims, and maybe not even then.

Why? People are, in fact, prosocial; they give money to, say, puppy pounds. Science is one of the great social interests, and people are even widely aware of this—why not Science, then?

Any particular science project—say, studying the genetics of trypanotolerance in cattle—is not a good emotional fit for individual charity. Science has a long time horizon that requires continual support. The interim or even final press releases may not sound all that emotionally arousing. You can’t volunteer; it’s a job for specialists. Being shown a picture of the scientist you’re supporting at or somewhat below the market price for their salary lacks the impact of being shown the wide-eyed puppy that you helped usher to a new home. You don’t get the immediate feedback and the sense of immediate accomplishment that’s required to keep an individual spending their own money.

Ironically, I finally realized this, not from my own work, but from thinking “Why don’t Seth Roberts’s readers come together to support experimental tests of Roberts’s hypothesis about obesity? Why aren’t individual philanthropists paying to test Bussard’s polywell fusor?” These are examples of obviously ridiculously underfunded science, with applications (if true) that would be relevant to many, many individuals. That was when it occurred to me that, in full generality, Science is not a good emotional fit for people spending their own money.

In fact very few things are, with the individuals we have now. It seems to me that this is key to understanding how the world works the way it does—why so many individual interests are poorly protected—why 200 million adult Americans have such tremendous trouble supervising the 535 members of Congress, for example.

So how does Science actually get funded? By governments that think they ought to spend some amount of money on Science, with legislatures or executives deciding to do so—it’s not quite their own money they’re spending. Sufficiently large corporations decide to throw some amount of money at blue-sky R&D. Large grassroots organizations built around affective death spirals may look at science that suits their ideals. Large private foundations, based on money block-allocated by wealthy individuals to their reputations, spend money on Science that promises to sound very charitable, sort of like allocating money to orchestras or modern art. And then the individual scientists (or individual scientific task-forces) fight it out for control of that pre-allocated money supply, given into the hands of grant committee members who seem like the sort of people who ought to be judging scientists.

You rarely see a scientific project making a direct bid for some portion of society’s resource flow; rather, it first gets allocated to Science, and then scientists fight over who actually gets it. Even the exceptions to this rule are more likely to be driven by politicians (moonshot) or military purposes (Manhattan project) than by the appeal of scientists to the public.

Now I’m sure that if the general public were in the habit of funding particular science by individual donations, a whole lotta money would be wasted on e.g. quantum gibberish—assuming that the general public somehow acquired the habit of funding science without changing any other facts about the people or the society.

But it’s still an interesting point that Science manages to survive not because it is in our collective individual interest to see Science get done, but rather, because Science has fastened itself as a parasite onto the few forms of large organization that can exist in our world. There are plenty of other projects that simply fail to exist in the first place.

It seems to me that modern humanity manages to put forth very little in the way of coordinated effort to serve collective individual interests. It’s just too non-ancestral a problem when you scale to more than 50 people. There are only big taxers, big traders, supermemes, occasional individuals of great power; and a few other organizations, like Science, that can fasten parasitically onto them.

324
Money: The Unit of Caring

Steve Omohundro has suggested a folk theorem to the effect that, within the interior of any approximately rational self-modifying agent, the marginal benefit of investing additional resources in anything ought to be about equal. Or, to put it a bit more exactly, shifting a unit of resource between any two tasks should produce no increase in expected utility, relative to the agent’s utility function and its probabilistic expectations about its own algorithms.

This resource balance principle implies that—over a very wide range of approximately rational systems, including even the interior of a self-modifying mind—there will exist some common currency of expected utilons, by which everything worth doing can be measured.

In our society, this common currency of expected utilons is called “money.” It is the measure of how much society cares about something.

This is a brutal yet obvious point, which many are motivated to deny.

With this audience, I hope, I can simply state it and move on. It’s not as if you thought “society” was intelligent, benevolent, and sane up until this point, right?

I say this to make a certain point held in common across many good causes. Any charitable institution you’ve ever had a kind word for, certainly wishes you would appreciate this point, whether or not they’ve ever said anything out loud. For I have listened to others in the nonprofit world, and I know that I am not speaking only for myself here . . .

Many people, when they see something that they think is worth doing, would like to volunteer a few hours of spare time, or maybe mail in a five-year-old laptop and some canned goods, or walk in a march somewhere, but at any rate, not spend money.

Believe me, I understand the feeling. Every time I spend money I feel like I’m losing hit points. That’s the problem with having a unified quantity describing your net worth: Seeing that number go down is not a pleasant feeling, even though it has to fluctuate in the ordinary course of your existence. There ought to be a fun-theoretic principle against it.

But, well . . .

There is this very, very old puzzle/observation in economics about the lawyer who spends an hour volunteering at the soup kitchen, instead of working an extra hour and donating the money to hire someone to work for five hours at the soup kitchen.

There’s this thing called “Ricardo’s Law of Comparative Advantage.” There’s this idea called “professional specialization.” There’s this notion of “economies of scale.” There’s this concept of “gains from trade.” The whole reason why we have money is to realize the tremendous gains possible from each of us doing what we do best.

This is what grownups do. This is what you do when you want something to actually get done. You use money to employ full-time specialists.

Yes, people are sometimes limited in their ability to trade time for money (underemployed), so that it is better for them if they can directly donate that which they would usually trade for money. If the soup kitchen needed a lawyer, and the lawyer donated a large contiguous high-priority block of lawyering, then that sort of volunteering makes sense—that’s the same specialized capability the lawyer ordinarily trades for money. But “volunteering” just one hour of legal work, constantly delayed, spread across three weeks in casual minutes between other jobs? This is not the way something gets done when anyone actually cares about it, or to state it near-equivalently, when money is involved.

To the extent that individuals fail to grasp this principle on a gut level, they may think that the use of money is somehow optional in the pursuit of things that merely seem morally desirable—as opposed to tasks like feeding ourselves, whose desirability seems to be treated oddly differently. This factor may be sufficient by itself to prevent us from pursuing our collective common interest in groups larger than 40 people.

Economies of trade and professional specialization are not just vaguely good yet unnatural-sounding ideas, they are the only way that anything ever gets done in this world. Money is not pieces of paper, it is the common currency of caring.

Hence the old saying: “Money makes the world go ‘round, love barely keeps it from blowing up.”

Now, we do have the problem of akrasia—of not being able to do what we’ve decided to do—which is a part of the art of rationality that I hope someone else will develop; I specialize more in the impossible questions business. And yes, spending money is more painful than volunteering, because you can see the bank account number go down, whereas the remaining hours of our span are not visibly numbered. But when it comes time to feed yourself, do you think, “Hm, maybe I should try raising my own cattle, that’s less painful than spending money on beef?” Not everything can get done without invoking Ricardo’s Law; and on the other end of that trade are people who feel just the same pain at the thought of having less money.

It does seem to me offhand that there ought to be things doable to diminish the pain of losing hit points, and to increase the felt strength of the connection from donating money to “I did a good thing!” Some of that I am trying to accomplish right now, by emphasizing the true nature and power of money; and by inveighing against the poisonous meme saying that someone who gives mere money must not care enough to get personally involved. This is a mere reflection of a mind that doesn’t understand the post-hunter-gatherer concept of a market economy. The act of donating money is not the momentary act of writing the check; it is the act of every hour you spent to earn the money to write that check—just as though you worked at the charity itself in your professional capacity, at maximum, grownup efficiency.

If the lawyer needs to work an hour at the soup kitchen to keep themselves motivated and remind themselves why they’re doing what they’re doing, that’s fine. But they should also be donating some of the hours they worked at the office, because that is the power of professional specialization. One might consider the check as buying the right to volunteer at the soup kitchen, or validating the time spent at the soup kitchen. More on this later.

To a first approximation, money is the unit of caring up to a positive scalar factor—the unit of relative caring. Some people are frugal and spend less money on everything; but if you would, in fact, spend $5 on a burrito, then whatever you will not spend $5 on, you care about less than you care about the burrito. If you don’t spend two months’ salary on a diamond ring, it doesn’t mean you don’t love your Significant Other. (“De Beers: It’s Just A Rock.”) But conversely, if you’re always reluctant to spend any money on your Significant Other, and yet seem to have no emotional problems with spending $1,000 on a flat-screen TV, then yes, this does say something about your relative values.

Yes, frugality is a virtue. Yes, spending money hurts. But in the end, if you are never willing to spend any units of caring, it means you don’t care.

325
Purchase Fuzzies and Utilons Separately

Previously:

There is this very, very old puzzle/observation in economics about the lawyer who spends an hour volunteering at the soup kitchen, instead of working an extra hour and donating the money to hire someone . . .

If the lawyer needs to work an hour at the soup kitchen to keep themselves motivated and remind themselves why they’re doing what they’re doing, that’s fine. But they should also be donating some of the hours they worked at the office, because that is the power of professional specialization. One might consider the check as buying the right to volunteer at the soup kitchen, or validating the time spent at the soup kitchen. More on this later.

I hold open doors for little old ladies. I can’t actually remember the last time this happened literally (though I’m sure it has, sometime in the last year or so). But within the last month, say, I was out on a walk and discovered a station wagon parked in a driveway with its trunk completely open, giving full access to the car’s interior. I looked in to see if there were packages being taken out, but this was not so. I looked around to see if anyone was doing anything with the car. And finally I went up to the house and knocked, then rang the bell. And yes, the trunk had been accidentally left open.

Under other circumstances, this would be a simple act of altruism, which might signify true concern for another’s welfare, or fear of guilt for inaction, or a desire to signal trustworthiness to oneself or others, or finding altruism pleasurable. I think that these are all perfectly legitimate motives, by the way; I might give bonus points for the first, but I wouldn’t deduct any penalty points for the others. Just so long as people get helped.

But in my own case, since I already work in the nonprofit sector, the further question arises as to whether I could have better employed the same sixty seconds in a more specialized way, to bring greater benefit to others. That is: can I really defend this as the best use of my time, given the other things I claim to believe?

The obvious defense—or, perhaps, obvious rationalization—is that an act of altruism like this one acts as a willpower restorer, much more efficiently than, say, listening to music. I also mistrust my ability to be an altruist only in theory; I suspect that if I walk past problems, my altruism will start to fade. I’ve never pushed that far enough to test it; it doesn’t seem worth the risk.

But if that’s the defense, then my act can’t be defended as a good deed, can it? For these are self-directed benefits that I list.

Well—who said that I was defending the act as a selfless good deed? It’s a selfish good deed. If it restores my willpower, or if it keeps me altruistic, then there are indirect other-directed benefits from that (or so I believe). You could, of course, reply that you don’t trust selfish acts that are supposed to be other-benefiting as an “ulterior motive”; but then I could just as easily respond that, by the same principle, you should just look directly at the original good deed rather than its supposed ulterior motive.

Can I get away with that? That is, can I really get away with calling it a “selfish good deed,” and still derive willpower restoration therefrom, rather than feeling guilt about its being selfish? Apparently I can. I’m surprised it works out that way, but it does. So long as I knock to tell them about the open trunk, and so long as the one says “Thank you!,” my brain feels like it’s done its wonderful good deed for the day.

Your mileage may vary, of course. The problem with trying to work out an art of willpower restoration is that different things seem to work for different people. (That is: We’re probing around on the level of surface phenomena without understanding the deeper rules that would also predict the variations.)

But if you find that you are like me in this aspect—that selfish good deeds still work—then I recommend that you purchase warm fuzzies and utilons separately. Not at the same time. Trying to do both at the same time just means that neither ends up done well. If status matters to you, purchase status separately too!

If I had to give advice to some new-minted billionaire entering the realm of charity, my advice would go something like this:

To purchase warm fuzzies, find some hard-working but poverty-stricken woman who’s about to drop out of state college after her husband’s hours were cut back, and personally, but anonymously, give her a cashier’s check for $10,000. Repeat as desired.
To purchase status among your friends, donate $100,000 to the current sexiest X-Prize, or whatever other charity seems to offer the most stylishness for the least price. Make a big deal out of it, show up for their press events, and brag about it for the next five years.
Then—with absolute cold-blooded calculation—without scope insensitivity or ambiguity aversion—without concern for status or warm fuzzies—figuring out some common scheme for converting outcomes to utilons, and trying to express uncertainty in percentage probabilities—find the charity that offers the greatest expected utilons per dollar. Donate up to however much money you wanted to give to charity, until their marginal efficiency drops below that of the next charity on the list.

I would furthermore advise the billionaire that what they spend on utilons should be at least, say, 20 times what they spend on warm fuzzies—5% overhead on keeping yourself altruistic seems reasonable, and I, your dispassionate judge, would have no trouble validating the warm fuzzies against a multiplier that large. Save that the original fuzzy act really should be helpful rather than actively harmful.

(Purchasing status seems to me essentially unrelated to altruism. If giving money to the X-Prize gets you more awe from your friends than an equivalently priced speedboat, then there’s really no reason to buy the speedboat. Just put the money under the “impressing friends” column, and be aware that this is not the “altruism” column.)

But the main lesson is that all three of these things—warm fuzzies, status, and expected utilons—can be bought far more efficiently when you buy separately, optimizing for only one thing at a time. Writing a check for $10,000,000 to a breast-cancer charity—while far more laudable than spending the same $10,000,000 on, I don’t know, parties or something—won’t give you the concentrated euphoria of being present in person when you turn a single human’s life around, probably not anywhere close. It won’t give you as much to talk about at parties as donating to something sexy like an X-Prize—maybe a short nod from the other rich. And if you threw away all concern for warm fuzzies and status, there are probably at least a thousand underserved existing charities that could produce orders of magnitude more utilons with ten million dollars. Trying to optimize for all three criteria in one go only ensures that none of them end up optimized very well—just vague pushes along all three dimensions.

Of course, if you’re not a millionaire or even a billionaire—then you can’t be quite as efficient about things, can’t so easily purchase in bulk. But I would still say—for warm fuzzies, find a relatively cheap charity with bright, vivid, ideally in-person and direct beneficiaries. Volunteer at a soup kitchen. Or just get your warm fuzzies from holding open doors for little old ladies. Let that be validated by your other efforts to purchase utilons, but don’t confuse it with purchasing utilons. Status is probably cheaper to purchase by buying nice clothes.

And when it comes to purchasing expected utilons—then, of course, shut up and multiply.

326
Bystander Apathy

The bystander effect, also known as bystander apathy, is that larger groups are less likely to act in emergencies—not just individually, but collectively. Put an experimental subject alone in a room and let smoke start coming up from under the door. Seventy-five percent of the subjects will leave to report it. Now put three subjects in the room—real subjects, none of whom know what’s going on. On only 38% of the occasions will anyone report the smoke. Put the subject with two confederates who ignore the smoke, and they’ll only report it 10% on the time—even staying in the room until it becomes hazy.¹

On the standard model, the two primary drivers of bystander apathy are:

Diffusion of responsibility—everyone hopes that someone else will be first to step up and incur any costs of acting. When no one does act, being part of a crowd provides an excuse and reduces the chance of being held personally responsible for the results.
Pluralistic ignorance—people try to appear calm while looking for cues, and see . . . that the others appear calm.

Cialdini:²

Very often an emergency is not obviously an emergency. Is the man lying in the alley a heart-attack victim or a drunk sleeping one off? . . . In times of such uncertainty, the natural tendency is to look around at the actions of others for clues. We can learn from the way the other witnesses are reacting whether the event is or is not an emergency. What is easy to forget, though, is that everybody else observing the event is likely to be looking for social evidence, too. Because we all prefer to appear poised and unflustered among others, we are likely to search for that evidence placidly, with brief, camouflaged glances at those around us. Therefore everyone is likely to see everyone else looking unruffled and failing to act.

Cialdini suggests that if you’re ever in emergency need of help, you point to one single bystander and ask them for help—making it very clear to whom you’re referring. Remember that the total group, combined, may have less chance of helping than one individual.

I’ve mused a bit on the evolutionary psychology of the bystander effect. Suppose that in the ancestral environment, most people in your band were likely to be at least a little related to you—enough to be worth saving, if you were the only one who could do it. But if there are two others present, then the first person to act incurs a cost, while the other two both reap the genetic benefit of a partial relative being saved. Could there have been an arms race for who waited the longest?

As far as I’ve followed this line of speculation, it doesn’t seem to be a good explanation—at the point where the whole group is failing to act, a gene that helps immediately ought to be able to invade, I would think. The experimental result is not a long wait before helping, but simply failure to help: if it’s a genetic benefit to help when you’re the only person who can do it (as does happen in the experiments) then the group equilibrium should not be no one helping (as happens in the experiments).

So I don’t think an arms race of delay is a plausible evolutionary explanation. More likely, I think, is that we’re looking at a nonancestral problem. If the experimental subjects actually know the apparent victim, the chances of helping go way up (i.e., we’re not looking at the correlate of helping an actual fellow band member). If I recall correctly, if the experimental subjects know each other, the chances of action also go up.

Nervousness about public action may also play a role. If Robin Hanson is right about the evolutionary role of “choking,” then being first to act in an emergency might also be taken as a dangerous bid for high status. (Come to think, I can’t actually recall seeing shyness discussed in analyses of the bystander effect, but that’s probably just my poor memory.)

Can the bystander effect be explained primarily by diffusion of moral responsibility? We could be cynical and suggest that people are mostly interested in not being blamed for not helping, rather than having any positive desire to help—that they mainly wish to escape antiheroism and possible retribution. Something like this may well be a contributor, but two observations that mitigate against it are (a) the experimental subjects did not report smoke coming in from under the door, even though it could well have represented a strictly selfish threat and (b) telling people about the bystander effect reduces the bystander effect, even though they’re no more likely to be held publicly responsible thereby.

In fact, the bystander effect is one of the main cases I recall offhand where telling people about a bias actually seems able to strongly reduce it—maybe because the appropriate way to compensate is so obvious, and it’s not easy to overcompensate (as when you’re trying to e.g. adjust your calibration). So we should be careful not to be too cynical about the implications of the bystander effect and diffusion of responsibility, if we interpret individual action in terms of a cold, calculated attempt to avoid public censure. People seem at least to sometimes hold themselves responsible, once they realize they’re the only ones who know enough about the bystander effect to be likely to act.

Though I wonder what happens if you know that you’re part of a crowd where everyone has been told about the bystander effect . . .

1. Bibb Latané and John M. Darley, “Bystander ‘Apathy,’” American Scientist 57, no. 2 (1969): 244–268, http://www.jstor.org/stable/27828530.

2. Cialdini, Influence.

327
Collective Apathy and the Internet

In the last essay I covered the bystander effect, a.k.a. bystander apathy: given a fixed problem situation, a group of bystanders is actually less likely to act than a single bystander. The standard explanation for this result is in terms of pluralistic ignorance (if it’s not clear whether the situation is an emergency, each person tries to look calm while darting their eyes at the other bystanders, and sees other people looking calm) and diffusion of responsibility (everyone hopes that someone else will be first to act; being part of a crowd diminishes the individual pressure to the point where no one acts).

Which may be a symptom of our hunter-gatherer coordination mechanisms being defeated by modern conditions. You didn’t usually form task-forces with strangers back in the ancestral environment; it was mostly people you knew. And in fact, when all the subjects know each other, the bystander effect diminishes.

So I know this is an amazing and revolutionary observation, and I hope that I don’t kill any readers outright from shock by saying this: but people seem to have a hard time reacting constructively to problems encountered over the Internet.

Perhaps because our innate coordination instincts are not tuned for:

Being part of a group of strangers. (When all subjects know each other, the bystander effect diminishes.)
Being part of a group of unknown size, of strangers of unknown identity.
Not being in physical contact (or visual contact); not being able to exchange meaningful glances.
Not communicating in real time.
Not being much beholden to each other for other forms of help; not being codependent on the group you’re in.
Being shielded from reputational damage, or the fear of reputational damage, by your own apparent anonymity; no one is visibly looking at you, before whom your reputation might suffer from inaction.
Being part of a large collective of other inactives; no one will single out you to blame.
Not hearing a voiced plea for help.

Et cetera. I don’t have a brilliant solution to this problem. But it’s the sort of thing that I would wish for potential dot-com cofounders to ponder explicitly, rather than wondering how to throw sheep on Facebook. (Yes, I’m looking at you, Hacker News.) There are online activism web apps, but they tend to be along the lines of sign this petition! yay, you signed something! rather than how can we counteract the bystander effect, restore motivation, and work with native group-coordination instincts, over the Internet?

Some of the things that come to mind:

Put a video of someone asking for help online.
Put up names and photos or even brief videos if available of the first people who helped (or have some reddit-ish priority algorithm that depends on a combination of amount-helped and recency).
Give helpers a video thank-you from the founder of the cause that they can put up on their “people I’ve helped” page, which with enough standardization could be partially or wholly assembled automatically and easily embedded in their home webpage or Facebook account.
Find a non-annoying idiom for “Tell a friend about cause X”; allow referrer link codes; then show people how many others they’ve evangelized (how many people who initially got here using referrer code X actually contributed or took some other action).
(All of the above applies not just to donations, but to open-source projects to which people have contributed code. Or if people really do want nothing but signatures on a petition, then for signatures. There are ways to help besides money—even though money is usually the most effective. The main thing is that the form of help has to be verifiable online.)
Make it easier for people to offer monetary bounties on subtasks whose performance is verifiable.

But mostly I just hand you an open, unsolved problem: make it possible/easier for groups of strangers to coalesce into an effective task force over the Internet, in defiance of the usual failure modes and the default reasons why this is a non-ancestral problem. Think of that old statistic about Wikipedia representing 1/2,000 of the time spent in the US alone on watching television. There’s quite a lot of fuel out there, if there were only such a thing as an effective engine . . .

328
Incremental Progress and the Valley

Rationality is systematized winning.

“But,” you protest, “the reasonable person doesn’t always win!”

What do you mean by this? Do you mean that every week or two, someone who bought a lottery ticket with negative expected value wins the lottery and becomes much richer than you? That is not a systematic loss; it is selective reporting by the media. From a statistical standpoint, lottery winners don’t exist—you would never encounter one in your lifetime, if it weren’t for the selective reporting.

Even perfectly rational agents can lose. They just can’t know in advance that they’ll lose. They can’t expect to underperform any other performable strategy, or they would simply perform it.

“No,” you say, “I’m talking about how startup founders strike it rich by believing in themselves and their ideas more strongly than any reasonable person would. I’m talking about how religious people are happier—”

Ah. Well, here’s the thing: An incremental step in the direction of rationality, if the result is still irrational in other ways, does not have to yield incrementally more winning.

The optimality theorems that we have for probability theory and decision theory are for perfect probability theory and decision theory. There is no companion theorem which says that, starting from some flawed initial form, every incremental modification of the algorithm that takes the structure closer to the ideal must yield an incremental improvement in performance. This has not yet been proven, because it is not, in fact, true.

“So,” you say, “what point is there then in striving to be more rational? We won’t reach the perfect ideal. So we have no guarantee that our steps forward are helping.”

You have no guarantee that a step backward will help you win, either. Guarantees don’t exist in the world of flesh; but, contrary to popular misconceptions, judgment under uncertainty is what rationality is all about.

“But we have several cases where, based on either vaguely plausible-sounding reasoning, or survey data, it looks like an incremental step forward in rationality is going to make us worse off. If it’s really all about winning—if you have something to protect more important than any ritual of cognition—then why take that step?”

Ah, and now we come to the meat of it.

I can’t necessarily answer for everyone, but . . .

My first reason is that, on a professional basis, I deal with deeply confused problems that make huge demands on precision of thought. One small mistake can lead you astray for years, and there are worse penalties waiting in the wings. An unimproved level of performance isn’t enough; my choice is to try to do better, or give up and go home.

“But that’s just you. Not all of us lead that kind of life. What if you’re just trying some ordinary human task like an Internet startup?”

My second reason is that I am trying to push some aspects of my art further than I have seen done. I don’t know where these improvements lead. The loss of failing to take a step forward is not that one step. It is all the other steps forward you could have taken, beyond that point. Robin Hanson has a saying: The problem with slipping on the stairs is not falling the height of the first step; it is that falling one step leads to falling another step. In the same way, refusing to climb one step up forfeits not the height of that step but the height of the staircase.

“But again—that’s just you. Not all of us are trying to push the art into uncharted territory.”

My third reason is that once I realize I have been deceived, I can’t just shut my eyes and pretend I haven’t seen it. I have already taken that step forward; what use to deny it to myself? I couldn’t believe in God if I tried, any more than I could believe the sky above me was green while looking straight at it. If you know everything you need to know in order to know that you are better off deceiving yourself, it’s much too late to deceive yourself.

“But that realization is unusual; other people have an easier time of doublethink because they don’t realize it’s impossible. You go around trying to actively sponsor the collapse of doublethink. You, from a higher vantage point, may know enough to expect that this will make them unhappier. So is this out of a sadistic desire to hurt your readers, or what?”

Then I finally reply that my experience so far—even in this realm of merely human possibility—does seem to indicate that, once you sort yourself out a bit and you aren’t doing quite so many other things wrong, striving for more rationality actually will make you better off. The long road leads out of the valley and higher than before, even in the human lands.

The more I know about some particular facet of the Art, the more I can see this is so. As I’ve previously remarked, my essays may be unreflective of what a true martial art of rationality would be like, because I have only focused on answering confusing questions—not fighting akrasia, coordinating groups, or being happy. In the field of answering confusing questions—the area where I have most intensely practiced the Art—it now seems massively obvious that anyone who thought they were better off “staying optimistic about solving the problem” would get stomped into the ground. By a casual student.

When it comes to keeping motivated, or being happy, I can’t guarantee that someone who loses their illusions will be better off—because my knowledge of these facets of rationality is still crude. If these parts of the Art have been developed systematically, I do not know of it. But even here I have gone to some considerable pains to dispel half-rational half-mistaken ideas that could get in a beginner’s way, like the idea that rationality opposes feeling, or the idea that rationality opposes value, or the idea that sophisticated thinkers should be angsty and cynical.

And if, as I hope, someone goes on to develop the art of fighting akrasia or achieving mental well-being as thoroughly as I have developed the art of answering impossible questions, I do fully expect that those who wrap themselves in their illusions will not begin to compete. Meanwhile—others may do better than I, if happiness is their dearest desire, for I myself have invested little effort here.

I find it hard to believe that the optimally motivated individual, the strongest entrepreneur a human being can become, is still wrapped up in a blanket of comforting overconfidence. I think they’ve probably thrown that blanket out the window and organized their mind a little differently. I find it hard to believe that the happiest we can possibly live, even in the realms of human possibility, involves a tiny awareness lurking in the corner of your mind that it’s all a lie. I’d rather stake my hopes on neurofeedback or Zen meditation, though I’ve tried neither.

But it cannot be denied that this is a very real issue in very real life. Consider this pair of comments from Less Wrong:

I’ll be honest—my life has taken a sharp downturn since I deconverted. My theist girlfriend, with whom I was very much in love, couldn’t deal with this change in me, and after six months of painful vacillation, she left me for a co-worker. That was another six months ago, and I have been heartbroken, miserable, unfocused, and extremely ineffective since.

Perhaps this is an example of the valley of bad rationality of which PhilGoetz spoke, but I still hold my current situation higher in my preference ranking than happiness with false beliefs.

And:

My empathies: that happened to me about 6 years ago (though thankfully without as much visible vacillation).

My sister, who had some Cognitive Behaviour Therapy training, reminded me that relationships are forming and breaking all the time, and given I wasn’t unattractive and hadn’t retreated into monastic seclusion, it wasn’t rational to think I’d be alone for the rest of my life (she turned out to be right). That was helpful at the times when my feelings hadn’t completely got the better of me.

So—in practice, in real life, in sober fact—those first steps can, in fact, be painful. And then things can, in fact, get better. And there is, in fact, no guarantee that you’ll end up higher than before. Even if in principle the path must go further, there is no guarantee that any given person will get that far.

If you don’t prefer truth to happiness with false beliefs . . .

Well . . . and if you are not doing anything especially precarious or confusing . . . and if you are not buying lottery tickets . . . and if you’re already signed up for cryonics, a sudden ultra-high-stakes confusing acid test of rationality that illustrates the Black Swan quality of trying to bet on ignorance in ignorance . . .

Then it’s not guaranteed that taking all the incremental steps toward rationality that you can find will leave you better off. But the vaguely plausible-sounding arguments against losing your illusions generally do consider just one single step, without postulating any further steps, without suggesting any attempt to regain everything that was lost and go it one better. Even the surveys are comparing the average religious person to the average atheist, not the most advanced theologians to the most advanced rationalists.

But if you don’t care about the truth—and you have nothing to protect—and you’re not attracted to the thought of pushing your art as far as it can go—and your current life seems to be going fine—and you have a sense that your mental well-being depends on illusions you’d rather not think about—

Then you’re probably not reading this. But if you are, then, I guess . . . well . . . (a) sign up for cryonics, and then (b) stop reading Less Wrong before your illusions collapse! RUN AWAY!

329
Bayesians vs. Barbarians

Previously:

Let’s say we have two groups of soldiers. In group 1, the privates are ignorant of tactics and strategy; only the sergeants know anything about tactics and only the officers know anything about strategy. In group 2, everyone at all levels knows all about tactics and strategy.

Should we expect group 1 to defeat group 2, because group 1 will follow orders, while everyone in group 2 comes up with better ideas than whatever orders they were given?

In this case I have to question how much group 2 really understands about military theory, because it is an elementary proposition that an uncoordinated mob gets slaughtered.

Suppose that a country of rationalists is attacked by a country of Evil Barbarians who know nothing of probability theory or decision theory.

Now there’s a certain viewpoint on “rationality” or “rationalism” which would say something like this:

“Obviously, the rationalists will lose. The Barbarians believe in an afterlife where they’ll be rewarded for courage; so they’ll throw themselves into battle without hesitation or remorse. Thanks to their affective death spirals around their Cause and Great Leader Bob, their warriors will obey orders, and their citizens at home will produce enthusiastically and at full capacity for the war; anyone caught skimming or holding back will be burned at the stake in accordance with Barbarian tradition. They’ll believe in each other’s goodness and hate the enemy more strongly than any sane person would, binding themselves into a tight group. Meanwhile, the rationalists will realize that there’s no conceivable reward to be had from dying in battle; they’ll wish that others would fight, but not want to fight themselves. Even if they can find soldiers, their civilians won’t be as cooperative: So long as any one sausage almost certainly doesn’t lead to the collapse of the war effort, they’ll want to keep that sausage for themselves, and so not contribute as much as they could. No matter how refined, elegant, civilized, productive, and nonviolent their culture was to start with, they won’t be able to resist the Barbarian invasion; sane discussion is no match for a frothing lunatic armed with a gun. In the end, the Barbarians will win because they want to fight, they want to hurt the rationalists, they want to conquer and their whole society is united around conquest; they care about that more than any sane person would.”

War is not fun. As many, many people have found since the dawn of recorded history, as many, many people have found before the dawn of recorded history, as some community somewhere is finding out right now in some sad little country whose internal agonies don’t even make the front pages any more.

War is not fun. Losing a war is even less fun. And it was said since the ancient times: “If thou would have peace, prepare for war.” Your opponents don’t have to believe that you’ll win, that you’ll conquer; but they have to believe you’ll put up enough of a fight to make it not worth their while.

You perceive, then, that if it were genuinely the lot of “rationalists” to always lose in war, that I could not in good conscience advocate the widespread public adoption of “rationality.”

This is probably the dirtiest topic I’ve discussed or plan to discuss here. War is not clean. Current high-tech militaries—by this I mean the US military—are unique in the overwhelmingly superior force they can bring to bear on opponents, which allows for a historically extraordinary degree of concern about enemy casualties and civilian casualties.

Winning in war has not always meant tossing aside all morality. Wars have been won without using torture. The unfunness of war does not imply, say, that questioning the President is unpatriotic. We’re used to “war” being exploited as an excuse for bad behavior, because in recent US history that pretty much is exactly what it’s been used for . . .

But reversed stupidity is not intelligence. And reversed evil is not intelligence either. It remains true that real wars cannot be won by refined politeness. If “rationalists” can’t prepare themselves for that mental shock, the Barbarians really will win; and the “rationalists” . . . I don’t want to say, “deserve to lose.” But they will have failed that test of their society’s existence.

Let me start by disposing of the idea that, in principle, ideal rational agents cannot fight a war, because each of them prefers being a civilian to being a soldier.

As has already been discussed at some length, I one-box on Newcomb’s Problem.

Consistently, I do not believe that if an election is settled by 100,000 to 99,998 votes, that all of the voters were irrational in expending effort to go to the polling place because “my staying home would not have affected the outcome.” (Nor do I believe that if the election came out 100,000 to 99,999, then 100,000 people were all, individually, solely responsible for the outcome.)

Consistently, I also hold that two rational AIs (that use my kind of decision theory), even if they had completely different utility functions and were designed by different creators, will cooperate on the true Prisoner’s Dilemma if they have common knowledge of each other’s source code. (Or even just common knowledge of each other’s rationality in the appropriate sense.)

Consistently, I believe that rational agents are capable of coordinating on group projects whenever the (expected probabilistic) outcome is better than it would be without such coordination. A society of agents that use my kind of decision theory, and have common knowledge of this fact, will end up at Pareto optima instead of Nash equilibria. If all rational agents agree that they are better off fighting than surrendering, they will fight the Barbarians rather than surrender.

Imagine a community of self-modifying AIs who collectively prefer fighting to surrender, but individually prefer being a civilian to fighting. One solution is to run a lottery, unpredictable to any agent, to select warriors. Before the lottery is run, all the AIs change their code, in advance, so that if selected they will fight as a warrior in the most communally efficient possible way—even if it means calmly marching into their own death.

(A reflectively consistent decision theory works the same way, only without the self-modification.)

You reply: “But in the real, human world, agents are not perfectly rational, nor do they have common knowledge of each other’s source code. Cooperation in the Prisoner’s Dilemma requires certain conditions according to your decision theory (which these margins are too small to contain) and these conditions are not met in real life.”

I reply: The pure, true Prisoner’s Dilemma is incredibly rare in real life. In real life you usually have knock-on effects—what you do affects your reputation. In real life most people care to some degree about what happens to other people. And in real life you have an opportunity to set up incentive mechanisms.

And in real life, I do think that a community of human rationalists could manage to produce soldiers willing to die to defend the community. So long as children aren’t told in school that ideal rationalists are supposed to defect against each other in the Prisoner’s Dilemma. Let it be widely believed—and I do believe it, for exactly the same reason I one-box on Newcomb’s Problem—that if people decided as individuals not to be soldiers or if soldiers decided to run away, then that is the same as deciding for the Barbarians to win. By that same theory whereby, if an election is won by 100,000 votes to 99,998 votes, it does not make sense for every voter to say “my vote made no difference.” Let it be said (for it is true) that utility functions don’t need to be solipsistic, and that a rational agent can fight to the death if they care enough about what they’re protecting. Let them not be told that rationalists should expect to lose reasonably.

If this is the culture and the mores of the rationalist society, then, I think, ordinary human beings in that society would volunteer to be soldiers. That also seems to be built into human beings, after all. You only need to ensure that the cultural training does not get in the way.

And if I’m wrong, and that doesn’t get you enough volunteers?

Then so long as people still prefer, on the whole, fighting to surrender, they have an opportunity to set up incentive mechanisms, and avert the True Prisoner’s Dilemma.

You can have lotteries for who gets elected as a warrior. Sort of like the example above with AIs changing their own code. Except that if “be reflectively consistent; do that which you would precommit to do” is not sufficient motivation for humans to obey the lottery, then . . .

. . . well, in advance of the lottery actually running, we can perhaps all agree that it is a good idea to give the selectees drugs that will induce extra courage, and shoot them if they run away. Even considering that we ourselves might be selected in the lottery. Because in advance of the lottery, this is the general policy that gives us the highest expectation of survival.

. . . like I said: Real wars = not fun, losing wars = less fun.

Let’s be clear, by the way, that I’m not endorsing the draft as practiced nowadays. Those drafts are not collective attempts by a populace to move from a Nash equilibrium to a Pareto optimum. Drafts are a tool of kings playing games in need of toy soldiers. The Vietnam draftees who fled to Canada, I hold to have been in the right. But a society that considers itself too smart for kings does not have to be too smart to survive. Even if the Barbarian hordes are invading, and the Barbarians do practice the draft.

Will rational soldiers obey orders? What if the commanding officer makes a mistake?

Soldiers march. Everyone’s feet hitting the ground in the same rhythm. Even, perhaps, against their own inclinations, since people left to themselves would walk all at separate paces. Lasers made out of people. That’s marching.

If it’s possible to invent some method of group decisionmaking that is superior to the captain handing down orders, then a company of rational soldiers might implement that procedure. If there is no proven method better than a captain, then a company of rational soldiers commit to obey the captain, even against their own separate inclinations. And if human beings aren’t that rational . . . then in advance of the lottery, the general policy that gives you the highest personal expectation of survival is to shoot soldiers who disobey orders. This is not to say that those who fragged their own officers in Vietnam were in the wrong; for they could have consistently held that they preferred no one to participate in the draft lottery.

But an uncoordinated mob gets slaughtered, and so the soldiers need some way of all doing the same thing at the same time in the pursuit of the same goal, even though, left to their own devices, they might march off in all directions. The orders may not come from a captain like a superior tribal chief, but unified orders have to come from somewhere. A society whose soldiers are too clever to obey orders is a society that is too clever to survive. Just like a society whose people are too clever to be soldiers. That is why I say “clever,” which I often use as a term of opprobrium, rather than “rational.”

(Though I do think it’s an important question as to whether you can come up with a small-group coordination method that really genuinely in practice works better than having a leader. The more people can trust the group decision method—the more they can believe that it really is superior to people going their own way—the more coherently they can behave even in the absence of enforceable penalties for disobedience.)

I say all this, even though I certainly don’t expect rationalists to take over a country any time soon, because I think that what we believe about a society of “people like us” has some reflection on what we think of ourselves. If you believe that a society of people like you would be too reasonable to survive in the long run . . . that’s one sort of self-image. And it’s a different sort of self-image if you think that a society of people all like you could fight the vicious Evil Barbarians and win—not just by dint of superior technology, but because your people care about each other and about their collective society—and because they can face the realities of war without losing themselves—and because they would calculate the group-rational thing to do and make sure it got done—and because there’s nothing in the rules of probability theory or decision theory that says you can’t sacrifice yourself for a cause—and because if you really are smarter than the Enemy and not just flattering yourself about that, then you should be able to exploit the blind spots that the Enemy does not allow itself to think about—and because no matter how heavily the Enemy hypes itself up before battle, you think that just maybe a coherent mind, undivided within itself, and perhaps practicing something akin to meditation or self-hypnosis, can fight as hard in practice as someone who theoretically believes they’ve got seventy-two virgins waiting for them.

Then you’ll expect more of yourself and people like you operating in groups; and then you can see yourself as something more than a cultural dead end.

So look at it this way: Jeffreyssai probably wouldn’t give up against the Evil Barbarians if he were fighting alone. A whole army of beisutsukai masters ought to be a force that no one would mess with. That’s the motivating vision. The question is how, exactly, that works.

330
Beware of OtherOptimizing

I’ve noticed a serious problem in which aspiring rationalists vastly overestimate their ability to optimize other people’s lives. And I think I have some idea of how the problem arises.

You read nineteen different webpages advising you about personal improvement—productivity, dieting, saving money. And the writers all sound bright and enthusiastic about Their Method, they tell tales of how it worked for them and promise amazing results . . .

But most of the advice rings so false as to not even seem worth considering. So you sigh, mournfully pondering the wild, childish enthusiasm that people can seem to work up for just about anything, no matter how silly. Pieces of advice #4 and #15 sound interesting, and you try them, but . . . they don’t . . . quite . . . well, it fails miserably. The advice was wrong, or you couldn’t do it, and either way you’re not any better off.

And then you read the twentieth piece of advice—or even more, you discover a twentieth method that wasn’t in any of the pages—and STARS ABOVE IT ACTUALLY WORKS THIS TIME.

At long, long last you have discovered the real way, the right way, the way that actually works. And when someone else gets into the sort of trouble you used to have—well, this time you know how to help them. You can save them all the trouble of reading through nineteen useless pieces of advice and skip directly to the correct answer. As an aspiring rationalist you’ve already learned that most people don’t listen, and you usually don’t bother—but this person is a friend, someone you know, someone you trust and respect to listen.

And so you put a comradely hand on their shoulder, look them straight in the eyes, and tell them how to do it.

I, personally, get quite a lot of this. Because you see . . . when you’ve discovered the way that really works . . . well, you know better by now than to run out and tell your friends and family. But you’ve got to try telling Eliezer Yudkowsky. He needs it, and there’s a pretty good chance that he’ll understand.

It actually did take me a while to understand. One of the critical events was when someone on the Board of the Machine Intelligence Research Institute told me that I didn’t need a salary increase to keep up with inflation—because I could be spending substantially less money on food if I used an online coupon service. And I believed this, because it was a friend I trusted, and it was delivered in a tone of such confidence. So my girlfriend started trying to use the service, and a couple of weeks later she gave up.

Now here’s the thing: if I’d run across exactly the same advice about using coupons on some blog somewhere, I probably wouldn’t even have paid much attention, just read it and moved on. Even if it were written by Scott Aaronson or some similar person known to be intelligent, I still would have read it and moved on. But because it was delivered to me personally, by a friend who I knew, my brain processed it differently—as though I were being told the secret; and that indeed is the tone in which it was told to me. And it was something of a delayed reaction to realize that I’d simply been told, as personal advice, what otherwise would have been just a blog post somewhere; no more and no less likely to work for me, than a productivity blog post written by any other intelligent person.

And because I have encountered a great many people trying to optimize me, I can attest that the advice I get is as wide-ranging as the productivity blogosphere. But others don’t see this plethora of productivity advice as indicating that people are diverse in which advice works for them. Instead they see a lot of obviously wrong poor advice. And then they finally discover the right way—the way that works, unlike all those other blog posts that don’t work—and then, quite often, they decide to use it to optimize Eliezer Yudkowsky.

Don’t get me wrong. Sometimes the advice is helpful. Sometimes it works. “Stuck In The Middle With Bruce”—that resonated, for me. It may prove to be the most helpful thing I’ve read on the new Less Wrong so far, though that has yet to be determined.

It’s just that your earnest personal advice, that amazing thing you’ve found to actually work by golly, is no more and no less likely to work for me than a random personal improvement blog post written by an intelligent author is likely to work for you.

“Different things work for different people.” That sentence may give you a squicky feeling; I know it gives me one. Because this sentence is a tool wielded by Dark Side Epistemology to shield from criticism, used in a way closely akin to “Different things are true for different people” (which is simply false).

But until you grasp the laws that are near-universal generalizations, sometimes you end up messing around with surface tricks that work for one person and not another, without your understanding why, because you don’t know the general laws that would dictate what works for who. And the best you can do is remember that, and be willing to take “No” for an answer.

You especially had better be willing to take “No” for an answer, if you have power over the Other. Power is, in general, a very dangerous thing, which is tremendously easy to abuse, without your being aware that you’re abusing it. There are things you can do to prevent yourself from abusing power, but you have to actually do them or they don’t work. There was a post on Overcoming Bias on how being in a position of power has been shown to decrease our ability to empathize with and understand the other, though I can’t seem to locate it now. I have seen a rationalist who did not think he had power, and so did not think he needed to be cautious, who was amazed to learn that he might be feared . . .

It’s even worse when their discovery that works for them requires a little willpower. Then if you say it doesn’t work for you, the answer is clear and obvious: you’re just being lazy, and they need to exert some pressure on you to get you to do the correct thing, the advice they’ve found that actually works.

Sometimes—I suppose—people are being lazy. But be very, very, very careful before you assume that’s the case and wield power over others to “get them moving.” Bosses who can tell when something actually is in your capacity if you’re a little more motivated, without it burning you out or making your life incredibly painful—these are the bosses who are a pleasure to work under. That ability is extremely rare, and the bosses who have it are worth their weight in silver. It’s a high-level interpersonal technique that most people do not have. I surely don’t have it. Do not assume you have it because your intentions are good. Do not assume you have it because you’d never do anything to others that you didn’t want done to yourself. Do not assume you have it because no one has ever complained to you. Maybe they’re just scared. That rationalist of whom I spoke—who did not think he held power and threat, though it was certainly obvious enough to me—he did not realize that anyone could be scared of him.

Be careful even when you hold leverage, when you hold an important decision in your hand, or a threat, or something that the other person needs, and all of a sudden the temptation to optimize them seems overwhelming.

Consider, if you would, that Ayn Rand’s whole reign of terror over Objectivists can be seen in just this light—that she found herself with power and leverage, and could not resist the temptation to optimize.

We underestimate the distance between ourselves and others. Not just inferential distance, but distances of temperament and ability, distances of situation and resource, distances of unspoken knowledge and unnoticed skills and luck, distances of interior landscape.

Even I am often surprised to find that X, which worked so well for me, doesn’t work for someone else. But with so many others having tried to optimize me, I can at least recognize distance when I’m hit over the head with it.

Maybe being pushed on does work . . . for you. Maybe you don’t get sick to the stomach when someone with power over you starts helpfully trying to reorganize your life the correct way. I don’t know what makes you tick. In the realm of willpower and akrasia and productivity, as in other realms, I don’t know the generalizations deep enough to hold almost always. I don’t possess the deep keys that would tell me when and why and for who a technique works or doesn’t work. All I can do is be willing to accept it when someone tells me it doesn’t work . . . and go on looking for the deeper generalizations that will hold everywhere, the deeper laws governing both the rule and the exception, waiting to be found, someday.

331
Practical Advice Backed by Deep Theories

Once upon a time, Seth Roberts took a European vacation and found that he started losing weight while drinking unfamiliar-tasting caloric fruit juices.

Now suppose Roberts had not known, and never did know, anything about metabolic set points or flavor-calorie associations—all this high-falutin’ scientific experimental research that had been done on rats and occasionally humans.

He would have posted to his blog, “Gosh, everyone! You should try these amazing fruit juices that are making me lose weight!” And that would have been the end of it. Some people would have tried it, it would have worked temporarily for some of them (until the flavor-calorie association kicked in) and there never would have been a ShangriLa Diet per se.

The existing ShangriLa Diet is visibly incomplete—for some people, like me, it doesn’t seem to work, and there is no apparent reason for this or any logic permitting it. But the reason why as many people have benefited as they have—the reason why there was more than just one more blog post describing a trick that seemed to work for one person and didn’t work for anyone else—is that Roberts knew the experimental science that let him interpret what he was seeing, in terms of deep factors that actually did exist.

One of the pieces of advice on Overcoming Bias / Less Wrong that was frequently cited as the most important thing learned, was the idea of “the bottom line”—that once a conclusion is written in your mind, it is already true or already false, already wise or already stupid, and no amount of later argument can change that except by changing the conclusion. And this ties directly into another oft-cited most important thing, which is the idea of “engines of cognition,” minds as mapping engines that require evidence as fuel.

Suppose I had merely written one more blog post that said, “You know, you really should be more open to changing your mind—it’s pretty important—and oh yes, you should pay attention to the evidence too.” This would not have been as useful. Not just because it was less persuasive, but because the actual operations would have been much less clear without the explicit theory backing it up. What constitutes evidence, for example? Is it anything that seems like a forceful argument? Having an explicit probability theory and an explicit causal account of what makes reasoning effective makes a large difference in the forcefulness and implementational details of the old advice to “Keep an open mind and pay attention to the evidence.”

It is also important to realize that causal theories are much more likely to be true when they are picked up from a science textbook than when invented on the fly—it is very easy to invent cognitive structures that look like causal theories but are not even anticipation-controlling, let alone true.

This is the signature style I want to convey from all those essays that entangled cognitive science experiments and probability theory and epistemology with the practical advice—that practical advice actually becomes practically more powerful if you go out and read up on cognitive science experiments, or probability theory, or even materialist epistemology, and realize what you’re seeing. This is the brand that can distinguish Less Wrong from ten thousand other blogs purporting to offer advice.

I could tell you, “You know, how much you’re satisfied with your food probably depends more on the quality of the food than on how much of it you eat.” And you would read it and forget about it, and the impulse to finish off a whole plate would still feel just as strong. But if I tell you about scope insensitivity, and duration neglect and the Peak/End rule, you are suddenly aware in a very concrete way, looking at your plate, that you will form almost exactly the same retrospective memory whether your portion size is large or small; you now possess a deep theory about the rules governing your memory, and you know that this is what the rules say. (You also know to save the dessert for last.)

I want to hear how I can overcome akrasia—how I can have more willpower, or get more done with less mental pain. But there are ten thousand people purporting to give advice on this, and for the most part, it is on the level of that alternate Seth Roberts who just tells people about the amazing effects of drinking fruit juice. Or actually, somewhat worse than that—it’s people trying to describe internal mental levers that they pulled, for which there are no standard words, and which they do not actually know how to point to. See also the illusion of transparency, inferential distance, and double illusion of transparency. (Notice how “You overestimate how much you’re explaining and your listeners overestimate how much they’re hearing” becomes much more forceful as advice, after I back it up with a cognitive science experiment and some evolutionary psychology?)

I think that the advice I need is from someone who reads up on a whole lot of experimental psychology dealing with willpower, mental conflicts, ego depletion, preference reversals, hyperbolic discounting, the breakdown of the self, picoeconomics, et cetera, and who, in the process of overcoming their own akrasia, manages to understand what they did in truly general terms—thanks to experiments that give them a vocabulary of cognitive phenomena that actually exist, as opposed to phenomena they just made up. And moreover, someone who can explain what they did to someone else, thanks again to the experimental and theoretical vocabulary that lets them point to replicable experiments that ground the ideas in very concrete results, or mathematically clear ideas.

Note the grade of increasing difficulty in citing:

Concrete experimental results (for which one need merely consult a paper, hopefully one that reported p < 0.01 because p < 0.05 may fail to replicate);
Causal accounts that are actually true (which may be most reliably obtained by looking for the theories that are used by a majority within a given science);
Math validly interpreted (on which I have trouble offering useful advice because so much of my own math talent is intuition that kicks in before I get a chance to deliberate).

If you don’t know who to trust, or you don’t trust yourself, you should concentrate on experimental results to start with, move on to thinking in terms of causal theories that are widely used within a science, and dip your toes into math and epistemology with extreme caution.

But practical advice really, really does become a lot more powerful when it’s backed up by concrete experimental results, causal accounts that are actually true, and math validly interpreted.

332
The Sin of Underconfidence

There are three great besetting sins of rationalists in particular, and the third of these is underconfidence. Michael Vassar regularly accuses me of this sin, which makes him unique among the entire population of the Earth.

But he’s actually quite right to worry, and I worry too, and any adept rationalist will probably spend a fair amount of time worying about it. When subjects know about a bias or are warned about a bias, overcorrection is not unheard of as an experimental result. That’s what makes a lot of cognitive subtasks so troublesome—you know you’re biased but you’re not sure how much, and you don’t know if you’re correcting enough—and so perhaps you ought to correct a little more, and then a little more, but is that enough? Or have you, perhaps, far overshot? Are you now perhaps worse off than if you hadn’t tried any correction?

You contemplate the matter, feeling more and more lost, and the very task of estimation begins to feel increasingly futile . . .

And when it comes to the particular questions of confidence, overconfidence, and underconfidence—being interpreted now in the broader sense, not just calibrated confidence intervals—then there is a natural tendency to cast overconfidence as the sin of pride, out of that other list which never warned against the improper use of humility or the abuse of doubt. To place yourself too high—to overreach your proper place—to think too much of yourself—to put yourself forward—to put down your fellows by implicit comparison—and the consequences of humiliation and being cast down, perhaps publicly—are these not loathesome and fearsome things?

To be too modest—seems lighter by comparison; it wouldn’t be so humiliating to be called on it publicly. Indeed, finding out that you’re better than you imagined might come as a warm surprise; and to put yourself down, and others implicitly above, has a positive tinge of niceness about it. It’s the sort of thing that Gandalf would do.

So if you have learned a thousand ways that humans fall into error and read a hundred experimental results in which anonymous subjects are humiliated of their overconfidence—heck, even if you’ve just read a couple of dozen—and you don’t know exactly how overconfident you are—then yes, you might genuinely be in danger of nudging yourself a step too far down.

I have no perfect formula to give you that will counteract this. But I have an item or two of advice.

What is the danger of underconfidence?

Passing up opportunities. Not doing things you could have done, but didn’t try (hard enough).

So here’s a first item of advice: If there’s a way to find out how good you are, the thing to do is test it. A hypothesis affords testing; hypotheses about your own abilities likewise. Once upon a time it seemed to me that I ought to be able to win at the AI-Box Experiment; and it seemed like a very doubtful and hubristic thought; so I tested it. Then later it seemed to me that I might be able to win even with large sums of money at stake, and I tested that, but I only won one time out of three. So that was the limit of my ability at that time, and it was not necessary to argue myself upward or downward, because I could just test it.

One of the chief ways that smart people end up stupid is by getting so used to winning that they stick to places where they know they can win—meaning that they never stretch their abilities, they never try anything difficult.

It is said that this is linked to defining yourself in terms of your “intelligence” rather than “effort,” because then winning easily is a sign of your “intelligence,” where failing on a hard problem could have been interpreted in terms of a good effort.

Now, I am not quite sure this is how an adept rationalist should think about these things: rationality is systematized winning and trying to try seems like a path to failure. I would put it this way: A hypothesis affords testing! If you don’t know whether you’ll win on a hard problem—then challenge your rationality to discover your current level. I don’t usually hold with congratulating yourself on having tried—it seems like a bad mental habit to me—but surely not trying is even worse. If you have cultivated a general habit of confronting challenges, and won on at least some of them, then you may, perhaps, think to yourself, “I did keep up my habit of confronting challenges, and will do so next time as well.” You may also think to yourself “I have gained valuable information about my current level and where I need improvement,” so long as you properly complete the thought, “I shall try not to gain this same valuable information again next time.”

If you win every time, it means you aren’t stretching yourself enough. But you should seriously try to win every time. And if you console yourself too much for failure, you lose your winning spirit and become a scrub.

When I try to imagine what a fictional master of the Competitive Conspiracy would say about this, it comes out something like: “It’s not okay to lose. But the hurt of losing is not something so scary that you should flee the challenge for fear of it. It’s not so scary that you have to carefully avoid feeling it, or refuse to admit that you lost and lost hard. Losing is supposed to hurt. If it didn’t hurt you wouldn’t be a Competitor. And there’s no Competitor who never knows the pain of losing. Now get out there and win.”

Cultivate a habit of confronting challenges—not the ones that can kill you outright, perhaps, but perhaps ones that can potentially humiliate you. I recently read of a certain theist that he had defeated Christopher Hitchens in a debate (severely so; this was said by atheists). And so I wrote at once to the Bloggingheads folks and asked if they could arrange a debate. This seemed like someone I wanted to test myself against. Also, it was said by them that Christopher Hitchens should have watched the theist’s earlier debates and been prepared, so I decided not to do that, because I think I should be able to handle damn near anything on the fly, and I desire to learn whether this thought is correct; and I am willing to risk public humiliation to find out. Note that this is not self-handicapping in the classic sense—if the debate is indeed arranged (I haven’t yet heard back), and I do not prepare, and I fail, then I do lose those stakes of myself that I have put up; I gain information about my limits; I have not given myself anything I consider an excuse for losing.

Of course this is only a way to think when you really are confronting a challenge just to test yourself, and not because you have to win at any cost. In that case you make everything as easy for yourself as possible. To do otherwise would be spectacular overconfidence, even if you’re playing tic-tac-toe against a three-year-old.

A subtler form of underconfidence is losing your forward momentum—amid all the things you realize that humans are doing wrong, that you used to be doing wrong, of which you are probably still doing some wrong. You become timid; you question yourself but don’t answer the self-questions and move on; when you hypothesize your own inability you do not put that hypothesis to the test.

Perhaps without there ever being a watershed moment when you deliberately, self-visibly decide not to try at some particular test . . . you just . . . . slow . . . . . down . . . . . . .

It doesn’t seem worthwhile any more, to go on trying to fix one thing when there are a dozen other things that will still be wrong . . .

There’s not enough hope of triumph to inspire you to try hard . . .

When you consider doing any new thing, a dozen questions about your ability at once leap into your mind, and it does not occur to you that you could answer the questions by testing yourself . . .

And having read so much wisdom of human flaws, it seems that the course of wisdom is ever doubting (never resolving doubts), ever the humility of refusal (never the humility of preparation), and just generally, that it is wise to say worse and worse things about human abilities, to pass into feel-good feel-bad cynicism.

And so my last piece of advice is another perspective from which to view the problem—by which to judge any potential habit of thought you might adopt—and that is to ask:

Does this way of thinking make me stronger, or weaker? Really truly?

I have previously spoken of the danger of reasonableness—the reasonable-sounding argument that we should two-box on Newcomb’s problem, the reasonable-sounding argument that we can’t know anything due to the problem of induction, the reasonable-sounding argument that we will be better off on average if we always adopt the majority belief, and other such impediments to the Way. “Does it win?” is one question you could ask to get an alternate perspective. Another, slightly different perspective is to ask, “Does this way of thinking make me stronger, or weaker?” Does constantly reminding yourself to doubt everything make you stronger, or weaker? Does never resolving or decreasing those doubts make you stronger, or weaker? Does undergoing a deliberate crisis of faith in the face of uncertainty make you stronger, or weaker? Does answering every objection with a humble confession of you fallibility make you stronger, or weaker?

Are your current attempts to compensate for possible overconfidence making you stronger, or weaker? Hint: If you are taking more precautions, more scrupulously trying to test yourself, asking friends for advice, working your way up to big things incrementally, or still failing sometimes but less often then you used to, you are probably getting stronger. If you are never failing, avoiding challenges, and feeling generally hopeless and dispirited, you are probably getting weaker.

I learned the first form of this rule at a very early age, when I was practicing for a certain math test, and found that my score was going down with each practice test I took, and noticed going over the answer sheet that I had been pencilling in the correct answers and erasing them. So I said to myself, “All right, this time I’m going to use the Force and act on instinct,” and my score shot up to above what it had been in the beginning, and on the real test it was higher still. So that was how I learned that doubting yourself does not always make you stronger—especially if it interferes with your ability to be moved by good information, such as your math intuitions. (But I did need the test to tell me this!)

Underconfidence is not a unique sin of rationalists alone. But it is a particular danger into which the attempt to be rational can lead you. And it is a stopping mistake—an error that prevents you from gaining that further experience that would correct the error.

Because underconfidence actually does seem quite common among aspiring rationalists who I meet—though rather less common among rationalists who have become famous role models—I would indeed name it third among the three besetting sins of rationalists.

333
Go Forth and Create the Art!

I have said a thing or two about rationality, these past months. I have said a thing or two about how to untangle questions that have become confused, and how to tell the difference between real reasoning and fake reasoning, and the will to become stronger that leads you to try before you flee; I have said something about doing the impossible.

And these are all techniques that I developed in the course of my own projects—which is why there is so much about cognitive reductionism, say—and it is possible that your mileage may vary in trying to apply it yourself. The one’s mileage may vary. Still, those wandering about asking “But what good is it?” might consider rereading some of the earlier essays; knowing about e.g. the conjunction fallacy, and how to spot it in an argument, hardly seems esoteric. Understanding why motivated skepticism is bad for you can constitute the whole difference, I suspect, between a smart person who ends up smart and a smart person who ends up stupid. Affective death spirals consume many among the unwary . . .

Yet there is, I think, more absent than present in this “art of rationality”—defeating akrasia and coordinating groups are two of the deficits I feel most keenly. I’ve concentrated more heavily on epistemic rationality than instrumental rationality, in general. And then there’s training, teaching, verification, and becoming a proper experimental science based on that. And if you generalize a bit further, then building the Art could also be taken to include issues like developing better introductory literature, developing better slogans for public relations, establishing common cause with other Enlightenment subtasks, analyzing and addressing the gender imbalance problem . . .

But those small pieces of rationality that I’ve set out . . . I hope . . . just maybe . . .

I suspect—you could even call it a guess—that there is a barrier to getting started, in this matter of rationality. Where by default, in the beginning, you don’t have enough to build on. Indeed so little that you don’t have a clue that more exists, that there is an Art to be found. And if you do begin to sense that more is possible—then you may just instantaneously go wrong. As David Stove observes, most “great thinkers” in philosophy, e.g., Hegel, are properly objects of pity.¹ That’s what happens by default to anyone who sets out to develop the art of thinking; they develop fake answers.

When you try to develop part of the human art of thinking . . . then you are doing something not too dissimilar to what I was doing over in Artificial Intelligence. You will be tempted by fake explanations of the mind, fake accounts of causality, mysterious holy words, and the amazing idea that solves everything.

It’s not that the particular, epistemic, fake-detecting methods that I use are so good for every particular problem; but they seem like they might be helpful for discriminating good and bad systems of thinking.

I hope that someone who learns the part of the Art that I’ve set down here will not instantaneously and automatically go wrong if they start asking themselves, “How should people think, in order to solve new problem X that I’m working on?” They will not immediately run away; they will not just make stuff up at random; they may be moved to consult the literature in experimental psychology; they will not automatically go into an affective death spiral around their Brilliant Idea; they will have some idea of what distinguishes a fake explanation from a real one. They will get a saving throw.

It’s this sort of barrier, perhaps, that prevents people from beginning to develop an art of rationality, if they are not already rational.

And so instead they . . . go off and invent Freudian psychoanalysis. Or a new religion. Or something. That’s what happens by default, when people start thinking about thinking.

I hope that the part of the Art I have set down, as incomplete as it may be, can surpass that preliminary barrier—give people a base to build on; give them an idea that an Art exists, and somewhat of how it ought to be developed; and give them at least a saving throw before they instantaneously go astray.

That’s my dream—that this highly-specialized-seeming art of answering confused questions may be some of what is needed, in the very beginning, to go and complete the rest.

A task which I am leaving to you. Probably, anyway. I make no promises as to where my attention may turn in the future. But y’know, there are certain other things I need to do. Even if I develop yet more Art by accident, it may be that I will not have the time to write any of it up.

Beyond all that I have said of fake answers and traps, there are two things I would like you to keep in mind.

The first—that I drew on multiple sources to create my Art. I read many different authors, many different experiments, used analogies from many different fields. You will need to draw on multiple sources to create your portion of the Art. You should not be getting all your rationality from one author—though there might be, perhaps, a certain centralized website, where you went to post the links and papers that struck you as really important. And a maturing Art will need to draw from multiple sources. To the best of my knowledge there is no true science that draws its strength from only one person. To the best of my knowledge that is strictly an idiom of cults. A true science may have its heroes, it may even have its lonely defiant heroes, but it will have more than one.

The second—that I created my Art in the course of trying to do some particular thing that animated all my efforts. Maybe I’m being too idealistic—maybe thinking too much of the way the world should work—but even so, I somewhat suspect that you couldn’t develop the Art just by sitting around thinking to yourself, “Now how can I fight that akrasia thingy?” You’d develop the rest of the Art in the course of trying to do something. Maybe even—if I’m not overgeneralizing from my own history—some task difficult enough to strain and break your old understanding and force you to reinvent a few things. But maybe I’m wrong, and the next leg of the work will be done by direct, specific investigation of “rationality,” without any need of a specific application considered more important.

A past attempt of mine to describe this principle, in terms of maintaining a secret identity or day job in which one doesn’t teach rationality, was roundly rejected by my audience. Maybe “leave the house” would be more appropriate? It sounds to me like a really good, healthy idea. Still—perhaps I am deceived. We shall see where the next pieces of the Art do, in fact, come from.

I have striven for a long time now to convey, pass on, share a piece of the strange thing I touched, which seems to me so precious. And I’m not sure that I ever said the central rhythm into words. Maybe you can find it by listening to the notes. I can say these words but not the rule that generates them, or the rule behind the rule; one can only hope that by using the ideas, perhaps, similar machinery might be born inside you. Remember that all human efforts at learning arcana slide by default into passwords, hymns, and floating assertions.

I have striven for a long time now to convey my Art. Mostly without success, before this present effort. Earlier I made efforts only in passing, and got, perhaps, as much success as I deserved. Like throwing pebbles in a pond, that generate a few ripples, and then fade away . . . This time I put some back into it, and heaved a large rock. Time will tell if it was large enough—if I really disturbed anyone deeply enough that the waves of the impact will continue under their own motion. Time will tell if I have created anything that moves under its own power.

I want people to go forth, but also to return. Or maybe even to go forth and stay simultaneously, because this is the Internet and we can get away with that sort of thing; I’ve learned some interesting things on Less Wrong, lately, and if continuing motivation over years is any sort of problem, talking to others (or even seeing that others are also trying) does often help.

But at any rate, if I have affected you at all, then I hope you will go forth and confront challenges, and achieve somewhere beyond your armchair, and create new Art; and then, remembering whence you came, radio back to tell others what you learned.

1. David Charles Stove, The Plato Cult and Other Philosophical Follies (Cambridge University Press, 1991).

Bibliography

: Albert, David Z. Quantum Mechanics and Experience. Harvard University Press, 1994.
: Alexander, Scott. “Why I Am Not Rene Descartes.” Slate Star Codex (blog) (2014). http://slatestarcodex.com/2014/11/27/why-i-am-not-rene-descartes/.
: Allais, Maurice. “Le Comportement de l’Homme Rationnel devant le Risque: Critique des Postulats et Axiomes de l’Ecole Americaine.” Econometrica 21, no. 4 (1953): 503–546. doi:10.2307/1907921.
: Ariely, Dan. Predictably Irrational: The Hidden Forces That Shape Our Decisions. HarperCollins, 2008.
: Asch, Solomon E. “Studies of Independence and Conformity: A Minority of One Against a Unanimous Majority.” Psychological Monographs 70 (1956).
: Ashmore, Richard D., Vasantha Ramchandra, and Russell A. Jones. “Censorship as an Attitude Change Induction.” Paper presented at Eastern Psychological Association meeting (1971).
: Asimov, Isaac. The Relativity of Wrong. Oxford University Press, 1989.
: Baez, John. “The Crackpot Index.” 1998. http://math.ucr.edu/home/baez/crackpot.html.
: Banks, Iain. The Player of Games. Orbit, 1989.
: Baratz, Daphna. How Justified Is the “Obvious” Reaction? Stanford University, 1983.
: Barbour, Julian. The End of Time: The Next Revolution in Physics. 1st ed. New York: Oxford University Press, 1999.
: Baron, Jonathan. Thinking and Deciding. Cambridge University Press, 2007.
: Baron, Jonathan, and Joshua D. Greene. “Determinants of Insensitivity to Quantity in Valuation of Public Goods: Contribution, Warm Glow, Budget Constraints, Availability, and Prominence.” Journal of Experimental Psychology: Applied 2, no. 2 (1996): 107–125. doi:10.1037/1076-898X.2.2.107.
: Barrett, Jeffrey. Everett’s Relative-State Formulation of Quantum Mechanics. Edited by Edward N. Zalta. http://plato.stanford.edu/archives/fall2008/entries/qm-everett/.
: Benson, Peter L., Stuart A. Karabenick, and Richard M. Lerner. “Pretty Pleases: The Effects of Physical Attractiveness, Race, and Sex on Receiving Help.” Journal of Experimental Social Psychology 12 (5 1976): 409–415. doi:10.1016/0022-1031(76)90073-1.
: Bond, Rod, and Peter B. Smith. “Culture and Conformity: A Meta-Analysis of Studies Using Asch’s (1952b, 1956) Line Judgment Task.” Psychological Bulletin 119 (1996): 111–137.
: Bostrom, Nick. “A History of Transhumanist Thought.” Journal of Evolution and Technology 14, no. 1 (2005): 1–25. http://www.nickbostrom.com/papers/history.pdf.
: ———. “Existential Risks: Analyzing Human Extinction Scenarios and Related Hazards.” Journal of Evolution and Technology 9 (2002). http://www.jetpress.org/volume9/risks.html.
: ———. Superintelligence: Paths, Dangers, Strategies. Oxford University Press, 2014.
: Bostrom, Nick, and Milan M. Ćirković, eds. Global Catastrophic Risks. New York: Oxford University Press, 2008.
: Bostrom, Nick, and Julian Savulescu. “Human Enhancement Ethics: The State of the Debate.” In Human Enhancement, edited by Nick Bostrom and Julian Savulescu. 2009.
: Bostrom, Nick, and Eliezer Yudkowsky. “The Ethics of Artificial Intelligence.” In The Cambridge Handbook of Artificial Intelligence, edited by Keith Frankish and William Ramsey. New York: Cambridge University Press, 2014.
: Bourget, David, and David J. Chalmers. “What Do Philosophers Believe?” Philosophical Studies (2013): 1–36.
: Boynton, Robert S. “The Birth of an Idea: A Profile of Frank Sulloway.” The New Yorker (October 1999).
: Brehm, Sharon S., and Marsha Weintraub. “Physical Barriers and Psychological Reactance: Two-year-olds’ Responses to Threats to Freedom.” Journal of Personality and Social Psychology 35 (1977): 830–836.
: Broeder, Dale. “The University of Chicago Jury Project.” Nebraska Law Review 38 (1959): 760–774.
: Brown, Kevin. Reflections On Relativity. Raleigh, NC: printed by author, 2011. http://www.mathpages.com/rr/rrtoc.htm.
: Brust, Steven. The Paths of the Dead. Vol. 1 of The Viscount of Adrilankha. Tor Books, 2002.
: Budesheim, Thomas Lee, and Stephen DePaola. “Beauty or the Beast?: The Effects of Appearance, Personality, and Issue Information on Evaluations of Political Candidates.” Personality and Social Psychology Bulletin 20 (4 1994): 339–348. doi:10.1177/0146167294204001.
: Buehler, Roger, Dale Griffin, and Michael Ross. “Exploring the ‘Planning Fallacy’: Why People Underestimate Their Task Completion Times.” Journal of Personality and Social Psychology 67, no. 3 (1994): 366–381. doi:10.1037/0022-3514.67.3.366.
: ———. “Inside the Planning Fallacy: The Causes and Consequences of Optimistic Time Predictions.” In Gilovich, Griffin, and Kahneman, Heuristics and Biases, 250–270.
: ———. “It’s About Time: Optimistic Predictions in Work and Love.” European Review of Social Psychology 6, no. 1 (1995): 1–32. doi:10.1080/14792779343000112.
: Bujold, Lois McMaster. Komarr. Miles Vorkosigan Adventures. Baen, 1999.
: Burton, Ian, Robert W. Kates, and Gilbert F. White. The Environment as Hazard. 1st ed. New York: Oxford University Press, 1978.
: Campbell, Richmond, and Lanning Snowden, eds. Paradoxes of Rationality and Cooperation: Prisoner’s Dilemma and Newcomb’s Problem. Vancouver: University of British Columbia Press, 1985.
: Carson, Richard T., and Robert Cameron Mitchell. “Sequencing and Nesting in Contingent Valuation Surveys.” Journal of Environmental Economics and Management 28, no. 2 (1995): 155–173. doi:10.1006/jeem.1995.1011.
: Casscells, Ward, Arno Schoenberger, and Thomas Graboys. “Interpretation by Physicians of Clinical Laboratory Results.” New England Journal of Medicine 299 (1978): 999–1001.
: Castellow, Wilbur A., Karl L. Wuensch, and Charles H. Moore. “Effects of Physical Attractiveness of the Plaintiff and Defendant in Sexual Harassment Judgments.” Journal of Social Behavior and Personality 5 (6 1990): 547–562.
: Chaiken, Shelly. “Communicator Physical Attractiveness and Persuasion.” Journal of Personality and Social Psychology 37 (8 1979): 1387–1397. doi:10.1037/0022-3514.37.8.1387.
: Chalmers, David J. The Conscious Mind: In Search of a Fundamental Theory. New York: Oxford University Press, 1996.
: Chapman, Graham, et al. Monty Python’s The Life of Brian (of Nazareth). Eyre Methuen, 1979.
: Chapman, Gretchen B., and Eric J. Johnson. “Incorporating the Irrelevant: Anchors in Judgments of Belief and Value.” In Gilovich, Griffin, and Kahneman, Heuristics and Biases, 120–138.
: Cherryh, Carolyn J. The Paladin. Baen, 2002.
: Cialdini, Robert B. Influence: Science and Practice. Boston: Allyn & Bacon, 2001.
: ———. Influence: The Psychology of Persuasion: Revised Edition. New York: Quill, 1993.
: Cleaver, Jerry. Immediate Fiction: A Complete Writing Course. Macmillan, 2004.
: Combs, Barbara, and Paul Slovic. “Newspaper Coverage of Causes of Death.” Journalism & Mass Communication Quarterly 56, no. 4 (1979): 837–849. doi:10.1177/107769907905600420.
: Crawford, Charles B., Brenda E. Salter, and Kerry L. Jang. “Human Grief: Is Its Intensity Related to the Reproductive Value of the Deceased?” Ethology and Sociobiology 10, no. 4 (1989): 297–307.
: Darwin, Charles. On the Origin of Species by Means of Natural Selection; or, The Preservation of Favoured Races in the Struggle for Life. 1st ed. London: John Murray, 1859. http://darwin-online.org.uk/content/frameset?viewtype=text&itemID=F373&pageseq=1.
: ———. The Descent of Man, and Selection in Relation to Sex. 2nd ed. London: John Murray, 1874. http://darwin-online.org.uk/content/frameset?itemID=F944&viewtype=text&pageseq=1.
: Darwin, Francis, ed. The Life and Letters of Charles Darwin. John Murray, 1887.
: Dawes, Robyn M. House of Cards: Psychology and Psychotherapy Built on Myth. Free Press, 1996.
: ———. Rational Choice in An Uncertain World. 1st ed. Edited by Jerome Kagan. San Diego, CA: Harcourt Brace Jovanovich, 1988.
: De Camp, Lyon Sprague, and Fletcher Pratt. The Incomplete Enchanter. New York: Henry Holt & Company, 1941.
: Denes-Raj, Veronika, and Seymour Epstein. “Conflict between Intuitive and Rational Processing: When People Behave against Their Better Judgment.” Journal of Personality and Social Psychology 66 (5 1994): 819–829. doi:10.1037/0022-3514.66.5.819.
: Dennett, Daniel C. Breaking the Spell: Religion as a Natural Phenomenon. Penguin, 2006.
: ———. Darwin’s Dangerous Idea: Evolution and the Meanings of Life. Simon & Schuster, 1995.
: ———. Freedom Evolves. Viking Books, 2003.
: ———. “The Unimagined Preposterousness of Zombies.” Journal of Consciousness Studies 2 (4 1995): 322–26.
: Descartes, René. Discours de la Méthode. Librairie des Bibliophiles, 1887.
: Desvousges, William H., F. Reed Johnson, Richard W. Dunford, Kevin J. Boyle, Sara P. Hudson, and K. Nicole Wilson. Measuring Nonuse Damages Using Contingent Valuation: An Experimental Evaluation of Accuracy. Technical report. Research Triangle Park, NC: RTI International, 2010. doi:10.3768/rtipress.2009.bk.0001.1009.
: Downs, A. Chris, and Phillip M. Lyons. “Natural Observations of the Links Between Attractiveness and Initial Legal Judgments.” Personality and Social Psychology Bulletin 17 (5 1991): 541–547. doi:10.1177/0146167291175009.
: Drescher, Gary L. Good and Real: Demystifying Paradoxes from Physics to Ethics. Cambridge, MA: MIT Press, 2006.
: Eagly, Alice H., Richard D. Ashmore, Mona G. Makhijani, and Laura C. Longo. “What Is Beautiful Is Good, But . . . A Meta-analytic Review of Research on the Physical Attractiveness Stereotype.” Psychological Bulletin 110 (1 1991): 109–128. doi:10.1037/0033-2909.110.1.109.
: Eddy, David M. “Probabilistic Reasoning in Clinical Medicine: Problems and Opportunities.” In Judgement Under Uncertainty: Heuristics and Biases, edited by Daniel Kahneman, Paul Slovic, and Amos Tversky. Cambridge University Press, 1982.
: Efran, M. G., and E. W. J. Patterson. “The Politics of Appearance.” Unpublished PhD thesis, 1976.
: Egan, Greg. Quarantine. London: Legend Press, 1992.
: Ehrlinger, Joyce, Thomas Gilovich, and Lee Ross. “Peering Into the Bias Blind Spot: People’s Assessments of Bias in Themselves and Others.” Personality and Social Psychology Bulletin 31, no. 5 (2005): 680–692.
: Eidelman, Scott, and Christian S. Crandall. “Bias in Favor of the Status Quo.” Social and Personality Psychology Compass 6, no. 3 (2012): 270–281.
: Epley, Nicholas, and Thomas Gilovich. “Putting Adjustment Back in the Anchoring and Adjustment Heuristic: Differential Processing of Self-Generated and Experimentor-Provided Anchors.” Psychological Science 12 (5 2001): 391–396. doi:10.1111/1467-9280.00372.
: Epstein, Lewis Carroll. Thinking Physics: Understandable Practical Reality, 3rd Edition. Insight Press, 2009.
: Feldman, Richard. “Naturalized Epistemology.” In The Stanford Encyclopedia of Philosophy, Summer 2012, edited by Edward N. Zalta.
: Festinger, Leon, Henry W. Riecken, and Stanley Schachter. When Prophecy Fails: A Social and Psychological Study of a Modern Group That Predicted the Destruction of the World. Harper-Torchbooks, 1956.
: Fetherstonhaugh, David, Paul Slovic, Stephen M. Johnson, and James Friedrich. “Insensitivity to the Value of Human Life: A Study of Psychophysical Numbing.” Journal of Risk and Uncertainty 14, no. 3 (1997): 283–300. doi:10.1023/A:1007744326393.
: Feynman, Richard P. “Judging Books by Their Covers.” In Surely You’re Joking, Mr. Feynman! New York: W. W. Norton & Company, 1985.
: Feynman, Richard P., Robert B. Leighton, and Matthew L. Sands. The Feynman Lectures on Physics. 3 vols. Reading, MA: Addison-Wesley, 1963.
: Finucane, Melissa L., Ali Alhakami, Paul Slovic, and Stephen M. Johnson. “The Affect Heuristic in Judgments of Risks and Benefits.” Journal of Behavioral Decision Making 13, no. 1 (2000): 1–17.
: Fong, Geoffrey T., David H. Krantz, and Richard E. Nisbett. “The Effects of Statistical Training on Thinking about Everyday Problems.” Cognitive Psychology 18, no. 3 (1986): 253–292. doi:10.1016/0010-0285(86)90001-0.
: Frank, Adam. The Constant Fire: Beyond the Science vs. Religion Debate. University of California Press, 2009.
: Freire, Paulo. The Politics of Education: Culture, Power, and Liberation. Greenwood Publishing Group, 1985.
: Galbraith, John Kenneth. Economics, Peace and Laughter. Plume, 1981.
: Ganzach, Yoav. “Judging Risk and Return of Financial Assets.” Organizational Behavior and Human Decision Processes 83, no. 2 (2000): 353–370. doi:10.1006/obhd.2000.2914.
: Gendlin, Eugene T. Focusing. Bantam Books, 1982.
: Gibbon, Edward. The History of the Decline and Fall of the Roman Empire. J. & J. Harper, 1829.
: Gigerenzer, Gerd, and Ulrich Hoffrage. “How to Improve Bayesian Reasoning without Instruction: Frequency Formats.” Psychological Review 102 (1995): 684–704.
: Gilbert, Daniel T., Douglas S. Krull, and Patrick S. Malone. “Unbelieving the Unbelievable: Some Problems in the Rejection of False Information.” Journal of Personality and Social Psychology 59 (4 1990): 601–613. doi:10.1037/0022-3514.59.4.601.
: Gilbert, Daniel T., and Patrick S. Malone. “The Correspondence Bias.” Psychological Bulletin 117, no. 1 (1995): 21–38. http://www.wjh.harvard.edu/~dtg/Gilbert%20&%20Malone%20(CORRESPONDENCE%20BIAS).pdf.
: Gilbert, Daniel T., Romin W. Tafarodi, and Patrick S. Malone. “You Can’t Not Believe Everything You Read.” Journal of Personality and Social Psychology 65 (2 1993): 221–233. doi:10.1037/0022-3514.65.2.221.
: Gilbert, William S., and Arthur Sullivan. The Mikado. Opera, 1885.
: Gilovich, Thomas, Dale Griffin, and Daniel Kahneman, eds. Heuristics and Biases: The Psychology of Intuitive Judgment. New York: Cambridge University Press, 2002. doi:10.2277/0521796792.
: Goertzel, Ben, and Cassio Pennachin, eds. Artificial General Intelligence. Cognitive Technologies. Berlin: Springer, 2007. doi:10.1007/978-3-540-68677-4.
: Good, Irving John. “Speculations Concerning the First Ultraintelligent Machine.” In Advances in Computers, edited by Franz L. Alt and Morris Rubinoff, 6:31–88. New York: Academic Press, 1965. doi:10.1016/S0065-2458(08)60418-0.
: Graur, Dan, and Wen-Hsiung Li. Fundamentals of Molecular Evolution. 2nd ed. Sunderland, MA: Sinauer Associates, 2000.
: Griffin, Dale, and Amos Tversky. “The Weighing of Evidence and the Determinants of Confidence.” Cognitive Psychology 24, no. 3 (1992): 411–435. doi:10.1016/0010-0285(92)90013-R.
: Haidt, Jonathan. “The Emotional Dog and Its Rational Tail: A Social Intuitionist Approach to Moral Judgment.” Psychological Review 108, no. 4 (2001): 814–834. doi:10.1037/0033-295X.108.4.814.
: Halberstadt, Jamin Brett, and Gary M. Levine. “Effects of Reasons Analysis on the Accuracy of Predicting Basketball Games.” Journal of Applied Social Psychology 29, no. 3 (1999): 517–530.
: Haldane, John B. S. “A Mathematical Theory of Natural and Artificial Selection.” Mathematical Proceedings of the Cambridge Philosophical Society 23 (5 1927): 607–615. doi:10.1017/S0305004100011750.
: Hamermesh, Daniel S., and Jeff E. Biddle. “Beauty and the Labor Market.” The American Economic Review 84 (5 1994): 1174–1194.
: Hansen, Katherine, Margaret Gerbasi, Alexander Todorov, Elliott Kruse, and Emily Pronin. “People Claim Objectivity After Knowingly Using Biased Strategies.” Personality and Social Psychology Bulletin 40, no. 6 (2014): 691–699.
: Hanson, Robin. “You Are Never Entitled to Your Opinion.” Overcoming Bias (blog) (2006). http://www.overcomingbias.com/2006/12/you_are_never_e.html.
: Harris, Sam. The End of Faith: Religion, Terror, and the Future of Reason. WW Norton & Company, 2005.
: Hastorf, Albert, and Hadley Cantril. “They Saw a Game: A Case Study.” Journal of Abnormal and Social Psychology 49 (1954): 129–134. http://www2.psych.ubc.ca/~schaller/Psyc590Readings/Hastorf1954.pdf.
: Heuer, Richards J. Psychology of Intelligence Analysis. Center for the Study of Intelligence, Central Intelligence Agency, 1999.
: Hibbard, Bill. “Super-Intelligent Machines.” ACM SIGGRAPH Computer Graphics 35, no. 1 (2001): 13–15. http://www.siggraph.org/publications/newsletter/issues/v35/v35n1.pdf.
: Hintze, Daniel. “Problem Class Dominance in Predictive Dilemmas.” Honors thesis (2014).
: Hodgell, Patricia C. Seeker’s Mask. Meisha Merlin Publishing, Inc., 2001.
: Holt, Jim. “Thinking Inside the Boxes.” Slate (2002). http://www.slate.com/articles/arts/egghead/2002/02/thinkinginside%5C_the%5C_boxes.single.html.
: Holyoak, Keith J., and Robert G. Morrison. The Oxford Handbook of Thinking and Reasoning. Oxford University Press, 2013.
: Hsee, Christopher K. “Less Is Better: When Low-Value Options Are Valued More Highly than High-Value Options.” Behavioral Decision Making 11 (2 1998): 107–121.
: ———. “The Evaluability Hypothesis: An Explanation for Preference Reversals between Joint and Separate Evaluations of Alternatives.” Organizational Behavior and Human Decision Processes 67 (3 1996): 247–257. doi:10.1006/obhd.1996.0077.
: Hsee, Christopher K., and Howard C. Kunreuther. “The Affection Effect in Insurance Decisions.” Journal of Risk and Uncertainty 20 (2 2000): 141–159. doi:10.1023/A:1007876907268.
: Hutter, Marcus. Universal Artificial Intelligence: Sequential Decisions Based On Algorithmic Probability. Berlin: Springer, 2005. doi:10.1007/b138233.
: Huxley, Thomas Henry. Evolution and Ethics and Other Essays. Macmillan, 1894.
: Imagination Engines, Inc. “The Imagination Engine^®; or Imagitron^TM.” 2011. http://www.imagination-engines.com/ie.htm.
: Jaynes, Edwin T. Probability Theory: The Logic of Science. Edited by George Larry Bretthorst. New York: Cambridge University Press, 2003. doi:10.2277/0521592712.
: ———. “Probability Theory as Logic.” In Maximum Entropy and Bayesian Methods, edited by Paul F. Fougère. Springer Netherlands, 1990.
: ———. “Probability Theory, with Applications in Science and Engineering.” Unpublished manuscript (1974).
: Jones, Edward E., and Victor A. Harris. “The Attribution of Attitudes.” Journal of Experimental Social Psychology 3 (1967): 1–24. http://www.radford.edu/~jaspelme/443/spring-2007/Articles/Jones_n_Harris_1967.pdf.
: Joyce, James M. The Foundations of Causal Decision Theory. New York: Cambridge University Press, 1999. doi:10.1017/CBO9780511498497.
: Kahneman, Daniel. “Comments by Professor Daniel Kahneman.” In Valuing Environmental Goods: An Assessment of the Contingent Valuation Method, edited by Ronald G. Cummings, David S. Brookshire, and William D. Schulze, 1.B:226–235. Experimental Methods for Assessing Environmental Benefits. Totowa, NJ: Rowman & Allanheld, 1986. http://yosemite.epa.gov/ee/epa/eerm.nsf/vwAN/EE-0280B-04.pdf/$file/EE-0280B-04.pdf.
: Kahneman, Daniel, Ilana Ritov, and David Schkade. “Economic Preferences or Attitude Expressions?: An Analysis of Dollar Responses to Public Issues.” Journal of Risk and Uncertainty 19, nos. 1–3 (1999): 203–235. doi:10.1023/A:1007835629236.
: Kahneman, Daniel, David A. Schkade, and Cass R. Sunstein. “Shared Outrage and Erratic Awards: The Psychology of Punitive Damages.” Journal of Risk and Uncertainty 16 (1 1998): 48–86. doi:10.1023/A:1007710408413.
: Kahneman, Daniel, and Amos Tversky. “Prospect Theory: An Analysis of Decision Under Risk.” Econometrica 47 (1979): 263–292.
: Keats, John. “Lamia.” The Poetical Works of John Keats (London: Macmillan) (1884).
: Keysar, Boaz. “Language Users as Problem Solvers: Just What Ambiguity Problem Do They Solve?” In Social and Cognitive Approaches to Interpersonal Communication, edited by Susan R. Fussell and Roger J. Kreuz, 175–200. Mahwah, NJ: Lawrence Erlbaum Associates, 1998.
: ———. “The Illusory Transparency of Intention: Linguistic Perspective Taking in Text.” Cognitive Psychology 26 (2 1994): 165–208. doi:10.1006/cogp.1994.1006.
: Keysar, Boaz, and Dale J. Barr. “Self-Anchoring in Conversation: Why Language Users Do Not Do What They ‘Should.’” In Gilovich, Griffin, and Kahneman, Heuristics and Biases, 150–166.
: Keysar, Boaz, and Bridget Bly. “Intuitions of the Transparency of Idioms: Can One Keep a Secret by Spilling the Beans?” Journal of Memory and Language 34 (1 1995): 89–109. doi:10.1006/jmla.1995.1005.
: Keysar, Boaz, and Anne S. Henly. “Speakers’ Overestimation of Their Effectiveness.” Psychological Science 13 (3 2002): 207–212. doi:10.1111/1467-9280.00439.
: Kirk, Robert. Mind and Body. McGill-Queen’s University Press, 2003.
: Knishinsky, A. “The Effects of Scarcity of Material and Exclusivity of Information on Industrial Buyer Perceived Risk in Provoking a Purchase Decision.” Doctoral dissertation, Arizona State University, 1982.
: Kosslyn, Stephen M. Image and Brain: The Resolution of the Imagery Debate. Cambridge, MA: MIT Press, 1994.
: Krips, Henry. “Measurement in Quantum Theory.” In The Stanford Encyclopedia of Philosophy, Fall 2013, edited by Edward N. Zalta.
: Kruschke, John K. Doing Bayesian Data Analysis, Second Edition: A Tutorial with R, JAGS, and Stan. Academic Press, 2014.
: ———. “What to Believe: Bayesian Methods for Data Analysis.” Trends in Cognitive Sciences 14, no. 7 (2010): 293–300.
: Kulka, Richard A., and Joan B. Kessler. “Is Justice Really Blind?: The Effect of Litigant Physical Attractiveness on Judicial Judgment.” Journal of Applied Social Psychology 8 (4 1978): 366–381. doi:10.1111/j.1559-1816.1978.tb00790.x.
: Kunreuther, Howard, Robin Hogarth, and Jacqueline Meszaros. “Insurer Ambiguity and Market Failure.” Journal of Risk and Uncertainty 7 (1 1993): 71–87. doi:10.1007/BF01065315.
: Lakoff, George. Women, Fire, and Dangerous Things: What Categories Reveal about the Mind. Chicago: Chicago University Press, 1987.
: Latané, Bibb, and John M. Darley. “Bystander ‘Apathy.’” American Scientist 57, no. 2 (1969): 244–268. http://www.jstor.org/stable/27828530.
: Lazarsfeld, Paul F. “The American Solidier—An Expository Review.” Public Opinion Quarterly 13, no. 3 (1949): 377–404.
: Le Guin, Ursula K. The Farthest Shore. Saga Press, 2001.
: Ledwig, Marion. “Newcomb’s Problem.” PhD diss., University of Constance, 2000.
: Lichtenstein, Sarah, and Paul Slovic. “Reversals of Preference Between Bids and Choices in Gambing Decisions.” Journal of Experimental Psychology 89, no. 1 (1971): 46–55.
: ———, eds. The Construction of Preference. Cambridge University Press, 2006.
: Lichtenstein, Sarah, Paul Slovic, Baruch Fischhoff, Mark Layman, and Barbara Combs. “Judged Frequency of Lethal Events.” Journal of Experimental Psychology: Human Learning and Memory 4, no. 6 (1978): 551–578. doi:10.1037/0278-7393.4.6.551.
: Liersch, Michael J., and Craig R. M. McKenzie. “Duration Neglect by Numbers and Its Elimination by Graphs.” Organizational Behavior and Human Decision Processes 108, no. 2 (2009): 303–314.
: Mack, Denise, and David Rainey. “Female Applicants’ Grooming and Personnel Selection.” Journal of Social Behavior and Personality 5 (5 1990): 399–407.
: MacKay, David J. C. Information Theory, Inference, and Learning Algorithms. New York: Cambridge University Press, 2003.
: Matthews, Robert. “Do We Need to Change the Definition of Science?” New Scientist (May 2008).
: Mazis, Michael B. “Antipollution Measures and Psychological Reactance Theory: A Field Experiment.” Journal of Personality and Social Psychology 31 (1975): 654–666.
: Mazis, Michael B., Robert B. Settle, and Dennis C. Leslie. “Elimination of Phosphate Detergents and Psychological Reactance.” Journal of Marketing Research 10 (1973): 390–395.
: McDermott, Drew. “Artificial Intelligence Meets Natural Stupidity.” SIGART Newsletter, no. 57 (1976): 4–9. doi:10.1145/1045339.1045340.
: McFadden, Daniel L., and Gregory K. Leonard. “Issues in the Contingent Valuation of Environmental Goods: Methodologies for Data Collection and Analysis.” In Contingent Valuation: A Critical Assessment, edited by Jerry A. Hausman, 165–215. Contributions to Economic Analysis220. New York: North-Holland, 1993. doi:10.1108/S0573-8555(1993)0000220007.
: Mercier, Hugo, and Dan Sperber. “Why Do Humans Reason? Arguments for an Argumentative Theory.” Behavioral and Brain Sciences 34 (2011): 57–74. https://hal.archives-ouvertes.fr/file/index/docid/904097/filename/MercierSperberWhydohumansreason.pdf.
: Meyers, David G. Exploring Social Psychology. New York: McGraw-Hill, 1994.
: Mitchell, Tom M. Machine Learning. McGraw-Hill Science/Engineering/Math, 1997.
: Moore, John. Slay and Rescue. Xlibris Corp, 2000.
: Muehlhauser, Luke. “The Power of Agency.” Less Wrong (blog) (2011). http://lesswrong.com/lw/5i8/the_power_of_agency/.
: Musashi, Miyamoto. Book of Five Rings. New Line Publishing, 2003.
: Mussweiler, Thomas, and Fritz Strack. “Comparing Is Believing: A Selective Accessibility Model of Judgmental Anchoring.” European Review of Social Psychology 10 (1 1999): 135–167. doi:10.1080/14792779943000044.
: Nagel, Thomas. “What Is It Like to Be a Bat?” Philosophical Review 83, no. 4 (1974): 435–450. http://www.jstor.org/stable/2183914.
: Newby-Clark, Ian R., Michael Ross, Roger Buehler, Derek J. Koehler, and Dale Griffin. “People Focus on Optimistic Scenarios and Disregard Pessimistic Scenarios While Predicting Task Completion Times.” Journal of Experimental Psychology: Applied 6, no. 3 (2000): 171–182. doi:10.1037/1076-898X.6.3.171.
: Nickerson, Raymond S. “Confirmation Bias: A Ubiquitous Phenomenon in Many Guises.” Review of General Psychology 2, no. 2 (1998): 175.
: Nisbett, Richard E., and Timothy D. Wilson. “Telling More than We Can Know: Verbal Reports on Mental Processes.” Psychological Review 84 (1977): 231–259. http://people.virginia.edu/~tdw/nisbett&wilson.pdf.
: Orwell, George. 1984. Signet Classic, 1950.
: ———. “Politics and the English Language.” Horizon (April 1946).
: ———. “Why Socialists Don’t Believe in Fun.” Tribune (December 1943).
: Pearce, David. The Hedonistic Imperative. http://www.hedweb.com/, 1995.
: Pearl, Judea. Causality: Models, Reasoning, and Inference. 2nd ed. New York: Cambridge University Press, 2009.
: ———. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. San Mateo, CA: Morgan Kaufmann, 1988.
: Peirce, Charles Sanders. Collected Papers. Harvard University Press, 1931.
: Pinker, Steven. The Blank Slate: The Modern Denial of Human Nature. New York: Viking, 2002.
: Piper, Henry Beam. “Police Operation.” Astounding Science Fiction (July 1948).
: Pirsig, Robert M. Zen and the Art of Motorcycle Maintenance: An Inquiry Into Values. 1st ed. New York: Morrow, 1974.
: Planck, Max. Scientific Autobiography and Other Papers. New York: Philosophical Library, 1949.
: Plato. Great Dialogues of Plato. Edited by Eric H. Warmington and Philip G. Rouse. Signet Classic, 1999.
: Popper, Karl R. The Logic of Scientific Discovery. New York: Basic Books, 1959.
: Poundstone, William. Priceless: The Myth of Fair Value (and How to Take Advantage of It). Hill & Wang, 2010.
: Pratchett, Terry. Maskerade. Discworld Series. ISIS, 1997.
: ———. Witches Abroad. London: Corgi Books, 1992.
: Procopius. History of the Wars. Edited by Henry B. Dewing. Harvard University Press, 1914.
: Pronin, Emily. “How We See Ourselves and How We See Others.” Science 320 (2008): 1177–1180. http://psych.princeton.edu/psychology/research/pronin/pubs/2008%20Self%20and%20Other.pdf.
: Pronin, Emily, Daniel Y. Lin, and Lee Ross. “The Bias Blind Spot: Perceptions of Bias in Self versus Others.” Personality and Social Psychology Bulletin 28, no. 3 (2002): 369–381.
: Putnam, Hilary. “The Meaning of Meaning.” In The Twin Earth Chronicles, edited by Andrew Pessin and Sanford Goldberg, 3–52. M. E. Sharpe, Inc., 1996.
: Quattrone, George A., Cheryl P. Lawrence, Steven E. Finkel, and David C. Andrus. “Explorations in Anchoring: The Effects of Prior Range, Anchor Extremity, and Suggestive Hints.” Unpublished manuscript, Stanford University, 1981.
: Rhodes, Richard. The Making of the Atomic Bomb. New York: Simon & Schuster, 1986.
: Rips, Lance J. “Inductive Judgments about Natural Categories.” Journal of Verbal Learning and Verbal Behavior 14 (1975): 665–681.
: Roberts, Seth. “What Makes Food Fattening?: A Pavlovian Theory of Weight Control.” Unpublished manuscript, 2005. http://media.sethroberts.net/about/whatmakesfoodfattening.pdf.
: Robinson, Dave, and Judy Groves. Philosophy for Beginners. 1st ed. Cambridge: Icon Books, 1998.
: Rorty, Richard. “Out of the Matrix: How the Late Philosopher Donald Davidson Showed That Reality Can’t Be an Illusion.” The Boston Globe (October 2003).
: Rosch, Eleanor. “Principles of Categorization.” In Cognition and Categorization, edited by Eleanor Rosch and Barbara B. Lloyd. Hillsdale, NJ: Lawrence Erlbaum, 1978.
: Russell, Gillian. “Epistemic Viciousness in the Martial Arts.” In Martial Arts and Philosophy: Beating and Nothingness, edited by Graham Priest and Damon A. Young. Open Court, 2010.
: Russell, Stuart J., and Peter Norvig. Artificial Intelligence: A Modern Approach. 3rd ed. Upper Saddle River, NJ: Prentice-Hall, 2010.
: Ryle, Gilbert. The Concept of Mind. University of Chicago Press, 1949.
: Sadock, Jerrold. “Truth and Approximations.” Papers from the Third Annual Meeting of the Berkeley Linguistics Society (1977): 430–439.
: Sagan, Carl. The Demon-Haunted World: Science as a Candle in the Dark. 1st ed. New York: Random House, 1995.
: Saint-Exupery, Antoine de. Terre des Hommes. Paris: Gallimard, 1939.
: Sandel, Michael. “What’s Wrong With Enhancement.” Background material for the President’s Council on Bioethics. (2002).
: Schoemaker, Paul J. H. “The Role of Statistical Knowledge in Gambling Decisions: Moment vs. Risk Dimension Approaches.” Organizational Behavior and Human Performance 24, no. 1 (1979): 1–17.
: Schul, Yaacov, and Ruth Mayo. “Searching for Certainty in an Uncertain World: The Difficulty of Giving Up the Experiential for the Rational Mode of Thinking.” Journal of Behavioral Decision Making 16, no. 2 (2003): 93–106. doi:10.1002/bdm.434.
: Schwitzgebel, Eric. Perplexities of Consciousness. MIT Press, 2011.
: Serfas, Sebastian. Cognitive Biases in the Capital Investment Context: Theoretical Considerations and Empirical Experiments on Violations of Normative Rationality. Springer, 2010.
: Sherif, Muzafer, Oliver J. Harvey, B. Jack White, William R. Hood, and Carolyn W. Sherif. “Study of Positive and Negative Intergroup Attitudes Between Experimentally Produced Groups: Robbers Cave Study.” Unpublished manuscript (1954).
: Shermer, Michael. “The Unlikeliest Cult in History.” Skeptic 2, no. 2 (1993): 74–81. http://www.2think.org/02_2_she.shtml.
: Shimabukuro, Masayuki. Flashing Steel: Mastering Eishin-Ryu Swordsmanship. Frog Books, 1995.
: Slovic, Paul. “Numbed by Numbers.” Foreign Policy (March 2007). http://foreignpolicy.com/2007/03/13/numbed-by-numbers/.
: Slovic, Paul, Melissa Finucane, Ellen Peters, and Donald G. MacGregor. “Rational Actors or Rational Fools: Implications of the Affect Heuristic for Behavioral Economics.” Journal of Socio-Economics 31, no. 4 (2002): 329–342. doi:10.1016/S1053-5357(02)00174-9.
: Smith, Edward Elmer. Second Stage Lensmen. Old Earth Books, 1998.
: Smith, Edward Elmer, and Ric Binkley. Gray Lensman. Old Earth Books, 1998.
: Smith, Edward Elmer, and A. J. Donnell. First Lensman. Old Earth Books, 1997.
: Smullyan, Raymond M. What Is the Name of This Book?: The Riddle of Dracula and Other Logical Puzzles. Penguin Books, 1990.
: Soares, Nate, and Benja Fallenstein. “Toward Idealized Decision Theory.” Technical report. Berkeley, CA: Machine Intelligence Research Institute (2014). http://intelligence.org/files/TowardIdealizedDecisionTheory.pdf.
: Spee, Friedrich. Cautio Criminalis; or, A Book on Witch Trials. Edited and translated by Marcus Hellyer. Studies in Early Modern German History. 1631. Charlottesville: University of Virginia Press, 2003.
: Stanovich, Keith E., and Richard F. West. “Individual Differences in Reasoning: Implications for the Rationality Debate?” Behavioral and Brain Sciences 23, no. 5 (2000): 645–665. http://journals.cambridge.org/abstract_S0140525X00003435.
: Stewart, John E. “Defendants’ Attractiveness as a Factor in the Outcome of Trials: An Observational Study.” Journal of Applied Social Psychology 10 (4 1980): 348–361. doi:10.1111/j.1559-1816.1980.tb00715.x.
: Stiegler, Marc. David’s Sling. Baen, 1988.
: Stove, David Charles. The Plato Cult and Other Philosophical Follies. Cambridge University Press, 1991.
: Strack, Fritz, and Thomas Mussweiler. “Explaining the Enigmatic Anchoring Effect: Mechanisms of Selective Accessibility.” Journal of Personality and Social Psychology 73, no. 3 (1997): 437–446.
: Sunstein, Cass R. “Probability Neglect: Emotions, Worst Cases, and Law.” Yale Law Journal (2002): 61–107.
: Taber, Charles S., and Milton Lodge. “Motivated Skepticism in the Evaluation of Political Beliefs.” American Journal of Political Science 50, no. 3 (2006): 755–769. doi:10.1111/j.1540-5907.2006.00214.x.
: Talbott, William. “Bayesian Epistemology.” In The Stanford Encyclopedia of Philosophy, Fall 2013, edited by Edward N. Zalta.
: TalkOrigins Foundation. “Frequently Asked Questions about Creationism and Evolution.” http://www.talkorigins.org/origins/faqs-qa.html.
: Tegmark, Max. Our Mathematical Universe: My Quest for the Ultimate Nature of Reality. Random House LLC, 2014.
: ———. “Parallel Universes.” In Science and Ultimate Reality: Quantum Theory, Cosmology, and Complexity, edited by John D. Barrow, Paul C. W. Davies, and Charles L. Harper Jr., 459–491. New York: Cambridge University Press, 2004.
: Thompson, Silvanus Phillips. The Life of Lord Kelvin. American Mathematical Society, 2005.
: Thornton, Stephen. “Karl Popper.” In The Stanford Encyclopedia of Philosophy, Winter 2002, edited by Edward N. Zalta. Stanford University. http://plato.stanford.edu/archives/win2002/entries/popper/.
: Tooby, John, and Leda Cosmides. “The Psychological Foundations of Culture.” In The Adapted Mind: Evolutionary Psychology and the Generation of Culture, edited by Jerome H. Barkow, Leda Cosmides, and John Tooby, 19–136. New York: Oxford University Press, 1992.
: Tversky, Amos, and Ward Edwards. “Information versus Reward in Binary Choices.” Journal of Experimental Psychology 71, no. 5 (1966): 680–683. doi:10.1037/h0023123.
: Tversky, Amos, and Itamar Gati. “Studies of Similarity.” In Cognition and Categorization, edited by Eleanor Rosch and Barbara Lloyd, 79–98. Hillsdale, NJ: Lawrence Erlbaum Associates, Inc., 1978.
: Tversky, Amos, and Daniel Kahneman. “Extensional Versus Intuitive Reasoning: The Conjunction Fallacy in Probability Judgment.” Psychological Review 90, no. 4 (1983): 293–315. doi:10.1037/0033-295X.90.4.293.
: ———. “Judgment Under Uncertainty: Heuristics and Biases.” Science 185, no. 4157 (1974): 1124–1131. doi:10.1126/science.185.4157.1124.
: ———. “Judgments of and by Representativeness.” In Judgment Under Uncertainty: Heuristics and Biases, edited by Daniel Kahneman, Paul Slovic, and Amos Tversky, 84–98. New York: Cambridge University Press, 1982.
: Tzu, Sun. The Art of War. Cloud Hands, Inc., 2004.
: Uhlmann, Eric Luis, and Geoffrey L. Cohen. “‘I think it, therefore it’s true’: Effects of Self-perceived Objectivity on Hiring Discrimination.” Organizational Behavior and Human Decision Processes 104, no. 2 (2007): 207–223.
: Vaidman, Lev. “Many-Worlds Interpretation of Quantum Mechanics.” In The Stanford Encyclopedia of Philosophy, Fall 2008, edited by Edward N. Zalta.
: Vallone, Robert P., Lee Ross, and Mark R. Lepper. “The Hostile Media Phenomenon: Biased Perception and Perceptions of Media Bias in Coverage of the Beirut Massacre.” Journal of Personality and Social Psychology 49 (1985): 577–585. http://ssc.wisc.edu/~jpiliavi/965/hwang.pdf.
: Verhagen, Joachim. http://web.archive.org/web/20060424082937/http://www.nvon.nl/scheik/best/diversen/scijokes/scijokes.txt. Archived version, October 27, 2001.
: Wade, Michael J. “Group selections among laboratory populations of Tribolium.” Proceedings of the National Academy of Sciences of the United States of America 73, no. 12 (1976): 4604–4607. doi:10.1073/pnas.73.12.4604.
: Wansink, Brian, Robert J. Kent, and Stephen J. Hoch. “An Anchoring and Adjustment Model of Purchase Quantity Decisions.” Journal of Marketing Research 35, no. 1 (1998): 71–81. http://www.jstor.org/stable/3151931.
: Warren, Adam. Empowered. Dark Horse Books, 2007.
: Wason, Peter Cathcart. “On the Failure to Eliminate Hypotheses in a Conceptual Task.” Quarterly Journal of Experimental Psychology 12, no. 3 (1960): 129–140. doi:10.1080/17470216008416717.
: Weiten, Wayne. Psychology: Themes and Variations, Briefer Version, Eighth Edition. Cengage Learning, 2010.
: West, Richard F., Russell J. Meserve, and Keith E. Stanovich. “Cognitive Sophistication Does Not Attenuate the Bias Blind Spot.” Journal of Personality and Social Psychology 103, no. 3 (2012): 506.
: Williams, George C. Adaptation and Natural Selection: A Critique of Some Current Evolutionary Thought. Princeton Science Library. Princeton, NJ: Princeton University Press, 1966.
: Wilson, David Sloan. “A Theory of Group Selection.” Proceedings of the National Academy of Sciences of the United States of America 72, no. 1 (1975): 143–146.
: Wilson, Timothy D., David B. Centerbar, and Nancy Brekke. “Mental Contamination and the Debiasing Problem.” In Heuristics and Biases: The Psychology of Intuitive Judgment, edited by Thomas Gilovich, Dale Griffin, and Daniel Kahneman. Cambridge University Press, 2002.
: Wilson, Timothy D., Douglas J. Lisle, Jonathan W. Schooler, Sara D. Hodges, Kristen J. Klaaren, and Suzanne J. LaFleur. “Introspecting About Reasons Can Reduce Post-choice Satisfaction.” Personality and Social Psychology Bulletin 19 (1993): 331–331.
: Wittgenstein, Ludwig. Philosophical Investigations. Translated by Gertrude E. M. Anscombe. Oxford: Blackwell, 1953.
: Wright, Robert. The Moral Animal: Why We Are the Way We Are: The New Science of Evolutionary Psychology. Pantheon Books, 1994.
: Yamagishi, Kimihiko. “When a 12.86% Mortality Is More Dangerous than 24.14%: Implications for Risk Communication.” Applied Cognitive Psychology 11 (6 1997): 461–554.
: Yates, J. Frank, Ju-Whei Lee, Winston R. Sieck, Incheol Choi, and Paul C. Price. “Probability Judgment Across Cultures.” In Gilovich, Griffin, and Kahneman, Heuristics and Biases, 271–291.
: Yudkowsky, Eliezer. “Artificial Intelligence as a Positive and Negative Factor in Global Risk.” In Bostrom and Ćirković, Global Catastrophic Risks, 308–345.
: ———. “Cognitive Biases Potentially Affecting Judgment of Global Risks.” In Bostrom and Ćirković, Global Catastrophic Risks, 91–119.
: ———. Timeless Decision Theory. Unpublished manuscript. Machine Intelligence Research Institute, Berkeley, CA, 2010. http://intelligence.org/files/TDT.pdf.
: Yuzan, Daidoji, William Scott Wilson, Jack Vaughn, and Gary Miller Haskins. Budoshoshinshu: The Warrior’s Primer of Daidoji Yuzan. Black Belt Communications Inc., 1984.
: Zapato, Lyle. “Lord Kelvin Quotations.” 2008. http://zapatopi.net/kelvin/quotes/.
: Zelazny, Roger. Prince of Chaos. Thorndike Press, 2001.
: Zhuangzi and Thomas Merton. The Way of Chuang Tzu. New Directions Publishing, 1965.
: Zhuangzi and Burton Watson. The Complete Works of Zhuangzi. Columbia University Press, 1968.

Contents

Preface

Biases: An Introduction by Rob Bensinger

Rational Feelings

The Many Faces of Bias

A Word About This Text

Map and Territory

Acknowledgments

Book I Map and Territory

Part A Predictably Wrong

1 What Do I Mean By “Rationality”?

2 Feeling Rational

3 Why Truth? And . . .

4 . . . What’s a Bias, Again?

5 Availability

6 Burdensome Details

7 Planning Fallacy

8 Illusion of Transparency: Why No One Understands You

9 Expecting Short Inferential Distances

10 The Lens That Sees Its Own Flaws

Part B Fake Beliefs

11 Making Beliefs Pay Rent (in Anticipated Experiences)

12 A Fable of Science and Politics

13 Belief in Belief

14 Bayesian Judo

15 Pretending to be Wise

16 Religion’s Claim to be NonDisprovable

17 Professing and Cheering

18 Belief as Attire

19 Applause Lights

Part C Noticing Confusion

20 Focus Your Uncertainty

21 What Is Evidence?

22 Scientific Evidence, Legal Evidence, Rational Evidence

23 How Much Evidence Does It Take?

24 Einstein’s Arrogance

25 Occam’s Razor

26 Your Strength as a Rationalist

27 Absence of Evidence Is Evidence of Absence

28 Conservation of Expected Evidence

29 Hindsight Devalues Science

Part D Mysterious Answers

30 Fake Explanations

31 Guessing the Teacher’s Password

32 Science as Attire

33 Fake Causality

34 Semantic Stopsigns

35 Mysterious Answers to Mysterious Questions

36 The Futility of Emergence

37 Say Not “Complexity”

38 Positive Bias: Look into the Dark

39 Lawful Uncertainty

40 My Wild and Reckless Youth

41 Failing to Learn from History

42 Making History Available

43 Explain/Worship/Ignore?

44 “Science” as CuriosityStopper

45 Truly Part of You

Interlude The Simple Truth

Book II How to Actually Change Your Mind

Rationality: An Introduction by Rob Bensinger

How to Not Actually Change Your Mind

The Mathematics of Rationality

Rationality Applied

Part E Overly Convenient Excuses

46 The Proper Use of Humility

47 The Third Alternative

48 Lotteries: A Waste of Hope

49 New Improved Lottery

50 But There’s Still a Chance, Right?

51 The Fallacy of Gray

52 Absolute Authority

53 How to Convince Me That 2 + 2 = 3

54 Infinite Certainty

55 0 And 1 Are Not Probabilities

56 Your Rationality Is My Business

Part F Politics and Rationality

57 Politics is the MindKiller

58 Policy Debates Should Not Appear OneSided

59 The Scales of Justice, the Notebook of Rationality

Biases: An Introduction
by Rob Bensinger

Book I
Map and Territory

Part A
Predictably Wrong

1
What Do I Mean By “Rationality”?

2
Feeling Rational

3
Why Truth? And . . .

4
. . . What’s a Bias, Again?

5
Availability

6
Burdensome Details

7
Planning Fallacy

8
Illusion of Transparency: Why No One Understands You

9
Expecting Short Inferential Distances

10
The Lens That Sees Its Own Flaws

Part B
Fake Beliefs

11
Making Beliefs Pay Rent (in Anticipated Experiences)

12
A Fable of Science and Politics

13
Belief in Belief

14
Bayesian Judo

15
Pretending to be Wise

16
Religion’s Claim to be NonDisprovable

17
Professing and Cheering

18
Belief as Attire

19
Applause Lights

Part C
Noticing Confusion

20
Focus Your Uncertainty

21
What Is Evidence?

22
Scientific Evidence, Legal Evidence, Rational Evidence

23
How Much Evidence Does It Take?

24
Einstein’s Arrogance

25
Occam’s Razor

26
Your Strength as a Rationalist

27
Absence of Evidence Is Evidence of Absence

28
Conservation of Expected Evidence

29
Hindsight Devalues Science

Part D
Mysterious Answers

30
Fake Explanations

31
Guessing the Teacher’s Password

32
Science as Attire

33
Fake Causality

34
Semantic Stopsigns

35
Mysterious Answers to Mysterious Questions

36
The Futility of Emergence

37
Say Not “Complexity”

38
Positive Bias: Look into the Dark

39
Lawful Uncertainty

40
My Wild and Reckless Youth

41
Failing to Learn from History

42
Making History Available

43
Explain/Worship/Ignore?

44
“Science” as CuriosityStopper

45
Truly Part of You

Interlude
The Simple Truth

Book II
How to Actually Change Your Mind

Rationality: An Introduction
by Rob Bensinger

Part E
Overly Convenient Excuses

46
The Proper Use of Humility

47
The Third Alternative

48
Lotteries: A Waste of Hope

49
New Improved Lottery

50
But There’s Still a Chance, Right?

51
The Fallacy of Gray

52
Absolute Authority

53
How to Convince Me That 2 + 2 = 3

54
Infinite Certainty

55
0 And 1 Are Not Probabilities

56
Your Rationality Is My Business

Part F
Politics and Rationality

57
Politics is the MindKiller

58
Policy Debates Should Not Appear OneSided

59
The Scales of Justice, the Notebook of Rationality

60
Correspondence Bias

61
Are Your Enemies Innately Evil?

62
Reversed Stupidity Is Not Intelligence

63
Argument Screens Off Authority

64
Hug the Query

65
Rationality and the English Language

66
Human Evil and Muddled Thinking

Part G
Against Rationalization

67
Knowing About Biases Can Hurt People

68
Update Yourself Incrementally